1

Complex numbers

Complex numbers can be interpreted in two

ways:

•Analitically - as ‘special numbers’

which solve polynomial equations.

•Geometrically - as points on a 2-plane

(which can be added and multiplied).

Mysterious ‘e’.

Lecture 2

2

Consider a simple equation:

x

2

+ 1= 0

Wouldn’t it be nice to be able to solve it

It doesn’t have any solutions

 !!!

Lets imagine that we can solve it, and lets name the
solution ‘

i’

i

2

=

-1

1. Analytical interpretation ‘intro’

z = x + i·y

where

x

and

y

are Real Numbers

 

  

 

3



 

 

 



.

v

y

i

u

x

iv

u

iy

x





















)

(

yu

xv

i

yv

xu

yv

i

iyu

ixv

xu

iv

u

iy

x

2





















The addition of complex
numbers

The multiplication of complex
numbers

.

Let z = x + i·y, w = u + i·v be two complex numbers

How do we add and multiply such numbers?

Can a "thing" z = x + iy be treated like a number ?

Yes

, we call it a

complex number

.

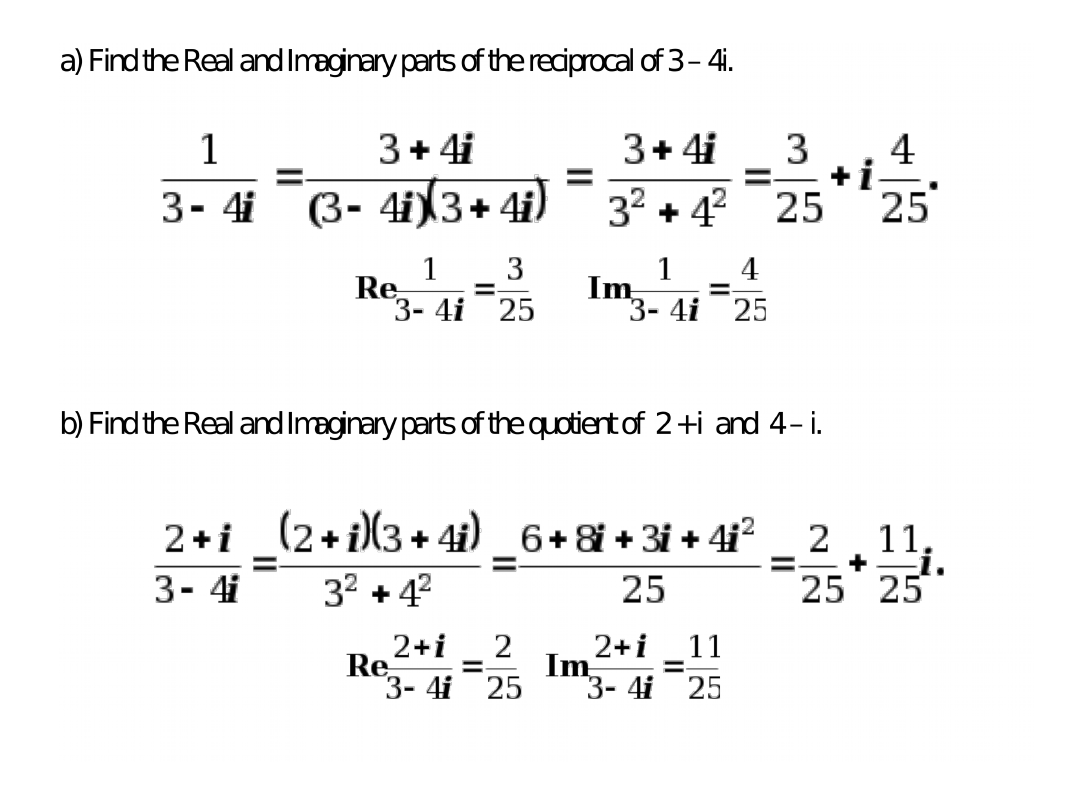
4

5

Definition
The complex conjugate of

z = a + ib

is the

number

a – i b

.

Notation:

.

Two numbers of which one is a conjugate of the other,

are called

conjugate numbers.

ib

a

z





6

Solve the equation

i

z

i

z

3

1

)

1

(

2









Let

y

i

x

z





i

y

x

i

y

x

y

ix

iy

x

iy

x

y

i

x

i

y

i

x

z

i

z

3

1

)

(

)

3

(

2

2

)

)(

1

(

)

(

2

)

1

(

2









































then

Because the real and imaginary parts on the right hand side
must be equal to the real and imaginary parts on the left hand side

















3

1

3

y

x

y

x

The solution is

5

,

2





 y

x

Example

7

z

z

z

Im

i

2

z

z

z

Re

2

)

4

z

)

z

(

)

3

w

z

w

z

w

z

w

z

)

2

w

z

w

z

w

z

w

z

)

1































Properties

8

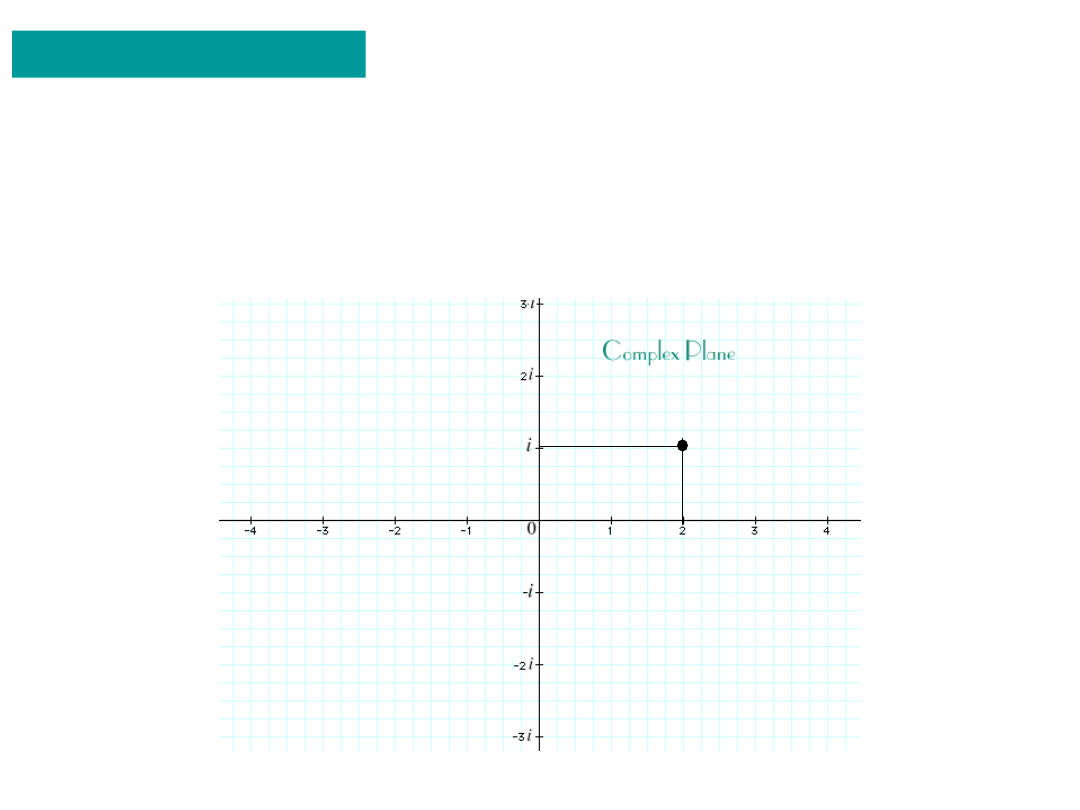
z = (2,1) = 2+i

Real axis

Imaginary axis

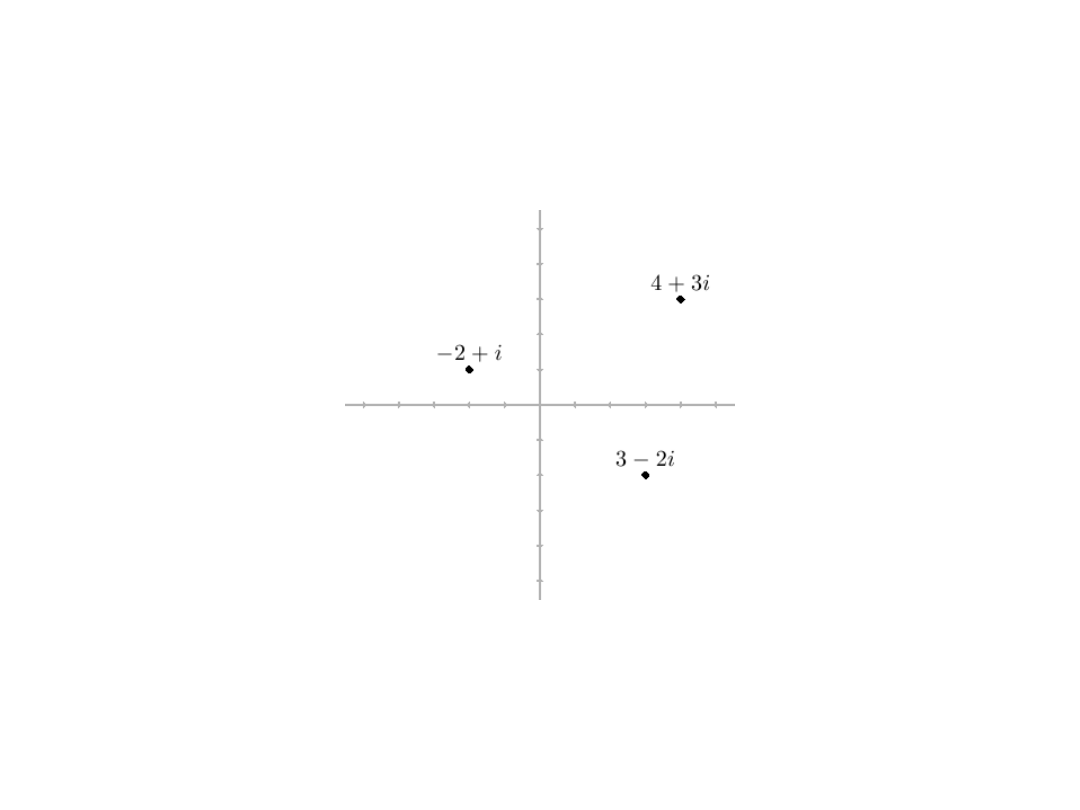
A complex number z can be viewed as a point or a position vector
in a two-dimensional Cartesian coordinate system called
the Complex Plane or Argand diagram.

1. Geometrical ‘Intro’

The point z is described by two coordinates:

• x - the Real axis coordinate

• y - the Imaginary axis coordinate

9

10

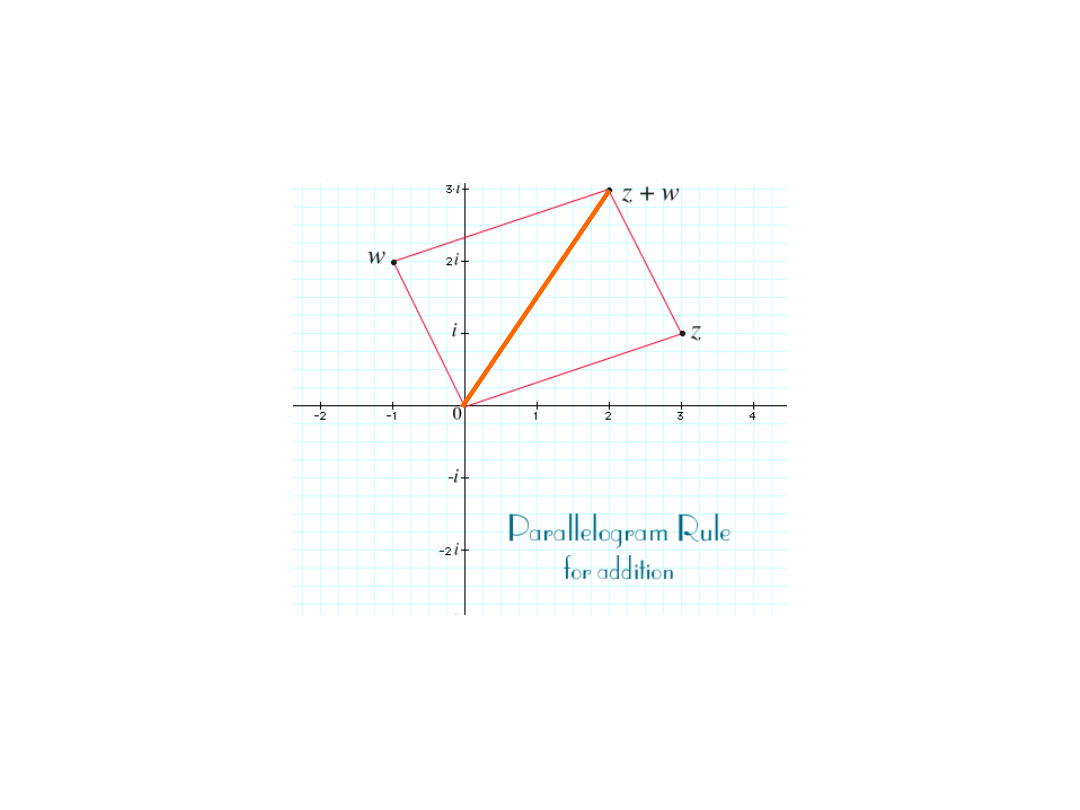
The sum of complex numbers

z+

w

(you add them like vectors)

Analitical interpretation:

z = x+iy, w = u+iv z + w = (x+u) + i(y+v)

Vector interpretation:

z = (x,y) w = (u,v) z+w = (x+u, y+v)

11

is the mirror reflection of

z

z

Re z

Im z

y

i

x

z





y

i

x

z





12

r

b

a

z

2

2







 

.

5

4

3

i

4

3

2

2











Definition

The modulus (or absolute value) of a complex
number
z = a + i b, is denoted by |z| or r,

Example
Find the modulus of the complex number 3 - 4i.

Similarity:  1 = 1, i = 1,  0 = 0.

Fact
A complex number is equal to zero iff its modulus is zero:
z = 0

 |z| = 0.

13

Properties of the modulus (absolute value) of

z, |z|

w

z

w

z

)

2

w

z

w

z

)

2

w

z

w

z

)

1















x +iy

2

2

y

x

z

r







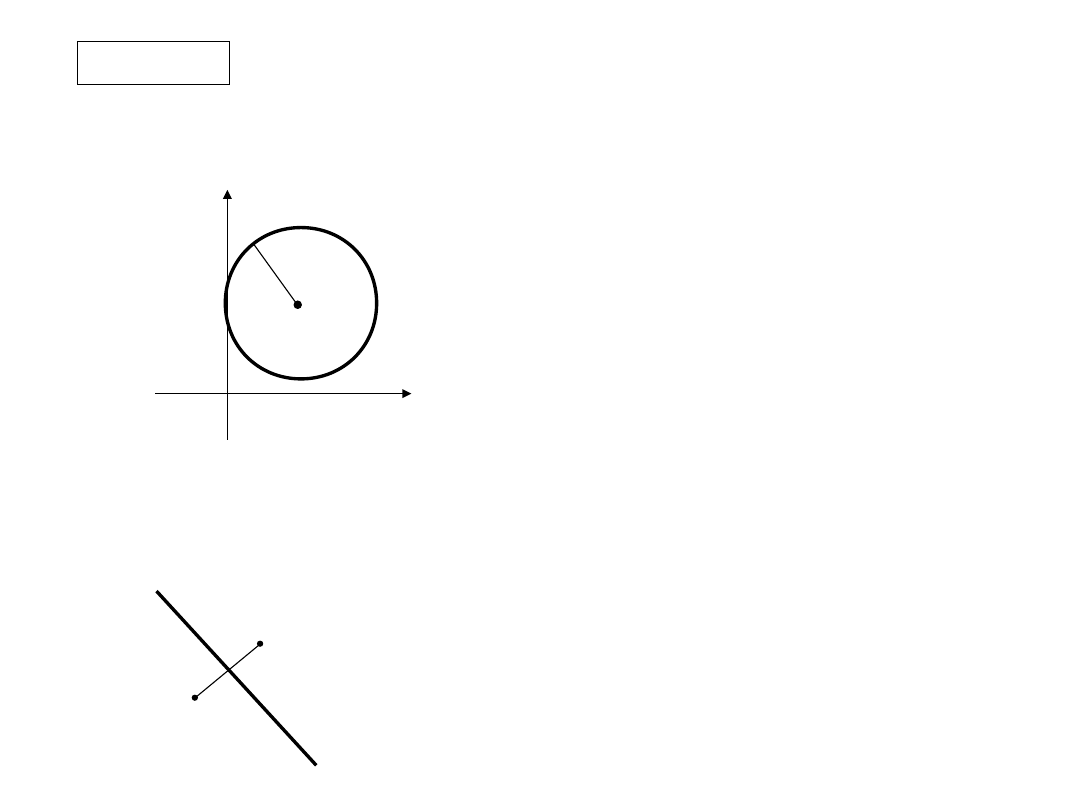
14

Examples

1. Draw in the complex plane the set of points 'z' which satisfy:
|z-z

0

|=R

z

0

R

Re z

Im z

A circle with centre z

0

and radius R

2. Draw in the complex plane the set of points S
S={z: |z - z

1

| = |z - z

2

|}

z

1

z

2

Line symmetrical to segment [z

1

, z

2

]

15

Fact
(i) Conjugate numbers have the same modulus:

(ii) The product of conjugate numbers is the square of the

modulus:

bi

a

z





z

z 

2

z

z

z 









.

b

a

bi

a

bi

a

2

2









16

TRIGONOMETRIC REPRESENTATION

OF COMPLEX NUMBERS

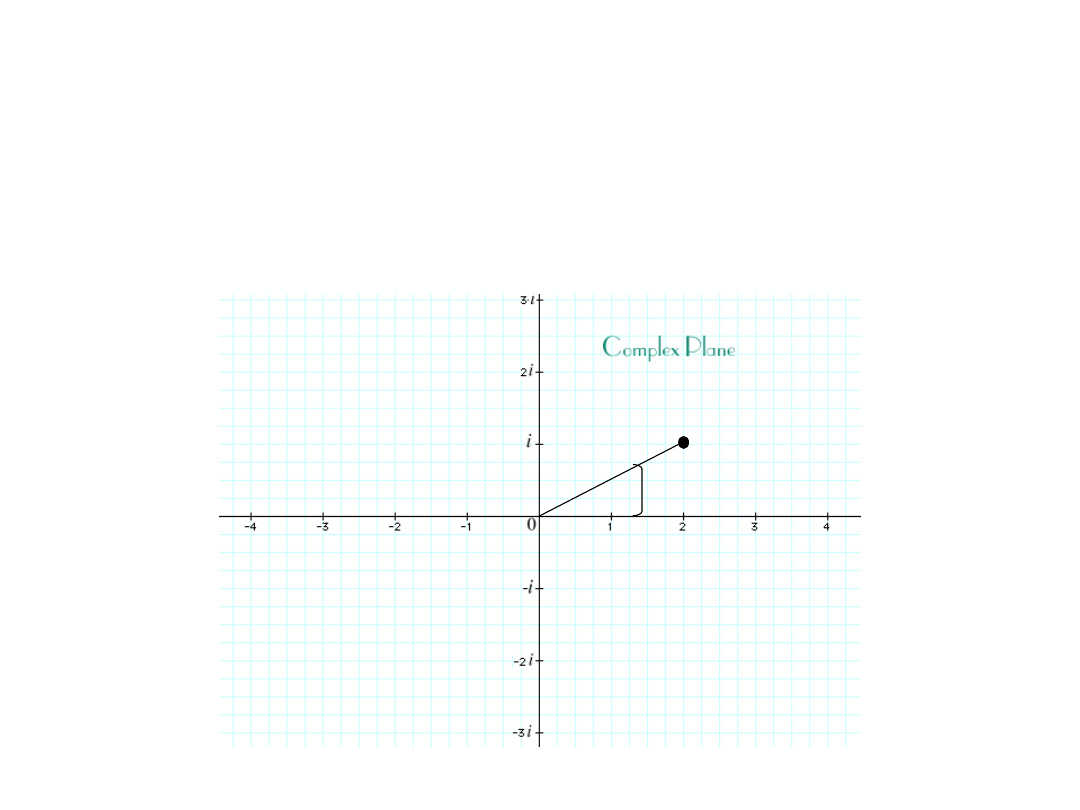
17

z = (2,1) = 2+ i

Real axis

Imaginary axis

The complex point

z = x + i y

can be also described

by:
• the distance

r

from the origin of the Coordinate

System
• the angle



between the vector

z = [x,y]

and the

Real Axis



r

18

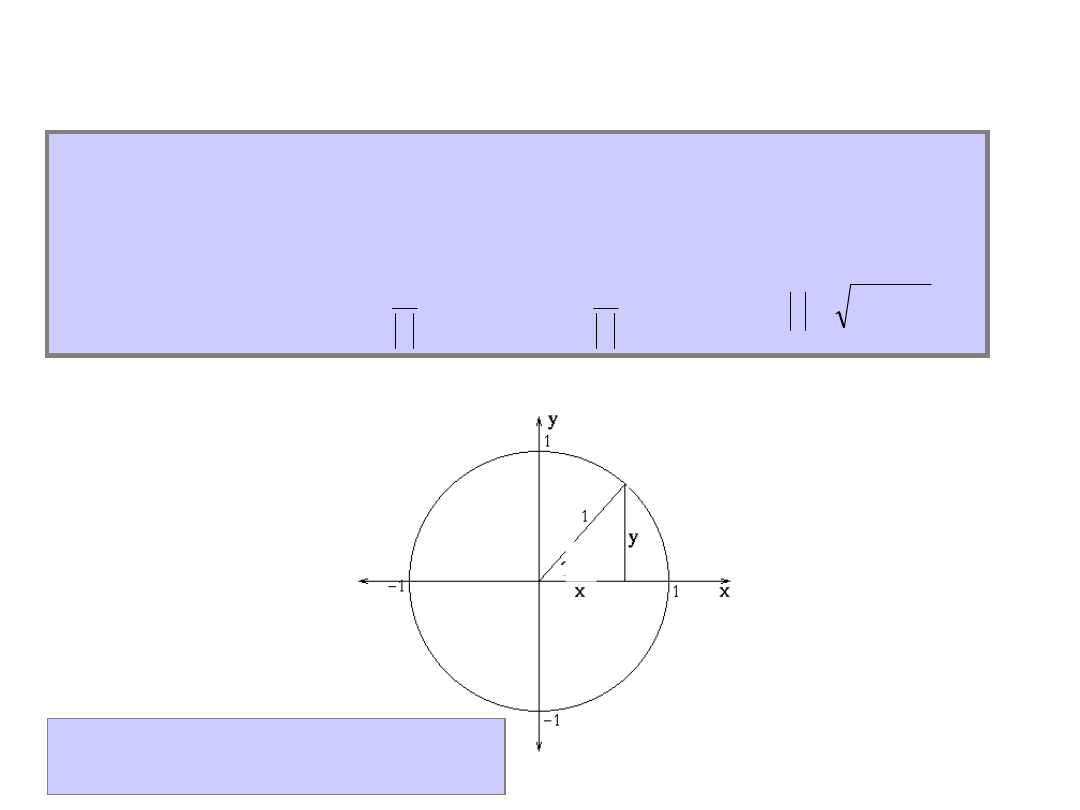
THE TRIGONOMETRIC REPRESENTATION OF COMPLEX NUMBERS

(POLAR FORM)

,

z

x

cos 



,

z

y

sin 



0

y

x

z

2

2







Definition
The argument of a number z = x +i y, denoted by arg
z = α is any real number α which meets the conditions:

where

The argument of number 0
is undefined.

(cos

α, sin α)

α

19

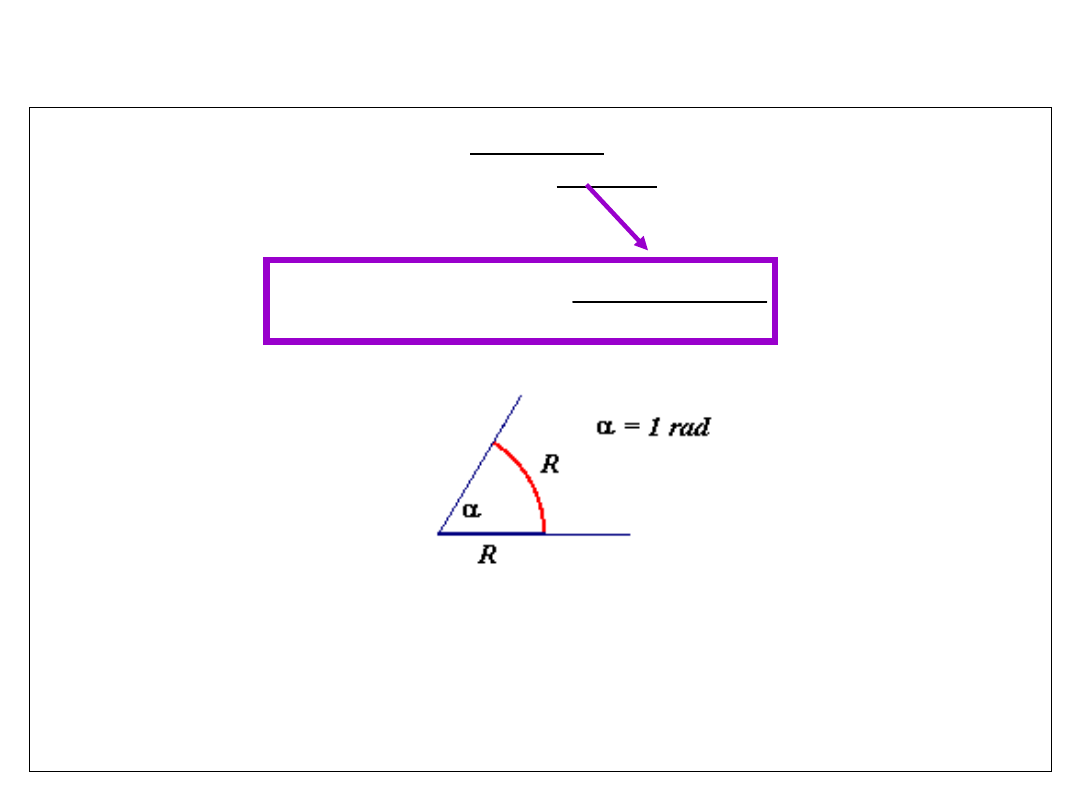
ANGLES

The angle is measured in radians, not degrees.

radius

arc

an

of

length

of

measure

radian





Notation:
We say, in geometry, that an arc or curve "subtends" an angle, (stretches under).
A line or curve AC subtends angle ABC at point B.

20

360 degrees = 2  =

6.28319...
180 degrees =  =

3.14159...
90 degrees = /2 =

1.5708...
60 degrees = /3 =

1.0472...
30 degrees = /6 =

0.523599...
45 degrees = /4 =

0.785398...

1 radian = 57.2957 degrees
1 degree = 0.0174532 radians

In mathematics if you write the size of an angle as a pure number,

without the degree unit marker after it, then the angle is taken to be in
radians.

So, if someone were to write down:
 = 4

Then that would mean that angle  has a measurement of 4

radians and not 4 degrees.

21

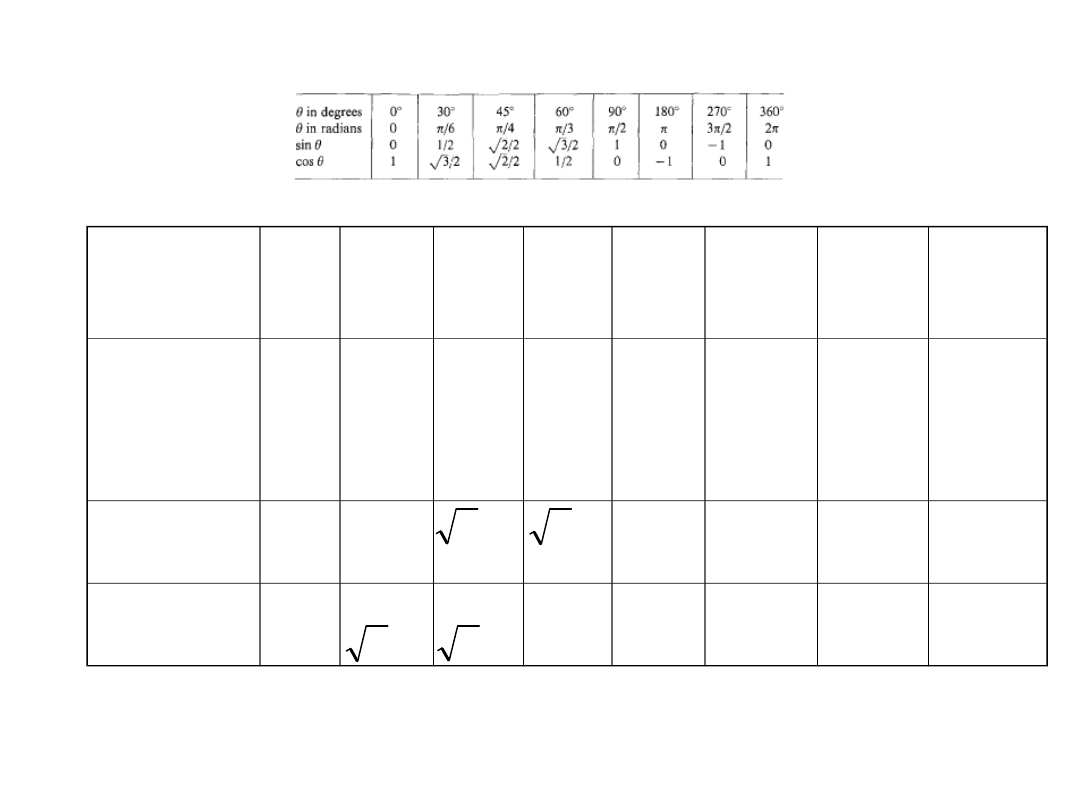
α in

degrees

0

0

30

0

45

0

60

0

90

0

180

0

270

0

360

0

α in

radians

0

π/6

π/4

π/

3

π/2

π 3π/

2

2π

sin α

0

1/2

1

0

-1

0

cos α

1

1/2

0

-1

0

1

/2

2

/2

3

/2

3

/2

2

22

Definition
The

main argument

of the complex number

z

is the

argument of

z

taken from the interval

( - , ].

The

main argument

is denoted by

Arg z

,

thus

-  < Argz  

and

arg z = Arg z + 2k ,

k =
0, 1, ...

o

o

o

o

360

k

90

i

90

i

Arg

360

k

1

0

1

Arg

k

2

2

i

2

i

Arg

k

2

1

0

1

Arg





























arg

,

,

arg

,

.

/

arg

,

/

,

arg

,

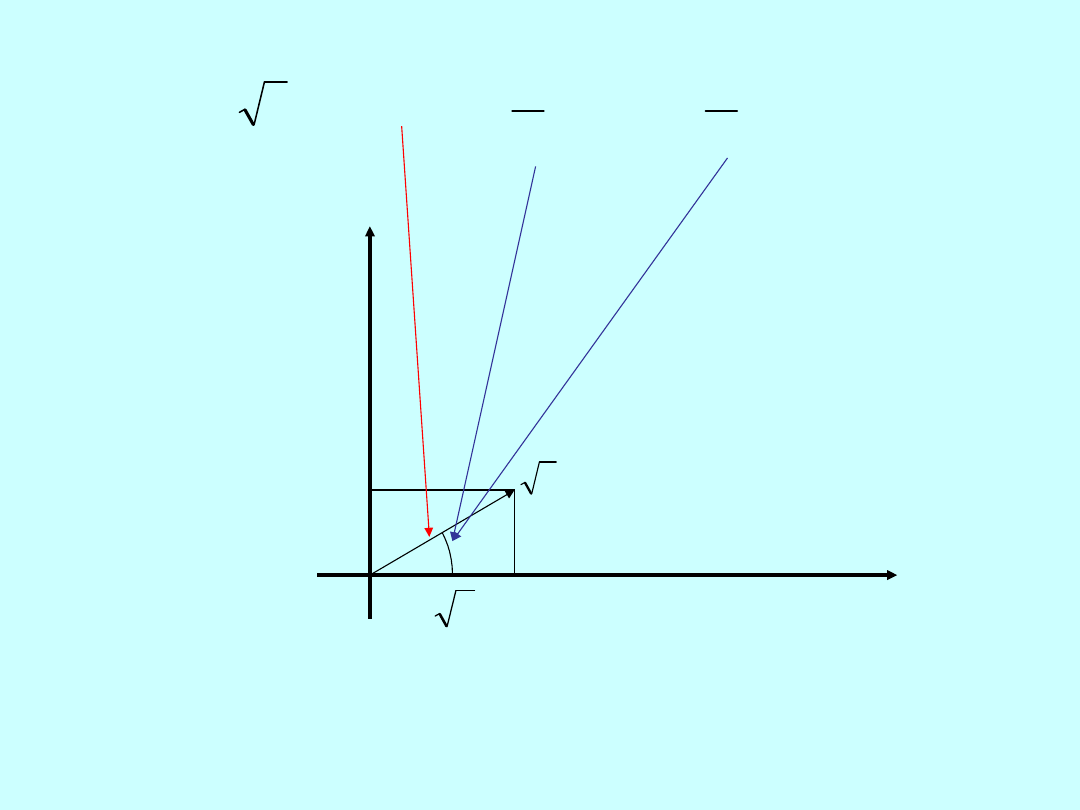
Example:

i

1

/2

23

DEFINITION
The polar form (trigonomeric representation) of a complex number

z = x + i y

, is

z = r ( cos  + i sin )

,

where r is the modulus r = |z| , and



is the argument of

z

.

x = r cos
,
y = r sin




x

y

r

24

i

3

z





.

2

1

3

z

r









o

o

360

k

30

k

2

6

2

1

sin

2

3

cos

















































































6

sin

i

6

cos

2

i

3





Example

Find the polar form of

use the main argument.

The argument of the complex number i.e. the angle

α

which satisfies:

Thus:

1.

2.

The radius (modulus)

25

.

sin

cos











































6

6

2

3





i

i

3

1

/6

i



3

Re

Im

26

MULTIPLICATION IN POLAR FORM

27

Theorem

Let

z

1

= r

1

(cos α

1

+ i∙sin α

1

)

and

z

2

= r

2

(cos

α

2

+ i∙sin α

2

).

Then:

.

0

z

for

)],

sin(

i

)

[cos(

r

r

z

z

)],

sin(

i

)

[cos(

r

r

z

z

2

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1







































Multiplying

complex numbers we

multiply their modules

and

add their arguments

.

Dividing

complex numbers we

divide their modules

and

subtract their arguments.

28

How can we ‘multiply’

points???

Imaginary axis

z

w

Real Axis

1

z · w

The angle of ‘z·w’ is  + β



β



Lets start with the
‘multiplication’ of points
located on the unit circle

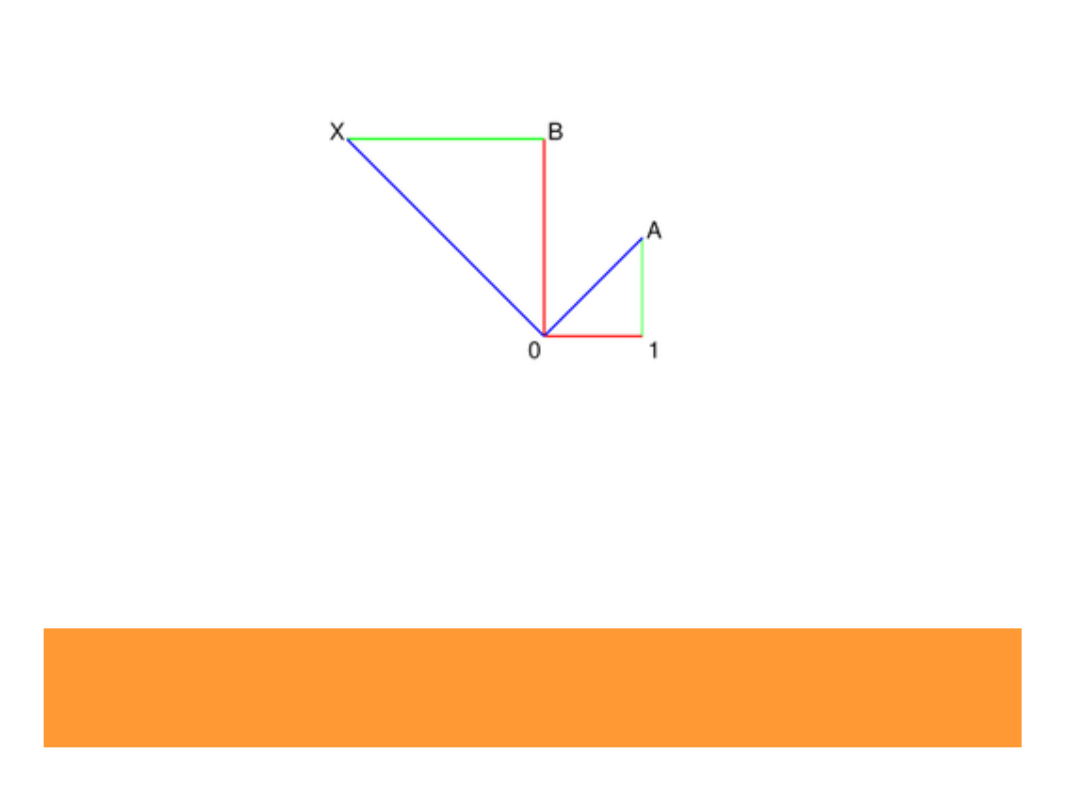
29

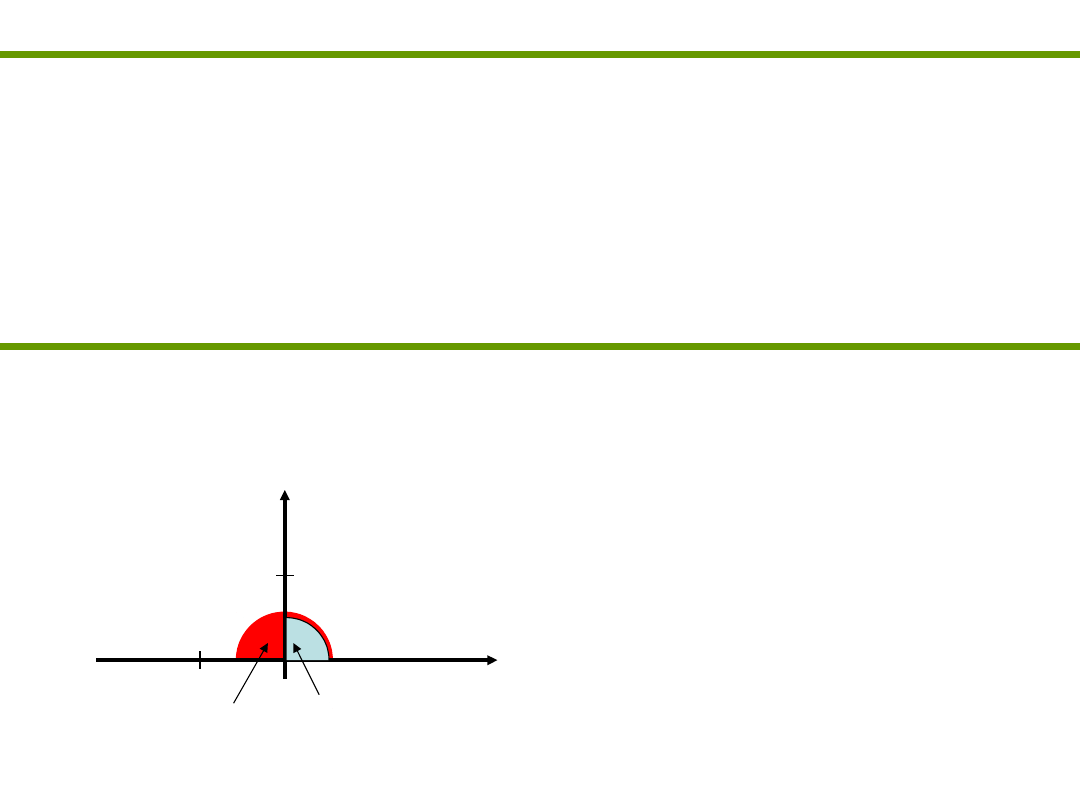
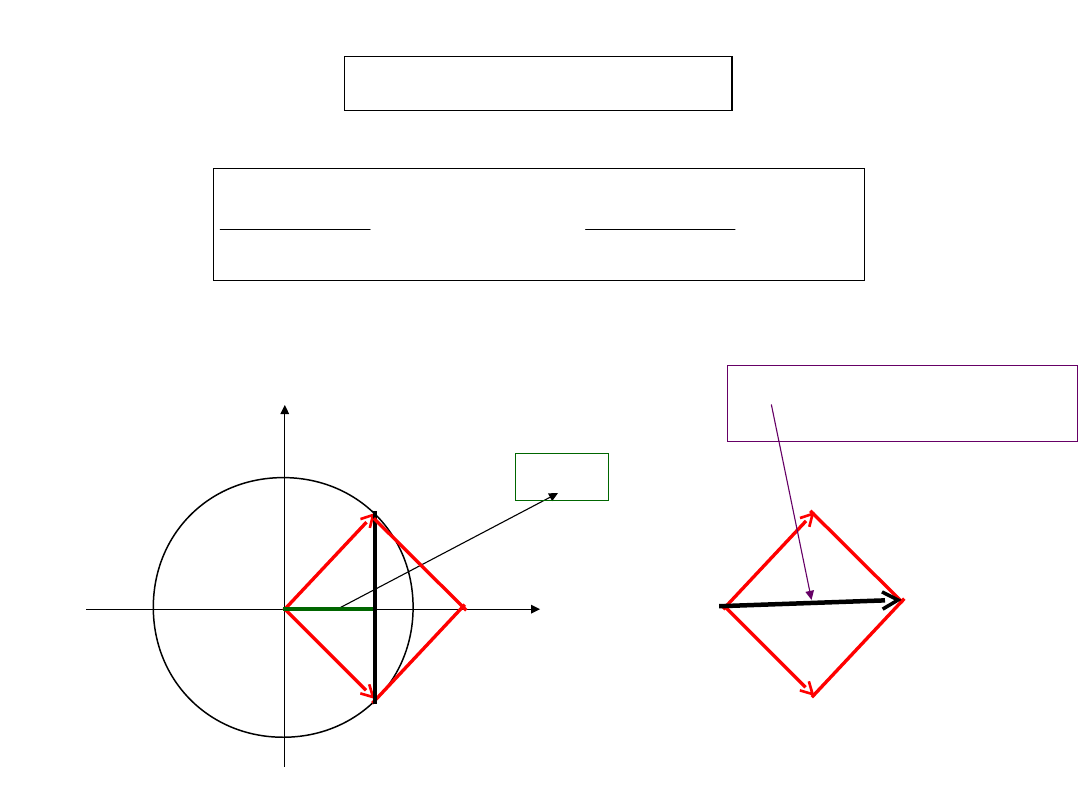
The point X is the product of A and B.
The length of X is the length of A times length
of B.
The angle of X is the angle of A plus the angle of
B.

The product of complex numbers of arbitrary length.

Points on a 2-dimension plane with addition and
multiplication defined as above form the complex
number system.

30

Theorem ( de Moivré's)
For every complex number

z = r (cos

α

+ i sin

α

)

and natural number

n = 0, 1, 2, 3, ... , the powers of

z

are given by:

z

n

= r

n

(cos n

α

+ i sin n

α

).

The above theorem is also true for negative integers.

EXAMPLE

i

2

= ( cos(/2) + i sin (/2) )

2

= {de Moivre’s} = cos  + i sin  = -1

i

-1

/2



31

32

)

sin

(cos









2

i

2

r

z

2

2

A formula for

cos 2, sin 2

)

sin

(cos









i

r

z

1. Let

)

cos

sin

sin

(cos

)

sin

(cos





















i

2

a

r

i

r

z

2

2

2

2

2

2

then its square is

2. On the other hand from the d'Moivre's theorem:

)

sin

(cos

cos









2

2

2

2

a

r

2

r









cos

sin

sin

2

r

2

r

2

2

We equate the real and imaginary parts:









2

2

a

2

sin

cos

cos

so









cos

sin

sin

2

2

Re

Im

so

33

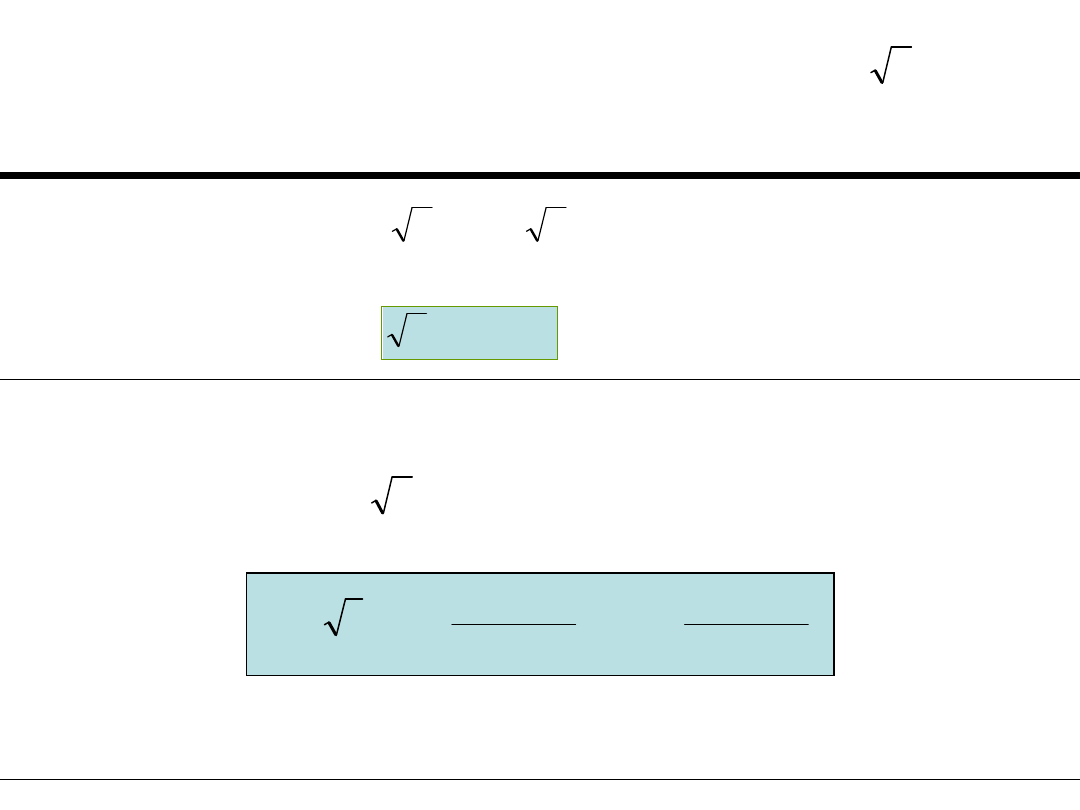
N-TH ROOTS OF COMPLEX

NUMBERS

34

THE n-TH ROOT OF A COMPLEX NUMBER
is a set of numbers,

it is not a function in the strict meaning of this word.

For real numbers

2

4

2

4

2

2





 ,

This means that





2

2

4

2



 ,

n

z

w

























n

k

2

sin

i

n

k

2

cos

r

z

n

k













k

2

1

0

n

z

z

z

z

z

...

,

,

,



where

1

n

2

1

0

k





...

,

,

,

For complex numbers

35

1

2

1

0





n

k

...

,

,

,

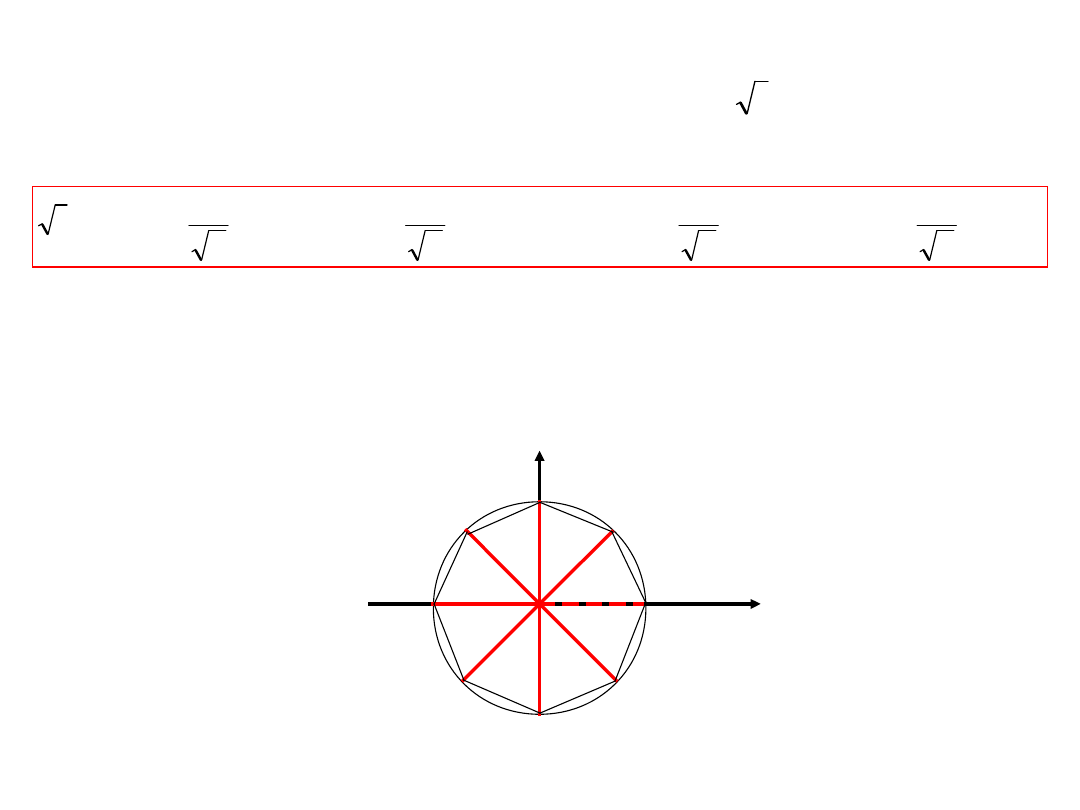
The roots 

0

, ...., 

n-1

are the vertices of a

regular n – gon inscribed in a circle of radius 1
and centre at (0, 0).

d'Moivre's theorem

The set of n-th roots of 1

The number 1 is written as a complex number
1 = 1 + 0 i = 1(cos 0 + i sin 0).
The successive n-th roots of 1 are denoted by 

0

, 

1

, ..., 

n-1

.

From the d'Moivre's theorem we obtain

n

k

2

i

n

k

2

k













sin

cos

k = 0,1,...,n-1.

REP.

























n

k

2

sin

i

n

k

2

cos

r

z

n

k









36



 





 

  

i

1

2

1

i

i

1

2

1

1

i

1

2

1

i

i

1

2

1

1

1

8



















,

,

,

,

,

,

,

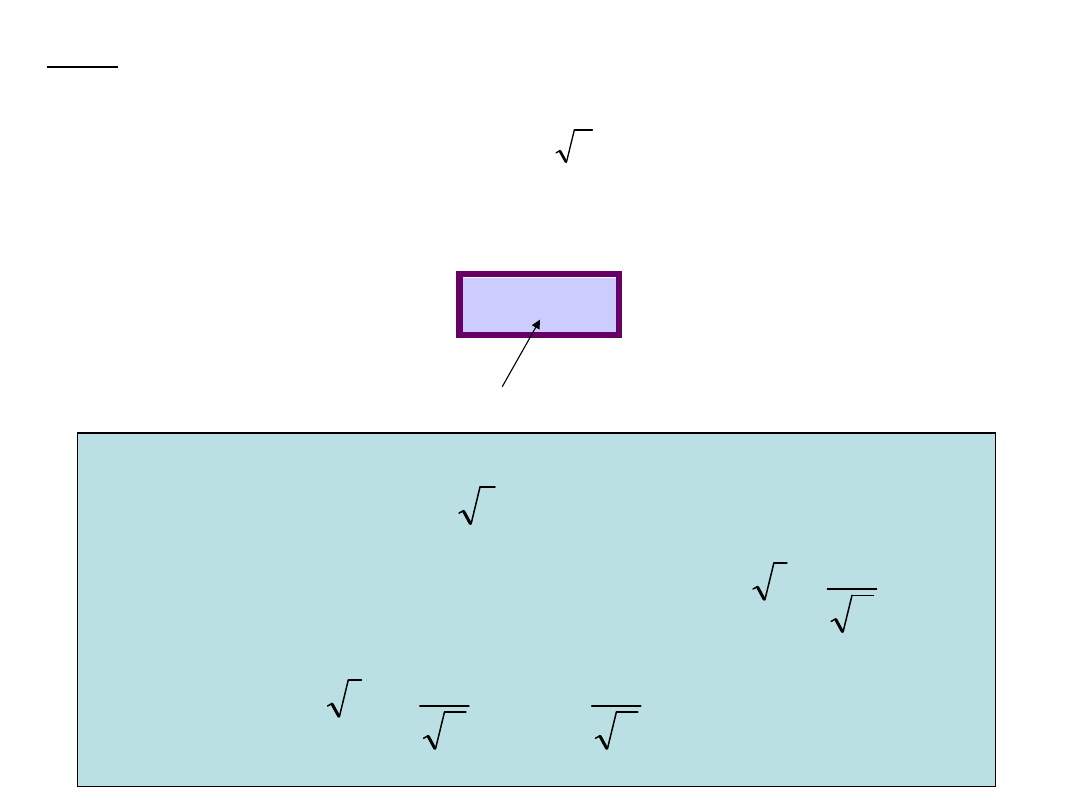
The roots of degree 8 of unity:

8

1

Each root is a vertex of a regular polygon. In the above case an
octagon.

Re

Im

37

If we have some n-th root of a complex number

:

n

s

z

z 

z

then the other roots can be expressed as

s

k

k

z

z





some root of unity

 

 





















i

1

2

1

i

1

2

1

i

2

,

Example





1

1

1

2



 ,

 

i

1

2

1

i

2





Note

Then, because one of the square roots of

i

is:

38

EXPONENTIAL FORM

39

w

z

w

z

e

e

e

.

1







w

z

w

z

e

e

e

.

2





 

n

z

n

z

e

e

.

3





,

.

PROPERTIES OF THE EXPONENTIAL FUNCTION

1

e

.

4

0



40

Argz

i

i

e

z

e

r

z













The exponential form of a complex number

z = r(cos α + i sinα)

The exponential form is the ‘friendliest’ form of the complex number!!!







sin

i

cos

e

i





Let

Example: e

iπ

= cosπ + i sinπ = -1, e

iπ/2

= cos π/2 + i sin π /2 = i

41



























i

)

k

2

(

i

n

i

n

i

)

(

i

i

i

)

(

i

i

i

e

e

e

)

e

(

e

e

/

e

e

e

e

















42

,

.

Examples:

1) -1·i = e

i

· e

i/2

= e

i3/2

= -i

2)

Find the real and imaginary parts of

e

-

i

:

e

-i

=cos(-1) + i sin(-1) = 0.540 + i

0.841
(in
radians)

3) 1= e

2kπ

43

 

0.20788...

e

e

e

i

2

/

2

/

i

i

i

2

/

i

i

















44

)

(

i

2

1

2

1

i

ik

k

k

i

2

2

2

)

(

i

i

2

1

e

r

r

z

z

.

7

e

r

1

z

1

.

6

e

r

z

.

5

e

r

z

.

4

e

r

z

.

3

e

r

z

.

2

r

z

.

1











































45





.

9

,

)

(

:

3

4

4

z

z

z

z

C

z

S









Use the exponential representation of a complex number to
sketch the following set.

Example

3

r

9

r

r

9

r

r

9

z

9

z

r

2

4

7

4

5

4

4

4

3

4

2

4

4

0

4

k

e

1

e

e

r

e

r

1

re

z

re

z

Let

2

3

3

3

k

2

i

i

8

i

4

4

i

4

4

i

i



































































































)

,...,

,

,

,

,

,

)

,

46

3

Re

Im

47

EULER FORMULAS

























sin

cos

i

2

e

e

2

e

e

i

i

i

i

e

i

e

-i

cosφ

the sum of two vectors
e

i

+ e

-i

= 2 cosφ

48

Euler's identity is remarkable for its mathematical beauty.

Three basic arithmetic functions are present exactly once:
addition, multiplication, and exponentiation.

The identity links five fundamental mathematical constants:

•The number 0.

•The number 1.

•The number π,.

•The number e, the base of natural logarithms,

•The number i, imaginary unit of the complex numbers

.

Euler's identity

0

1





i

e