Metody analizy

danych

eksperymentalnych

Transformacja danych

Podstawowymi pojęciami w eksploracji danych są pojęcia

obiektu

i

cechy

(atrybutu)

.

Obiektem

będzie się nazywać element

pewnego zbioru, badany ze względu na pewne swoje właściwości,
które noszą nazwę

cech

(atrybutów). Te same cechy dla różnych

obiektów mogą przyjmować różne

wartości

. Reprezentantem

obiektu w bazie danych jest zwykle rekord, a wartości cech
charakteryzujących ten obiekt – pola tego rekordu, przy czym
cechami są nazwy pół rekordu, jednakowe dla wszystkich
obiektów-rekordów.
Przyjmuje się następujące oznaczenia:

•I={1,2,…,n}

– zbiór numerów obiektów, będących przedmiotem

eksploracji,

•J={1,2,…,m}

– zbiór numerów cech opisujących każdy obiekt ze

zbioru

O

,

•X={X

1

,X

2

,…,X

m

}

- zbiór wektorów wartości cech obiektów postaci:

przy czym wiersz (rekord)

X

i

=(x

i1

, x

i2

, …, x

im

)

odpowiada

jednemu obiektowi o numerze

i

, a kolumna

X

j

=(x

1j

, x

2j

, …, x

nj

)

–

wektorowi wartości cechy o numerze

j

.

Pojęcia podstawowe

11

12

1m

21

22

2m

ij n m

n1

n2

nm

x

x

… x

x

x

… x

X = x

,

…

…

… …

x

x

… x

�

�

�

�

�

�

�

� � =

� �

�

�

�

�

�

�

2

GK (MADE(02) - 2010)

Metody eksploracji danych takie, jak klasyfikacja,

grupowanie czy rangowanie należą do metod

statystycznej analizy

wielowymiarowej

, który to termin oznacza grupę metod

statystycznych, umożliwiających jednoczesną analizę przynajmniej
dwóch cech (własności, atrybutów) obiektów wielocechowych, przy
czym takimi obiektami mogą być określone rzeczy, osoby,
kategorie abstrakcyjne lub zdarzenia, np. produkty spożywcze,
studenci, zjawiska przyrody, przestępstwa.

Ze względu na to, że metody eksploracji danych (ogólnie:

statystycznej analizy wielowymiarowej) z zasady wymagają, aby
wartości cech (atrybutów) badanych obiektów były liczbami
rzeczywistymi, zachodzi potrzeba uprzedniego rozpoznania skali
pomiarowej, w której są wyrażone wartości cechy obiektu.
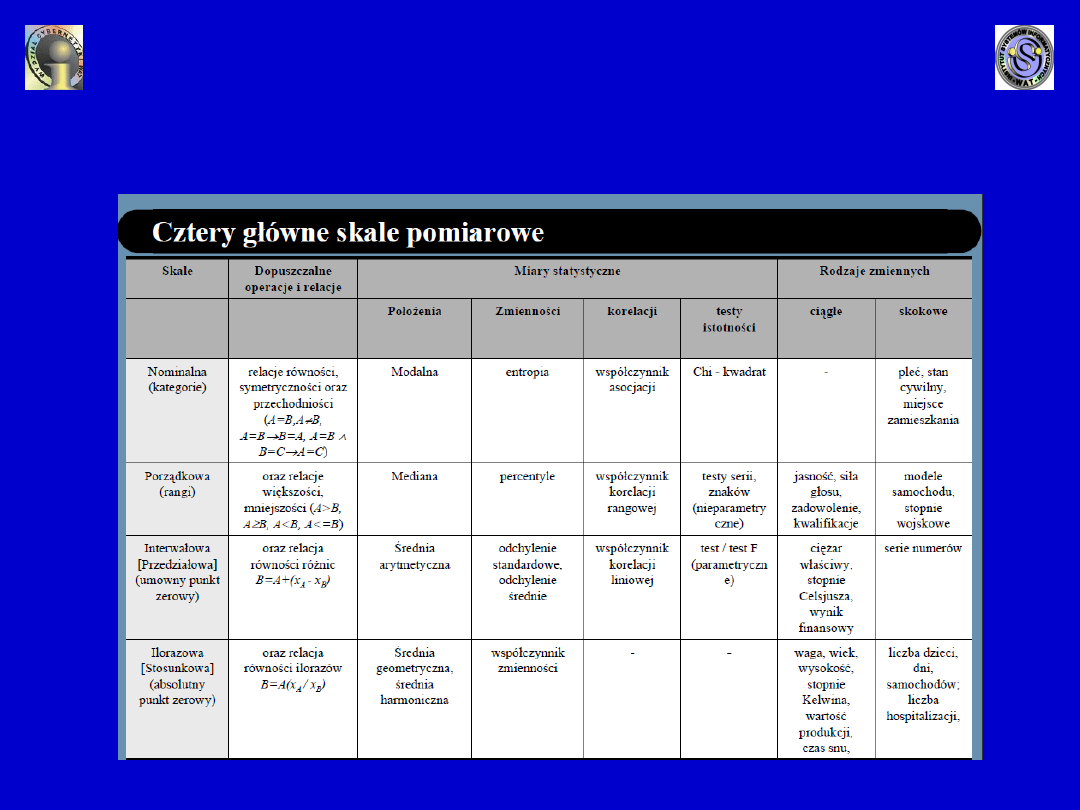
Podstawowy katalog skal pomiarowych obejmuje skale [Stevens,
1959]:

•nominalną,

•porządkową (rangową),

•przedziałową (interwałową),

•ilorazową (stosunkową).
Skale są uporządkowane od najsłabszej do najmocniejszej według
przekształceń dopuszczalnych na wartościach cechy (danych).
Dwie pierwsze z nich noszą często nazwę skal

niemierzalnych

, a

dwie ostatnie –

mierzalnych

, co przekłada się na nazewnictwo

cech.

Skale pomiarowe

3

GK (MADE(02) - 2010)

Skala nominalna:

- przyporządkowuje poszczególnym wartościom cechy wyłącznie

nazwy,

- pozwala jedynie na stwierdzenie identyczności lub różnic

porównywanych obiektów oraz na zliczanie obiektów
identycznych i różnych,

- przykład pomiaru na tej skali: przyporządkowanie płci (kobieta,

mężczyzna) porównywanym ze względu na tę cechę osobom,

- jedyną dopuszczalną procedurą arytmetyczną jest zliczanie, a

spośród procedur statystycznych - tylko te, które oparte są na
zliczaniu.

Skala porządkowa (rangowa):

- wartości cechy (liczby) oznaczają rangi, tj. kolejność obiektów,

przy czym rangi odwzorowują nie tylko równość obiektów, ale też
ich uporządkowanie pod względem rozpatrywanej cechy

(liniowe

porządkowanie obiektów), zatem można stwierdzać, czy obiekt
jest lepszy (większy) od innego, czy też gorszy (mniejszy),

- umożliwia zliczanie obiektów uporządkowanych (liczby relacji

równości (identyczności), większości i mniejszości),

- nie pozwala określić odległości między obiektami,

- przykład pomiaru na tej skali: poziom wykształcenia,

- dozwolone są w tej skali wszelkie przekształcenia liczb nie

zmieniające porządku obiektów, np. potęgowanie,
pierwiastkowanie, logarytmowanie itp.

Skale pomiarowe

4

GK (MADE(02) - 2010)

Skala przedziałowa

(interwałowa):

- pozwala dodatkowo, w stosunku do skali porządkowej, obliczyć

odległości między obiektami, dokonując pomiaru wartości cech
za pomocą liczb rzeczywistych,

- dla skali tej możliwe jest, obok operacji arytmetycznych

dopuszczalnych dla skal poprzednich, także dodawanie i
odejmowanie,

- wartość zerowa na tej skali ma charakter umowny (np. 0

o

w skali

Celsjusza), co prowadzi do zachowania różnic między
wartościami cechy przy zmianie jednostek miary,

- przykład pomiaru na tej skali: średnie dochody pracowników w

przemyśle,

- wartości cech mogą być przekształcane liniowo, ponieważ

transformacja liniowa zachowuje nie tylko kolejność mierzonych
wartości cech, ale także względne ich odległości. Nie jest
natomiast dozwolone ani mnożenie, ani dzielenie, gdyż operacje
te wynikają z założenia o istnieniu rzeczywistego punktu
zerowego. Dopuszczalnymi technikami statystycznymi dla tej
skali, oprócz odpowiednich dla skal poprzednich są: średnia
arytmetyczna, wariancja, rachunek korelacji i regresji oraz
wiele testów parametrycznych

,

Skale pomiarowe

5

GK (MADE(02) - 2010)

Skala ilorazowa

(stosunkowa):

- ma podobny charakter jak skala przedziałowa z tym, że

występuje na niej zero bezwzględne (zero ogranicza
lewostronnie zakres tej skali),

- pozwala dodatkowo, w stosunku do skal poprzednich,

dokonywać także dzielenia i mnożenia, a tym samym
przedstawiać dowolną wartość cechy danego obiektu jako
wielokrotność wartości cechy dla innego obiektu,

- przykład pomiaru na tej skali: waga ludzi,

- wartości cech w skali ilorazowej traktować można jako odległość

mierzoną od bezwzględnego zera. Dozwolone są tym przypadku
wszelkie operacje arytmetyczne, z mnożeniem i dzieleniem
włącznie. Również możliwe jest stosowanie dowolnych technik
statystycznych

.

Skale pomiarowe

6

GK (MADE(02) - 2010)

Skale pomiarowe

Skale pomiarowe są uporządkowane od najsłabszej do
najmocniejszej: nominalna, porządkowa, przedziałowa i
ilorazowa.

7

GK (MADE(02) - 2010)

Ponieważ wartości cech niemierzalnych (skala nominalna i

porządkowa) są wyrażane w postaci kategorii (poziomów) (np.
kolor oczu) ich bezpośrednie wykorzystanie w algorytmach
statystycznej analizy wielowymiarowej jest bardzo ograniczone,
zachodzi więc konieczność ich uprzedniego przekodowania na
liczby rzeczywiste. W tym zakresie wykorzystuje się najczęściej
dwa następujące sposoby przekodowywania wartości cech
niemierzalnych na liczby:

•bez względu na liczbę kategorii (poziomów) cechy,
poszczególnym jej kategoriom można przypisać kolejne liczby
naturalne w sposób dowolny, bez względu na to, czy te kategorie
można uporządkować według intensywności oddziaływania, czy
nie. Np. dla cechy zachowanie ucznia, która ma cztery kategorie:
niepoprawne, poprawne, dobre i bardzo dobre, poszczególnym
kategoriom przypisuje się kolejne liczby naturalne od 1 do 4
(niepoprawne - 1, poprawne - 2, dobre – 3, bardzo dobre – 4),

•jeżeli cecha ma tylko dwie kategorie (cecha binarna, np. płeć),
można ją zamienić na pojedynczą tzw. cechę sztuczną, najczęściej
zero-jedynkową, poprzez nadanie jednej kategorii wartości 0, a
drugiej – 1 (np. mężczyzna – 0, kobieta – 1),

Skale pomiarowe

8

GK (MADE(02) - 2010)

• jeżeli cecha ma więcej niż dwie kategorie, można ją zamienić

nie

na pojedynczą cechę sztuczną, ale na zespół takich cech, także
najczęściej zero-jedynkowych, przy czym liczba wprowadzanych
cech sztucznych musi być najmniejszą liczbą całkowitą,
spełniającą następujący warunek:

2

liczba cech sztucznych

≥ liczba kategorii cechy

przekodowywanej

.

W takim przypadku reprezentowanie poszczególnych kategorii

cechy wymaga nadania odpowiednich wartości wszystkim
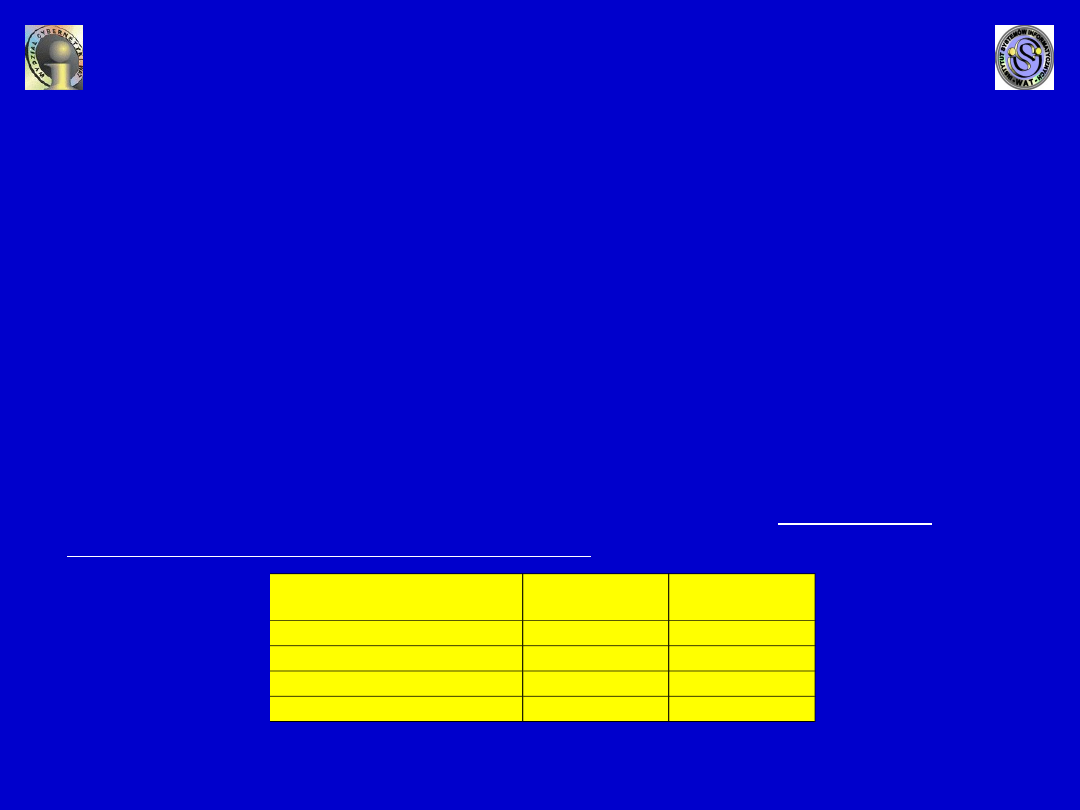
wprowadzonym cechom sztucznym. Np. dla cechy zachowanie
ucznia, która ma cztery kategorie: niepoprawne, poprawne,
dobre i bardzo dobre, wprowadza się 2 sztuczne cechy,
zdefiniowane następująco:

Pojęcia podstawowe

Zachowanie ucznia

Cecha

sztuczna 1

Cecha

sztuczna 2

Niepoprawne

0

0

Poprawne

0

1

Dobre

1

0

Bardzo dobre

1

1

9

GK (MADE(02) - 2010)

P

odstawą stosowania wielu metod eksploracji danych jak

np. klasyfikacja, grupowanie czy rangowanie obiektów
wielocechowych jest macierz wartości cech obiektów (macierz

X

).

Istotą tych metod jest porównywanie ze sobą cech różniących się
wartościami i mianami. Aby takie porównanie było sensowne,
należy wszystkie cechy sprowadzić do porównywalnej postaci
poprzez tzw.

transformację danych

.

Cele transformacji danych:

•ujednolicenie charakteru ech obiektów (postulat jednolitej
preferencji),

•doprowadzenie różnoimiennych cech do wzajemnej
porównywalności (postulat addytywności),

•zastąpienie zróżnicowanych zakresów zmienności poszczególnych
cech zakresem stałym (postulat stałości rozstępu lub stałości
wartości ekstremalnych),

•wyeliminowanie z obliczeń wartości ujemnych (postulat
dodatniości).

Transformacja danych, w zależności od skali pomiarowej

cechy może być realizowana za pomocą wielu metod spośród,
których najczęściej stosuje się: rangowanie, normowanie
analityczne i ważenie cech.

Transformacja danych

10

GK (MADE(02) - 2010)

Rangowanie cech

jest najprostszym sposobem

transformowania cech i polega na przypisaniu każdej wartości
(kategorii) cechy pewnej liczby, tzw.

rangi

, która określa pozycję

zajmowaną przez daną wartość cechy w uporządkowanym ciągu
wartości tej cechy. Najczęściej stosuje się

rangi normalne

(rangi w

postaci kolejnych liczb naturalnych)

lub

rangi Spearmana

.

Normowanie przez rangowanie można stosować do cech
mierzonych w skali porządkowej lub silniejszej.

Normowanie analityczne.

Niech oznacza

wektor wartości

j

-tej cechy obiektów przed unormowaniem, a

oznacza ten wektor z unormowanymi wartościami

j

-tej cechy.

Normowanie analityczne opiera się na przekształceniu
wyrażającym się następującą formułą:

gdzie:

•A

j

– parametr zmiany skali wartości cechy,

•B

j

– parametr skalujący wartości cechy (pozbawia cechę miana),

•p

– parametry przekształcenia (na ogół p = 1). Większe wartości

parametru powodują zwiększenie wariancji. Parzyste naturalne
wartości parametru dają w wyniku wszystkie dodatnie wartości
cechy po unormowaniu.

(

)

j

1j

2j

nj

X = x ,x ,…x

(

)

'

'

'

'

j

1j

2j

nj

X = x ,x ,…,x

p

ij

j

'

ij

j

i=1,2,...,n; j=1,2,...m,

x

A

x

,

B

�

�

-

=�

�

�

�

�

�

Transformacja danych

11

GK (MADE(02) - 2010)

Parametr

A

j

najczęściej przybiera następujące wartości:

stałą równą

0

,

wartość oczekiwaną

(średnią arytmetyczną)

wartości cech (elementów wektora

X

), mini

m

aln

ą

(

x

min

), bą

dź

maksymalną (

x

max

) wartość spośród aktualnych wartości

cechy

(elementów wektor

a

X

)

.

Parametr

B

j

najczęściej przybiera następujące wartości:

mini

m

aln

ą

(

x

min

), bą

dź

maksymalną (

x

max

) wartość spośród

aktualnych wartości

cechy

(elementów wektor

a

X

)

, różnicę

wartości maksymalnej i minimalnej (

x

max

- x

min

),

sumę

wszystkich

aktualnych wartości cechy (elementów wektora

X

),

wartość

oczekiwaną

(średnią arytmetyczną) oraz

odchylenie standardowe

(

s

) obliczone na podstawie wszystkich aktualnych wartości cechy

(elementów wektora

X

).

Szczególnym przypadkiem normalizacji jest

standaryzacja

, która

jest przeprowadzana według następującej formuły:

Wektor wartości cechy po standaryzacji ma następujące własności:
jego elementy są liczbami na ogół z przedziału

(-3,3)

, wartość

średnia z wszystkich elementów jest równa

0

, a odchylenie

standardowe – równe

1

.

Transformacja danych

ij

j

'

ij

j

i=1,2,...,n; j=1,2,...,m.

x

x

x

,

s

-

=

12

GK (MADE(02) - 2010)

Innym przypadkiem normowania analitycznego jest

unitaryzacja

, która jest realizowana przy następujących

wartościach parametrów

A

,

B

i

p

:

Na ogół w praktyce przyjmuje się

A

=

x

min

oraz

p

=

1

, uzyskując

unitaryzację zerową

,

której formuła przekształcająca przyjmie

postać:

Unitaryzacja zerowa powoduje, że elementy wektora

X

j



mają

następujące własności: wszystkie elementy są liczbami przedziału

[0,1]

, wartość maksymalna jest równa

1

, a minimalna

0

.

Przykład

: wartości cechy:

2.0, -3.4, 5.8, 2.4, -6.2, 0.0, 1.2, -4.2

.

Wartości cech po:

•standaryzacji:

0.7967, -0.6868, 1.8406, -0.4121, -1.456, 0.2472,

0.5769, -0.9066

,

•unitaryzacji:

0.6833, 0.2333, 1, 0.3167, 0, 0.5167, 0.6167,

0.1667

.

Transformacja danych

min

max

min

j

j

j

j

j

max

j

j=1,2,...,m

0

A

x , B =x

- x , p=0.5,1,2...;

.

x

�

�

=�

�

�

min

ij

j

'

ij

max

min

j

j

i=1,2,...,n; j=1,2,...,m

x

x

x

,

.

x

x

-

=

-

13

GK (MADE(02) - 2010)

Kolejny przypadkiem normowania analitycznego jest

normalizacja w przedziale[-1,1]

, która jest realizowana przy

następujących wartościach parametrów

A

,

B

i

p

:

Formuła rozpatrywanej normalizacji przyjmie postać:

Normalizacja w przedziale

[-1,1]

powoduje, że elementy wektora

X

j



mają następujące własności: wszystkie elementy są liczbami

przedziału

[-1,1]

o

wartości oczekiwanej równej

0

.

W ramach normowania analitycznego stosuje się też wiele

metod zorientowanych na cechy mierzone tylko w skali ilorazowej;
noszą one wspólną nazwę

przekształceń ilorazowych

. Przykłady

przekształceń:

Transformacja danych

j

j

j

ij

j

i

j=1,2,...,m

A

x , B

max x

x , p=1;

.

=

=

-

ij

j

'

ij

ij

j

i

i=1,2,...,n; j=1,2,...,m

x

x

x

,

.

max x

x

-

=

-

1

ij

ij

ij

ij

ij

'

'

'

'

'

ij

ij

ij

ij

ij

n

max

min

j

j

j

j

ij

i

ij

i

i=1,2,...,n; j=1,2,...,m.

x

x

x

x

x

x

, x

, x

, x

, x

,

s

x

x

x

max x

x

=

=

=

=

=

=

-

�

14

GK (MADE(02) - 2010)

Ważenie cech

jest stosowane w przypadkach, gdy zachodzi

potrzeba określenia, na ile są ważne cechy z punktu widzenia
przyjętego kryterium oraz takiego przekształcenia wartości tych
cech, aby cechy po przekształceniu mogły zachować swój wpływ
proporcjonalny do ważności w końcowych wynikach eksploracji.
Najczęściej ważenie cech jest stosowane w procesie
konstruowania uogólnionych ocen obiektów, stanowiących
podstawę ich porównywania. Ważność cech na ogół ustala się za
pomocą

wag

.

Ważenie cech powinno być przeprowadzane dopiero po ich

transformacji,
najlepiej po standaryzacji.

Przyjmuje się, że waga przypisana dowolnej cesze jest

dowolną liczbą nieujemną (

 0

). Niech wektor

W=(w

1

,w

2

,...,w

m

)

będzie wektorem wag (tzw. wag surowych), a jego element

w

j

,

(j=1,2,…,m)

– surową wagą przypisaną cesze

X

i

. Ocena wpływu wag

na określenie hierarchii ważności cech w zbiorze cech wymaga ich
unormowania. Niech wektor

W

 =(w

1

,w



2

,...,w



m

)

będzie wektorem

wag unormowanych.

Ważoną macierz danych

X



uzyskuje się przez

przemożenie każdego elementu macierzy unormowanej (lub
zestandaryzowanej)

X



przez odpowiednią wagę unormowaną, tj.

Transformacja danych

''

'

'

ij

ij

j

i=1,2,...,n; j=1,2,...,m

x

x w ,

.

= �

15

GK (MADE(02) - 2010)

Istnieje wiele sposobów normowania wag, ale najczęściej

stosowane są następujące:

1. Suma unormowanych wag wynosi

1

:

2. Suma kwadratów unormowanych wag wynosi

1

:

3. Suma wag jest równa dowolnej wartości

c > 0

:

Transformacja danych

( )

m

2

j

'

'

j

j

m

j=1

2

j

j=1

j =1,2,...,m

w

w =

,

w

=1.

w

�

�

�

m

j

'

'

j

j

m

j=1

j

j=1

c >0; j =1,2,...,m

w

w =

c,

w =c.

w

�

�

�

�

m

j

'

'

j

j

m

j=1

j

j=1

j =1,2,...,m

w

w =

,

w =1.

w

�

�

�

16

GK (MADE(02) - 2010)

Ustalanie wag surowych

w

j

, (j=1,2,…,m)

może być

dokonywane przez ekspertów lub statystycznie. W przypadku
ustalania wartości wag na drodze statystycznej, uwzględnia się
naturalną zmienność cechy mierzoną za pomocą współczynnika
zmienności

v

j

, (j=1,2,…,m)

lub siłę naturalnego powiązania cechy

z pozostałymi, mierzoną za pomocą współczynnika korelacji

r

ij

,

(i,j=1,2,…,m)

.

1.Wagi uwzględniające naturalną zmienność cechy (wagi są
wyznaczane na podstawie wartości cech

przed

ich normalizacją

):

2.Wagi uwzględniające skorelowanie cechy z pozostałymi (wagi
są wyznaczane na podstawie wartości cech

po ich normalizacji

):

Transformacja danych

j

j

j

m

j

j

j=1

s

j

x

j =1,2,...,m; v

v

w =

,

.

v

=

�

m

ij

i=1

j

m m

ij

i=1 j=1

i, j =1,2,...,m.

r

w =

,

r

�

��

17

GK (MADE(02) - 2010)

W procesie badania obiektów wielocechowych istotne jest
określenie ich liniowego uporządkowania (nadanie rangi) w

m

-

wymiarowej unormowanej przestrzeni cech.

Przed wykonaniem

działań zmierzających do rangowania obiektów konieczne jest
określenie charakteru poszczególnych cech i zakwalifikowanie
ich do jednej z następujących grup:

•stymulant,

•destymulant,

•nominant.

Stymulantą

nazywana jest taka cecha, której wysokie

wartości są pożądane z punktu widzenia celu rangowania. Wyższe
wartości stymulanty (np. średnia płaca) kwalifikują obiekt jako
lepszy ze względu na tę cechę.

Destymulantą

nazywana jest taka cecha, której niskie

wartości są pożądane z punktu widzenia celu rangowania. Niższe
wartości destymulanty (np. poziom bezrobocia) kwalifikują
obiekt jako lepszy ze względu na tę cechę.

Nominantą

nazywana jest taka cecha, której „normalne”

wartości (np. normalna temperatura ciała człowieka) są
pożądane z punktu widzenia celu rangowania; nie są pożądane
natomiast wartości stanowiące duże odchylenia w dół i w górę od
wartości „normalnych”. Wartość cechy uważana za „normalną”
(najlepszą) może być wyznaczana arbitralnie lub na podstawie
wartości średniej (oczekiwanej).

Zmiana charakteru cech

18

GK (MADE(02) - 2010)

K

walifikacja cech powinna odpowiedzieć na pytanie, czy

wszystkie cechy rangowanych obiektów są

stymulantami

(destymulantami)

, gdyż tylko taka „jednokierunkowość” cech

zapewnia właściwe rangowanie. Jeżeli przyjąć, że rangowanie
będzie oparte na stymulantach, to wszystkie wykryte w trakcie
analizy cechy będące

destymulantami

i

nominantami

będą

musiały być przetransformowane na

stymulanty

przed

rozpoczęciem rangowania.

Zamiana destymulanty na stymulantę

. Rozpatruje się

jedną cechę

X

j

o wartościach

x

ij

, (i=1,2,…,n; j=1,2,…,m)

,

będącą

destymulantą. Można ją zamienić na stymulatę

Z

j

o wartościach

z

ij

,

stosując najczęściej jedno z dwóch następujących

przekształceń:

Zmiana charakteru cech

{ }

(

)

{ }

{ }

0

ij

i=1,2,...,n

ij

ij

ij

j

i=1,2,...,n

ij

ij

i=1,2,...,n

min x

ij

a= max x

i=1,2,...,m; j=1,2,...,m

a =0, a = max x , a =2x ,

a =1,

,

z

a x ,

a

z

,

.

x

�

= -

�

�

�

�

=

�

�

�

�

19

GK (MADE(02) - 2010)

Zamiana nominanty na stymulantę

. Niech cecha

X

j

o

wartościach

x

ij

, (i=1,2,…,n; j=1,2,…,m)

będzie nominantą.

Pożądaną („normalną”) wartością nominaty może być jedna
wartość (nominanta punktowa) lub przedział wartości
(nominanta przedziałowa). Niech rozpatrywana nominanta

X

j

będzie nomintą przedziałową, która przyjmuje wartości
„normalne” z

przedziału pożądanego

[x

d

, x

g

], (d,g=1,2,…,m; d



g)

. Nominanta punktowa przyjmowałaby jedną wartość pożądaną

równą

x = x

d

= x

g

.

Lewym przedziałem

nominanty

X

j

nazywa się

przedział

[x

1j

, x

d

)

, a

prawym przedziałem

– przedział

(x

g

, x

nj

]

.

Niech wektor

Z

j

o wartościach

z

ij

oznacza stymulatę.

Przekształcenia nominanty

X

j

w stymulantę

Z

j

można dokonać

stosując np. formułę:

gdzie:

a, b

- miejsca zerowe funkcji

f(x)

,

p

1

, p

2

– parametry odpowiedzialne za typ funkcji, odpowiednio

lewego i prawego przedziału nominanty.

Zmiana charakteru cech

( )

(

)

(

)

1

2

p

d

ij

ij

d

d

ij

ij

d

g

p

ij

g

ij

g

g

,

x

dla x

,x

dla x

x ,x

dla x

x

x -

1-

x -a

z

f x

1

x - x

1-

b- x

+�

� - �

�

�

� �

�

� �

�

� �

�

�

�

�

�

=

=�

�

�

�

� �

�

�

�

� �

�

� �

�

�

20

GK (MADE(02) - 2010)

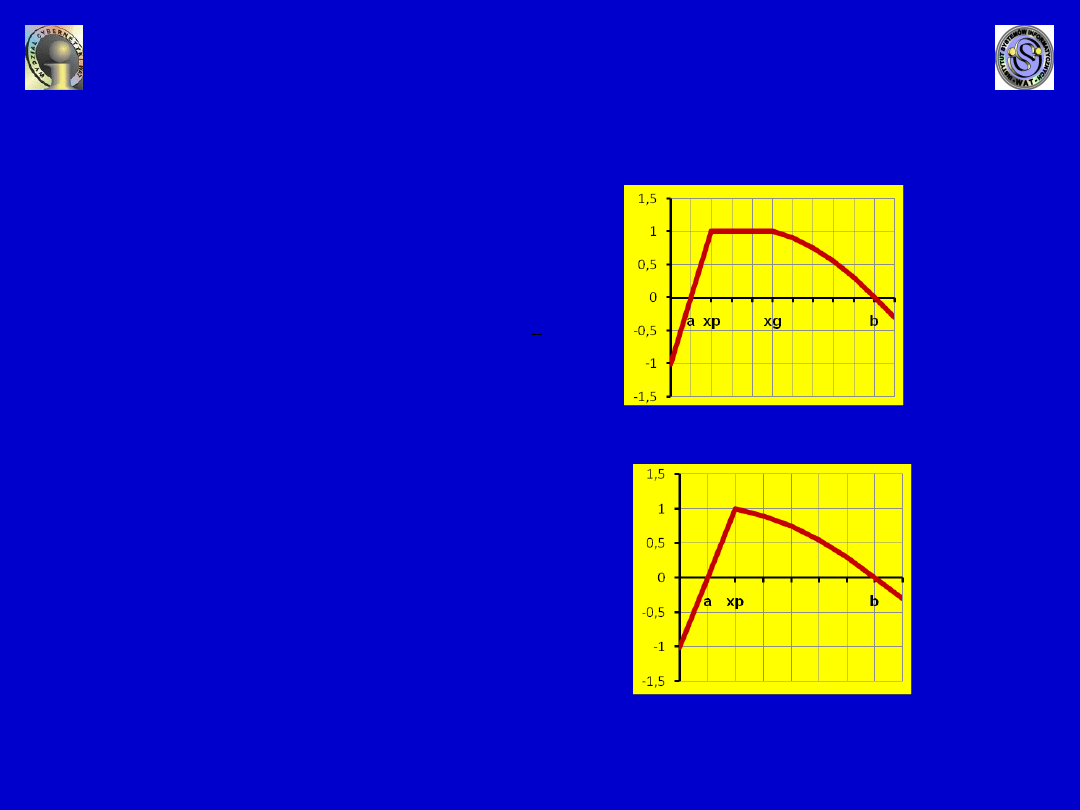
W przypadku, gdy nominanta
przyjmuje tylko jedną „normalną”
wartość,

pożądany przedział

jej

wartości sprowadza się do jednej
wartości (jednego elementu)

x

p

takiej, że

x

p

= x

d

= x

g

. Przykładowy

wykres funkcji

f(x)

dla

rozpatrywanego przypadku
nominanty, przy założeniu, że

p

1

=

1

i

p

2

= 2

.

Zmiana charakteru cech

Przykładowy wykres funkcji

f(x)

przekształcenia nominanty w
stymulantę przy założeniu, że

p

1

=

1

i

p

2

= 2

.

21

GK (MADE(02) - 2010)

Możliwość stosowania funkcji

f(x)

przekształcania

nominanty w stymulantę wymaga określenia wartości progowych

a

i

b

, występujących w tej funkcji. Jednym z częściej stosowanych

sposobów wyznaczania tych wartości jest sposób przedstawiony
niżej:



jeżeli spełniona jest nierówność

to



jeżeli spełniona jest nierówność

to

Zmiana charakteru cech

{ }

{ }

d

ij

ij

g

i=1,2,...,n

i=1,2,...,n

x - min x

max x - x ,

�

{ }

{ }

d

g

ij

i=1,2,...,n

ij

i=1,2,...,n

a x

x

max x ,

b max x ,

=

+ -

=

{ }

{ }

ij

i=1,2,...,n

d

g

ij

i=1,2,...,n

a

min x ,

b x

x

min x .

=

=

+ -

{ }

{ }

d

ij

ij

g

i=1,2,...,n

i=1,2,...,n

x - min x

max x - x ,

>

22

GK (MADE(02) - 2010)

W analizie danych opartej na klasyfikacji, bądź grupowaniu

istotną rolę odgrywa określanie

odległości

(podobieństwa) między

obiektami. Do określania tych odległości służy

metryka

. Niech

d

oznacza metrykę, a

d(o

i

,o

k

)

- odległość metryczną obiektu

o

k

od

obiektu

o

i

.

Metryką nazywa się funkcję dwuargumentową

d

, która

spełnia następujące własności:

1.d(o

i

,o

k

) > 0

– odległość między dwoma różnymi obiektami jest

zawsze dodatnia,

2.d(o

i

,o

k

) = d(o

k

,o

i

)

– odległość od obiektu

o

i

do obiektu

o

k

jest

taka sama jak odległość od obiektu

o

k

do obiektu

o

i

,

3.d(o

i

,o

i

) = 0

– odległość od punktu

o

i

do siebie jest równa

0

,

4.d(o

i

,o

q

)

 d(o

i

,o

k

) + d(o

j

,o

q

)

– odległość między dowolnymi trzema

obiektami

o

i

,

o

q

i

o

k

spełnia własność trójkąta: suma dowolnych

dwóch odległości jest nie mniejsza od odległości trzeciej.
Dogodną formą przedstawiania odległości między obiektami jest
macierz odległości

D

. Jest to macierz kwadratowa, symetryczna, z

zerowymi wartościami na głównej przekątnej (to wynika z
własności 1, 2 i 3 metryki). Ponadto każda podmacierz

3

3

macierzy

D

spełnia następującą własność: suma każdych dwóch

spośród trzech elementów nad główną przekątną podmacierzy jest
nie mniejsza od elementu trzeciego (własność trójkąta – 4-ta
własność metryki).

Miary odległości dla

obiektów

23

GK (MADE(02) - 2010)

Macierz

D

odległości między obiektami:

Macierz

D

jest tworzona tylko na podstawie unormowanej

macierzy

X



. Elementami macierzy

D

są liczby określające

odległości między obiektami reprezentowanymi przez jej wiersze a
obiektami reprezentowanymi przez jej kolumny. Istnieje wiele
mierników odległości, a ich stosowanie zależy od:

•skali pomiarowej wartości cech; istnieje wiele miar odległości dla
przypadku, gdy wartości wszystkich cech obiektu są mierzone w
takiej samej skali pomiarowej,

•zastosowanej formuły transformacji danych do przekształcenia
wartości cech,

•spełnienia przez formułę obliczeniową dodatkowych wymagań,
np. nierówności trójkąta,

•skal pomiarowych wartości cech obiektu, gdy te skale są inne.

Miary odległości dla

obiektów

12

1n

21

2n

n1

n2

0

d

... d

d

0

... d

D

...

...

... ...

d

d

... 0

�

�

�

�

�

�

=

�

�

�

�

�

�

24

GK (MADE(02) - 2010)

W przypadku

cech mierzalnych

najczęściej stosuje się:

1.Odległość Minkowskiego:

gdzie:

d

ik

– odległość obiektu

o

i

od obiektu

o

k

,

x



ij

,

x



kj

– wartości unormowanej

k

-tej cechy obiektów, odpowiednio

o

i

oraz

o

j

(elementy macierzy

X



),

p

– parametr (

p = 1

– odległość miejska (Hamminga),

p = 2

–

odległość euklidesowa (stosowana najczęściej),

p =



- odległość

Czebyszewa).

Największą wartość elementy

d

ik

macierzy

D

osiągają dla

p = 1

,

która maleje wraz ze wzrostem

p

, a dla

p =



wyraża się

zależnością:

Miary odległości dla

obiektów

1

m

p

'

'

p

ik

ij

kj

j

i,k=1,2,...,n; j=1,2,...,m,

d

x

x

,

=

=

-

�

{

}

'

'

ik

ij

kj

j 1,2,...,m

i,k=1,2,...,n

d

max x

x ,

.

�

=

-

25

GK (MADE(02) - 2010)

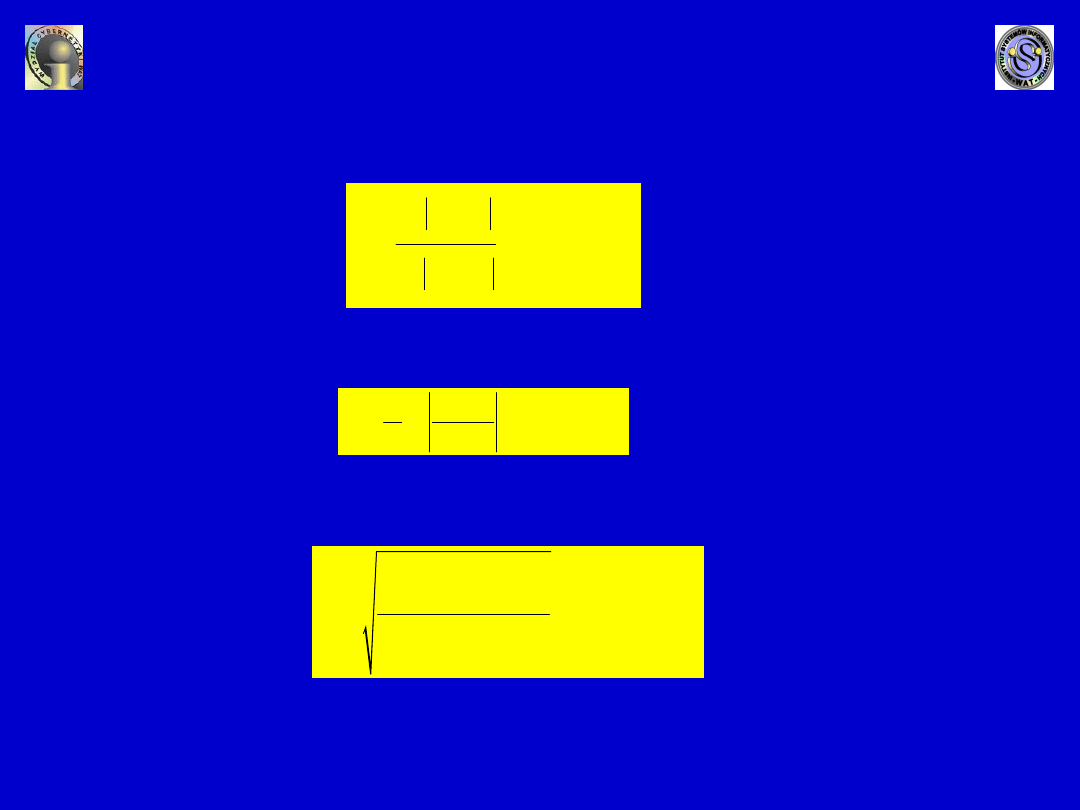
2. Odległość Braya-Curtisa:

3. Odległość Canberry:

4. Odległość łukowa:

m

'

'

ij

kj

j=1

ik

m

'

'

ij

kj

j=1

i,k =1,2,...,n

x - x

d =

,

.

x

x

+

�

�

'

'

m

ij

kj

ik

'

'

j=1

ij

kj

i,k =1,2,...,n

x - x

1

d =

,

.

m

x

x

+

�

(

)

( )

( )

m

'

'

ij

kj

j=1

ik

m

m

2

2

'

'

ij

kj

j=1

j=1

i,k =1,2,...,n

1-

x x

d =

,

.

x

x

�

�

�

�

�

Miary odległości dla

obiektów

26

GK (MADE(02) - 2010)

5. Odległość Mahalanobisa:

gdzie:

•

Z

ik

–

m

-elementowy wektor, którego elementami

z

j

są różnice

unormowanych wartości cech obiektów

o

i

oraz

o

k

:

•

C

-1

– macierz odwrotna do macierzy kowariancji utworzona na

podstawie nieunormowanej macierzy

X

, tj. macierz

kwadratowa

m

m

o elementach:

przy czym

Odległość ta powinna być stosowana w przypadku, gdy cechy

mają rozkłady normalne oraz zachodzi potrzeba
uwzględnienia korelacji między nimi.

-1

T

ik

ik

ik

i,k=1,2,...,n,

d =Z C Z

'

'

j

ij

kj

j=1,2,...,m

z =x - x ,

,

(

)

(

)

n

jl

ij

j

il

l

i=1

j,l=1,2,...,m

1

c =

x - x

x - x ,

,

n

�

�

n

j

ij

i=1

j =1,2,...,m

1

x =

x ,

.

n

�

Miary odległości dla

obiektów

27

GK (MADE(02) - 2010)

6. Odległość miejska (taksówkowa, manhatańska):

W przypadku

cech niemierzalnych

(skala nominalna lub

porządkowa, cechy jakościowe)

najczęściej stosowaną miarą

podobieństwa obiektów

O

i

oraz

O

k

jest

współczynnik

podobieństwa Sneatha

, definiowany jako:

gdzie

(warunek)

indykator (funkcja) postaci:

Miary odległości dla

obiektów

(

)

m

ik

ij

kj

j=1

i,k =1,2,...,n

1

d =

x

x ,

.

m

�

�

I

(

)

warunek = prawda

warunek

inaczej .

1,

,

=

0,

�

�

�

I

m

'

'

ik

ij

kj

j=1

i,k =1,2,...,n

d =

x - x ,

.

�

28

GK (MADE(02) - 2010)

W przypadku

cech niemierzalnych

(skala nominalna, cechy

binarne)

konieczne

jest ustalenie sposobu kodowania wartości

tych cech, tj. ich kategorii: cecha „występuje” (+) i cecha „nie
występuje” (-) w badanych obiektach:

Przyjmuje się oznaczenia:

gdzie:

a

,

d

– liczba przypadków jednoczesnego występowania (

a

) lub nie

występowania (

b

) cechy w badanych obiektach

O

i

oraz

O

k

,

b

,

c

– liczba przypadków występowania cechy w obiekcie

O

i

i nie

występowania w obiekcie

O

k

(

b

) lub nie występowania cechy w

obiekcie

O

i

i występowania w obiekcie

O

k

(

c

).

Miary odległości dla

obiektów

Cecha X

j

a

j

b

j

c

j

d

j

Obiekt

O

i

Obiekt

O

k

+

+

1

0

0

0

+

-

0

1

0

0

-

+

0

0

1

0

-

-

0

0

0

1

,

,

,

,

1

1

1

1

























m

j

j

m

j

j

m

j

j

m

j

j

d

d

c

c

b

b

a

a

29

GK (MADE(02) - 2010)

W przypadku

cech niemierzalnych binarnych

najczęściej stosuje się:

1.Odległość Czekanowskiego:

2.Odległość Jaccarda:

3.Odległość Sokala i Michenera:

4.Odległość Russela i Rao:

Miary odległości dla

obiektów

ik

i,k=1,2,...,n,

2 a

d

1-

,

2 a+b+c

�

=

�

ik

i,k=1,2,...,n,

a

d

1-

,

a+b+c

=

ik

i,k=1,2,...,n,

a d

d

1-

,

a+b+c d

+

=

+

ik

i,k=1,2,...,n.

a

d

1-

,

a+b+c d

=

+

30

GK (MADE(02) - 2010)

W celu określenia

podobieństwa cech

badanych obiektów

stosuje się miary odległości, które są

semimetrykami

, ponieważ

nie spełniają własności trójkąta. Miary te są oparte na
współczynnikach korelacji między cechami. Do konstrukcji

macierzy odległości

D dla cech

stosuje się zwykle następujące

semimetryki:

•semimetryka 1:

gdzie:

r

jl

– współczynnik korelacji dla

j

-tej i

l

-tej cechy obiektu,

•semimetryka 2:

•semimetryka 3:

•semimetryka 4:

Miary odległości dla cech

obiektów





m,

1,2,...,

l

j,

,

r

1

2

d









jl

jl

m,

1,2,...,

l

j,

,

r

1

d

2

jl







jl

m,

1,2,...,

l

j,

,

r

1

d

2

jl







jl

.

m

1,2,...,

l

j,

,

r

1

d







jl

jl

31

GK (MADE(02) - 2010)

32

GK (MADE(02) - 2010)