
Statystyka w analizie i planowaniu eksperymentu
Wykład 3
Transformacje danych i metody ich prezentacji
Przemysław Biecek
Dla 1 roku studentów Biotechnologii

Wejściówka
Proszę na (niewielkiej) kartce napisać:
1
Imię, nazwisko,
2
Nr. indeksu,
3
Nazwisko osoby prowadzącej ćwiczenia
Podstawy rachunku prawdopodobieństwa
2/34

Wejściówka
Proszę na (niewielkiej) kartce napisać:
1
Imię, nazwisko,
2
Nr. indeksu,
3
Nazwisko osoby prowadzącej ćwiczenia
Zadanie
Proszę wyznaczyć wariancję dla cyfr swojego numeru indeksu.
Zadanie
Przyjmując, że liczba jagód w jagodziance ma rozkład w
przybliżeniu normalny N (µ = 50, σ = 10), proszę oszacować
prawdopodobieństwo, że w kupionej jagodziance jest od 30 do 80
jagód.
Podstawy rachunku prawdopodobieństwa
3/34

Podstawowe statystyki opisowe
Podstawowymi statystykami opisowymi są (patrz wykład 1)
min,
max,
średnia,
mediana,
kwartyle,
IQR,
odchylenie standardowe sd,
wariancja var,
kowariancja cov,
korelacja cor.
Podstawy rachunku prawdopodobieństwa
4/34

Podstawowe statystyki
Zobaczmy jak wygląda rozkład koloru oczy i rozkład płci w pewnej
populacji 45 osób. Aby podsumować wystąpienia dwóch zmiennych
jakościowych, wygodnie jest wykorzystać tablice kontyngencji
(nazywaną też tablicą wielodzielczą).
niebieskie
brązowe
Σ
mężczyzna
15
8
23
kobieta
10
12
22
Σ
25
20
45
W komórkach macierzy wypisane są liczby osób o odpowiednich
atrybutach. W ostatniej kolumnie i ostatnim wierszu wypisane są
liczebności brzegowe.
Podstawy rachunku prawdopodobieństwa
5/34
Podstawowe statystyki
Dla tej macierzy, możemy wyznaczyć jako procent osób mających
niebieskie oczy to mężczyźni a jaki procent to kobiety.
niebieskie
brązowe
mężczyzna
15
8
23
kobieta
10
12
22
25
20
45
niebieskie
brązowe
mężczyzna
60%
40%
kobieta
40%
60%
100%
100%
Pr (kobieta|oczy niebieskie) =???
Podstawy rachunku prawdopodobieństwa
6/34

Podstawowe statystyki
Dla tej macierzy, możemy też wyznaczyć procent mężczyzn mające
niebieski kolor oczu lub brązowy kolor oczu.
niebieskie
brązowe
mężczyzna
15
8
23
kobieta
10
12
22
25
20
45
niebieskie
brązowe
mężczyzna
65.2%
34.8%
100%
kobieta
45.5%
54.5%
100%
Pr (oczy niebieskie|kobieta) =???
Podstawy rachunku prawdopodobieństwa
7/34

Podstawowe statystyki graficzne
Jeden obrazek jest wart więcej niż tysiąc słów.
Podstawy rachunku prawdopodobieństwa
8/34
Wykres mozaikowy mosaicplot()
Pola kwadratów odpowiadają liczebności klas.
mezczyzna
kobieta
niebieskie
brazowe
Podstawy rachunku prawdopodobieństwa
9/34

Wykres balonowy balloonplot()
Pola kół odpowiadają liczebności klas.
25
20
23
22
45
mezczyzna
kobieta
niebieskie
brazowe
y
x
15
8
10
12
Podstawy rachunku prawdopodobieństwa
10/34
Wykres słupkowy barplot()
Wysokości słupków opisują liczebności lub frakcje występowania
poszczególnych poziomów zmiennej.
wysokie
średnie
niskie
0
5
10
15
20
Podstawy rachunku prawdopodobieństwa
11/34
Wykres słupkowy barplot()
Możemy przedstawiać zmienne w rozbiciu na podgrupy.
podstawowe
srednie
wyzsze
zawodowe
0
20
40
60
80
Podstawy rachunku prawdopodobieństwa
12/34
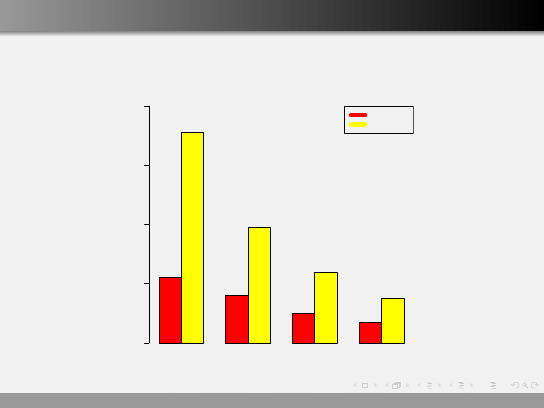
Wykres słupkowy barplot()
Możemy przedstawiać zmienne w rozbiciu na podgrupy.
podstawowe
srednie
wyzsze
zawodowe
0
20
40
60
80
kobieta
mezczyzna
22
71
16
39
10
24
7
15
Podstawy rachunku prawdopodobieństwa
13/34

Wykres pudełkowy boxplot()
Wykres pudełkowy to jeden z najpopularniejszych sposobów
przedstawiania danych.
20
30
40
50
60
70
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Podstawy rachunku prawdopodobieństwa
14/34

Wykres pudełkowy boxplot()
●
●
●
●
●
●
60
70
80
90
100
ciś nienie rozkurczowe
min. bez obs. odst.
1. kwartyl
mediana
3. kwartyl
max. bez obs. odst.
95% p. ufn. dla med.
95% p. ufn. dla med.
obs. odstają ca
obs. odstają ca
obs. odstają caobs. odstają ca
obs. odstają ca
obs. odstają ca
Podstawy rachunku prawdopodobieństwa
15/34
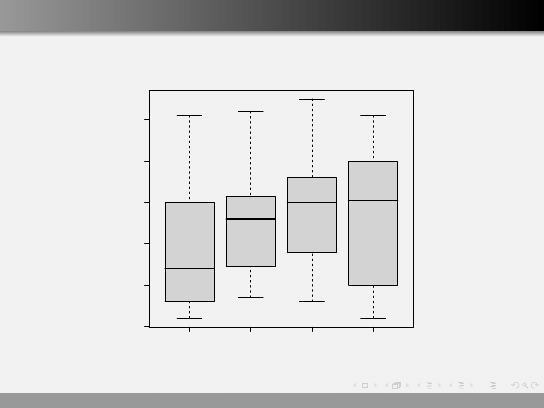
Wykres pudełkowy boxplot()
podstawowe
srednie
wyzsze
zawodowe
20
30
40
50
60
70
Podstawy rachunku prawdopodobieństwa
16/34
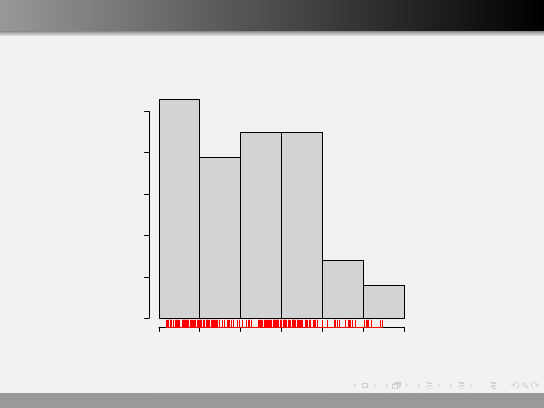
Histogram hist()
Histogram zmiennej wiek
wiek
liczebnosci
20
30
40
50
60
70
80
0
10
20
30
40
50
Podstawy rachunku prawdopodobieństwa
17/34
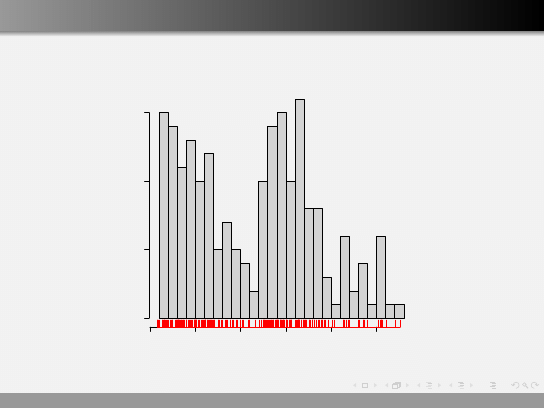
Histogram hist()
Histogram zmiennej wiek
wiek
liczebnosci
20
30
40
50
60
70
0
5
10
15
Podstawy rachunku prawdopodobieństwa
18/34
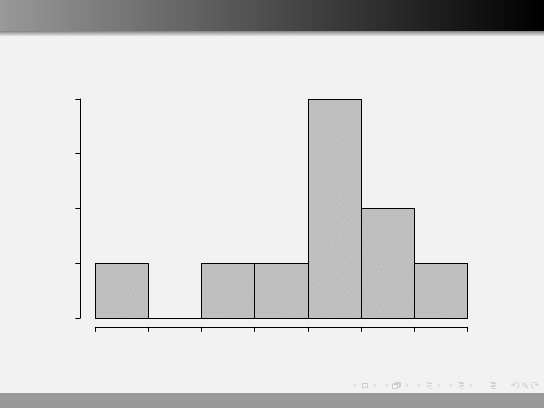
Histogram hist()
Histogram of IQ
IQ
Frequency
60
70
80
90
100
110
120
130
0
1
2
3
4
Podstawy rachunku prawdopodobieństwa
19/34
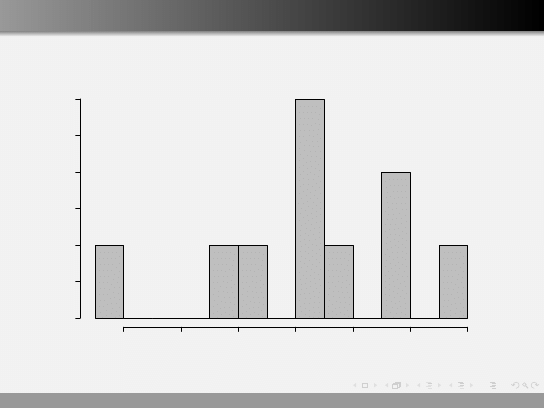
Histogram hist()
Histogram of IQ
IQ
Frequency
70
80
90
100
110
120
130
0.0
0.5
1.0
1.5
2.0
2.5
3.0
Podstawy rachunku prawdopodobieństwa
20/34
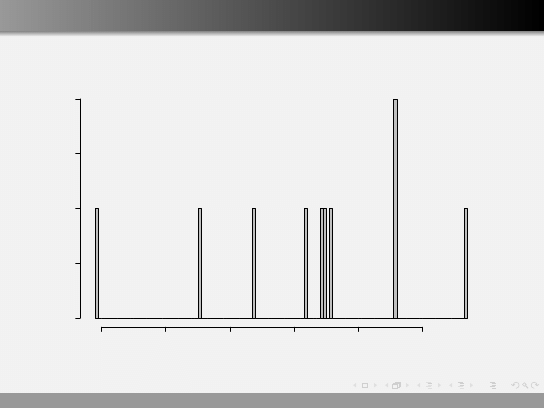
Histogram hist()
Histogram of IQ
IQ
Frequency
70
80
90
100
110
120
0.0
0.5
1.0
1.5
2.0
Podstawy rachunku prawdopodobieństwa
21/34
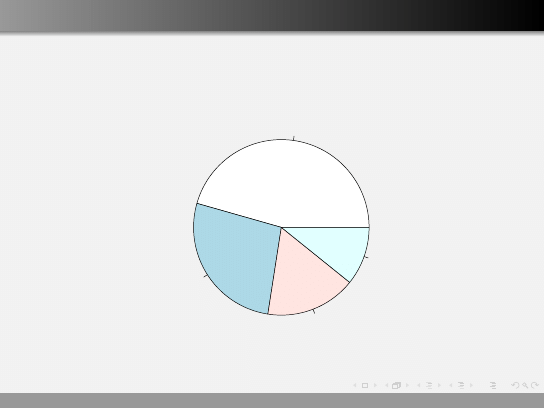
Wykres kołowy pie()
Niestety, popularny sposób opisu danych.
podstawowe
srednie
wyzsze
zawodowe
Podstawy rachunku prawdopodobieństwa
22/34

Wykres kołowy
Są sytuacje w których nie powinno się stosować wykresów
kołowych.
1
2
3
1
2
3
Podstawy rachunku prawdopodobieństwa
23/34

Wykres rozrzutu sp(), plot()
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
100
120
140
160
180
60
70
80
90
100
dat$cisnienie.skurczowe
dat$cisnienie.rozkurczowe
●
●
Podstawy rachunku prawdopodobieństwa
24/34
Wykres rozrzutu sp(), plot()
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
100
120
140
160
180
60
70
80
90
100
dane$cisnienie.skurczowe
dane$cisnienie.rozkurczowe
●
●
●
●
●
●
●
●
●
●
Podstawy rachunku prawdopodobieństwa
25/34
Wykres rozrzutu
●
●
●
●
●
●
100
120
140
160
180
60
70
80
90
100
cisnienie.skurczowe
cisnienie.rozkurczowe
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
plec
kobieta
mezczyzna
Podstawy rachunku prawdopodobieństwa
26/34
Macierz wykresów rozrzutu pairs()
|
|
|
|
| |
|
| |
|
||
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
| ||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| ||
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|| |
|
|
|
| | |
|
|
|
|
|
|
|
|
|
wiek
100
120
140
160
180
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
20
30
40
50
60
70
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
100
120
140
160
180
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
||
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
||
|
|
||
|| |
|
|
|
|
|
|
|
|
|
|
| |
|
| | |
|
|
|
|
|
|
| ||
|
|
|
||
|
|
||
|
|
|
|
|
|
|
| |
|
|
| |
|
|
|
| |
| |
|
| |
|
|
|
|
|
|
| |
|
| |
|
|
|
||
|
cisnienie.skurczowe
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
20
30
40
50
60
70
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
60
70
80
90
100
60
70
80
90
100
|
||
|
|
|
|
|
|
|
|
|| |
|
|
| |
|
|
|
|
|
|
|
|
||
|
||
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
||
|
|
|
|
|
|
||
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|||
|
|
|
|
|
|
|
||| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
cisnienie.rozkurczowe
Podstawy rachunku prawdopodobieństwa
27/34

Wykres słonecznikowy sunflowerplot()
0
1
2
3
4
5
0
1
2
3
4
5
zm1
zm2
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Podstawy rachunku prawdopodobieństwa
28/34
Transformacje zmiennych
●
●
● ● ●
●●●
●●●
●●
●●●
●●●●●
●
●●●●
●●●●
●●●
●●●
●
●
●●
●
●
●
●
● ●
●
●
●
●
−2
−1
0
1
2
0
5
10
15
Pierwiastkowa
norm quantiles
y
●
●
● ● ● ●●
●●●●●●
●●●
●●●●●●●●
●●●●●●
●●●
●●●
●
●
●●
●
●
●
●
●
●
●
●
●
●
−2
−1
0
1
2
0
20
40
60
Logarytmiczna
norm quantiles
y
●
●
● ●
● ●
●●
●
●
●●
●
●
●●●
●●●
●●●●●
●●●
●●●
●●●
●●
●
●●●
●
●
●
●
●
● ●
●
●
●
−2
−1
0
1
2
0.15
0.25
0.35
0.45
Odwrotna
norm quantiles
y
●
●
● ●
● ●●
●●●
●
●●
●●●
●
●●
●
●
●
●●
●●
●
●●
●●
●●
●
●
●
●●
●●
●●●
●● ●
● ●
●
●
−2
−1
0
1
2
−1.0
−0.5
0.0
0.5
1.0
Arcsin
norm quantiles
y
Podstawy rachunku prawdopodobieństwa
29/34
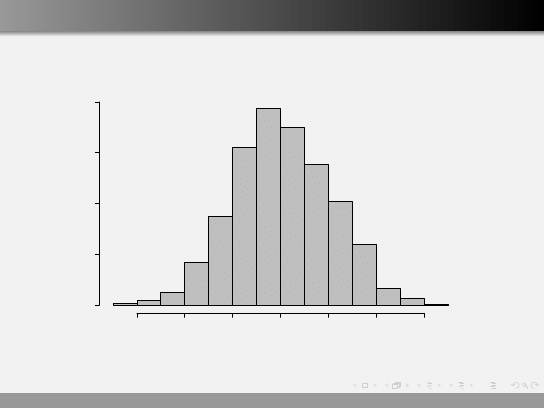
Transformacje zmiennych
Frequency
0
1
2
3
4
5
6
0
50
100
150
200
Podstawy rachunku prawdopodobieństwa
30/34
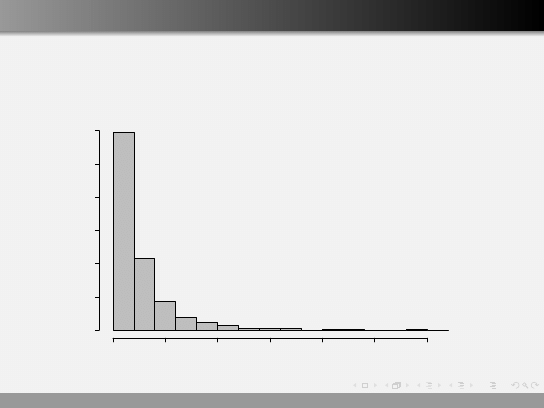
Transformacje logarytmiczna
Y = log(X )
Frequency
0
500
1000
1500
2000
2500
3000
0
100
200
300
400
500
600
Podstawy rachunku prawdopodobieństwa
31/34
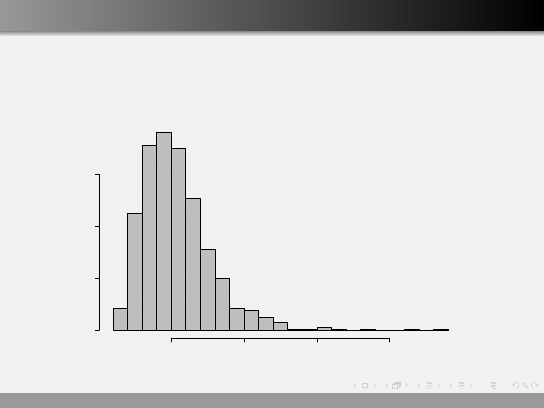
Transformacja odwrotna
Y = 1/X
Frequency
0.2
0.3
0.4
0.5
0
50
100
150
Podstawy rachunku prawdopodobieństwa
32/34

Popularne transformacje nieliniowe
Nazwa
Zmienna
przyjmuje
wartości dodatnie
Zmienna
przyjmuje
wartości nieujemne
Logarytmiczna
x
0
= log(x )
x
0
= log(x + 1)
Odwrotna
x
0
= 1/x
x
0
= 1/(x + 1)
Pierwiastkowa
x
0
=
√
x
x
0
=
√
x + 0.5
Arcsin
x
0
= arc sin(
√
x )
Podstawy rachunku prawdopodobieństwa
33/34

Co trzeba zapamiętać?
Jakimi statystykami możemy opisać zmienną jakościową?
Jakimi statystykami możemy opisać zmienną ilościową?
Jakimi statystykami możemy opisać pary zmiennych?
Jakie i kiedy transformacje stosować?
Podstawy rachunku prawdopodobieństwa
34/34
Wyszukiwarka
Podobne podstrony:
Metody opracowywania i prezentacji danych statystycznych
Metody graficznej prezentacji danych statystycznych
Planowanie zadań i metody ich obrazowania
instrumenty ochrony powietrza oraz metody ich wykorzystania
ZWIĄZKI REFRAKCYJNE I METODY ICH USUWANIA ZE ŚCIEKÓW, Technologia Wody i Ścieków
Autentyczność i zafałszowania produktów zbożowych i jaj oraz metody ich wykrywania(1)(1)(1)
PRZEMIANY CHEMICZNE ZANIECZYSZCZEŃ W TROPOSFERZE I METODY ICH OPISU W MODELACH(1)
3 Mechanizm powstawania odruchów warunkowych oraz metody ich badania
ćwiczenia rozluźniajace i metody naurofizjologiczne, Metody neurofizjologiczne - prezentacje
Obniľka cen towar˘w w zaleľnoci od przyj©tej metody ich ewidencji i wyceny, Wynagrodzenia za grudzi
Białka i metody ich oznaczania w mleku
bd 02 03 Hurtownie danych Ix
MADE(02) Transformacja danych
Środki konserwujące w zywności i metody ich oznaczania
kołaczek,bezpieczeństwo i ochrona danych, metody progowe
więcej podobnych podstron