Zastosowanie matematyki 

w finansach i  bankowości

Wykład 2

Procent składany

Zasady procentu 

składanego (1)

• Procent składany wykorzystywany jest w 

analizach inwestycji średnio- i długoterminowych 

• Warunki oprocentowania wymagają określenia: 

- stopy procentowej (jak dla procentu prostego) 
- okresu kapitalizacji (dodatkowo)

• Kapitalizacja ( i procent składany) oznacza 

wielokrotne dopisywanie odsetek do kapitału 
początkowego

Zasady procentu 

składanego (2)

• Kapitalizacja (k) najczęściej ma miejsce:

- co kwartał (k=4)
- co miesiąc (k=12)
- codziennie (k=360)

• Kapitał  końcowy  (FV)  przy  oprocentowaniu 

składanym  (r),  dla  kapitału  początkowego  (PV), 

okresu  oprocentowania  (n)  lat  i  liczby  kapitalizacji 

w roku (k) wyraża się wzorem:

)

(

)

1

(

n

k

k

r

PV

FV









Zasady procentu składanego 

(3)

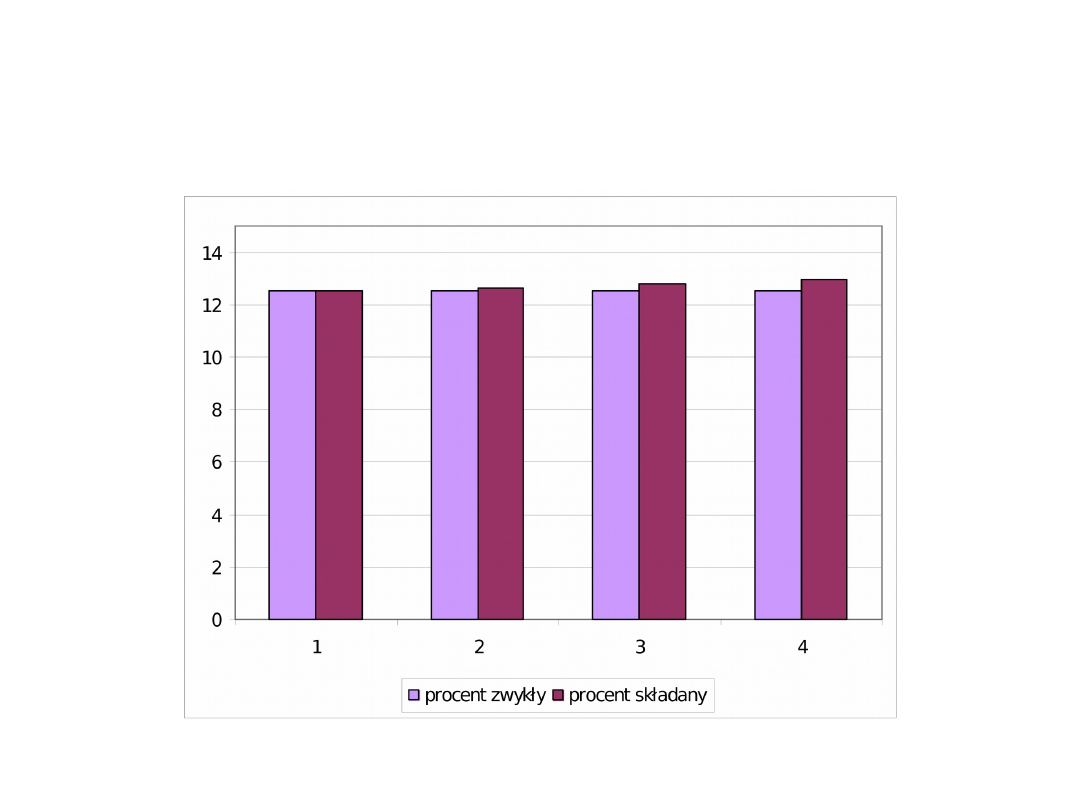
Przykład:
        Wylicz  kapitał  końcowy  lokaty  rocznej  przy 

kapitalizacji  kwartalnej,  stopie  5%  w  skali  roku  dla 
kapitału  początkowego  1000  zł.  Porównaj  wynik  z 
oprocentowaniem prostym.

Zasady procentu 

składanego (4)

Zasady procentu 

składanego (5)

    Okres oprocentowania (n), stopa procentowa (r), 

kapitał początkowy (PV) i końcowy (FV) są ze sobą 
ściśle powiązane. 

1





n

P

F

r

)

1

ln(

)

ln(

r

P

F

n





Zasady procentu 

składanego (6)

Przykład:
    Wpłacasz 1000 zł i chcesz wyjąć 1500 zł. Ile czasu 

musisz  trzymać  pieniądze  na  koncie,  jeśli  stopa 
procentowa wynosi 5% w skali roku, a kapitalizacja 
jest miesięczna.

41

.

0

)

5

.

1

ln(

)

1000

1500

ln(

)

ln(







P

F

0042

.

0

)

0042

.

1

ln(

)

12

/

05

,

0

1

ln(

)

1

ln(









 r

98

5

.

97

0042

.

0

41

.

0







n

16

.

8

12

98

'





n

)

1

ln(

)

ln(

r

P

F

n





Zasady procentu 

składanego (7)

Aby szybko sprawdzić, w jakim czasie 

kapitał początkowy podwoi swoją 
wartość można skorzystać z „reguły 
70”

(%)

70

r

n 

Zasady procentu 

składanego (8)

Przykład:
    Sprawdź, w ile lat podwoi się 1000zł, przy stopie 

5% i kapitalizacji rocznej. O ile lat podwajanie się 
przyspieszy, 

jeżeli 

kapitalizacja 

będzie 

miesięczna?

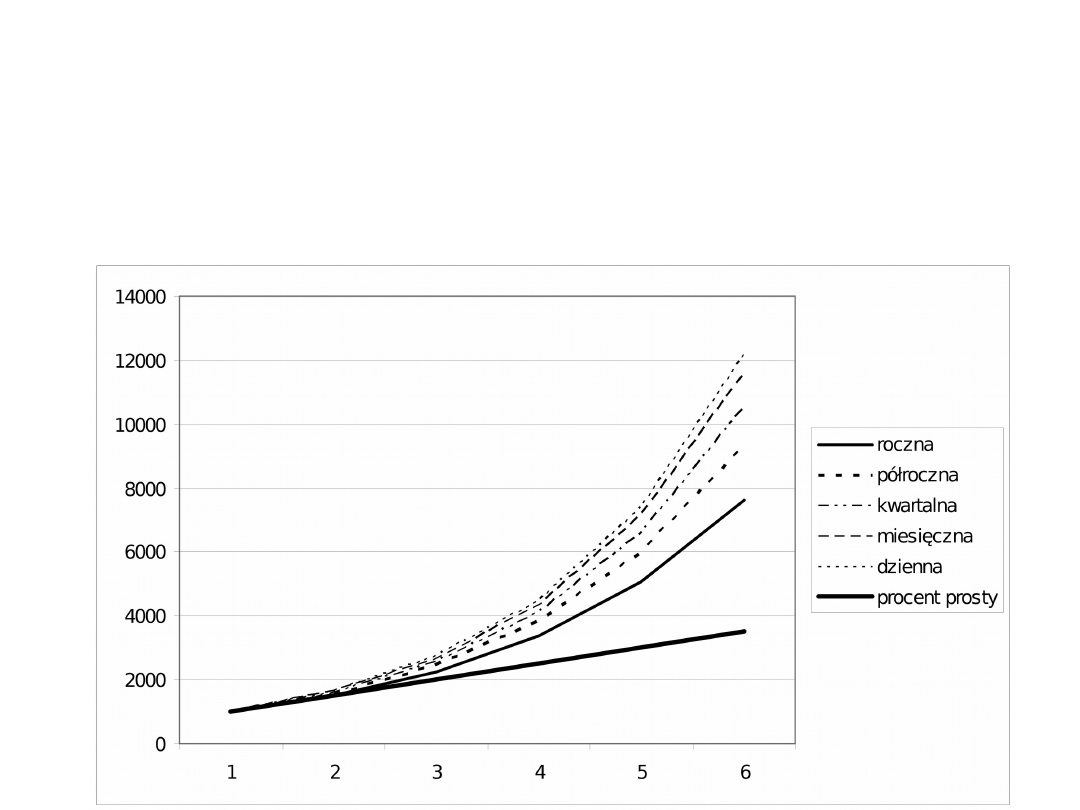
Kapitalizacja a odsetki

     Liczba kapitalizacji dodatnio wpływa na wysokość odsetek – im 

częściej odsetki dopisywane są do kapitału początkowego tym 
wyższy kapitał końcowy

Roczny czynnik 

oprocentowania (1)

        Wygodnym  narzędziem  w  wyznaczaniu  FV  jest 

roczny  czynnik  oprocentowania  (future  value 
interest  factor,  FVIF).  Wskazuje  on,  ilokrotnie 
rośnie  wartość  kapitału  początkowego  w  ciągu 
roku / okresu oprocentowania.

k

k

k

r

)

1

( 





n

k

PV

FV

)

(







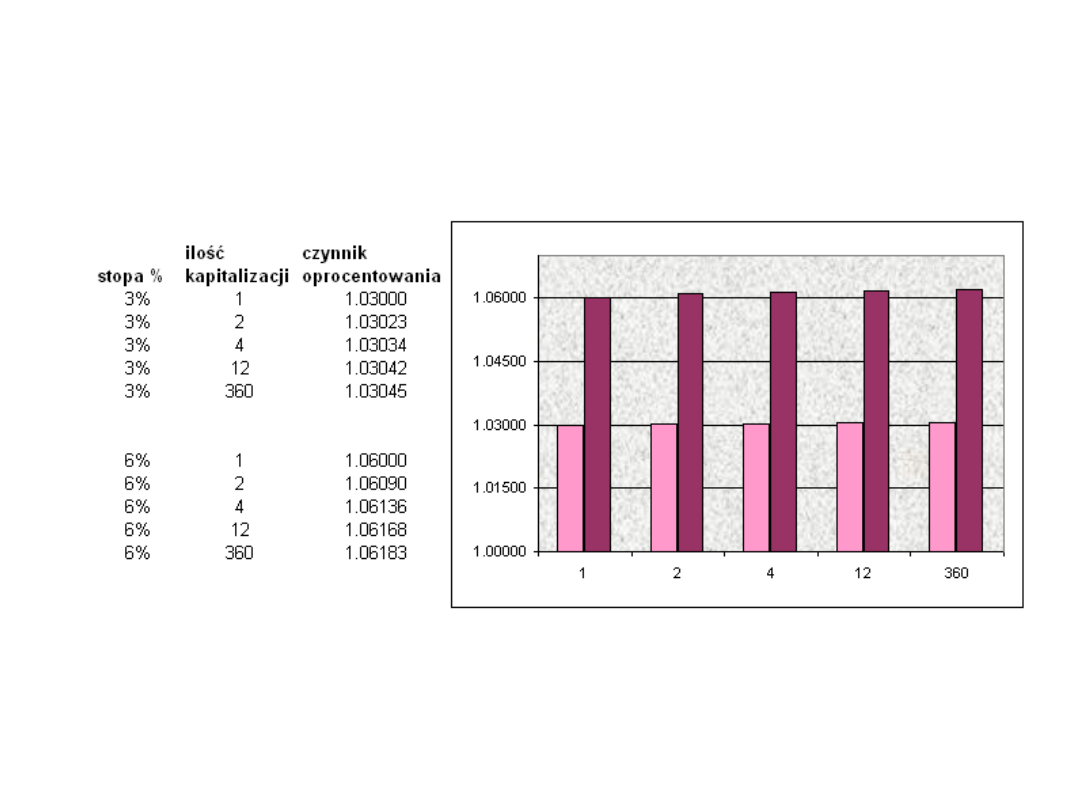
Roczny czynnik 

oprocentowania (2)

Roczny czynnik 

oprocentowania (3)

Przykład:
    Wyznacz kapitał końcowy za 3 lata dla stopy 6 %, 

kapitalizacji  co  miesiąc,  korzystając  z  czynników 
oprocentowania

Równoważność stóp procentowych 

(1)

- Aby stopy procentowe składane były 

równoważne, ich roczne czynniki oprocentowania 
muszą być równe

- Równoważność stóp procentowych zależy od 

dwóch parametrów: kapitalizacji oraz stopy 
nominalnej. 

- Równoważność nie zależy od kapitału 

początkowego ani czasu oprocentowania

Równoważność stóp procentowych 

(2)

Przykład:
       Sprawdź  – „na oko” lub obliczeniowo – 

równoważność par składanych stóp 
procentowych:

a) stopa kwartalna 3%, kapitalizacja kwartalna
b) stopa nominalna (roczna) 12%, kapitalizacja 

kwartalna

c) stopa nominalna (roczna) 11%, kapitalizacja 

miesięczna

d) stopa miesięczna 1%, kapitalizacja miesięczna

Równoważność stóp procentowych 

(3)

    Równoważność oprocentowania składanego i 

prostego

 obie stopy mogą być równoważne w określonym 

czasie n, ale już nie koniecznie w czasie n’.

 

 Z tego względu wyznacza się stopę efektywną

Stopa efektywna (1)

•

Stopa efektywna – wskazuje, o ile % zwiększa się 

wartość kapitału w ciągu jednego roku, uwzględniając 

liczbę kapitalizacji

•

Stopa efektywna wyraża się wzorem:

•

Jest to roczny czynnik oprocentowania minus 1

•

Gdy  stopy  efektywne  są  równe  to  występuje 

równoważność oprocentowania składanego

1

)

1

(







k

ef

k

r

r

Stopa efektywna (2)

Przykład
   Pan Kowalski ma lokatę oprocentowaną 6% w skali 

roku  z  kapitalizacją  miesięczną.  Zastanawia  się 
nad  inną  lokatą  –  oprocentowaną  6,5%  z 
kapitalizacją  półroczną.  Czy  opłaca  się  mu  taka 
zmiana?

Analiza procentu 

składanego (1)

Przykład:
        Jak  często  trzeba  kapitalizować  odsetki  przy 

nominalnej  stopie  11%,  aby  wartość  2-letnich 
odsetek  od  kwoty  3300  zł  wyniosła  przynajmniej 
820 zł?