Zastosowanie matematyki

w finansach i bankowości

Wykład 1

Procent prosty

Istnienie procentu

• Istnienie procentu oznacza, że wartość pieniądza

w czasie zmienia się

• W matematyce finansowej wykorzystuje się

procent prosty lub składany

• Analizując zmiany wartości pieniądza w czasie

należy brać pod uwagę: kapitał początkowy,

kapitał końcowy, czas oprocentowania, odsetki,

stopę procentową roczną, kapitalizację, stopę

podokresową

Zmiana procentowa cen

- Istnieje różnica pomiędzy zmianą o x %, a zmianą o

x p.p.

Przykład:
- Produkt A kosztował 20 zł i zdrożał o 25%. O ile zł

zdrożał produkt A?

- Produkt B kosztował 20 zł i zdrożał o 60 zł. O ile %

zdrożał produkt B?

- Jaka jest różnica w zmianach cen obu produktów?

Zasada oprocentowania

prostego

Zasada oprocentowania prostego
1) Procent za każdy okres dodawany jest do kapitału

początkowego

po

zakończeniu

czasu

oprocentowania

2) Procent należny za dany okres naliczany jest od

kapitału początkowego proporcjonalnie do trwania

tego okresu

• Procent prosty wykorzystywany jest w bankowych

transakcjach krótkoterminowych, w umowach

zawieranych poza sektorem bankowym, w

dyskoncie weksli i bonów skarbowych

Wartość przyszła pieniądza

• Znając wartość bieżącą pieniądza (PV) (kapitał

początkowy),

stopę

procentową

(r),

czas

odsetkowy (n) i metodę obliczeniową (tu procent
prosty) można wyznaczyć wartość przyszłą
pieniądza (FV).

)

1

(

n

r

PV

FV









Zasada oprocentowania

prostego

Przykład:
Jaką wartość osiągnie kapitał początkowy 300 zł po:
a) 2 miesiącach,
b) po 15 dniach.
Stopa procentowa wynosi 7% w skali roku,

oprocentowanie proste

Czas w matematyce finansowej

(1)

W matematyce finansowej problem czasu pojawia się

przy określeniu podokresowej stopy procentowej na

podstawie rocznej stopy procentowej.

Zwykle wykonuje się takie przeliczenia jak:
1) obliczenie liczby dni pomiędzy dwiema datami
2) zamiana liczby dni/tygodni na liczbę lat (część roku)

Wyróżnia się dwa czasy:
- Czas bankowy (360 dni)
- Czas kalendarzowy (365/366 dni)

Czas w matematyce finansowej

(2)

Obliczenie dokładnej liczby dni pomiędzy dwiema

datami jest różne w zależności od przyjętej metody

Dni wg czasu kalendarzowego > dni wg czasu

bankowego

Uwaga techniczna:
- Procent nie jest naliczany za dzień początkowy, za to

uwzględniany jest dzień końcowy, czyli za dzień
odsetkowy uważa się dzień np. wypłaty z konta,
spłaty raty kredytu etc.

Czas w matematyce finansowej

(3)

Przyjęcie typu przeliczeń dla liczby dni między

dwiema datami nie jest obojętne dla stron
transakcji finansowej:

- Dla wierzyciela (kredytodawcy) korzystniejsze jest

obliczenie dokładnej liczby dni wg czasu
kalendarzowego (na dłużej pożycza komuś
pieniądze)

- Dla dłużnika (kredytobiorcy) korzystniejsze jest

obliczenie liczby dni wg czasu bankowego (na
krócej pożycza od kogoś pieniądze)

Czas w matematyce finansowej

(4)

Zamiana liczby dni na część roku może odbywać się

także dwiema metodami:

- Dla wierzyciela (kredytodawcy) korzystniejsze jest

przeliczanie dni na lata wg czasu bankowego
(dzieli się przez mniejszą liczbę dni, więc część
roku jest dłuższa)

- Dla dłużnika (kredytobiorcy) korzystniejsze jest

przeliczanie dni na lata wg czasu kalendarzowego
(dzieli się przez większą liczbę dni, więc część
roku jest krótsza)

Czas w matematyce finansowej

(5)

Obliczanie liczby dni

pomiędzy dwiema datami

Przeliczanie liczby dni na

część roku

- na podstawie tabeli

numerów dni w roku (czas

kalendarzowy)

- arytmetyka liczby dni w

miesiącu względem 30

(czas bankowy)

- dzielenie liczby dni przez

365 (czas kalendarzowy)

- dzielenie liczby dni przez

360 (czas bankowy)

Czas w matematyce finansowej

(6)

Możliwe są cztery kombinacje czasów:

Bank gra rolę wierzyciela (kredytodawcy), a nie
dłużnika (instytucji przyjmującej lokaty)

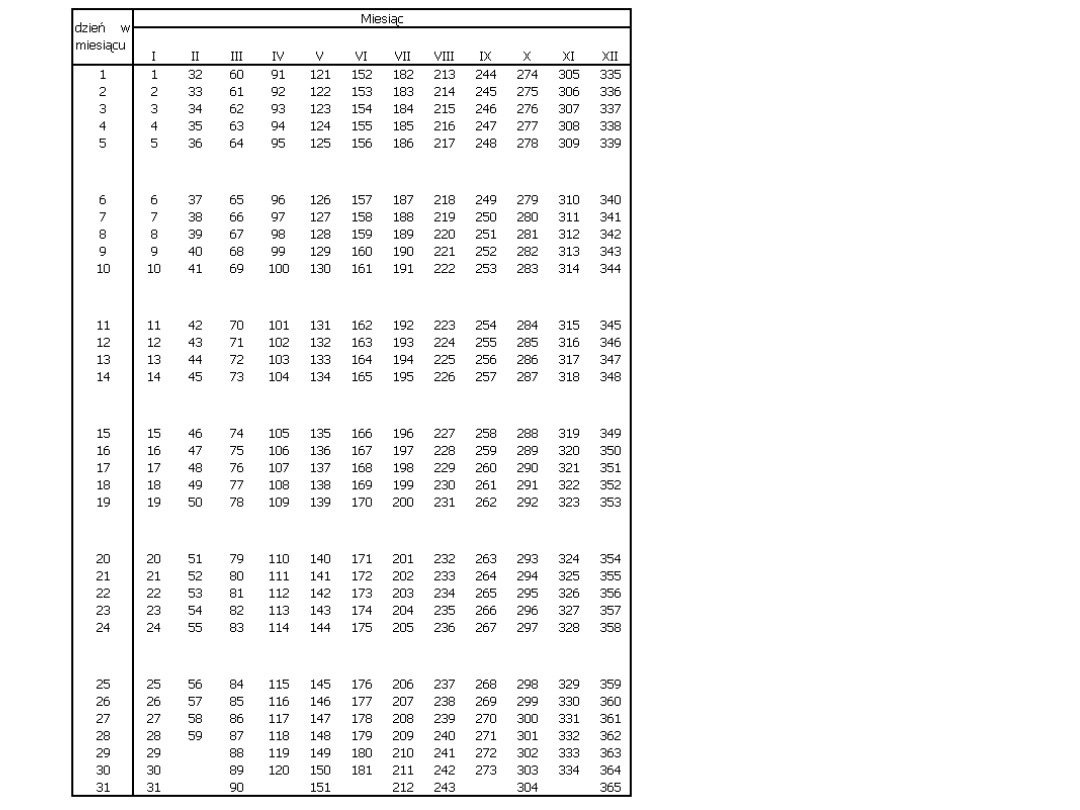
Tabela dni
miesiąca / roku

Czas w matematyce finansowej

(7)

Przykład:

Pan Nowak zaciągnął kredyt w wysokości 10 000

zł przy rocznej stopie 12% na okres od 7.04 do
15.11. Jakie odsetki zapłaci od kredytu w
zależności od metody obliczeniowej?

Zasada równoważności stóp

procentowych (1)

Zasada równoważności stóp procentowych –

stopy procentowe są równoważne, jeśli przy

każdej z nich dany kapitał początkowy generuje w

określonym czasie identyczne odsetki

 Stopy oprocentowania prostego są równoważne

wtedy i tylko wtedy, gdy są proporcjonalne

 Stopy podokresowe są proporcjonalne, gdy

stosunek ich wysokości jest taki, jak stosunek

odpowiadających im podokresów

Zasada równoważności stóp

procentowych (2)

Przykład:
Klient szukając oferty lokat otrzymał takie propozycje:

a) Lokata na 3 tygodnie na 1,5%*
b) Lokata na 2 miesiące na 2,4%
c) Lokata na 25 tygodni na 7%

Sprawdź, czy podane stopy procentowe są równoważne.

* Podane stopy % są podokresowe

Rozliczenia bankowe

Przykład:

Pan Nowak 31.03 miał na koncie bieżącym 1000

zł. Dnia 15.04 wpłacił 700 zł, dnia 19.04 wypłacił
150 zł, dnia 22.04 wpłacił 400 zł.

Wyznacz saldo na dzień 30.04, uwzględniając

miesięczne rozliczenie odsetek. Przyjmij, że
odsetki

naliczane

są

za

każdy

dzień.

Oprocentowanie rachunku w skali roku 3%.

Dyskonto i dyskontowanie

(1)

Dyskontowanie to obliczanie kapitału

początkowego na podstawie kapitału końcowego.
Jest to operacja przeciwna do oprocentowania.
Różnica pomiędzy kapitałem końcowym a
kapitałem początkowym to dyskonto (jest to
przeciwieństwo odsetek).

)

1

(

r

FV

PV





Dyskonto i dyskontowanie

(2)

Przykład:

Pan Kowalski chce mieć po trzech miesiącach

1000 zł na koncie. Stopa procentowa roczna
wynosi 5%. Ile musi wpłacić? Ile wynosi dyskonto?

Bony skarbowe

Bony skarbowe sprzedawane są z dyskontem

(tzn. są tańsze niż ich nominalna cena w dniu
wykupu.

Przykład:
Pan Kowalski kupił bon 26-tygodniowy o wartości

nominalnej 1000 zł za 952,10 zł. Oblicz stopę
rentowności (roczną) tej inwestycji. Wykorzystaj
czas bankowy.