Jak uczyć
rozwiązywania

zadań z treścią

Rozwiązujemy zadania, bo one
stanowią treść i sens matematyki



Wprowadzenie większości pojęć matematycznych,
odbywa się poprzez zadania tekstowe.



Uczeń klasy I –III ma opanować umiejętność
rozwiązywania najprostszych zadań tekstowych.



Większość sytuacji matematycznych,
np..wprowadzanie kolejnych liczb naturalnych,
obliczenia pieniężne, kalendarzowe i zegarowe
wiążą się
z sytuacjami opisanymi w formie zadań tekstowych.

Zadanie tekstowe



Składa się z sytuacji życiowej i warunków
matematycznych określonych za pomocą
wielkości danych i wielkości poszukiwanej
i powiązanych ze sobą takimi zależnościami
logicznymi, których ustalenie prowadzi do
odpowiedzi na główne pytanie w zadaniu.



/Zofia Cydzik/

Podział zadań ze względu na strukturę



Zadania poprawnie skonstruowane



W warstwie treściowej zawarte są wszystkie
niezbędne informacje do rozwiązania



Na drzewie siedziało 15 wróbli po 3 na gałęzi. Na
ilu gałęziach siedziały wróble?



Paweł ma 12 znaczków. Agata ma o 7 znaczków
więcej. Ile znaczków maja razem?

Podział zadań ze względu na strukturę

Zadania z niedoborem danych



Zadania nie można rozwiązać, gdyż informacje
w zadaniu nie wystarczają do znalezienia
odpowiedzi na pytanie.



Uczeń powinien m.in. wskazać, jakich danych
brakuje do rozwiązania

Paweł ma 12 znaczków. Agata ma o kilka znaczków

więcej. Ile znaczków maj razem?

Podział zadań ze względu na strukturę

Zadania ze zbyt dużą liczbą danych

niesprzecznych



Zadanie zawiera dane niemające znaczenia dla
rozwiązania zadania, wprowadzające tzw. „szum
informacyjny”.
Uczeń powinien m.in. wskazać zbędne dane.



Paweł ma 12 znaczków. Agata ma o 7 znaczków
więcej, a Kasia o 2 mniej niż Paweł i o 9 mniej niż
Agata. Ile znaczków ma Kasia?

Podział zadań ze względu na strukturę

Zadania z danymi wzajemnie sprzecznymi



Zadania nie można rozwiązać. Uczeń powinien
dostrzec sprzeczność miedzy danymi w zadaniu
i wskazać sposób poprawienia konstrukcji
zadania.

Janek ma 12 znaczków. Agata ma o 7 znaczków

więcej, a Kasia o 4 mniej niż Agata i o 8 więcej niż
Paweł.
Ile znaczków ma Kasia?

Podział zadań ze względu na strukturę

Zadania otwarte



Zadania, w których odpowiedź nie jest jednoznaczna
lub istnieje kilka rozwiązań poprawnych



Janek ma 12 znaczków, Agata ma o 7 znaczków
więcej, a Kasia ma mniej niż Agata, ale więcej niż
Paweł. Ile znaczków ma Kasia?



Władek miał 50 zł i kupił zeszyty za 22 zł. Resztę
otrzymał w monetach o wartości 2 zł i 5 zł. Ile
otrzymał monet każdego rodzaju?

Podział zadań ze względu na złożoność
konstrukcyjną:



zadania proste, zadania złożone łańcuchowo

i właściwe zadania złożone

Zadania proste
Odpowiadający im model matematyczny zawiera tylko

jedno działanie arytmetyczne wiążące niewiadomą
z dwiema danymi liczbami, np.

Na talerzu leżał 12 jabłek. Dzieci zjadły 7 jabłek.

Ile jabłek zostało?

Model matematyczny przyjmuje postać działania: 12-7 =

Podział zadań ze względu na złożoność
konstrukcyjną:

Zadania złożone łańcuchowo

Dają się w naturalny sposób rozłożyć na ciąg zadań

prostych, tak że liczba znaleziona jako wartość niewiadomej

jednego zadania prostego staje się daną do następnego

zadania w łańcuchu.



W sklepie było 8 skrzynek, a w każdej po 10 kg jabłek.

Szkoła zakupiła 25 kg jabłek. Ile kg jabłek zostało w

sklepie?



Najpierw należy obliczyć wagę jabłek będących w sklepie, a

następnie od otrzymanej wartości odjąć masę sprzedanych

jabłek. Rozwiązanie można zapisać w postaci dwóch działań:

8 x 10 kg = 80 kg

80 kg – 25 kg = 55 kg



Rozwiązanie tego zadania można przedstawić w postaci

jednego zapisu: 8 x1 0 kg – 25 kg = 55kg



Zadania złożone łańcuchowo można zilustrować grafem

Podział zadań ze względu na złożoność
konstrukcyjną:

Właściwe zadania złożone
charakteryzują się tym, że co najmniej dwa warunki

zadania określają związki między niewiadomymi, np.

Do sklepu przywieziono jabłka i gruszki, razem 27 kg
owoców. Jabłek było 2 razy więcej niż gruszek.
Ile kilogramów gruszek przywieziono do sklepu?

Niewiadomymi w zadaniu są ilości przywiezionych do

sklepu jabłek – j i gruszek – g, choć polecenie
dotyczy tylko jabłek. Zależności można zapisać w
postaci dwóch równań: j + g =27 oraz 2 x g = j

Układ ten jest naturalnym modelem matematycznym

Podział zadań ze względu na formę
zadania:



statyczne i dynamiczne



W początkowej fazie kształcenia staramy się aby
z treści zadania wynikało działanie, które należy wykonać,
aby rozwiązać zadanie.
Mówimy o takich zadaniach,

że mają charakter dynamiczny

,

są opisem pewnej akcji.
Używa się zwrotów, takich jak:

dołożyć, zabrać, przynieść,

dojść, zwiększyć

itp.

Na talerzu leżało 7 jabłek.
Mama dołożyła jeszcze 6 jabłek.

Ile jabłek jest na talerzu?

Podział zadań ze względu na formę zadania:

statyczne i dynamiczne



W dalszej fazie kształcenia pojawiają się zadania

statyczne,

opisujące sytuacje bez akcji, tym

samym nie sugerują one operacji matematycznej,
którą należy wykonać

W wazonie były tulipany i róże, razem 15

kwiatów. Tulipanów było 7.
Ile róż było w wazonie?

Inne podziały zdań tekstowych,
np. ze względu na:



treść: realne i fikcyjne,



dane: problemowe i bezproblemowe,



układ danych w tekście: arytmetyczne
i algebraiczne,



sposób rozwiązania: typowe (rozwiązanie jednym
ze znanych sposobów) i nietypowe (do których nie
daje się zastosować żaden z poznanych wcześniej
sposobów

rozwiązania),



problemy związane z treścią: zamknięte ( z
jednym lub wieloma rozwiązaniami) i otwarte
(problemy matematyczne w nich zawarte nie są do
końca określone i pozwalają na swobodę przy ich
rozwiązywaniu).

Układanie zadań tekstowych przez
uczniów



Aby opanować umiejętność rozwiązywania zadań
tekstowych, trzeba znać i rozumieć ich strukturę.

Nauczyć się tego można układając zdania.



Umiejętność tę uczniowie powinni zdobywać
równolegle z poznawaniem sztuki rozwiązywania
zadań.



Umiejętność układania zadań można kształtować
na wiele sposobów

Układanie zadań analogicznych do
danych z wykorzystaniem tych samych
liczb lub działań



Układanie zadań analogicznych do zadania, czyli

przekształcanie zadania, dotyczy zmiany treści zadania bez

zmiany liczb

i sposobu rozwiązania.

Np. Uczniowie rozwiązują na lekcji zadanie:

Na talerzu leżało 6 jabłek i 3 gruszki.

Ile owoców leżało na talerzu?

Podczas rozwiązywania ustalono, że w zadaniu dane są liczby 6

(jabłka ) i 3 (gruszki), natomiast aby odpowiedzieć na pytanie,

należy wykonać dodawanie: 6+3 =

W analogiczny sposób można rozwiązać wiele zadań. Uczeń

powinien dobrze to zrozumieć, dlatego proponujemy ułożenie

zadań z tymi samymi danymi – liczbami i o tym samym

sposobie rozwiązania – działaniem 6 + 3

Ułóżcie zadanie z tymi samymi liczbami, które można rozwiązać

w taki sam sposób, ale o innej treści. Mogą to być zadania

o zbieraniu kasztanów, kupowaniu ołówków…

Układanie zadań z rozsypanki



Jednym ze sposobów poznawania struktury zadania
tekstowego mogą być sytuacje, w których dziecko
otrzymuje tekst zadania w postaci tekstu pociętego
na fragmenty, najlepiej jednakowej wielkości
(na paskach papieru tej samej długości), by nie
sugerować mechanicznego układania, lecz
zastanowienia się nad treścią, konstrukcją zadania.

Ania kupiła 12 kwiatków. Poukładała je do wazonów

tak, aby w każdym wazonie było tyle samo kwiatów.
Ile kwiatów było w każdym wazonie?

Układanie zadań do konkretnej sytuacji
związanej z czynnościami



Układając zadania, sugerujemy uczniom odwołanie się
do znanych im sytuacji z życia codziennego, podając
tematykę i nie ograniczając zakresu działań, które
trzeba będzie wykonać podczas rozwiązywania.
Można to zrobić, dając polecenie: ułóżcie zadanie o:

kupowaniu zeszytów, liczeniu jabłek, samochodach na

parkingu…

Takie zadanie może być poprzedzone rozmową na

dany temat, czy wcześniej odbyta wycieczką.
Można wykorzystać tematy omawiane wcześniej
w ramach edukacji polonistycznej lub środowiskowej.

Układanie zadań do ilustracji



Podstawą jest ilustracja, mniej lub bardziej
naturalistyczna, która powinna sugerować pewne
działania matematyczne. Do poniższego rysunku
(przedstawia 5 papug i poniżej 3 strusie)

można ułożyć wiele zadań.



Przykłady zadań:

W ZOO było 5 papug i 3 strusie.
Ile ptaków było razem?



W ZOO jest 5 papug i 3 strusie.
O ile więcej jest papug niż strusi?



W ZOO jest 8 ptaków. Jest 5 ptaków, a reszta to
strusie. Ile jest strusi?

Układanie zadań do działania



Układając zadania do działania, należy zwracać

uwagę na kolejność pojawiania się w treści zadania

informacji liczbowych zgodnie z występowaniem

tych liczb

w działaniu, choć czasem może to sprawiać pewną

trudność.



Ułóż zadanie, które można rozwiązać za pomocą

działania: 24 + 8 : 4 =

W koszyku były 24 jabłka, a 8 jabłek było

rozłożonych po tyle samo na 4 talerzykach. Mama

dołożyła do koszyka jabłka z jednego talerzyka.

Ile jabłek jest teraz w koszyku?

Układanie zadań do sytuacji ogólnej, gdy
trzeba wybrać pewne elementy np. kupowanie
z cennikiem



Układanie zadań do sytuacji ogólnej, gdy trzeba wybrać
pewne elementy spośród podanych wymaga od dziecka
wyobraźni i umiejętności przewidywania. Można założyć, że
układając zadanie z cennikiem, dziecko nie będzie ograniczać
wyboru kupowanych przedmiotów ani wartości zakupów.



Cennik: zeszyt 3 zł, pisaki 12 zł, gumka 1 zł, linijka 4 zł,
ołówek 2 zł długopis 8 zł



Korzystając z cennika, ułóżcie zadanie o kupowaniu, mogą
powstać zadania typu:



Janek kupił linijkę, dwa zeszyty i długopis. Ile zapłacił za
zakupy? Co jest droższe linijka i ołówek czy zeszyt i długopis?



Można określić ile Janek miał pieniędzy na zakupy np.. 20 zł

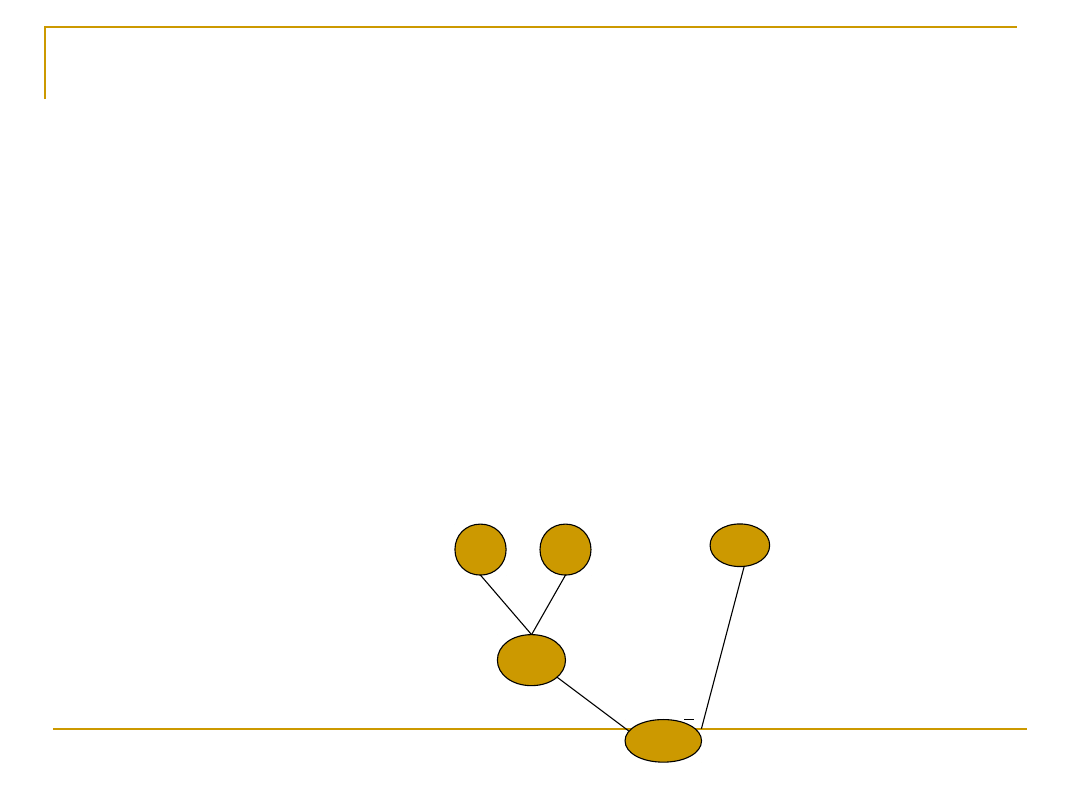
Układanie zadań do schematu



Wiele zadań tekstowych podczas rozwiązywania
ilustruje się schematami, np. grafem, drzewkiem,
tabelką lub na osi liczbowej.



Warto, aby uczniowie próbowali również
przekładać schematy na zadania tekstowe.
Czasem będzie to konkretny graf a czasem może
to być tylko przedstawienie działań bez liczb, co
wymaga od dziecka wyobraźni.