1

Podstawowe charakterystyki

• Miary tendencji centralnej
 Średnie
 Modalna
 Mediana

ZAGADNIENIA OMAWIANE NA 
ĆWICZENIACH

2

• Miary zróżnicowania (dyspersji)
Wariancja
Odchylenie standardowe
Współczynnik zmienności
• Miary asymetrii
Skośność
•Miary skupienia
Kurtoza
• Błąd standardowy
Zadania do wykonania

3

Główne działy statystyki opisowej

1.

Kompleksowa analiza struktury zbiorowości,

2.

Analiza korelacji i regresji,

3.

Analiza  dynamiki  zjawisk  (badanie  szeregów  czasowych, 
tendencji rozwojowej).

Kompleksowa 

analiza 

struktury 

zbiorowości 

powinna 

doprowadzić 

do 

zwięzłego 

przedstawienia 

ogólnej 

charakterystyki  istotnych  właściwości  badanej  zbiorowości. 
Parametry  tak  charakteryzują  zbiorowość,  że  porównanie 
różnych  zbiorowości  statystycznych  można  sprowadzić  do  ich 
porównań. Podstawowe zadania tych parametrów opisowych to :

•

  określenie  przeciętnego  rozmiaru  i  rozmieszczenia  wartości 
zmiennej. Dokonujemy tego przez obliczenie miar położenia.

•

  określenie  granic  obszaru  zmienności  wartości  zmiennej. 
Dokonujemy tego przez obliczenie miar zmienności.

•

  określenie  skupienia  i  spłaszczenia  (w  stosunku  do  kształtu 
krzywej  normalnej)  oraz  stopnia  zmiany  od  idealnej  symetrii. 
Dokonujemy tego przez obliczenie miar asymetrii i koncentracji.

STATYSTYKA OPISOWA

4

Kompleksowa analiza struktury 

zbiorowości c.d.

Wszystkie miary (parametry), którymi się posługujemy w kompleksowej analizie 

struktury zbiorowości można podzielić na dwie zasadnicze grupy:

• miary klasyczne,
• miary pozycyjne.

Miary klasyczne są wypadkową ze wszystkich wartości cechy badanej (pomiarów).
Budowa ich jest oparta na momentach statystycznych (zwykłych i centralnych).

Miary pozycyjne są wyznaczone na podstawie pozycji w szeregu statystycznym 

niektórych

jednostek lub grup jednostek. Miary te z jednej strony stanowią uzupełnienie miar
klasycznych a z drugiej – umożliwiają przeprowadzenia analizy struktury w sytuacji, 

gdy nie

jest możliwe obliczenie średniej arytmetycznej lub gdy nie ma ona wartości 

poznawczej

(otwarte przedziały klasowe, silna lub skrajna asymetria, silne zróżnicowanie i
niejednorodność zbiorowości).

5

 Miary tendencji centralnej

Miary średnie

Średnia arytmetyczna jest najlepszą miarą charakteryzującą rozkład cechy i 
dlatego  jest  miarą  najczęściej  używaną.  Obliczanie  jej  opiera  się  na 
wszystkich  obserwacjach  i  ma  ogromne  znaczenie  teoretyczne  i  praktyczne. 
Jedyną  poważniejszą  jej  wadą  jest  to,  że  duży  wpływ  na  nią  wywierają 
najmniejsza  i  największa  wartość  badanego  szeregu,  czyli  tzw.  skrajne 
wartości cechy. 

 

dla szeregów prostych, gdy dane nie są uporządkowane, wyraża się wzorem

Wzór:

Dodać  wszystkie  wartości  danych  (x)  i  podzielić  przez  ich  liczbę

x

i

 – wartość badanej cechy i-tej jednostki statystycznej,

N – liczba badanych jednostek statystycznych.

PRZYKŁAD 1:

Obliczyć średni wzrost mężczyzn (10 elementów)

x1 = 168 x2 = 178

x3 = 171

x4 = 185

x5 =180

x6 = 171 x7 = 179

x8 =183

x9 =180

x10 =175

168+178+171+185+180+171+179+183+180+175 = 1770
1770 10 = 177

___

1

n

i

i

N

x

x







6

• dla szeregu rozdzielczego – jeżeli w wyniku odpowiedniego grupowania 

danych nieuporządkowanych w szereg rozdzielczy w postaci:

Wzór:

n

i

 – liczebność i-tego przedziału klasowego (suma  ni równa się N)

    – środek i-tego przedziału klasowego

Średnią oblicza się jako sumę iloczynów liczności (n

i

) klas mnożonych przez 

środki klas x

i

(średnia cząstkowa podzielona przez liczność wyrazów (N) w całym szeregu.

PRZYKŁAD 2

Średnia arytmetyczna jest miarą prawidłową tylko dla zbiorowości 

jednorodnych, tj. o

Umiarkowanym zróżnicowaniu wartości cechy zmiennej. W rozkładach 

asymetrycznych,

silnie zróżnicowanych, bimodalnych i wielomodalnych średnia arytmetyczna 

traci wartość

poznawczą. Średniej arytmetycznej nie można obliczyć dla szeregu o otwartych
przedziałach klasowych. Średnia arytmetyczna jest momentem zwykłym rzędu 

pierwszego.









n

i

i

i

x

n

N

x

1

1

x

i

7

Średnia arytmetyczna ważona

• Gdy liczebność w obrębie dwóch (lub więcej) prób jest jednakowa, to 

średnia obliczona z prób, tzw. średnia ogólna równa się sumie 
średnich prób podzielonej przez liczbę grup, czyli równa się średniej 
arytmetycznej średnich grupowych.

W przypadku gdy liczebność w obrębie prób nie jest jednakowa, to 

wówczas średnia ogólna

jest średnią arytmetyczną ważoną, którą obliczamy w następujący 

sposób. Średnią dla

każdej grupy (tzw. średnią próby, cząstkową) mnożymy przez liczebność, 

zwaną również

„wagą”. Iloczyny należy dodać i sumę podzielić przez liczebność 

zbiorowości (N).

8

Średnią geometryczną oblicza się wówczas, gdy wyniki w trakcie badań 

zmieniają się w

postępie geometrycznym i gdy zjawiska ujmowane są dynamicznie (np. średnie 

tempo

zmian). Średniej tej nie stosuje się, gdy mamy wartości ujemne lub równe zeru.

Wzór:

gdzie x

i

 >0

(∏ oznacza iloczyn x

1

, x

2

, x

3 

… x

n

)

Średnia geometryczna:
•

obliczana na podstawie wszystkich danych szeregu,

•

wartości skrajne mają na nią mniejszy wpływ niż na średnią 

arytmetyczną,

•

jest mniejsza lub równa średniej arytmetycznej,

•

istnieje dla xi > 0,

•

jest pomocna przy obliczaniu średnich wskaźników

•

ma szerokie zastosowanie w badaniach serologicznych, gdzie 

wprowadzono pojęcie „miana” .

i

n

n

i

x

G







1

9

Średnia harmoniczna jest odwrotnością średniej arytmetycznej – 

stosujemy gdy dane są 

podane jako odwrotność np. zużycie paliwa na jednostkę, wydajność na 

godzinę.

Wzór:

gdzie x

i

 0

Średnia harmoniczna:
•

obliczana na podstawie wszystkich danych szeregu,

•

nadaje się do przekształceń algebraicznych,

•

jest mniejsze lub równe średniej arytmetycznej, przy czym równość 
zachodzi tylko dla identycznych wszystkich wartości.







n

i

i

x

N

H

1

1

10

Modalna (moda, dominanta, typowa)

To  taka  wartość  badanej  cechy  statystycznej,  której  odpowiada  największa 

liczebność.

Oznaczona jest symbolem M

o

.  Należy do pozycyjnych miar średnich.

Sposób wyznaczania dominanty dla szeregu prostego

1.

uporządkować szereg rosnąco (czasami malejąco),

2.

podsumować jednostki, które maja tę samą wartość.

3.

Dominantą będzie wartość występująca najczęściej.

 

 Liczebność (% lub 

liczby 
rzeczywist
e

Wartość badanej cechy 

(cecha 
mierzalna

Dominanta

wartość

11

W szeregach szczegółowych i

 

rozdzielczych jest to wartość cechy, której 

odpowiada największa liczebność. Można, więc łatwo określić przedział, 

w którym modalna występuje.

Wzór:

gdzie  x

o

 – dolna granica przedziału, w którym występuje modalna,

n

m

 – liczebność przedziału modalnej,

n

m-1

 – liczebność klasy poprzedzającej przedział modalnej,

n

m+1

 – liczebność klasy następującej po przedziale modalnej,

k

m

 – rozpiętość przedziału klasowego modalnej.

 



 



1

1

1

*

m

m

o

o

m

m

m

m

m

n n

x

k

M

n n

n n



















12

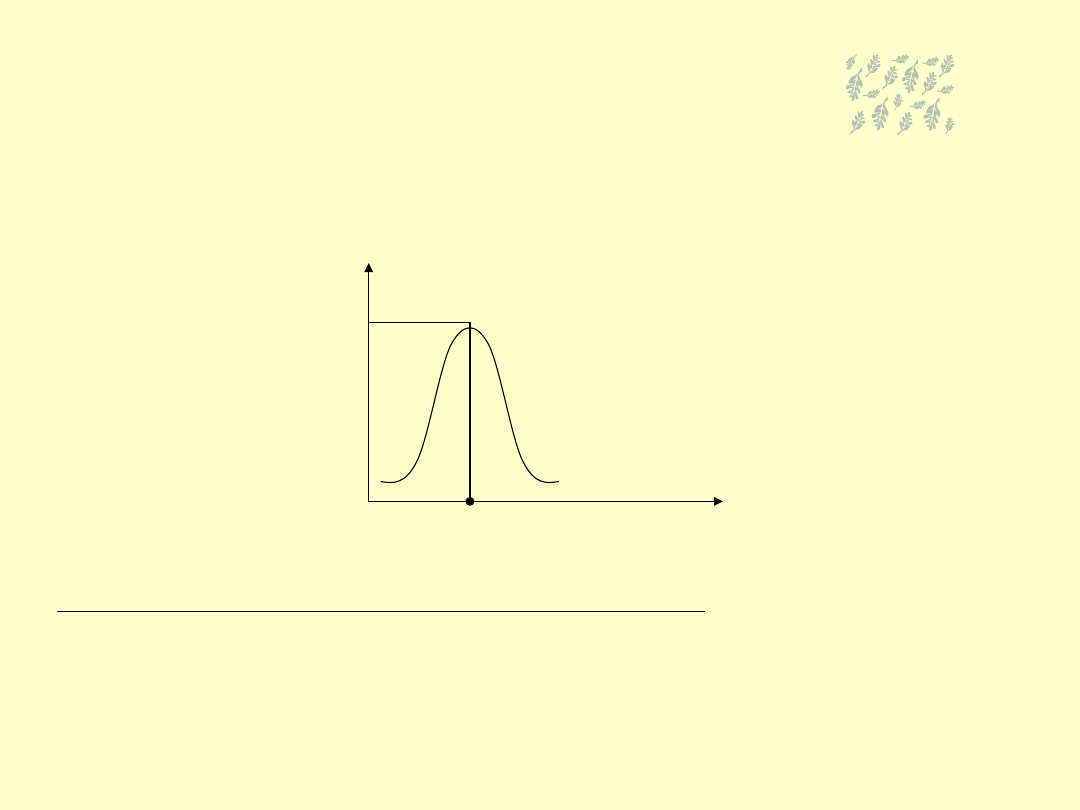
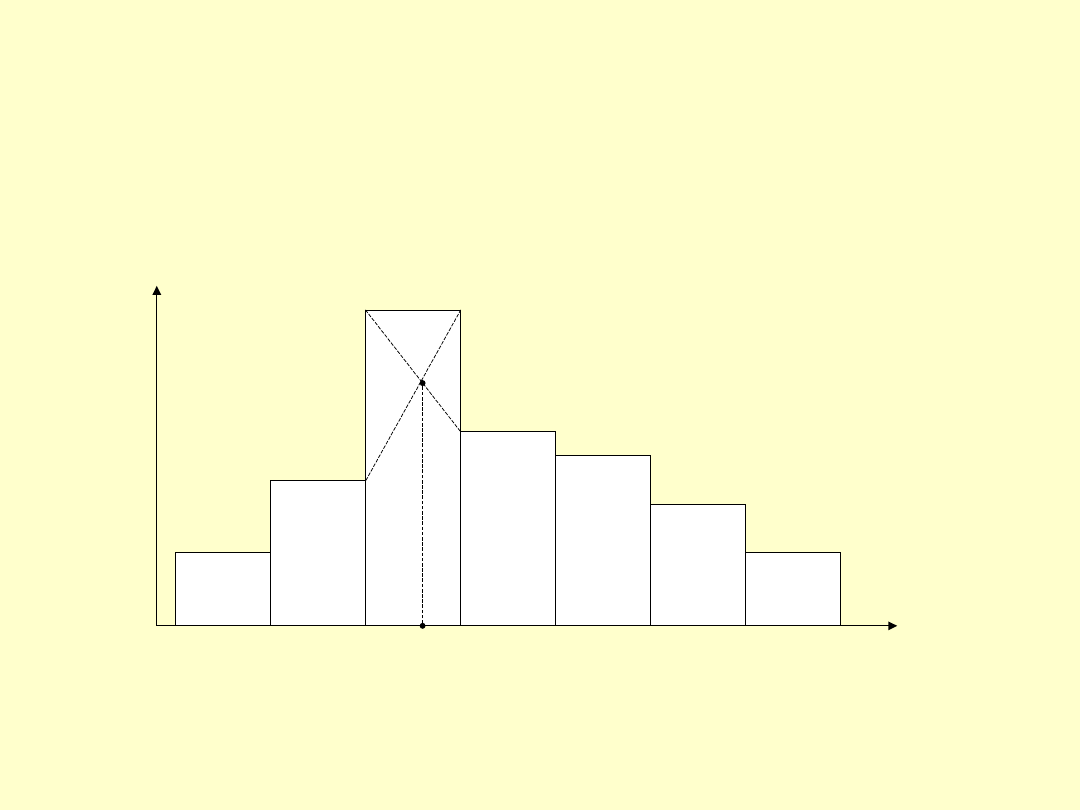
Dominantę z szeregu rozdzielczego można w przybliżeniu wyznaczyć 

także w sposób graficzny.

Dominanta

x

n

13

Znalezienie klasy o największej liczebności nie jest sprawą trudną, określona 
jest  przez  wyraźny  punkt  –  szczyt  reprezentujący  największą  liczbę 
obserwacji. Jeśli histogram ma 2,  3 lub więcej szczytów, to mówimy, że jest 
bimodalny, trimodalny lub wielomodalny itd. To świadczy o niejednorodności 
badanej zbiorowości.

Przykład 3

W  tabeli  umieszczono  liczbę  pacjentów  pogrupowanych  według  czasu 
działania pewnego leku.

Liczymy  modalną.  Jak  wynika  z  tabeli  –  modalna  znajduje  się  w  czwartym 
przedziale.

Arkusz programu 

Microsoft Excel

Arkusz programu 

Microsoft Excel



 



81 39

23

*5 25,386

81 39

81 35

o

M



 









14

Mediana (symbole: Me, M, me)

Wartość  środkowa  –  mediana  (jeśli  uporządkujemy  posiadane  wartości 
rosnąco lub malejąco i wybierzemy wartość środkową)

 Mediana  dzieli  uporządkowany  szereg  liczbowy  na  połowę,  jest  więc  to 

wartość  środkowa  szeregu  (kwartyl  drugi)  Jest  to  taka  liczba,  od  której 
połowa jednostek szeregu statystycznego jest mniejsza a druga większa.

  Wyznaczenie  Me  musi  poprzedzić  ustalenie  jej  pozycji.  Jest  to  przedział, 

dla  którego  liczebność  skumulowana  jest  mniejsza  lub  równa  liczbie  n/2 
(gdzie n to liczebność zbiorowości.

Wzór:

 

 

 

gdzie: m – numer klasy, w której występuje Me,

x

m

 – dolna granica tej klasy,

n

m

 – liczebność tej klasy,

k

m

 – rozpiętość tej klasy

 – liczebność skumulowana do przedziału poprzedzającego klasę, w 

której występuje      Me.

1

1

2

m

m

e

m

i

i

m

n

k

x

n

M

n

























1

1

m

i

i

n







15

Mediana obok średniej arytmetycznej jest najczęściej stosowanym 
parametrem statystycznym. Wartość mediany nie zależy od wartości 
krańcowych. Możemy ją wyznaczać nawet wtedy, gdy nie wszystkie 
obserwacje są dokładnie znane, np. z szeregów, w których występują nie 
zamknięte przedziały klasowe. Mediana wysuwa się na czoło w zastosowaniu 
do wszystkich wzrokowo uchwytnych, a trudno mierzalnych wielkości. 
Mediany używamy również do analizy cech jakościowych.

 Przykład 

Wykorzystując dane z poprzedniego przykładu obliczyć medianę.

Me = 23 + 5/81 * [201/2-72] = 24,759

Oznacza  to,  że  dla  połowy  pacjentów  czas  działania  leku  nie  przekracza  24,75 

minut i dla takiej samej liczby pacjentów nie mniejszy od tej wartości. 

Sposób wyznaczania mediany dla szeregu prostego

•

uporządkować dane w sposób rosnący,

•

zauważyć (przeliczyć) czy liczba obserwacji jest parzysta czy nieparzysta

Jeżeli szereg jest nieparzysty wartość mediany stanowi wartość cechy wyrazu środkowego

168, 178, 171, 185, 180, 171, 179, 183, 180, 175, 186

168, 171, 171, 175, 178,  179,  180, 180, 183, 185, 186

Me = 179

Jeżeli szereg jest parzysty są dwa wyrazy środkowe a medianę stanowi średnia arytmetyczna 

wartości badanej cechy wyznaczona z obu wyrazów środkowych

159, 168, 171, 171, 175, 178, 179, 180, 180, 183, 185, 186

Me = (178+179)  2 = 178,5  179

16

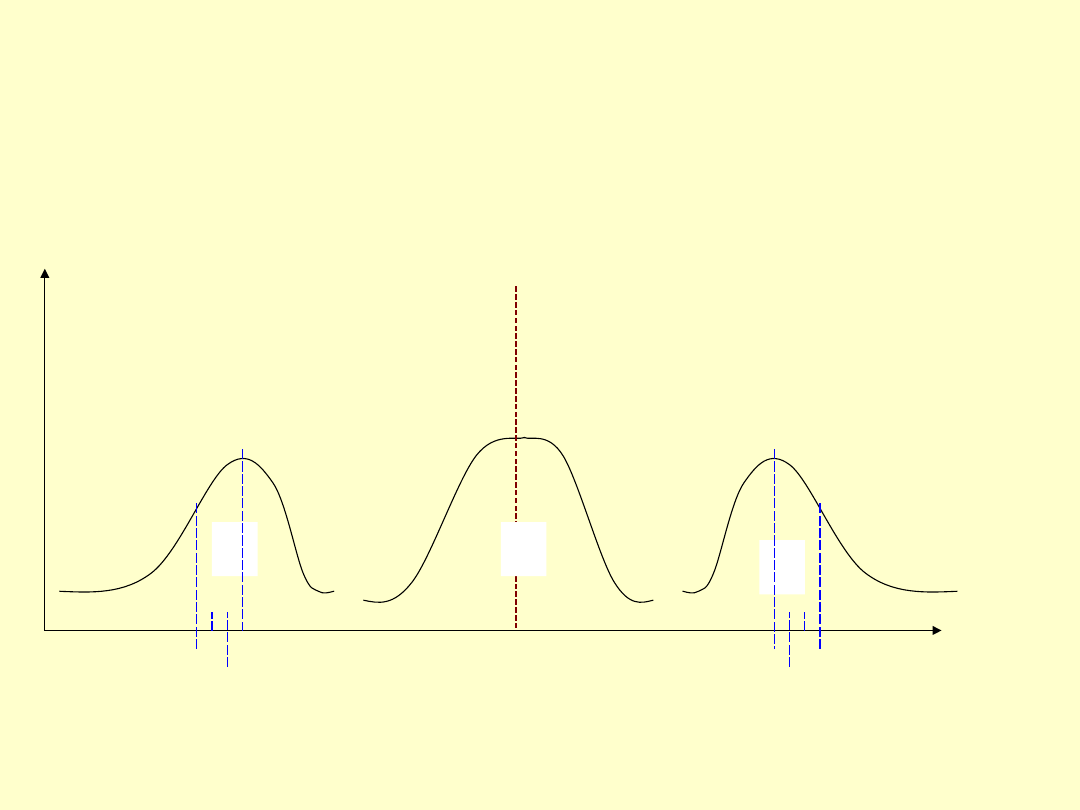
Wzajemne położenie średniej, dominanty i mediany 

w rozkładzie

b

a

c

        x

 n

i

D

D

Me

średnia

średnia

Me

17

Do pozycyjnych miar średnich zalicza się kwantyle i dominantę. 

Kwantylami nazywamy wartości cechy badanej zbiorowości, które 

dzielą uporządkowaną (według rosnących wartości cechy 

statystycznej) zbiorowość na określone części pod względem liczby 

jednostek. Wśród kwantyli wyróżnia się:

• kwartyle (dzielą zbiorowość na 4 części), 

• kwintyle (dzielą zbiorowość na 5 części), 

• decyle (dzielą zbiorowość na 10 części),

• centyle lub percentyle (dzielą zbiorowość na 100 części).

• Najpowszechniej stosowanymi kwantylami są kwartyle:

• Pierwszy kwartyl – Q1 to taka wartość badanej cechy, która dzieli 

populację na dwie części w sposób następujący – 25% jednostek 

statystycznych jeszcze tej wartości nie osiągnęło a pozostałe 75% 

tę wartość przekroczyło.

• Drugi kwartyl – Q2 – Me (mediana) to taka wartość badanej 

cechy, która dzieli populację na połowy, inaczej mówiąc jest to 

wartość środkowa. W medianie połowa populacji jeszcze nie 

osiągnęła wartości badanej cechy a druga połowa już tę wartość 

przekroczyła.

• Trzeci kwartyl – Q3 to taka wartość badanej cechy, której 75% 

liczebności jeszcze nie osiągnęło tej wielkości a 25% ją 

przekroczyło.

18

 Miary rozproszenia (zmienności)

Najprostszą miarą jest odchylenie średnie (przeciętne) do jego wyliczenia 
dodajemy do siebie wartości bezwzględne różnic między kolejnymi pomiarami 
i średnią a następnie dzielimy sumę tych różnic przez liczbę pomiarów.

Najpowszechniej 

używaną 

miarą 

rozproszenia 

jest 

odchylenie 

standardowe, jest ono większe od odchylenia przeciętnego, gdyż na nie mają 
większy wpływ wartości skrajne, tzn. bardzo odbiegające od średniej; dlatego 
odchylenie  średnie  bywa  lepsza  miarą  rozproszenia  niż  odchylenie 
standardowe.

Teoretycznie miarą odchylenia jest wariancja, a odchylenie standardowe jest 
jej  pierwiastkiem.  Do  obliczania  odchylenia  wykorzystujemy  wszystkie  dane, 
to znaczy wszystkie wartości zarejestrowane w trakcie pomiarów.

Wariancją zmiennej X nazywamy średnią arytmetyczną kwadratów odchyleń 
poszczególnych  wartości  zmiennej  od  średniej  arytmetycznej  całej 
zbiorowości:

Wzór:

 

 

Wariancja jest momentem centralnym rzędu drugiego. Miara ta nie ma 
interpretacji, ponieważ jej miano nie jest zgodne z mianem badanej cechy. W 
związku z tym do oceny wykorzystuje się odchylenie standardowe.

2

__

2

1

1

n

i

i

N

x x

s























19

Pierwiastek 

kwadratowy 

z 

wariancji 

zwany 

jest 

odchyleniem 

standardowym i określony jest wzorem:

 

  

Gdzie: 

        

- suma kwadratów odchyleń

        

- suma kwadratów tych pomiarów

        

- kwadrat sumy pomiarów

    N 

- elementy zbioru

ODCHYLENIE 

STANDARDOWE 

jest 

miarą 

bezwzględną, 

czyli 

mianowaną,  wyrażoną  w  takich samych jednostkach jak  badana  cecha (np. 
zarobki w zł, waga w kg).

2

1

x

s

N











2

2

2

X

x

X

N











2

x



2

X







2

X



20

Współczynnik zmienności

Za pomocą tego współczynnika można porównywać zmienność 

pomiarów różniących się średnią, na przykład zmienność 

osobników z gatunków różniących się wymiarami.

 

Wzór:

jeżeli:
• Vx  35%

to średnia jest „bardzo dobra” (bardzo dobrze opisuje badaną 

rzeczywistość),

• 35%  Vx  68%

to średnia jest „dobra”,

• 68%  Vx  75%

to średnia jest „do przyjęcia”,

• Vx > 75%

to średnia traci swój sens poznawczy.

Współczynnik zmienności służy do porównywania różnych cech jednej zbiorowości 
lub jednej cechy w różnych zbiorowościach. Określa on siłę zróżnicowania 
(dyspersji). Im większe wartości tego współczynnika, tym zbiorowość statystyczna 
jest mniej jednorodna z punktu widzenia danej cechy i jednocześnie tym jest 
większe uzasadnienie dla stosowania pozycyjnych miar dyspersji oraz pozycyjnych 
miar średnich.

100





x

V

x

x



__

s

CV

X



21

Jeśli  rozkład  danej  cechy  jest  jednomodalny  i  symetryczny,  to  średnia  i 
odchylenia  są  w  zasadzie  wystarczającymi  charakterystykami  tego 
rozkładu.  Jeśli  natomiast  nie  jest  on  symetryczny,  czyli  średnia  nie 
pokrywa się z medianą, to nazywamy go asymetrycznym:

     Lewostronnie, jeśli mediana jest większa od średniej
     Prawostronnie, jeśli mediana jest mniejsza od średniej

• Miary asymetrii

Są  sytuacje,  w  których  badanie  średniego  poziomu  zmiennej  i 
rozproszenia  jej  wartości  nie  wskazuje  na  istnienie  różnic  między 
badanymi zbiorowościami. Obserwacja zaś rozkładów tych cech wyklucza 
podobieństwo rozważanych zbiorowości.

 

Przykład 5 

Badano czas reakcji na lek w trzech grupach 100-osobowych. W tabeli są 
umieszczone dane.

Oblicz średnią arytmetyczną i wariancje.

22

Wynik: oba te parametry są jednakowe dla wszystkich grup i wynoszą:

X = 35, s

2

 = 120

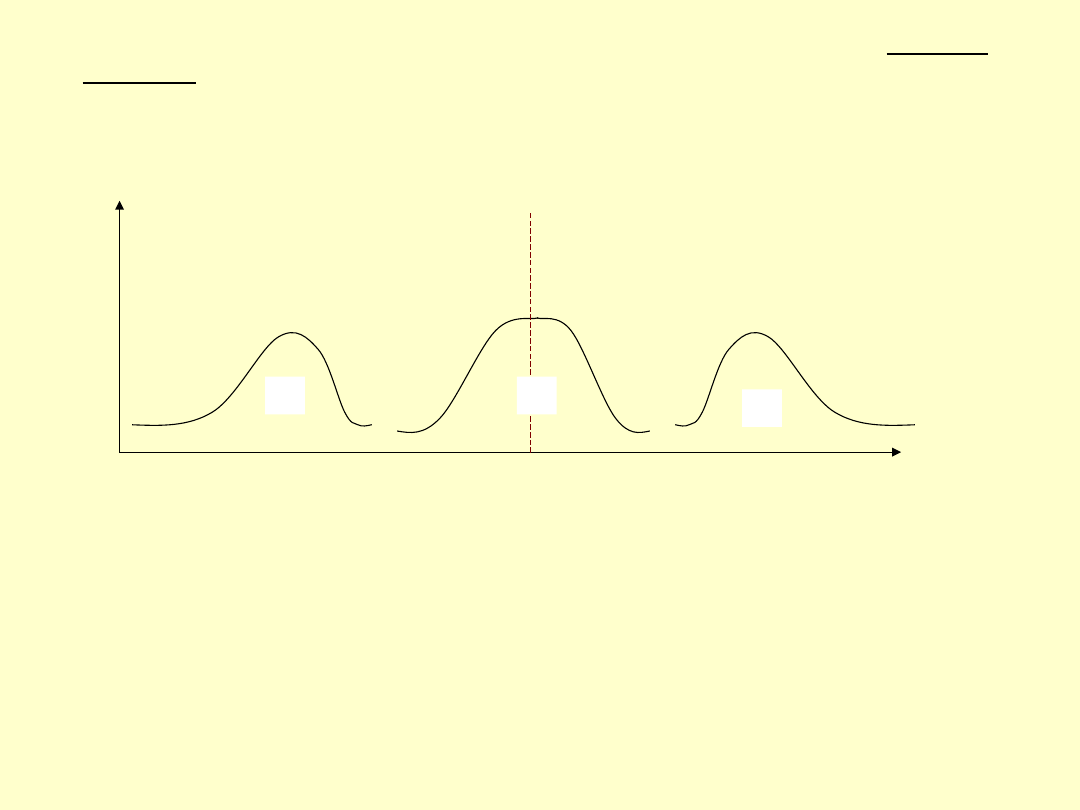
Mimo to występują różnice – widać to wyraźnie na histogramach. 

Wnioski:  w  grupie  2  u  większości  osób  czas  reakcji  na  lek  jest  niższy  od 
przeciętnego, natomiast w grupie trzeciej u większości osób czas reakcji na 
lek  jest  wyższy  od  przeciętnego.  Związane  jest  to  oczywiście  z  asymetrią 
rozkładu. 

Asymetrię  można  określić  porównując  średnią  arytmetyczną  z  medianą  i 
modalną.

Można wyróżnić trzy przypadki:

X  = Me = Mo – dla rozkładu symetrycznego

X  > Me > Mo – dla rozkładu o asymetrii prawostronnej

X  < Me < Mo – dla rozkładu o asymetrii lewostronnej

23

Dla  określenia  odchylenia  od  symetrii  rozkładu  stosuje  się  mierniki 
asymetrii.  Typowym  przykładem  jest  parametr  nazywany  skośnością 
rozkładu.  Przyjmuje  on  wartości  ujemne  dla  rozkładu  asymetrycznego 
lewostronnie,  dodatnie  dla  rozkładu  asymetrycznego  prawostronnie, 
natomiast dla rozkładów symetrycznych jest równa zero. Jeśli s (skośność) 
< 0,3 to uważamy asymetrię za nieznaczną.

b – rozkład symetryczny (osią symetrii byłaby rzędna)

a, c – rozkłady asymetryczne; a – ma asymetrię lewostronną, c – asymetrię prawostronną 

Kiedy stosować średnią a kiedy inne wskaźniki?

Istnieje prosta reguła.

     Jeśli rozkład jest jednomodalny i względnie symetryczny – stosujemy 

średnią;

      Jeśli  rozkład  jest  jednomodalny,  ale  niesymetryczny  –  stosujemy 

medianę;

     Jeśli rozkład jest wielomodalny– stosujemy modalną;

b

a

c

cecha

liczebnoś

ć

24

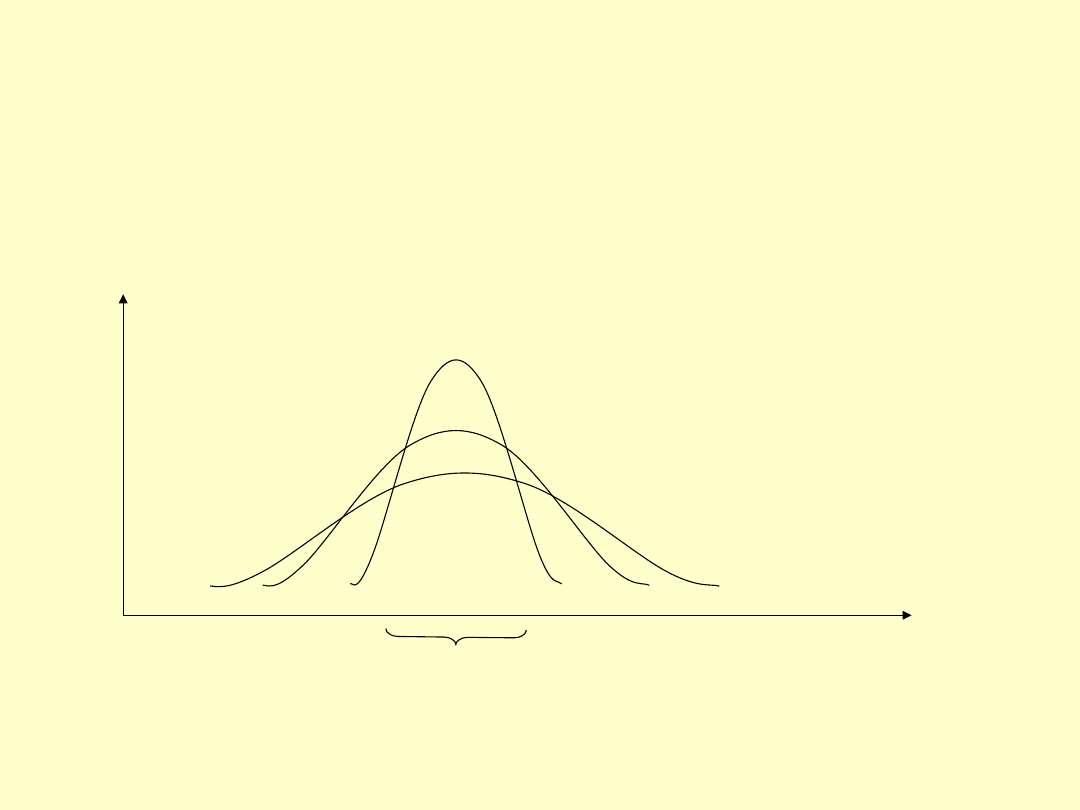
Miary spłaszczenia 

(koncentracji wokół średniej)

a

b

c

Największa 

koncentr

acja

Im bardziej układ wysmukły, tym 

mniejsze rozproszenie

25

Opis struktury zjawisk może być dokonany z punktu 

widzenia skupienia, które jest rozumiane jako skupienie 

jednostek zbiorowości wokół wartości średniej. Tak 

określona koncentrację nazywa się kurtozą.

Koncentracja (kurtoza) wartości zmiennej odnosi się tylko do 
rozkładów symetrycznych lub co najwyżej słabo 
asymetrycznych.

 

Za taki typowy punkt odniesienia przyjęto rozkład normalny. 
Jeżeli dla pewnego rozkładu skupienie wartości zmiennej 
wokół średniej jest większe niż w rozkładzie normalnym, to 
taki rozkład nazywamy wysmukłym (leptokurtycznym). 
Natomiast gdy skupienie wartości zmiennej wokół średniej 
jest mniejsze niż w rozkładzie normalnym, to taki rozkład 
nazywamy spłaszczonym (platokurtycznym). 

26

    Błąd standardowy [standard error of the mean]

Określony jest wzorem:

Błąd  standardowy  (SEM)  wskazuje  na  prawdopodobną  odległość  uzyskanej 
średniej od rzeczywistej średniej populacyjnej.

Wielkość  SEM  jest  zależna  od  liczebności  badanej  grupy,  dlatego  w  dużych 
grupach SEM jest zwykle mniejsze. 

SEM jako taki jest trudny do interpetacji. Ze względu na mniejszą wartość od 
odchylenia  standardowego  często  jest  wykorzystywany  do  prezentacji 
wyników,  które  "stają  się"  przez  to  ładniejsze.  Poprawia  to  samopoczucie 
badacza i ma "wywierać" dobre wrażenie na pozostałych. 

Uważa  się,  że  jeśli  obok  średniej  podano  SEM  wówczas  powinna  znaleźć  się 
również liczba przypadków, np. średnia wielkość lewej komory w rozkurczu 47 
mm,  SEM  ±  7  mm,  liczba  przebadanych  9.  SEM  odpowiada  ilorazowi  SD  i 
pierwiastka z liczby przypadków. 

Wynik  W  opisanym  przykładzie  SD  jest  więc  równy  21  mm.  O  ileż  mniej 
"atrakcyjny"  jest  wynik  47  ±  21  mm  (średnia±SD)  niż  47±7  mm 
(średnia±SEM).

Zadania do wykonania

 

*

N





