Kod uzupełnień do dwóch

Kod uzupełnień do dwóch (w skrócie
U2) jest obecnie najpopularniejszym
sposobem zapisu liczb całkowitych na
bitach. Jego popularność wynika z
faktu, że operacje dodawania i
odejmowania są w nim wykonywane
tak samo jak dla liczb binarnych bez
znaku. Z tego też powodu oszczędza
się na kodach rozkazów procesora.

Zapis liczb

W dwójkowym systemie liczbowym
najstarszy bit liczby n-cyfrowej ma wagę
2n–1. Jedyną różnicą, jaką wprowadza tu
kod U2, jest zmiana wagi tego bitu na
przeciwną (–2n–1). Bit ten jest nazywany
bitem znaku, ponieważ świadczy o znaku
całej liczby – jeśli jest ustawiony (=1) cała
liczba jest ujemna, jeśli jest skasowany
(=0) – liczba jest dodatnia lub równa 0.

STAŁOPOZYCYJ NA REPREZENTACJ A LICZB

STAŁOPOZYCYJ NA REPREZENTACJ A LICZB

(kod U2)

(kod U2)

W zapisie U2 (uzupełnień do 2) liczbę binarną można
przedstawić jako:

a

n-1

...a

0

= -a

n-1

.

2

n-1

+a

n-2

.

2

n-2

+

...

+a

0

.

2

0

Najstarszy bit nie jest tylko bitem znaku ale niesie wraz ze
swoją wagą wartość ujemną

W zapisie

W zapisie

U2

U2

(uzupełnień do 2) liczbę binarną można

(uzupełnień do 2) liczbę binarną można

przedstawić jako:

przedstawić jako:

a

a

n

n

-

-

1

1

...a

...a

0

0

=

=

-

-

a

a

n

n

-

-

1

1

.

.

2

2

n

n

-

-

1

1

+

+

a

a

n

n

-

-

2

2

.

.

2

2

n

n

-

-

2

2

+

+

...

...

+a

+a

0

0

.

.

2

2

0

0

Najstarszy bit nie jest tylko bitem znaku ale niesie wraz ze

Najstarszy bit nie jest tylko bitem znaku ale niesie wraz ze

swoją wagą wartość ujemną

swoją wagą wartość ujemną

1101

1101

U2

U2

=

=

-

-

1

1

.

.

2

2

3

3

+1

+1

.

.

2

2

2

2

+0

+0

.

.

2

2

1

1

+1

+1

.

.

2

2

0

0

=

=

-

-

8+4+1 =

8+4+1 =

-

-

3

3

D

D

0111

0111

U2

U2

=

=

-

-

0

0

.

.

2

2

3

3

+1

+1

.

.

2

2

2

2

+1

+1

.

.

2

2

1

1

+1

+1

.

.

2

2

0

0

=

=

4+2+1 = 7

4+2+1 = 7

D

D

Ponieważ: a

Ponieważ: a

-

-

b=a+(

b=a+(

-

-

b);

b);

-

-

a+b=(

a+b=(

-

-

a)+b;

a)+b;

-

-

a

a

-

-

b=(

b=(

-

-

a)+(

a)+(

-

-

b) to korzystnie jest

b) to korzystnie jest

stosować liczbę przeciwną (oznaczanej symbolem ~) do danej

stosować liczbę przeciwną (oznaczanej symbolem ~) do danej

~0111

~0111

U2

U2

1000

1000

+ 1

+ 1

1001

1001

U2

U2

negacja wszystkich bitów i dodanie 1

negacja wszystkich bitów i dodanie 1

-

-

7

7

D

D

7

7

D

D

Kod uzupełnień do 2 zyskał swoją popularność

dzięki prostym zasadom przeprowadzania
operacji

arytmetycznych. Dodawanie i odejmowanie w
systemie

U2 jest analogiczne do wykonywania działań w
zwykłym

systemie dwójkowym. Pojawiające się
przeniesienia

poza bit znaku możemy zwyczajnie
zignorować. Oto

przykład:

00111001

+ 11110011

00101100

Reprezentacja liczb
rzeczywistych

Liczby rzeczywiste mają część całkowitą i ułamkową;
można je przedstawić:

•

         

W postaci kodu stałoprzecinkowego (stałopozycyjnego)

•

         

W postaci kodu zmiennoprzecinkowego

(zmiennopozycyjnego)
Nie jest możliwe przedstawienie nieskończonych zbiorów za
pomocą skończonej liczby bitów. Do obliczeń w komputerach
stosuje się reprezentację skończonych podzbiorów liczb
rzeczywistych.
Zgodne jest to ze standardem

IEEE - 754

, gdzie określony

został standard zapisu i działań arytmetycznych na liczbach
zmiennoprzecinkowych

ZAPIS UŁAMKÓW

Aby umożliwić zapis liczb ułamkowych, musimy rozszerzyć wagi

pozycji w stronę ujemnych potęg podstawy. Część ułamkową

oddzielimy od części całkowitej zapisu za pomocą znaku przecinka.

wagi

p

n-1

p

2

p

1

p

0

p

-1

p

-2

p

-m

cyfry

c

n-1

...

c

2

c

1

c

0

, c

-1

c

-2

...

c

-m

n cyfr

m cyfr

Obliczenie wartości tak zapisanej liczby prowadzimy według

zasady

c

n-1

...c

2

c

1

c

0

,c

-1

c

-2

...c

-m

= c

-m

p

-m

+ ... + c

-2

p

-2

+ c

-1

p

-1

+ c

0

p

0

+ c

1

p

1

+ c

2

p

2

+

... + c

n-1

p

n-1

c

n-1

c

n-2

...c

2

c

1

c

0

, c

-1

c

-2

...c

-m

=

n-1

i=-m

c

i

p

i

PRZYKŁAD:

Obliczyć wartość liczby stałoprzecinkowej 245,133 zapisanej w systemie

pozycyjnym o podstawie p = 6.

245,133

(6)

= 3 x 6

-3

+ 3 x 6

-2

+ 1 x 6

-1

+ 5 x 6

0

+ 4 x 6

1

+ 2 x 6

2

245,133

(6)

= 3 x 1/216 + 3 x 1/36 + 1 x 1/6 + 5 x 1+ 4 x 6 + 2 x 32

245,133

(6)

=

3

/

216

+

3

/

36

+

1

/

6

+ 5 + 24 + 64

245,133

(6)

=

1

/

72

+

1

/

12

+

1

/

6

+ 5 + 24 + 64

245,133

(6)

=

(1 + 6 + 12)

/

72

+ 93

245,133

(6)

= 93

19

/

72

= 93,263888888888...

(10)

Zapis stałoprzecinkowy

Zapis stałoprzecinkowy

Załóżmy , że dla zapisu liczby dysponujemy ośmioma bitami.

W zapisie stałoprzecinkowym liczbę zapisujemy w kodzie

znak- moduł, więc najstarszy bit będzie bitem znaku.

Pozostałe bity wykorzystujemy w następujący sposób:

o       dwa najmłodsze bity stanowią część ułamkową

(umowa)

o       pozostałe bity część całkowitą.

PRZYKŁAD

011111,11

(2)

=31,75

(10)

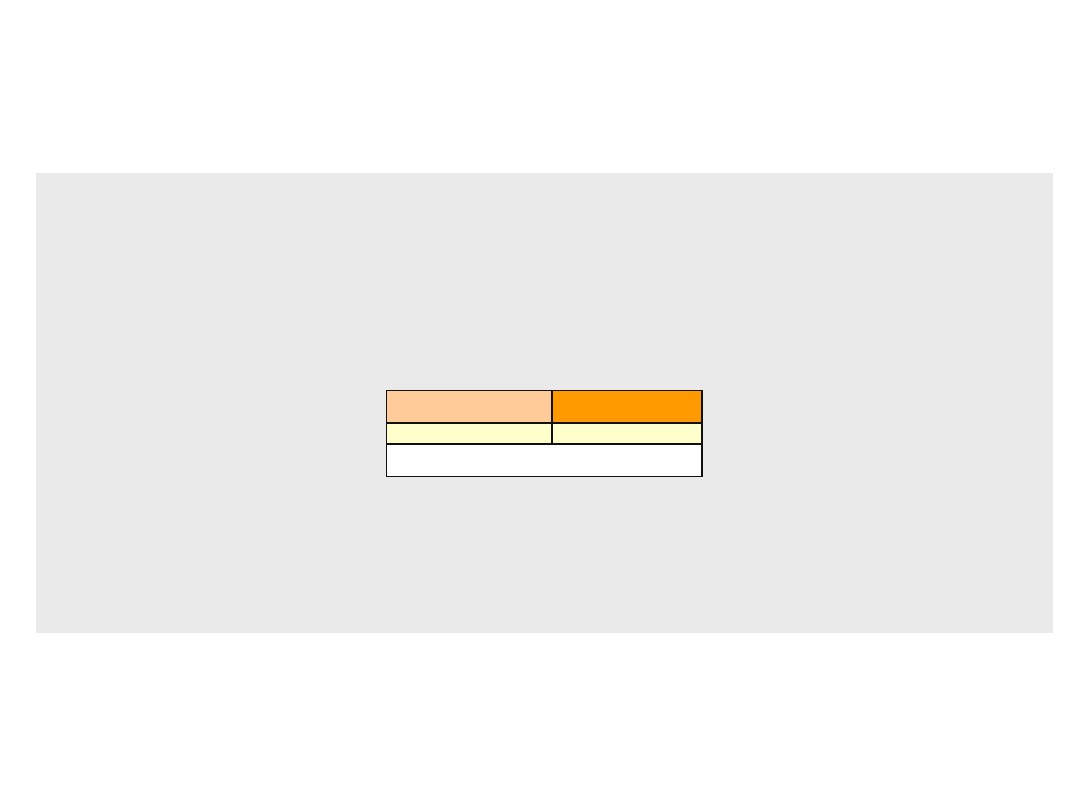
Dwójkowy system zmiennoprzecinkowy

Dwójkowa liczba zmiennoprzecinkowa zbudowana jest z dwóch części: z

mantysy m i wykładnika potęgowego e (zwanego również cechą). Ponieważ

podstawa systemu liczenia jest znana i wynosi 2, więc nie ma potrzeby

umieszczać jej w zapisie liczby. Mantysa m jest liczbą stałoprzecinkową na

moduł mniejszą od 1. Wykładnik e jest liczbą całkowitą. Obie części mogą być

zapisane np. w kodzie U2 lub kodzie Z-M.

wykładnik e

mantysa m

n-bitów

m-bitów

liczba zmiennoprzecinkowa

Wartość liczby liczymy wg poznanego wcześniej wzoru:

w = m x 2

e

Przykład

00110111

(ZP)

= ...?

(10)

Najpierw wydobywamy z liczby wykładnik e i mantysę m:

0011

e

0111

m

Teraz obliczamy kolejno wartość wykładnika i mantysy:

e

=

0011

(U2)

=

0

x -8 +

0

x 4 +

1

x 2 +

1

x 1

e

=

0011

(U2)

= 2 + 1

e

=

0011

(U2)

= 3

(10)

m

=

0

,

111

(U2)

= - 0 +

1

/

2

+

1

/

4

+

1

/

8

m

=

0

,

111

(U2)

=

1

/

2

+

1

/

4

+

1

/

8

m

=

0

,

111

(U2)

=

4

/

8

+

2

/

8

+

1

/

8

m

=

0

,

111

(U2)

=

7

/

8

Mając wykładnik i mantysę mogę podstawić je do wzoru i obliczyć wartość

liczby:

w =

m

x 2

e

w =

7

/

8

x 2

3

w =

7

/

8

x

8

w = 7, więc ostatecznie:

00110111

(ZP)

= 7

(10)