Ekonomiczny, a rzeczywisty

wiek rębności, na przykładzie

nadleśnictwa Brzeziny

Piotr Popielarz

Sławomir

Wygnał

Rzeczywisty wiek rębności – wiek, w

którym drzewostan danego gatunku
powinien być przeznaczony do wyrębu (do
użytkowania rębnego). W drzewostanach
mieszanych wiek rębności dostosowuje się
do gatunku panującego.

Ekonomiczny wiek rębności - stan

drzewostanu najbardziej pożądany z punktu
widzenia założonego celu gospodarczego
[Klocek, Rutkowski 1986]. Oznacza to, że
wiek rębności powinien być traktowany jako
jeden z czynników zapewniających
maksymalną realizację celu prowadzonej
działalności gospodarczej

wieku rębności drzewostanów

sosnowych jako typowy problem
inwestycyjny, którego celem jest
maksymali− zacja dochodu netto
uzyskiwanego w ramach produkcji
drewna, tj. właściwy moment
wycięcia drzewostanu umożliwia
uzyskanie maksymalnego czystego
dochodu z tytułu upłynnienia kapi−
tału zgromadzonego w zapasie
rosnącym.

Wartość drzewostanu według klas bonitacji

obliczono z podziałem na dwie grupy

wiekowe:

Pierwszą stanowiły drzewostany młodszych klas

wieku, których wartość Gm(t) w wieku t określono

według wzoru:

Gm(t) = Wk(t) · Z · C
gdzie:
Wk(t) – tabelaryczny wskaźnik wartości

drzewostanu w wieku t i w danej klasie bonitacji

określony według kosztów poniesionych na

założenie i pielęgnację [m3/ha],

Z – współczynnik zadrzewienia,
C – przeciętna cena sprzedaży surowca

drzewnego w [zł/m3].

Z kolei wartość drzewostanów starszych klas

wieku Gs(t) obliczono zgodnie ze wzorem:

Gs(t) = Ws(t) · Z · C
gdzie:
Ws(t) – tabelaryczny wskaźnik wartości

drzewostanu w wieku t i w danej klasie bonitacji

okre− ślony według wartości sprzedażnej [m3/ha].

W dalszej kolejności należało określić wartość

drzewostanu podrzędnego. Niezmiernie istotnym

elementem w tej części obliczeń okazała się

możliwość wykorzystania już istniejących danych

zawartych w Systemie Informatycznym Lasów

Państwowych (SILP), który rejestruje zdarzenia

gospodarcze zarówno dotyczące przychodów, jak i

kosztów związanych z pozyskaniem, sprzedażą i

zrywką drewna

Na podstawie tych informacji, w połączeniu z

opisem taksacyjnym (lokalizacja,
powierzchnia, wiek, skład gatunkowy, klasa
bonitacji), wartość drzewostanu podrzędnego
P(t) w wieku t określono zgodnie ze wzorem:

P(t) = T(t) – [M(t) · K(t)]
gdzie:
T(t) – wartość pozyskanego drewna w wieku t

i w danej klasie bonitacji [zł], M(t) – miąższość
pozyskanego drewna w wieku t i w danej
klasie bonitacji [m3], K(t) – przeciętny koszt
pozyskania i zrywki drewna w wieku t [zł/m3].

Tak obliczona wartość drzewostanów głównego i

podrzędnego stanowiła podstawę do określe− nia

wartości produkcji sumarycznej drzewostanu w

wieku t.

Wartość produkcji sumarycznej drzewostanu S(t) w

wieku t umożliwia określenie wzrostu jego wartości, a

ściślej – bieżącego przyrostu wartości drzewostanu.

Jest to przyrost wartości pro− dukcji sumarycznej

obserwowany w kolejnych latach życia drzewostanu:

S(t) = S(t + 1) – S(t) [4]
W ekonomii przyrost ten inaczej określany jest

mianem przychodu krańcowego czy też margi−

nalnego i oznacza, o ile wzrośnie wartość

drzewostanu, jeśli jego użytkowanie zostanie

odłożone do roku następnego, przy czym wartość

tego przyrostu jest też zmienna w czasie życia

drzewo− stanu.

Chcąc zatem ustalić najkorzystniejszy wiek

wyrębu w gospodarstwie leśnym, należy wziąć

pod uwagę kształtowanie się krańcowych wartości

przychodów oraz krańcowych wartości kosztów w

przypadku przetrzymywania drzewostanu z roku

na rok. Ściślej, dla każdego roku oddzielnie trzeba

porównać wzrost wartości kapitału leśnego

uzyskany dzięki wstrzymaniu się od wyrębu przez

okres jednego roku z kosztami wynikającymi z tej

decyzji. Kosztem ponoszo− nym przez

gospodarstwo leśne w związku z

przetrzymywaniem drzewostanu jest procent, jaki

mogłoby ono uzyskać od kapitału

zmaterializowanego w wartości drzewostanu,

jeśliby został on spieniężony, a następnie

zainwestowany przy bieżącej stopie procentowej

p.

W ekonomii tego rodzaju koszt nosi nazwę

kosztu alternatywnego lub też utraconych
możliwości. Stanowi on sumę dochodów
utraconych w wyniku niewykorzystania
posiadanych zasobów (pracy i kapitału) w
najlepszym z istniejących alternatywnych
zastosowań. Inaczej rzecz ujmując jest to
ilość innego dobra, z której trzeba
zrezygnować, aby możliwe stało się
wytworzenie dodatkowej jed− nostki dobra
pierwszego [Begg i in. 1993]

W związku z powyższym, przy założeniu dążenia do

maksymalizacji dochodów (zysków) w tym gospodarstwie,

należałoby przetrzymywać drzewo− stan jedynie tak długo,

jak stopa zwrotu S(t)/S(t), uzyskiwana w rezultacie wzrostu

wartości hodowanego drzewostanu, przewyższać będzie

wysokość żądanej stopy procentowej p.

p S t
S t

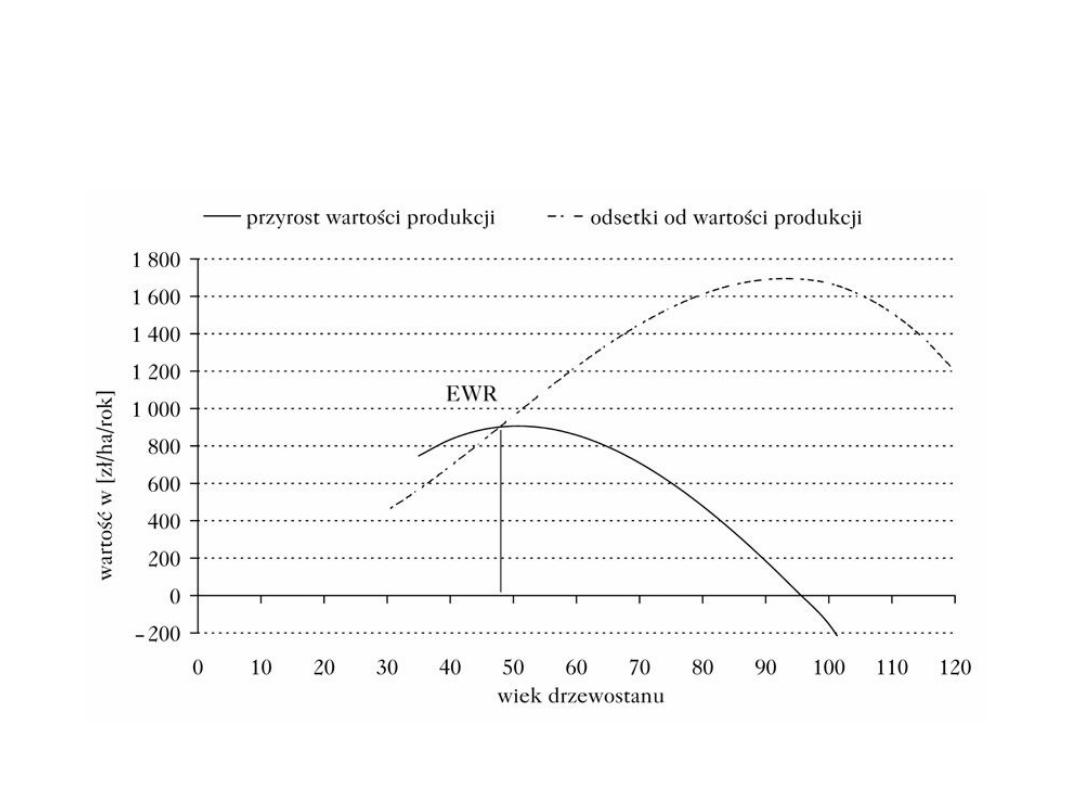
Wiek, w którym stopa zwrotu od wartości kapitału leśnego

(procent charakteryzujący przyrost wartości drzewostanu)

pokrywa się z wysokością stopy procentowej, stanowi

ekonomiczny wiek rębności (EWR). Na podstawie wzoru [5]

można stwierdzić, że optymalny wiek rębności jest tym

dłuższy, im wyższy i bardziej wydłużony w czasie jest

procent przyrostu wartości, a jedno− cześnie im niższa jest

stopa procentowa. Można także, przekształcając to

równanie, dokonać próby sformułowania zasady

umożliwiającej wyznaczenie optymalnego wieku rębności,

który przypa− da na taki moment życia drzewostanu, w

którym następuje zrównanie przychodów krańcowych

S(t) w rezultacie przetrzymywania zapasu

rosnącego jeszcze o rok dłużej z kosztem

alternaty−

wnym kapitału reprezentowanego przez

ten zapas, co można zapisać w postaci

równania:

S(t) = S(t) · p
Zatem drzewostan powinien być

przetrzymywany na pniu tak długo, aż

oczekiwany w roku następnym bieżący

przyrost wartości tego drzewostanu

zrówna się z alternatywnym kosztem

kapitału [Chang 1984; Klemperer 1996]

Kształtowanie się wartości drzewostanu głównego i

podrzędnego w zależności od ich wieku t i w ramach

poszczególnych bonitacji przedstawiono w formie funkcji

charakteryzujących się następującymi równaniami:

Ia/I G(t) = –0,1545 · t3 + 25,535 · t2 – 777,48 · t + 17935 II

G(t) = 0,0059 · t3 – 5,035 · t2 + 976,69 · t – 19388 III/IV

G(t) = –0,0096 · t3 – 0,271 · t2 + 499,80 · t – 11478 Ia/I

P(t) = 0,0159 · t3 – 3,0683 · t2 + 156,81 · t – 635

II

P(t) = 0,0212 · t3 – 4,7234 · t2 + 305,84 · t – 4333 III/IV

P(t) = 0,051 · t3 – 13,054 · t2 + 1038,90 · t – 24227

gdzie:
G – drzewostan główny,
P – drzewostan podrzędny.

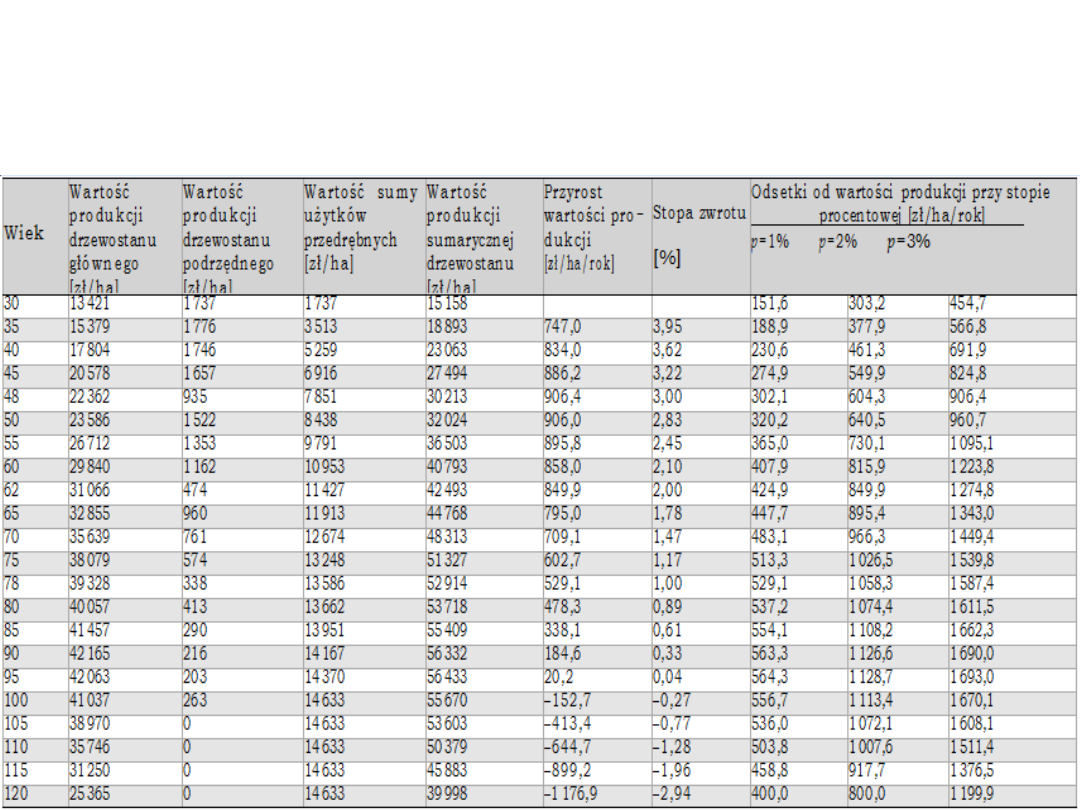
Punktem wyjścia do wyznaczenia ekonomicznego

wieku rębności są zachodzące z biegiem czasu zmiany

wartości drzewostanu głównego i podrzędnego oraz

kosztów alternatywnych będących odzwierciedleniem

wartości możliwych do uzyskania odsetek w rezultacie

upłynnie− nia tegoż drzewostanu. W celu określenia

najkorzystniejszego wieku rębności przeanalizowano

kształtowanie się krańcowych wartości przychodów

oraz krańcowych wartości kosztów związanych z

przetrzymywaniem drzewostanu z roku na rok (tab. 1).

Drzewostan należy wyciąć w momencie, kiedy

przyrost wartości produkcji zrówna się z odsetkami od

wartości produkcji (ryc. 1−3), czy też inaczej: w

momencie, w którym stopa zwrotu uzyskiwana w

rezultacie wzro− stu hodowanego drzewostanu

pokryje się z wysokością stopy procentowej

przedsięwzięcia alter− natywnego

W przypadku drzewostanów

sosnowych Ia/I klasy bonitacji ma to
miejsce, przy stopach procentowych
p=1, 2 i 3%, odpowiednio w wieku:
78, 62 i 48 lat. Z kolei dla pozo−
stałych klas bonitacji wiek ten,
według przyjętych stóp
procentowych, wynosi odpowiednio:
80, 64 i 54 lata (bonitacja II) oraz 89,
75 i 65 lat (bonitacja III/IV)

Ekonomiczny wiek rębności dla drzewostanu sosnowego Ia/I

klasy bonitacji przy stopach procentowych p=1%, 2% i 3%

Economical rotation age of Scots pine stand for Ia/I stand

quality and rate of return p=1%, 2% and 3%

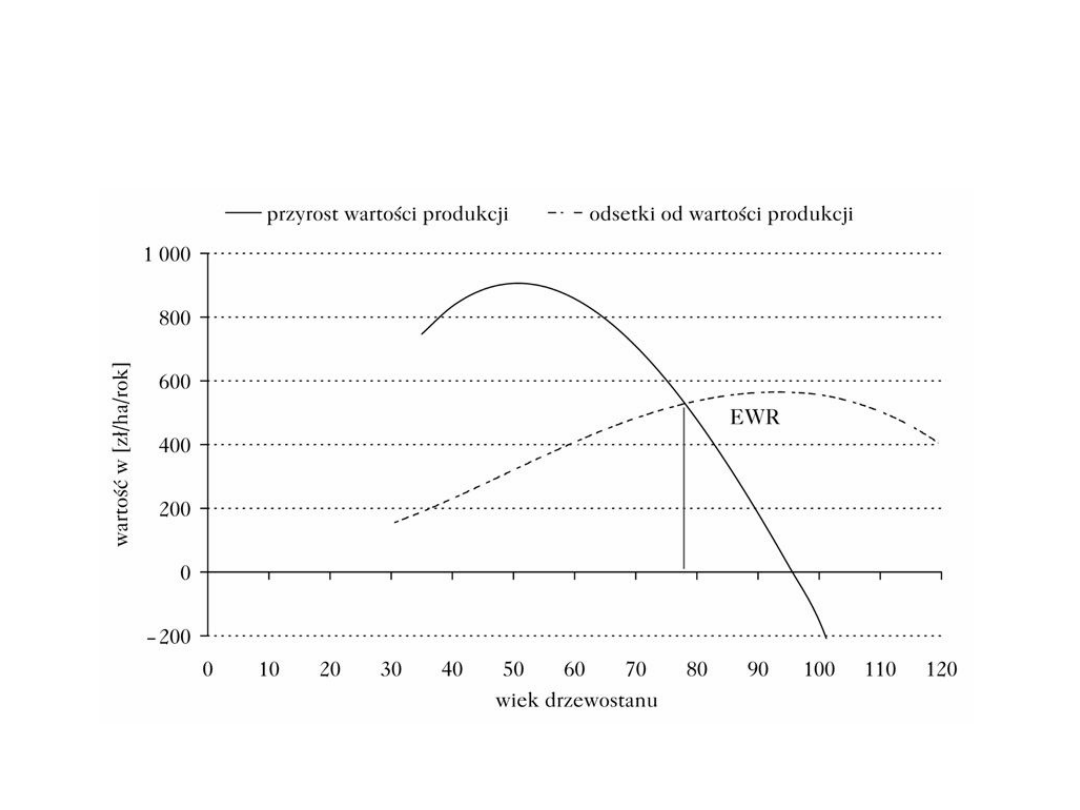
I klasa bonitacji przy stopie

1%

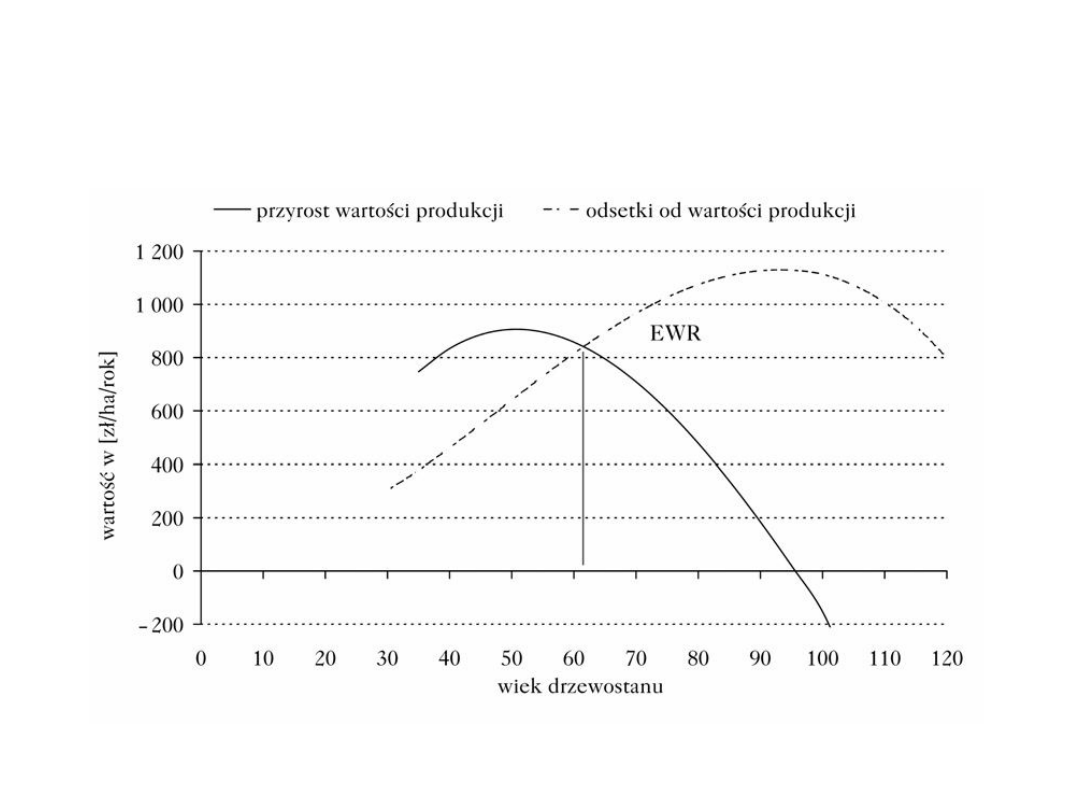
I klasa bonitacji przy stopie

2%

I klasa bonitacji przy stopie

3%

Ekonomiczny wiek rębności dla drzewostanów

sosnowych według klas bonitacji i stóp

procentowych p

Z przeprowadzonych wyliczeń wynika, że

optymalny wiek rębności dla sosny w
Nadle− śnictwie Brzeziny waha się od 48
do 89 lat. Kłóci się to jednak z postulatami
ochrony przyrody, sugerującymi koncepcję
wydłużania wieku rębności oraz z
wartościami stosowanymi w praktyce
gospodarstwa leśnego. Przyjęty w planie
urządzania lasu Nadleśnictwa Brzeziny
wiek rębności dla sosny zwyczajnej wynosi
110 lat. Postulaty te nie są jednak
ekonomicznie poprawne, ponieważ nie
uwzględniają kilku ważnych faktów

Przede wszystkim nie biorą pod uwagę
„zamrożenia” kapitału leśnego, bo przecież

odnowienie czy zalesienie gruntu kosztuje,
podob− nie rzecz się ma z zabiegami
pielęgnacyjnymi. Przychodów zaś nie
uzyskuje się natychmiast, tylko po wielu
latach. Stąd też poprawna ekonomicznie
decyzja o wyrębie drzewostanu powinna
uwzględniać również stopę procentową.
Jednak ustalenie racjonalnej wysokości
stopy procen− towej dla gospodarstwa
leśnego stanowi wciąż poważny problem

Inne ważne okoliczności, które należy uwzględnić

w obliczeniach dotyczących wieku rębno− ści, to

koszty zabiegów pielęgnacyjnych. Im dłużej las

pozostaje na pniu, tym bardziej obciążają go tego

rodzaju nakłady. Jeszcze inne czynniki

zniechęcające do wydłużenia wieku rębności

związane są z ryzykiem zniszczenia drzewostanu

przez pożar albo masowy rozwój szkodników.

Wymienione okoliczności sugerują, że las należy

wyciąć i sprzedać w momencie, gdy tempo wzrostu

jego wartości zmaleje do poziomu stopy

dyskontowej. Wycinając las wcześniej, zarządca

(właściciel) pozbawia się przyrostu wartości

korzystniejszego niż zwrot z inwestycji alternatyw−

nej, mierzony stopą dyskontową. Z kolei

wstrzymanie się z wyrębem do okresu późniejszego

będzie skutkowało mniejszym zwrotem w

porównaniu z inwestycją alternatywną.

Na wysokość ekonomicznego wieku rębności wpływ

ma klasa bonitacji drzewostanu – im drze− wostany

mają lepsze warunki wzrostu i rozwoju, tym

ekonomiczny wiek rębności jest krótszy i odwrotnie.

W tym przypadku różnice między klasami bonitacji w

zależności od przyjętej stopy procentowej wahają się

w granicach od 2 do 11 lat. Znaczenie ma także

stopa procentowa. Wraz z jej wzrostem cykl

produkcyjny drzewostanu ulega skróceniu i

odwrotnie. Różnice te, w zależ− ności od klasy

bonitacji, przy zmianie stopy procentowej o jeden

punkt wynoszą od 10 do 16 lat. Jednak zastosowanie

wysokiej stopy procentowej, tzn. ostrzejszego

kryterium ekonomicznego, pociąga za sobą określone

konsekwencje gospodarcze w postaci preferowania

gatunków iglastych (bardziej rentowne) i krótkich

cykli produkcyjnych (przy 3% w zależności od klasy

bonitacji wiek rębności wynosi 48, 54 i 65 lat).

Stąd też, po uwzględnieniu aktualnej stopy

procentowej dla gospo− darstwa leśnego,

kształtującej się na poziomie około 1%,

należy przyjąć, że ekonomiczny wiek rębności

dla drzewostanów sosnowych powinien

wynosić od 78 do 89 lat w zależności od klasy

bonitacji.

W przedstawionym rozwiązaniu brano pod

uwagę tylko jeden rodzaj kosztu, wynikający z

faktu wiązania („zamrożenia”) kapitału w

formie wartości drzewostanu. Jednakże

oprócz drze− wostanu w gospodarstwie

leśnym podstawowym czynnikiem produkcji

jest również grunt leśny. Stąd też w tego typu

analizach zachodzi potrzeba włączenia

kosztów użycia gruntu leśnego. W przypadku

uwzględnienia wspomnianych kosztów

nastąpiłoby obniżenie wieku rębności.