KOWARIANCJA
dxdy
y
x
f
m
y
m
x
p
m
y
m
x
Y
X
i
j
ij
)
,
(
)
)(
(
)
)(
(
)
,
cov(
01
10
01
10
Współczynnik korelacji
Y
X
Y
X
Y
D
X
D
Y
X
)
,
cov(
)
(
)
(
)
,
cov(
2
2
02
20
11
1
1
Współczynnik korelacji dla
zmiennych losowych liniowo
zależnych
1
b
aX
Y
P
b
aX
Y
b
aEX
EY
)
)(
(
)
)(
(
)
,
cov(
b
aEX
b
aX
EX
X
E
EY
Y
EX
X
E
Y
X
EX
aEX
EX
X
aE
EX
X
aE
XX
aE
aEX
aX
EX
X
E
)
(
)
(
)
(
)
)(
(
X
aD
EX
a
aEX
EX
a
EX
a
EX
a
aEX
2
2
2
2
2
2
2
)
(
)
(
)
(
)
(
X
D
a
b
aX
D
Y
D
2
2
2
2
)
(
1
)
(
)
(
)
(
)
(
)
,
cov(
2
2
2
2
2
2
2
2
2
02
20
11
a
a
X
D
a
X
aD
X
D
a
X
D
X
aD
Y
D
X
D
Y
X
XY
Funkcja regresji zmiennej losowej Y względem
zmiennej losowej X.
)
(
)
(
x
X
Y
E
x
g
dy
x
y
yf
x
X
Y
E
x
g
)
(
)
(
)
(
)
( x
y
f
rozkład warunkowy
Dla funkcji regresji zachodzi własność
min
)
(
2
x
g
Y
E
Własność ta jest podstawą szacowania metodą
najmniejszych
kwadratów
funkcji regresji II rodzaju, tzn. funkcji g(x) o
przyjętym z góry typie i o parametrach wyznaczonych tak, by dla
wyników (x
i
,y
i
)
(i=1,2,...,n) n-elementowej próby z
dwuwymiarowego rozkładu (X,Y) zachodziło minimum funkcji:
n
i
i
i
x
g
y
S
1
2
)
(
x
x
g )
(
Parametr
liniowej funkcji regresji g(x) nazywa się
współczynnikiem regresji liniowej.
0
)
)(
(
)
(
)
(
)
)(
(
)
,
cov(
EY
EY
EX
EX
EY
Y
E
EX
X
E
EY
Y
EX
X
E
X
X
X,Y – stochastycznie niezależne
Parametry pozycyjne rozkładu
zmiennej losowej
Dla dowolnej liczby p ( 0 < p < 1 ) kwantylem rzędu p
rozkładu zmiennej losowej X nazywamy liczbę x
p
spełniającą nierówności:
1
oraz
p
x
X
P
p
x
X
P
p
p
Jeżeli istnieje (dla zmiennej losowej skokowej)
więcej niż jedna taka liczba x
p
, to przyjmuje się
najmniejszą z nich.
Dla zmiennej ciągłej mamy równość p=F(x
p
).
Podstawowymi kwantylami ważnymi zmiennej
losowej X w praktyce statystycznej są:
Centyle (p = 0.01 i 99 wielokrotności tej
liczby )
Decyle (p = 0.1 i 9 wielokrotności tej liczby
)
Kwartyle (p = 0.25 i 3 wielokrotności tej
liczby )
Najczęściej używanym kwantylem jest x
0.5
mediana
Podstawowe rozkłady skokowe
Rozkład dwupunktowy
p
q
X
P
p
X
P
1
)
0
(
)
1
(
Rozkład dwumianowy (Bernoulliego).
a) dokonuje się n niezależnych powtórzeń pewnego
doświadczenia losowego.
b) w każdym doświadczeniu mogą zajść tylko dwa
wykluczające się
zdarzenia :
A
( sukces) i
A’
(porażka)
c) oraz
Zmienna losowa przyjmuje wartości równe liczbie sukcesów w n
doświadczeniach
p
A
P
)
(
p
q
A
P
1
)
'
(
k
n
k
q
p
k
n
k
X
P
}
{
np
EX
npq
X
D
2
p
EX
pq
X
D
2
Rozkład Poissona
W schemacie doświadczeń typu Bernoulliego liczba niezależnych
doświadczeń
Prawdopodobieństwo sukcesu p maleje tak, że
Przy takim założeniu funkcja prawdopodobieństwa zmiennej
losowej o rozkładzie dwumianowym dąży do funkcji
prawdopodobieństwa w tzw. Rozkładzie Poissona:
dla k = 1,2,…
n
const
np
!
k
e
k
X
P
k
X
D
EX
2
Model rozpadu radioaktywnego.
Rad rozpada się w radon. Rozpadające się jądro radu wysyła
cząsteczkę α.
Odległości między atomami są stosunkowo duże, można zatem
przyjąć, że jądra rozpadają się niezależnie od stanu sąsiednich
atomów.
Załóżmy, że prawdopodobieństwo p(t) rozpadu danego atomu radu
w pewnym przedziale czasu o długości t zależy tylko od długości
tego przedziału. Jeżeli łącznie jest n atomów ( w jednym gramie 10
) to średnia liczba cząsteczek wysyłanych w czasie t jest równa a
= np(t). Jak pokazują doświadczenia, liczba ta przy t = 1 s jest
rzędu 10
10
, zatem p(1) = 10
-12
Sukces – rozpad atomu radu. Liczba wyemitowanych cząsteczek
jest równa licznie sukcesów w n doświadczeniach Bernoulliego.
Prawdopodobieństwo sukcesu p = p(t). Parametry n i p są takie,
że faktycznym rozkładem prawdopodobieństwa zmiennej losowej
X(t) – liczba wysłanych w czasie t cząsteczek będzie rozkład
Poissona z parametrem a = np(t):
Podstawowe rozkłady ciągłe
Rozkład gamma Rozkład beta
Rozkład t-Studenta
Rozkład χ
2
Rozkład normalny ( rozkład Gaussa)
)
2
)
(
exp(
2
1
2
1
)
(
2
2
2
)
(
2
2
m
x
e
x
f
m
x
)
2
exp(
2
1
)
(
2
x
x
f
2
2
X
D
m
EX
N(m,
)
N(0,1
)
m
X
U
Unormowany rozkład Gaussa
Centralne twierdzenie
graniczne
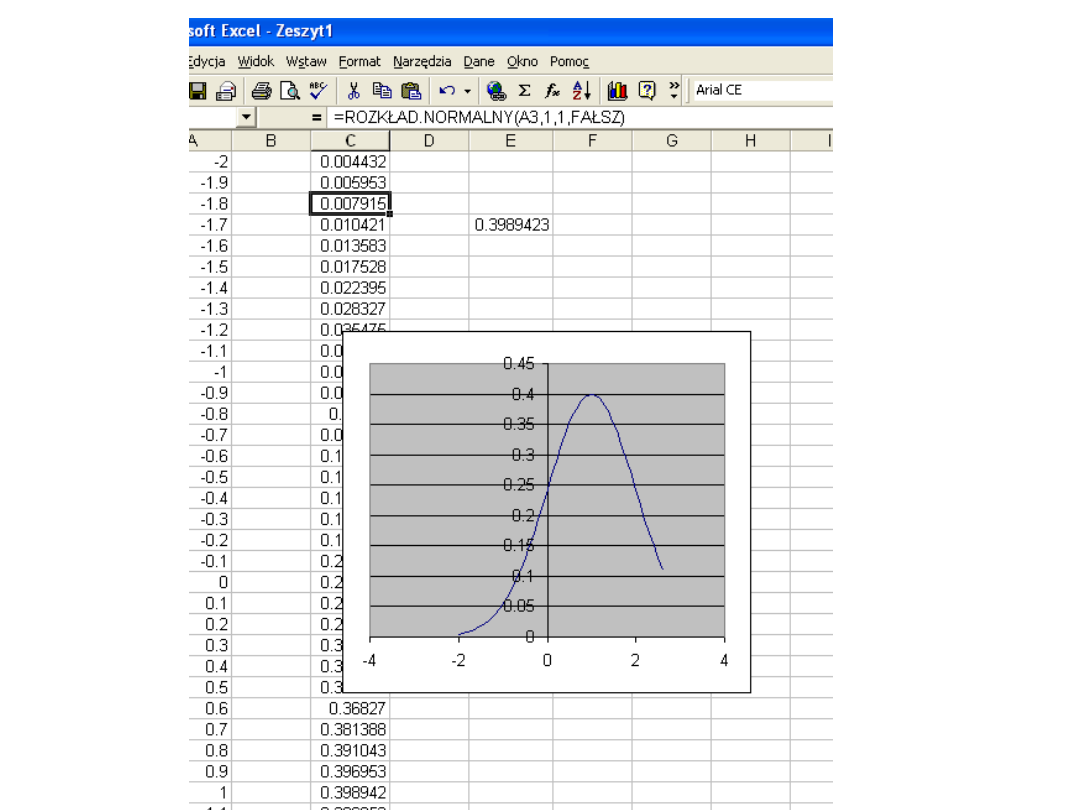
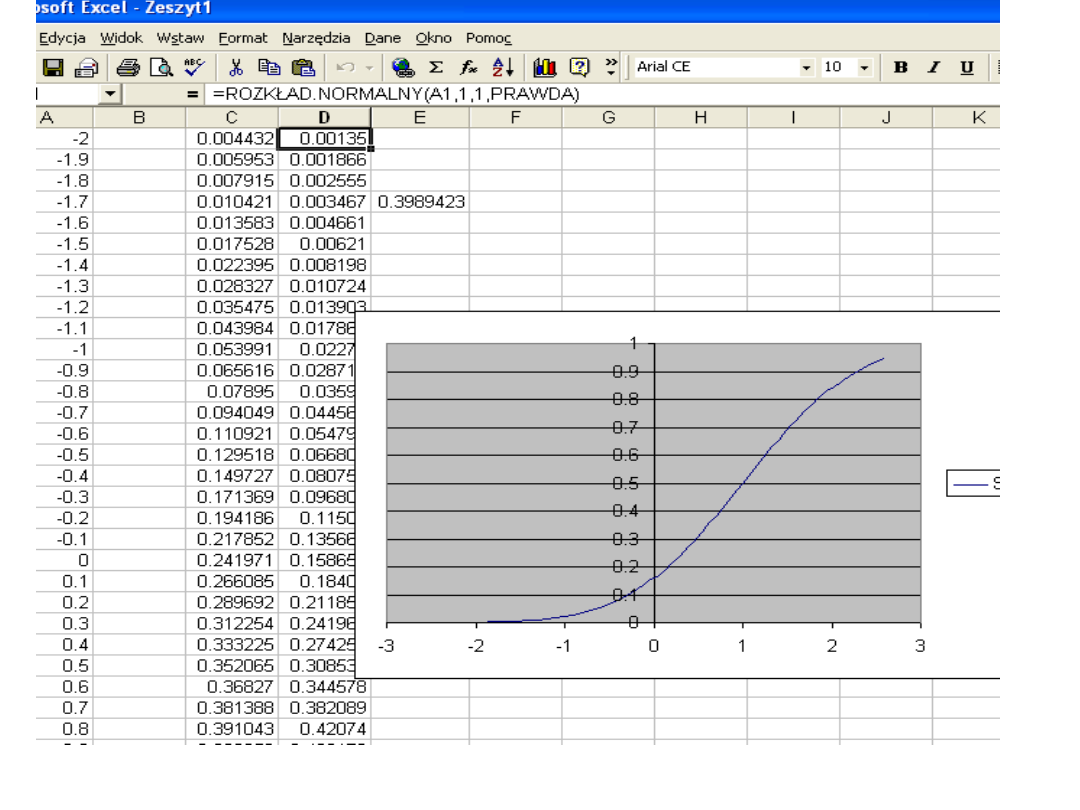
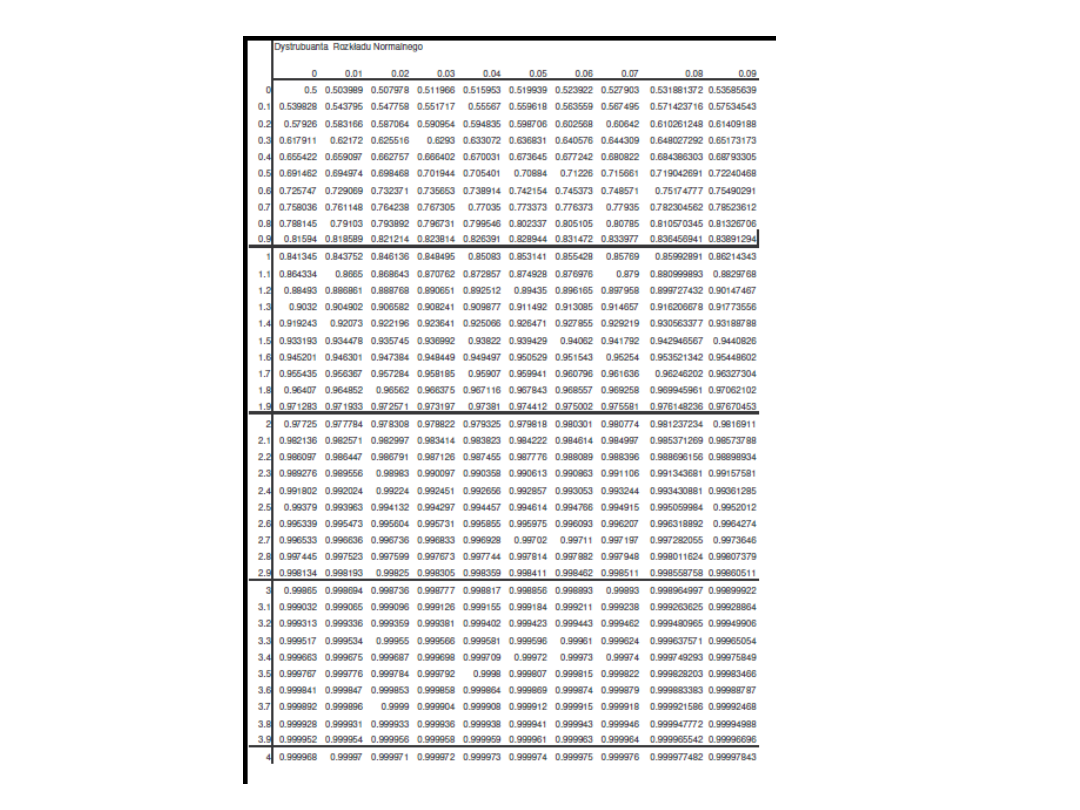
ROZKŁAD.NORMALNY
Daje w wyniku normalny rozkład łączny dla danej średniej i
normalnego odchylenia. Funkcja ta ma bardzo szeroki zakres
zastosowań w statystyce, łącznie z badaniem hipotez.
Składnia
X jest to wartość, dla której chcemy mieć rozkład.
Średnia jest to średnia arytmetyczna rozkładu.
Odchylenie_std jest to standardowe odchylenie rozkładu.
Skumulowany jest to wartość logiczna, która określa rodzaj funkcji.
Jeżeli skumulowany ma wartość PRAWDA, wówczas funkcja
ROZKŁAD.NORMALNY daje w wyniku łączną funkcję rozkładu, a jeśli
FAŁSZ, wówczas funkcja ta daje w wyniku funkcję gęstości
prawdopodobieństwa.
ROZKŁAD.NORMALNY(x;średnia;odchylenie_std;skumulowany)
ROZKŁAD.NORMALNY.S
Oblicza standardowy skumulowany rozkład
(dystrybuantę) normalny o zadanych
parametrach. Rozkład ten ma średnią zero i
odchylenie standardowe równe jeden. Funkcję tę
należy stosować zamiast tabeli obszarów
standardowych krzywych normalnych.
Składnia
Z jest to wartość, dla której chcemy określić
rozkład.
ROZKŁAD.NORMALNY.S(z)
ROZKŁAD.NORMALNY.ODW
Oblicza wartość funkcji odwrotnej
skumulowanego rozkładu normalnego.
Składnia.
ROZKŁAD.NORMALNY.S.ODW(prawdopodobie
ństwo)
Prawdopodobieństwo jest to
prawdopodobieństwo odpowiadające
rozkładowi normalnemu.
Średnia jest to średnia arytmetyczna
rozkładu.
Odchylenie_std jest to standardowe
odchylenie rozkładu
ROZKŁAD.NORMALNY.ODW(prawdopodobieństwo;średnia;odchyleni
e_std)
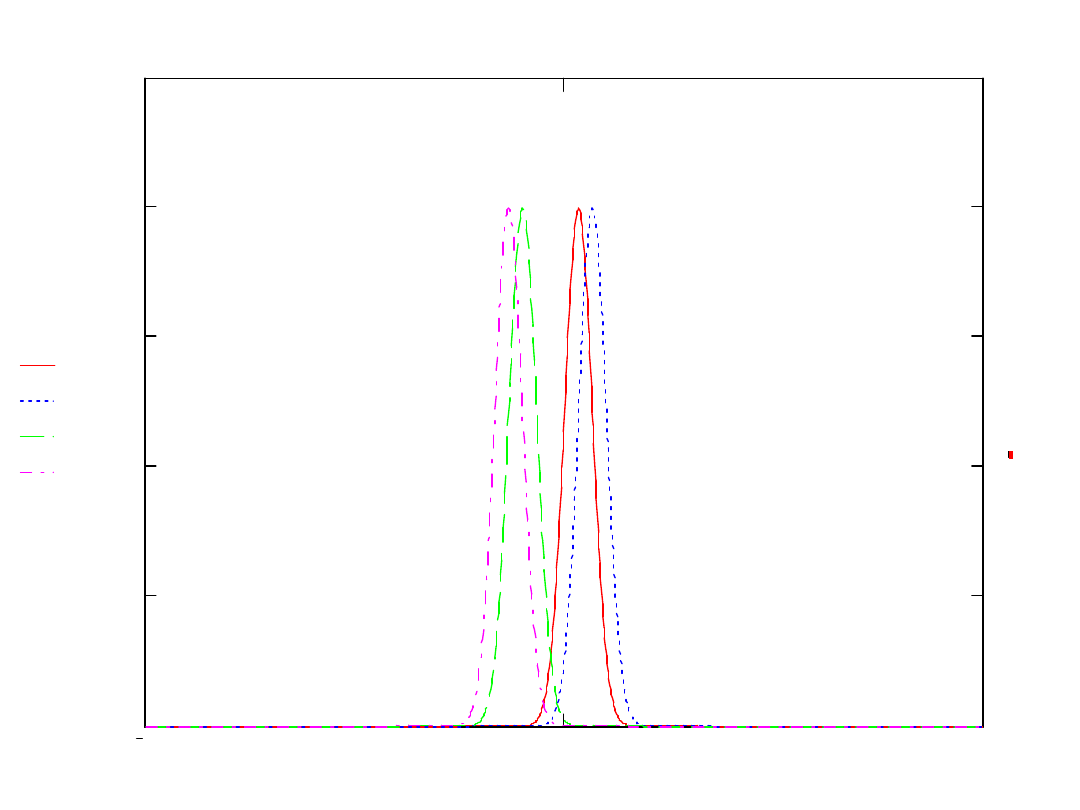
30
0
30
0
0.1
0.2
0.3
0.4
0.5
0
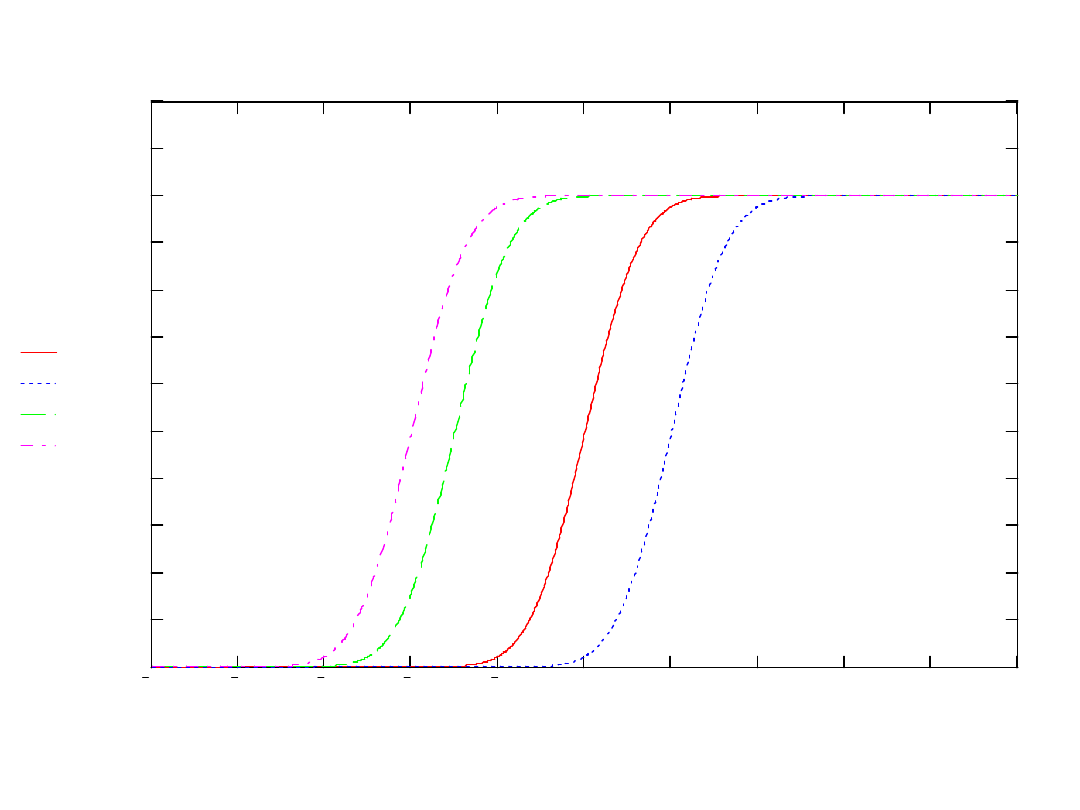
dnormx 1
1
(
)
dnormx 2
1
(
)
dnormx 3
1
(
)
dnormx 4
1
(
)
30
30
x
10
8
6
4
2
0
2
4
6
8
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.2
0
pnormx 0
1
(
)
pnormx 2
1
(
)
pnormx 3
1
(
)
pnormx 4
1
(
)
10
10
x
10
8
6
4
2
0
2
4
6
8
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
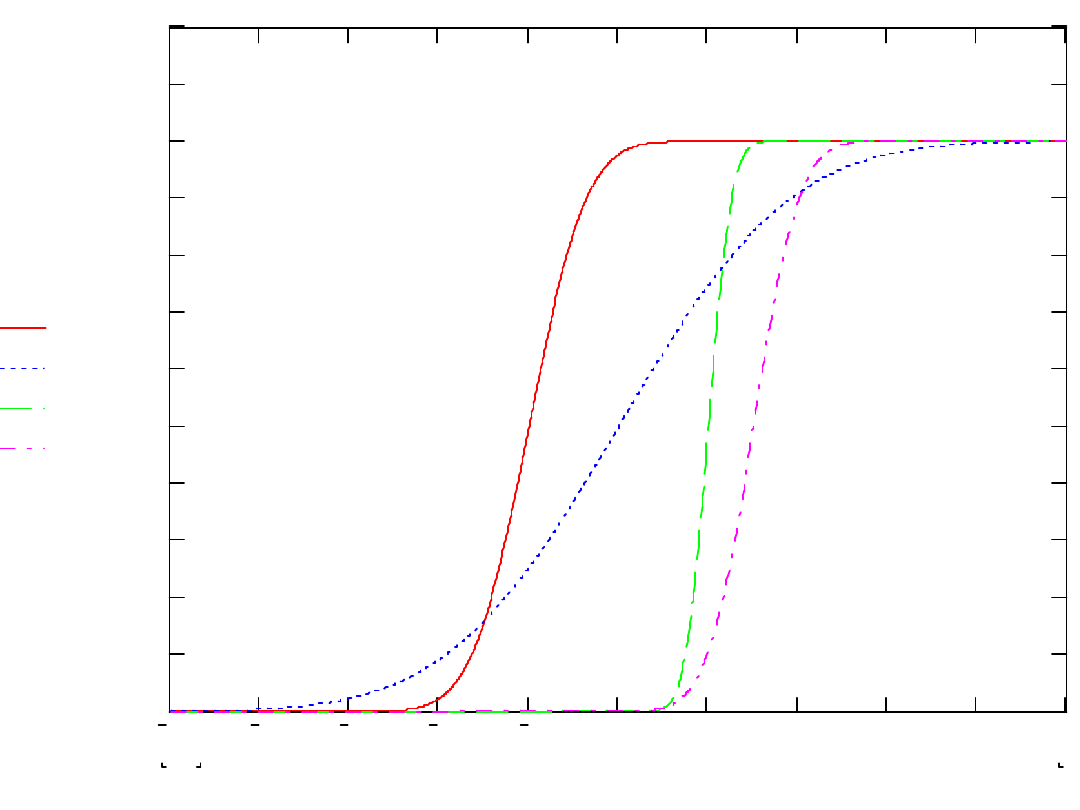
pnormx 2
1
(
)
pnormx 0
3
(
)
pnormx 2
0.4
(
)
pnormx 3
0.8
(
)
x x
x
x
10
8
6
4
2
0
2
4
6
8
10
0
0.2
0.4
0.6
0.8
1
1
0
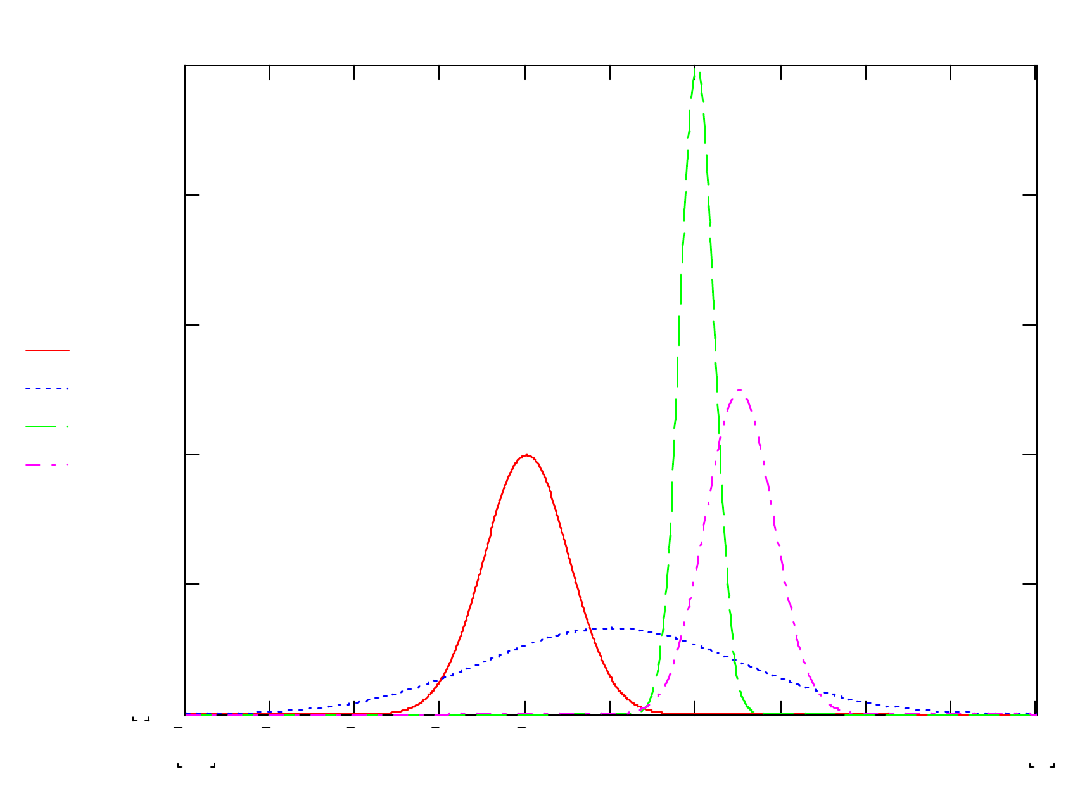
dnormx 2
1
(
)
dnormx 0
3
(
)
dnormx 2
0.4
(
)
dnormx 3
0.8
(
)
10
10
x x
x
x
10
8
6
4
2
0
2
4
6
8
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
pnormx 0
1
(
)
pnormx 2
1
(
)
pnormx 3
1
(
)
pnormx 4
1
(
)
x
10
8
6
4
2
0
2
4
6
8
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.2
0
pnormx 2
1
(
)
pnormx 0
3
(
)
pnormx 2
0.4
(
)
pnormx 3
0.8
(
)
10
10
x x
x
x
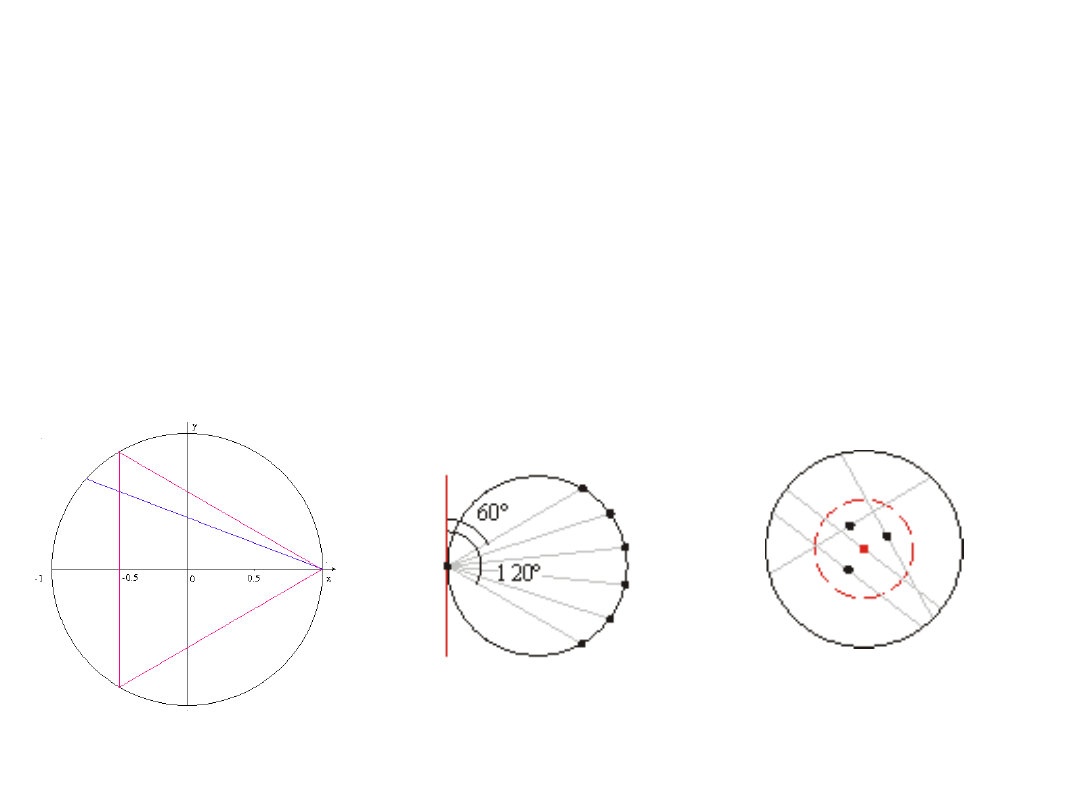
a) 1/2
b)
1/3
c) 1/4
Paradoks Bertranda