1

Linią długą nazywamy linię, której długość l jest
porównywalna z długością λ rozchodzącej się w
niej fali elektromagnetycznej.

Linię długą nazywamy linią długą jednorodną,
jeżeli wszystkie parametry linii są równomiernie
rozłożone wzdłuż linii.
W przypadku linii niejednorodnej parametry linii są
funkcją współrzędnej położenia x.

Linię długą nazywamy linią długą linearną, jeżeli
parametry linii nie zależą od wartości prądu ani
napięcia w danym punkcie linii.

LINIE DŁUGIE

2

LINIE DŁUGIE

Linię długą nazywamy linią długą symetryczną,
jeżeli parametry wszystkich przewodów linii są
jednakowe.

Linię długą nazywamy linią długą bezstratną,
jeżeli rezystancja przewodów linii R oraz
konduktacja między przewodami G są równe 0.

Linia

bezstratna

jest

wyidealizowanym

przypadkiem linii długiej, w którym nie uwzględnia
się parametrów rozpraszających energię R i G, a
jedynie parametry reaktancyjne L i C.

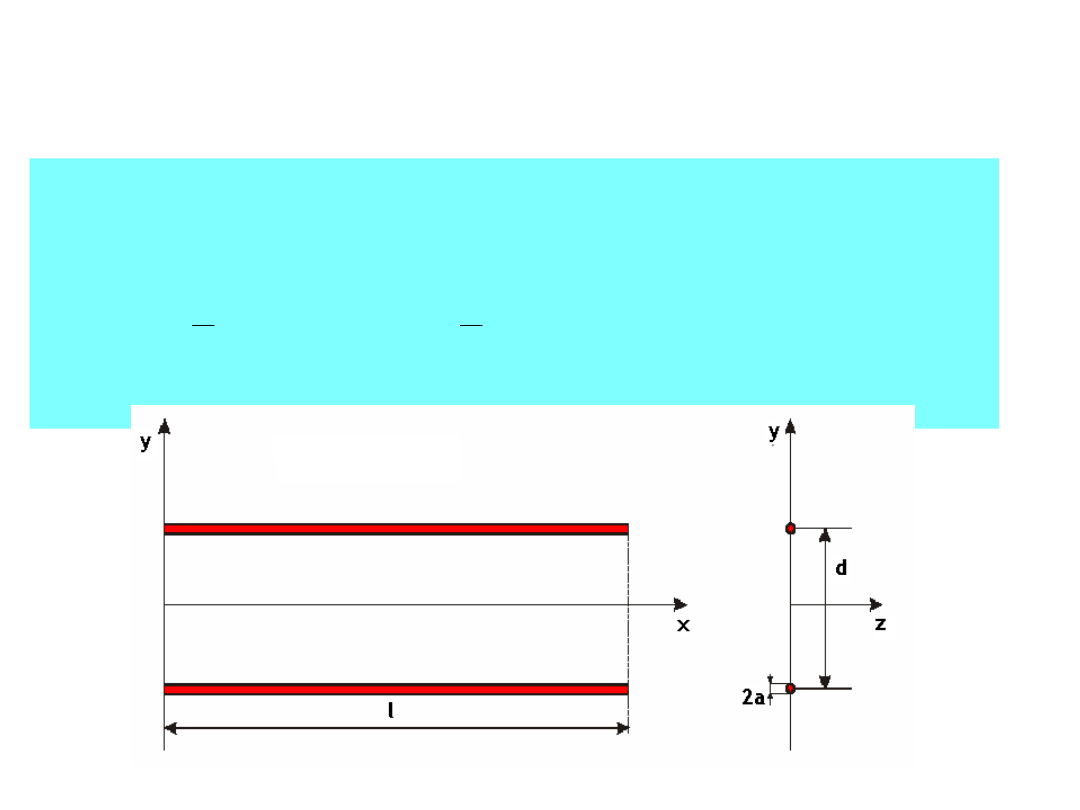
3

LINIE DŁUGIE

Linie przewodową można traktować jako linię
długą, gdy dla sygnałów występujących w linii
spełniony jest warunek:
przy

4





l

4





d

4

Jeżeli czas propagacji sygnału przez przewód
wynosi t

p

, to linią długą nazywamy takie

połączenie pomiędzy układami, w którym czas
propagacji sygnału jest większy niż połowa
średniego czasu trwania zbocza przenoszonego
sygnału t

T

, czyli t

p

>0.5t

T

.

W przypadku szybkich układów cyfrowych,
dla których czas trwania zbocza jest
mniejszy niż 1 ns, linią długą jest linia
paskowa (ścieżka obwodu drukowanego) lub
mikrolinia o długości ok. 9 cm oraz przewód
koncentryczny o długości ok. 7 cm.

LINIE DŁUGIE

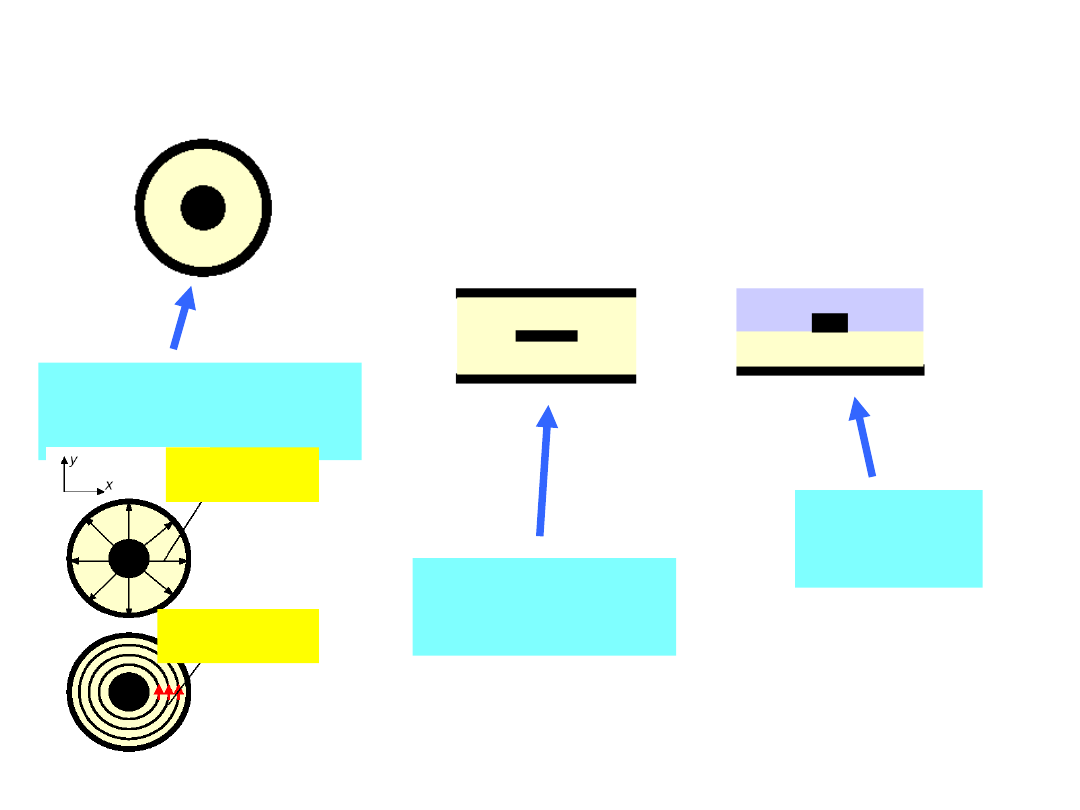
5

LINIE DŁUGIE

Linia
koncentryczna

Linia
paskowa

Mikrolin
ia

Pole
elektryczne

Pole
magnetyczne

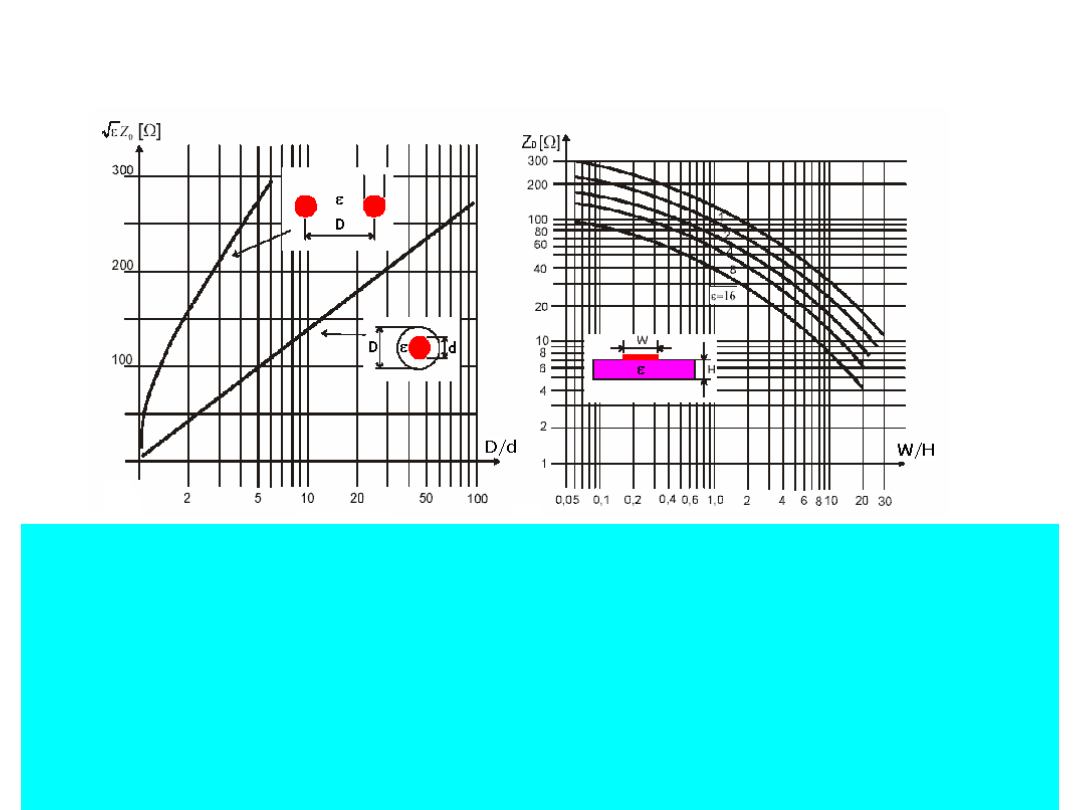
6

LINIE DŁUGIE

Użyteczny zakres Z

0

zamyka się w granicach 30 – 300 Ω.

Standardowe kable współosiowe mają Z

0

=50 Ω lub, rzadziej, 75

Ω. Opóźnienie jednostkowe powszechnie stosowanych linii nie
przekracza zwykle 5 ns/m. W praktyce, linia wysokiej jakości do
kilkunastu metrów), może być traktowana jako bezstratna do
kilku GHz. Linie paskowe na laminatach epoksydowych są
znacznie gorsze – straty są zauważalne już przy długości rzędu
kilkunastu cm.

7

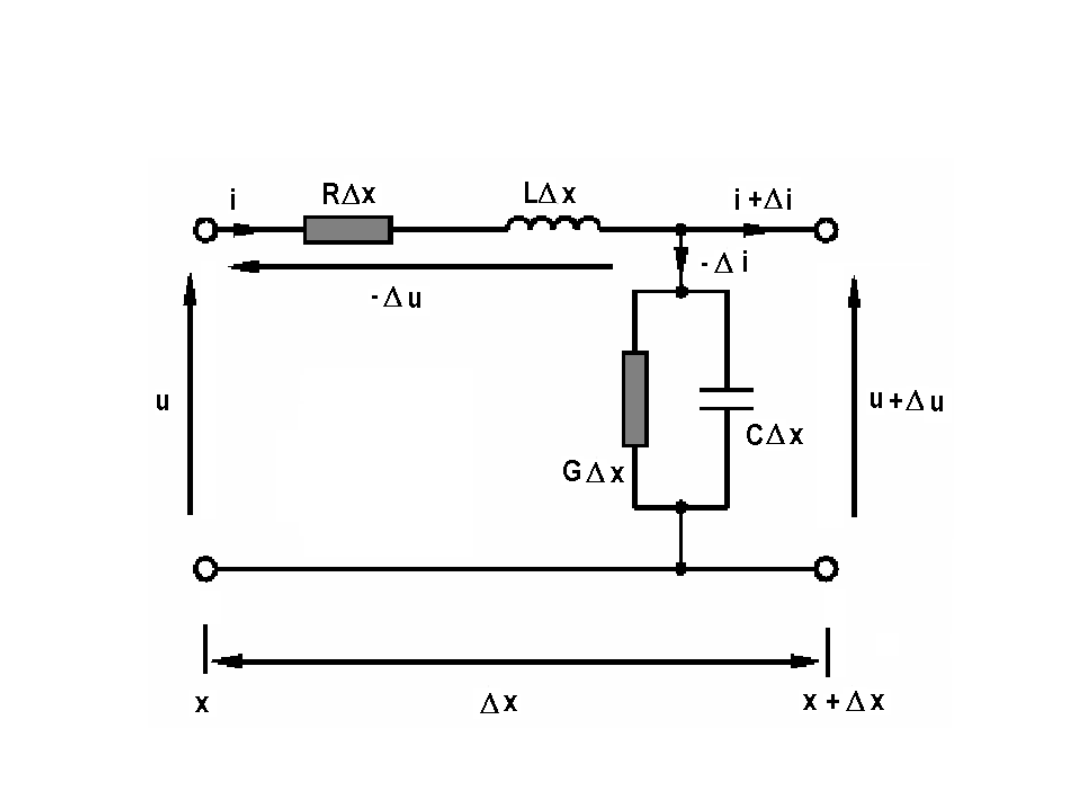
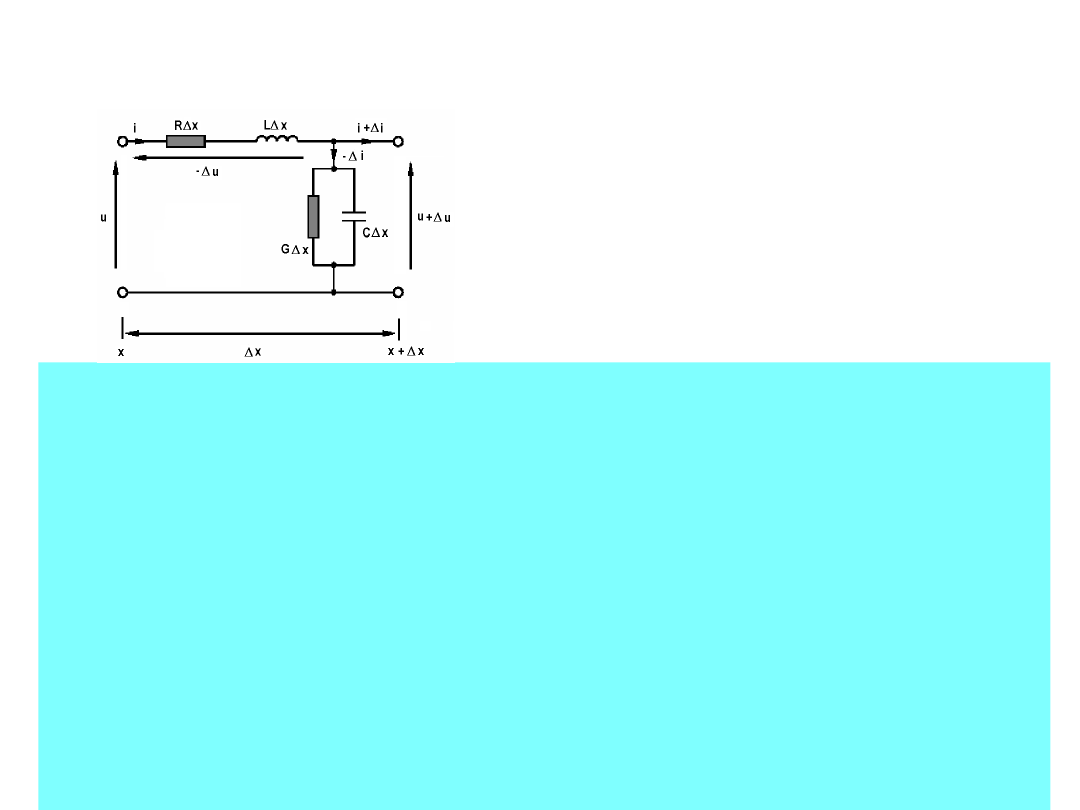
SCHEMAT ZASTĘPCZY LINII

DŁUGIEJ

8

SCHEMAT ZASTĘPCZY LINII

DŁUGIEJ

• R – rezystancja na jednostkę długości linii [Ω/m] –
reprezentująca
wszelkie straty cieplne w obu przewodach linii
• L – indukcyjność na jednostkę długości linii [H/m]–
reprezentująca pole magnetyczne obu
przewodów linii
• C – pojemność na jednostkę długości linii [F/m]–
reprezentująca
pole elektryczne w dielektryku między
przewodami linii
• G – upływność na jednostkę długości linii [S/m] –
reprezentująca ewentualne straty cieplne w
dielektryku.

9

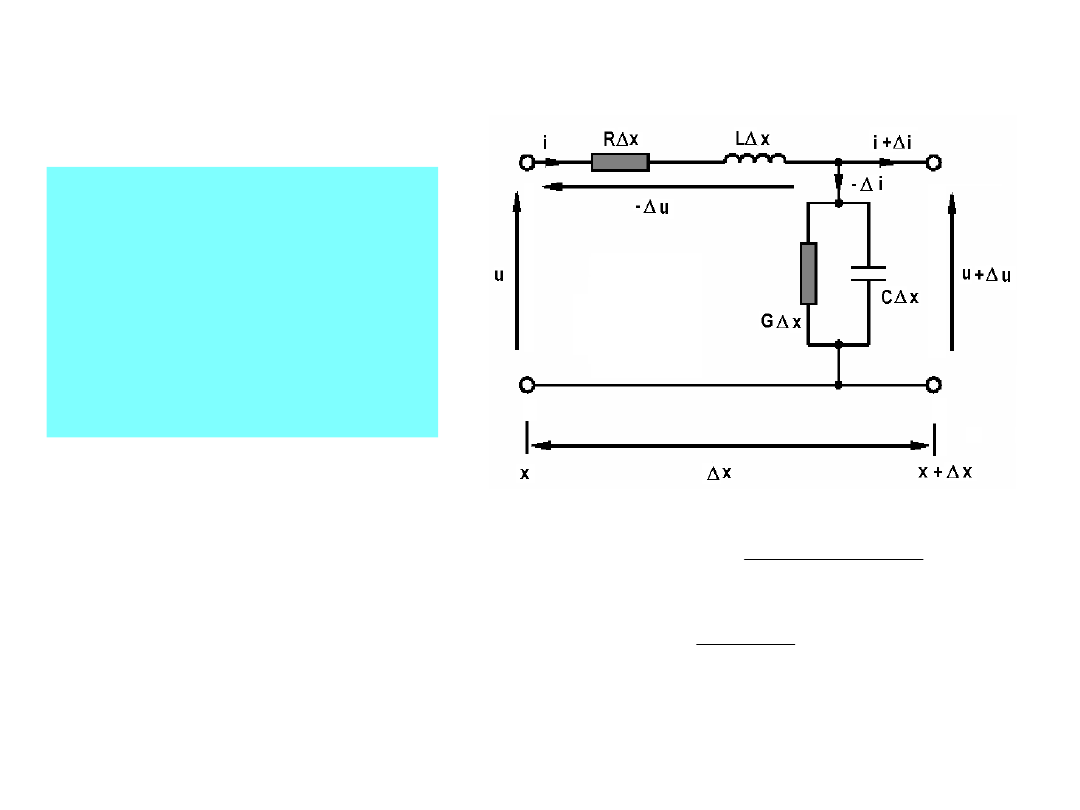
TEORIA LINII DŁUGIEJ

Przyrosty prądu
i napięcia na
odcinku
elementarnym Δx
można zapisać w
postaci:



  











  

 

 



























































t

t

x

i

x

L

t

x

i

x

R

t

x

u

t

x

x

u

t

t

x

x

u

x

C

t

x

x

u

x

G

t

x

i

t

x

x

i

,

,

,

,

,

,

,

,

10

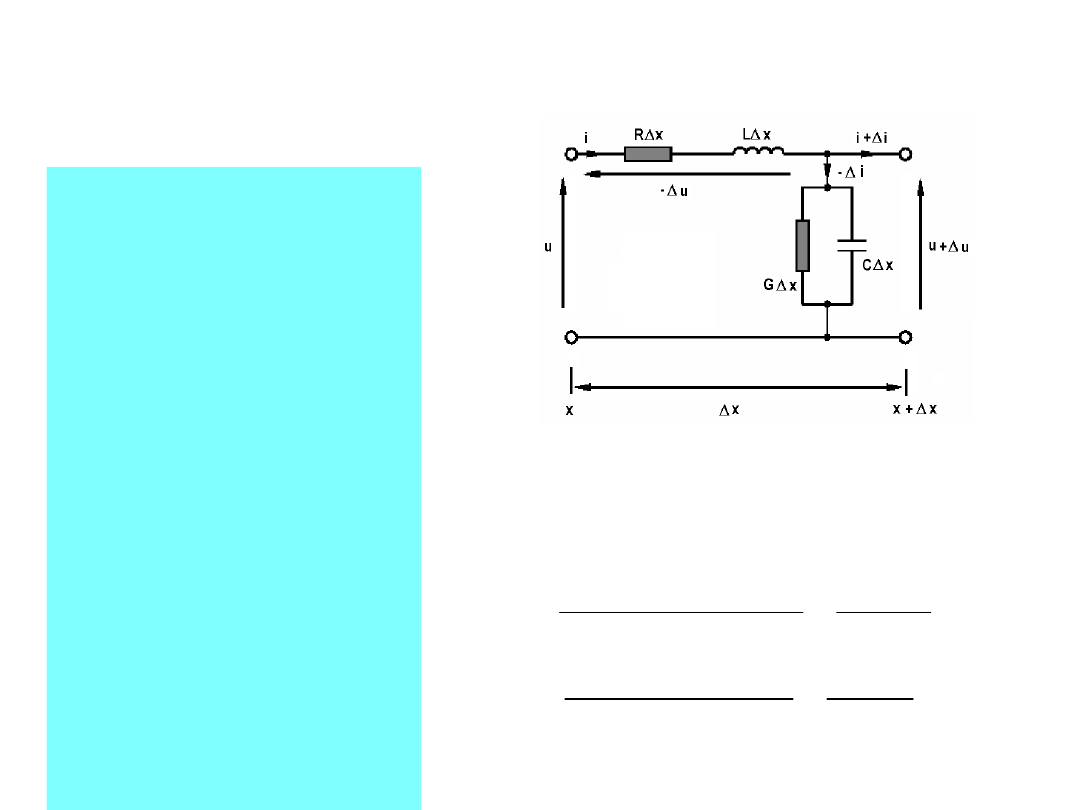
TEORIA LINII DŁUGIEJ

Równania na
zmianę napięcia
oraz na zmianę
prądu na
elementarnej
sekcji dzielimy
obustronnie przez
Δx i
przechodzimy do
granicy przy Δx
dążącym do 0.
Korzystamy z
warunku ciągłości
funkcji oraz
następujących
zależności:



  



  



  

 



  

 















































































x

t

x

i

x

t

x

i

t

x

x

i

x

t

x

u

x

t

x

u

t

x

x

u

t

x

i

t

x

x

i

t

x

u

t

x

x

u

x

x

x

x

,

,

,

,

,

,

,

,

,

,

lim

lim

lim

lim

0

0

0

0

11

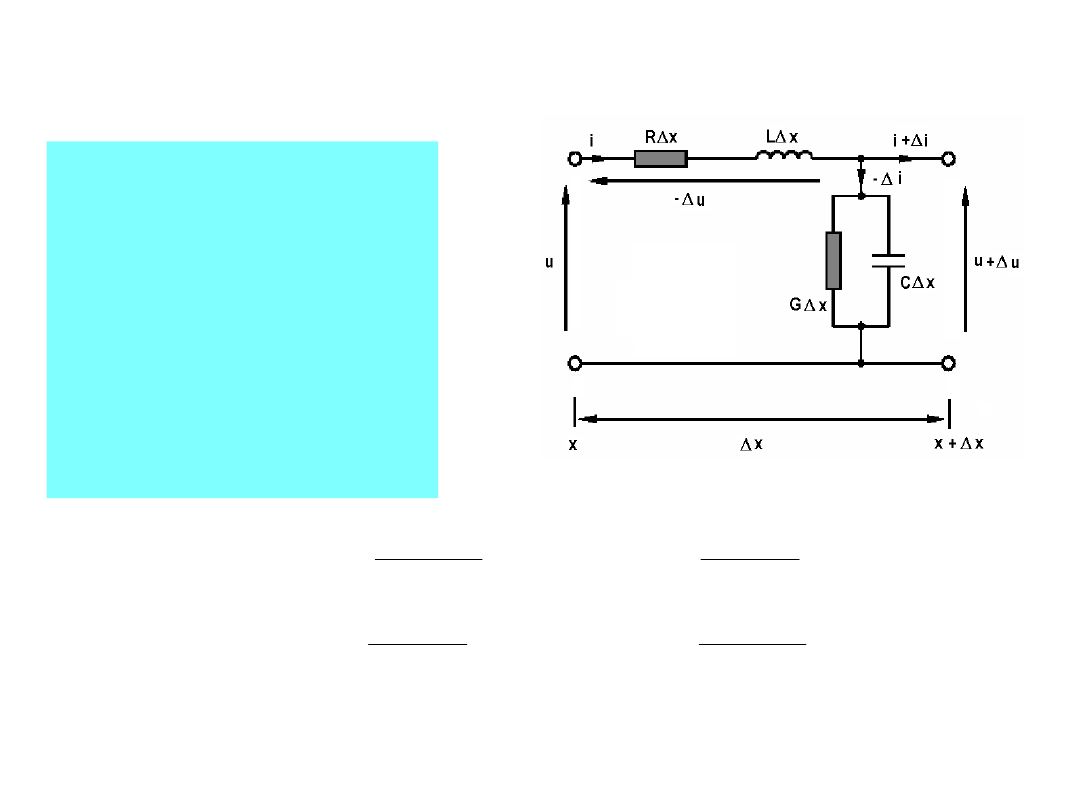
TEORIA LINII DŁUGIEJ

W rezultacie
otrzymuje się układ
dwóch równań
różniczkowych
cząstkowych dwóch
zmiennych (czasu t
i odległości od
początku linii x):

 

 

 

 

 

 







































t

t

x

u

C

t

x

Gu

x

t

x

i

t

t

x

i

L

t

x

Ri

x

t

x

u

,

,

,

,

,

,

12

TEORIA LINII DŁUGIEJ

Jeżeli jako U(x) i
I(x) oznaczmy
skuteczne
zespolone wartości
napięcia i prądu w
odległości x od
początku linii,
wtedy wartości
chwilowe można
obliczyć w sposób
następujący:

 

 

 

 

 

 























x

CU

j

x

GU

dx

x

dI

x

LI

j

x

RI

dx

x

dU





 

 

dx

x

dU

L

j

R

x

I







1

  



  

0

2

2









x

U

C

j

G

L

j

R

dx

x

U

d





13

TEORIA LINII DŁUGIEJ

Wprowadzając do
równania stałą
propagacji fali γ
opisaną zależnością

otrzymamy:







C

j

G

L

j

R













  



  

0

2

2









x

U

C

j

G

L

j

R

dx

x

U

d





 

 

0

2

2

2





x

U

dx

x

U

d



Analogicznie:

 

 

0

2

2

2





x

I

dx

x

I

d



14

TEORIA LINII DŁUGIEJ

Otrzymane
równanie
różniczkowe

posiada
rozwiązanie
następującej
postaci:

 

 

0

2

2

2





x

U

dx

x

U

d



 

x

x

e

A

e

A

x

U





2

1







 

 

dx

x

dU

L

j

R

x

I







1

 





x

x

o

e

A

e

A

Z

x

I





2

1

1







C

j

G

L

j

R

Z

o











15

TEORIA LINII DŁUGIEJ

Stała propagacji
γ

definiowana

jako:

Jest

liczbą

zespoloną
postaci:







C

j

G

L

j

R



















j





 









2

2

1

1

sin

2

sin

2

,































x

t

e

A

x

t

e

A

t

x

u

x

x

gdzie: ψ

1

, ψ

2

- argumenty liczb

zespolonych A1, A2

16

TEORIA LINII DŁUGIEJ

17

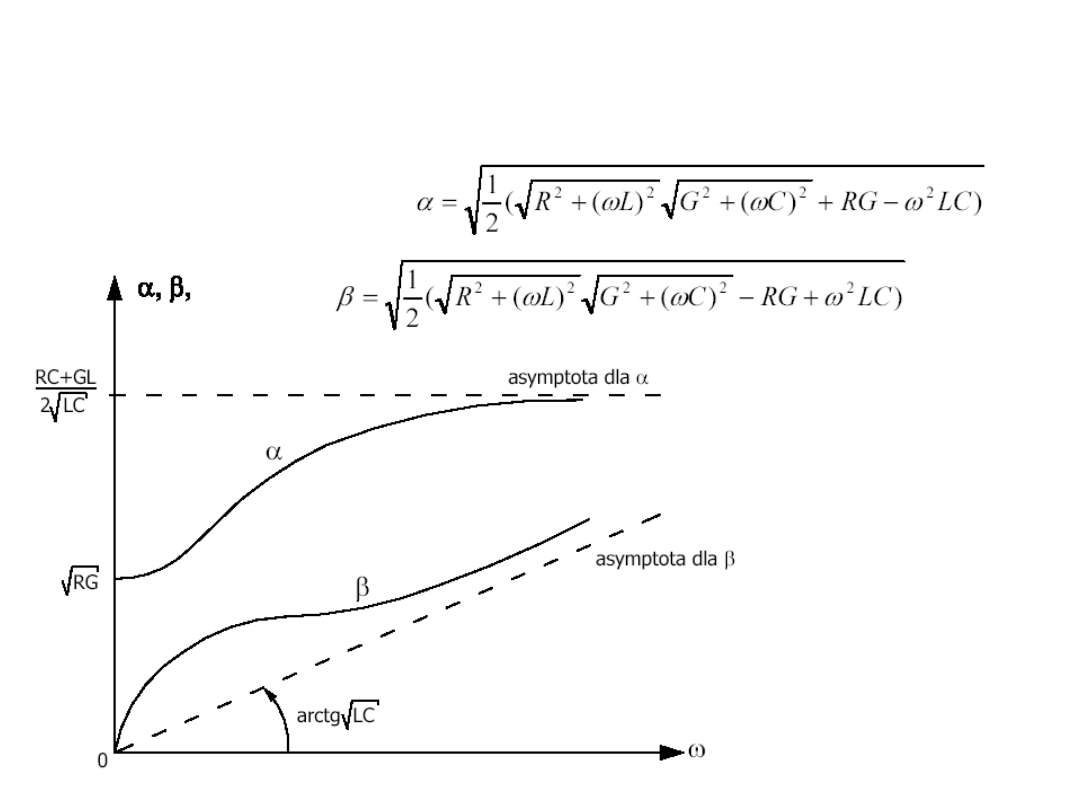
α - współczynnik tłumienia ( dla linii bez strat jest
równy 0)
β - współczynnik przesunięcia ( dla linii bez strat
wynosi ω ),

α, β i Z

0

decydują o parametrach fal napięcia i

prądu w linii długiej. Zależą one od parametrów
jednostkowych linii długiej czyli od R, L, G, C oraz
od częstotliwości.

Linie długie są stosowane w technice impulsowej
w postaci odcinków giętkiego kabla współosiowego
lub tzw. linii paskowych, utworzonych z płaskich
ścieżek przewodzących, umieszczonych na
powierzchni dielektryka. Niekiedy stosuje się
skręcone linie symetryczne dwuprzewodowe (tzw.
skrętki) i współosiowe linie sztywne typu
falowodowego.

TEORIA LINII DŁUGIEJ

LC

18

TEORIA LINII DŁUGIEJ

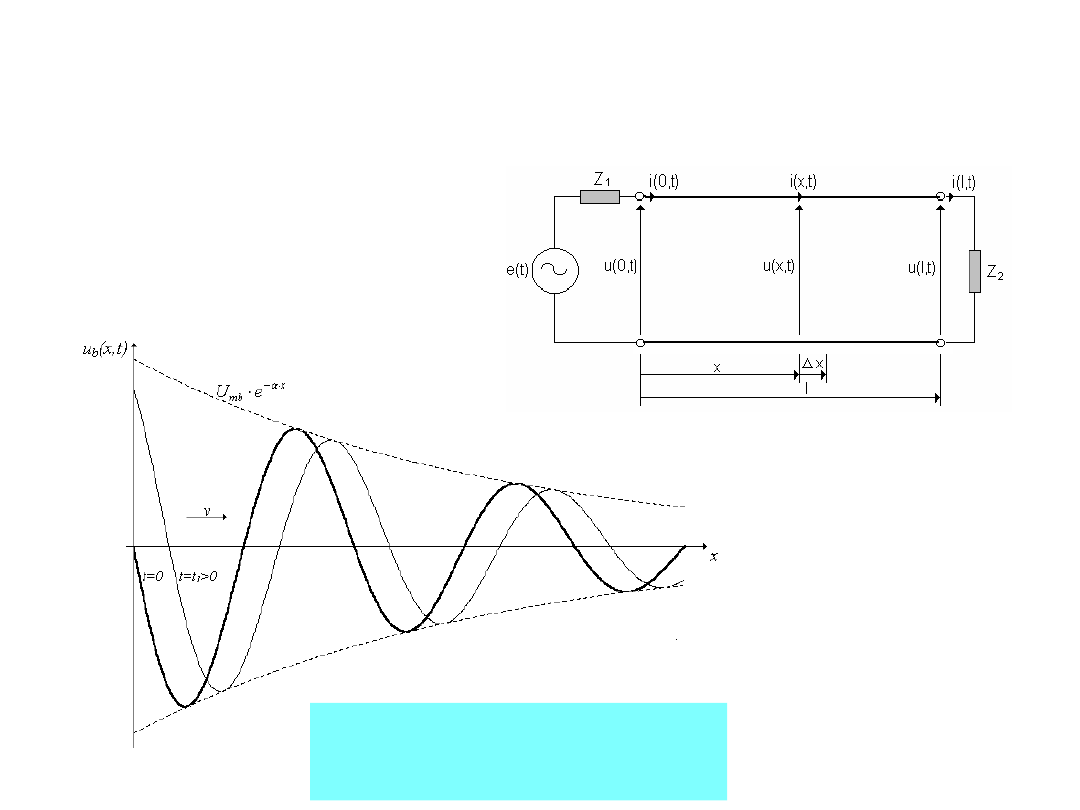
Ostatnie równanie można
przekształcić do postaci, w
której pierwsza składowa
przedstawia

falę,

o

amplitudzie zmniejszającej
się

ze

wzrostem

współrzędnej x, i
rosnącym

opóźnieniu

fazowym. Fala ta przesuwa
się w miarę upływu czasu t
od źródła do odbiornika.
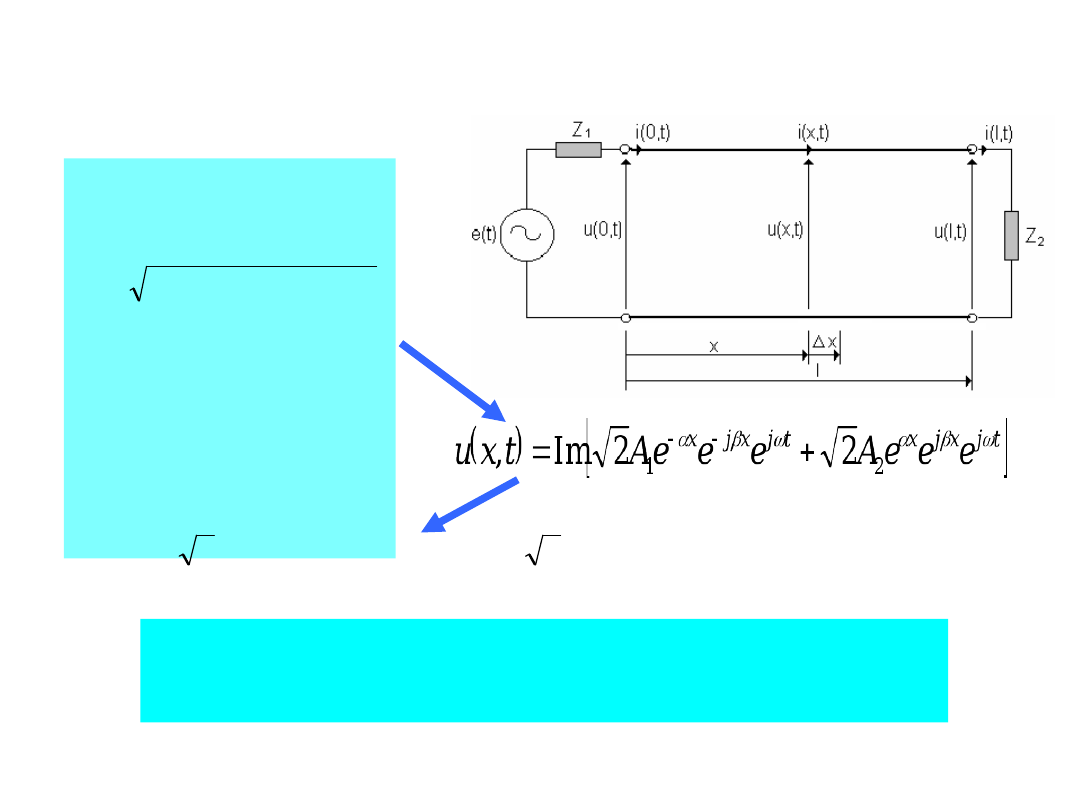
Jest

to

fala

bieżąca

(pierwotna).

 









x

t

e

U

x

t

e

U

t

x

u

x

mo

x

mb































2

1

sin

sin

,

19

TEORIA LINII DŁUGIEJ

Fala

bieżąca

(pierwotna).

20

TEORIA LINII DŁUGIEJ

Fala reprezentowana przez
drugą

składową

wzoru

przesuwa się w przeciwną
stronę - od odbiornika do
źródła. Jej amplituda rośnie
wraz ze wzrostem x, a faza
uzyskuje

większe

wyprzedzenie. Jest to fala
odbita (powrotna).

 









x

t

e

U

x

t

e

U

t

x

u

x

mo

x

mb































2

1

sin

sin

,

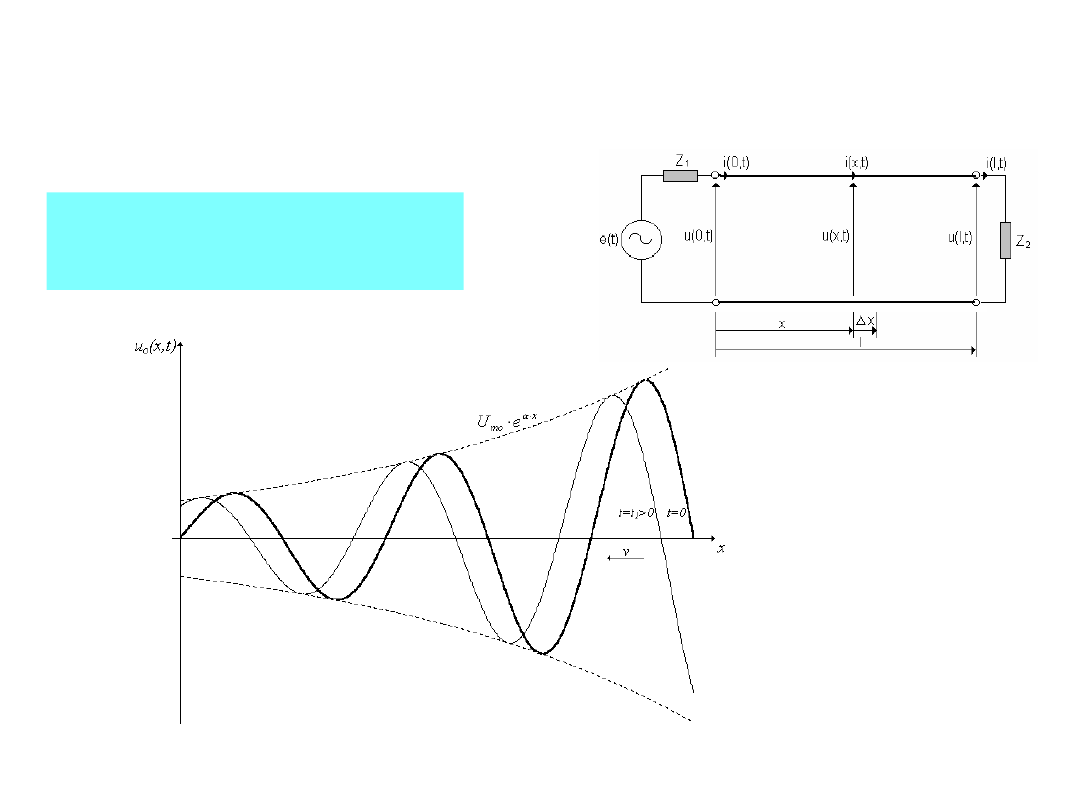
21

TEORIA LINII DŁUGIEJ

Fala

odbita

(pierwotna).

22

TEORIA LINII DŁUGIEJ

Występujące

we

wzorach stałe A1,
A2 wyznacza się z
warunków
granicznych
(brzegowych),
np. z napięcia
i

prądu

na

początku linii x=0:

 

2

1

1

0

A

A

U

U







 

2

1

1

0

0

0

A

A

I

Z

I

Z







2

1

0

1

1

I

Z

U

A





2

1

0

1

2

I

Z

U

A





23

TEORIA LINII DŁUGIEJ

 





x

x

e

e

Z

I

Z

U

x

I





1

0

1

0

1

2











 





x

x

e

e

I

Z

U

x

U





1

1

0

1

2











 





x

x

e

e

Z

I

Z

U

x

I















2

0

2

0

2

2

 





x

x

e

e

I

Z

U

x

U















2

2

0

2

2

0

1

0

1

1

Z

Z

Z

Z









0

2

0

2

2

Z

Z

Z

Z









Gdzie Γ

1

oraz Γ

2

stanowią współczynniki odbicia sygnału na początku i

końcu linii:

24

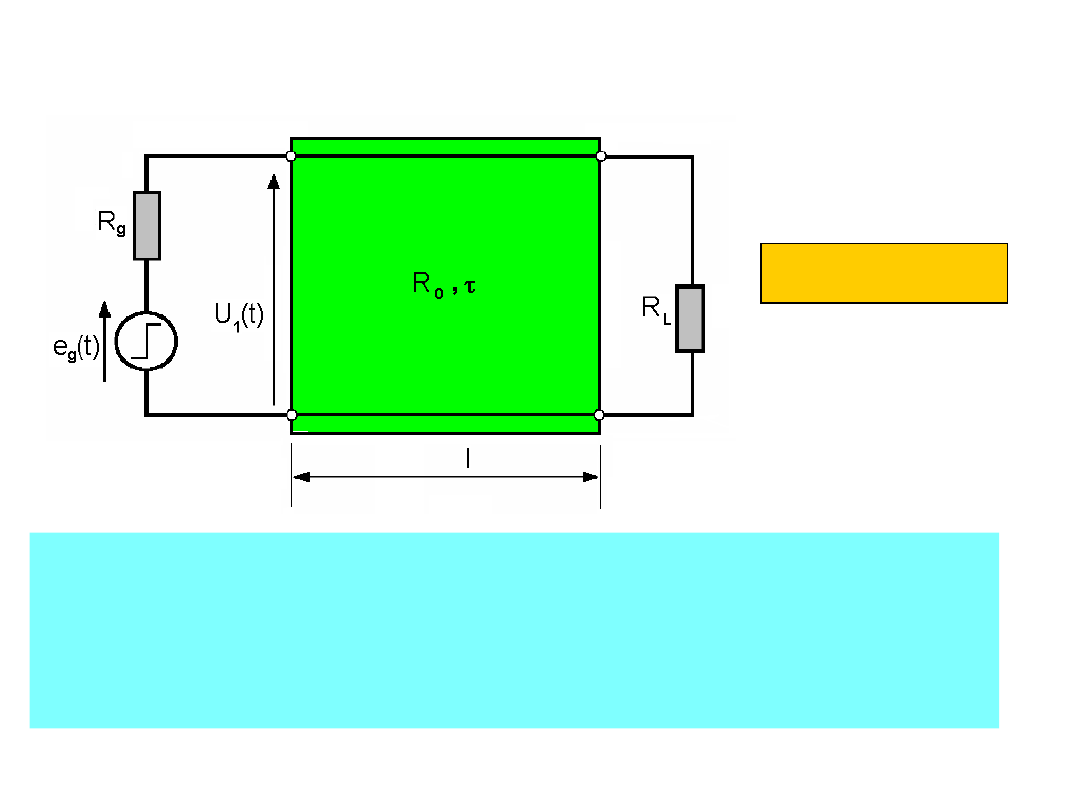
TEORIA LINII DŁUGIEJ

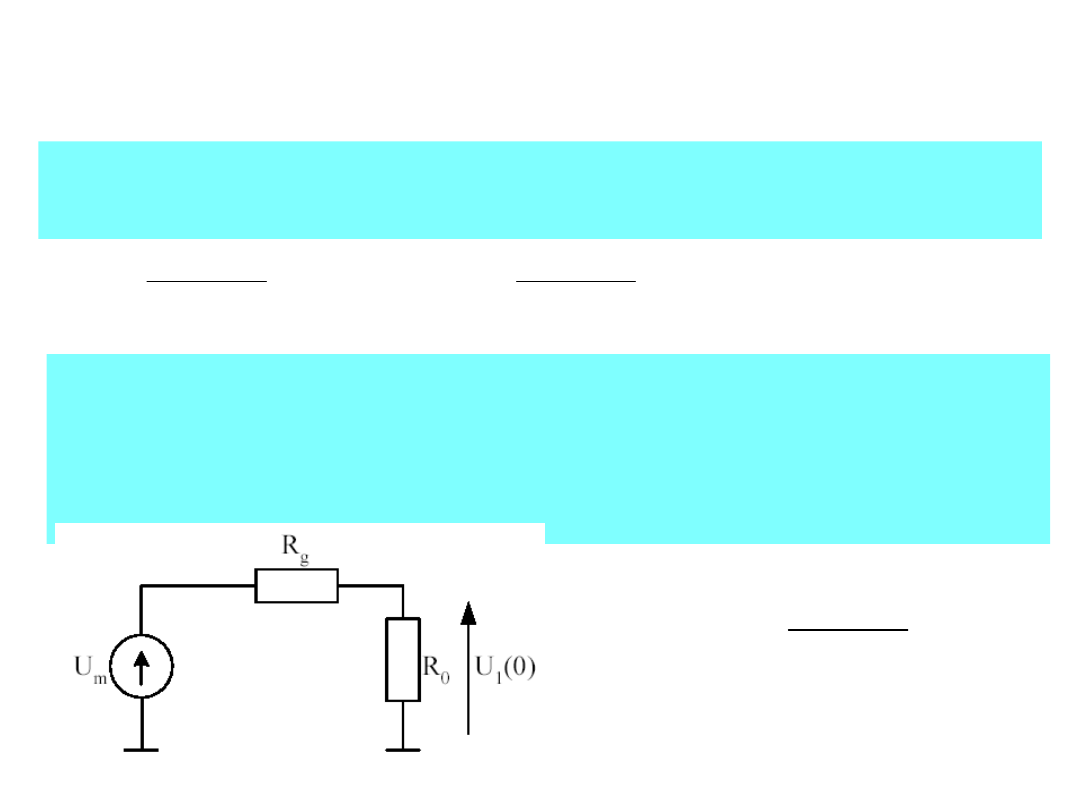
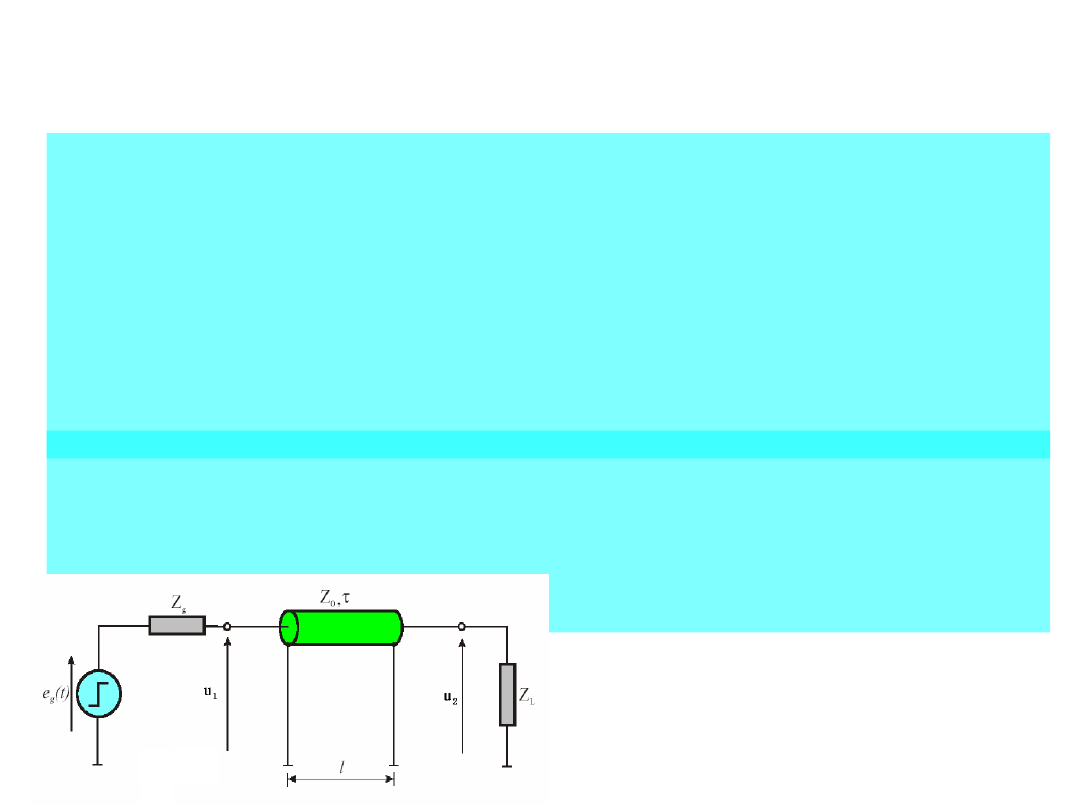
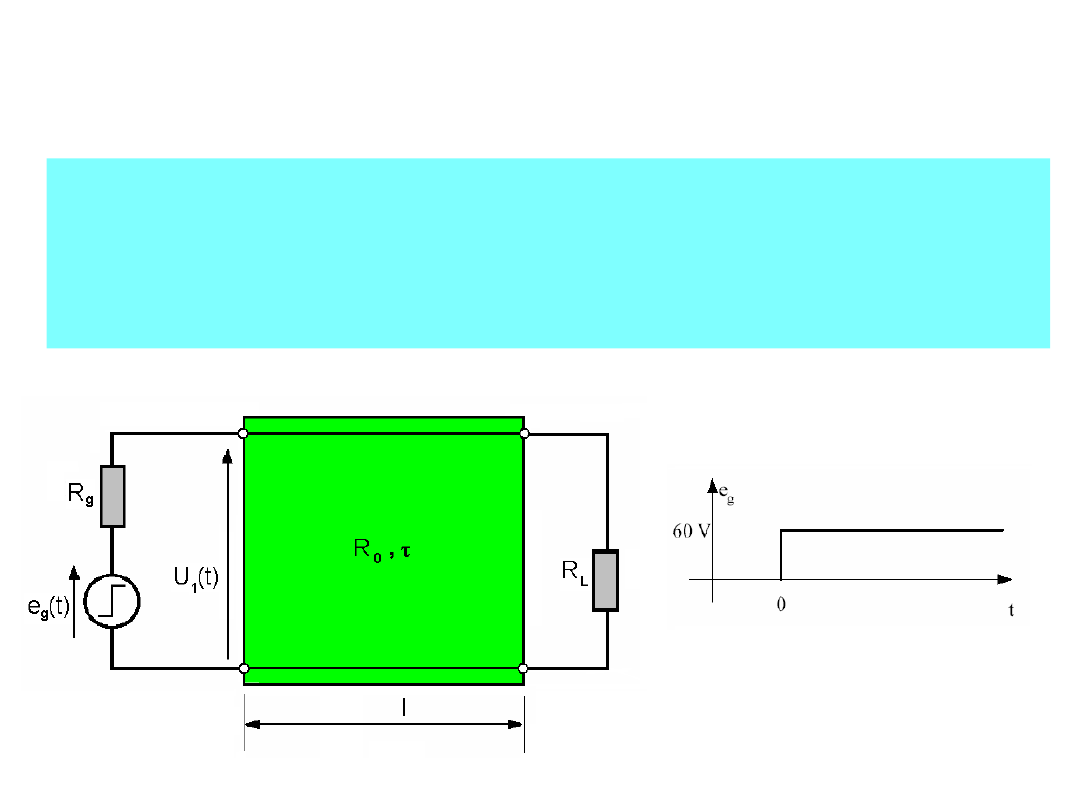
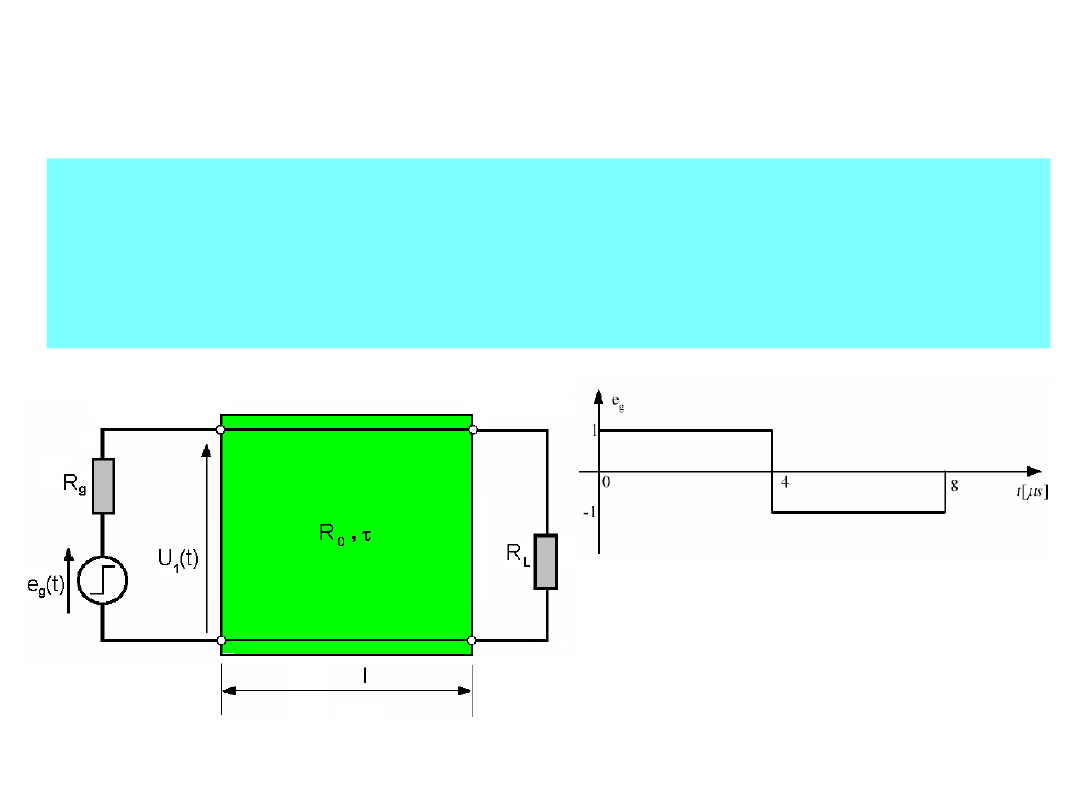
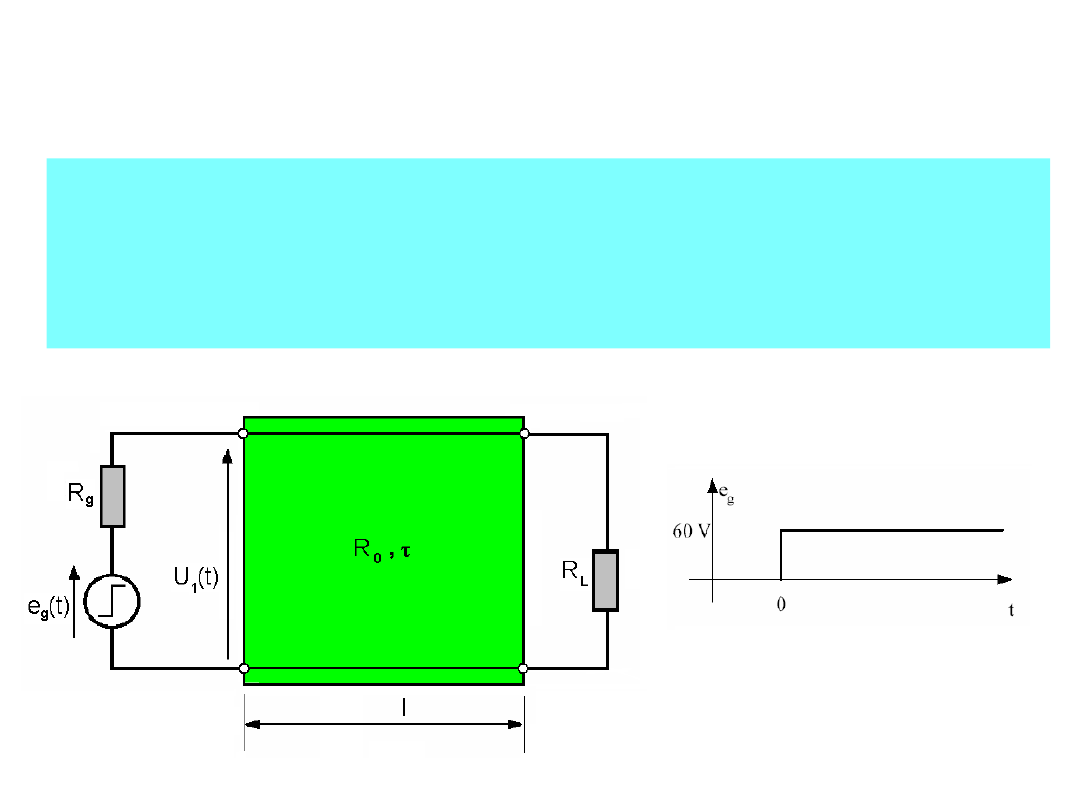
Rozważmy bezstratną linię długą:
o długości l i czasie propagacji τ, sterowaną ze
źródła napięcia e

g

(t) o rezystancji wejściowej R

g

,

przy rezystancji obciążenia R

L

.

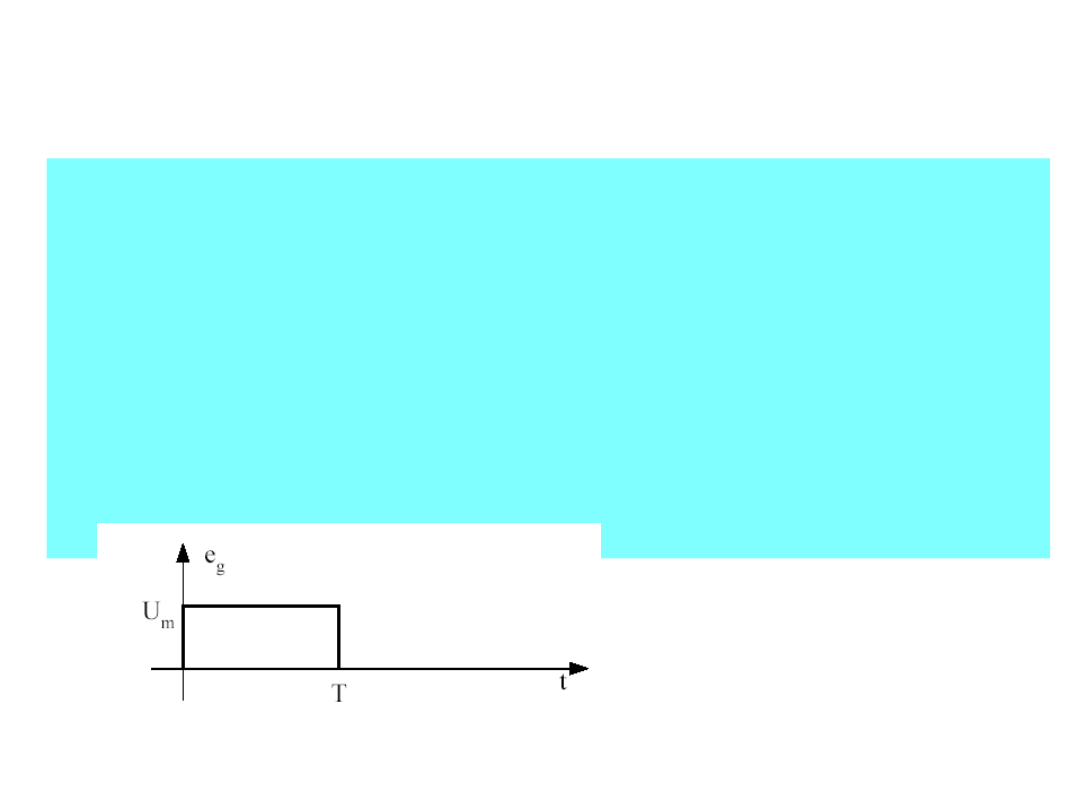
e

g

(t) = U

m

1(t)

25

TEORIA LINII DŁUGIEJ

Współczynniki odbicia na początku i końcu linii
długiej wynoszą:

o

g

o

g

R

R

R

R









1

o

L

o

L

R

R

R

R









2

Odcinek linii od momentu pobudzenia do chwili
powrotu fali odbitej od końca (0 < t < 2τ) obciąża
źródło e

g

(t) jako rezystancja równa R

0

. Schemat

zastępczy dla t = 0 przedstawia rysunek:

 

0

1

0

U

R

R

R

U

U

o

g

o

m







26

TEORIA LINII DŁUGIEJ

Fala napięciowa o amplitudzie U

0

przesuwa się ku

obciążeniu. W czasie od 0 do τ napięcie na
wyjściu linii długiej wynosi 0. Po czasie t=τ fala
dociera do obciążenia, gdzie następuje jej odbicie ze
współczynnikiem odbicia Г

2

. Amplituda napięcia na

końcu linii długiej jest superpozycją fali padającej i
odbitej stąd:

 

0

2

0

2

U

U

U









Na wejściu linii długiej amplituda napięcia wynosi U

0

aż do chwili kiedy fala odbita od końca (Г

2

U

0

) dotrze

do początku linii długiej. Wówczas do napięcia U

0

doda się fala padająca i odbita:

 

0

2

1

0

2

0

1

2

U

U

U

U















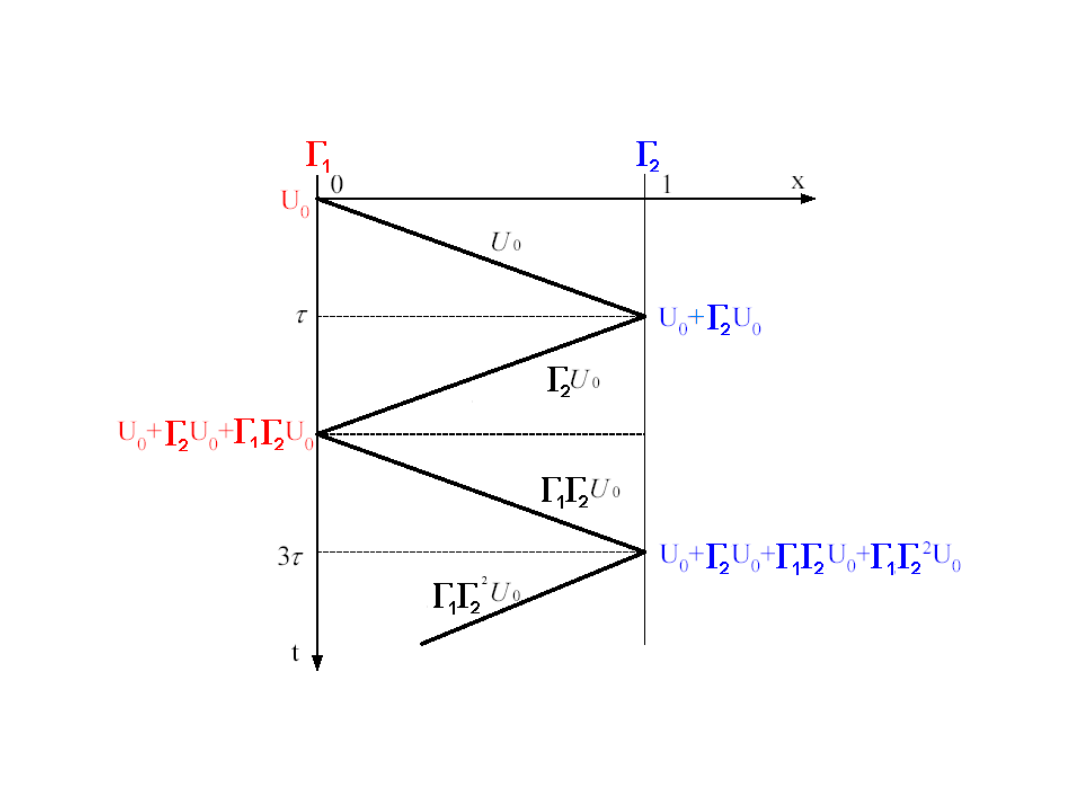
27

TEORIA LINII DŁUGIEJ

28

TEORIA LINII DŁUGIEJ

Napięcia dla na początku linii długiej w funkcji czasu
x = 0 (oznaczono kolorem czerwonym), natomiast
napięcia na końcu linii długiej dla x = l w funkcji
czasu (oznaczono kolorem niebieskim).
Napięcie na początku i końcu linii w funkcji czasu
przyjmie postać:

   



 

 







...

1

4

1

1

2

1

1

,

0

2

1

2

2

1

2

0

1

2

0

0































U

t

U

t

U

t

t

U





  

 

 







...

1

3

1

1

1

,

1

2

2

1

2

0

2

0



























U

t

U

t

t

l

U





29

TEORIA LINII DŁUGIEJ

W układach impulsowych o stałych rozłożonych
zwykle odcinek linii jest przynajmniej
jednostronnie dopasowany. Dzięki temu
osiągnięcie stanu ustalonego zachodzi w czasie nie
dłuższym niż 2τ. Z tych samych względów dąży się do
zapewnienia rzeczywistego charakteru obciążenia i
źródła.
Nigdy jednak nie jest możliwe całkowite uniknięcie
wpływu elementów reaktancyjnych.

   





m

m

g

U

T

t

U

t

t

e







1

1

Przy pobudzeniu o postaci:

30

TEORIA LINII DŁUGIEJ

31

TEORIA LINII DŁUGIEJ

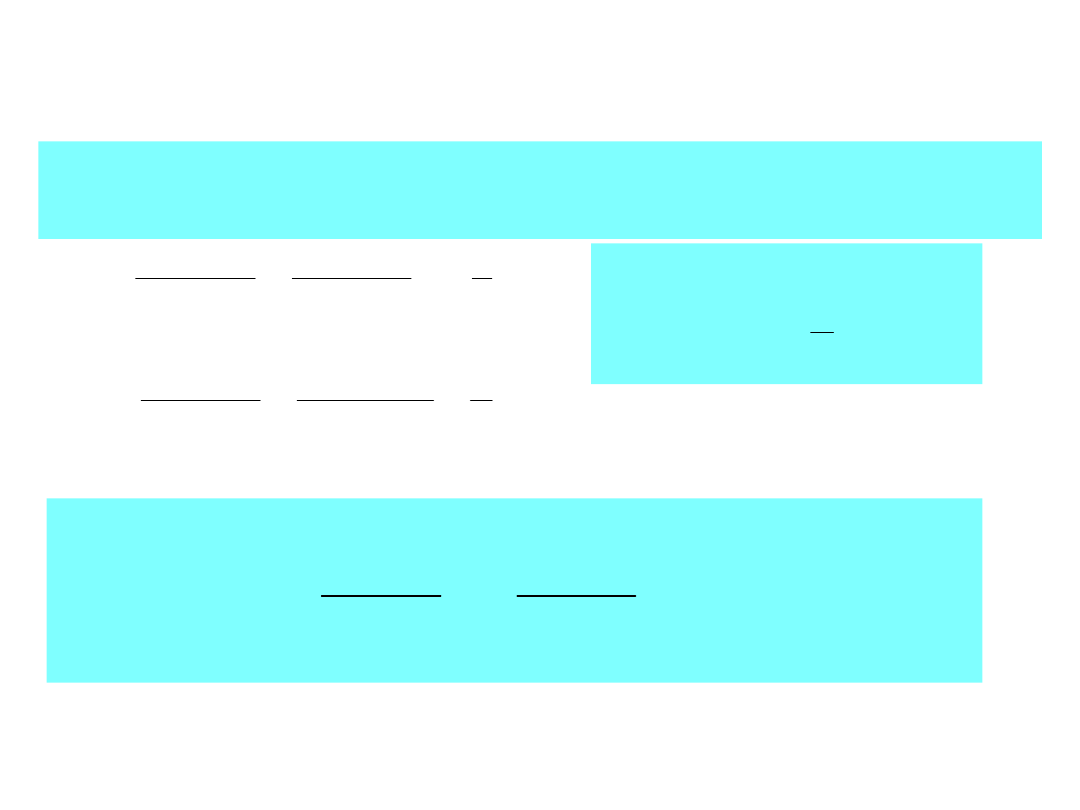
Przykład 1:
Obliczyć napięcia na początku i końcu bezstratnej
linii długiej przy – R

g

= 50Ω, R

L

= 300Ω, R

0

= 100Ω, l

= 10 cm, ν = 10

6

m/s.

32

Amplituda napięcia dla t = 0 wynosi:

TEORIA LINII DŁUGIEJ

Współczynniki odbicia na początku i końcu linii
długiej wynoszą:

3

1

100

50

100

50

1



















o

g

o

g

R

R

R

R

2

1

100

300

100

300

2

















o

L

o

L

R

R

R

R

Czas propagacji
linii wynosi:

s

l







1

,

0





V

R

R

R

U

U

o

g

o

m

40

100

50

100

60

0











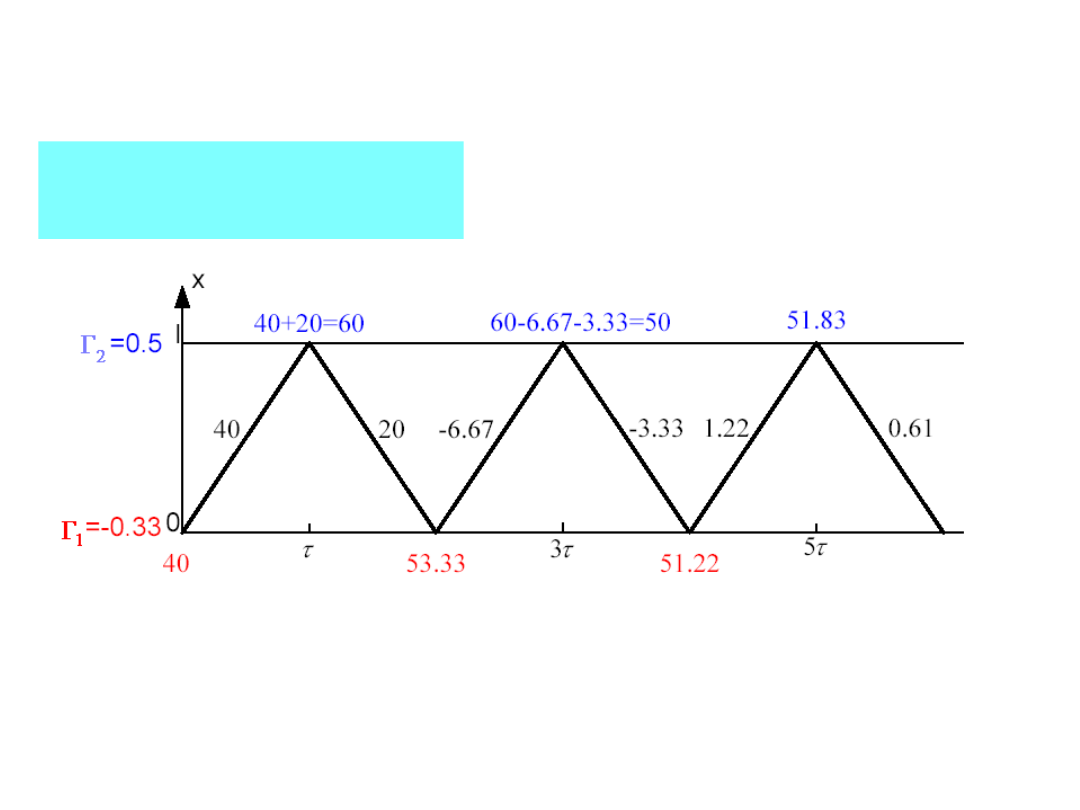
33

TEORIA LINII DŁUGIEJ

Schemat propagacji
fali:

34

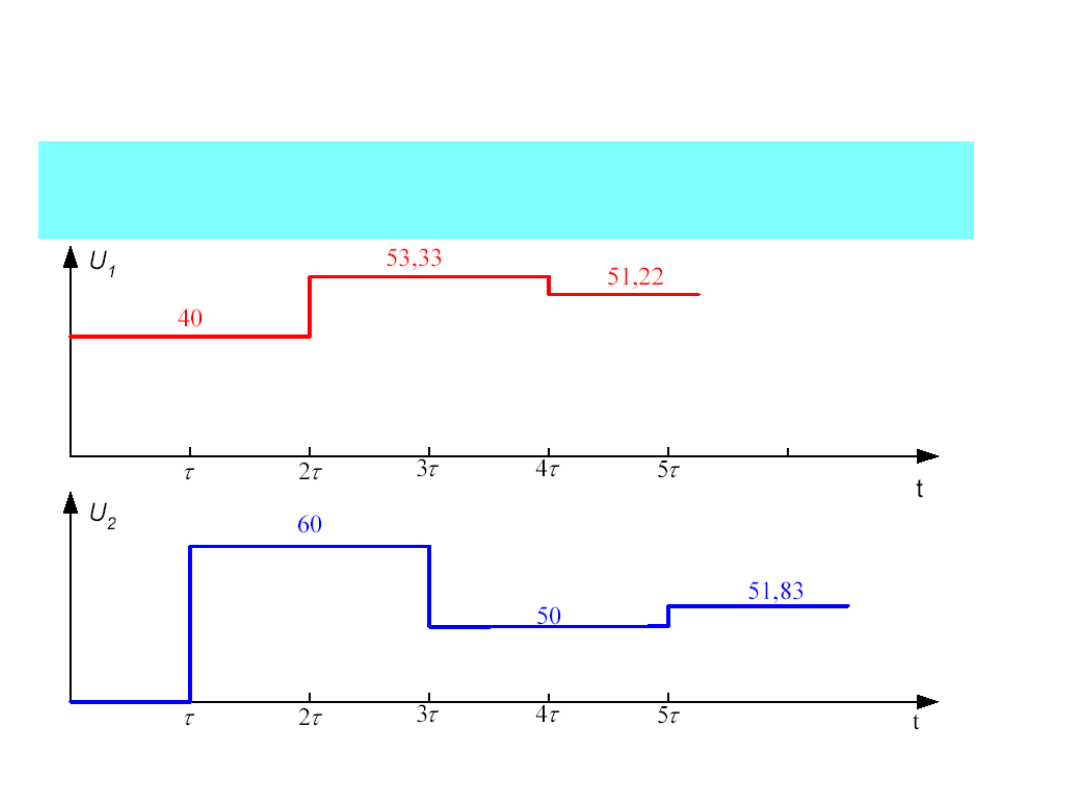
TEORIA LINII DŁUGIEJ

Napięcia na wejściu i wyjściu linii przedstawiono
poniżej:

35

TEORIA LINII DŁUGIEJ

Przykład 1:
Obliczyć napięcia na początku i końcu bezstratnej
linii długiej przy: R

g

= R

0

, R

L

= ∞, l = 100 cm, ν =

10

6

m/s.

36

TEORIA LINII DŁUGIEJ

Współczynniki odbicia na początku i końcu linii
długiej wynoszą:

0

1











o

g

o

g

R

R

R

R

1

2





















o

o

o

L

o

L

R

R

R

R

R

R

Czas propagacji
linii wynosi:

s

l







1





37

TEORIA LINII DŁUGIEJ

Wartości składowych napięcia na wejściu wynoszą
odpowiednio:

V

R

R

R

U

U

o

g

o

m

2

1

10







3

2

1

e

e

e

e

g







V

U

1

2

1

2

20









V

U

2

1

2

1

1

30





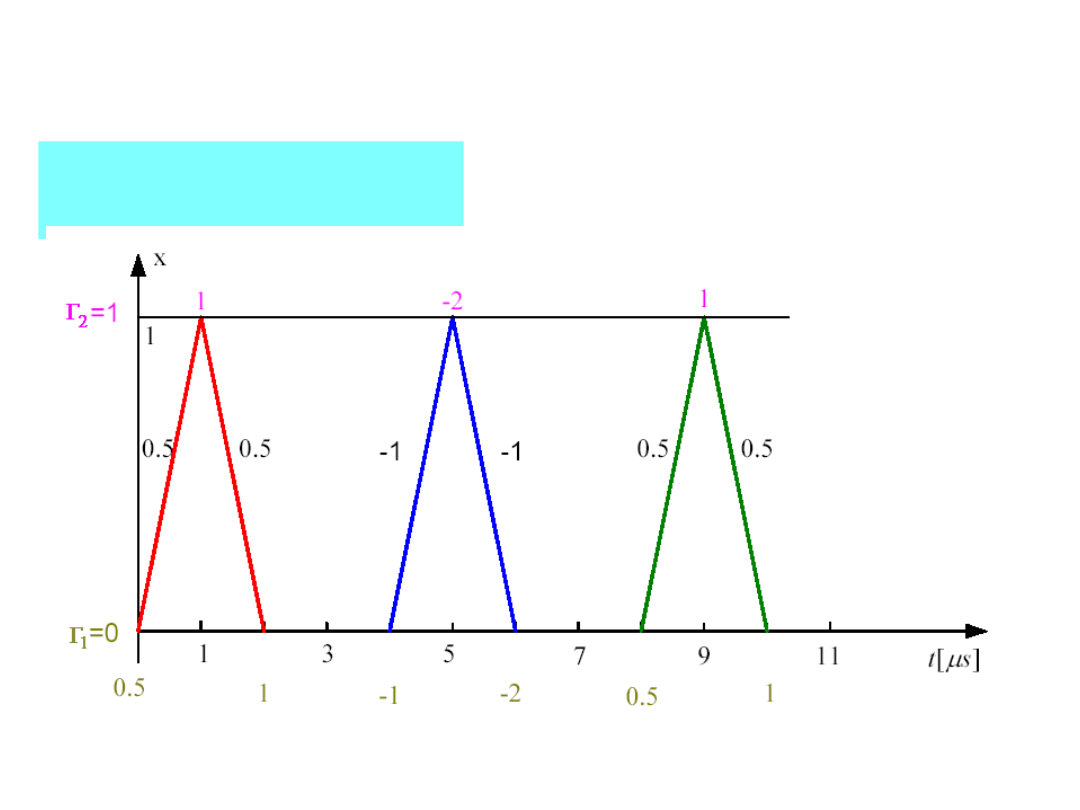
38

TEORIA LINII DŁUGIEJ

Schemat propagacji
fali:

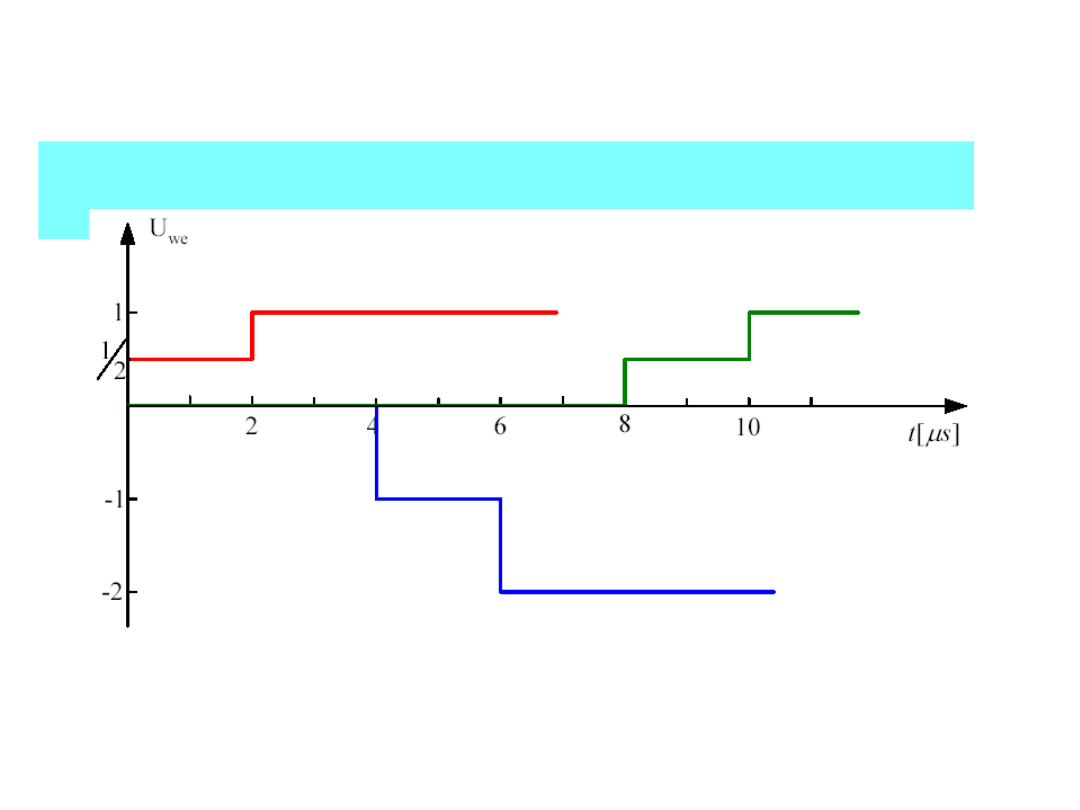
39

TEORIA LINII DŁUGIEJ

Składowe napięcia na wejściu linii przedstawiono
poniżej:

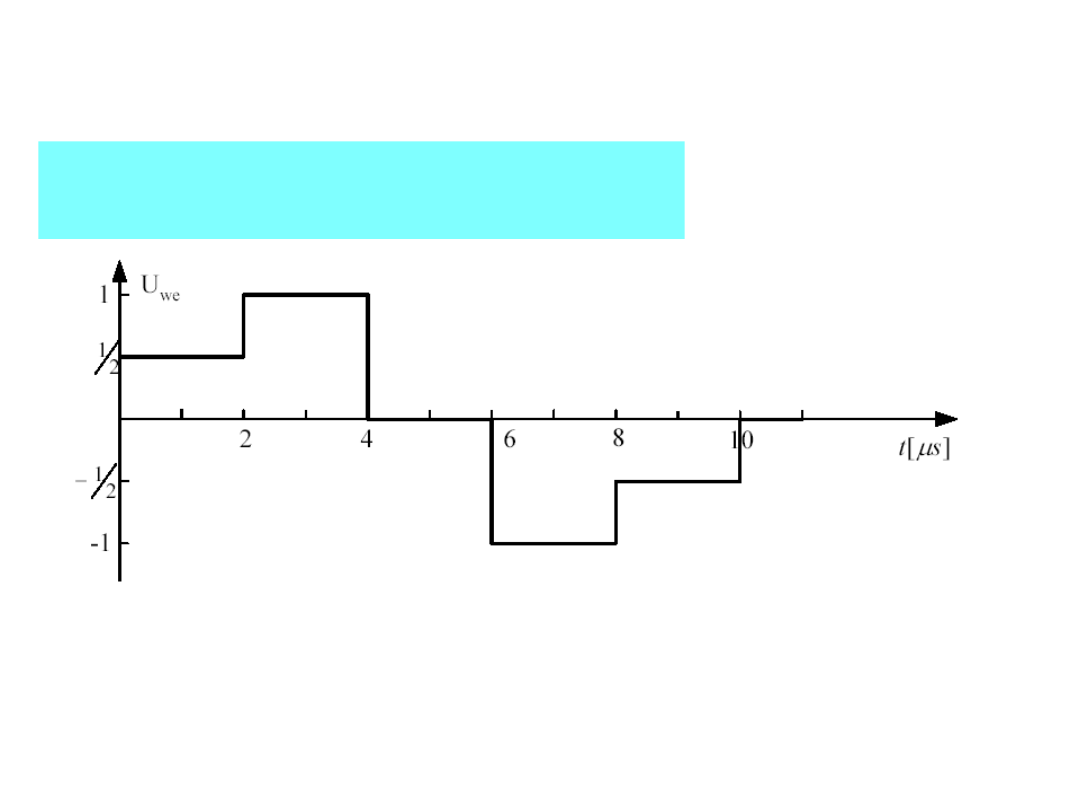
40

TEORIA LINII DŁUGIEJ

Napięcie na wejściu linii przyjmie
postać:

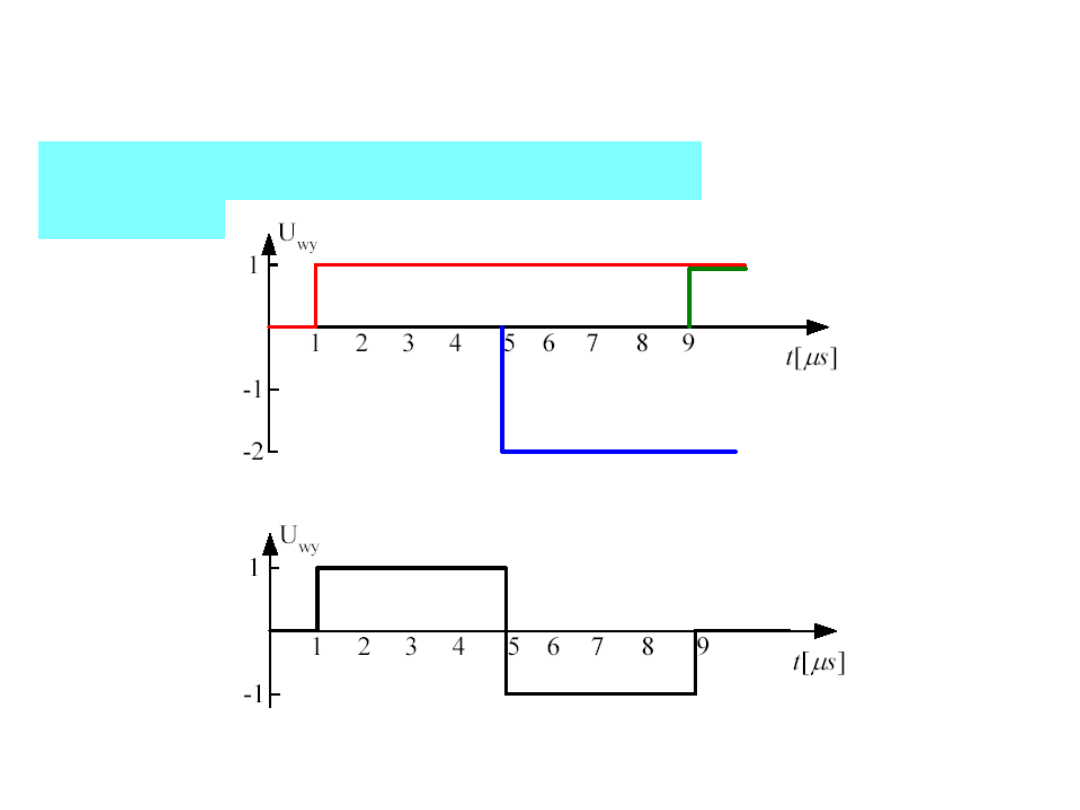
41

TEORIA LINII DŁUGIEJ

Napięcie na wyjściu linii przyjmie
postać:

42

TEORIA LINII DŁUGIEJ

Przykład 1:
Obliczyć napięcia na początku i końcu bezstratnej
linii długiej przy R

g

= R

0

= 100Ω, R

L

= 50Ω, α = 0,3

dB/m, l = 10 cm, ν = 10

6

m/s.

43

TEORIA LINII DŁUGIEJ

Współczynniki odbicia na początku i końcu linii
długiej wynoszą:

0

1











o

g

o

g

R

R

R

R

3

1

2













o

L

o

L

R

R

R

R

Czas propagacji
linii wynosi:

Współczynnik
tłumienia wynosi:

s

l







10





2





Zatem po czasie τ amplituda napięcia będzie
stłumiona raza.

2

V

R

R

R

e

U

o

g

o

g

we

30

2

1

60 







44

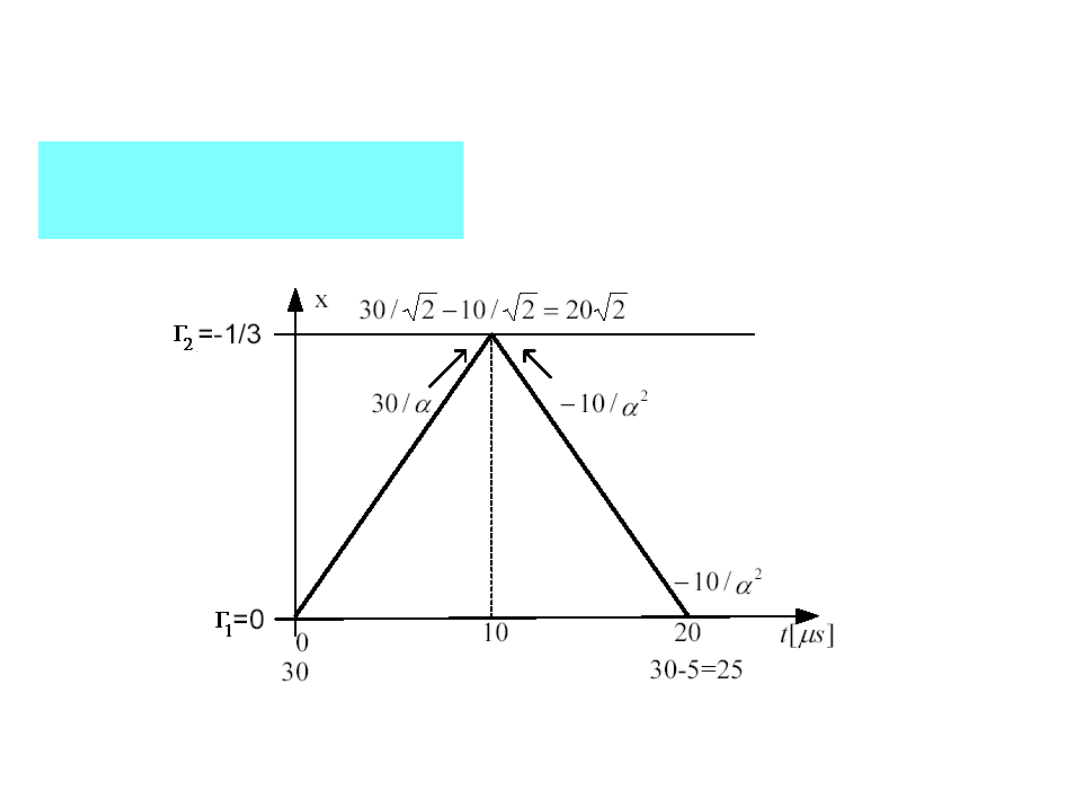
TEORIA LINII DŁUGIEJ

Schemat propagacji
fali:

45

TEORIA LINII DŁUGIEJ

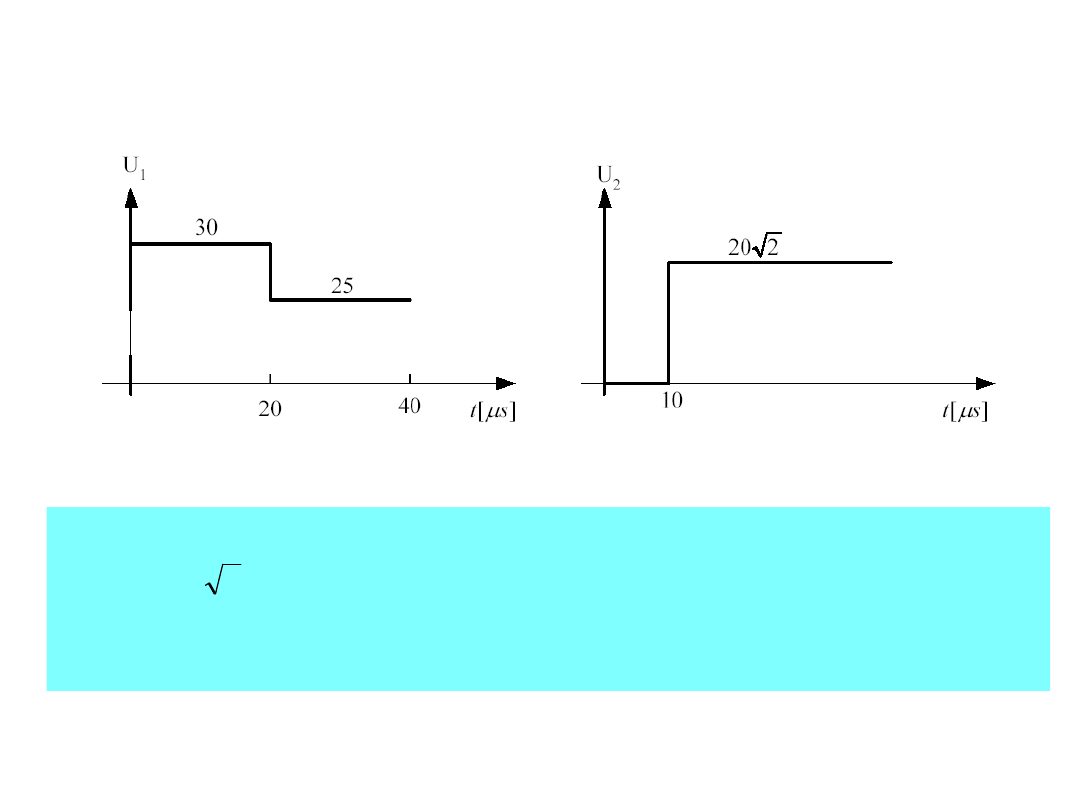
Zgodnie z rysunkiem fala odbita na wyjściu powraca
na wejście stłumiona -krotnie ale nie odbije się
dalej ponieważ współczynnik odbicia na wejściu linii
jest równy zero.

2

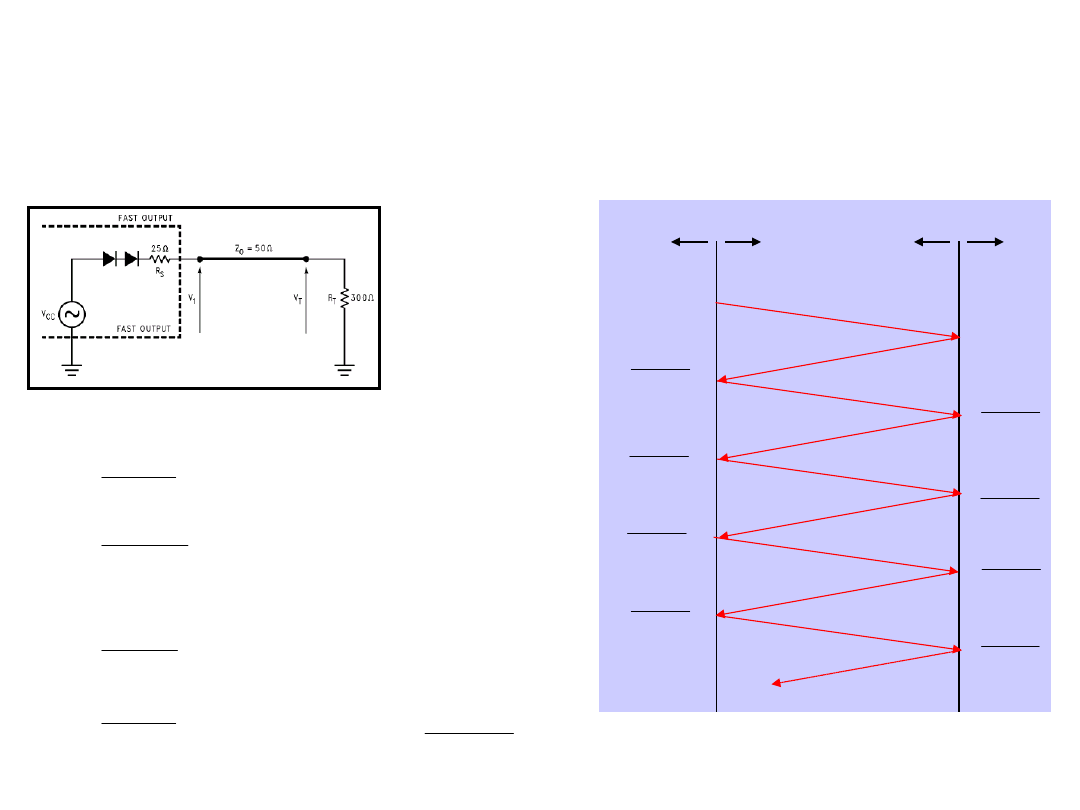
46

TEORIA LINII DŁUGIEJ

4

.

2

6

.

3

50

25

50

71

.

0

50

300

50

300

33

.

0

50

25

50

25

2

0

0

1

2

1





































V

Z

R

Z

V

V

VCC

Vo

s

BE

32

.

3

25

300

300

6

.

3

2







V

Początkowo:

Na końcu:

33

.

0

1







67

.

0

1

1







71

.

1

1

2







71

.

0

2





4

.

2

1



V

+2.40V

+1.70V

-0.56V

-0.40V

+0.13V

+0.09V

-0.03V

+0.02V

-0.03V

ETC

SUM

SUM

V

V

54

.

3

14

.

1





V

V

27

.

3

27

.

0





V

V

33

.

3

06

.

0





V

V

32

.

3

01

.

0





V

10

.

4



V

V

14

.

3

96

.

0





V

V

37

.

3

23

.

0





V

V

32

.

3

05

.

0





V

V

33

.

3

01

.

0





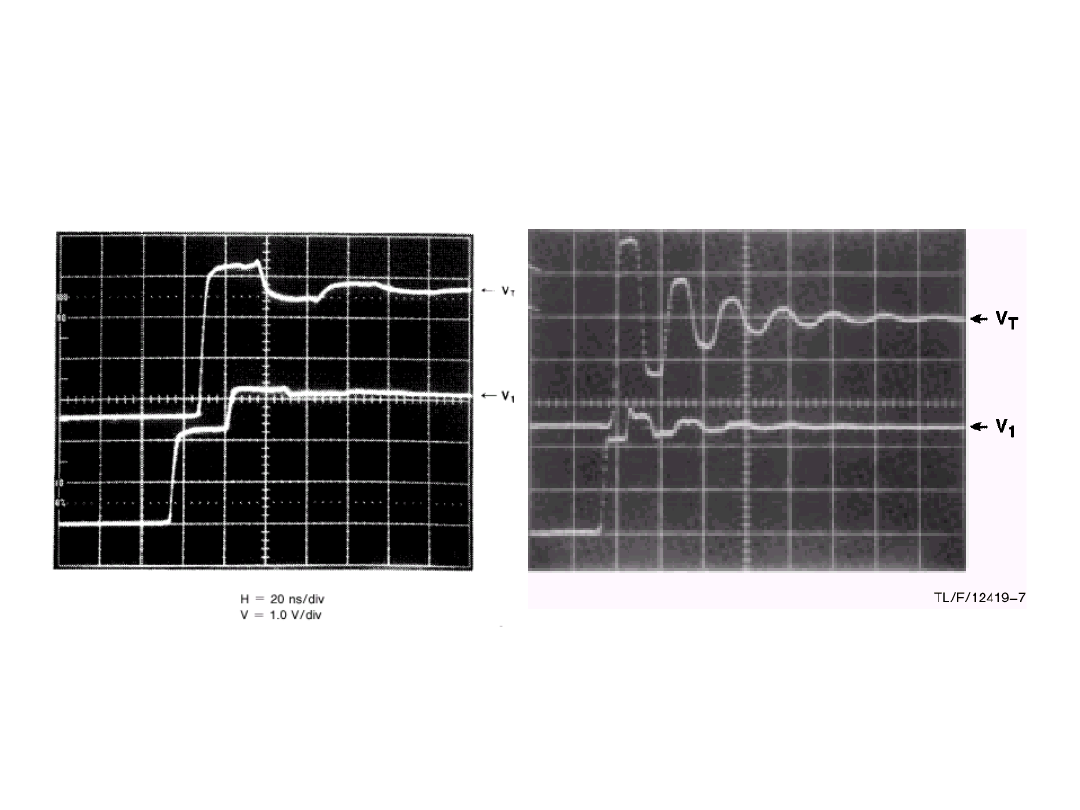
47

TEORIA LINII DŁUGIEJ



25

s

R



13

s

R

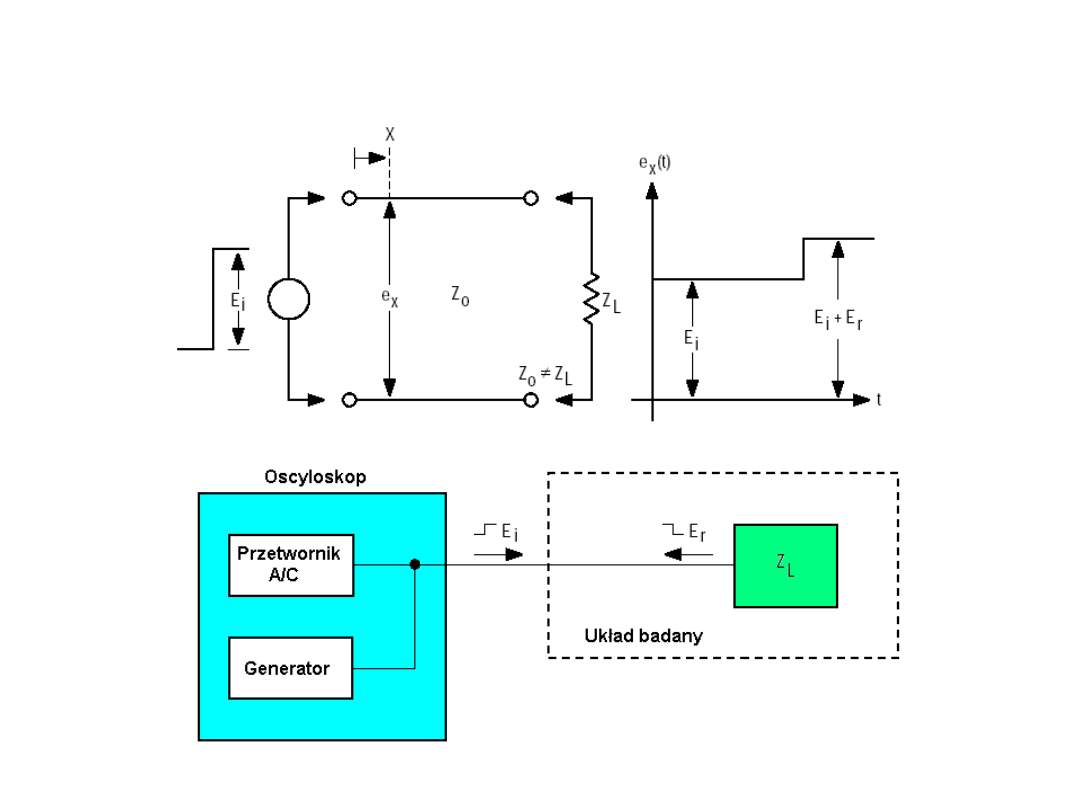
48

TEORIA LINII DŁUGIEJ

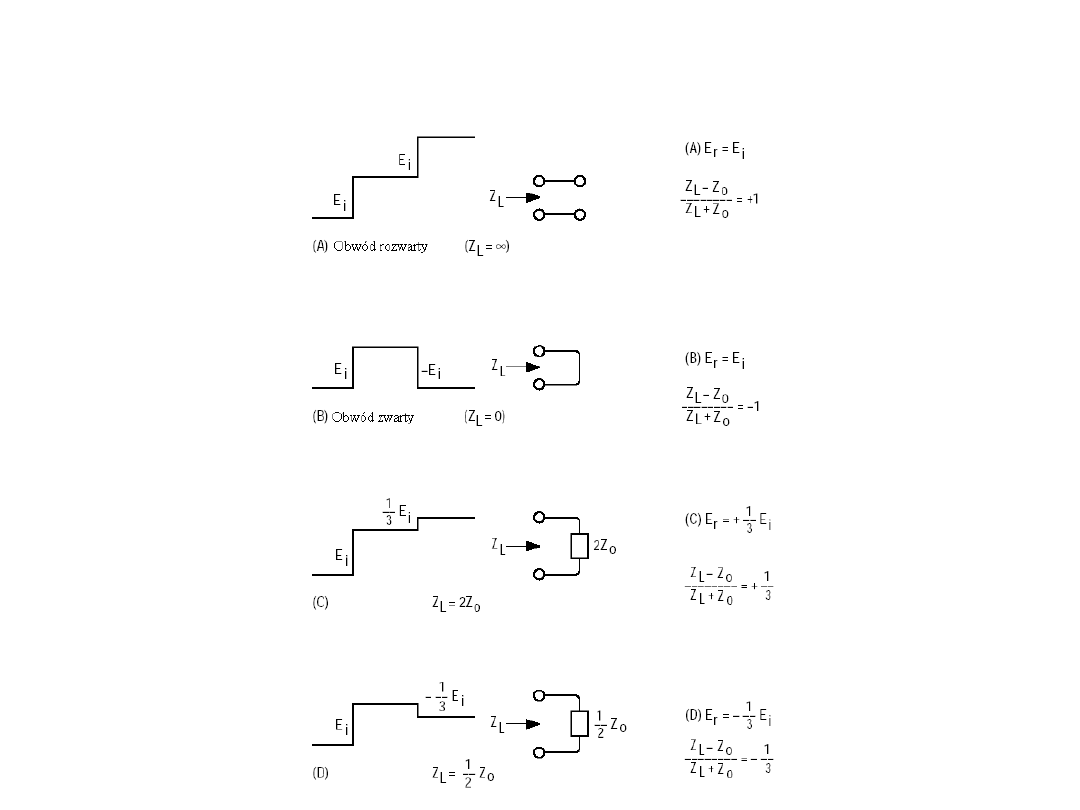
49

TEORIA LINII DŁUGIEJ

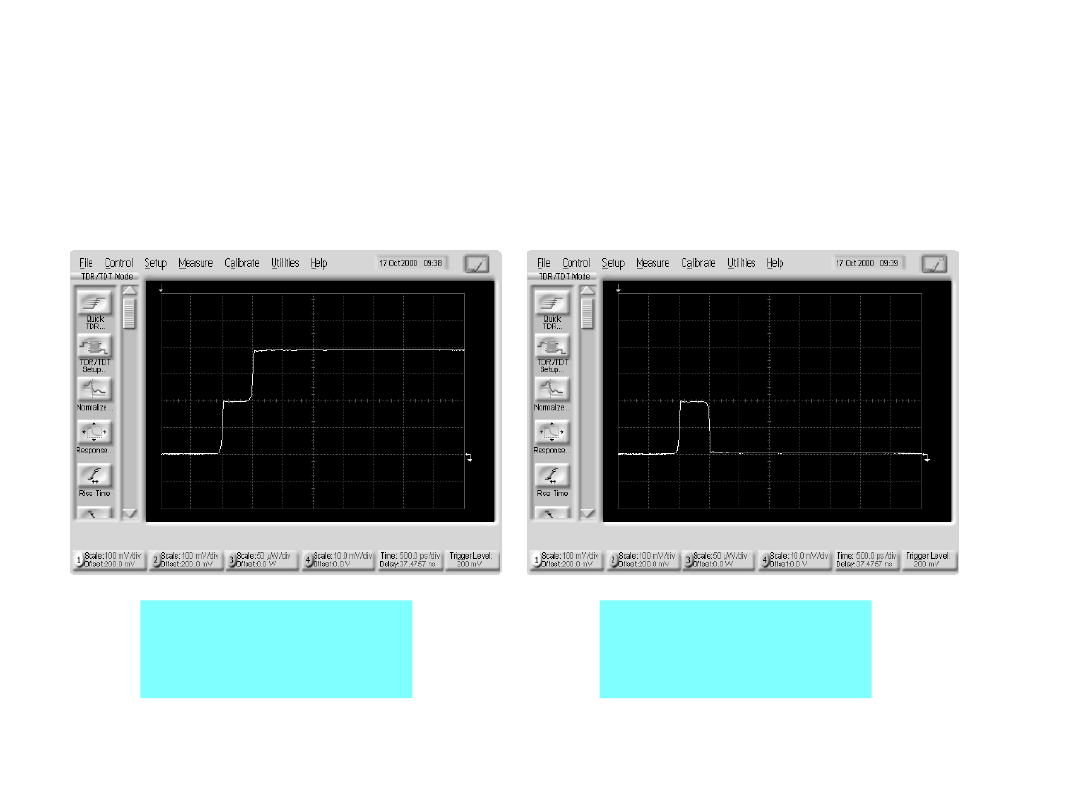
50

TEORIA LINII DŁUGIEJ

Obwód
rozwarty

Obwód
zwarty