czyli
Linie długie
czyli
nie zawsze bardzo długie
linie transmisyjne
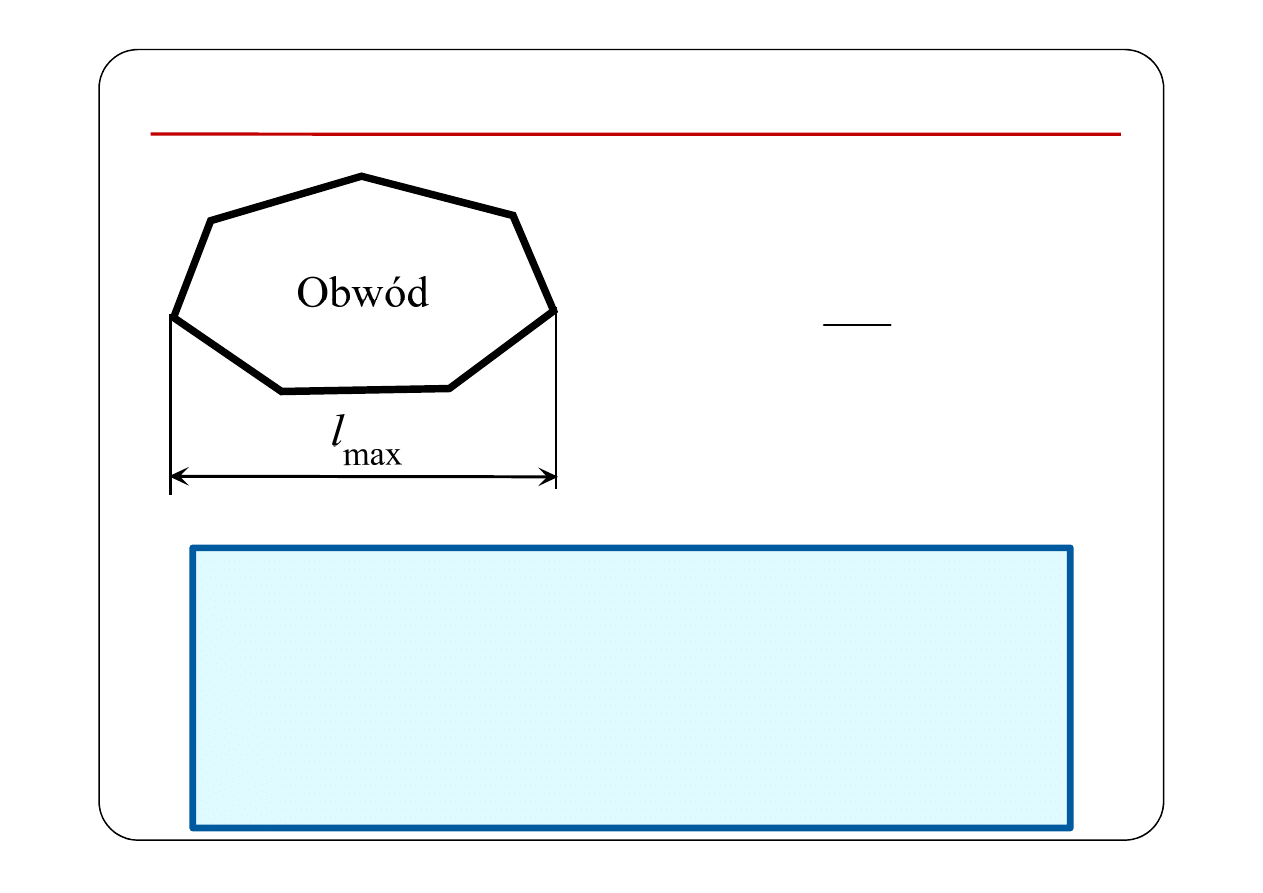
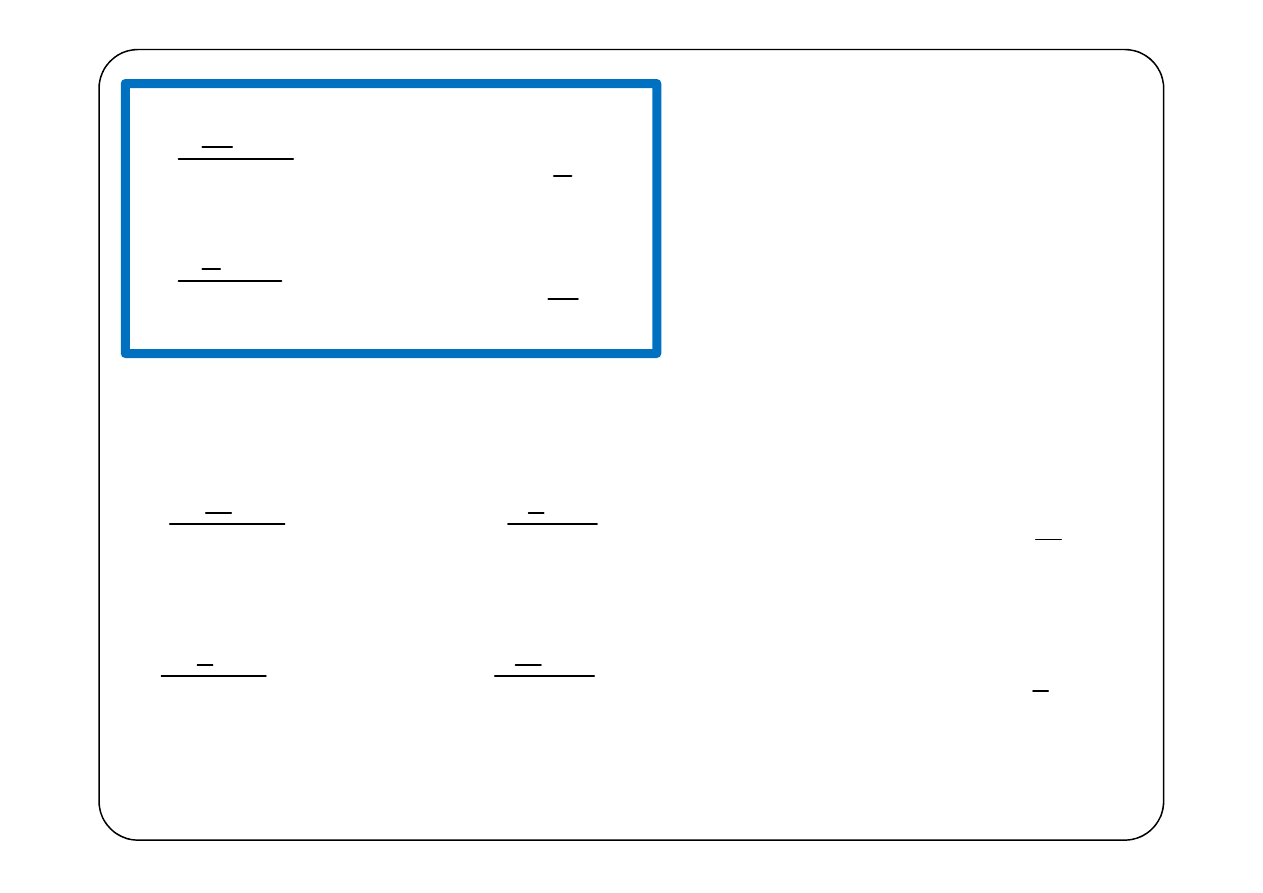
Kwazistacjonarność (przypomnienie)
max
l
c
τ
=
Czas potrzebny do przejścia
fali elektromagnetycznej
C
— prędkość światła
l
— maksymalny wymiar
l
max
— maksymalny wymiar
geometryczny obwodu
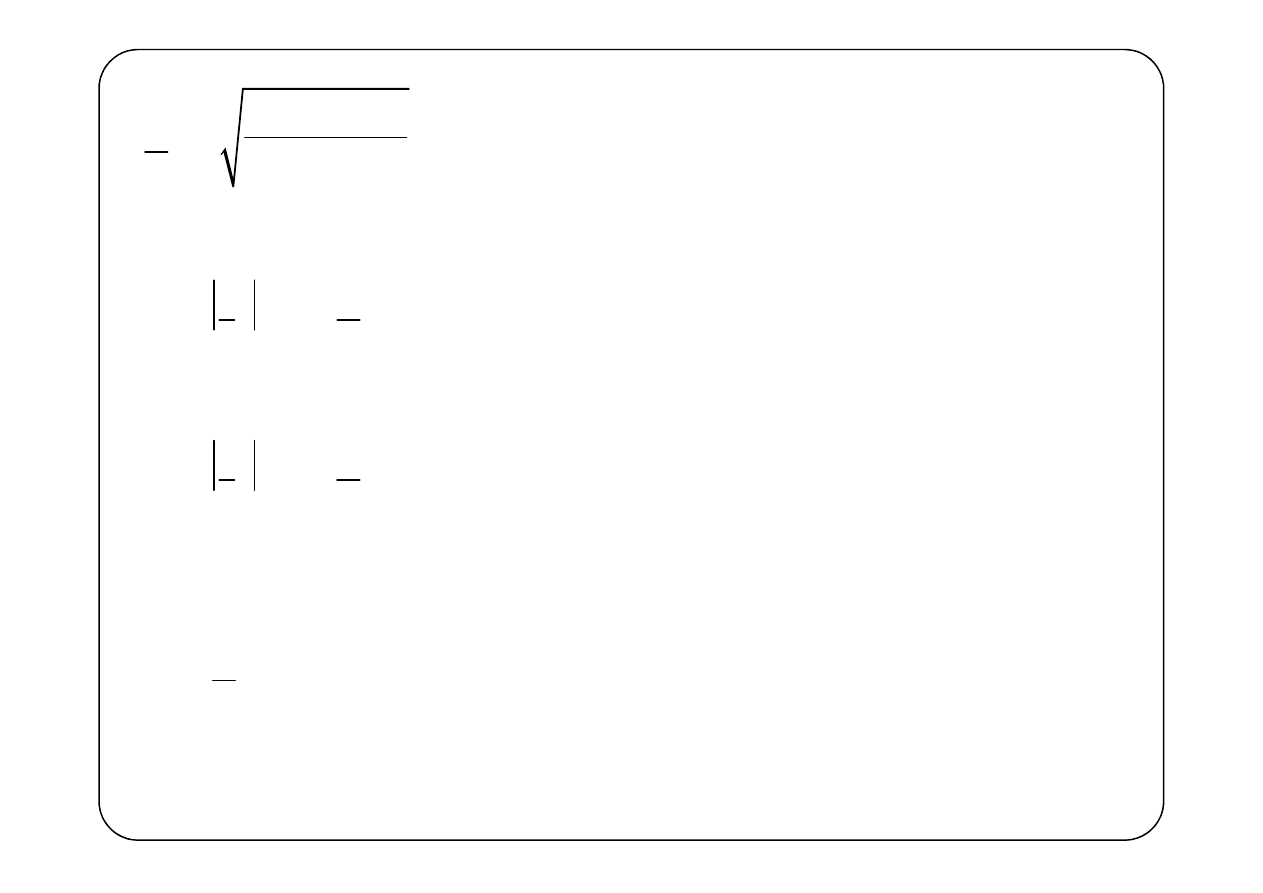
Obwód spełnia warunek kwazistacjonarności jeżeli
gdzie
oznaczają odpowiednio dowolny prąd
i dowolne napięcie w obwodzie. Obwód taki nazywać
będziemy
obwodem skupionym
.
( )
(
)
( )
(
)
,
k
k
k
k
i t
i t
u
t
u
t
τ
τ
≈
−
≈
−
( )
( )
k
k
i t
u
t
i
Warunek kwazistacjonarności będzie spełniony, gdy
gdzie
λ
jest długością fali elektromagnetycznej rozchodzącej
się w obwodzie.
max
max
0
czyli
c
l
l
f
λ
≪
≪
x
y
a
λ
≪
a
b
l
z
a
b
l
λ
λ
λ
≪
≪
∼

0
x
=
x
l
=
( )
,0
u t
( )
,0
i t
( )
,
u t x
( )
,
i t x
( )
,
u t l
( )
,
i t l
x
x
∆
( )
,
i t x
(
)
,
i t x
x
+ ∆
x
λ
∆
≪
( )
,
u t x
(
)
,
u t x
x
+ ∆
x
x
x
+ ∆
( )
,
u t x
( )
,
i t x
R
∆
L
∆
G
∆
C
∆
(
)
,
u t x
x
+ ∆
(
)
,
i t x
x
+ ∆

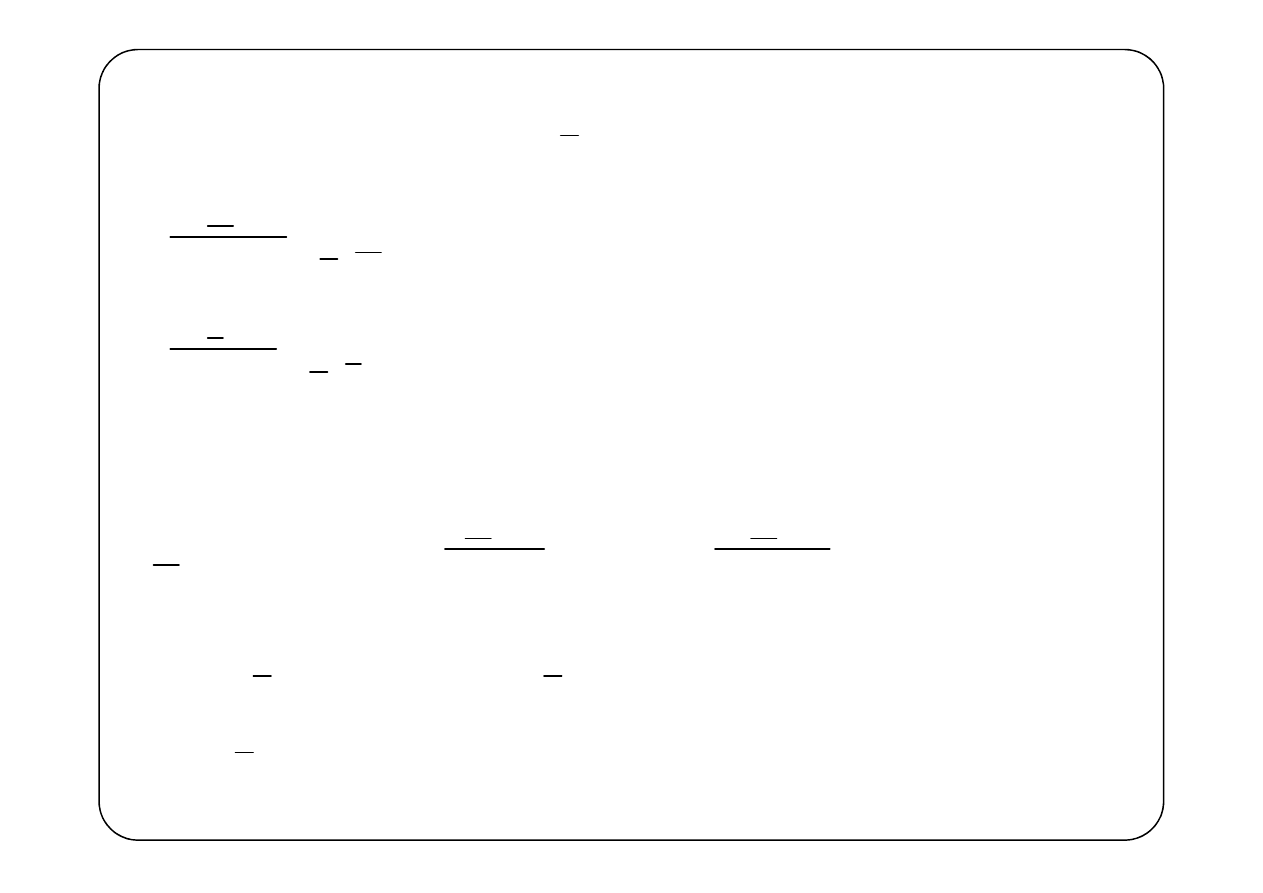
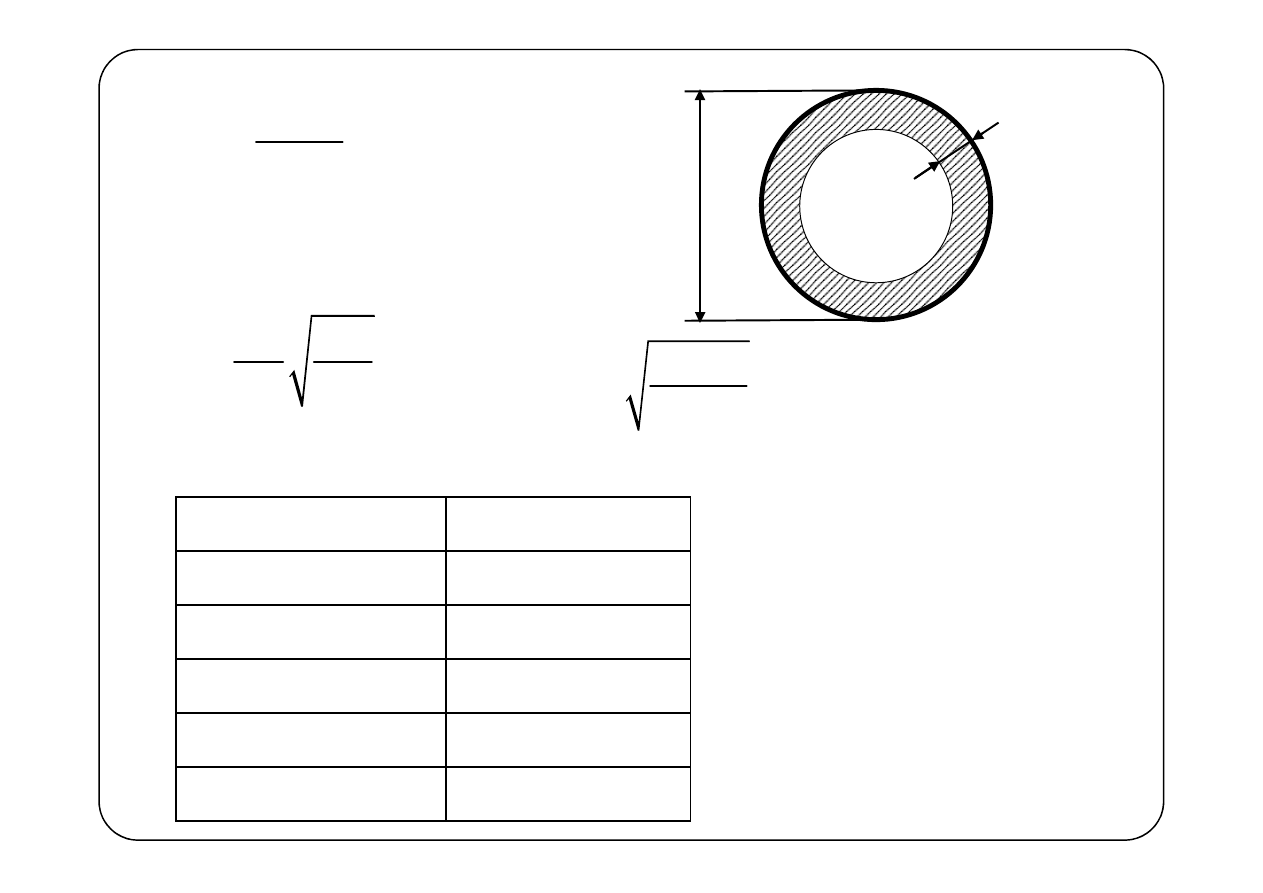
Parametry jednostkowe linii
0
0
lim
x
R
R
x
∆ →
∆
∆
≜
— rezystancja jednostkowa,
[ ]
0
Ω
m
R
=
0
0
lim
x
L
L
x
∆ →
∆
∆
≜
— indukcyjność jednostkowa,
[ ]
0
H
m
L
=
0
0
lim
x
G
G
x
∆ →
∆
∆
≜
— upływność jednostkowa,
[ ]
0
S
m
G
=
0
0
lim
x
C
C
x
∆ →
∆
∆
≜
— pojemność jednostkowa,
[ ]
0
F
m
C
=
Założymy, że linia jest jednorodna, czyli że parametry
jednostkowe nie zmieniają się wzdłuż linii. Wówczas
0
0
0
0
,
,
,
R
R
x
L
L x
G
G
x
C
C
x
∆ = ∆
∆ = ∆
∆ = ∆
∆ = ∆
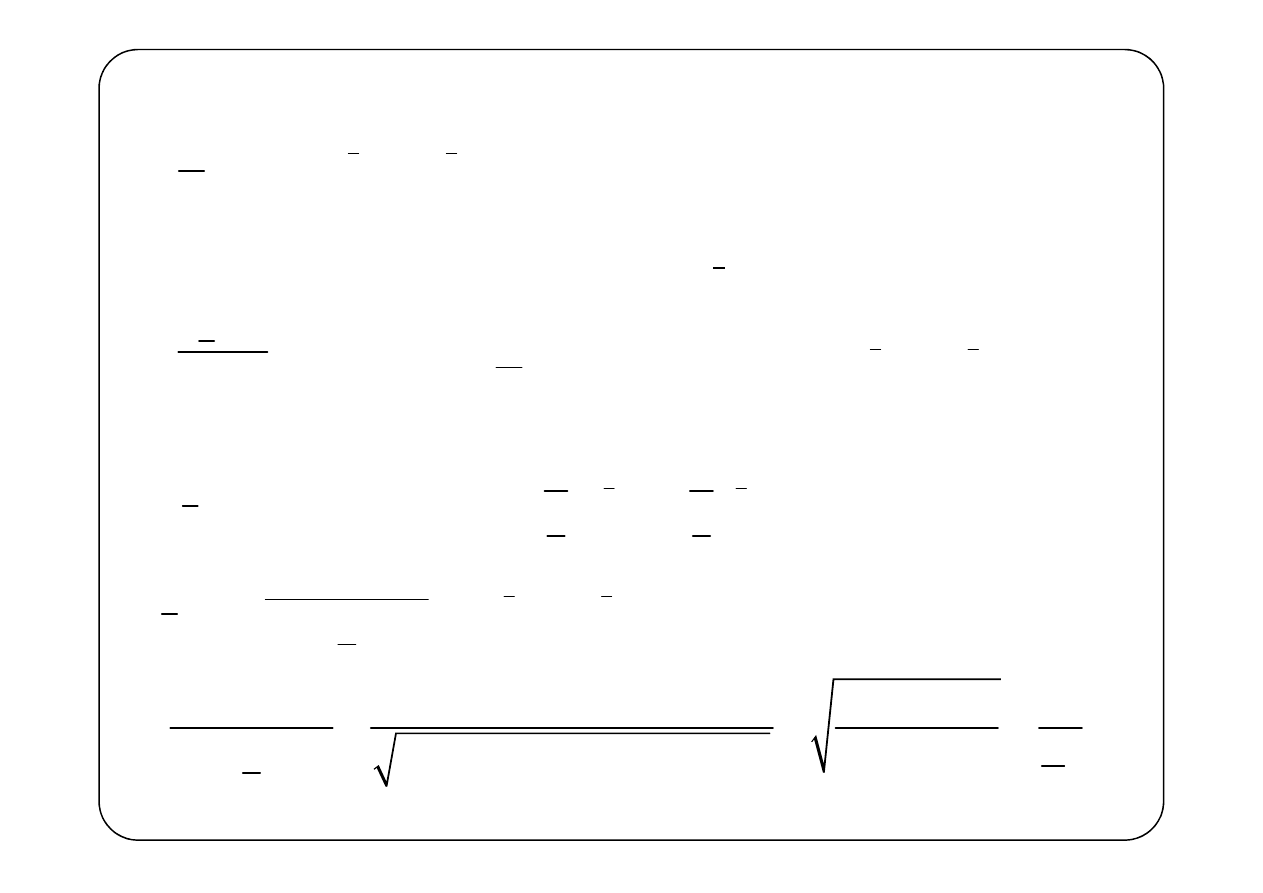
Równania linii długiej
0
R
x
∆
0
L
x
∆
0
G
x
∆
0
C
x
∆
( )
,
u t x
( )
,
i t x
( )
,
i t x
(
)
,
i t x
x
+ ∆
(
)
,
u t x
x
+ ∆
(
)
,
u t x
x
+ ∆
I prawo Kirchhoffa
I prawo Kirchhoffa
( )
(
)
(
) (
)
0
0
,
,
,
,
0
u t x
x
i t x
G
x u t x
x
C
x
i t x
x
t
∂
+ ∆
−
+ ∆
+ ∆ + ∆
+
+ ∆ =
∂
II prawo Kirchhoffa
( )
( )
( ) (
)
0
0
,
,
,
,
0
i t x
u t x
R
x i t x
L
x
u t x
x
t
∂
−
+ ∆
+ ∆
+
+ ∆ =
∂
(
) ( )
( )
( )( )
( )
( )
2
2
2
,
,
,
1
,
,
,
2
i t x
i t x
i t x
i t x
x
i t x
x
x
i t x
x
x
x
x
∂
∂
∂
+ ∆ =
+
∆ +
∆
+ ≈
+
∆
∂
∂
∂
⋯
(
) ( )
(
)
(
)
0
0
,
,
,
,
u t x
x
i t x
x
i t x
G u t x
x
C
x
t
∂
+ ∆
+ ∆ −
= −
+ ∆ +
∆
∂
(
) ( )
( )
( )
0
0
,
,
,
,
i t x
u t x
x
u t x
R i t x
L
x
t
∂
+ ∆ −
= −
+
∆
∂
(
) ( )
( )
( )( )
( )
( )
2
2
2
,
,
,
1
,
,
,
2
u t x
u t x
u t x
u t x
x
u t x
x
x
u t x
x
x
x
x
∂
∂
∂
+ ∆ =
+
∆ +
∆
+ ≈
+
∆
∂
∂
∂
⋯
( )
( )
( )
( )
( )
( )
( )
( ) ( )
0
0
2
2
0
0
0
0
,
,
,
,
,
,
,
,
u t x
i t x
x
R i t x
L
x
x
t
i t x
u t x
u t x
u t x
x
G u t x
C
x
G
C
x
x
t
x
x t
∂
∂
∆ = −
+
∆
∂
∂
∂
∂
∂
∂
∆ = −
+
∆ −
+
∆
∂
∂
∂
∂ ∂
( )
2
0
pomijamy
x
x
∆ →
⇒
∆
( )
( )
( )
( )
( )
( )
0
0
0
0
,
,
,
,
,
,
u t x
i t x
R i t x
L
x
t
i t x
u t x
G u t x
C
x
t
∂
∂
−
=
+
∂
∂
∂
∂
−
=
+
∂
∂
( )
( )
( )
( )
( )
( )
2
2
0
0
2
2
2
0
0
2
,
,
,
,
,
,
u t x
i t x
i
t x
R
L
x
t x
x
i
t x
u t x
u
t x
G
C
x t
t
t
∂
∂
∂
−
=
+
∂
∂ ∂
∂
∂
∂
∂
−
=
+
∂ ∂
∂
∂
( )
( )
( )
( )
( )
2
2
0
0
0
0
0
0
2
2
,
,
,
,
,
u t x
u t x
u t x
u
t x
R
G u t x
C
L
G
C
t
t
x
t
∂
∂
∂
∂
−
=
−
−
+
−
−
∂
∂
∂
∂
( ) (
) ( )
( )
( )
( ) (
) ( )
( )
( )
2
2
0
0
0
0
0
0
0
0
2
2
2
2
0
0
0
0
0
0
0
0
2
2
,
,
,
,
0
,
,
,
,
0
u t x
u t x
u t x
L C
R C
G L
R G u t x
t
t
x
i t x
i t x
i t x
L C
R C
G L
R G i t x
t
t
x
∂
∂
∂
+
+
+
−
=
∂
∂
∂
∂
∂
∂
+
+
+
−
=
∂
∂
∂
Równania telegrafistów
W szczególnym przypadku R
0
= 0 i G
0
= 0 (linia bezstratna)
( )
( )
( )
( )
2
2
0
0
2
2
2
2
0
0
2
2
,
,
0
,
,
0
u t x
u t x
L C
t
x
i t x
i t x
L C
t
x
∂
∂
−
=
∂
∂
∂
∂
−
=
∂
∂
Równania fali płaskiej
Rozwiązania równań linii długiej
Założymy, że przebiegi napięć i prądów, przy ustalonym x są
przebiegami sinusoidalnymi o postaci:
( )
( )
( )
( )
{
}
( )
( )
( )
( ) ( )
( )
( )
{
}
0
u
0
j
0
u
j
j
0
i
,
2 sin
2 Im
e
,
e
,
,
2 sin
2 Im
e
,
t
x
t
u t x
U x
t
x
U x
U x
U x
i t x
I x
t
x
I x
ω
ψ
ω
ω
ψ
ω
ψ
=
+
=
=
=
+
=
( ) ( )
( )
( )
{
}
( ) ( )
( )
i
0
i
j
e
,
x
I x
I x
ψ
=
Wówczas
( )
( )
{
}
( )
( )
0
0
j
0
j
,
2 Im j
e
,
d
2 Im
e
d
t
t
u t x
U x
t
u t x
U x
x
x
ω
ω
ω
∂
=
∂
∂
=
∂
( )
( )
{
}
( )
( )
0
0
j
0
j
,
2 Im j
e
,
d
2 Im
e
d
t
t
i t x
I x
t
i t x
I x
x
x
ω
ω
ω
∂
=
∂
∂
=
∂
( )
( )
( )
( )
( )
{
}
( )
{
}
0
0
0
0
0
j
j
j
0
0
0
,
,
,
d
2 Im
e
2 Im
e
2 Im j
e
d
t
t
t
u t x
i t x
R i t x
L
x
t
U x
R
I x
L
I x
t
ω
ω
ω
ω
∂
∂
−
=
+
∂
∂
⇓
−
=
+
( )
( )
( )
( )
( )
{
}
( )
{
}
0
0
0
0
0
j
j
j
0
0
0
,
,
,
d
2 Im
e
2 Im
e
2 Im j
e
d
t
t
t
i t x
u t x
G u t x
C
x
t
I x
G
U x
C
U x
t
ω
ω
ω
ω
∂
∂
−
=
+
∂
∂
⇓
−
=
+
Równania linii długiej
w postaci symbolicznej
( ) (
) ( )
( ) (
) ( )
0
0
0
0
0
0
d
j
d
d
j
d
U x
R
L I x
x
I x
G
C U x
x
ω
ω
−
=
+
−
=
+
Po zróżniczkowaniu każdego z równań otrzymujemy
( ) (
) ( )
(
)(
) ( )
2
0
0
0
0
0
0
0
0
0
2
d
d
j
j
j
d
d
U x
I x
R
L
R
L
G
C U x
x
x
ω
ω
ω
−
=
+
= −
+
+
( ) (
) ( )
(
)(
) ( )
2
0
0
0
0
0
0
0
0
0
2
d
d
j
j
j
d
d
I x
U x
G
C
R
L
G
C
I x
x
x
ω
ω
ω
−
=
+
= −
+
+
(
)(
)
2
0
0
0
0
0
0
j
j
R
L
G
C
ω
ω
γ
+
+
=
( )
( )
( )
( )
2
2
2
2
2
2
d
0
d
d
0
d
U x
U x
x
I x
I x
x
γ
γ
−
=
−
=
Poszukujemy rozwiązania o postaci
Poszukujemy rozwiązania o postaci
( )
( )
( )
2
2
2
d
d
e
e ,
e
d
d
rx
rx
rx
U x
U x
U x
r
r
x
x
=
⇒
=
=
2
2
2
2
e
e
0
0
rx
rx
r
r
γ
γ
−
=
⇒
−
=
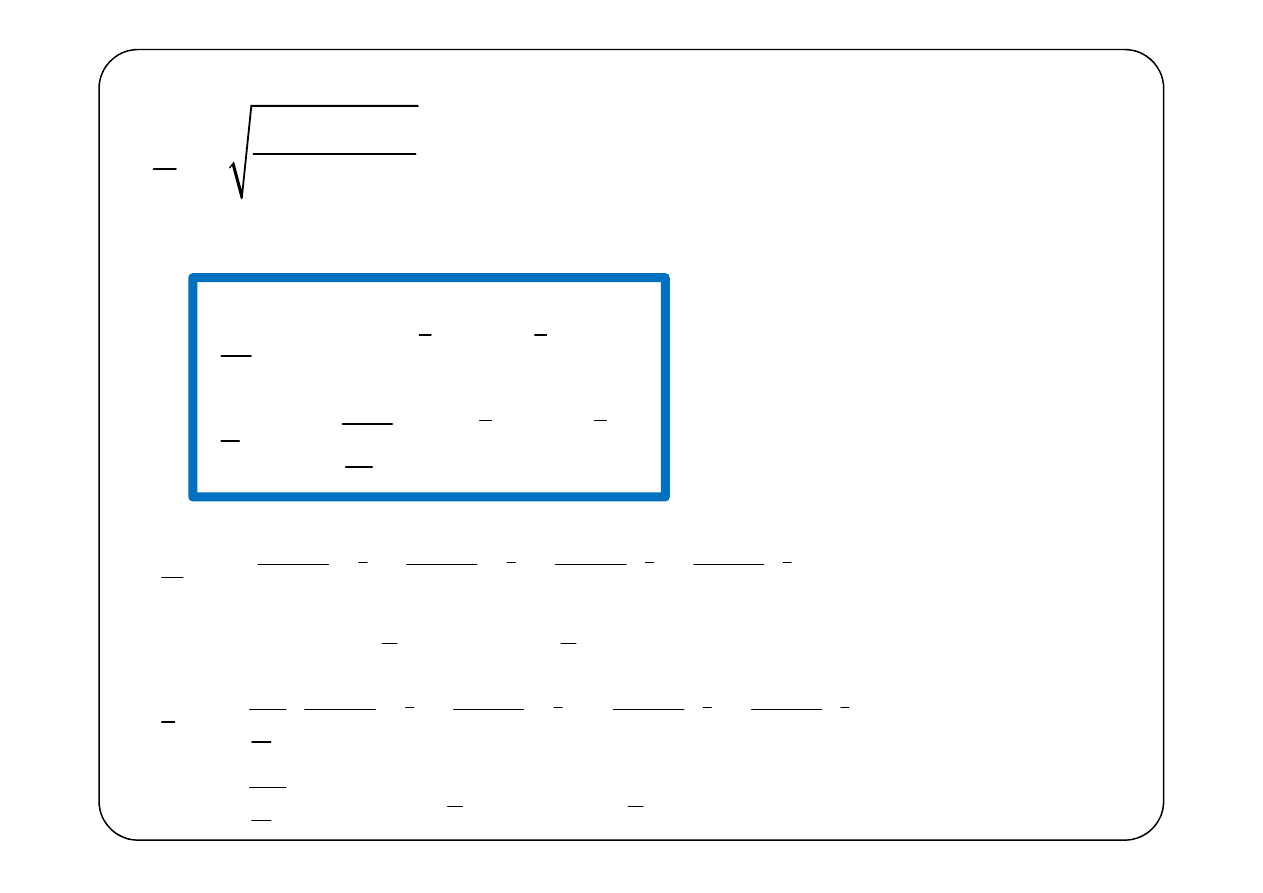
Równanie charakterystyczne
r
γ
= ±
Rozwiązanie ogólne równania na napięcie
( )
e
e
x
x
U x
A
B
γ
γ
−
=
+
( ) (
) ( ) (
)
(
)
0
0
0
0
0
0
d
j
j
e
e
d
x
x
I x
G
C U x
G
C
A
B
x
γ
γ
ω
ω
−
−
=
+
=
+
+
Po podstawieniu do równania na prąd I(x)
( )
(
)
( )
(
)
0
0
0
0
0
0
1
1
j
e
e
j
e
e
x
x
x
x
I x
G
C
A
B
G
C
I x
A
B
γ
γ
γ
γ
ω
γ
γ
ω
γ
−
−
−
=
+
−
+
+
=
−
(
)(
)
0
0
0
0
0
0
0
0
0
f
0
0
0
0
0
0
0
0
0
j
j
j
1
j
j
j
G
C
G
C
G
C
R
L
Z
R
L
G
C
ω
ω
ω
γ
ω
ω
ω
+
+
+
=
=
=
+
+
+
0
0
0
f
0
0
0
j
j
R
L
Z
G
C
ω
ω
+
=
+
— impedancja falowa linii
Ostatecznie
( )
( )
(
)
e
e
1
e
e
x
x
x
x
U x
A
B
I x
A
B
Z
γ
γ
γ
γ
−
−
=
+
=
−
Rozwiązania ogólne
równań linii długiej
( )
(
)
f
Z
( )
(
)
(
)
e
e
e
e
2
2
2
2
ch
sh
x
x
x
x
B
A
B
A
B
A
B
A
U x
B
A
x
B
A
x
γ
γ
γ
γ
γ
γ
−
−
+
−
+
−
=
−
+
+
=
=
+
+
−
( )
(
)
(
)
(
)
f
f
1
e
e
e
e
2
2
2
2
1
sh
ch
x
x
x
x
B
A
B
A
B
A
B
A
I x
Z
B
A
x
B
A
x
Z
γ
γ
γ
γ
γ
γ
−
−
+
−
+
−
=
−
−
+
=
=
−
+
−
−
,
A
B
A
B
B
A
′
′
= +
= −
Alternatywna postać
rozwiązań ogólnych
równań linii długiej
( )
( )
f
ch
sh
1
sh
ch
U x
A
x
B
x
I x
A
x
B
x
Z
γ
γ
γ
γ
′
′
=
+
′
′
= −
+
0
x
=
x
l
=
x
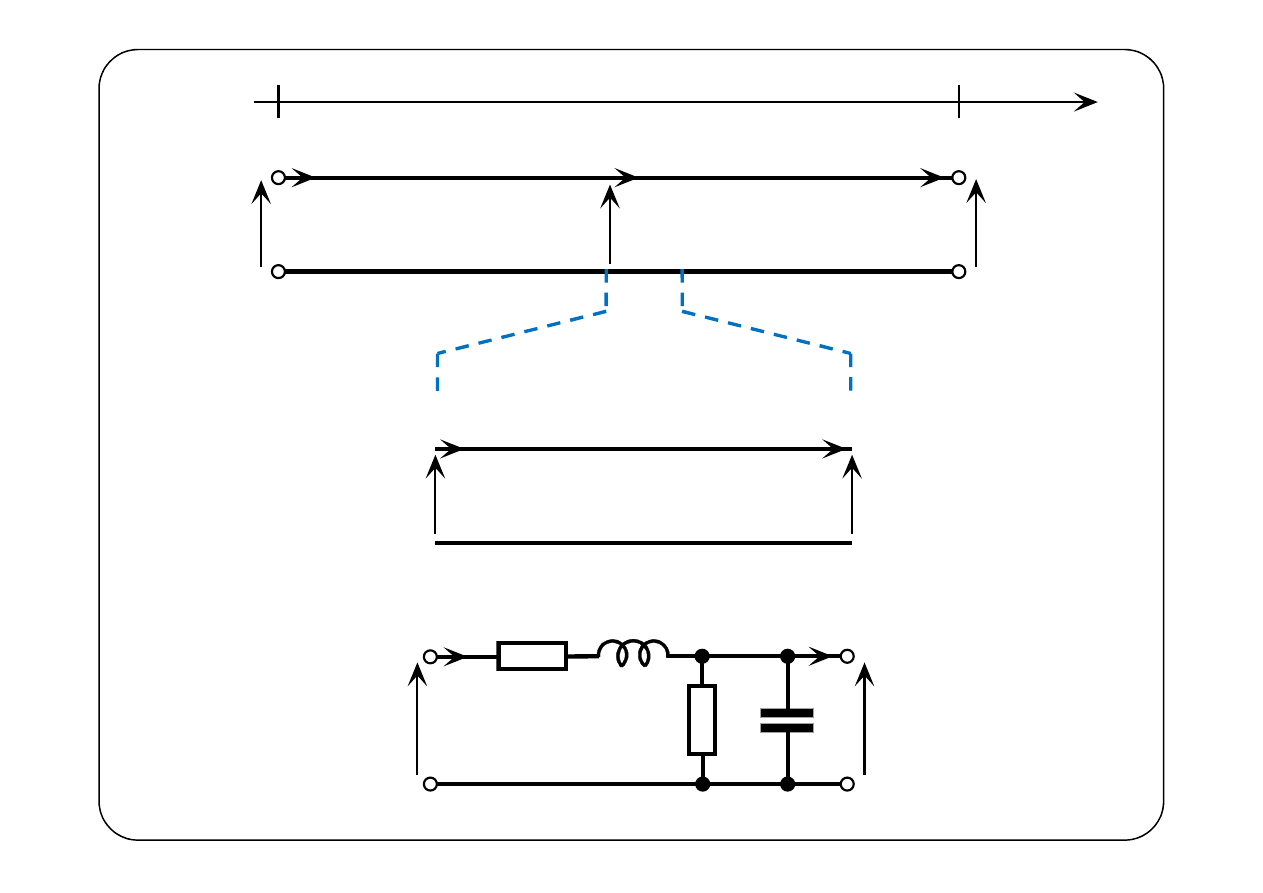
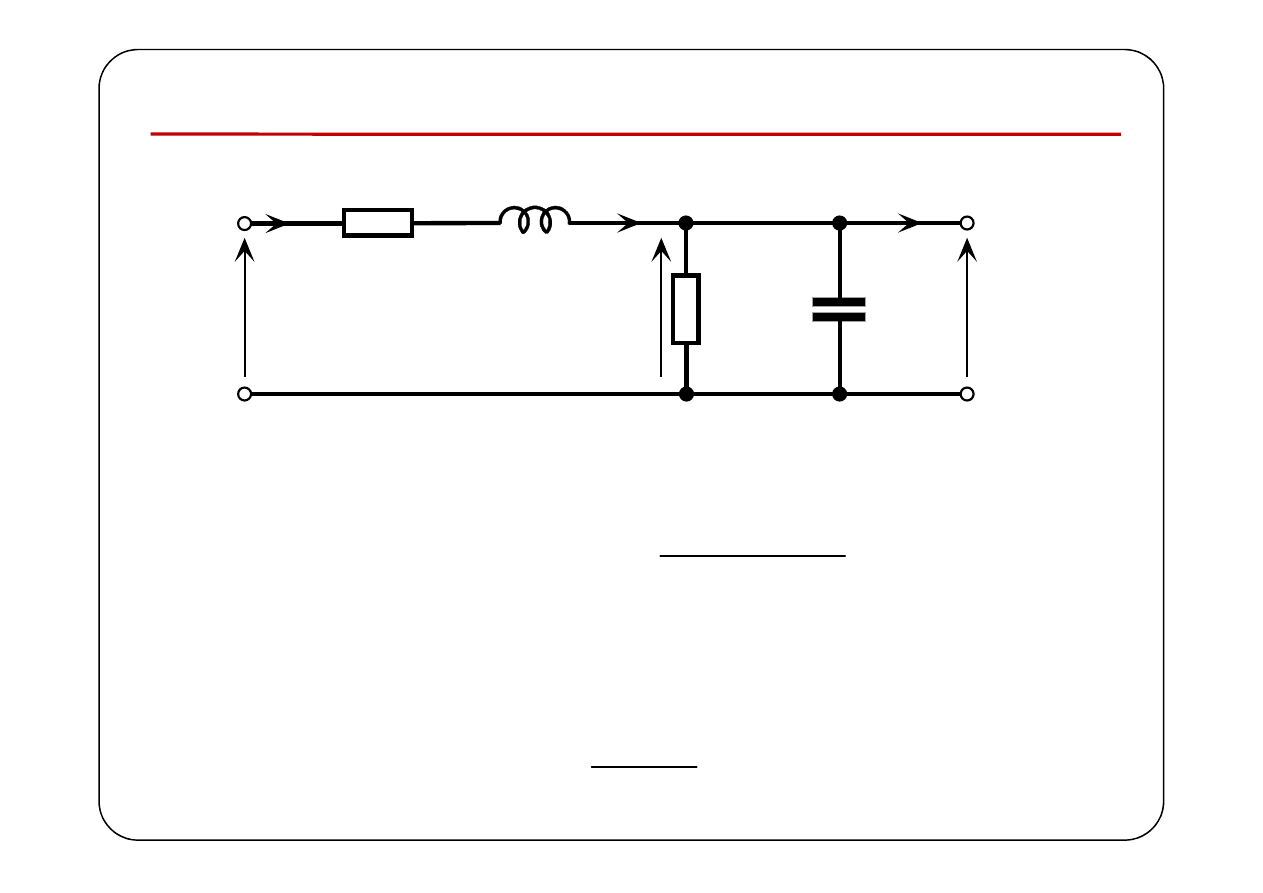
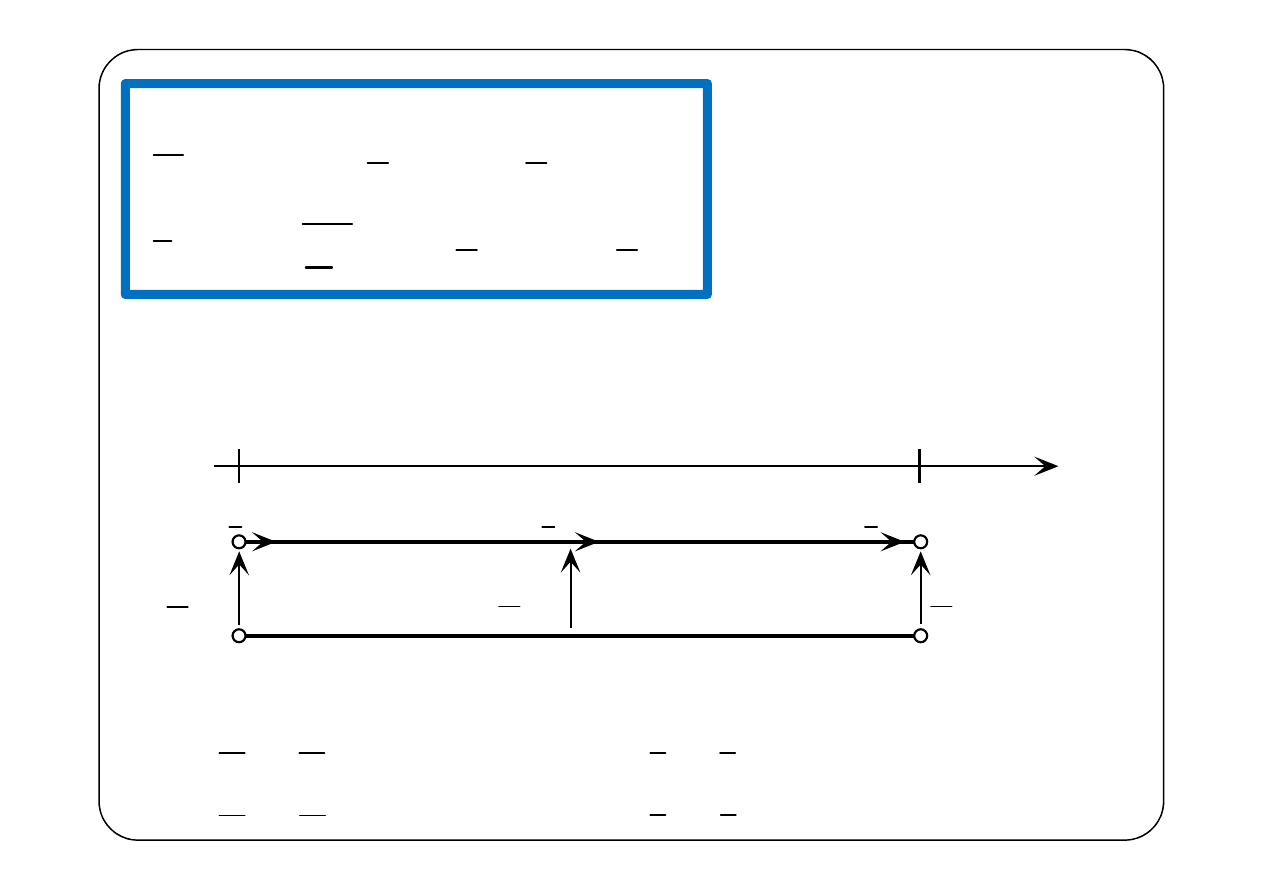
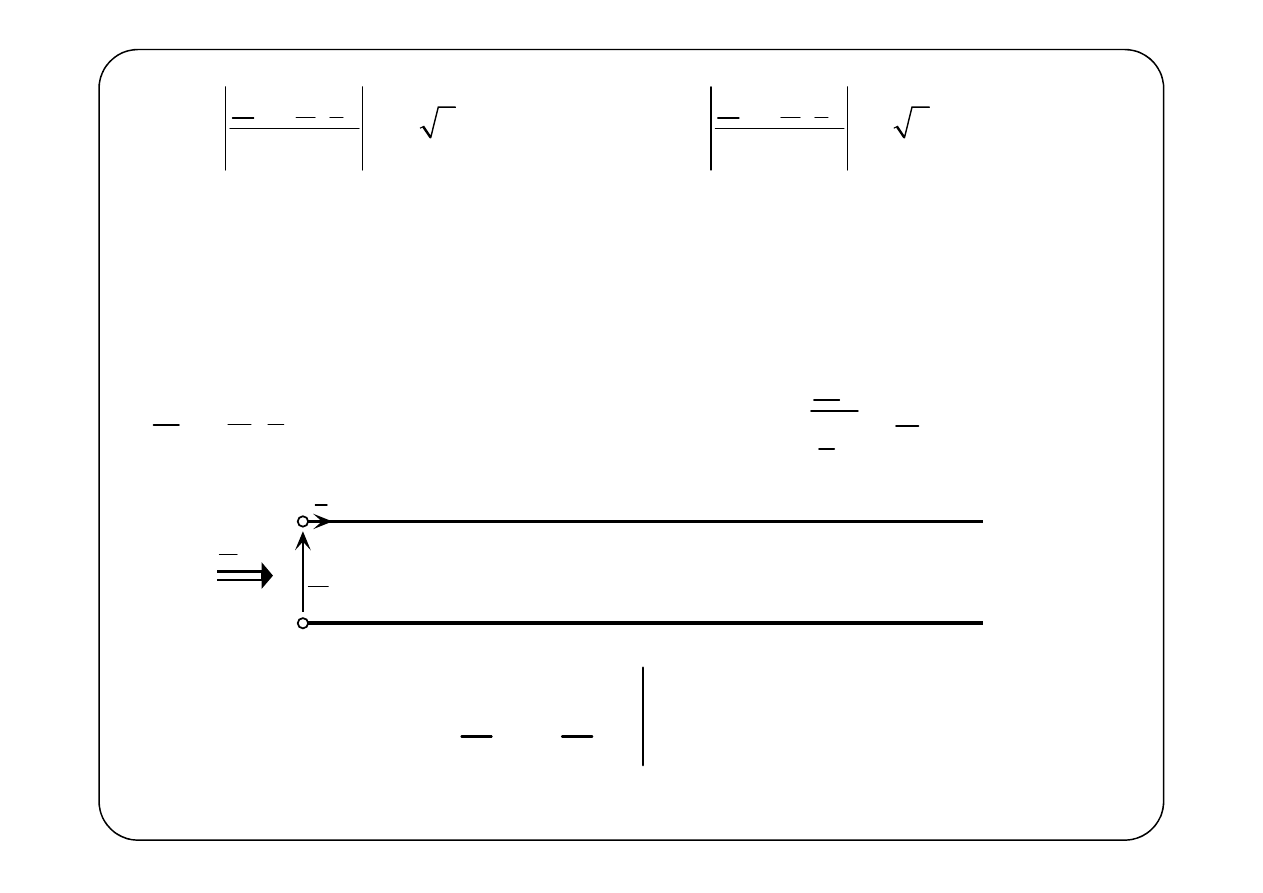
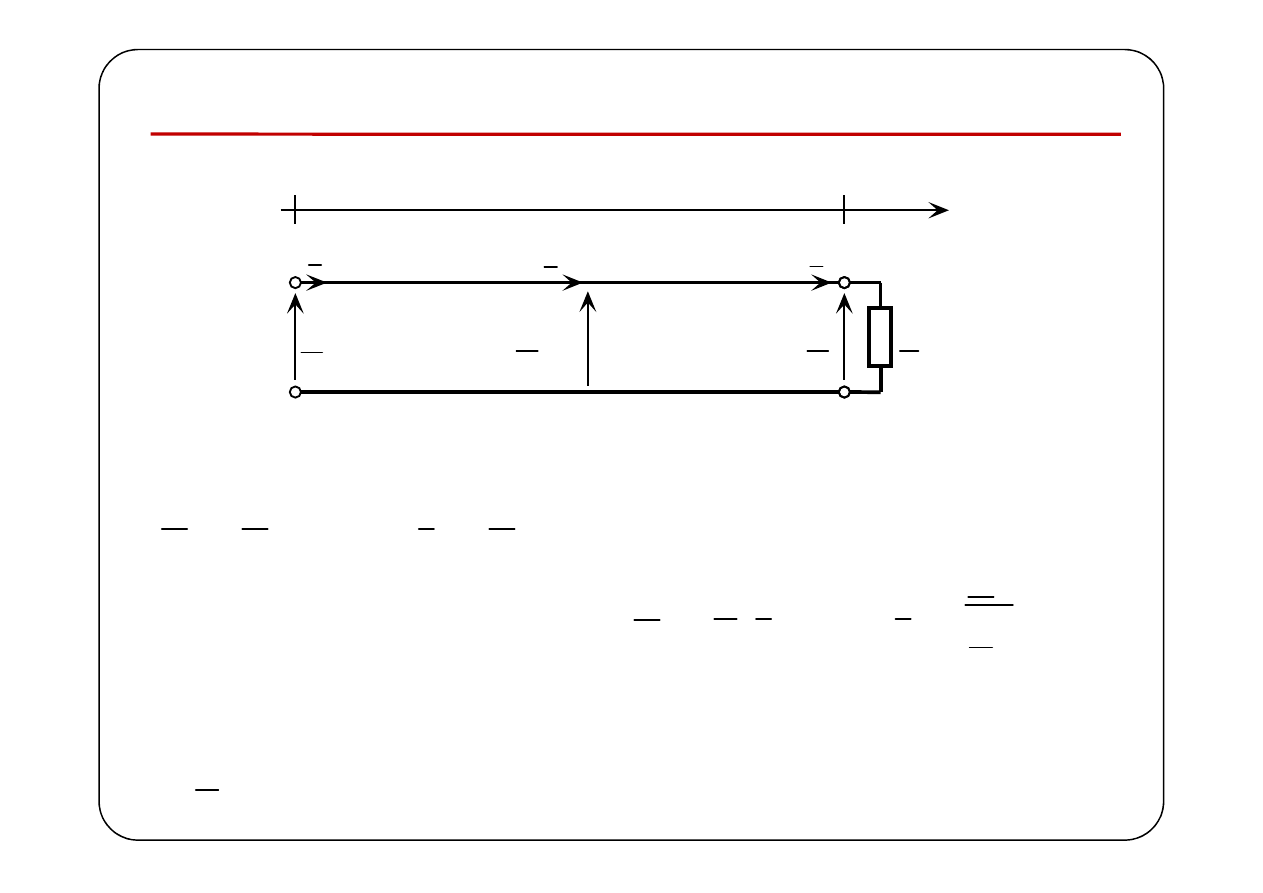
Symboliczny schemat zastępczy odcinka linii długiej
0
x
=
x
l
=
( )
0
U
( )
0
I
( )
U x
( )
I x
( )
U l
( )
I l
x
Będziemy oznaczać:
( )
( )
( )
( )
p
p
k
k
0
0
U
U
I
I
U
U l
I
I l
≜
≜
≜
≜

Aby wyznaczyć stałe A i B (lub A’ i B’) należy znać wartości
napięć i (lub) prądów w wybranych punktach linii.
( )
( )
(
)
f
e
e
1
e
e
x
x
x
x
U x
A
B
I x
A
B
Z
γ
γ
γ
γ
−
−
=
+
=
−
Załóżmy, że wielkościami znanymi (zadanymi) są
p
p
i
U
I
( )
( )
p
f
p
f
0
0
U
U
A
B
Z I
Z I
A B
=
= +
=
= −
f
p
p
f
p
p
2
2
U
Z I
A
U
Z I
B
+
=
−
=
( )
( )
f
p
f
p
p
p
p
p
p
p
f
p
f
p
p
p
f
f
f
e
e
2
2
1
e
e
e
e
2
2
2
2
x
x
x
x
x
x
U
Z I
U
Z I
U x
U
U
I
I
U
Z I
U
Z I
Z
Z
I x
Z
γ
γ
γ
γ
γ
γ
−
−
−
+
−
=
+
+
−
+
−
=
−
=
+
Oznaczmy
( )
( )
( )
1
2
e
e
x
x
A
B
U x
U
x
U
x
U
U
γ
γ
−
=
+
=
+
( )
( )
( )
1
2
A
B
(
)(
)
0
0
0
0
0
0
j
j
j
R
L
G
C
γ
ω
ω
α
β
=
+
+
= +
Rozważmy pierwszy składnik
( )
(
)
1
1
j
j
j
1
1
1
e
e
e
e
e
e
x
x
x
x
A
U
x
U
U
U
γ
ψ β
ψ
α
β
α
−
−
−
−
−
=
=
=

Postać czasowa
( )
( )
{
}
(
)
{
}
(
)
0
1
0
j
j
1
1
0
1
,
2 Im
e
2 Im
e
e
e
2 sin
t
x
t
x
A
A
x
u
t x
U
x
U
U
t
x
ω
β ψ
ω
α
α
ω
β ψ
−
+
−
−
=
=
=
=
−
+
Dla ustalonego x = x
0
— przebieg sinusoidalny o pulsacji
ω
0
,
fazie początkowej
ψ
1
–
β
x
0
i amplitudzie
0
1
e
2
x
U
α
−
Załóżmy (chwilowo), że linia jest bezstratna, czyli R = 0, G = 0.
Załóżmy (chwilowo), że linia jest bezstratna, czyli R
0
= 0, G
0
= 0.
Wówczas
0
0
0
0
0
0
0
j
j
j
j czyli
0.
L
C
L C
γ
ω
ω
ω
β
α
=
=
=
=
( )
(
)
( )
1
0
1
1
,
2 sin
2 sin
,
A
u
t x
U
t
x
U
t x
ω
β ψ
Φ
=
−
+
=
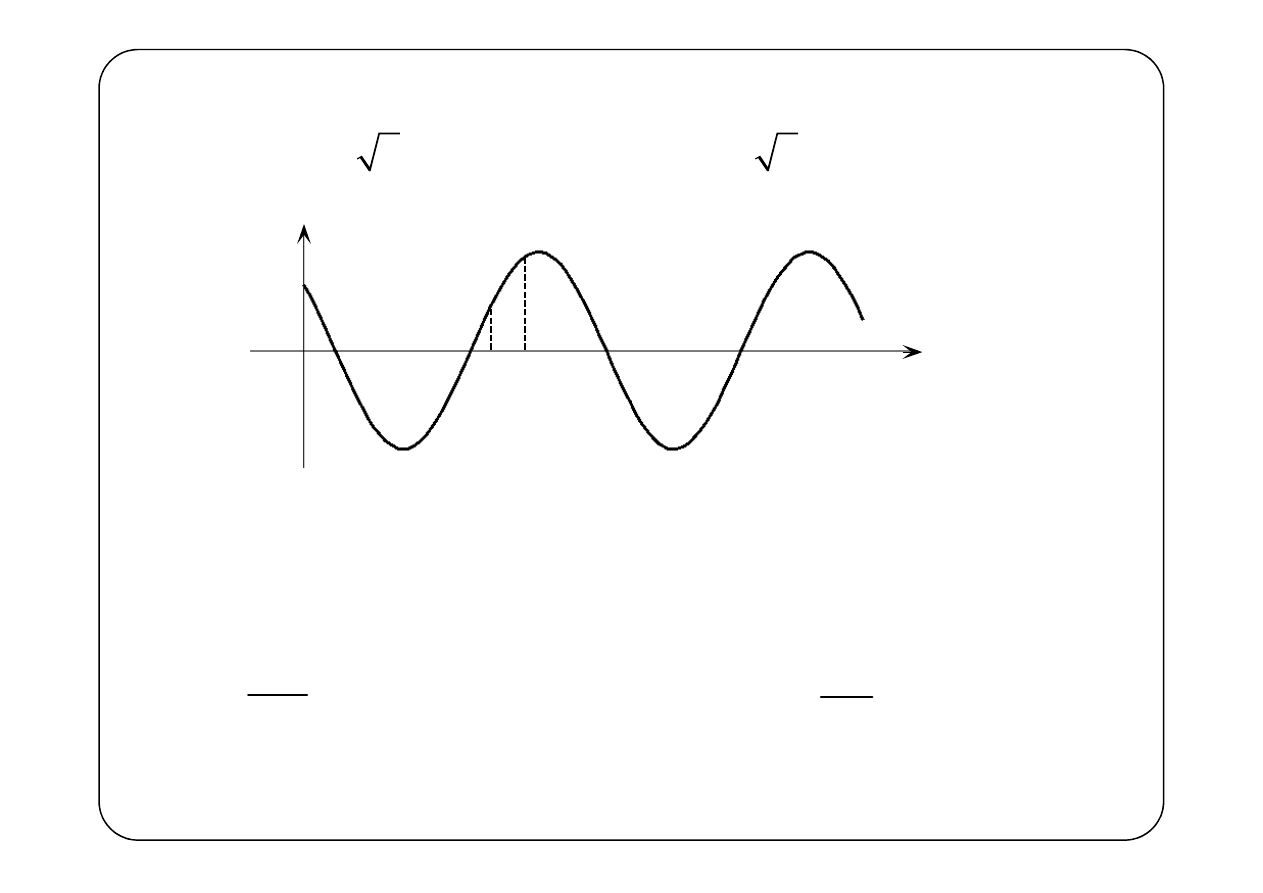
Dla ustalonego t = t
0
( )
(
)
( )
0
1
0 0
1
1
0
,
2 sin
2 sin
,
A
u
t x
U
t
x
U
t x
ω
β
ψ
Φ
=
−
+
=
( )
0
,
A
u
t x
x
x
x
x
+ ∆
Na odcinku
∆
x faza zmienia się o wartość
(
)
( )
(
)
0
0
,
,
t x
x
t x
x
x
x
x
Φ Φ
Φ
β
β
β
∆ =
+ ∆ −
= −
+ ∆ +
= − ∆
czyli
β
liczbowo określa zmianę fazy na jednostkę długości linii
x
Φ
β
∆
= − ∆
— przesuwność falowa,
[ ]
rad
m
β
=
Długość fali
λ
— odległość
∆
x , na której
∆
Φ
= 2
π
, czyli
2π
βλ
=
2π
2π
,
.
λ
β
β
λ
⇒
=
=
0
x
0
x
x
+∆
(
)
0
,
A
u
t x
(
)
0
,
A
u
t
t x
+ ∆
x
( )
,
A
u
t x
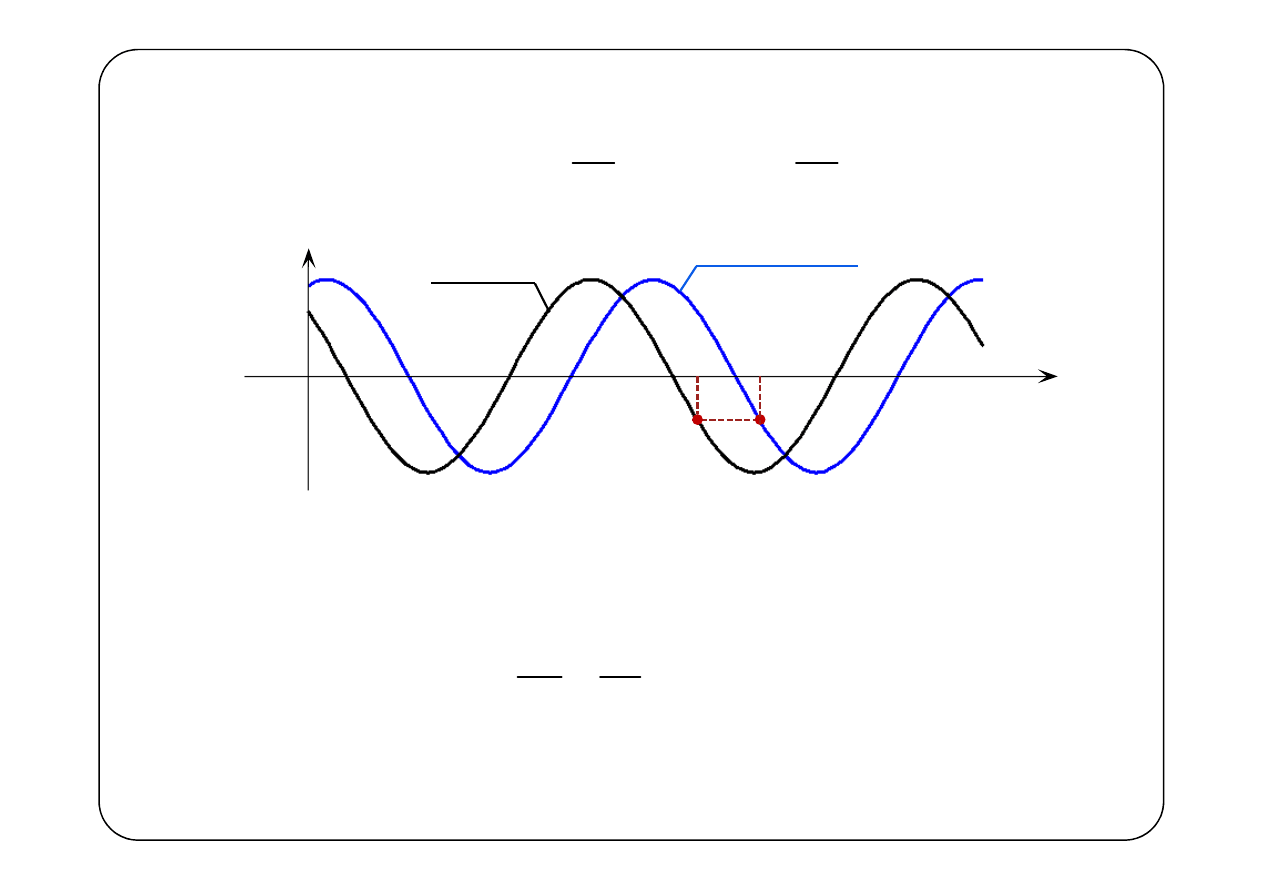
W czasie
∆
t punkt o stałej fazie przesunął się o odległość
∆
x
(
)
(
)
0
0
0
0
,
,
t x
t
t x
x
Φ
Φ
=
+ ∆
+ ∆
0
0
t
x
ω
β
∆ − ∆ =
0
f
x
v
t
ω
β
∆
⇒
=
=
∆
— prędkość fazowa
v
f
jest prędkością poruszania się punktu o stałej fazie
(np. wierzchołka sinusoidy) wzdłuż linii
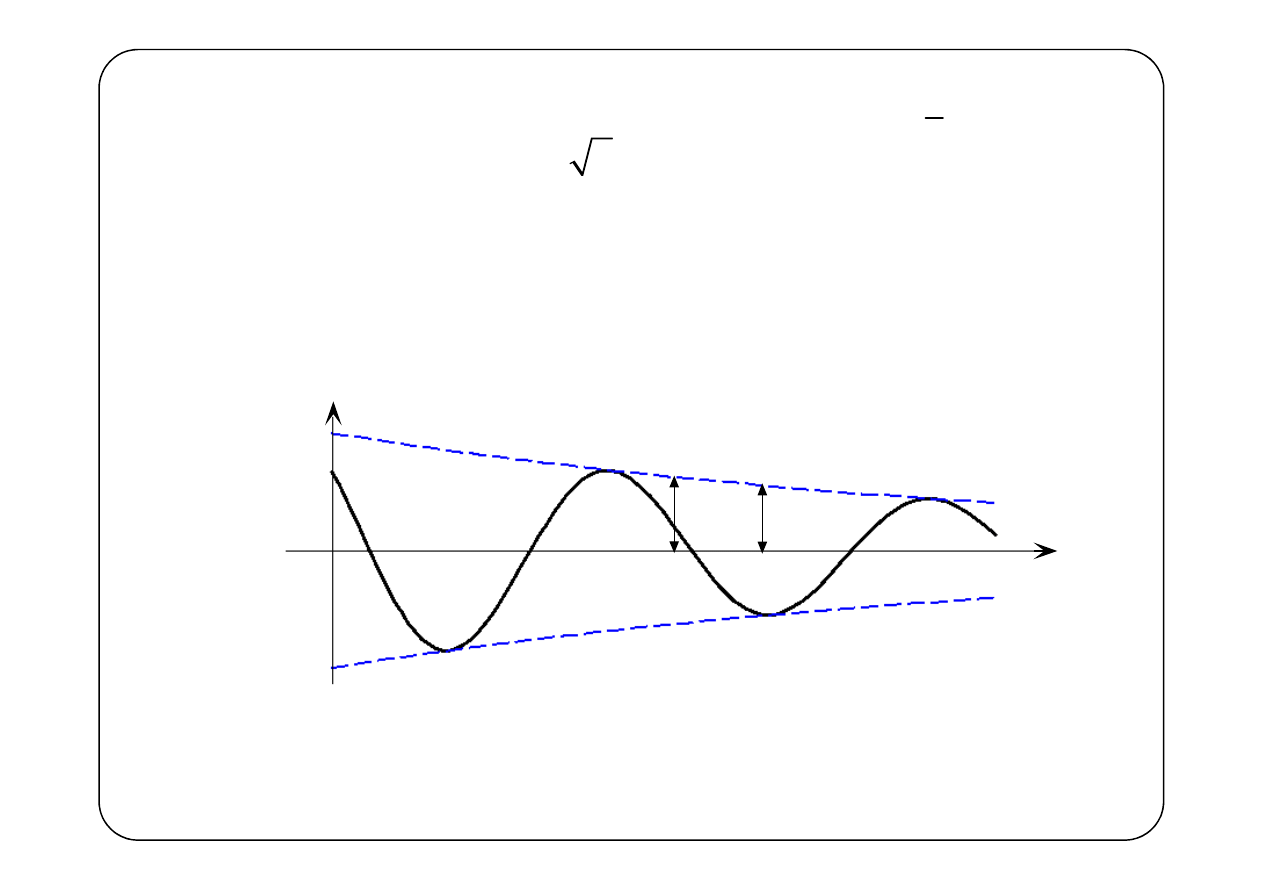
Rezygnujemy z założenia o bezstratności linii, czyli
j
γ α
β
= +
( )
(
)
1
0
1
,
e
2 sin
x
A
u
t x
U
t
x
α
ω
β
ψ
−
=
−
+
Amplituda fali zmienia się jak funkcja wykładnicza
Oczekujemy, że straty będą powodować zmniejszanie się amplitudy,
czyli
α
> 0.
e
x
α
−
( )
0
,
A
u
t x
( )
U
x
(
)
U
x
x
+∆
x
x
x
x
+∆
( )
A
U
x
(
)
A
U
x
x
+∆
( )
(
)
(
)
1
1
e
e
x
A
x
x
A
U
x
U
U
x
x
U
α
α
−
−
+∆
=
+ ∆ =
(
)
( )
(
)
( )
1
e
ln
A
A
x
A
A
U
x
x
U
x
x
x
U
x
U
x
α
α
− ∆
+ ∆
+ ∆
=
⇒
= −
∆
α
— tłumienność falowa — tłumienie w skali logarytmicznej na jednostkę
długości linii
Jeżeli to takie tłumienie historycznie nazywane jest
(
)
( )
ln
1
A
A
U
x
x
U
x
+ ∆
−
=
[ ]
Np
α
=
1 neperem. Zwykle więc przyjmuje się
( )
A
U
x
[ ]
Np
m
α
=
Niekiedy tłumienie linii określa się za pomocą współczynnika
wyrażanego w
(
)
( )
20 lg
A
A
U
x
x
x
U
x
α
+ ∆
′ −
∆
≜
dB
m
(
)
( )
ln
20
20
8, 686
0,1151
ln10
ln10
A
A
U
x
x
U
x
x
α
α
α
α
α
+ ∆
′
′
= −
=
≈
⇔
≈
∆
(!!!) Do wszystkich wzorów należy podstawiać
αααα
(
)(
)
0
0
0
0
0
0
j
j
j
R
L
G
C
γ
ω
ω
α
β
= ±
+
+
= +
Wybieramy taki znak aby
α
> 0 i
β
> 0
γ
— tamowność falowa,
1
m
γ
=
Podsumowanie:
Składnik rozwiązania
( )
(
)
1
0
1
,
e
2 sin
x
A
u
t x
U
t
x
α
ω
β
ψ
−
=
−
+
Składnik rozwiązania
reprezentuje falę o długości
, rozchodzącą się w kierunku
dodatnich x, z prędkością fazową
,
o
amplitudzie
malejącej wykładniczo (w kierunku rozchodzenia się fali).
0
f
v
ω
β
=
2π
λ β
=
Drugi składnik rozwiązania
( )
(
)
2
f
p
j
p
2
2
e
e
e e
2
x
x
x
x
B
U
Z I
U
x
U
U
γ
γ
β ψ
α
+
−
=
=
=
Będzie miał on taką sama postać jak pierwszy składnik jeżeli
zamienimy
2
1
i
U
U
x
x
→
→ −
Postać czasowa
( )
(
)
2
0
2
,
e
2 sin
x
B
u
t x
U
t
x
α
ω
β
ψ
=
+
+
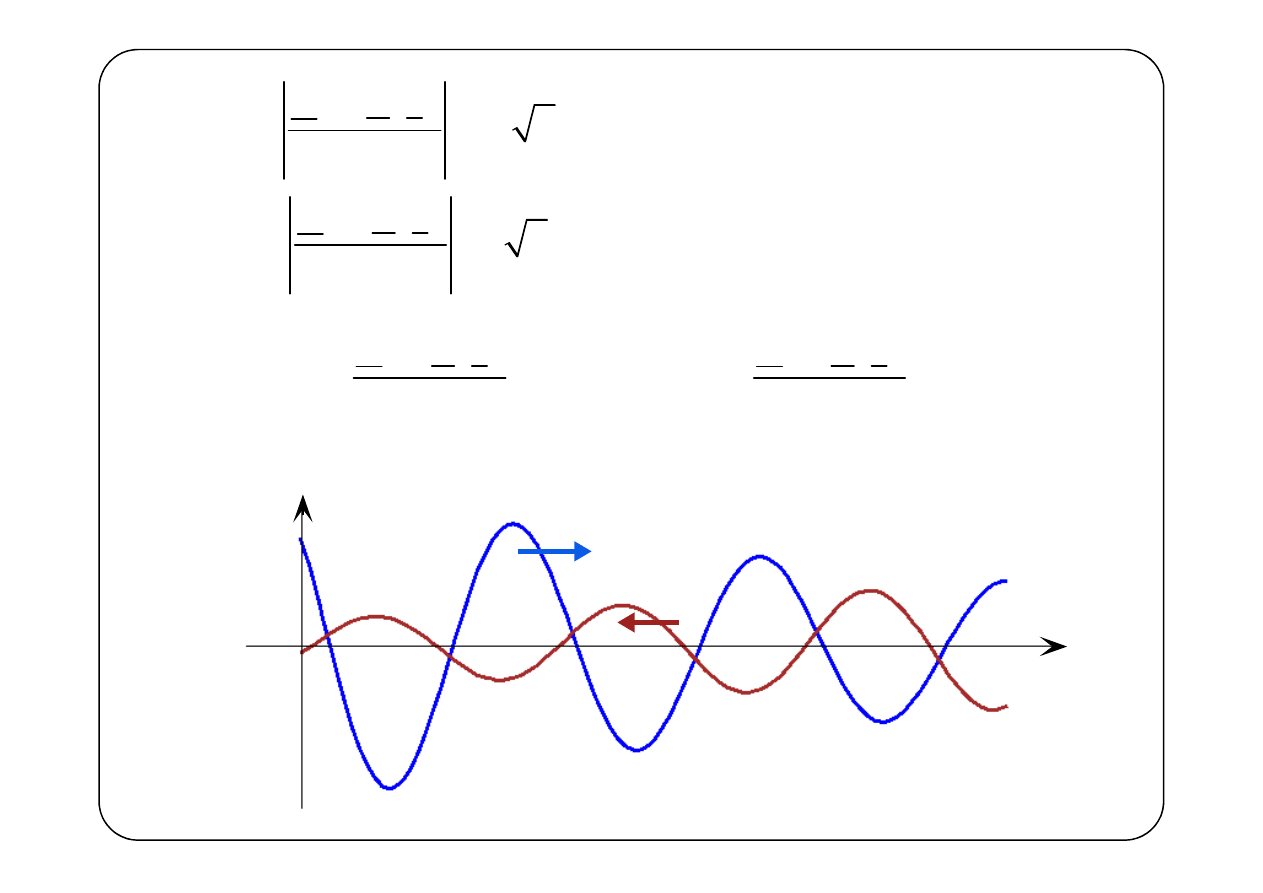
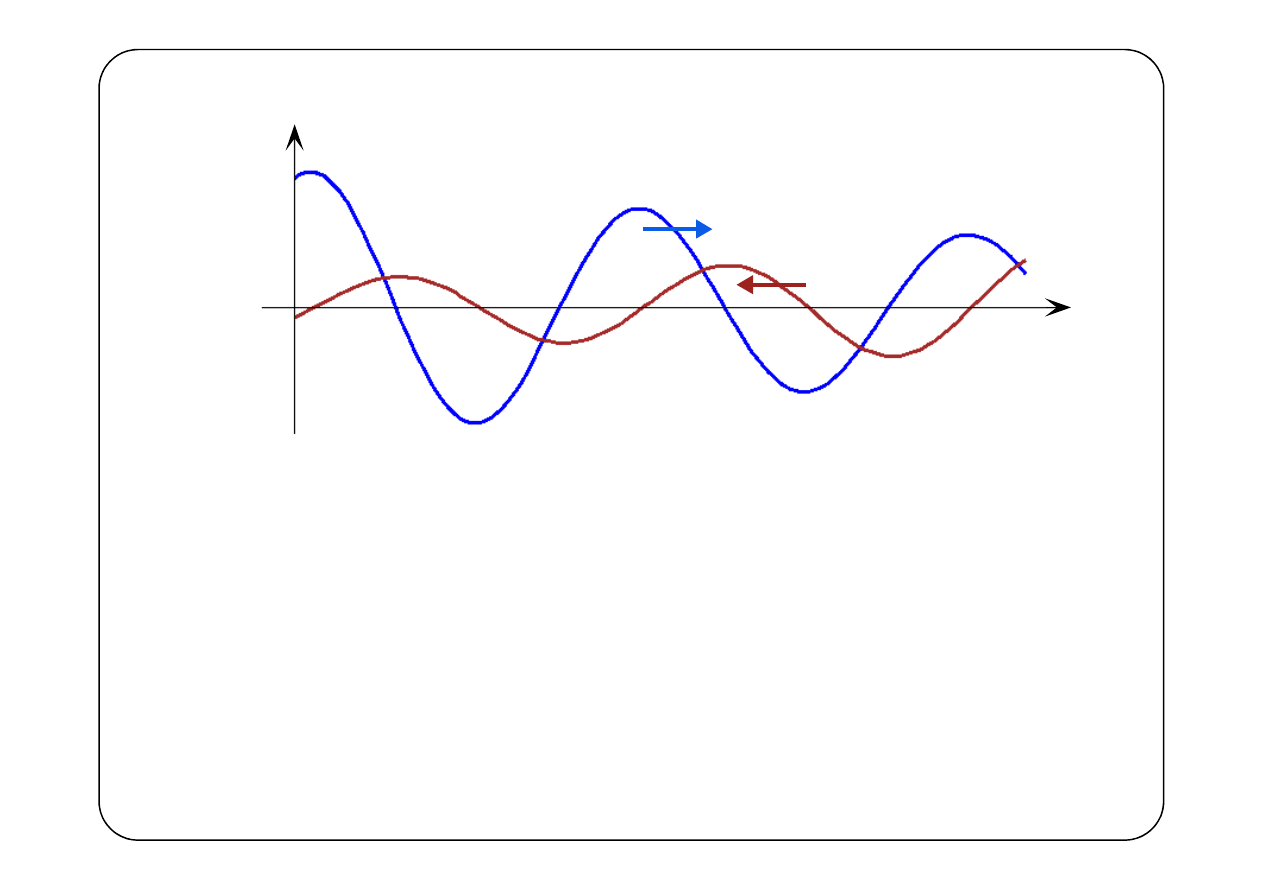
Jest to, z dokładnością do amplitudy i fazy początkowej, identyczna
fala, rozchodząca się w kierunku malejących wartości x. Jej
amplituda maleje w kierunku rozchodzenia się fali, czyli rośnie ze
wzrostem x.
(
)
( )
(
)
(
)
f
p
p
0
1
f
p
p
0
2
f
p
f
p
p
p
1
2
,
e
2 sin
2
e
2 sin
2
arg
,
arg
2
2
x
x
U
Z I
u t x
t
x
U
Z I
t
x
U
Z I
U
Z I
α
α
ω
β ψ
ω
β ψ
ψ
ψ
−
+
=
−
+
+
−
+
+
+
+
−
=
=
(
)
0
,
A
u
t x
(
)
0
,
B
u
t x
x
Rozwiązanie równania na prąd
( )
( )
( )
p
f
p
f
p
p
e
e
2
2
x
x
A
B
I
Y U
I
Y U
I x
I
x
I
x
γ
γ
−
+
−
=
+
=
+
( )
(
)
(
)
p
f
p
0
1
p
f
p
,
e
2 sin
2
e
2 sin
x
x
I
Y U
i t x
t
x
I
Y U
α
α
ω
β
ϕ
ω
β
ϕ
−
+
=
−
+
+
−
+
+
+
(
)
p
f
p
0
2
p
f
p
f
p
p
f
1
2
f
e
2 sin
2
1
arg
,
arg
,
2
2
x
I
Y U
t
x
I
Y U
I
Y U
Y
Z
α
ω
β
ϕ
ϕ
ϕ
−
+
+
+
+
−
=
=
=
x
(
)
0
,
A
i
t x
(
)
0
,
B
i
t x
Zarówno napięcie, jak i prąd rozchodzą się wzdłuż linii w postaci
dwóch fal, biegnących w przeciwnych kierunkach.
( )
(
)
(
)
f
p
f
p
p
p
0
1
0
2
,
e
2 sin
e
2 sin
2
2
x
x
U
Z I
U
Z I
u t x
t
x
t
x
α
α
ω
β
ψ
ω
β
ψ
−
+
−
=
−
+
+
+
+
Załóżmy, że zwiększamy nieograniczenie długość linii l, czyli
l
→ ∞
Aby drugi składnik rozwiązania nie wzrastał nieograniczenie
musi zachodzić
f
p
p
0
l
U
Z I
→∞
−
→
czyli w granicy
p
f
p
U
Z
I
=
p
I
l
→ ∞
p
U
p
I
we
Z
f
we
l
Z
Z
→ ∞
=
0
0
0
f
0
0
0
j
j
R
L
Z
G
C
ω
ω
+
=
+
Moc czynna dostarczona do linii
{ }
2
p
we
p
Re
P
I
Z
=
Gdy l
→ ∞
{ }
2
Re
P
I
Z
=
{ }
2
p
f
p
Re
P
I
Z
=
{ }
f
Re
0
Z
≥
Oczekujemy, że
, czyli że linia jest obwodem pasywnym.
Należy wybrać taki znak pierwiastka, aby
p
0
P
≥
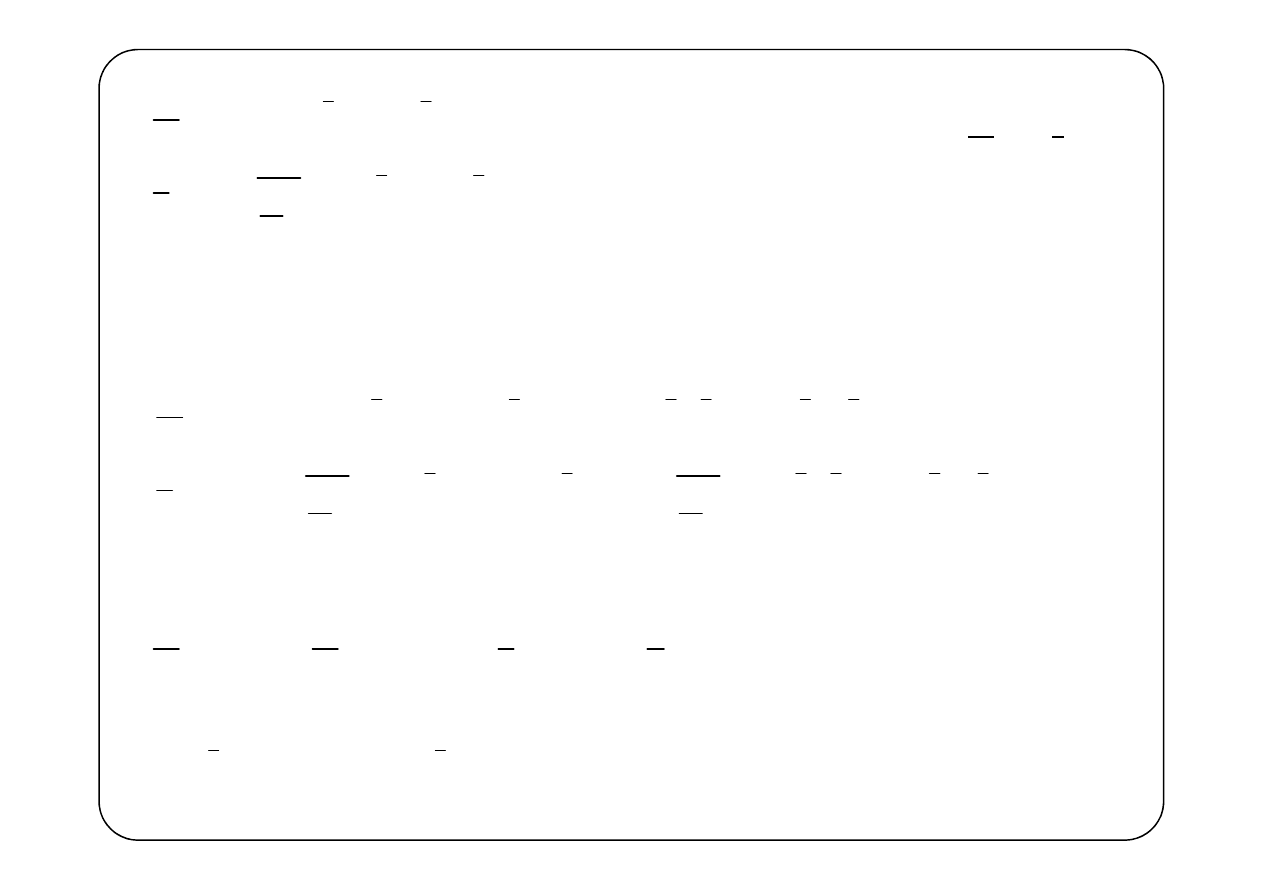
Linia obciążona
p
U
p
I
k
Z
k
I
k
U
0
x
=
x
l
=
x
( )
U x
( )
I x
Wprowadzimy oznaczenia
Wprowadzimy oznaczenia
( )
( )
k
k
U
U l
I
U l
≜
≜
Dodatkowo zachodzą związki
k
k
k
k
k
k
U
U
Z I
I
Z
=
=
Zakładać będziemy, że obciążeniem linii jest dwójnik pasywny, czyli
{ }
k
Re
0
Z
≥
( )
( )
(
)
f
e
e
1
e
e
x
x
x
x
U x
A
B
I x
A
B
Z
γ
γ
γ
γ
−
−
=
+
=
−
Przy założeniu, że znamy U
k
i I
k
można wyznaczyć A i B
Zrobimy inaczej
Podstawmy x = l – y
(
)
( )
( )
(
)
( )
( )
(
)
(
)
e
e
e
e
e e
1
1
l y
l y
l
y
l
y
U l
y
A
B
A
B
γ
γ
γ γ
γ
γ
γ
γ
γ γ
γ
γ
−
−
−
−
−
−
−
−
−
−
−
=
+
=
+
(
)
( )
( )
(
)
(
)
f
f
1
1
e
e
e
e
e e
l y
l y
l
y
l
y
I l
y
A
B
A
B
Z
Z
γ
γ
γ γ
γ
γ
−
−
−
−
−
−
=
−
=
−
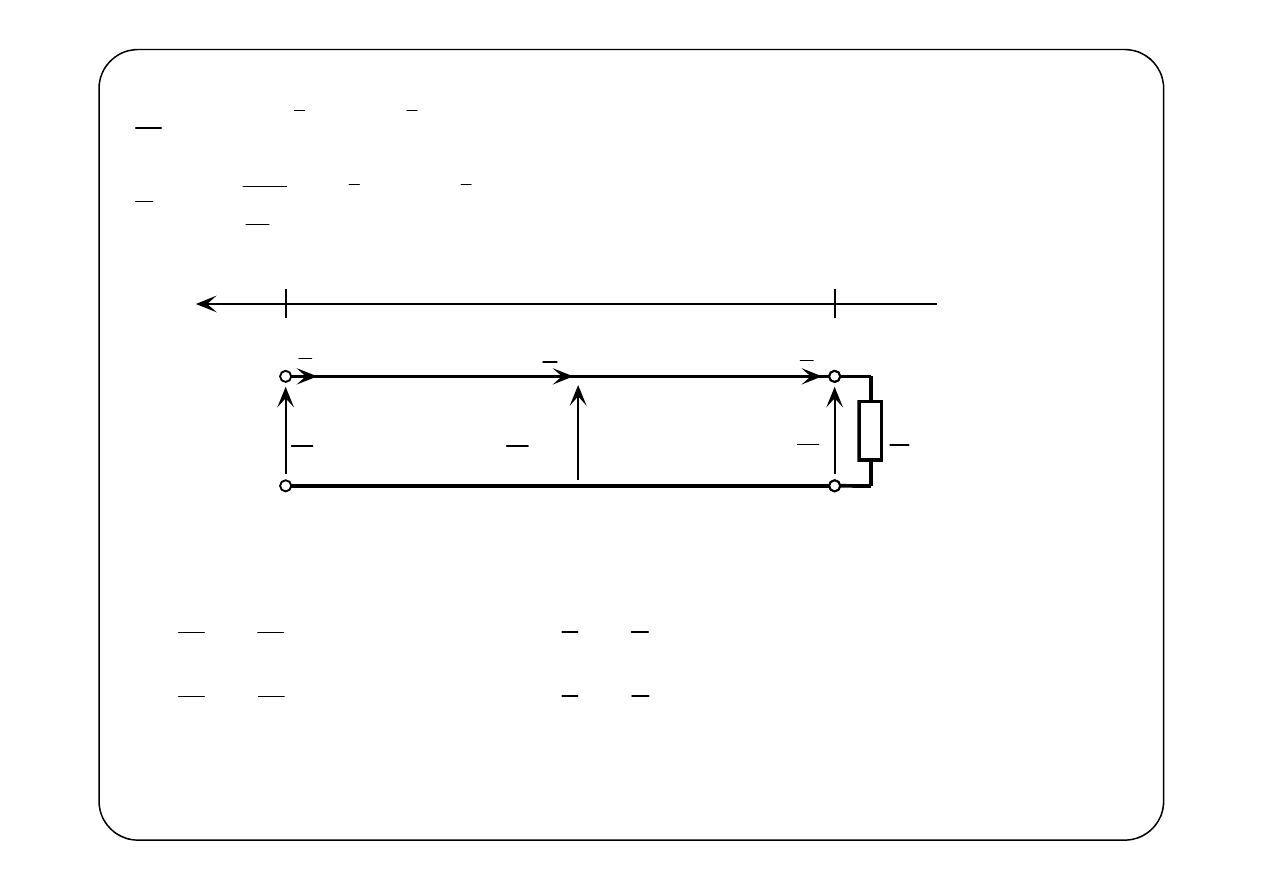
Wprowadzimy oznaczenia
(
)
( )
(
) ( )
oraz
e
e
l
l
U l
y
U y
I l
y
I y
A
A
B
B
γ
γ
−
−
=
−
=
=
=
ɶ
ɶ
ɶ
ɶ
( )
( )
(
)
f
e
e
1
e
e
y
y
y
y
U y
A
B
I y
A
B
Z
γ
γ
γ
γ
−
−
=
+
=
−
ɶ
ɶ
ɶ
ɶ
ɶ
ɶ
p
U
p
I
k
Z
k
I
k
U
0
y
=
y
l
=
y
( )
U y
ɶ
( )
I y
ɶ
p
U
k
Z
k
( )
U y
Teraz
( )
( )
( )
( )
p
p
k
k
0
0
U
U l
I
I l
U
U
I
I
=
=
=
=
ɶ
ɶ
ɶ
ɶ
k
f
k
U
A
B
Z I
A B
= +
= −
ɶ
ɶ
ɶ
ɶ
f
k
k
f
k
k
2
2
U
Z I
A
U
Z I
B
+
=
−
=
ɶ
ɶ
( )
f
k
f
k
k
k
e
e
2
2
y
y
U
Z I
U
Z I
U y
γ
γ
−
+
−
=
+
ɶ
( )
k
k
k
k
k
k
k
k
f
f
f
f
e
e
e
e
2
2
2
2
y
y
y
y
U
U
U
U
I
I
I
I
Z
Z
Z
Z
I y
γ
γ
γ
γ
−
−
+
−
+
−
=
−
=
+
ɶ
A
B
Znamy związek między U
k
i I
k
k
f
k
k
k
f
U
U
Z I
I
Z
=
=
( )
f
f
k
k
k
k
2
1
1
1
e
1
e
2
2
1
y
y
y
y
Z
Z
U y
U
U
Z
Z
Z
Z
Z
γ
γ
γ
γ
−
−
=
+
+
−
=
−
=
+
+
ɶ
( )
2
f
k
f
k
k
k
f
k
k
k
k
f
f
2
k
k
f
k
f
k
f
1
1
e
1
e
2
1
1
1 e
1 e
2
2
1
1 e
1
e
2
y
y
y
y
y
y
Z
Z
Z
U
Z
Z
Z
Z
Z
I y
I
I
Z
Z
Z
Z
Z
I
Z
Z
Z
γ
γ
γ
γ
γ
γ
−
−
−
−
=
+
+
+
=
+
−
−
=
−
=
+
−
+
ɶ
Oznaczymy:
( )
( )
2
2
k
f
k
k
f
k
f
k
k
f
e
e
czyli
0
y
y
Z
Z
y
Z
Z
Z
Z
Z
Z
γ
γ
Γ
Γ
Γ
Γ
−
−
−
=
=
+
−
=
=
+
( )
( )
( )
( )
f
k
k
1
1
e
1
2
y
A
B
Z
U y
U
y
U
y
U
y
Z
γ
Γ
=
+
+
=
+
ɶ
ɶ
ɶ
( )
( )
( )
( )
k
k
k
f
2
1
1 e
1
2
y
A
B
Z
Z
I y
I
y
I
y
I
y
Z
γ
Γ
=
+
−
=
+
ɶ
ɶ
ɶ
( )
( )
,
A
A
U
y
I
y
ɶ
ɶ
— reprezentują fale rozchodzące się w kierunku
malejących y, czyli od początku linii do końca
( )
( )
,
B
B
U
y
I
y
ɶ
ɶ
— reprezentują fale rozchodzące się w kierunku
malejących y, czyli od początku linii do końca
( )
( )
( )
( ) ( )
( )
( )
( )
( )
( )
f
k
k
f
k
k
k
k
f
k
k
1
1
e
2
1
1
e
2
1
1 e
2
1
1 e
2
y
A
y
B
A
y
A
y
B
A
Z
U
y
U
Z
Z
U
y
U
y
U
y
y
Z
Z
I
y
I
Z
Z
I
y
I
y
I
y
y
Z
γ
γ
γ
γ
Γ
Γ
Γ
Γ
=
+
=
+
=
=
+
=
+
−
=
−
ɶ
ɶ
ɶ
ɶ
ɶ
ɶ
( )
( )
( )
( )
k
f
2
B
A
Z
( )
( ) ( )
{
}
Re
A
A
A
P
y
U
y I
y
∗
=
ɶ
ɶ
— moc czynna fali A w odległości y od końca linii
( )
( ) ( )
{
}
( ) ( ) ( )
( )
{
}
( )
( )
2
Re
Re
B
A
B
B
A
A
P
y
U
y I
y
U
y
y I
y
y
y
P
y
Γ
Γ
Γ
∗
∗
∗
=
=
−
= −
ɶ
ɶ
ɶ
ɶ
— moc czynna fali B w odległości y od końca linii; znak minus oznacza, że
moc jest przenoszona od obciążenia do generatora
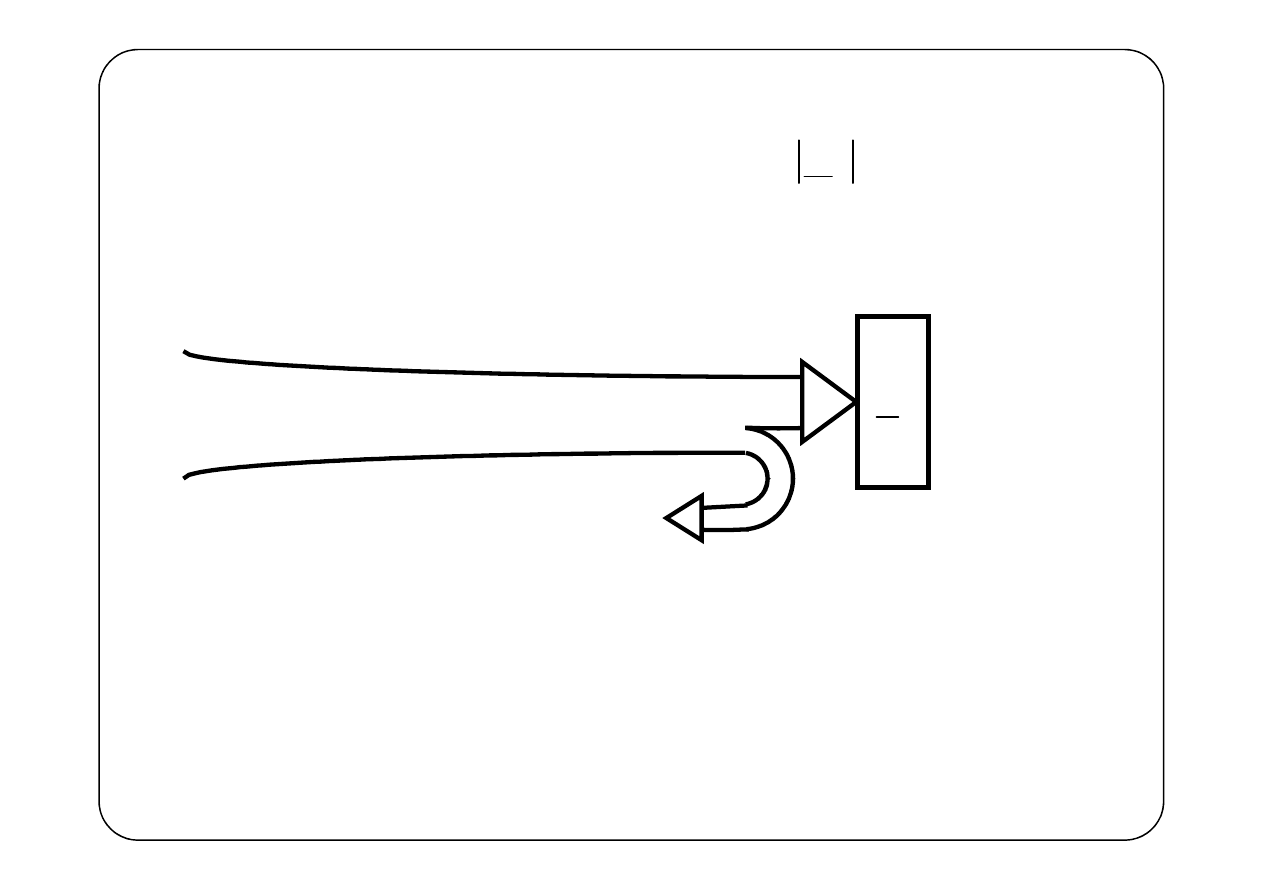
Bilans mocy na końcu linii (y = 0)
( )
( )
( )
(
)
2
k
k
k
0
0
0
0 1
A
B
A
P
P
P
P
P
Γ
+
−
=
⇒
=
−
P
k
— moc czynna dostarczona do obciążenia
k
Z
A
P
k
P
B
P
Fala A, poruszająca się od początku linii do jej końca nazywa się
falą padającą. Oznaczać będziemy indeksem i (incident wave)
Fala B, poruszająca się od końca linii do jej początku nazywa się
falą odbitą. Oznaczać będziemy indeksem r (reflected wave)
Przy „nowych” oznaczeniach równania na napięcie i prąd w linii
mają postać
( )
( )
( )
i
r
ik
rk
f
ik
k
k
e
e
,
gdzie
1
1
,
2
y
y
U y
U
y
U
y
U
U
Z
U
U
Z
γ
γ
−
=
+
=
+
=
+
ɶ
ɶ
ɶ
Wartość skuteczna zespolona napięcia fali
padającej na końcu linii
( )
(
)
f
k
rk
k
ik
k
2
k
ik
1
1
,
2
czyli
e
1
e
.
y
y
Z
U
U
U
Z
U y
U
γ
γ
Γ
Γ
−
=
−
=
=
+
ɶ
Wartość skuteczna zespolona napięcia fali
odbitej na końcu linii
I podobnie
( )
( )
( )
i
r
ik
rk
k
ik
k
f
k
rk
k
k
ik
f
e
e
,
gdzie
1
1 ,
2
1
1
,
2
y
y
I y
I
y
I
y
I
I
Z
I
I
Z
Z
I
I
I
Z
γ
γ
Γ
−
=
+
=
+
=
+
= −
− = −
ɶ
ɶ
ɶ
Wartość skuteczna zespolona prądu fali
padającej na końcu linii
Wartość skuteczna zespolona prądu fali
odbitej na końcu linii
( )
(
)
f
2
ik
k
czyli
e
1
e
y
y
I y
I
γ
γ
Γ
−
=
−
ɶ
odbitej na końcu linii
W każdym punkcie linii (czyli dla każdego y)
( )
( )
( )
( )
i
r
f
f
i
r
U
y
U
y
Z
Z
I
y
I
y
=
= −
ɶ
ɶ
ɶ
ɶ
k
f
k
k
f
Z
Z
Z
Z
Γ
−
=
+
— współczynnik odbicia na końcu linii
Jeżeli obciążeniem linii jest dwójnik pasywny, czyli
wówczas
{ }
k
Re
0,
Z
≥
k
f
k
k
f
1,
Z
Z
Z
Z
Γ
−
=
≤
+
( )
2
k
e
1
y
y
α
Γ
Γ
−
=
≤
( )
( ) ( )
( )
( )
2
r
i
r
i
Ponieważ
,
więc w każdym punkcie linii
P y
y
P y
P y
P y
Γ
= −
≤
Jeżeli
to oczywiście również
dla dowolnego y.
Oznacza to że w każdym punkcie linii napięcie i prąd fali odbitej są
równe zero, czyli w linii nie ma fali odbitej.
Taki stan w linii, kiedy nie ma fali odbitej, nazywa się stanem
dopasowania falowego.
k
0,
Γ
=
( )
0
y
Γ
=
Warunkiem dopasowania falowego będzie więc
k
f
k
0,
Z
Z
Z
Z
Γ
−
=
=
+
k
k
f
0,
Z
Z
Γ
=
=
+
czyli
k
f
Z
Z
=
W warunkach dopasowania moc fali padającej jest w całości
przekazywana do obciążenia.
Fale stojące w linii
( )
( )
( )
(
)
2
k
i
r
ik
e
1
e
y
y
U y
U
y
U
y
U
γ
γ
Γ
−
=
+
=
+
ɶ
ɶ
ɶ
( )
( )
( )
2
k
i
r
ik
e
1
e
y
y
U y
U
y
U
y
U
γ
γ
Γ
−
=
+
=
+
ɶ
ɶ
ɶ
Oznaczmy
k
j
k
k
e
θ
Γ
Γ
=
(
)
k
2
j
2
2
k
k
1
e
1
e
e
y
y
y
γ
θ
β
α
Γ
Γ
−
−
−
+
= +
=
(
)
(
)
(
)
(
)
(
)
2
2
k
k
k
k
2
2
2
2
k
k
k
k
2
2
4
k
k
k
1
e
cos
2
j
e
sin
2
1
e
cos
2
e
sin
2
1 2
e
cos
2
e
y
y
y
y
y
y
y
y
y
y
y
α
α
α
α
α
α
Γ
θ
β
Γ
θ
β
Γ
θ
β
Γ
θ
β
Γ
θ
β
Γ
−
−
−
−
−
−
= +
−
+
−
=
=
+
−
+
−
=
=
+
−
+
Po uwzględnieniu
j
e
e e
e
y
y
y
y
γ
α
β
α
=
=
( )
(
)
2
2
4
k
k
ik
k
e
1 2
e
cos
2
e
y
y
y
U y
U
y
α
α
α
Γ
θ
β
Γ
−
−
=
+
−
+
ɶ
Podobnie
( )
( )
( )
(
)
2
i
r
ik
k
e
1
e
y
y
I y
I
y
I
y
I
γ
γ
Γ
−
=
+
=
−
ɶ
ɶ
ɶ
( )
( )
( )
2
i
r
ik
k
e
1
e
y
y
I y
I
y
I
y
I
γ
γ
Γ
−
=
+
=
−
ɶ
ɶ
ɶ
(
)
k
j
π
k
k
e
θ
Γ
Γ
+
−
=
Po uwzględnieniu
( )
(
)
2
2
4
ik
k
k
k
e
1 2
e
cos
2
e
y
y
y
I y
I
y
α
α
α
Γ
θ
β
Γ
−
−
=
−
−
+
ɶ
k
k
e
Γ
Γ
−
=
Po uwzględnieniu
Wartość skuteczna (a więc również amplituda) napięcia i prądu
w ustalonym punkcie linii (dla ustalonego y) nie zależy od czasu
y
( )
U y
ɶ
( )
I y
ɶ
y
( )
U y
ɶ
( )
I y
ɶ
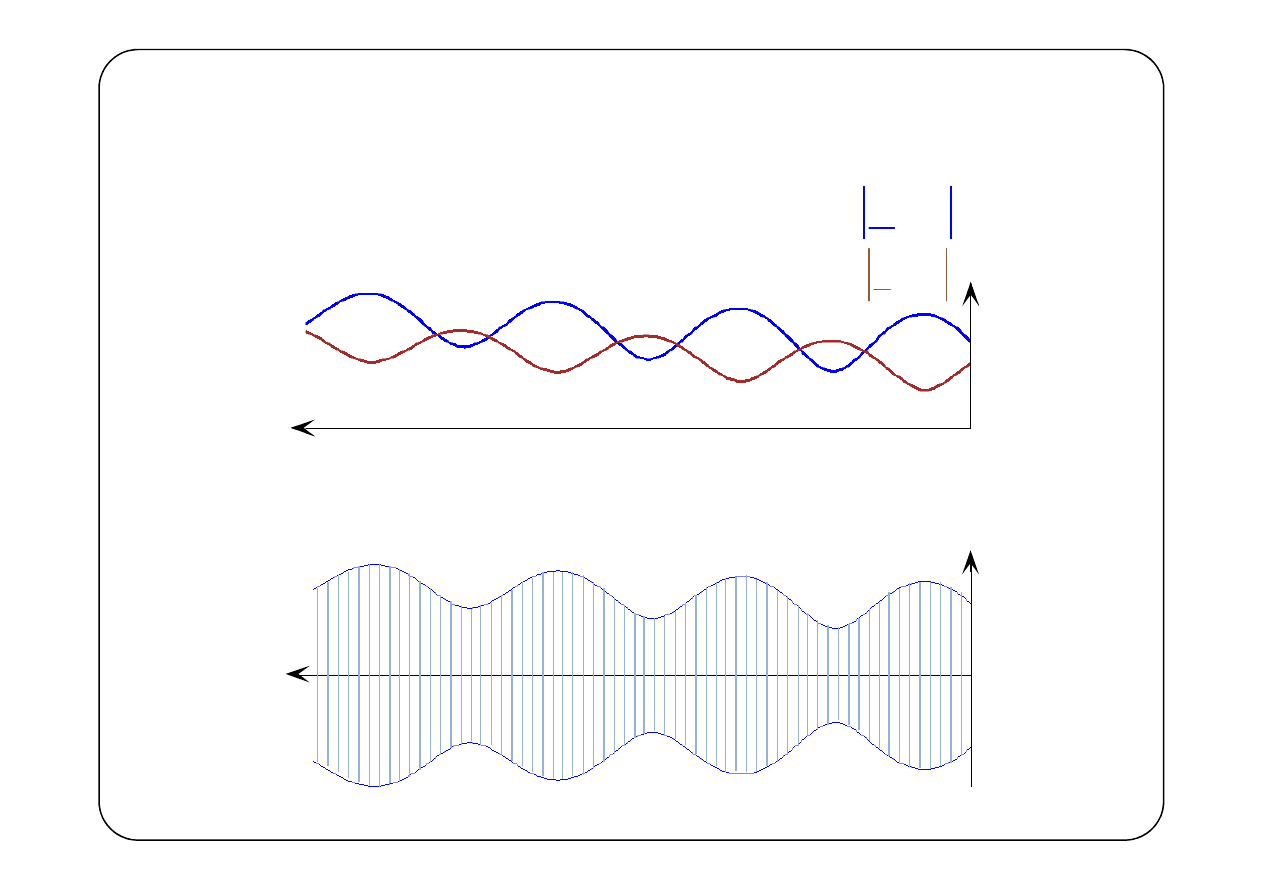
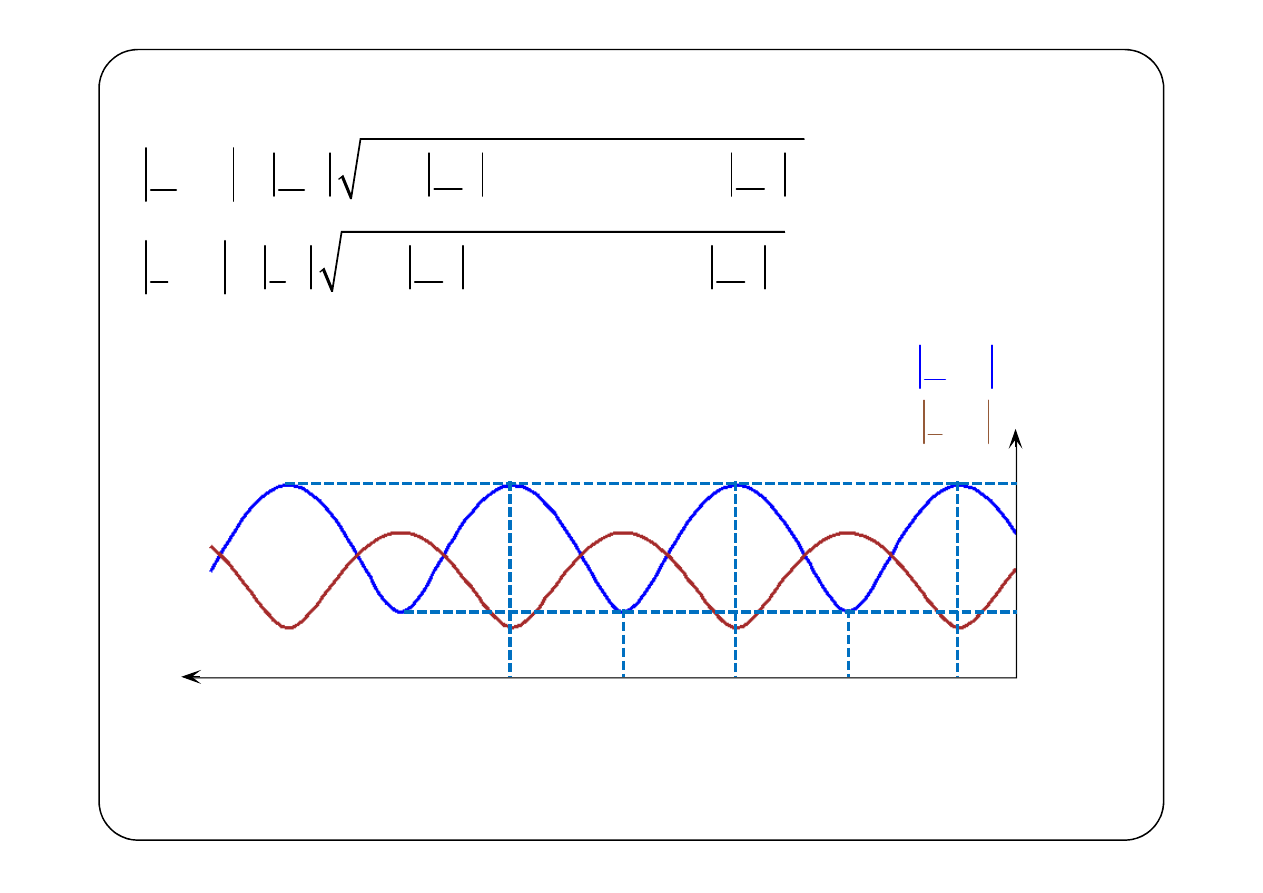
Prąd i napięcie w linii ma postać fali stojącej
( )
,
u t y
ɶ
y
Jeżeli linia jest bezstratna (
α
= 0)
( )
(
)
2
k
k
ik
k
1 2
cos
2
U y
U
y
Γ
θ
β
Γ
=
+
−
+
ɶ
( )
(
)
2
ik
k
k
k
1 2
cos
2
I y
I
y
Γ
θ
β
Γ
=
−
−
+
ɶ
( )
U y
ɶ
( )
I y
ɶ
y
max
U
min
U
max1
y
max2
y
max3
y
min1
y
min2
y

Położenie maksimów amplitudy fali stojącej napięcia
(
)
k
k
cos
2
1
2
2 π
y
y
n
θ
β
θ
β
−
=
⇒
−
= −
(
)
max
k
1
2 π
2
n
y
n
θ
β
=
+
Położenie minimów amplitudy fali stojącej napięcia
(
)
(
)
k
k
cos
2
1
2
2
1 π
y
y
n
θ
β
θ
β
−
= −
⇒
−
= −
−
(
)
(
)
k
k
cos
2
1
2
2
1 π
y
y
n
θ
β
θ
β
−
= −
⇒
−
= −
−
(
)
min
k
1
2
1 π
2
n
y
n
θ
β
=
+
−
Do powyższych wzorów należy podstawiać takie całkowite wartości n,
aby rozwiązania miały sens fizyczny, czyli
max
min
0
0
n
n
y
l
y
l
≤
≤
≤
≤
Fala stojąca prądu:
Położenia minimów i maksimów amplitudy prądu są zamienione
w stosunku do minimów i maksimów amplitudy napięcia
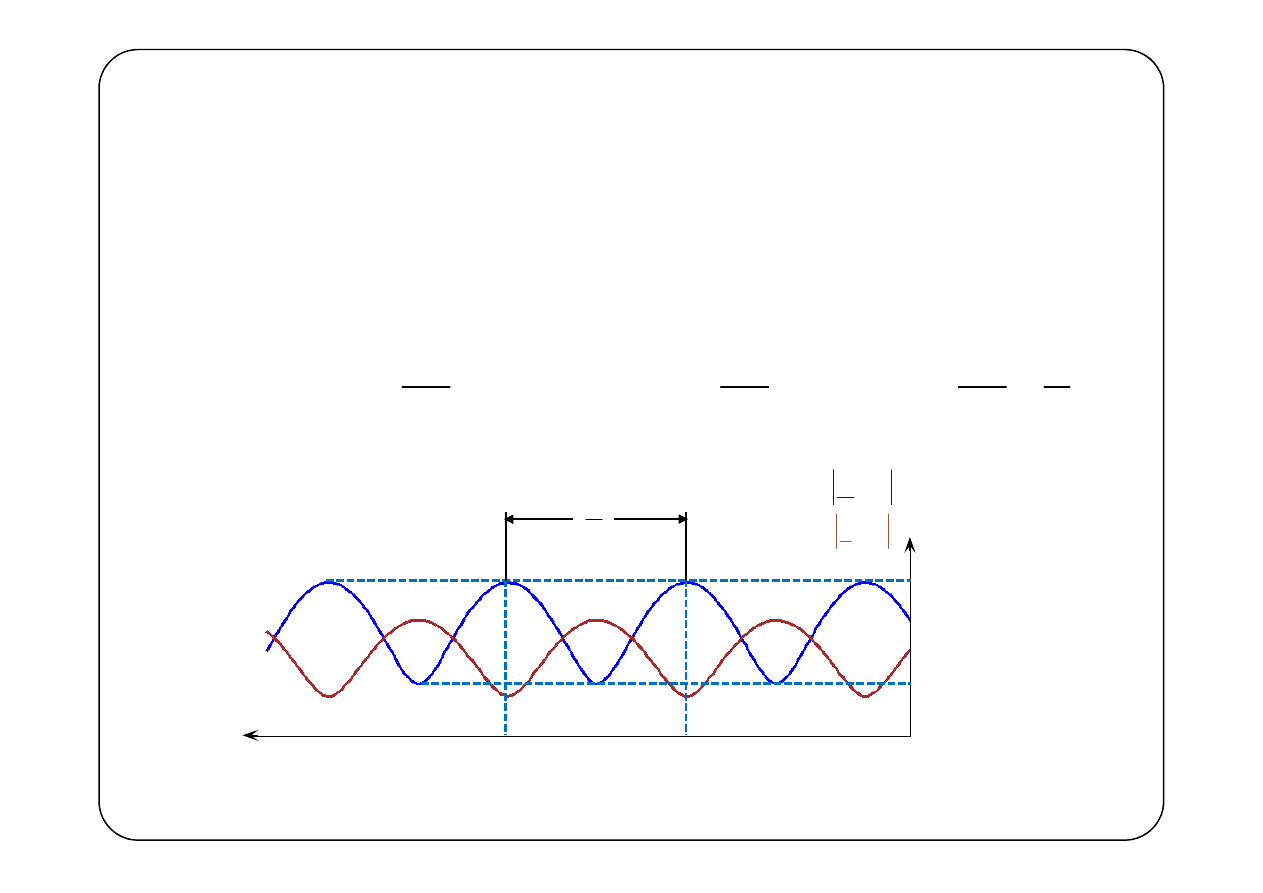
Odległość między sąsiednimi maksimami (minimami)
( )
(
)
(
)
max
k
k
max
1
1
1
2π
2
1 π
2 π
2
2
2
2
n
n
y
y
n
n
λ
θ
θ
β
β
β
+
−
=
+
+
−
+
=
=
( )
U y
ɶ
( )
I y
ɶ
y
max
U
min
U
max2
y
max3
y
2
λ
(
)
(
)
(
)
(
)
2
k
k
k
ik
ik
max
max
2
k
k
k
ik
ik
min
min
1 2
1
1 2
1
n
n
U
U y
U
U
U
U y
U
U
Γ
Γ
Γ
Γ
Γ
Γ
=
=
+
+
=
+
=
=
−
+
=
−
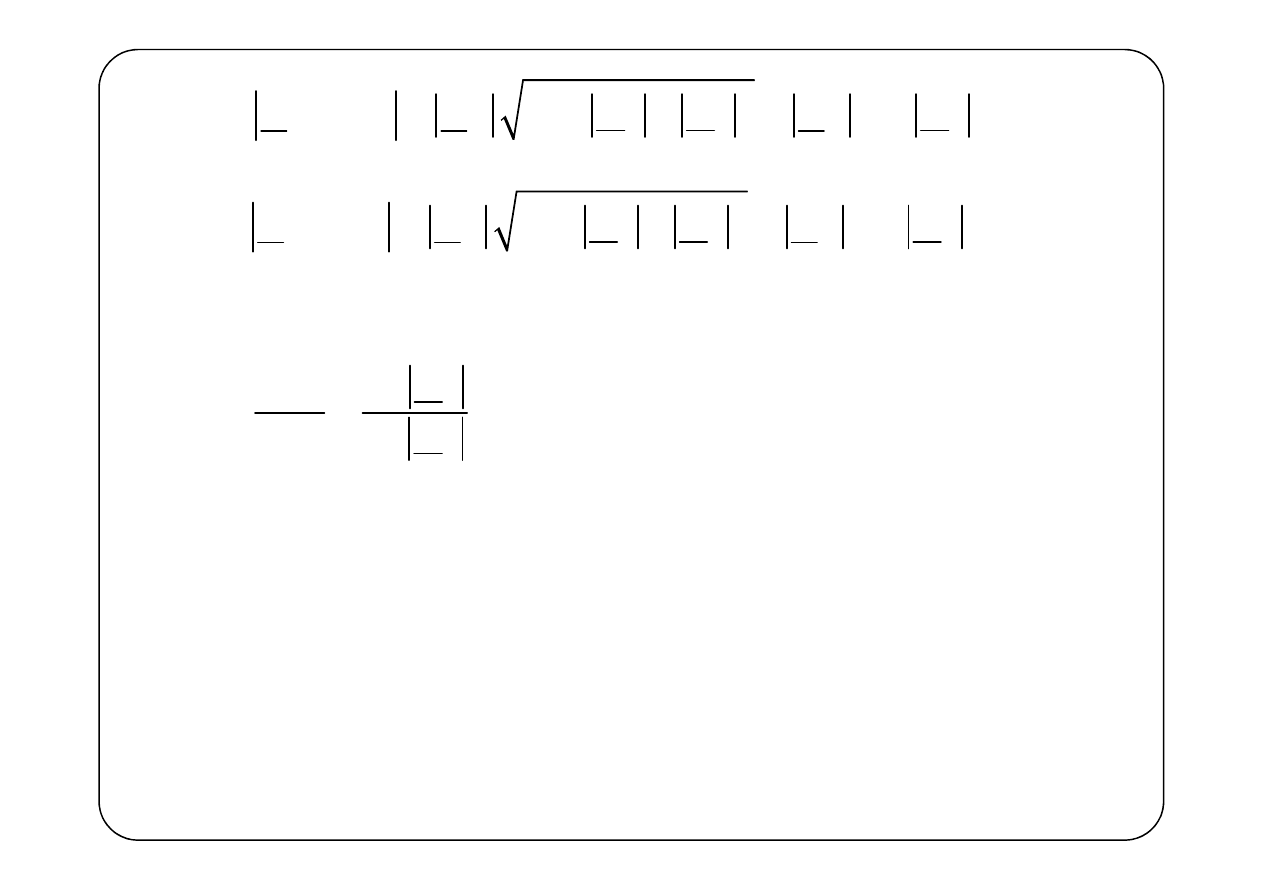
Współczynnik fali stojącej (WFS)
k
max
min
k
1
1
U
U
Γ
ρ
Γ
+
=
=
−
min
k
1
U
Γ
−
Jest popularną miarą niedopasowania linii
1
ρ
≤ < ∞
W linii dopasowanej
1
ρ
=
Zniekształcenia sygnałów w linii
Najczęściej
w
linii
transmisyjnej
rozchodzą
się
sygnały
przenoszące informację (przebiegi zmodulowane, impulsowe),
których widmo zawiera składowe o wielu różnych pulsacjach.
Każda ze składowych rozchodzi się z prędkością fazową
( )
( )
(
)(
)
{
}
f
0
0
0
0
,
Im
j
j
v
R
L
G
C
ω
ω
ω
β ω
ω
ω
=
=
+
+
która zależy od pulsacji. Może to spowodować zniekształcenie
kształtu przenoszonego sygnału, a w konsekwencji utrudnić lub
uniemożliwić poprawny odbiór przesyłanej informacji.
( )
(
)(
)
{
}
0
0
0
0
Im
j
j
R
L
G
C
β ω
ω
ω
+
+
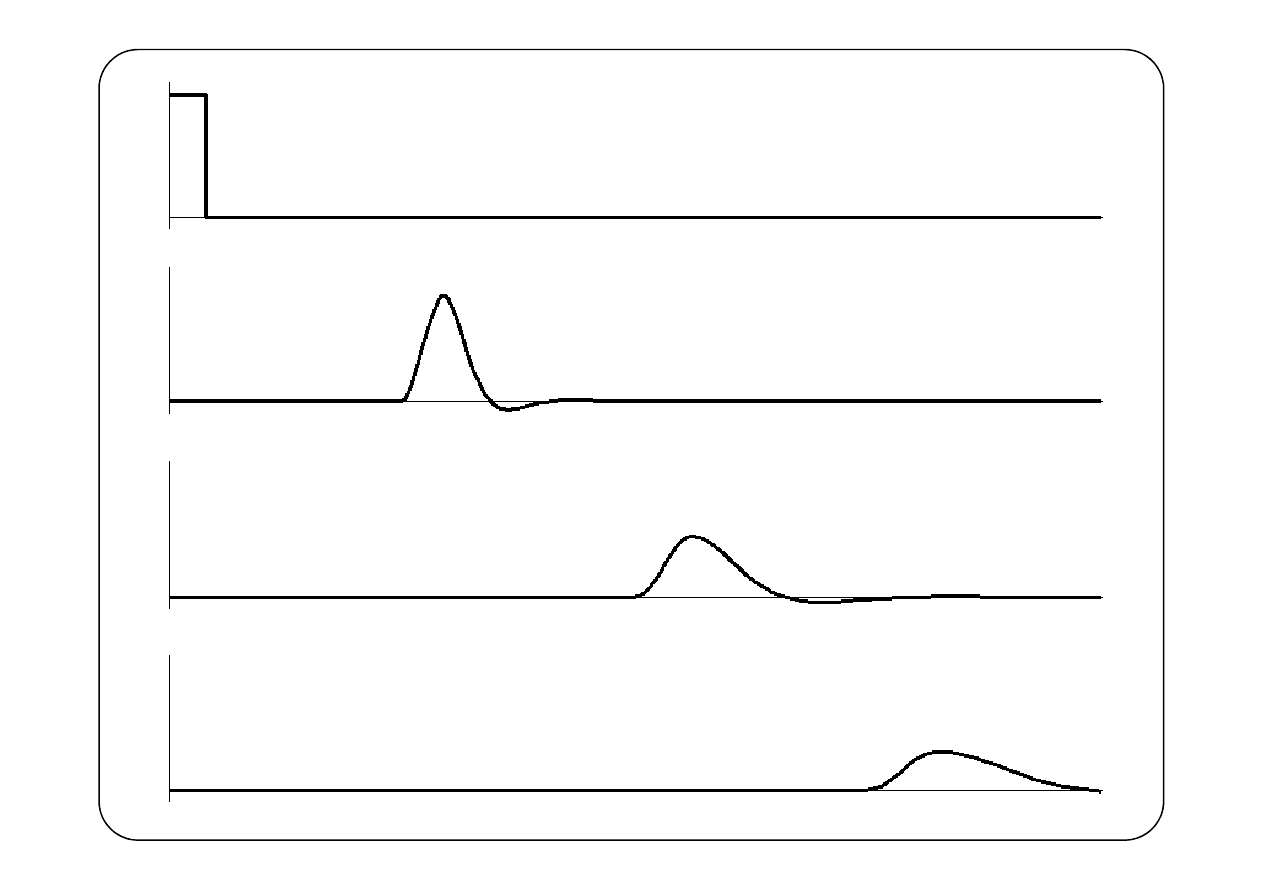
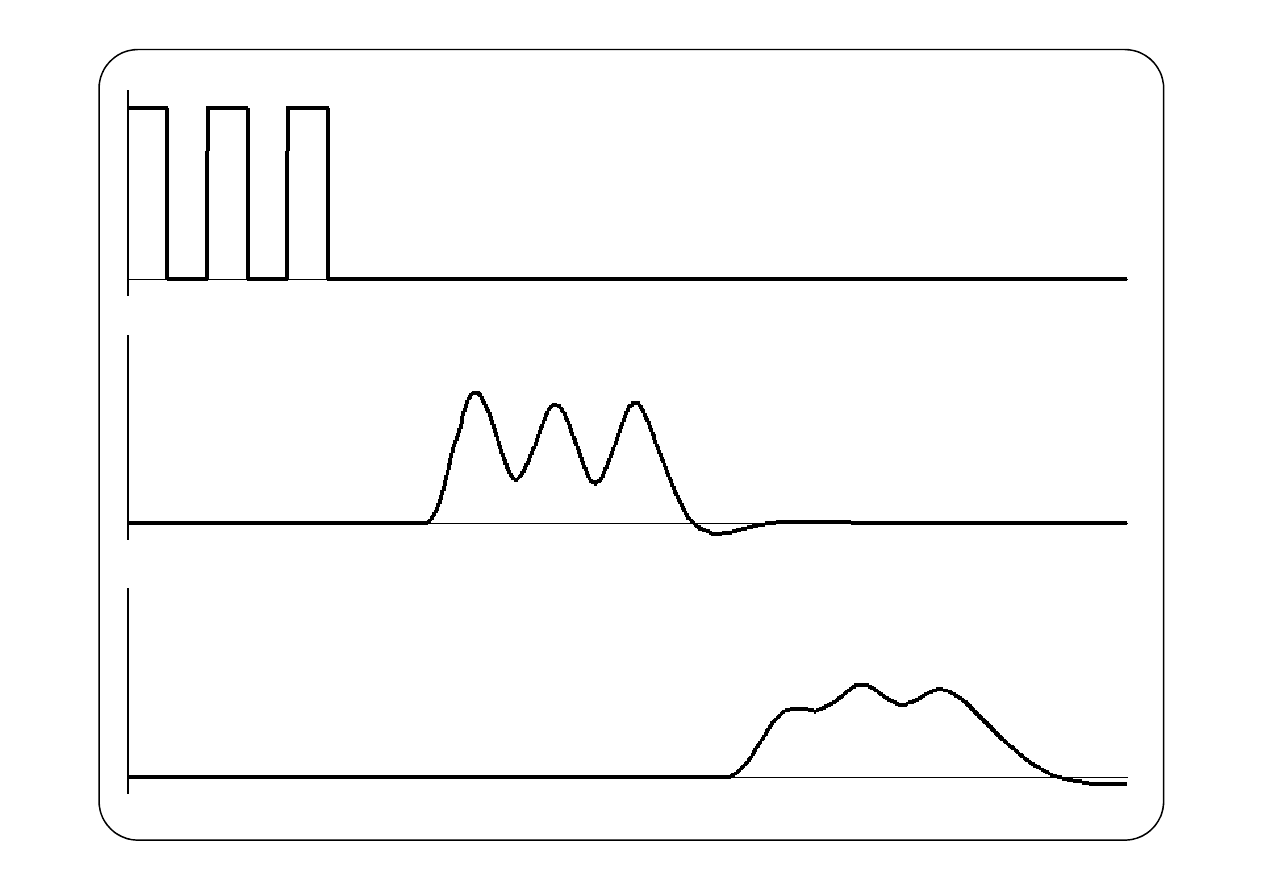
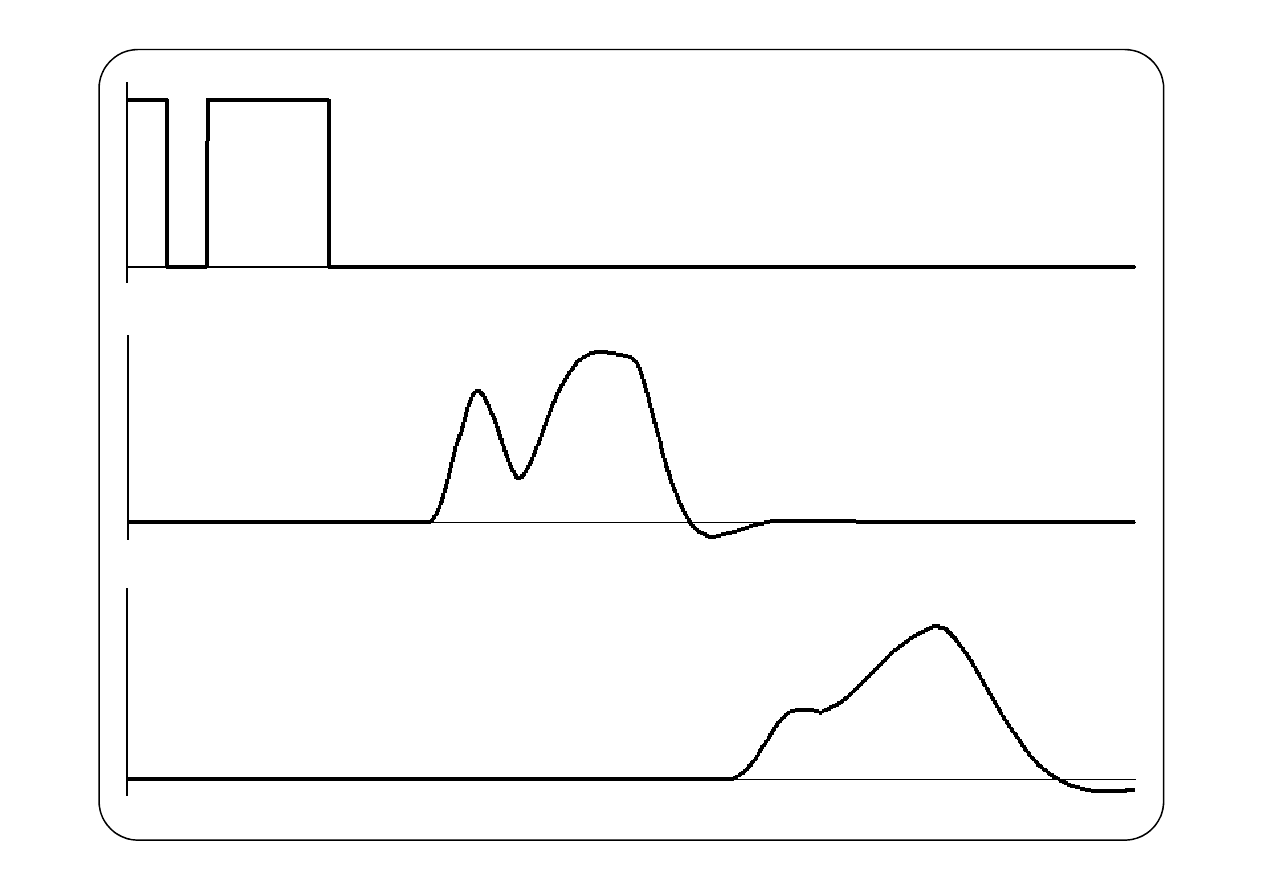
Załóżmy, że w linii nie występuje fala odbita oraz
( )
(
)
(
)
p
p1
0
1
p2
0
2
2 sin
2 sin
u t
U
t
U
t
ω
ψ
ω
ω
ψ
=
+
+
+ ∆
+
Wówczas, zgodnie z zasadą superpozycji:
( )
(
)
(
)
(
) (
)
p1
0
1
p2
0
2
,
2e
sin
2e
sin
,
x
x
u t x
U
t
x
U
t
x
α
α α
ω
β ψ
ω
ω
β
β
ψ
−
− +∆
=
−
+
+
+
+ ∆
−
+ ∆
+
gdzie
(
)(
)
(
)
(
)
(
)
0
0
0
0
0
0
0
0
0
0
0
0
j
j
j
j
j
j
R
L
G
C
R
L
G
C
ω
ω
α
β
ω
ω
ω
ω
α
α
β
β
+
+
= +
+
+ ∆
+
+ ∆
= + ∆ +
+ ∆

Założymy, że
p1
p2
p
0
1
2
,
,
0.
U
U
U
ω ω
ψ ψ
=
=
∆
=
=
≪
Wówczas można przyjąć e
1
x
α
−∆
≈
( )
(
)
(
)
p
0
0
,
2e
sin
sin
x
u t x
U
t
x
t
x
t
x
α
ω
β
ω
β
ω
β
−
=
−
+
−
+ ∆ − ∆
sin
sin
2 cos
sin
2
2
B
A
B
A
A
B
−
+
+
=
( )
(
)
p
0
,
2 2
e
cos
sin
2
2
x
u t x
U
t
x
t
x
α
β
ω
ω
β
−
∆
∆
=
−
−
(Przy uproszczeniach: )
0
0
2
2
,
2
2
ω
ω
β
β
ω
β
+ ∆
+ ∆
≈
≈
( )
(
)
p
0
,
2 2
e
cos
sin
2
2
x
u t x
U
t
x
t
x
α
β
ω
ω
β
−
∆
∆
=
−
−
( )
0
,
u t x
( )
,
A t x
Dla ustalonego t = t
0
x
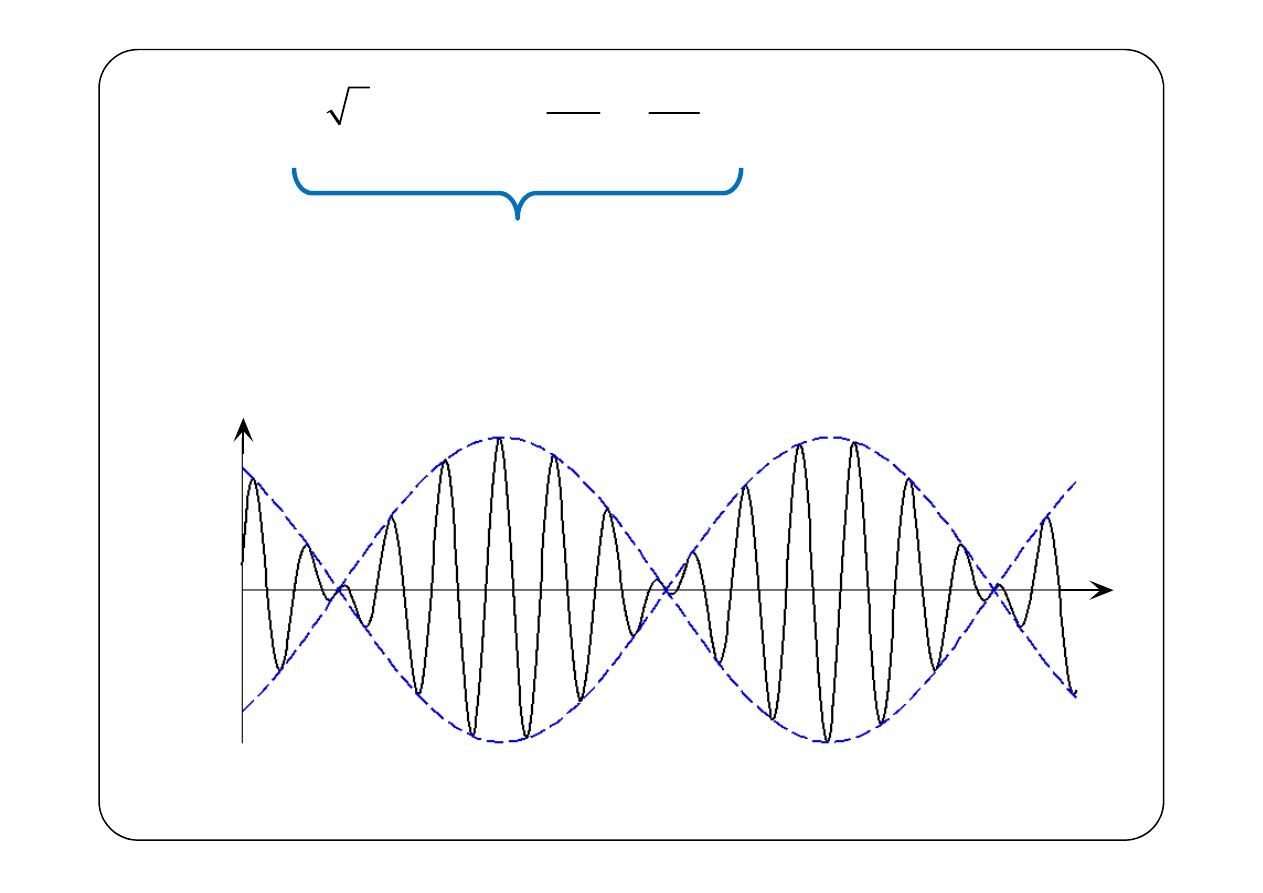
Równanie obwiedni
reprezentuje tłumioną falę, poruszającą się w kierunku dodatnich x.
( )
p
,
2 2
e
cos
2
2
x
A t x
U
t
x
α
β
ω
−
∆
∆
=
−
Punkt o stałej fazie obwiedni
const
t
x
β
ω
Φ
∆
∆
−
=
=
porusza się w kierunku dodatnich x z prędkością
0
const
2
2
t
x
β
ω
Φ
∆
∆
−
=
=
ω
β
∆
∆
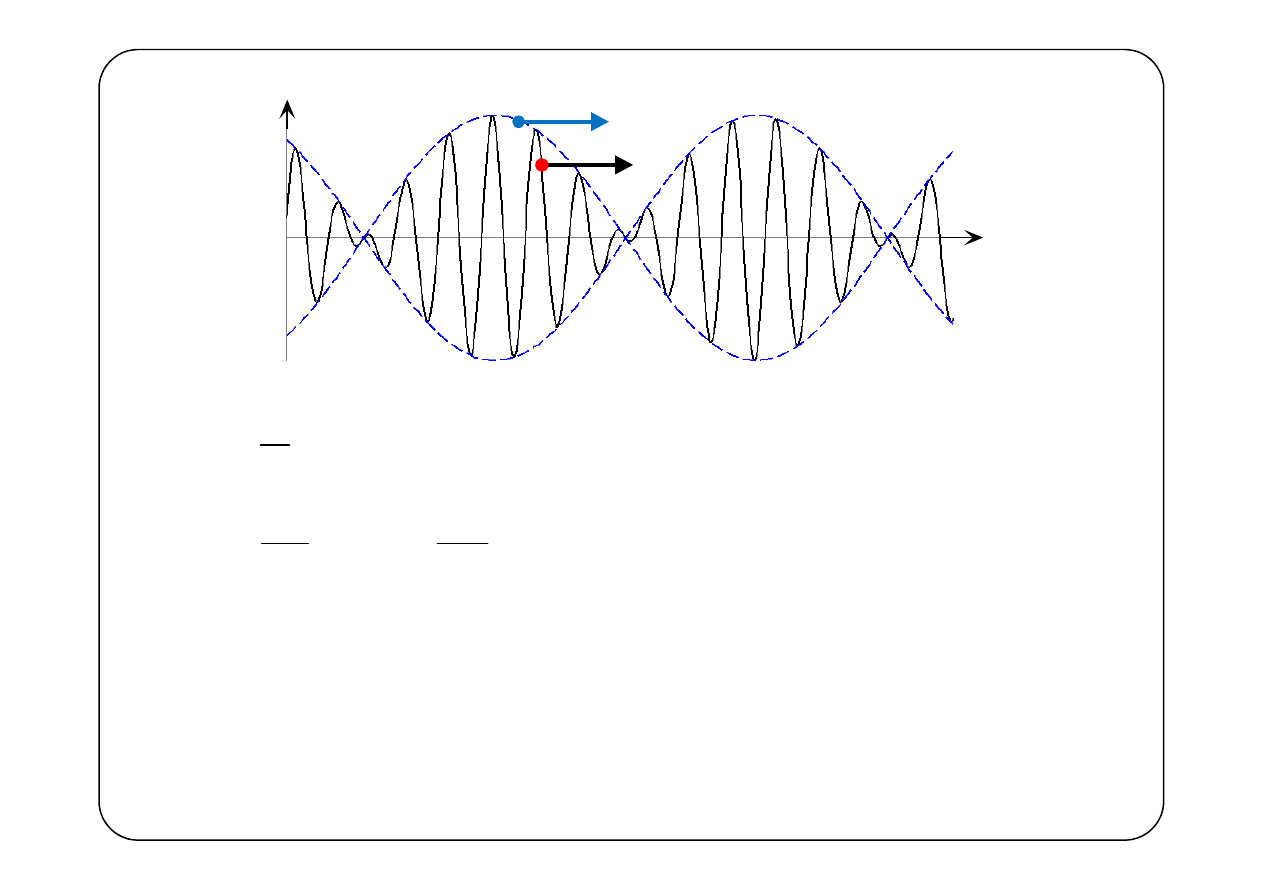
Definiuje się prędkość grupową jako
g
0
d
lim
d
v
β
ω
ω
β
β
∆ →
∆ =
∆
≜
( )
0
,
u t x
x
f
v
g
v
f
f
v
v
ω
ω β
β
=
⇒
=
f
f
f
g
f
d
d
d
d
v
v
v
v
v
ω β
β
ω
β
β
β
=
⇒
=
=
= +
Jeżeli v
g
≠
v
f
linia nazywa się linią dyspersyjną, przy czym
v
g
> v
f
— dyspersja anomalna
v
g
< v
f
— dyspersja normalna
W przypadku, gdy w linii rozchodzą się przebiegi których widmo
zawiera składowe o wielu różnych częstotliwościach, warunkiem
zachowania kształtu przebiegu jest zachowanie relacji między
fazami tych składowych, co wymaga aby
czyli
g
f
v
v
=
d
d
d
d
ω
ω
β
ω
β β
ω
β
=
⇒
=
ln
ln
ln ,
a
β
ω
=
+
a > 0 — dowolna stała
a
β
ω
=
Warunkiem na to, aby linia nie wprowadzała zniekształceń
obwiedni sygnałów będzie więc
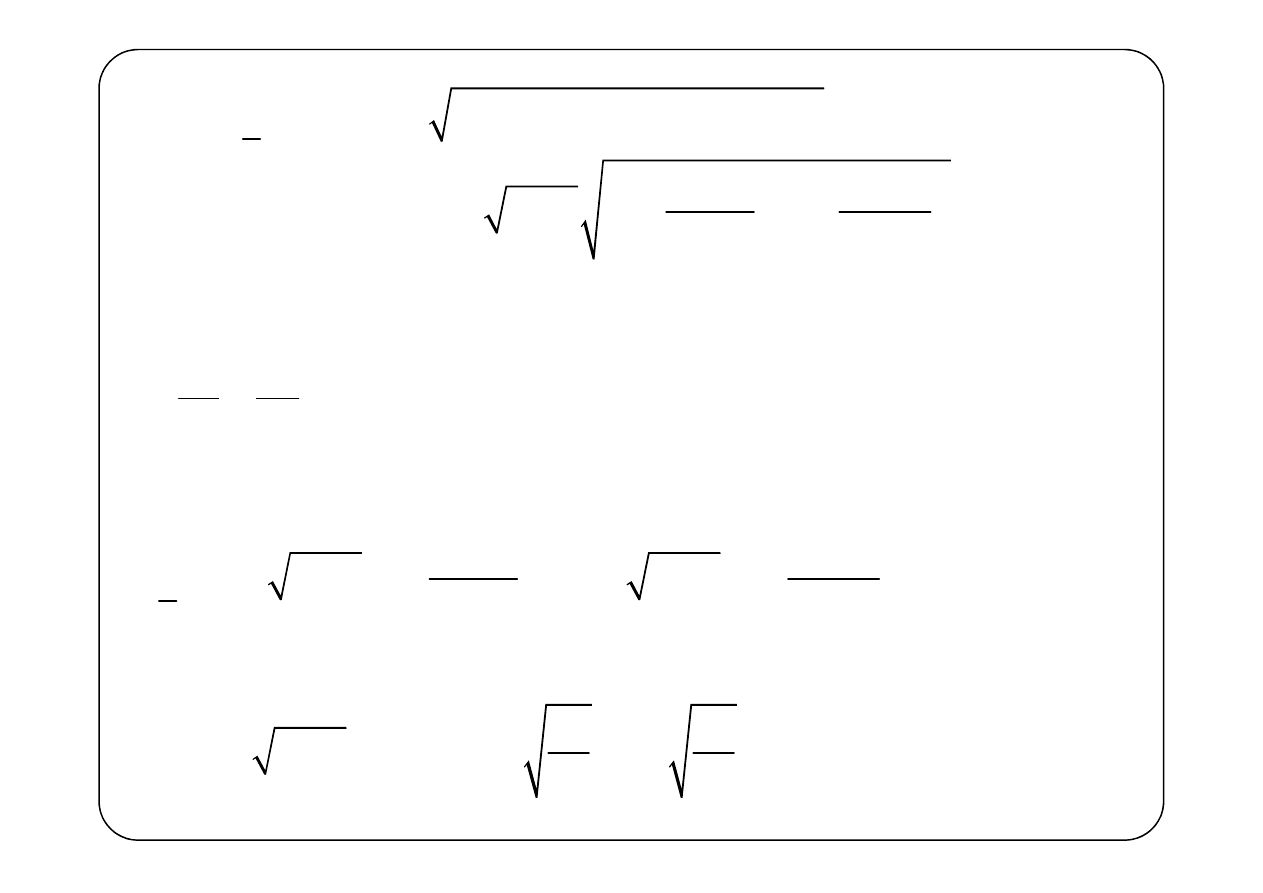
(
)(
)
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j
j
j
j
1
1
j
j
R
L
G
C
R
G
L C
L
C
γ α
β
ω
ω
ω
ω
ω
= +
=
+
+
=
=
+
+
Jeżeli zachodzić będzie równość
0
0
0
0
R
G
L
C
=
to wówczas
czyli
0
0
0
0
0
0
0
0
0
0
0
0
j
1
j
1
j
j
R
G
L C
L C
L
C
γ
ω
ω
ω
ω
=
+
=
+
0
0
0
0
0
0
0
0
0
,
C
L
L C
R
G
L
C
β ω
α
=
=
=
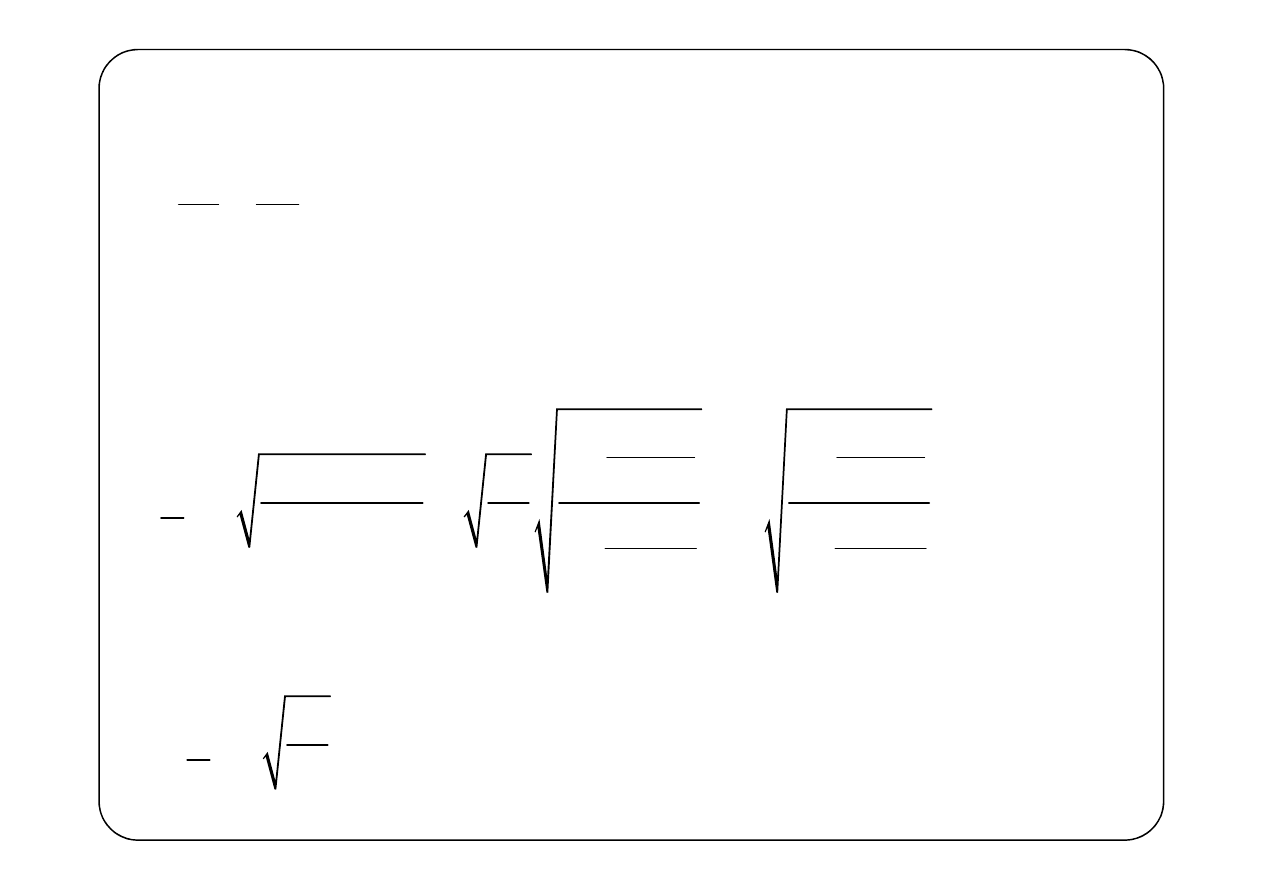
Linia transmisyjna, taka że
nazywa się linią zrównoważoną
0
0
0
0
R
G
L
C
=
Impedancja falowa
0
0
1
1
R
R
+
+
0
0
0
0
0
0
0
0
0
0
f
0
0
0
0
0
0
0
0
0
0
1
1
j
j
j
j
1
1
j
j
R
R
R
L
L
L
L
Z
G
C
C
G
G
C
C
ω
ω
ω
ζ
ω
ω
ω
+
+
+
=
=
=
+
+
+
W przypadku linii zrównoważonej
0
f
0
L
Z
C
ζ
=
=
— impedancja charakterystyczna
(liczba rzeczywista!)
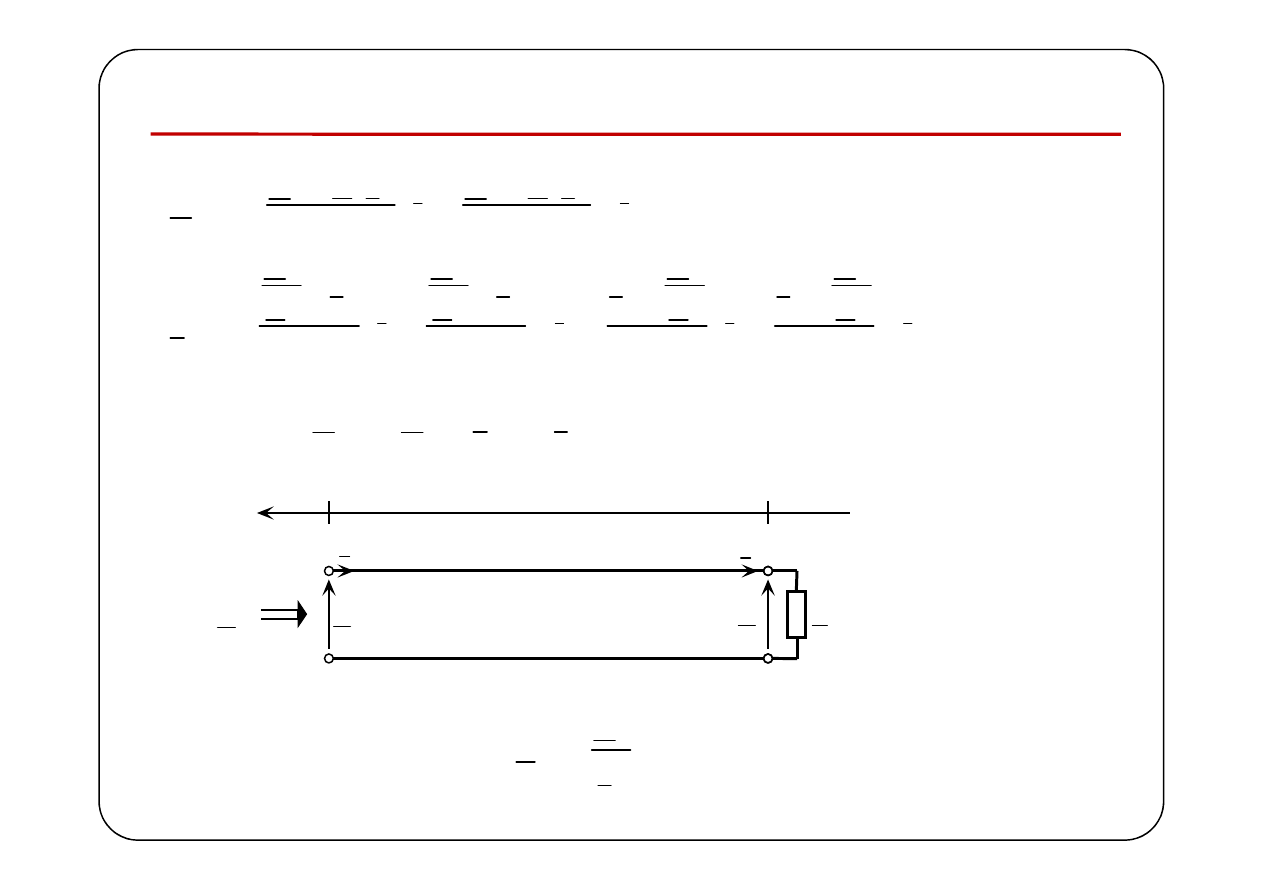
Impedancja wejściowa linii
( )
( )
f
k
f
k
k
k
k
k
k
k
k
k
k
k
f
f
f
f
e
e
2
2
e
e
e
e
2
2
2
2
y
y
y
y
y
y
U
Z I
U
Z I
U y
U
U
U
U
I
I
I
I
Z
Z
Z
Z
I y
γ
γ
γ
γ
γ
γ
−
−
−
+
−
=
+
+
−
+
−
=
−
=
+
ɶ
ɶ
( )
( )
p
p
,
y
l
U l
U
I l
I
=
⇒
=
=
ɶ
ɶ
p
U
p
I
k
Z
k
I
k
U
0
y
=
y
l
=
y
we
Z
p
we
p
U
Z
I
=
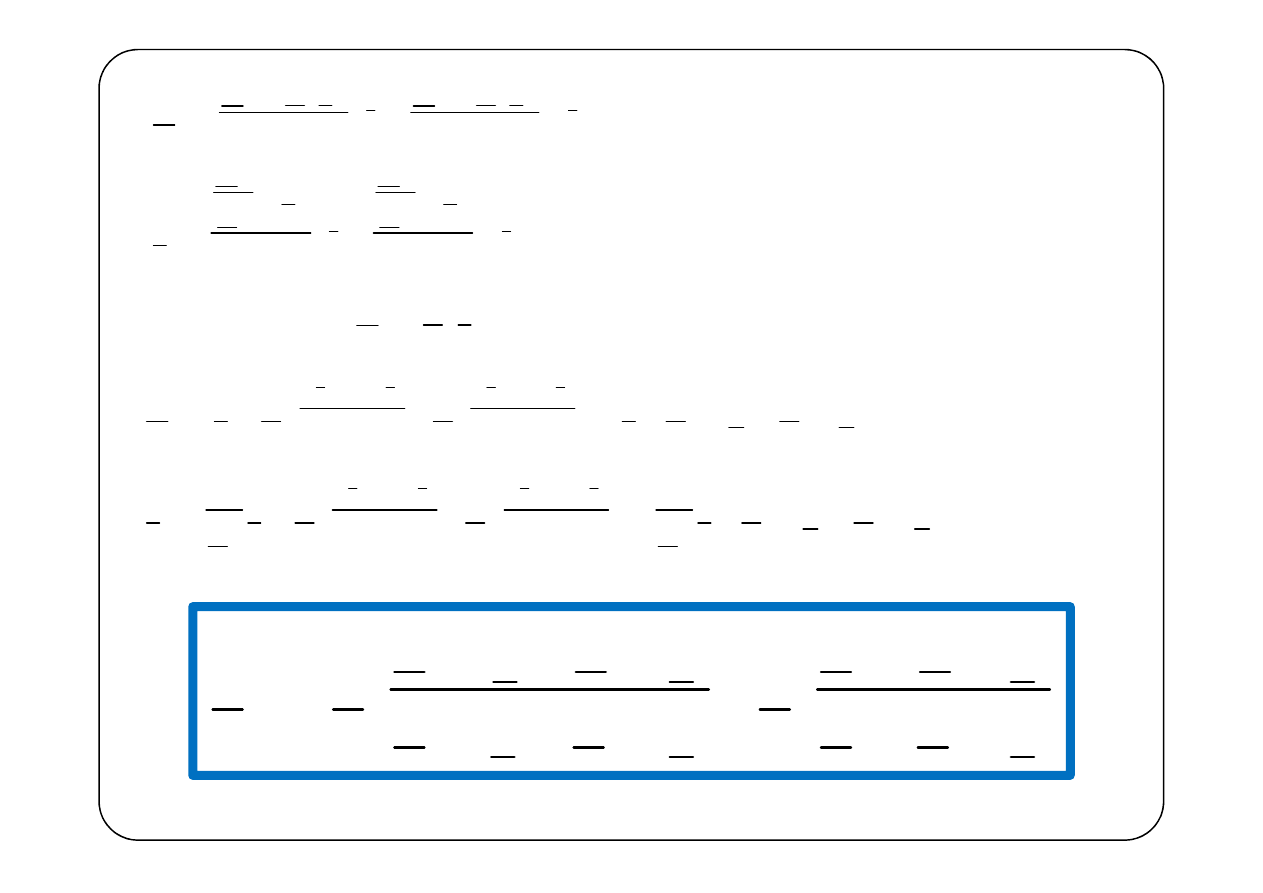
f
k
f
k
k
k
p
k
k
k
k
f
f
p
e
e
2
2
e
e
2
2
l
l
l
l
U
Z I
U
Z I
U
U
U
I
I
Z
Z
I
γ
γ
γ
γ
−
−
+
−
=
+
+
−
=
−
Po podstawieniu i uporządkowaniu
k
k
k
U
Z I
=
(
)
k
k
f
k
k
f
p
e
e
e
e
ch
sh
2
2
l
l
l
l
U
I
Z
Z
I
Z
l
Z
l
γ
γ
γ
γ
γ
γ
−
−
+
−
=
+
=
+
(
)
p
k
f
k
k
f
k
f
f
2
2
1
e
e
e
e
1
ch
sh
2
2
l
l
l
l
I
I
Z
Z
I
Z
l
Z
l
Z
Z
γ
γ
γ
γ
γ
γ
−
−
+
−
=
+
=
+
k
f
k
f
we
f
f
f
k
f
k
ch
sh
th
ch
sh
th
Z
l
Z
l
Z
Z
l
Z
Z
Z
Z
l
Z
l
Z
Z
l
γ
γ
γ
γ
γ
γ
+
+
=
=
+
+
Przyjmijmy (dopasowanie falowe)
k
f
Z
Z
=
Wówczas
f
f
we
f
f
f
f
th
th
Z
Z
l
Z
Z
Z
Z
Z
l
γ
γ
+
=
=
+
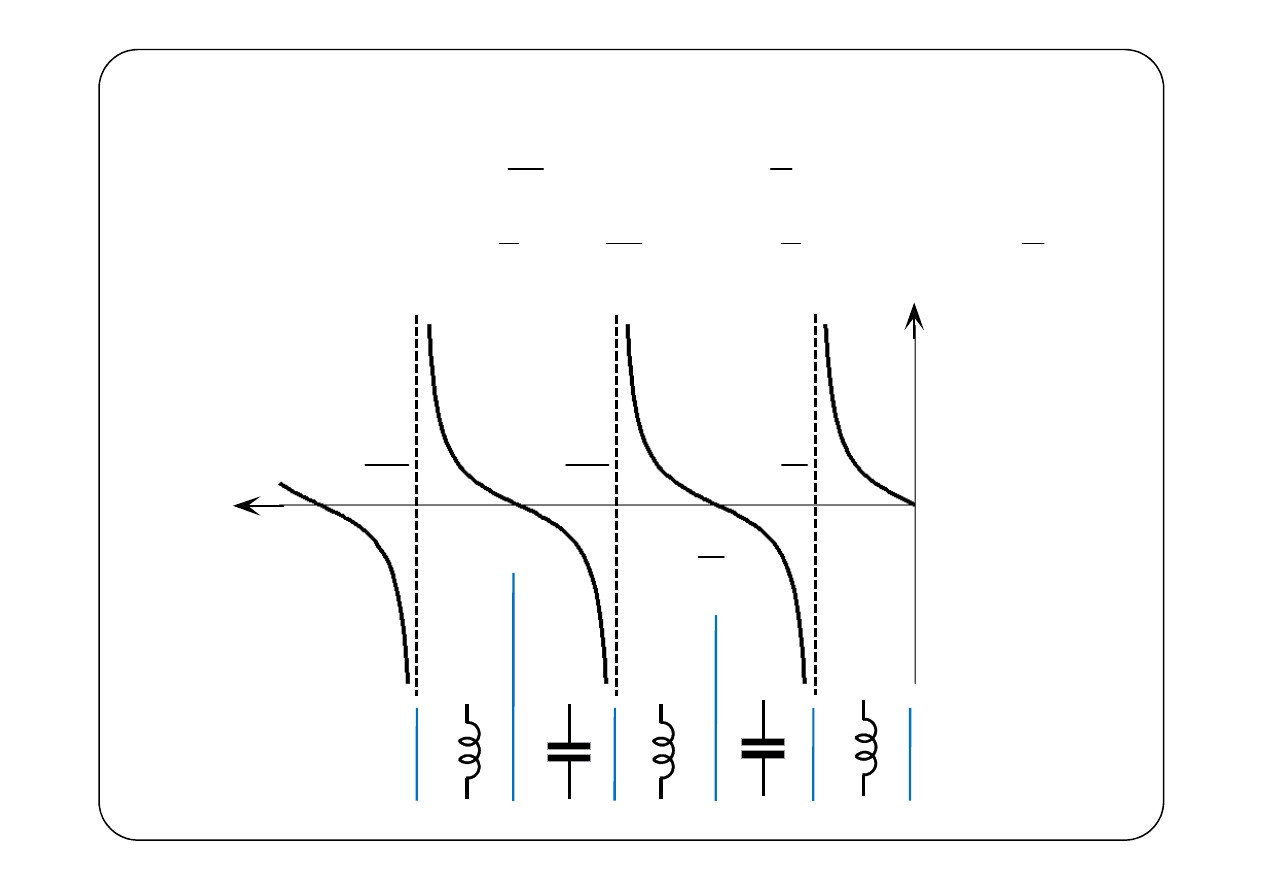
Linia zwarta na końcu —
k
0
Z
=
Linia zwarta na końcu —
k
0
Z
=
we
f
th
Z
Z
l
γ
=
Linia rozwarta na końcu —
k
Z
→ ∞
f
we
th
Z
Z
l
γ
=
k
we
k
j tg
j
tg
Z
l
Z
Z
l
ζ β
ζ ζ
β
+
=
+
Linia bezstratna
( )
( )
( )
0
f
0
j ,
sh j
jsin
,
ch j
cos
,
th j
jtg
l
l
l
l
l
l
L
Z
C
γ
β
β
β
β
β
β
β
ζ
=
=
=
=
=
=
Linia zwarta na końcu —
0
Z
=
Linia zwarta na końcu —
k
0
Z
=
we
we
j tg
j
Z
l
X
ζ β
=
=
Linia rozwarta na końcu —
k
Z
→ ∞
we
we
j
j ctg
j
tg
Z
l
X
l
ζ
ζ
β
β
= −
= −
=
we
X
λ
3
λ
5
λ
(
)
(
)
(
)
we
we
2π
0
π
π
2
π
2π
π
2
1
2
1
2
1
2
2
4
X
l
n
l
n
l
n
X
l
n
l
n
l
n
λ
β
λ
λ
β
λ
=
⇒
=
⇒
=
⇒
=
→ ∞
⇒
=
−
⇒
=
−
⇒
=
−
we
tg
X
l
ζ β
=
Linia zwarta —
l
4
λ
2
λ
3
4
λ
λ
5
4
λ
Zakres wielkich częstotliwości
„Wielkie częstotliwości” to takie, że
0
0
0
0
0
0
L
R
C
G
ω
ω
≫
≫
Wówczas
(
)(
)
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j
j
j
1
1
j
j
R
G
R
L
G
C
L C
L
C
γ
ω
ω
ω
ω
ω
=
+
+
=
+
+
0
0
0
0
0
0
0
0
0
0
f
0
0
0
0
0
0
0
0
0
0
1
1
j
j
j
j
1
1
j
j
R
R
R
L
L
L
L
Z
G
C
C
G
G
C
C
ω
ω
ω
ζ
ω
ω
ω
+
+
+
=
=
=
+
+
+
Skorzystamy z przybliżenia:
Jeżeli to
1
x
≪
1
1
1
1
2
2
1
x
x
x
x
+ ≈ +
≈ −
+
0
0
f
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
2 j
2 j
1
2 j
2 j
2 j
2 j
R
G
Z
L
C
R
G
R
G
L
C
L
C
ζ
ω
ω
ζ
ζ
ω
ω
ω
ω
=
+
−
=
=
+
−
−
≈
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j
1
1
2 j
2 j
j
1
2 j
2 j
2 j
2 j
j
j
j
2
2
2
R
G
L C
L
C
R
G
R
G
L C
L
C
L
C
R
G
R
L C
L C
γ
ω
ω
ω
ω
ω
ω
ω
ω
ζ
ω
ω
α
β
ζ
ζ
=
+
+
=
=
+
+
+
=
≈
+
+
≈
+
= +
W zakresie wielkich częstotliwości można przyjąć:
0
f
0
L
Z
R
ζ
= =
0
2
R
α
ζ
=
0
0
0
L C
β ω
=
— linia zrównoważona
0
0
0
L C
β ω
=
— linia zrównoważona
0
0
0
r
0
r
L C
µ µ ε ε
=
0 0
2
1
c
µ ε
=
najczęściej
µ
r
=1
0
r
0
f
f
0
r
0
r
r
v
c
c
v
c
f
f
ω ε
λ
β
λ
ε
ε
ε
=
=
=
=
=

Rzeczywiste linie transmisyjne
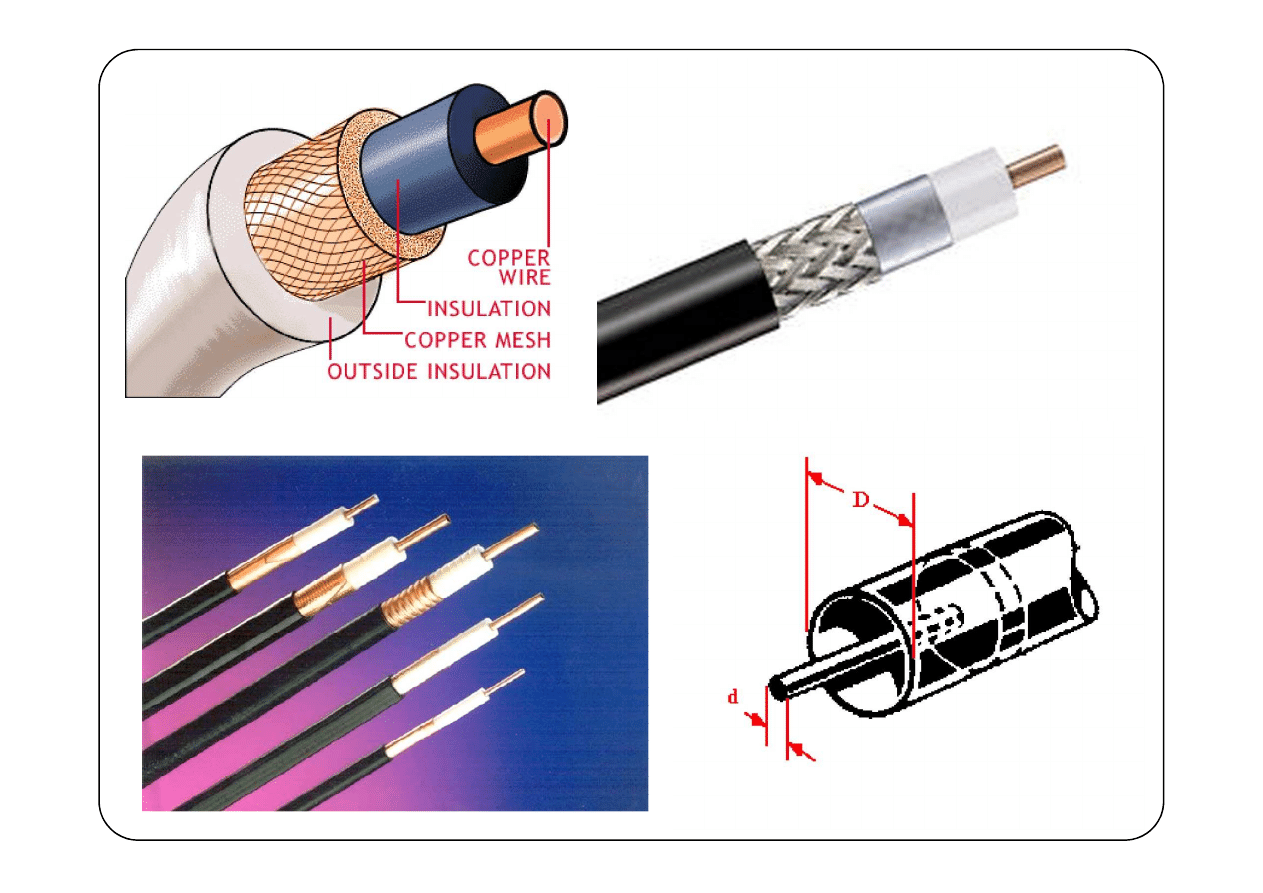
Linie dwuprzewodowe
r
ε
d
D
0
arch
π
D
L
d
µ
=
µ
— przenikalność magnetyczna ośrodka
7
r
0
0
H
,
4π 10
m
µ µ µ
µ
−
=
=
⋅
0
π
arch
C
D
d
ε
=
r
0
0
r
m
1
µ
≈
ε
— przenikalność dielektryczna ośrodka
12
r
0
0
2
0
1
F
,
8,8542 10
m
c
ε ε ε
ε
µ
−
=
=
≈
⋅
arch
π
D
d
µ
ζ
ε
=
ε
r
— względna przenikalność dielektryczna (stała dielektryczna)
Materiał
ε
r
Powietrze
∼
1
Guma
2,6
÷
3
Ebonit
2,5
÷
3,5
Porcelana elektrotechniczna
6
÷
8
Polistyren, polietylen
2,2
÷
2,4
Polistyren, polietylen
2,2
÷
2,4
Polietylen spieniony
1,45
µ
r
— względna przenikalność magnetyczna
Diamagnetyki, paramagnetyki —
µ
r
≈
1
Ferromagnetyki —
µ
r
= 5000
÷
100000
0
eff
c
1
2
R
S
σ
=
w
δ
d
w
c
2
δ
µωσ
=
— głębokość wnikania
w
eff
w
π
d
S
d
δ
δ
⇒
≈
≪
0
c
2
π
2
R
d
µω
σ
=
σ
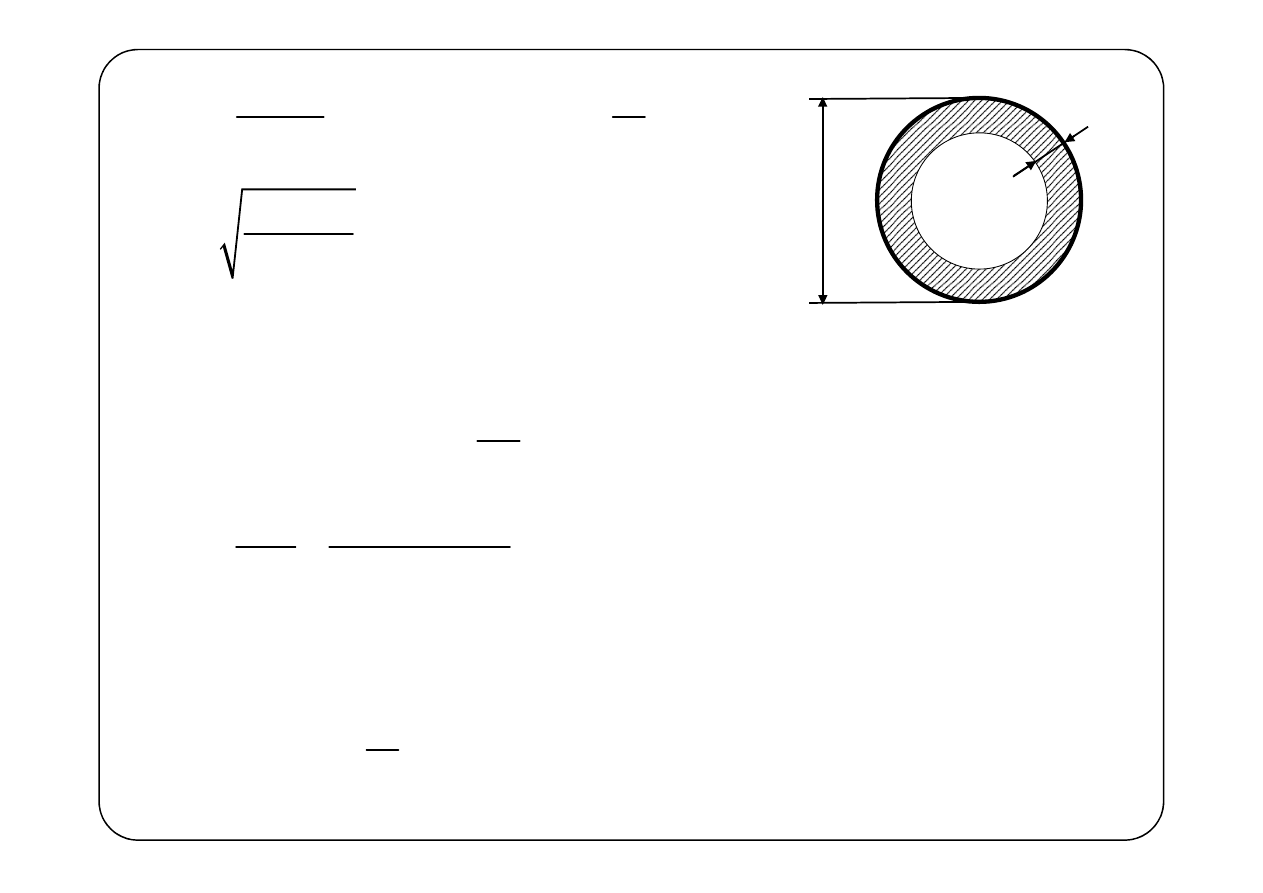
— konduktywność materiału przewodnika
c
σ
— konduktywność materiału przewodnika
Materiał
σσσσ
c
[S/m]
Aluminium
35,7
⋅
10
6
Miedź
58,8
⋅
10
6
Srebro
62,5
⋅
10
6
Złoto
41,7
⋅
10
6
Cyna
8,3
⋅
10
6

d
d
0
0
π
arch
G
C
D
d
σ
σ
ε
=
=
σ
d
— konduktywność dielektryka
Materiał
σσσσ
d
[S/m]
Guma
10
–13
Ebonit
10
–15
Ebonit
10
–15
Porcelana elektrotechniczna
(0,25
÷
1,5)
⋅
10
–9
Polistyren, polietylen
10
–15
÷
10
–13
Powietrze
?
Przykład 1
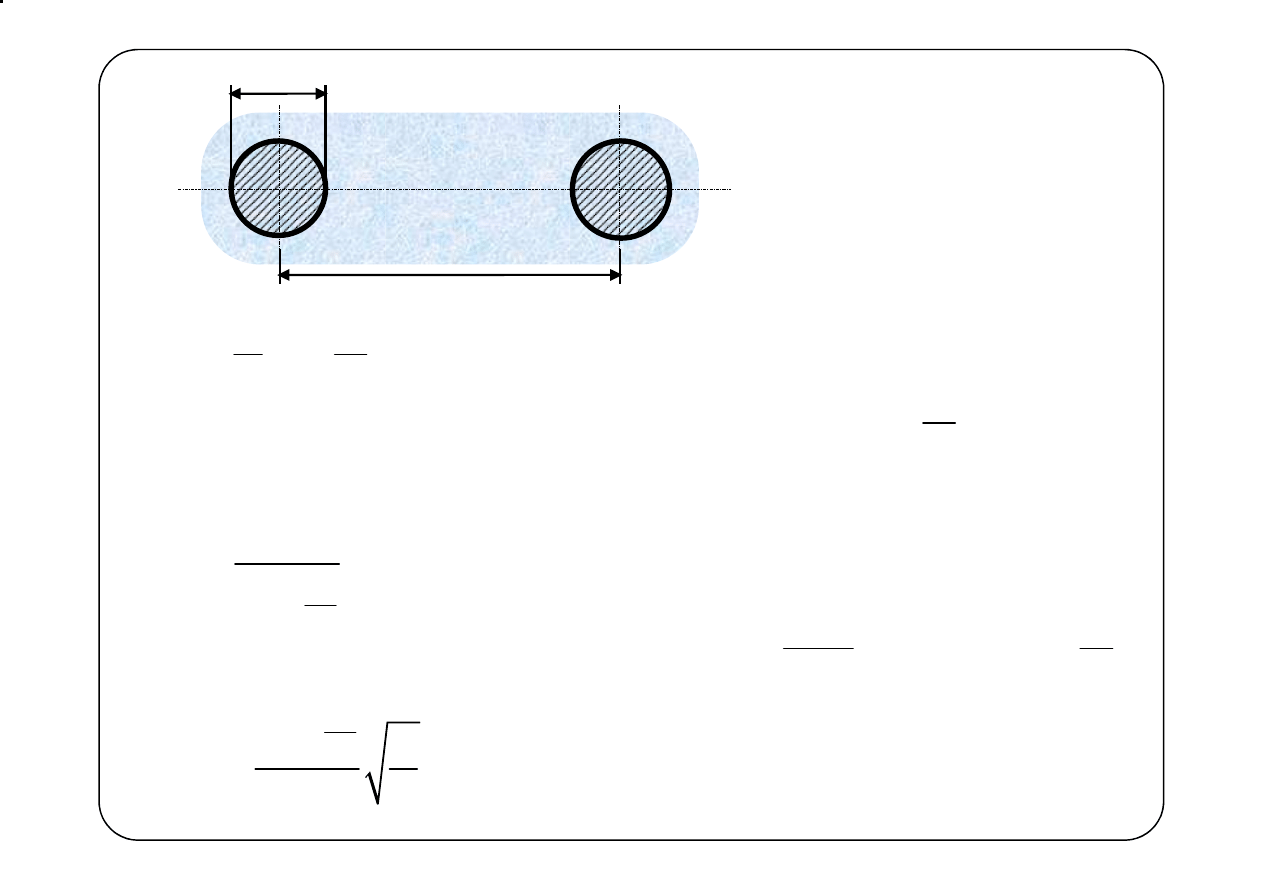
Wyznaczyć parametry jednostkowe linii napowietrznej, wykonanej
z przewodów aluminiowych o średnicy d = 4 mm, umieszczonych
w odległości D = 30 cm. Przeprowadzić obliczenia dla f
1
= 20 kHz
i f
2
=10 MHz.
Przyjmujemy
ε
r
=1,
µ
r
=1
6
0
H
arch
2 10
D
L
µ
−
=
= ⋅
6
0
0
H
arch
2 10
π
m
D
L
d
µ
−
=
= ⋅
12
0
0
π
F
5, 6 10
m
arch
C
D
d
ε
−
=
=
⋅
0
0
0
0
arch
600 Ω
π
D
L
d
C
µ
ζ
ε
=
=
=
6
0
c
eff
c
1
S
2
,
35, 7 10
m
R
S
σ
σ
=
=
⋅
w
δ
d
w
0
c
2
δ
µ ωσ
=
1. f
1
= 20 kHz
3
w
w
0,58 10 m,
0,15
d
δ
δ
−
=
⋅
=
w
0,58 10 m,
0,15
d
δ
=
⋅
=
(
)
2
2
w
6
2
eff
π
2
π
6, 24 10 m
4
4
d
d
S
δ
−
−
=
−
=
⋅
— wzór dokładny
3
0
Ω
8,55 10
m
R
−
=
⋅
6
2
eff
w
π
7,3 10 m
S
d
δ
−
≈
=
⋅
— wzór przybliżony, (błąd ok. 17
%
)
2. f
2
=10 MHz
6
w
w
26, 6 10 m,
0, 0067
d
δ
δ
−
=
⋅
=
(
)
2
2
w
6
2
eff
π
2
π
0,3299 10 m
4
4
d
d
S
δ
−
−
=
−
=
⋅
— wzór dokładny
6
2
eff
w
π
0,3346 10 m
S
d
δ
−
≈
=
⋅
— wzór przybliżony, (błąd ok. 1,4
%
)
Ω
0
Ω
0,17
m
R
=
G
0
można tylko oszacować — zależy m. in. od stanu izolatorów,
wilgotności i zanieczyszczenia powietrza.
Zwykle G
0
= (0,1
÷
1)
⋅
10
–9
S/m.
Przyjmijmy
9
0
S
0,5 10
m
G
−
=
⋅
Parametry falowe
1. f
1
= 20 kHz
(
)
(
)
f
6
3
6
597, 7
j9,9 Ω
1
7,3 10
j0, 421 10
m
Np
7,3 10
m
Z
γ
α
−
−
−
=
−
=
⋅
+
⋅
=
⋅
3
7,3 10
m
rad
0, 421 10
m
α
β
−
=
⋅
=
⋅
3
8
1
f
2π
2π
m
15 10 m,
2,99 10
s
f
v
c
λ β
β
=
= ⋅
=
=
⋅
=
3
dB
8, 686
0, 063 10
m
α
α
−
′ =
=
⋅
2. f
2
=10 MHz
(
)
(
)
f
3
3
600
j0, 4 Ω
1
0,1415 10
j0, 2096
m
Np
0,1415 10
m
rad
0, 2096
Z
ζ
γ
α
β
−
−
=
−
≈
=
⋅
+
=
⋅
=
rad
0, 2096
m
β
=
8
1
f
2π
2π
m
30 m,
2,9977 10
s
f
v
λ β
β
=
=
=
=
⋅
dB
8, 686
0, 00123
m
α
α
′ =
=
Przykład 2
Wyznaczyć
parametry
jednostkowe
kabla
symetrycznego,
przewody
o
ś
rednicy
d = 0,35 mm,
wykonane
z
miedzi
umieszczone w izolacji z polietylenu w odległości D = 7,5 mm.
Przeprowadzić obliczenia dla f
1
= 5 MHz i f
2
=100 MHz.
Miedź:
σ
c
= 58,8
⋅
10
6
S/m
Polietylen:
ε
r
= 2,25,
σ
d
= 10
–14
S/m
H
D
µ
6
0
0
H
arch
1,5 10
π
m
D
L
d
µ
−
=
=
⋅
12
0
r
0
π
F
16, 66 10
m
arch
C
D
d
ε ε
−
=
=
⋅
0
0
0
0
r
arch
300, 4 Ω
π
D
L
d
C
µ
ζ
ε ε
=
=
=
6
0
c
eff
c
1
S
2
,
58,8 10
m
R
S
σ
σ
=
=
⋅
w
0
c
2
δ
µ ωσ
=
1. f
1
= 5 MHz
6
w
w
29,35 10 m,
0, 084
d
δ
δ
−
=
⋅
≈
w
29,35 10 m,
0, 084
d
δ
=
⋅
≈
(
)
2
2
w
8
2
eff
π
2
π
2,956 10 m
4
4
d
d
S
δ
−
−
=
−
=
⋅
— wzór dokładny
8
2
eff
w
π
3, 23 10 m
S
d
δ
−
≈
=
⋅
— wzór przybliżony, (błąd ok. 9
%
)
0
Ω
1,15
m
R
=
2. f
2
=100 MHz
6
w
w
6,56 10 m,
0, 018
d
δ
δ
−
=
⋅
=
(
)
2
2
w
9
2
eff
π
2
π
7, 038 10 m
4
4
d
d
S
δ
−
−
=
−
=
⋅
— wzór dokładny
9
2
eff
w
π
7, 217 10 m
S
d
δ
−
≈
=
⋅
— wzór przybliżony, (błąd ok. 2,5
%
)
Ω
0
Ω
4,8
m
R
=
15
d
0
0
0
r
S
8,36 10
m
G
C
σ
ε ε
−
=
=
⋅
mało wiarygodne
Parametry falowe
1. f
1
= 5 MHz
(
)
(
)
f
3
3
300, 4
j3, 7 Ω
1
1,91 10
j0,1572
m
Np
1,91 10
m
Z
γ
α
−
−
=
−
=
⋅
+
=
⋅
1,91 10
m
rad
0,1572
m
α
β
=
⋅
=
8
1
f
2π
2π
m
40 m,
2 10
s
f
v
λ β
β
=
=
=
= ⋅
dB
8, 686
0, 0167
m
α
α
′ =
=
1. f
2
= 100 MHz
(
)
(
)
f
3
3
300, 4
j0, 77 Ω
1
8, 04 10
j3,1437
m
Np
8, 04 10
m
rad
3,1437
Z
γ
α
β
−
−
=
−
=
⋅
+
=
⋅
=
rad
3,1437
m
β
=
8
1
f
2π
2π
m
2 m,
2 10
s
f
v
λ β
β
=
=
=
= ⋅
dB
8, 686
0, 07
m
α
α
′ =
=

Kabel koncentryczny
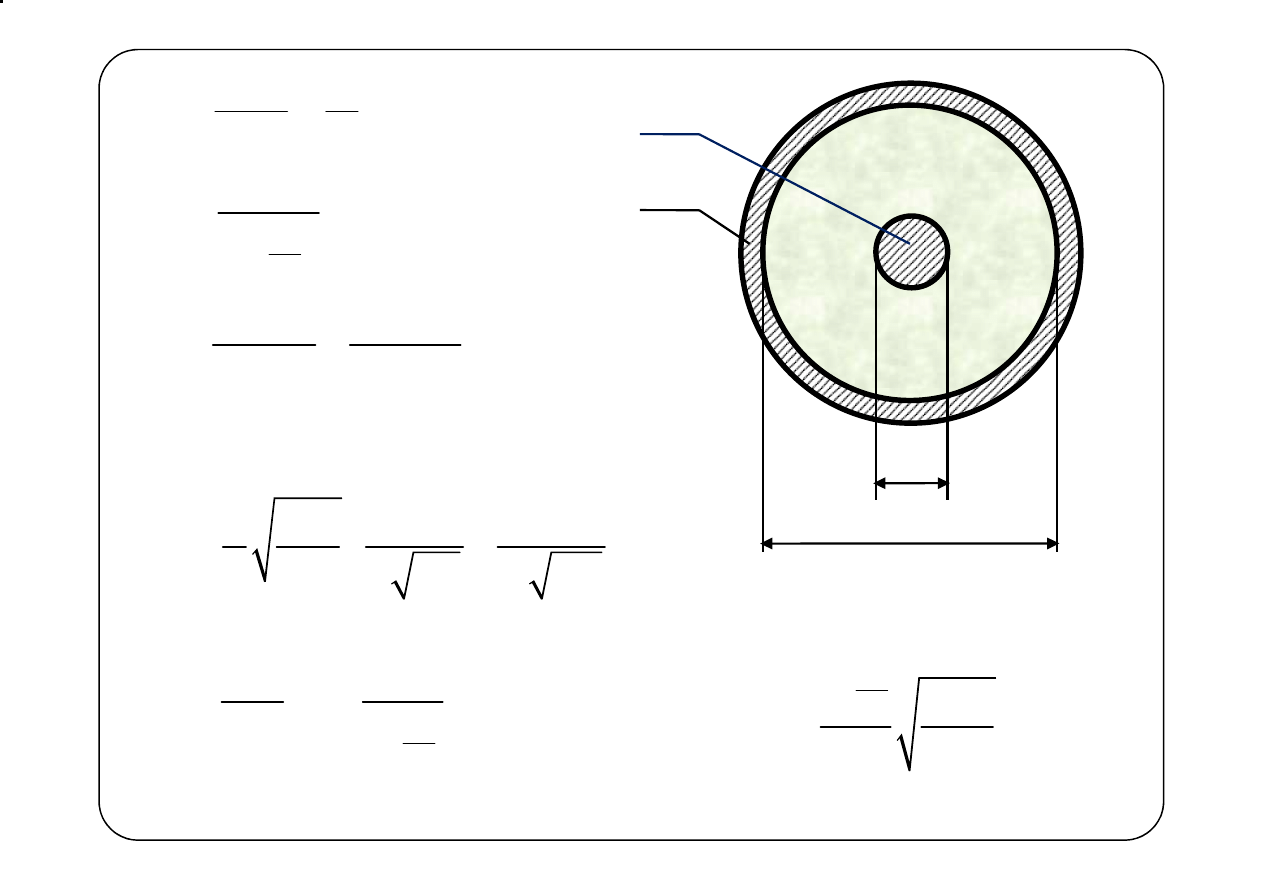
r
ε
0
r
0
ln
2π
D
L
d
µ µ
=
0
r
0
2π
ln
C
D
d
ε ε
=
0
eff 1
c1
eff 2
c2
1
1
R
S
S
σ
σ
=
+
eff 1
w1
eff 2
w 2
π
,
π
S
d
S
D
δ
δ
≈
≈
c1
σ
c2
σ
d
D
eff 1
w1
eff 2
w 2
π
,
π
S
d
S
D
δ
δ
≈
≈
0
0
c1
c2
1
1
1
π
2
R
d
D
µ ω
σ
σ
=
+
d
d
0
0
0
r
2π
ln
G
C
D
d
σ
σ
ε ε
≈
=
0
r
0
r
ln
2π
D
d
µ µ
ζ
ε ε
=
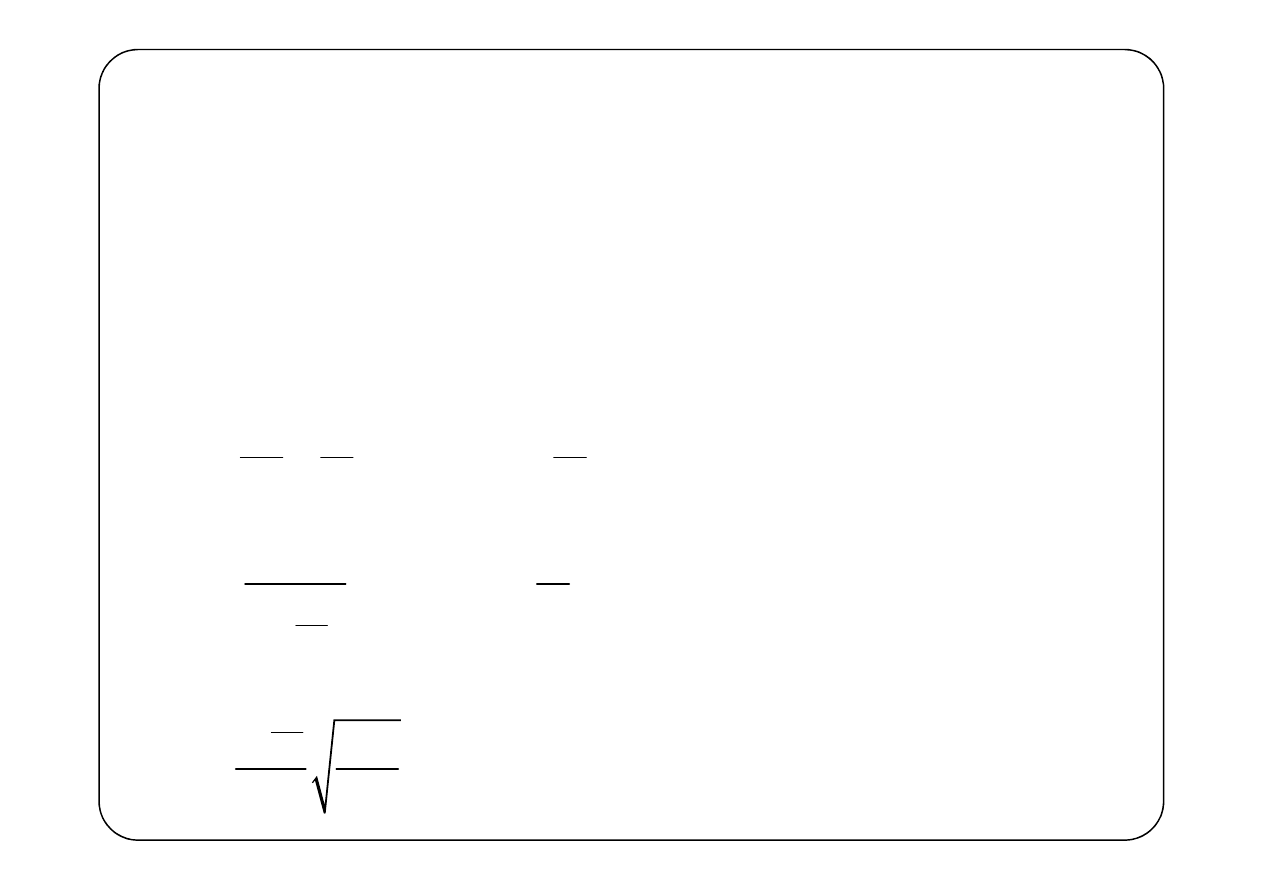
Przykład 3
Obliczyć parametry jednostkowe i falowe kabla koncentrycznego
o wymiarach: d = 1 mm,
D = 4,8 mm. Przewód wewnętrzny
wykonany z miedzi (
σ
c1
= 58,8
⋅
10
6
S/m), ekran z folii cynowej
o grubości 0,05 mm (
σ
c2
= 8,3
⋅
10
6
S/m). Izolatorem jest spieniony
polietylen (
σ
d
= 10
–14
S/m,
ε
r
= 1,45).
Przeprowadzić obliczenia dla f
1
= 100 MHz i f
2
= 500 MHz.
6
0
H
ln
0,314 10
D
L
µ
−
=
=
⋅
6
0
0
H
ln
0,314 10
2π
m
D
L
d
µ
−
=
=
⋅
12
0
r
0
2π
F
51, 4 10
m
ln
C
D
d
ε ε
−
=
=
⋅
0
0
r
ln
78,1Ω
2π
D
d
µ
ζ
ε ε
=
=
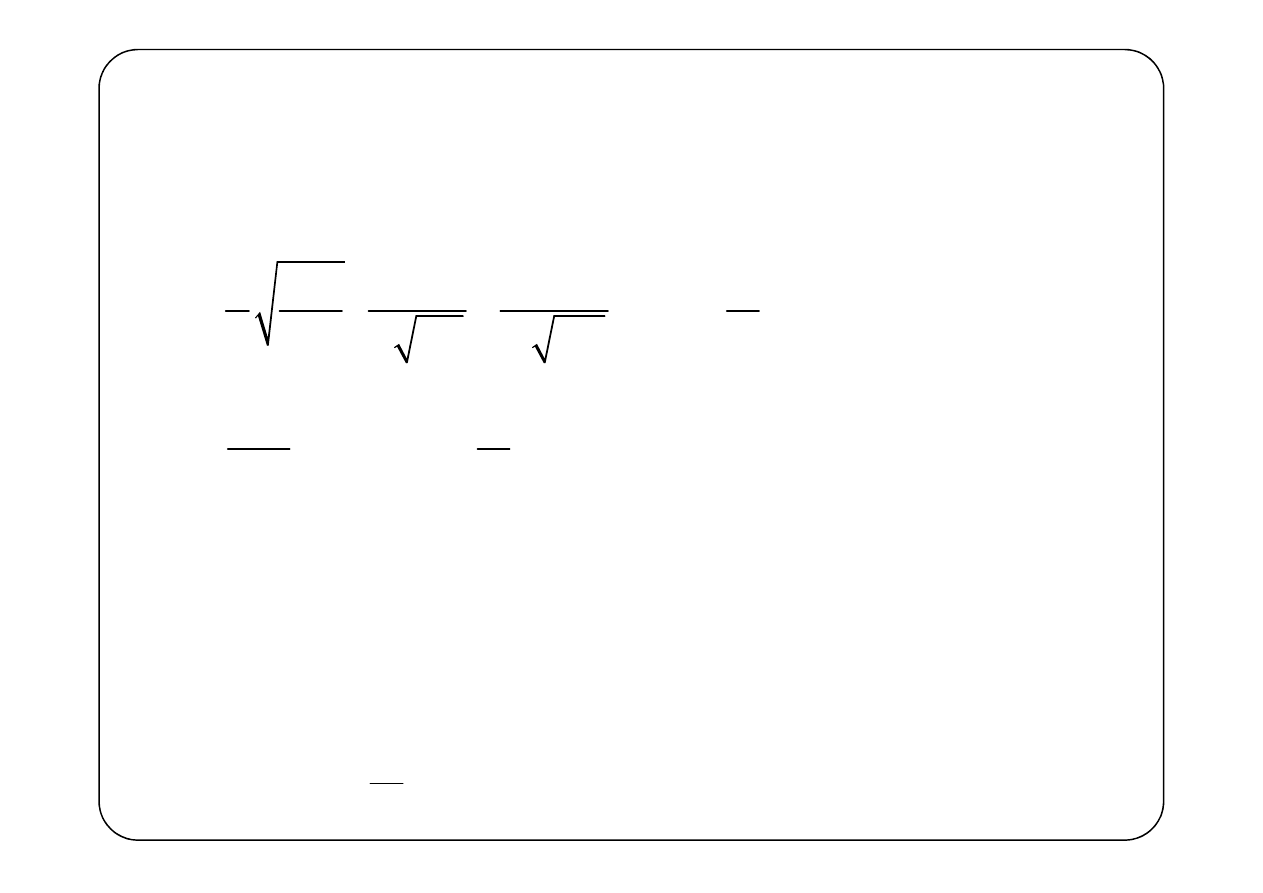
f
1
= 100 MHz
0
0
c1
c2
1
1
1
Ω
1, 28
π
2
m
R
d
D
µ ω
σ
σ
=
+
=
6
6
w1
w2
6,56 10 m,
17,5 10 m
δ
δ
−
−
=
⋅
=
⋅
14
d
S
4 10
G
C
σ
ε ε
−
=
= ⋅
14
d
0
0
0
r
S
4 10
m
G
C
ε ε
−
=
= ⋅
Według innych źródeł
0
0
tg
G
C
ω
δ
=
tg
δ
= 10
–6
÷
10
–3
,
δ
— katalogowy „kąt
stratności” dielektryka
Jeżeli przyjąć tg
δ
= 10
–6
6
0
S
0,3 10
m
G
−
=
⋅
Parametry falowe
(
)
(
)
f
78,1 j0, 25 Ω
1
0, 0082
j2,5242
m
Np
0, 0082
m
rad
2,5242
m
Z
γ
α
β
=
−
=
+
=
=
2,5242
m
β
=
8
1
f
2π
2π
m
2, 49 m,
2, 49 10
s
f
v
λ β
β
=
=
=
=
⋅
dB
8, 686
0, 071
m
α
α
′ =
=
Dane katalogowe:
f
7 dB 100 m
75 3Ω
Z
α
′ =
=
±
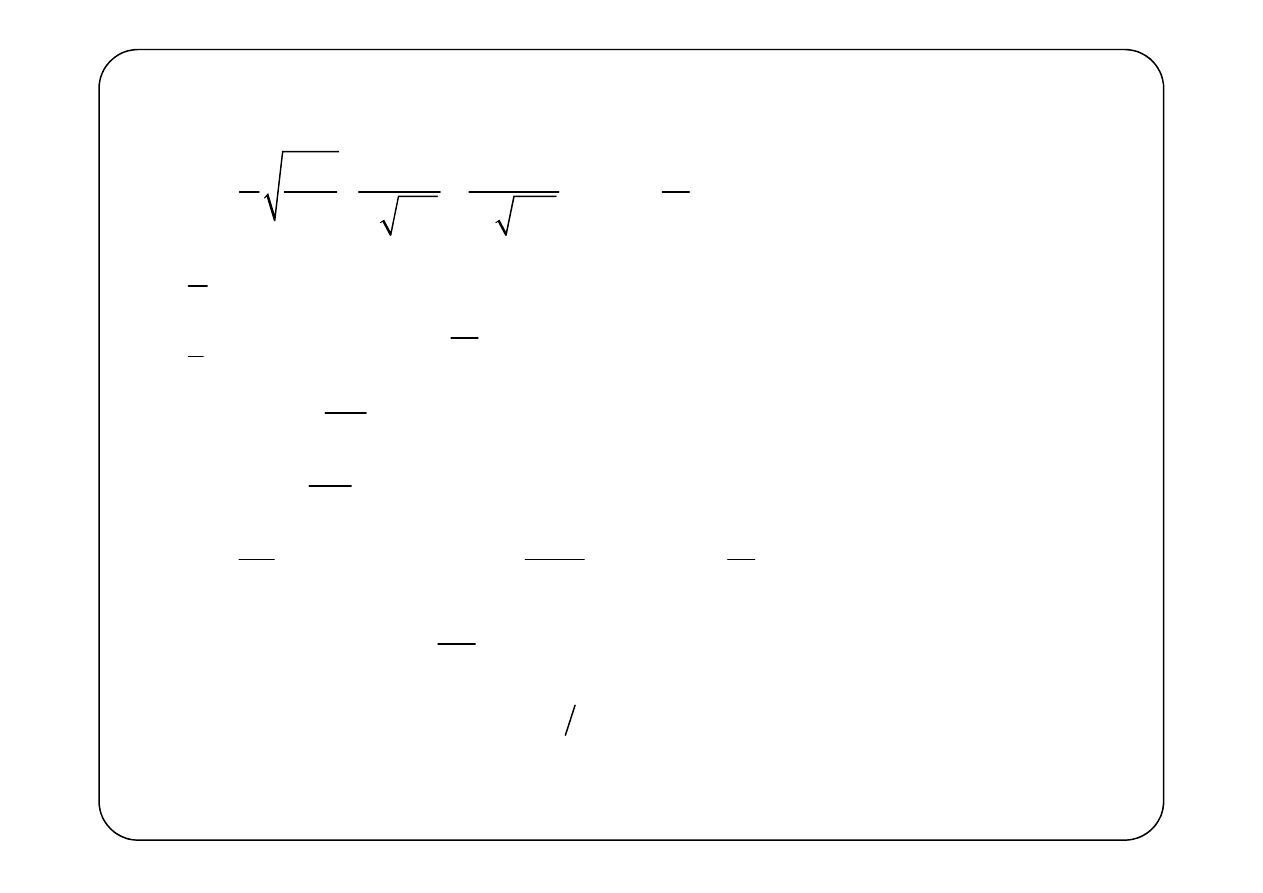
f
2
= 500 MHz
0
0
c1
c2
1
1
1
Ω
2,86
π
2
m
R
d
D
µ ω
σ
σ
=
+
=
6
6
w1
w2
2,9 10 m,
7,8 10 m
δ
δ
−
−
=
⋅
=
⋅
(
)
(
)
f
78,1
j0,11
Ω
1
0, 0183
j12, 62
m
Np
0, 0183
m
Z
γ
α
=
−
=
+
=
m
rad
12, 62
m
β
=
8
1
f
2π
2π
m
0, 498 m,
2, 49 10
s
f
v
λ β
β
=
=
=
=
⋅
dB
8, 686
0,159
m
α
α
′ =
=
Dane katalogowe:
f
15, 4 dB 100 m
75 3Ω
Z
α
′ =
=
±
Wyszukiwarka
Podobne podstrony:
Tois 11 Linie długie
Linie długie zadania
1 Linie długie
Tois 11 Linie długie
4 Linie wpływu wielkości statycznych w ustrojach prętowych
16 LINIE, PODZIAŁKI I RKUSZE RYSUNKOWE
Linie wplywowe w ukladach statycznie wyznaczalnych belka3
4 Co to są linie poślizgu widoczne na powierzchni próbki ze stali GX120Mn13
linie rysunkowe
problem dlugiego ogona
Budowa kości długiej
linie aga
ABY 0027 Linie wroga 2 Twierdza rebelii
Linie wpływu belka z teleskopem
Jak upinać długie włosy
Linie wplywowe w ukladach statycznie wyznaczalnych belka
linie wpływu zadanie
więcej podobnych podstron