Wykonała: Patrycja Bojarczuk

Plan prezentacji:

1. Definicja linii wpływu
2. Linie wpływu w układach statycznie wyznaczalnych
2.1 Belki proste
2.2 Belki gerberowskie
2.3 Kratownice
2.4 Ramy
3. Linie wpływu w ustrojach statycznie niewyznaczalnych
4. Zastosowanie linii wpływu

Definicja

Linią wpływu danej wielkości statycznej Z
(reakcji, momentu, siły poprzecznej, siły
osiowej) nazywamy wykres zależności
wielkości Z od położenia x czynnej siły
jednostkowej na ustalonym torze tej siły.

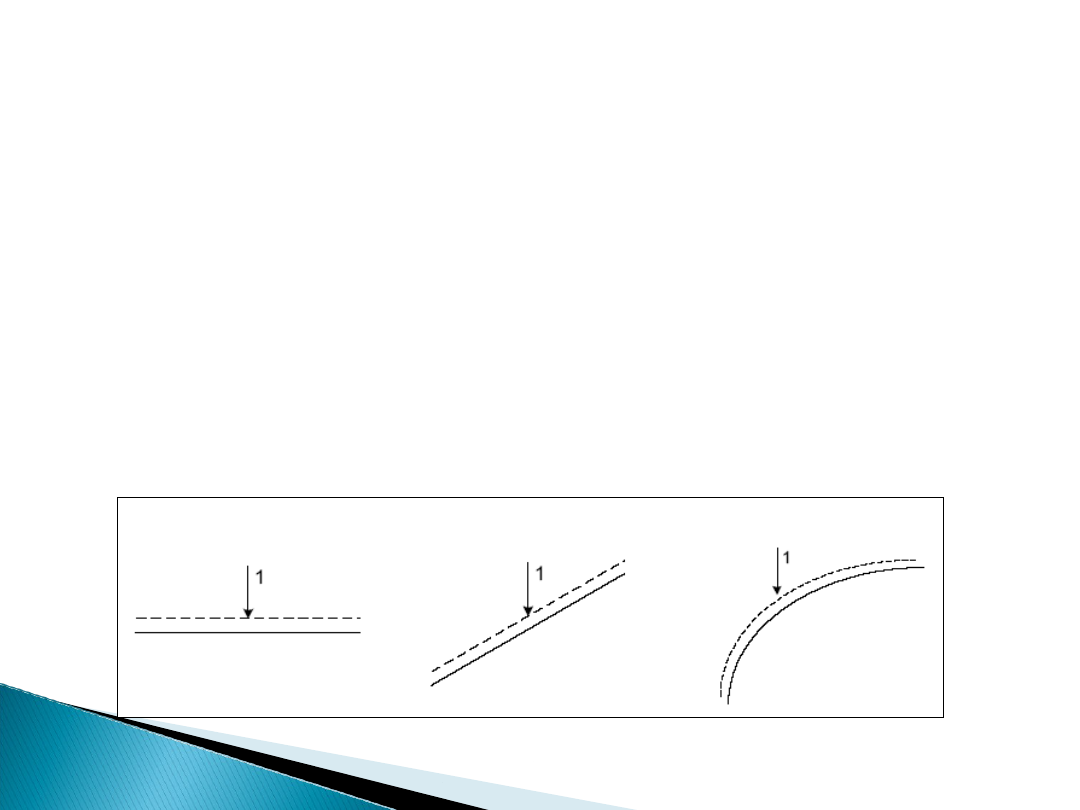
Zazwyczaj przyjmuje się, że siła jednostkowa P=1 jest pionowa.
Linią przerywaną zaznaczamy tor przesuwania się siły.

Ustroje statycznie

wyznaczalne

Dla układów statycznie wyznaczalnych wielkość
statyczna jest liniową funkcją położenia siły
jednostkowej.

Linie wpływu wielkości statycznej dla
ustrojów statycznie wyznaczalnych
składają się z odcinków prostych.

Przy rysowaniu linii wpływu

obowiązują następujące zasady:

1.Linię wpływu zaczynamy od postawienia siły w
miejscu, w którym będziemy liczyć. Następnie
przesuwamy siłę do drugiego punktu
charakterystycznego.

2.Na podporze „obcej’’ linia wpływu przyjmuje wartości
zerowe.

3.W miejscu przegubu następuje załamanie linii wpływu.

4.Kształt linii wpływu w przęśle jest
przedłużany na wsporniku.

5.Obciążenie z belki dolnej nie przenosi się na belkę górną
(w przypadku belek gerberowskich).

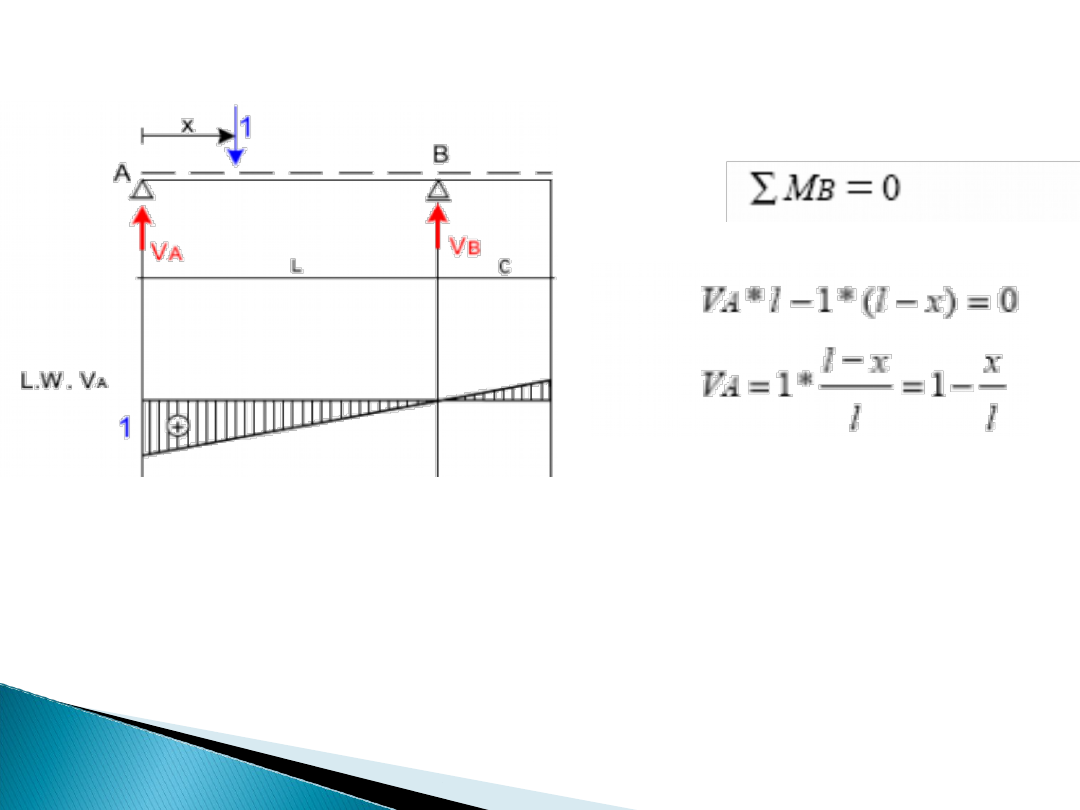
Belki proste

Linia wpływu V

A

określona jest powyższą zależnością.

Można jednak ją wyznaczyć stawiając siłę w punkcie A
otrzymując V

A

=1 oraz w punkcie B (na podporze „obcej”)

otrzymując V

A

=0

i następnie łącząc te dwie rzędne.

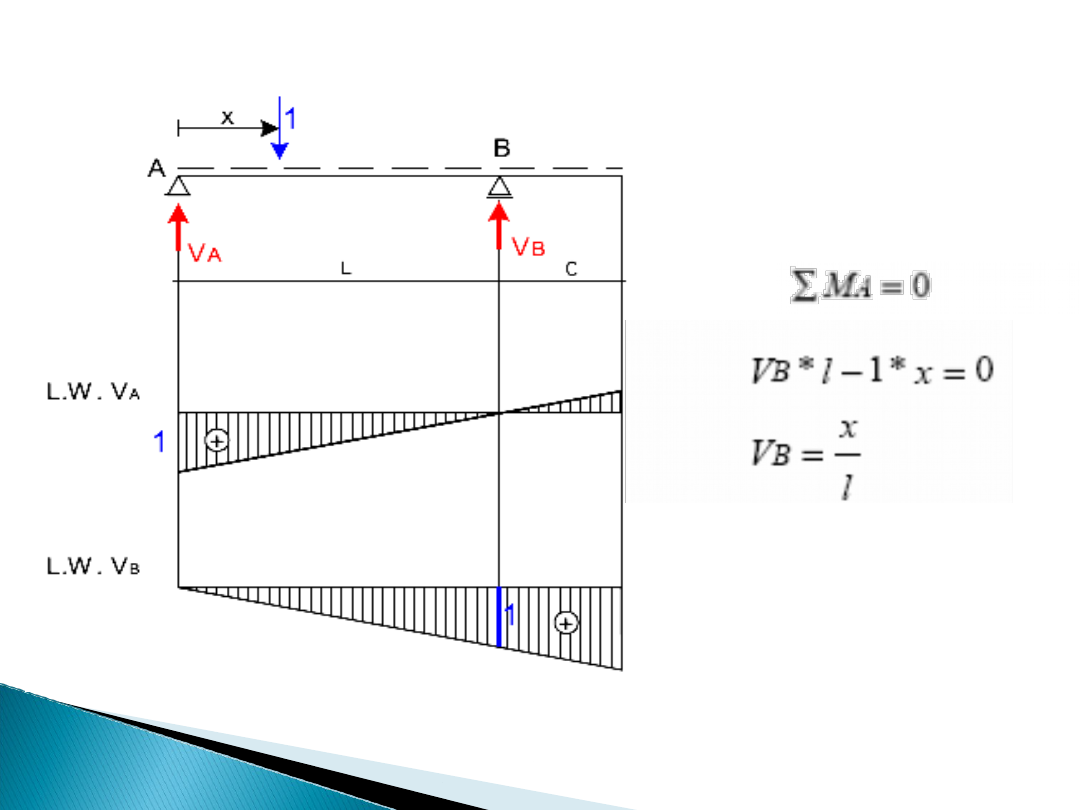
Podobnie postępujemy przy drugiej linii wpływu

.

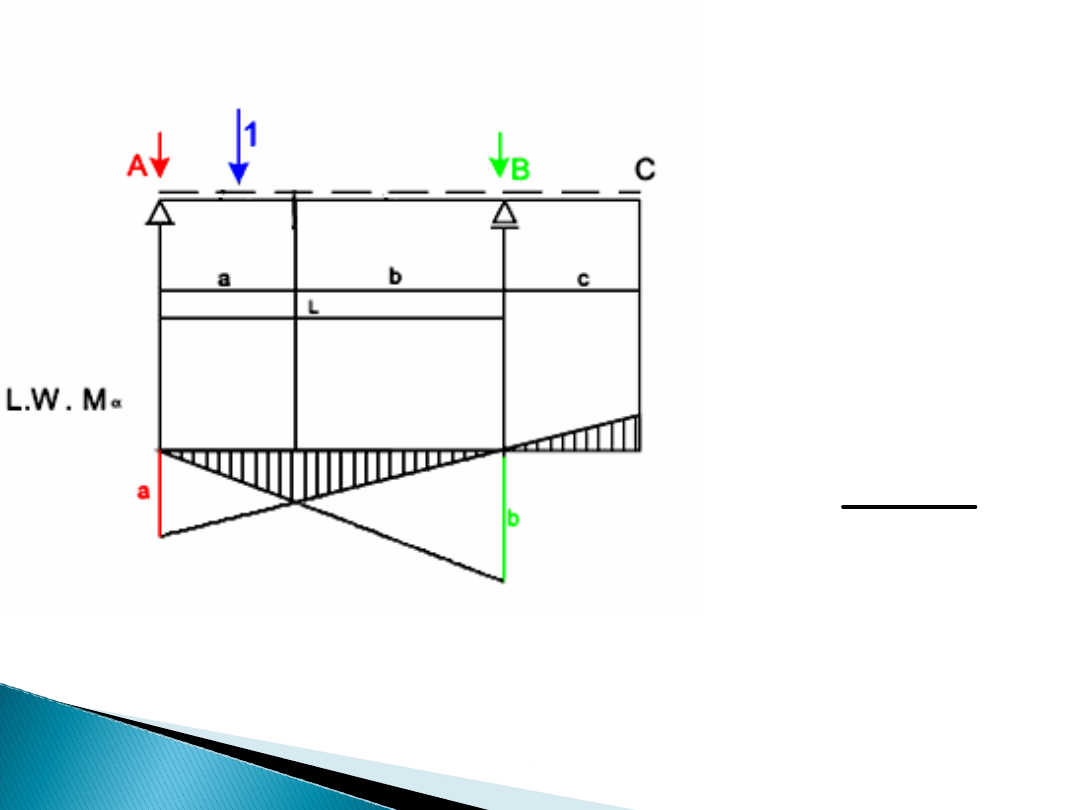
Linia wpływu momentu w przekroju α

M

P a

 b



(

)

L



P

P

Dla momentu w
miejscu przekroju
linia wpływu ma
załamanie. Rzędną
wykresu w tym
punkcie można
policzyć ze wzoru:

Rzędne odkładamy po
stronie włókien
rozciąganych.

Gdzie
P = 1
a, b, L – odpowiednie
odległości według
rysunku

α

α

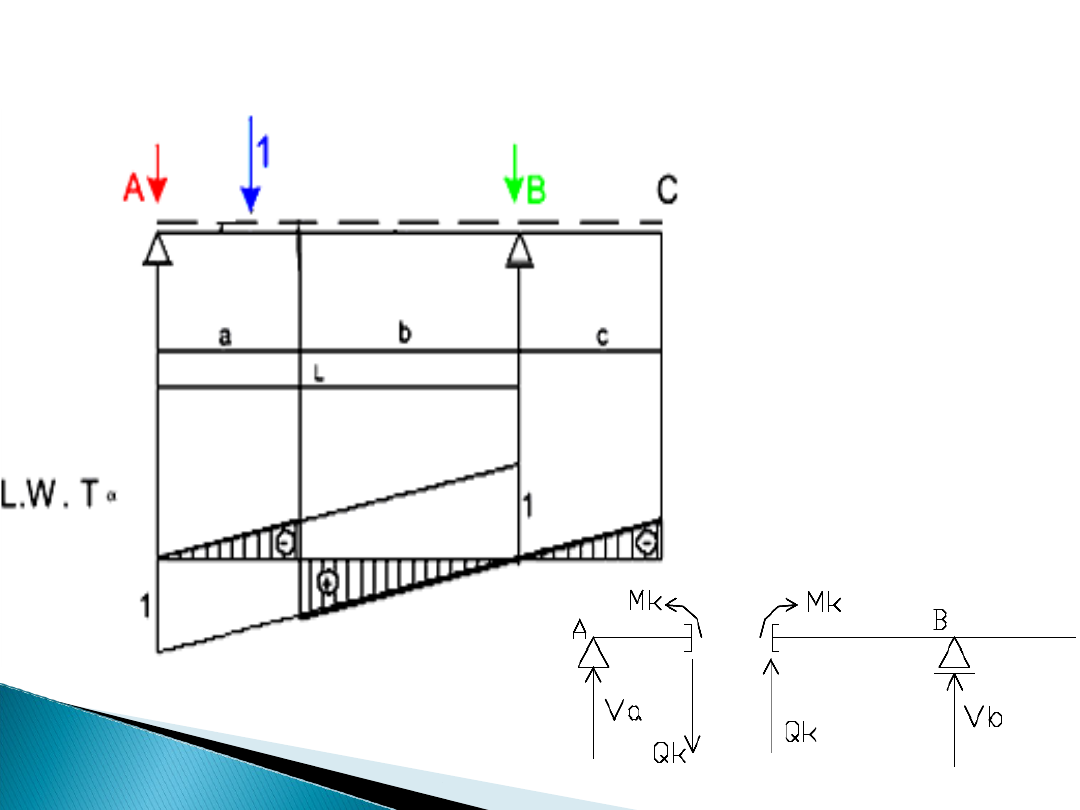
Linia wpływu siły tnącej w przekroju α

Dla siły tnącej linia
wpływu ma skok,
a dwie sąsiednie
gałęzie są
równoległe.

α

α

Dodatnie zwroty sił:

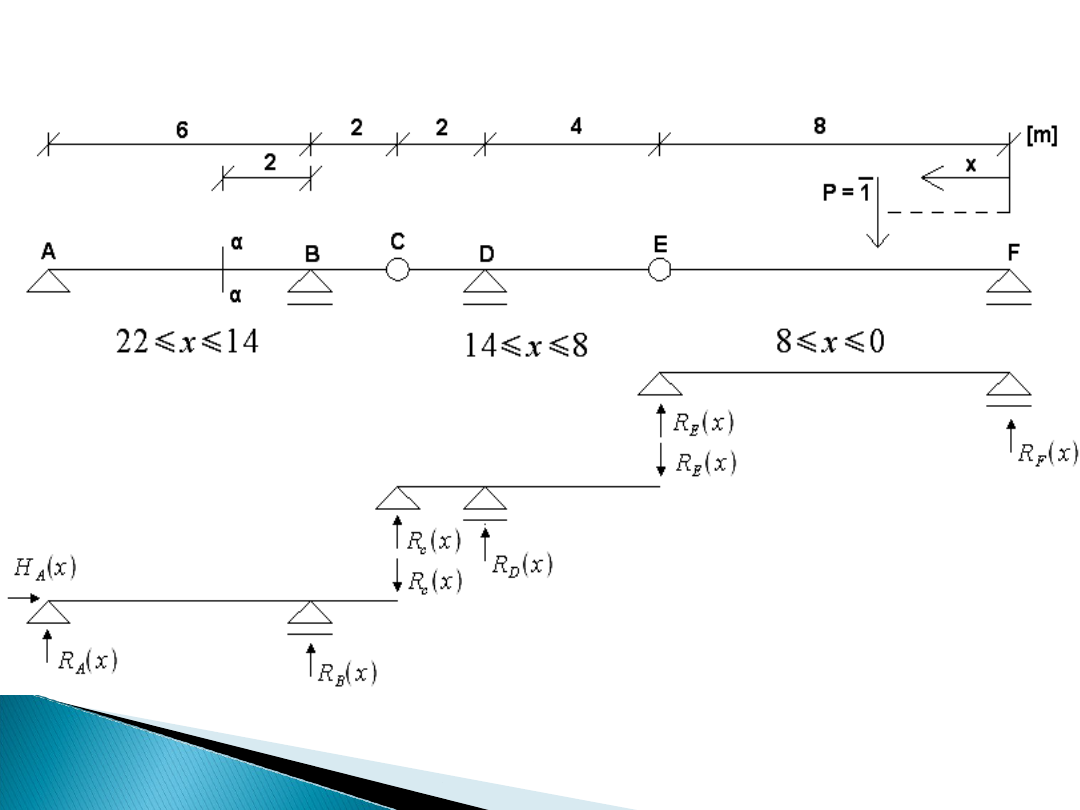
Belki gerberowskie

Rys.2

W przypadku belek
gerberowskich ważne jest
rozróżnienie opierania się belek.

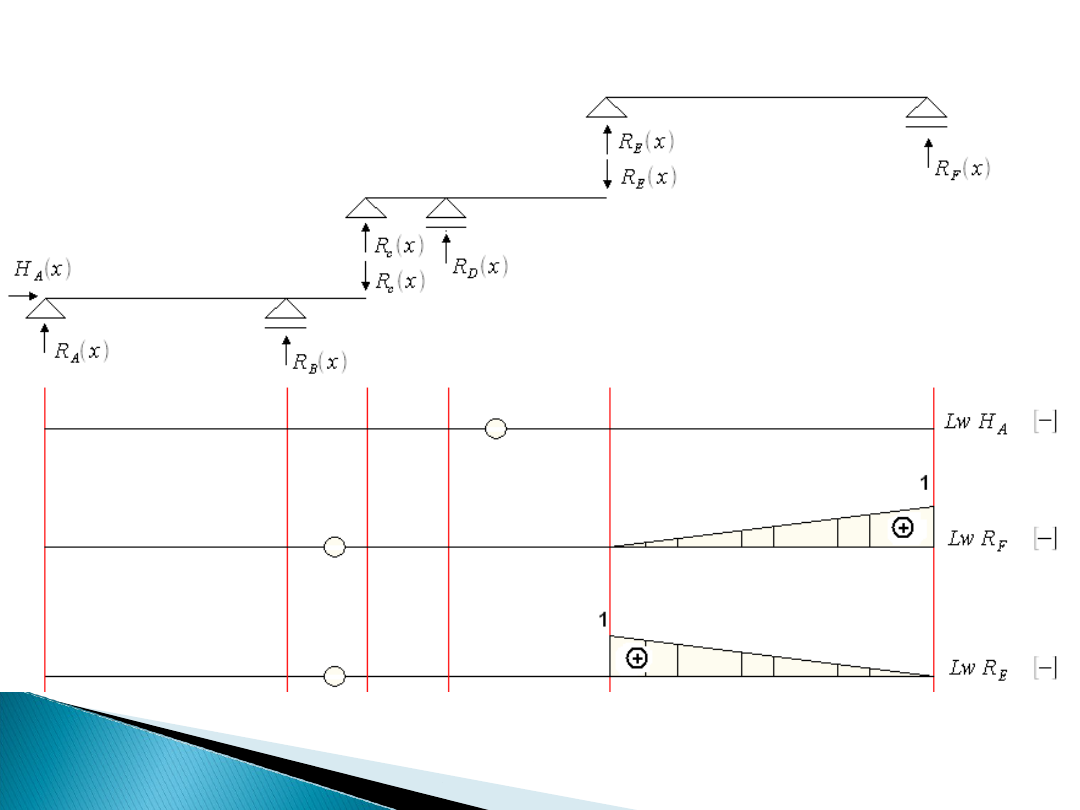
Linie wpływu reakcji podporowych

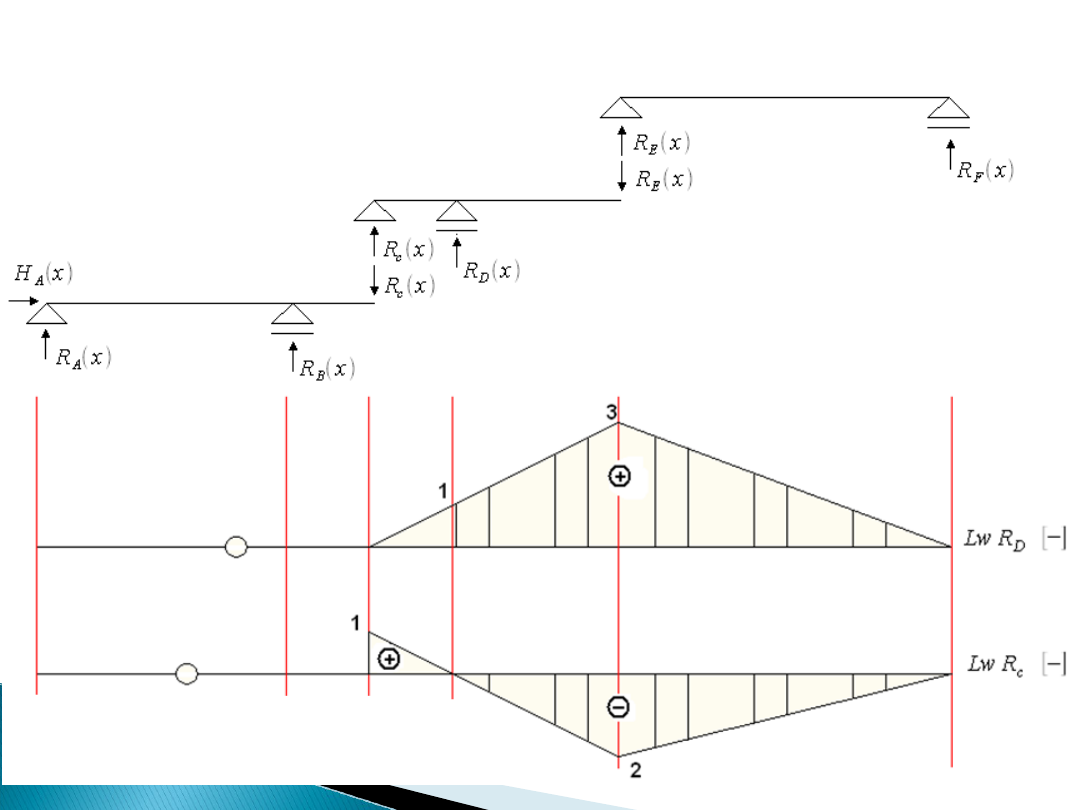
Linie wpływu reakcji podporowych

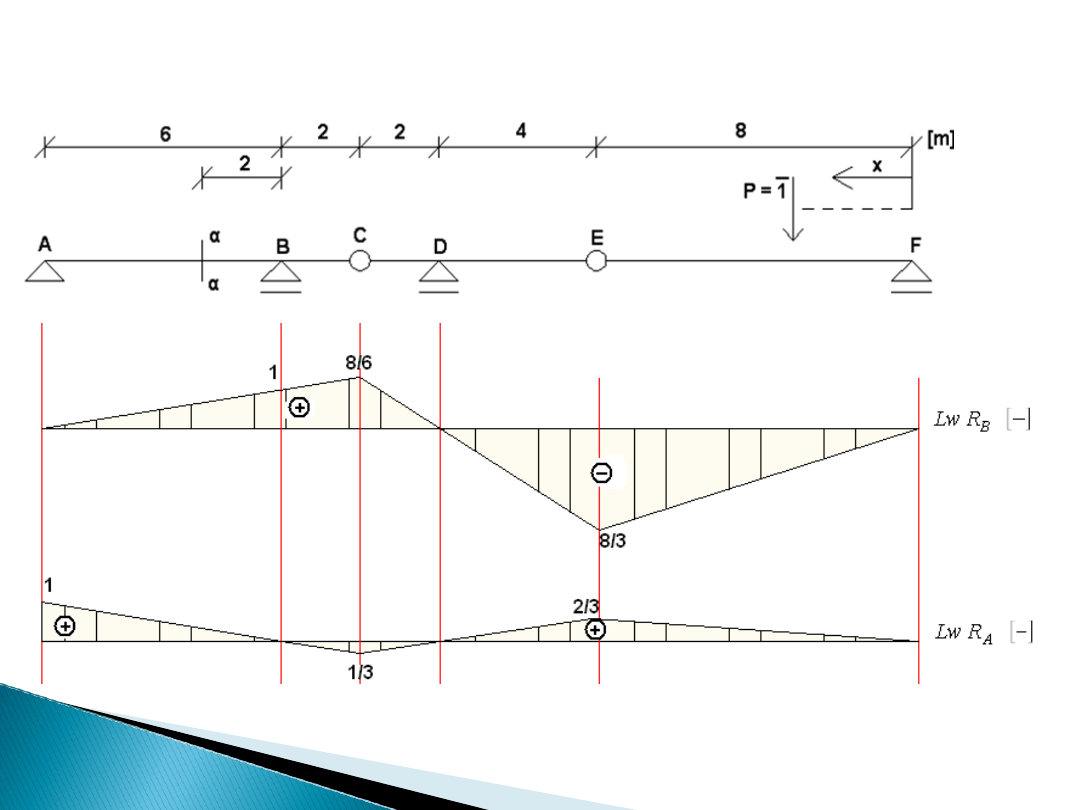
Linie wpływu reakcji podporowych

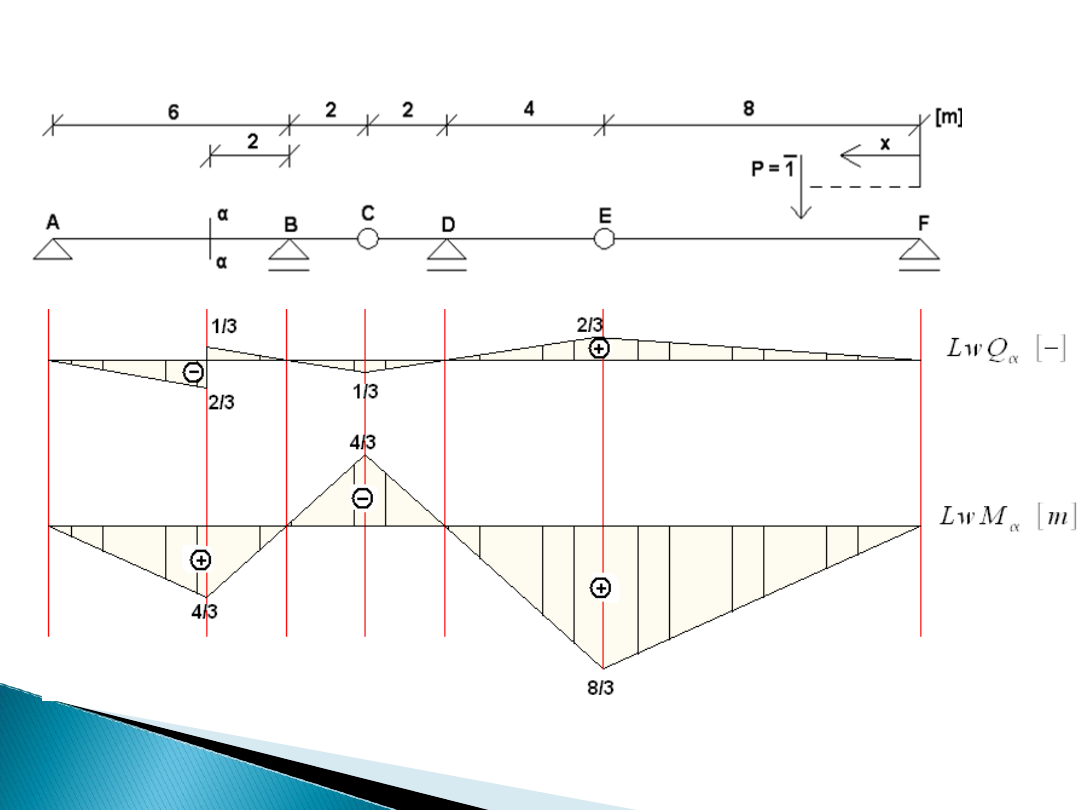
Linie wpływu sił przekrojowych

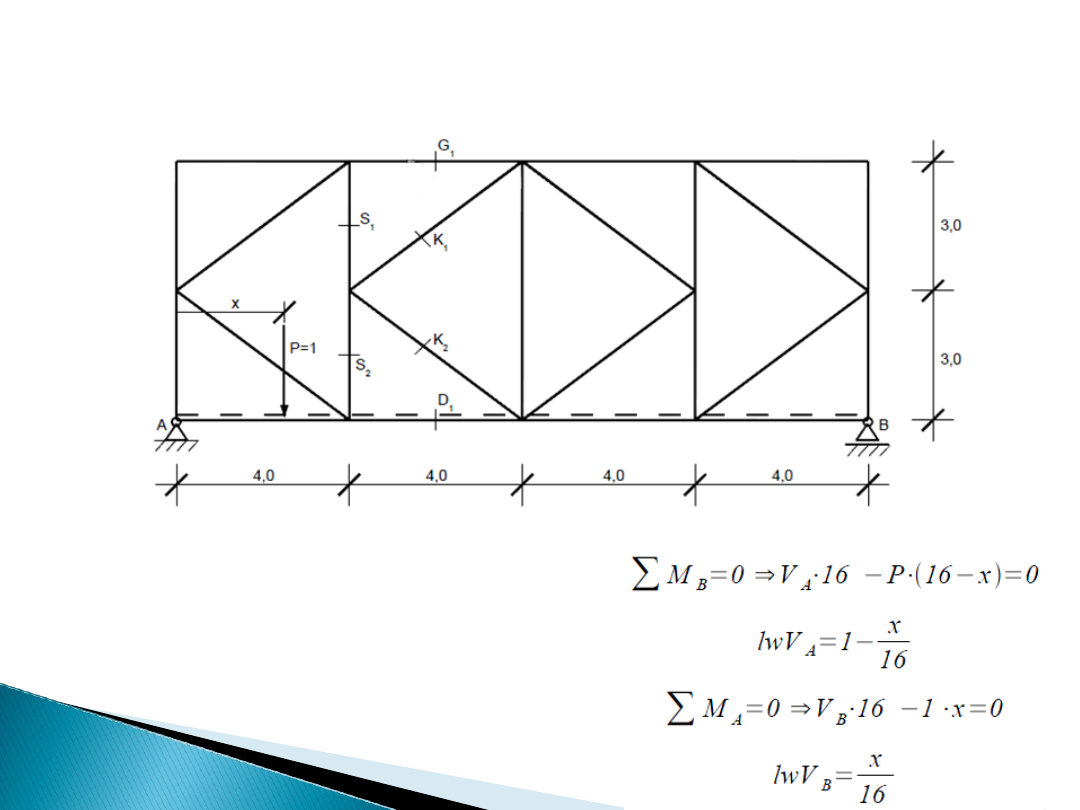
Kratownice

Linie wpływu reakcji podporowych
wyliczamy z sumy momentów
względem odpowiednich punktów:

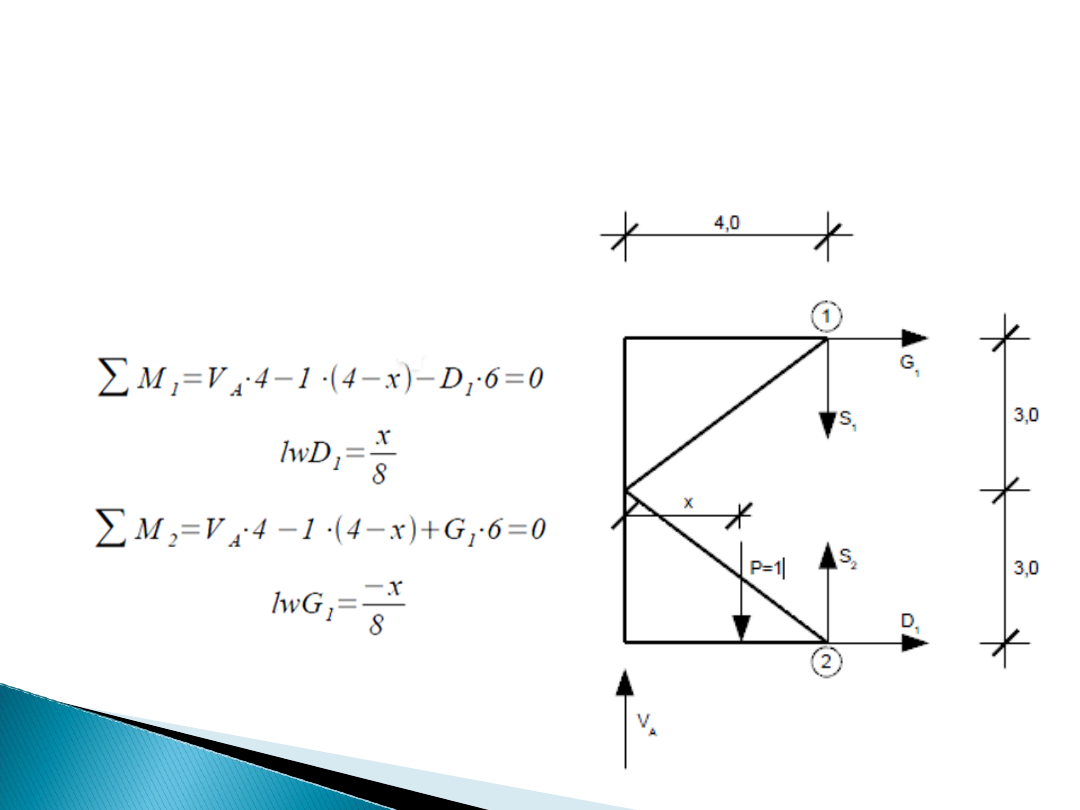
Linie wpływu sił wewnętrznych w kratownicy można
wyliczyć z równań równowagi zapisanych dla wyciętego
fragmentu kratownicy.

Linie wpływu prętów D1 oraz G1:
• x∈ 0 ; 4

〈

〉

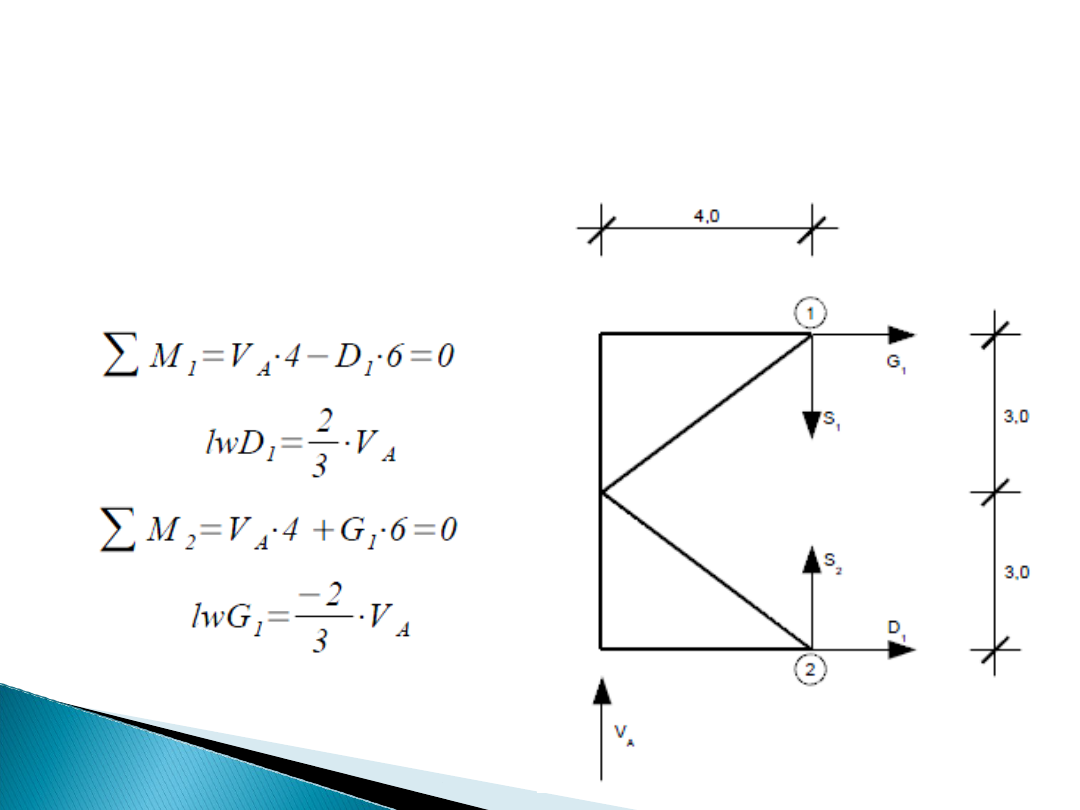
Równania równowagi można zapisywać zarówno dla
części po której porusza się siła jednostkowa jak i dla
pozostałego fragmentu układu.

• x∈ 8 ; 16

〈

〉

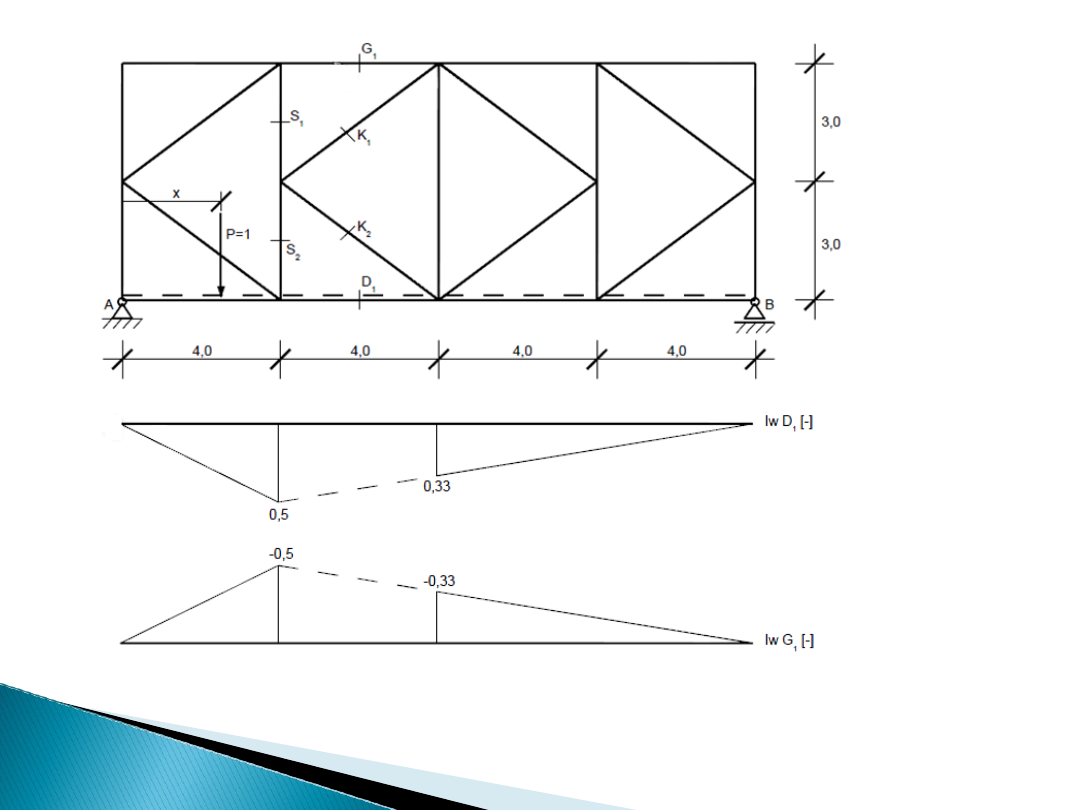
Dlatego łączymy punkty
charakterystyczne
po jego obu stronach linią przerywaną.

W miejscu przekroju nie znamy
przebiegu linii wpływu.

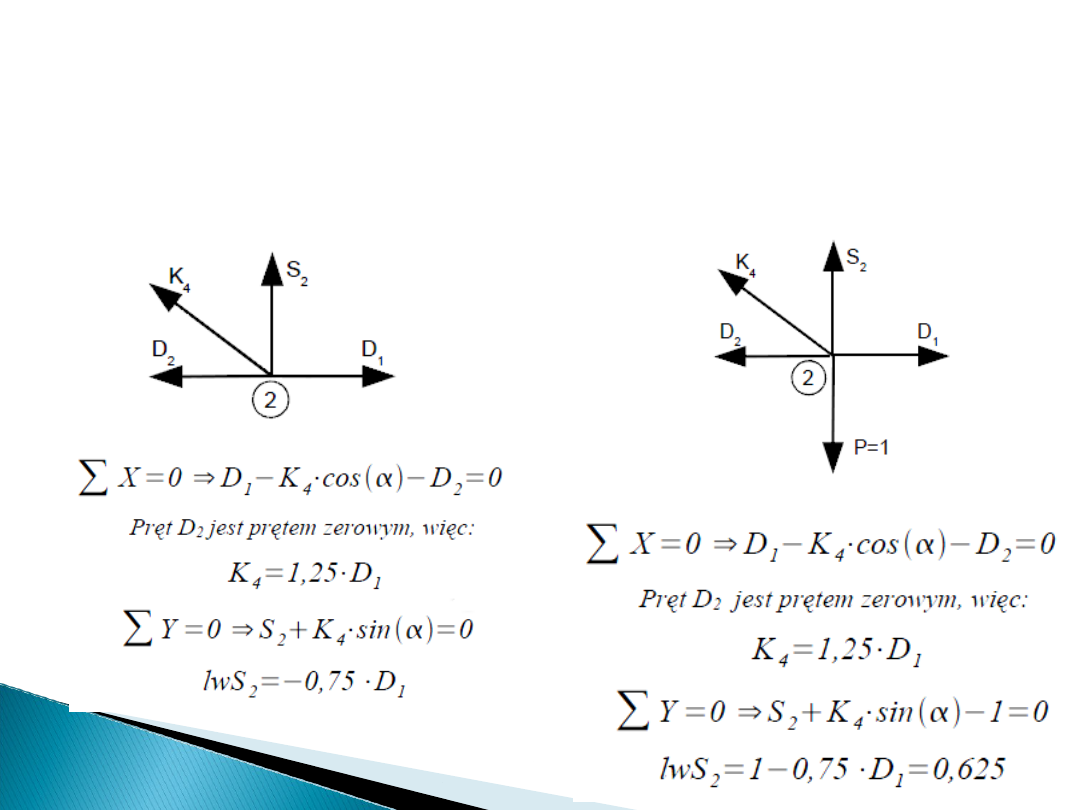
Linię wpływu w pręcie S2 wyznaczamy

przez myślowe wycięcie węzła 2:

• gdy poruszająca sie siła
znajduje się dokładnie w węźle
2

• gdy poruszająca sie siła
znajduje się poza węzłem 2

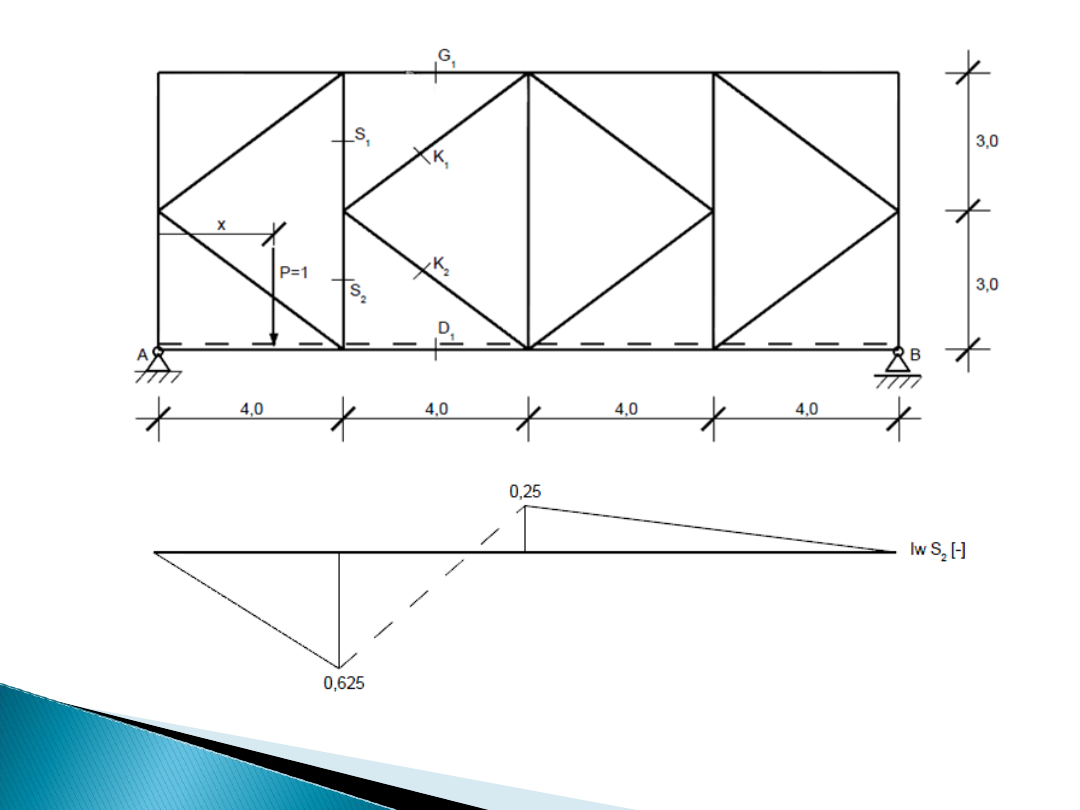
Linia wpływu siły w pręcie S

2

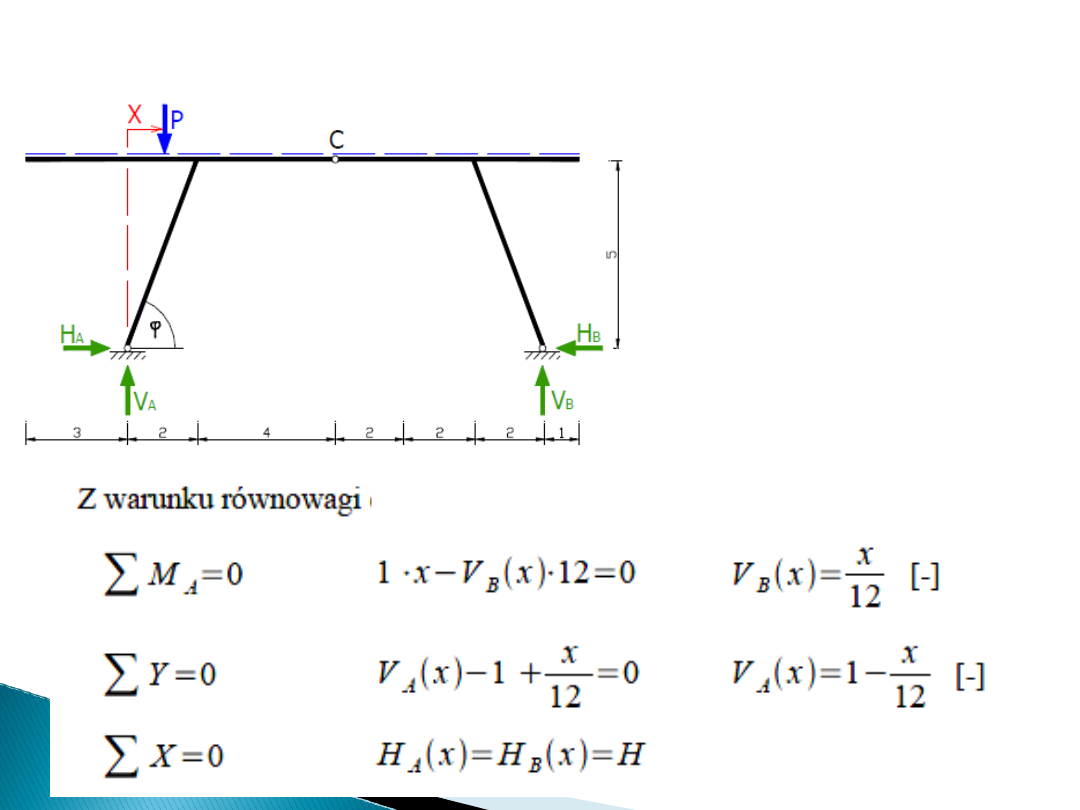
Ramy

Dziedzina współrzędnej:
X ∈ −3 ;13

〈

〉

Obliczenia należy zacząć
od przyjęcia
współrzędnej x
określającej położenie
jednostkowej siły P [-]

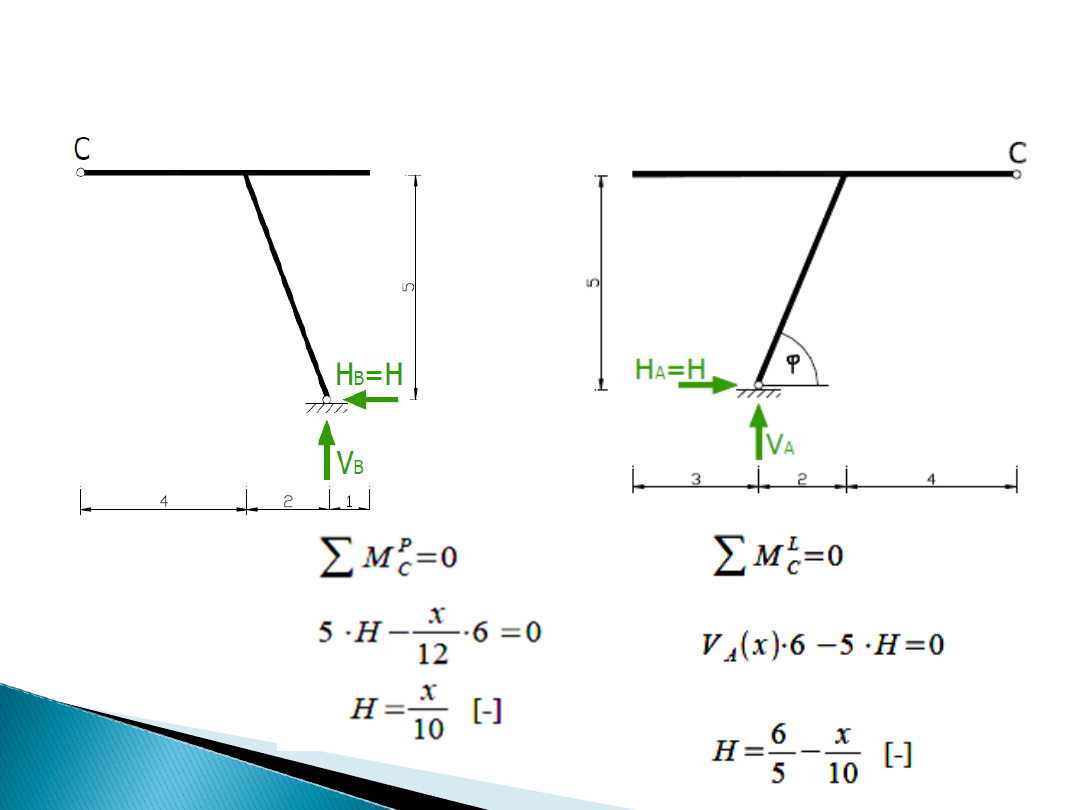
Z warunku równowagi dla
prawej części ramy gdy X ∈ −3 ;

〈

6 〉

Z warunku równowagi
dla
lewej części ramy gdy
X ∈ 6 ;13

〈

〉

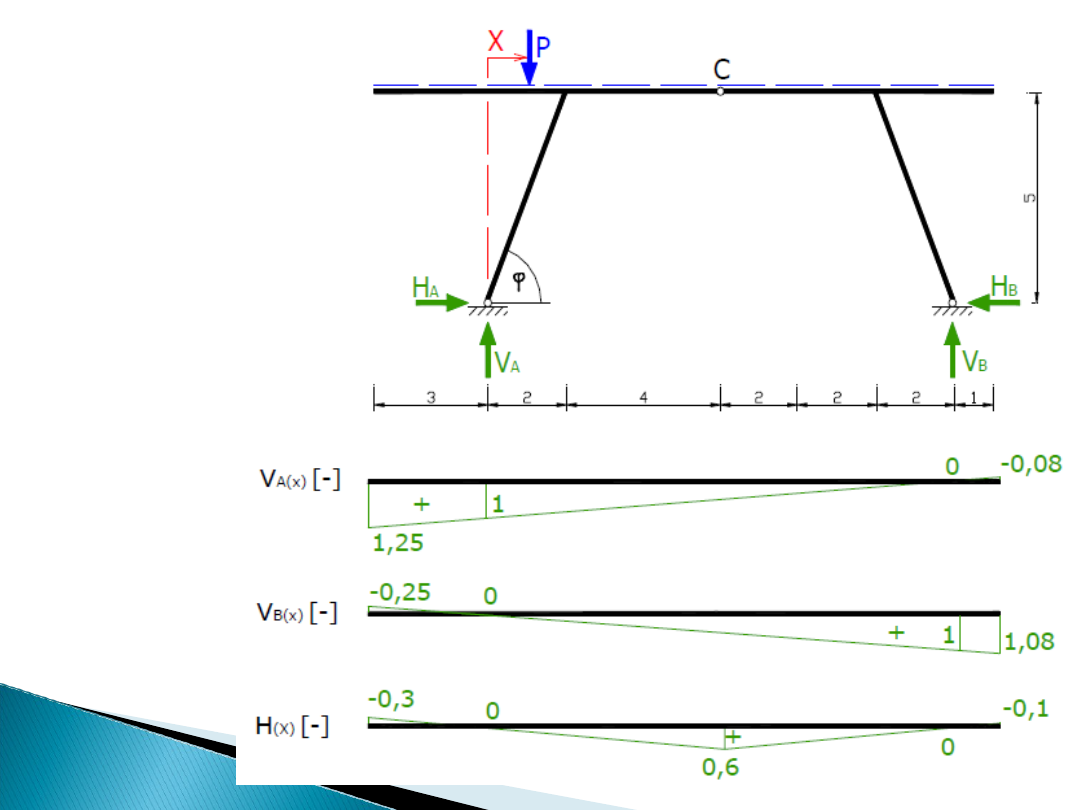
Linie wpływu
reakcji
podporowych

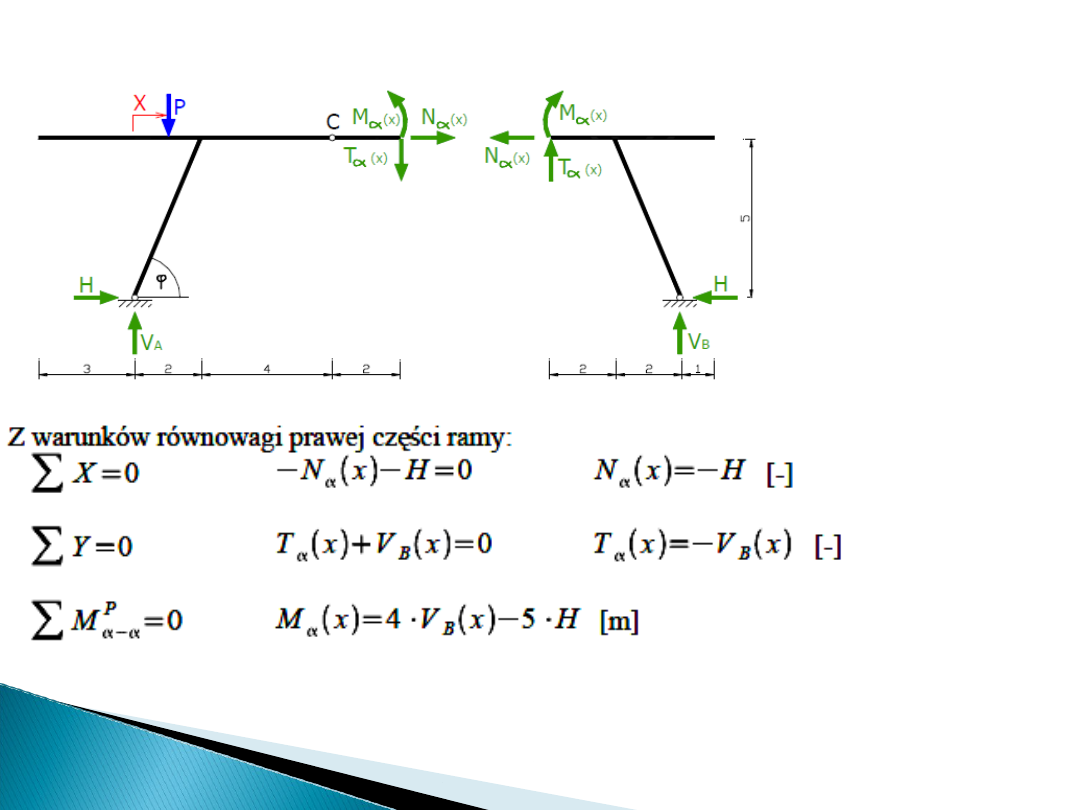
Obliczenie linii wpływowych sił
przekrojowych

Rozważamy dwa
przypadki położenia
siły: po lewej
lub prawej stronie
przekroju.
W obu przypadkach
możemy zapisywać
równania równowagi
dla obu części ramy.

Obliczamy funkcję linii wpływu sił przekrojowych
korzystając ze znanych reakcji podporowych.

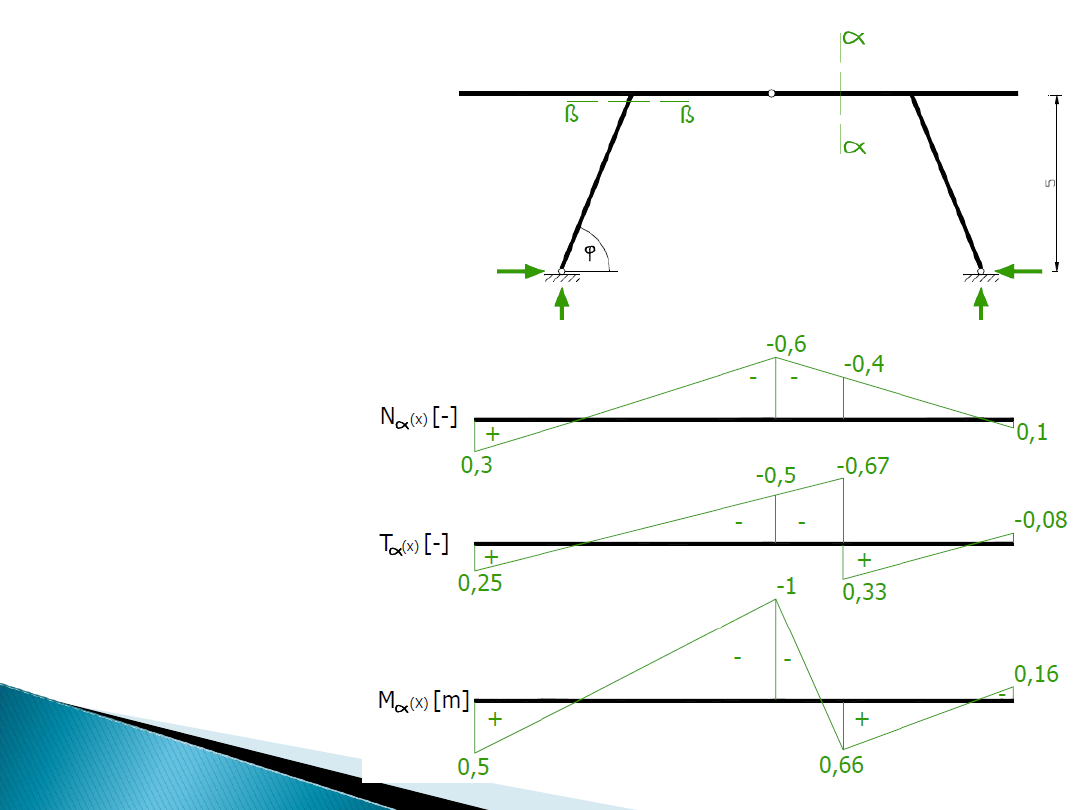
Linie wpływu dla
sił przekrojowych
Przekrój α - α

Wszystkie
omawiane
dotychczas zasady
mają zastosowanie
także w układach
ramowych.
Występuje skok na
linii wpływu sił
tnących, a także
załamanie na linii
wpływu momentu.

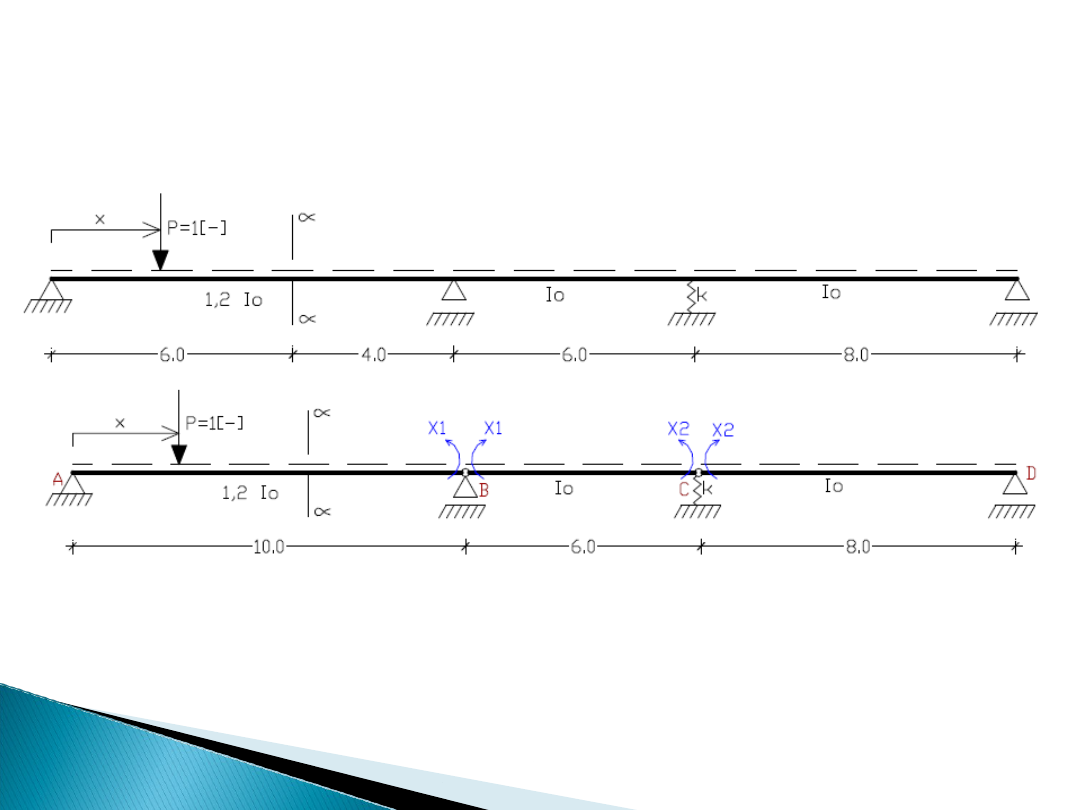
Ustroje statycznie

niewyznaczalne

Dobór statycznie wyznaczalnego okładu
podstawowego, w którym zaczepia się n niewiadomych
hiperstatycznych.

Metoda sił

Wyznaczanie w układach statycznie
niewyznaczalnych linii wpływu wielkości statycznych
metodą sił, należy rozpocząć od wyznaczenia linii
wpływu nadliczbowych niewiadomych X

k

, co w

dalszej kolejności umożliwi nam wyznaczenie linii
wszystkich innych wielkości.
Zmiennymi będą wyrazy wolne Δ

kP

i w konsekwencji

także X

k

przyjmą wartości zależne od położenia

obciążenia.

Układ równań kanonicznych zapewniających identyczność
kinematyczną obu układów przyjmuje postać:

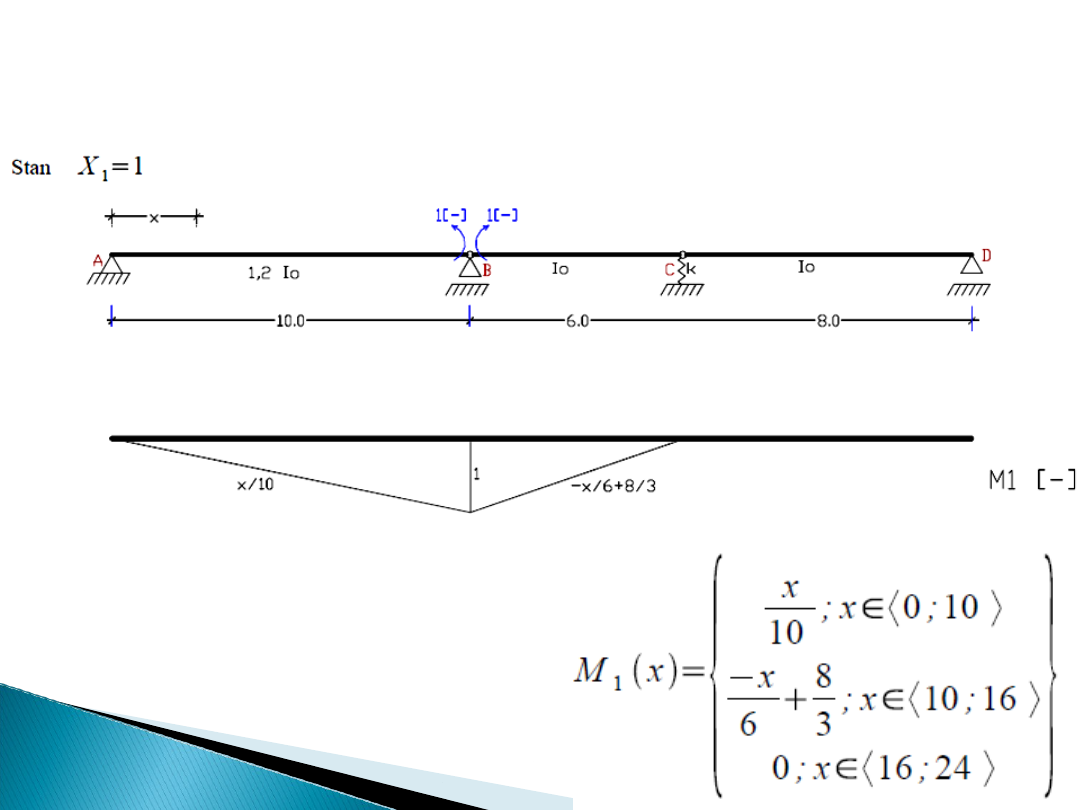
Wykres momentu M

1

dla stanu X

1

=1

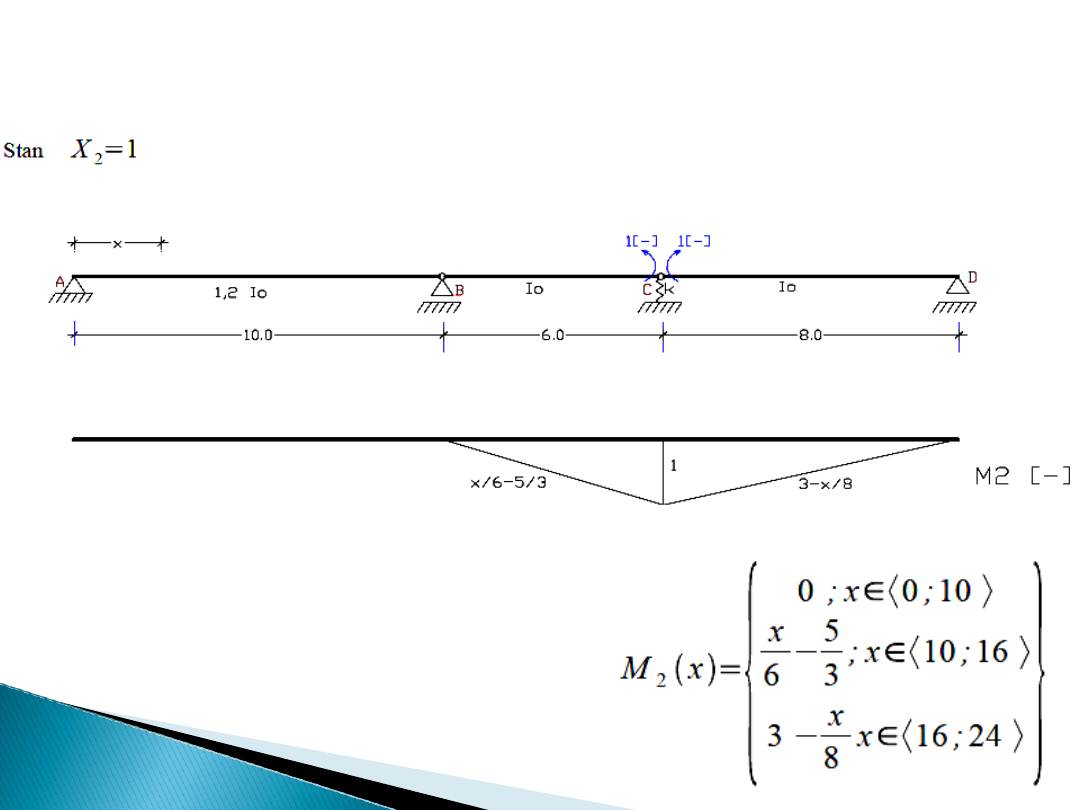
Wykres momentu M

2

dla stanu X

2

=1

Mając dane wykresy M

1

i M

2

wyznaczamy wartości

δ

11,

δ

12,

δ

22.

np. metodą całkowania
graficznego.

Aby je obliczyć rysujemy wykres momentu
w zależności od chwilowego położenia siły P.

Niewiadomymi w układzie równań pozostają wartości

Δ

1P,

Δ

2P.

M

P

1

0<x<10

Otrzymane wykresy całkujemy jak poprzednio,
dzięki czemu mamy wszystkie dane potrzebne
do rozwiązania układu.

Wynikiem jest funkcja opisująca wartości
ugięć belki pod wpływem przyłożonego
obciążenia jednostkowego X

1

i X

2

.

Podobne wykresy rysujemy dla położenia
siły na pozostałych odcinkach belki.

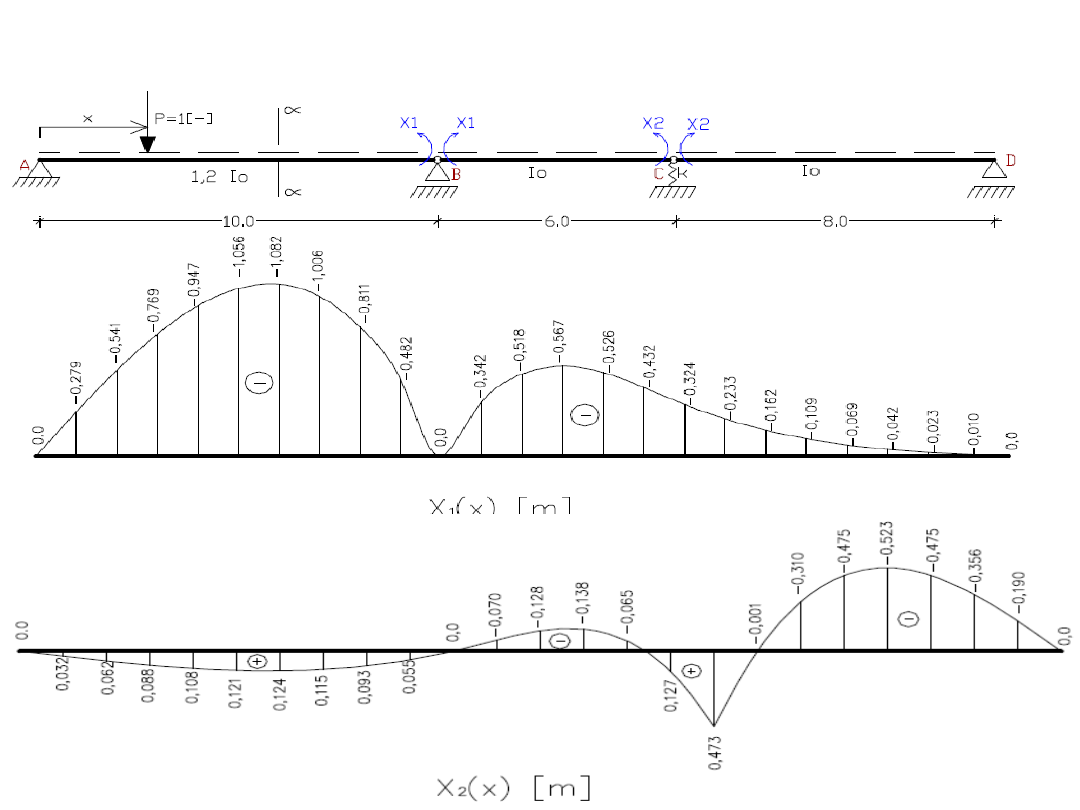
Linia ugięcia belki

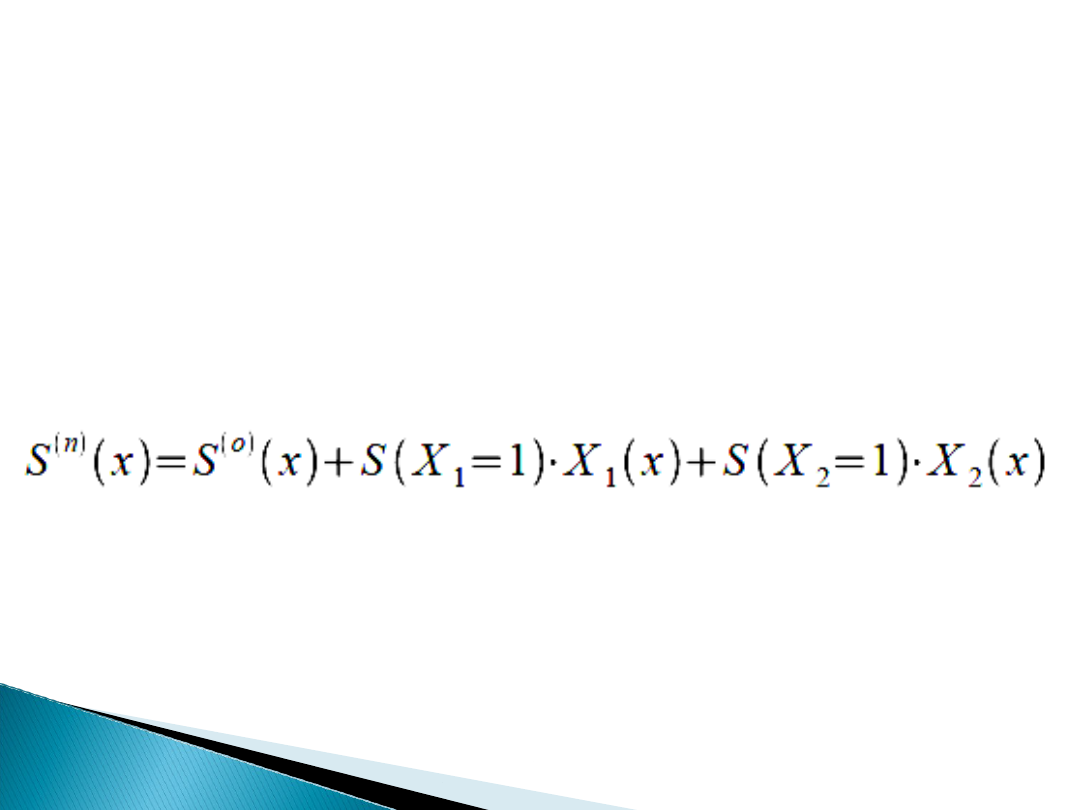
Linie wpływu reakcji oraz sił przekrojowych
wyznaczamy
z zasady superpozycji zgodnie ze wzorem

Gdzie S

(O)

(x) to linie wpływowe danych reakcji lub sił

przekrojowych w układzie statycznie wyznaczalnym.

Linie wpływu innych

wielkości

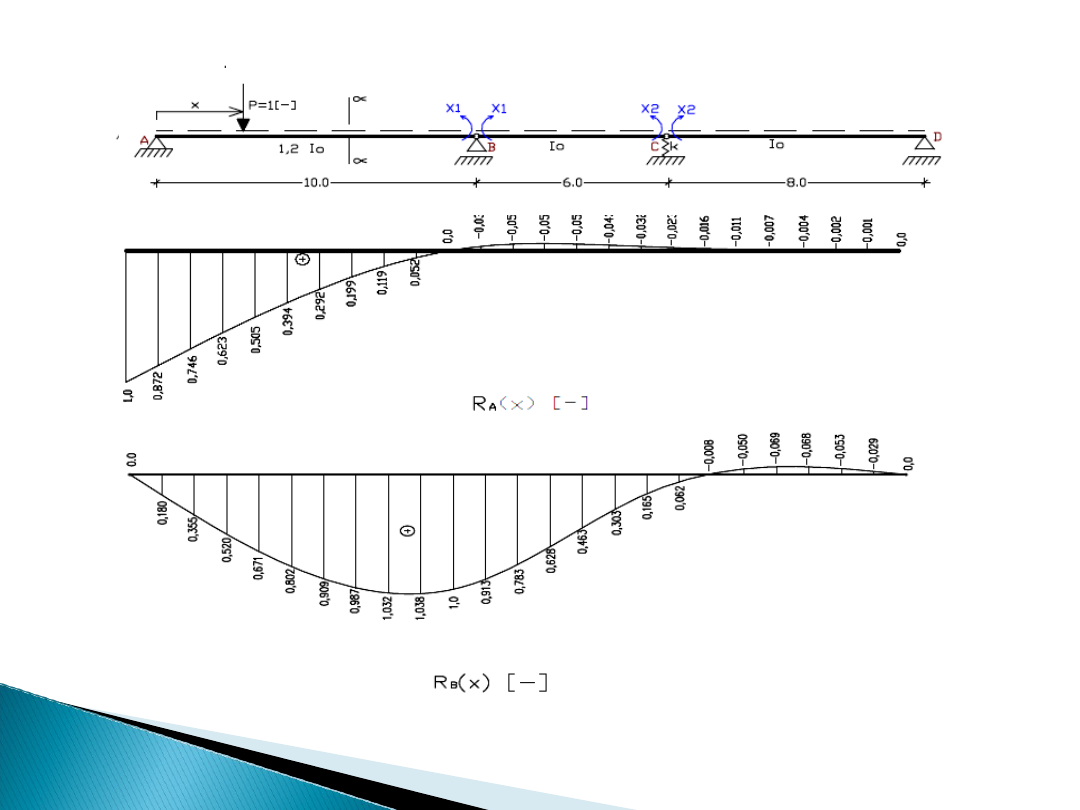
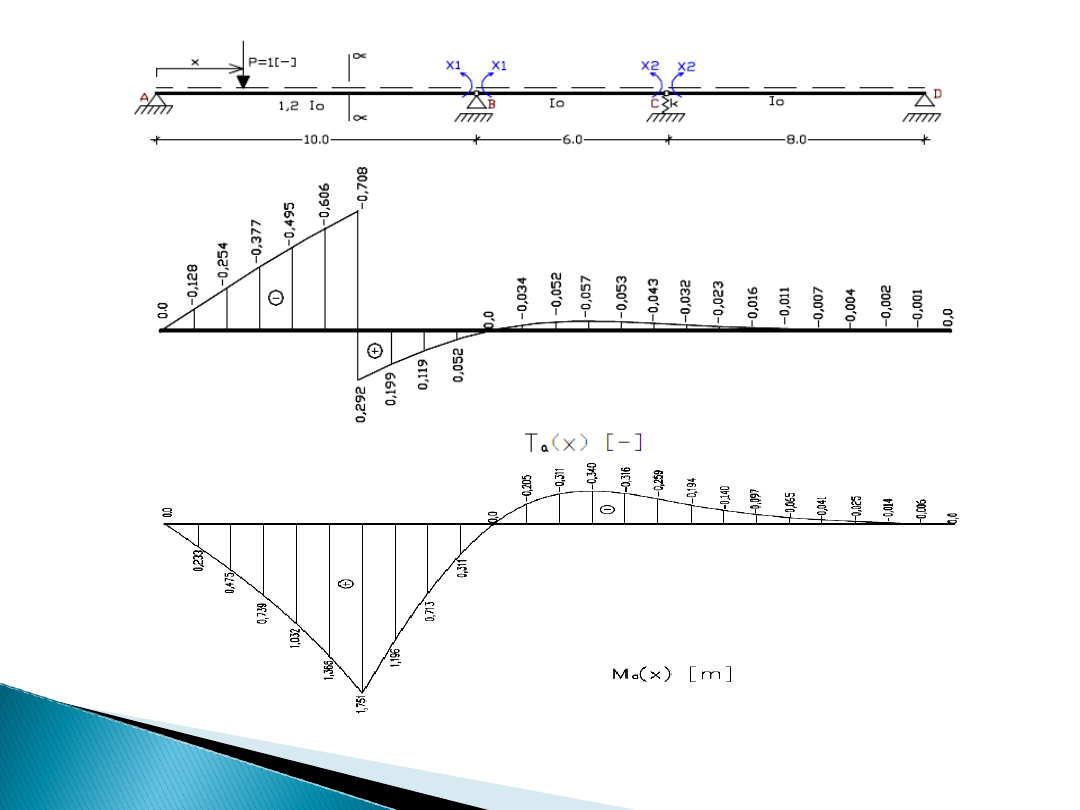
Linie wpływu szczególnie mają znaczenie przy wyznaczaniu
obwiedni sił przekrojowych (momentów, sił tnących, sił
osiowych).

Zastosowanie linii wpływu

Znajomość linii wpływu wielkości statycznej Z pozwala w
łatwy sposób wyznaczyć wielkość Z od danego programu
obciążenia.

Musimy uwzględnić fakt, że:

siły skupione w obciążeniu zmiennym mogą mieć różne

położenie, obciążenie rozłożone może być przerywane, a więc

występować

tylko na pewnych fragmentach konstrukcji,

a może także wcale nie występować.

W obciążeniu zmiennym wyróżniamy siły skupione
i obciążenie rozłożone.
Częstym zadaniem jest wyznaczenie wartości ekstremalnych
wielkości Z, a więc Z

max

i Z

min

.

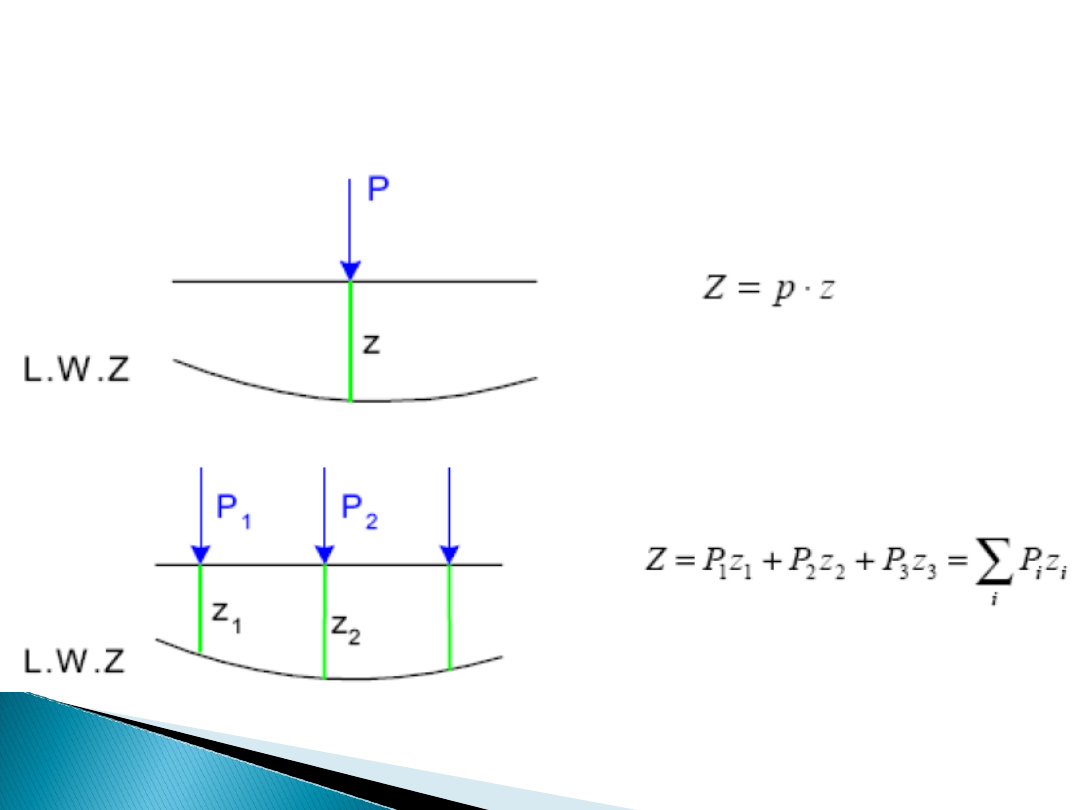
Grupa sił skupionych

Siła skupiona

Wyznaczanie wartości ekstremalnych:

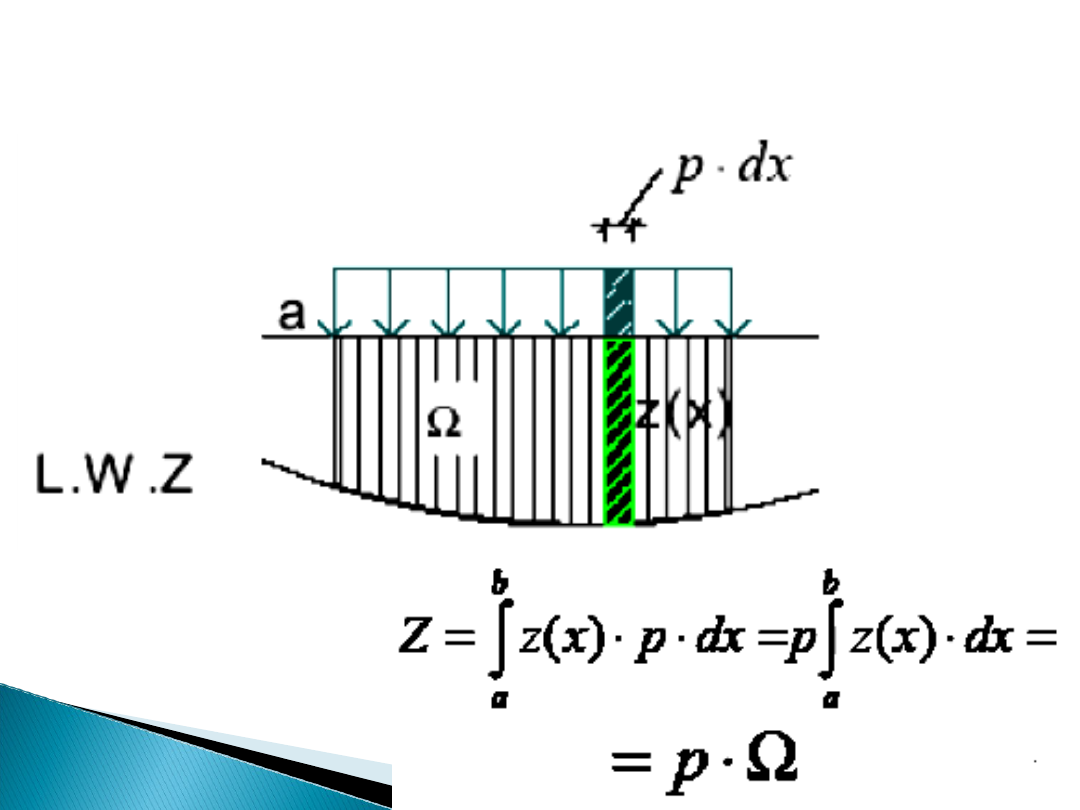
Obciążenie równomiernie rozłożone

Wyznaczanie wartości ekstremalnych:

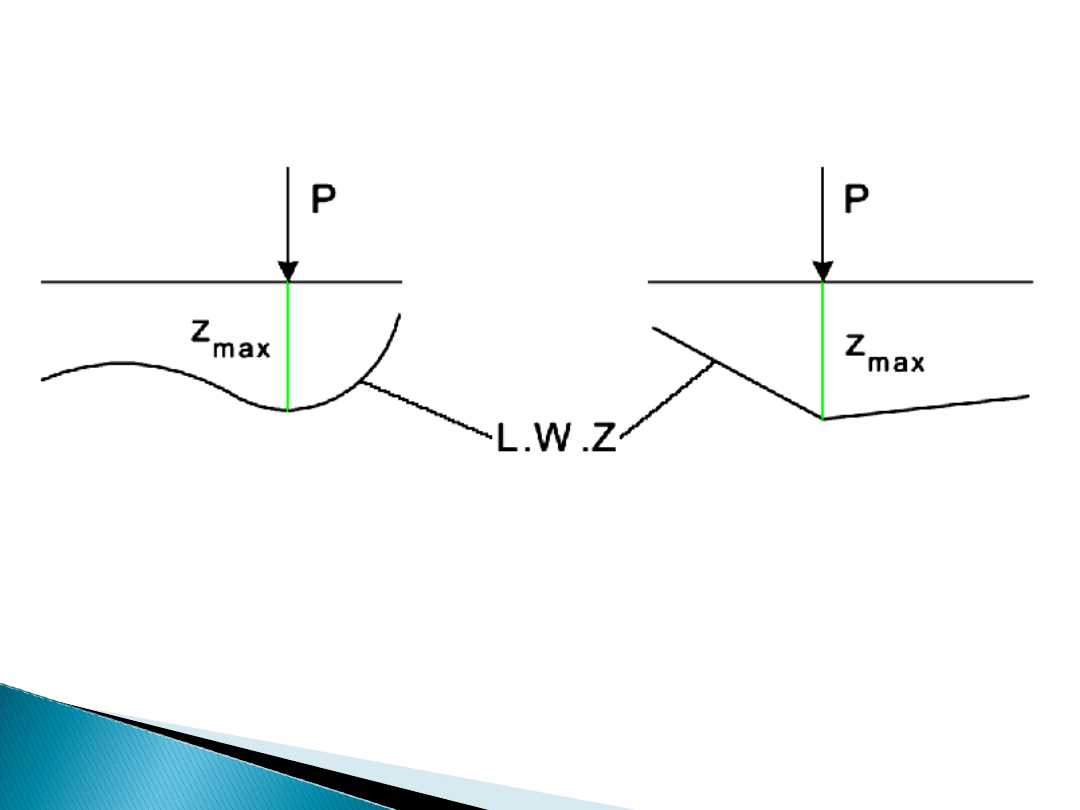
W przypadku sił skupionych najważniejszą zasadą
jest, aby jedną siłę skupioną (przeważnie
największą) ustawić w miejscu rzędnej
ekstremalnej.

Wyznaczanie wartości ekstremalnych:

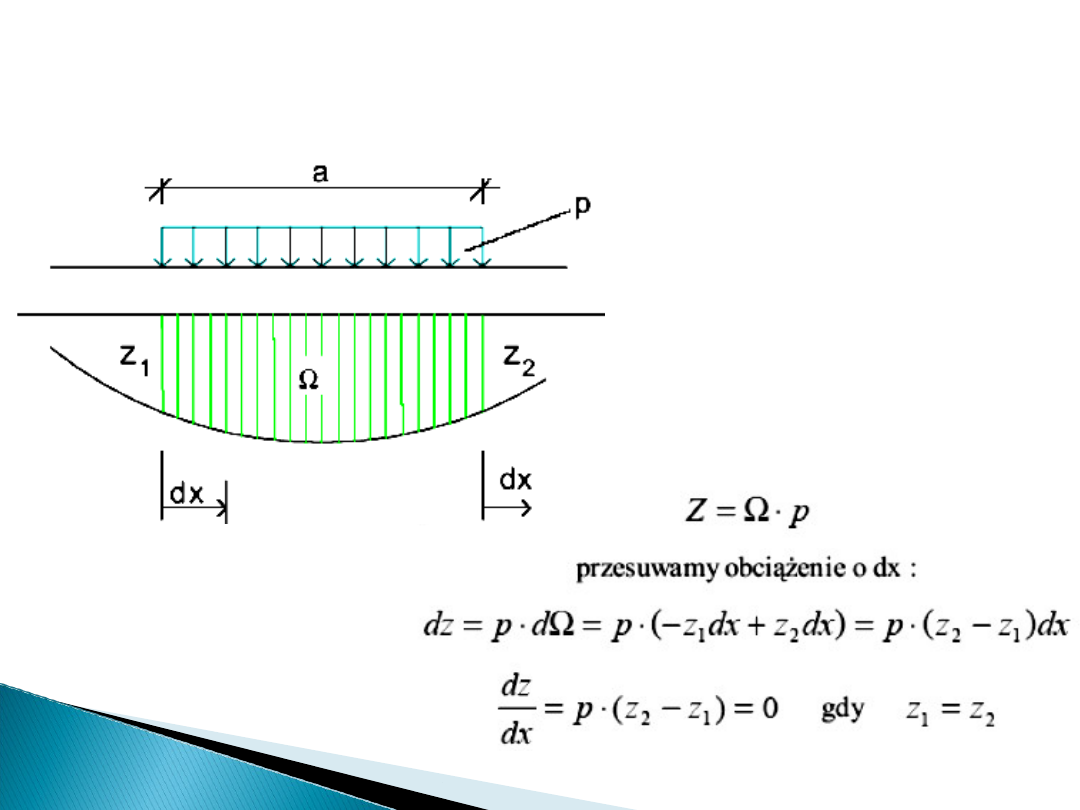
Wyznaczanie wartości ekstremalnych:

DZIĘKUJĘ

ZA UWAGĘ