Opracował:

Zygmunt Borkowski

1

Plan prezentacji:

1. Definicja linii wpływu
2. Linie wpływu w układach statycznie wyznaczalnych
2.1 Belki proste
2.2 Belki gerberowskie
2.3 Kratownice
2.4 Ramy
3. Linie wpływu w ustrojach statycznie niewyznaczalnych
4. Zastosowanie linii wpływu

2

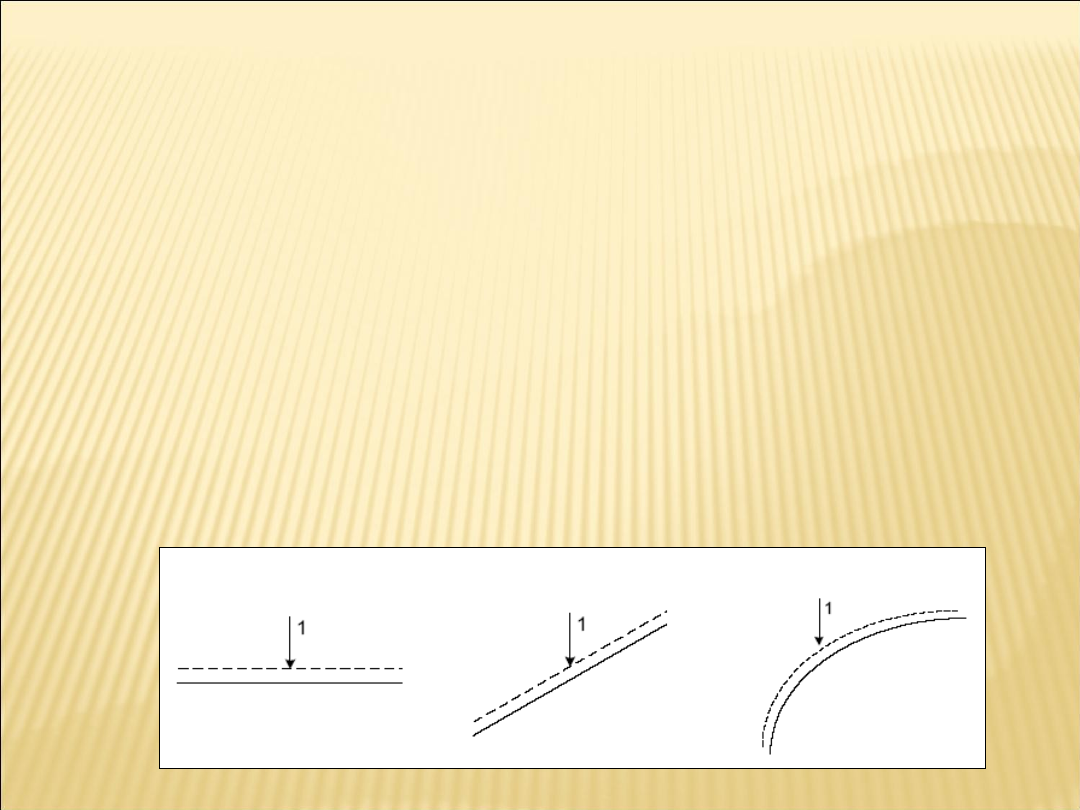
Definicja

Linią wpływu wielkości statycznej ” Z”
(reakcji, sił przekrojowych, jak momenty
zginające, siły tnące i
osiowe) nazywamy zależność wielkości ” Z”
od położenia czynnej siły jednostkowej na
ustalonym torze tej siły.

Zazwyczaj przyjmuje się, że siła jednostkowa P=1i jest pionowa.
Linią przerywaną zaznaczamy tor przesuwania się siły.

3

Ustroje statycznie

wyznaczalne

Dla układów statycznie wyznaczalnych wielkość
statyczna jest liniową funkcją położenia siły
jednostkowej.

Twierdzenie:

Linie wpływu wielkości statycznej dla
ustrojów statycznie wyznaczalnych
składają się z odcinków prostych.

4

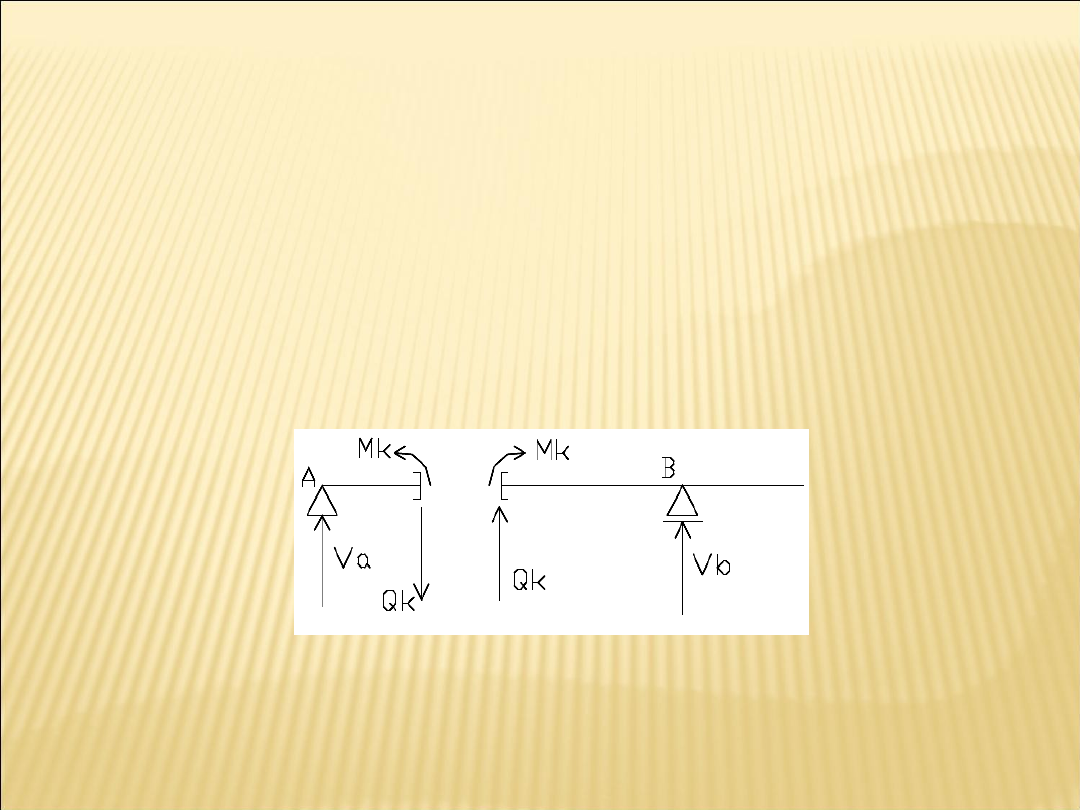
Dodatnie zwroty sił:

Ustroje statycznie

wyznaczalne

Linie wpływu można wyznaczać metodą
statyczną lub kinematyczną.

5

1.W miejscu podpory linia

wpływu przyjmuje wartość
równą sile jednostkowej = 1 i
wartości zerowe na podporze
„obcej”

2.Kształt linii wpływu w przęśle

jest przedłużany na
wsporniku.

3.Dla siły tnącej linia wpływu ma

skok, a dwie sąsiednie gałęzie
są równoległe

Przy rysowaniu linii wpływu
obowiązują następujące zasady:

6

4. Dla momentu w miejscu

przekroju linia wpływu
ma załamanie.

5.Obciążenie z belki dolnej

nie przekazuje się na
belkę górną

(w przypadku belek

gerberowskich).

Przy rysowaniu linii wpływu
obowiązują następujące zasady:

7

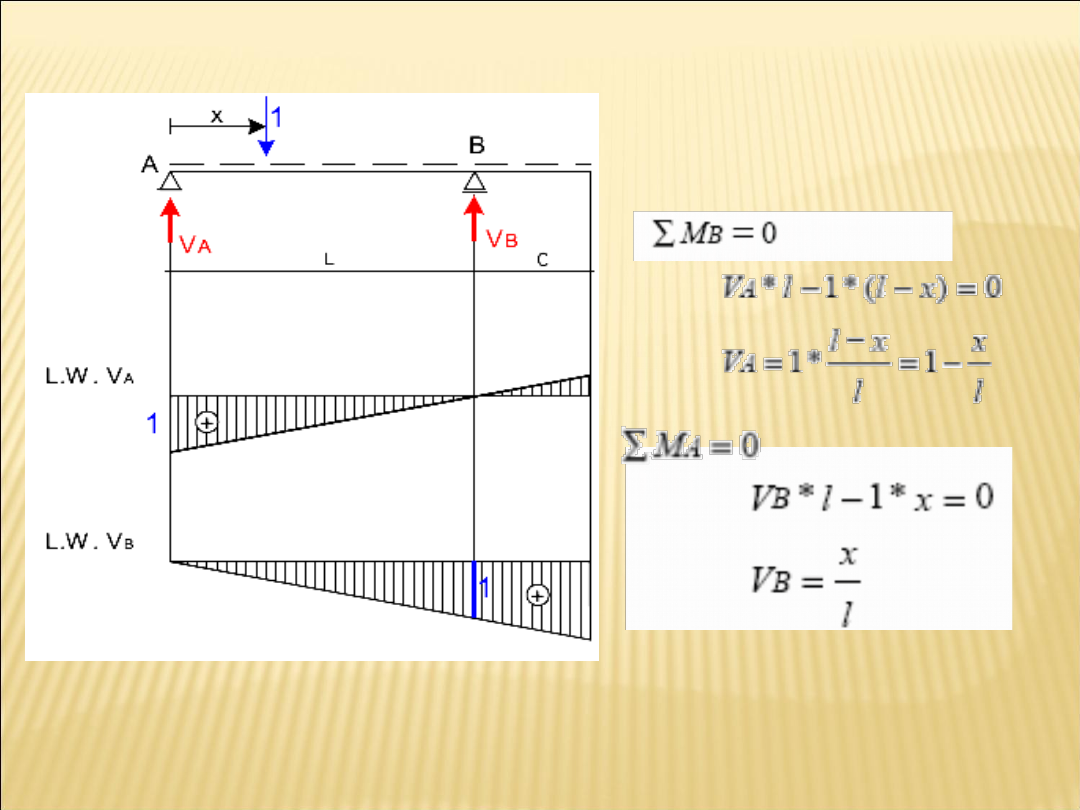
Gdy siła stoi w punkcie A, V

A

=1,a V

B

=0,łaczymy

rzędne i otrzymamy L.W. V

A

, gdy siła jest w punkcie B

wtedy
V

B

=1,a V

A

=0. łącząc te dwie rzędne – L.W. V

B

Belki proste

Metoda statyczna

Metoda kinematyczna

8

.

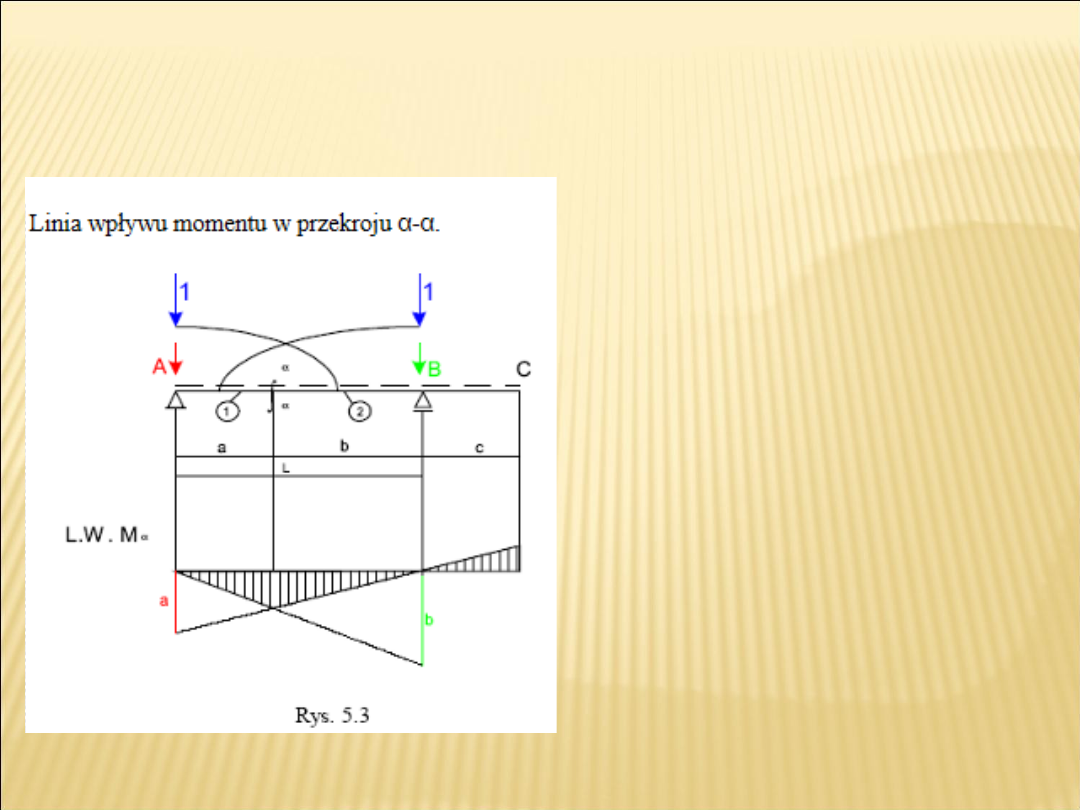
Linia wpływu momentu w przekroju α-α

Punktami
charakterystycznymi są
podpory A i B.
Przekrój α - α dzieli belkę
na dwie tarcze: (A- α )
=1

(tarcza)

i( α -C)=2

(tarcza)

. Dla

tarczy 1, gdy siła stoi nad
podporą w punkcie A M α
=0, a gdy stoi na „linii”
nad punktem B to
M α dla tarczy 1 w
punkcie B = b. Dla tarczy
2, gdy siła stoi nad
podporą w punkcie B
M α=0, gdy na „linii” nad
punktem A to M α dla
tarczy 2 w punkcie A = a.
Rzędne odkładamy po
stronie włókien
rozciąganych.

9

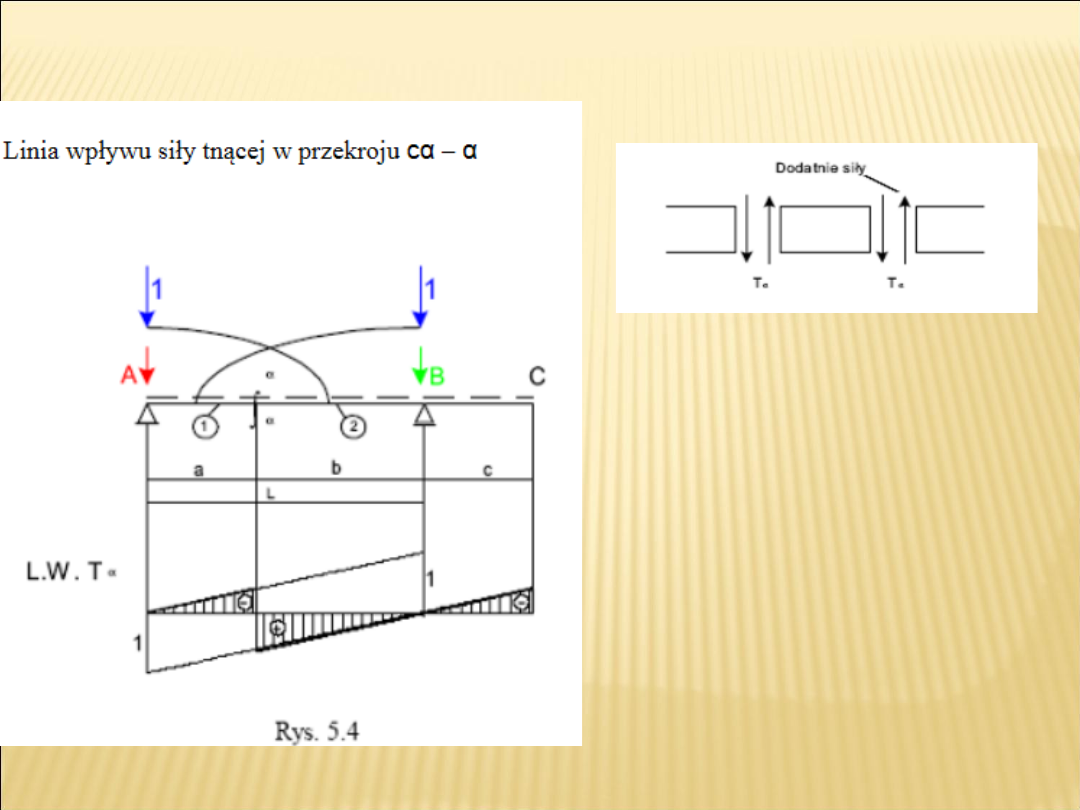
Linia wpływu siły tnącej w

przekroju α-α

Dla tarczy 1 = (A - α )siłę
stawiamy w punkcie A,
gdzie T α = 0 oraz na
”linii” w punkcie B, gdzie
T α = -1.
Dla tarczy 2 = ( α - C) w
punkcie A na „linii”,
gdzie siła tnąca T α = 1
oraz w punkcie B, gdzie T
α = 0

Znakowanie sił tnących

- 1

10

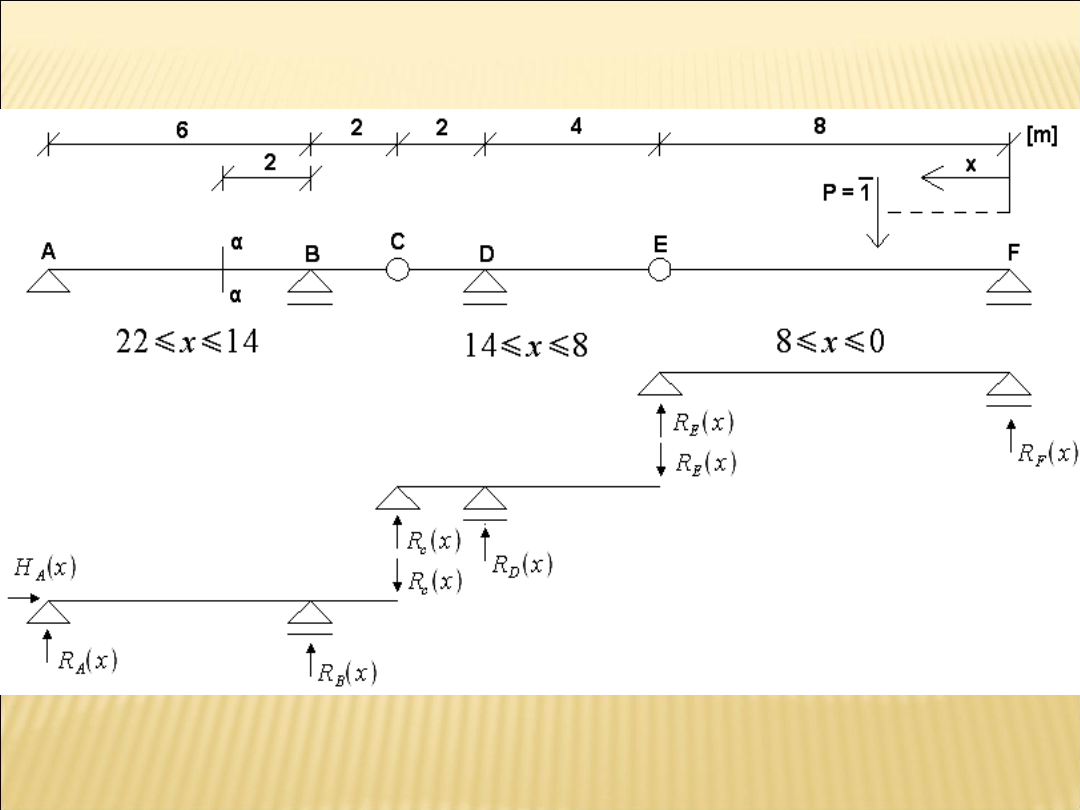
Belki gerberowskie

Rys.2

W przypadku belek
gerberowskich ważne jest
ustalenie zależności między
belkami.

11

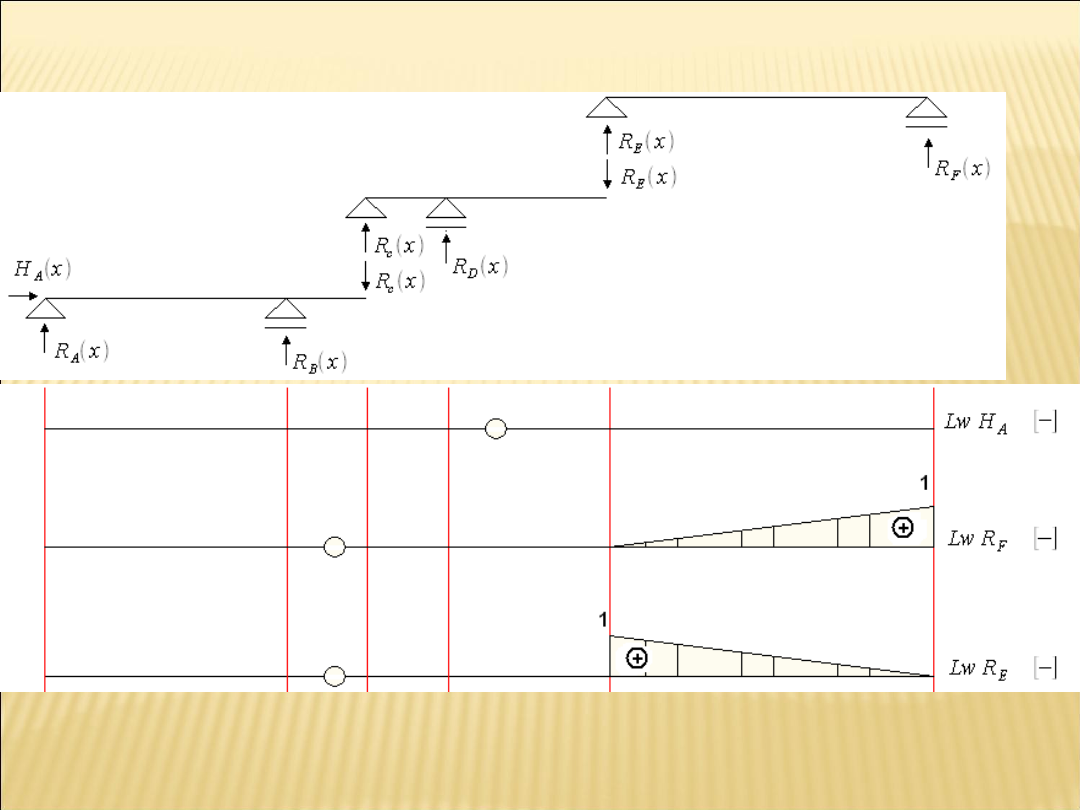
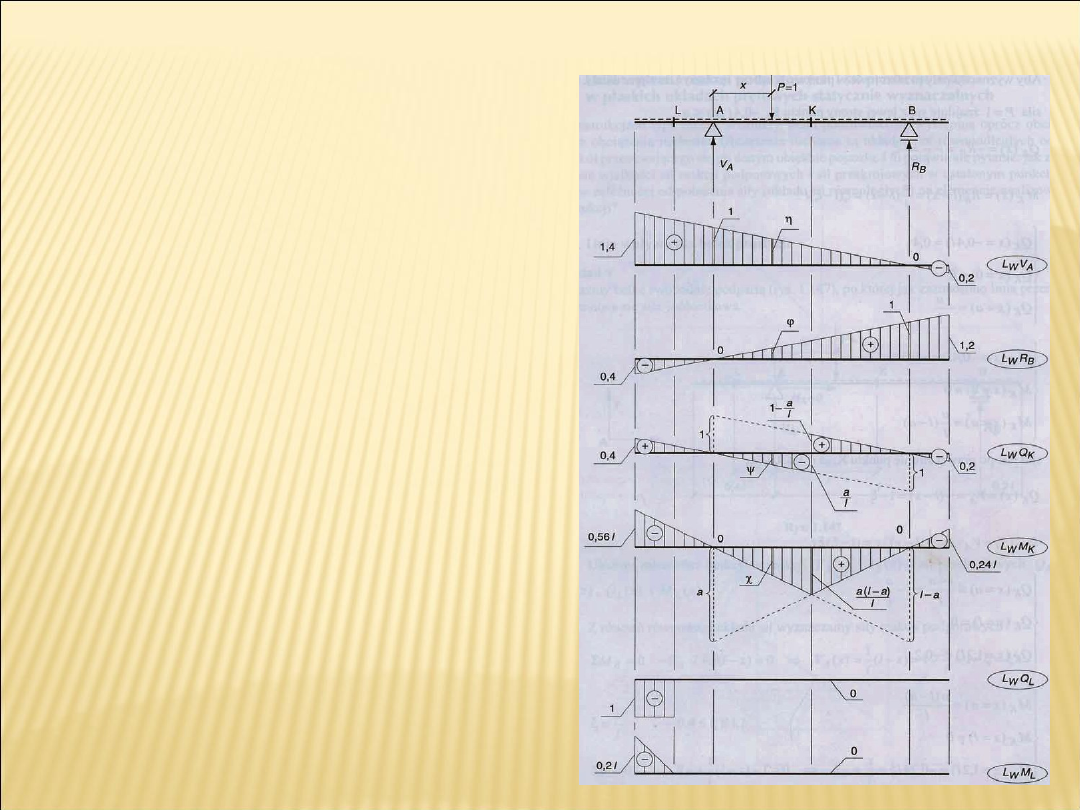
Linie wpływu reakcji podporowych

12

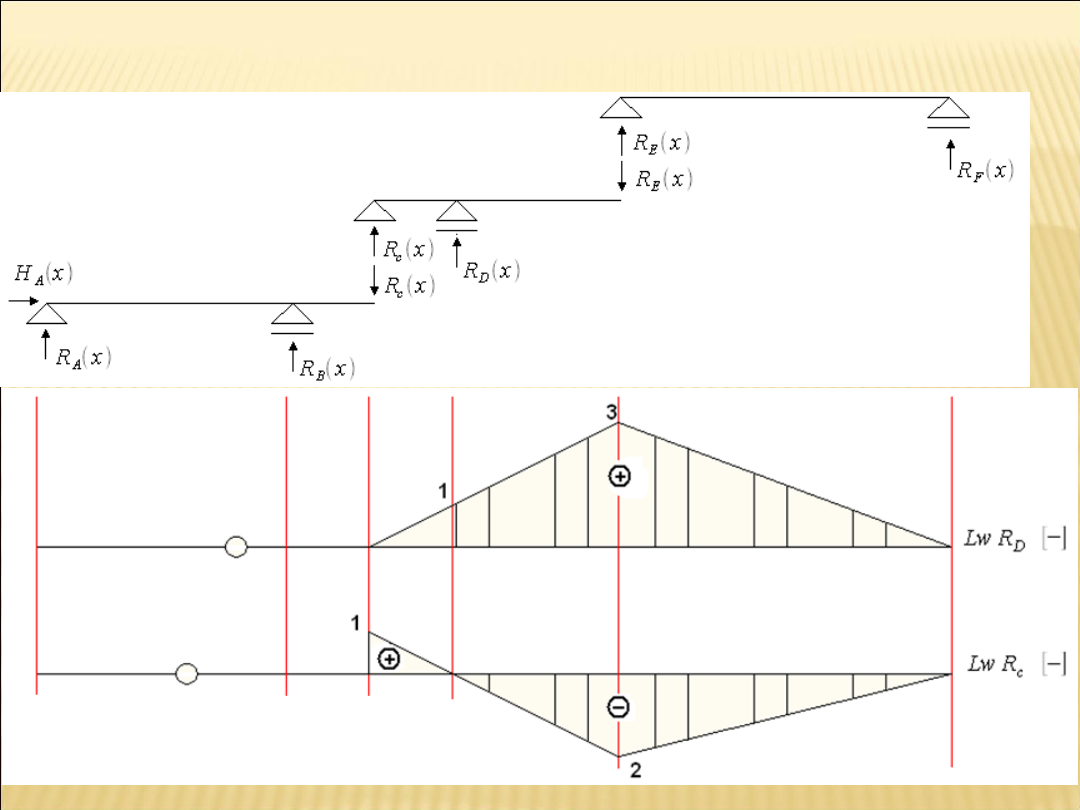
Linie wpływu reakcji podporowych

13

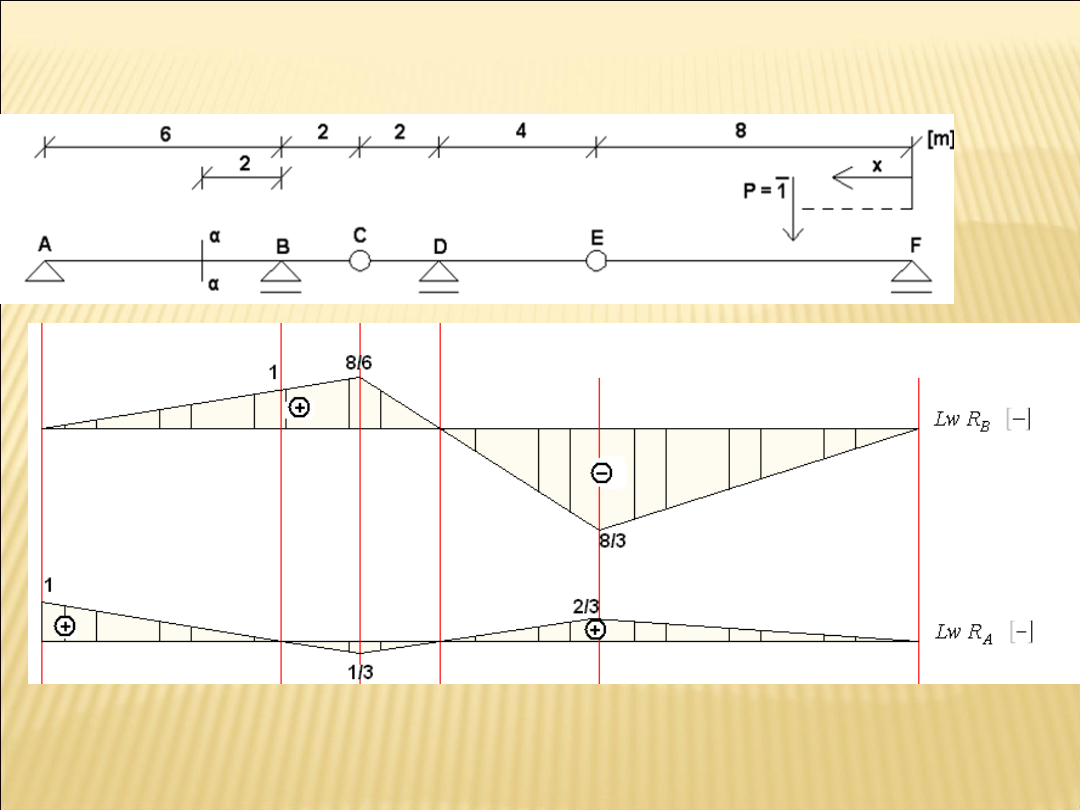
Linie wpływu reakcji podporowych

14

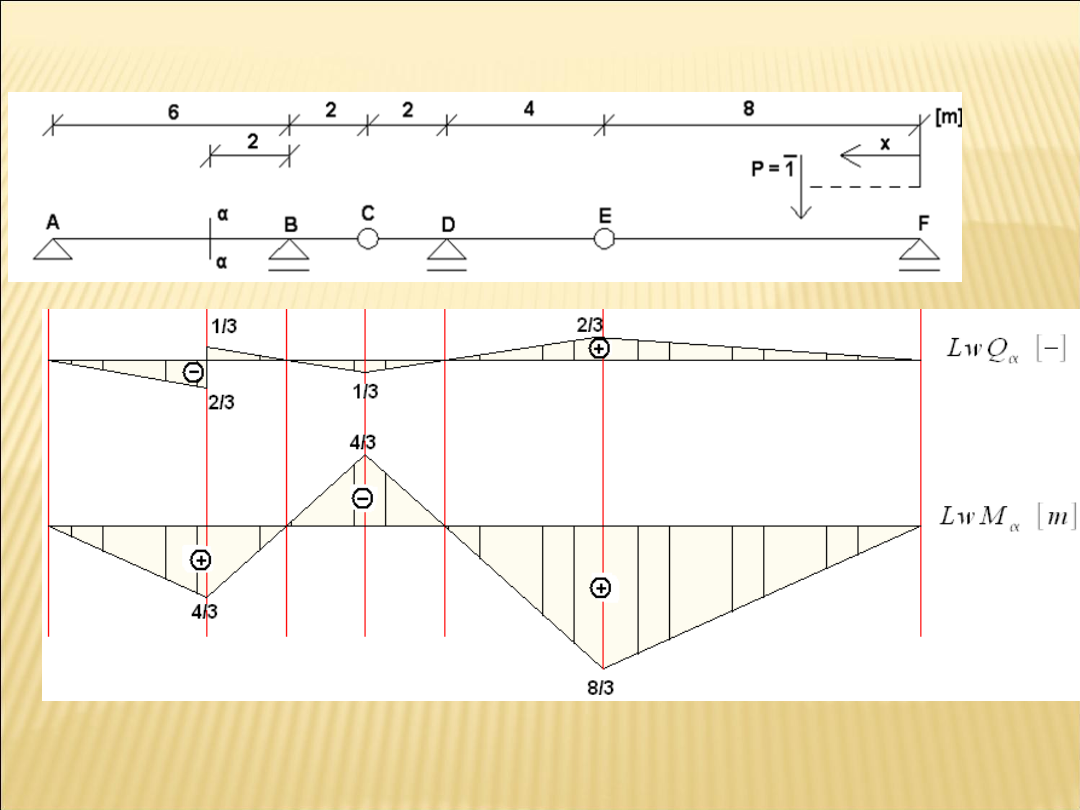
Linie wpływu sił przekrojowych

15

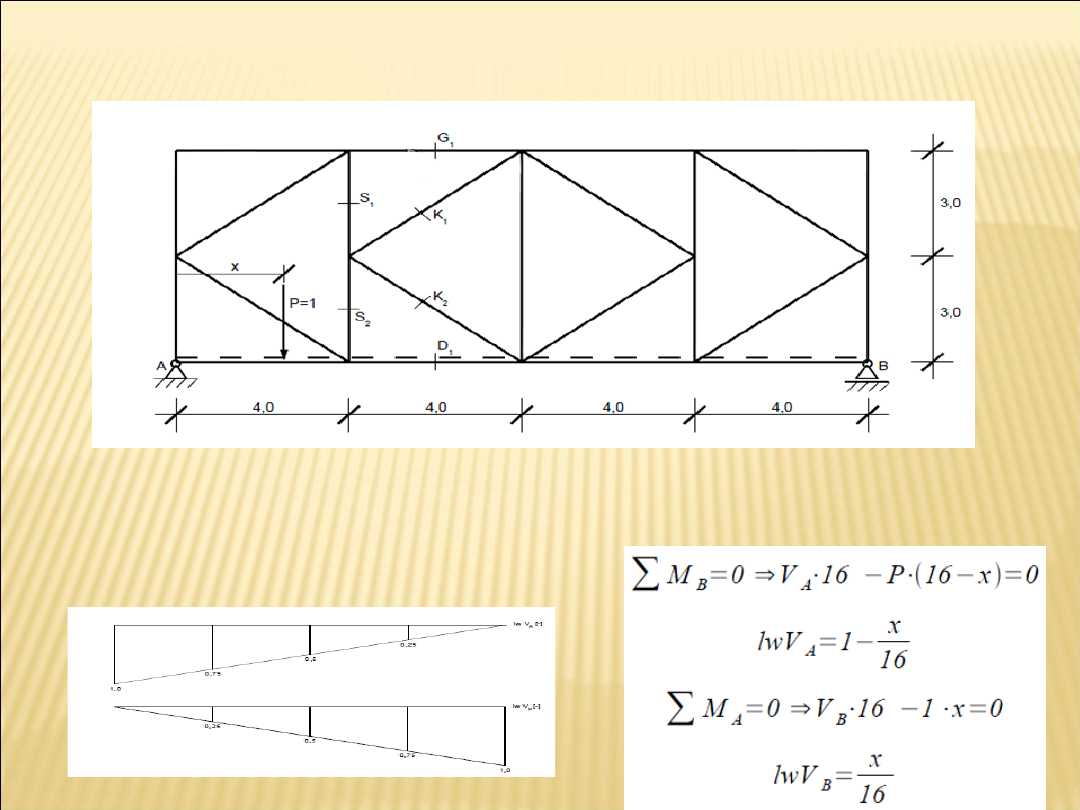
Kratownice

Linie wpływu reakcji podporowych
wyliczamy z sumy momentów
względem odpowiednich punktów:

16

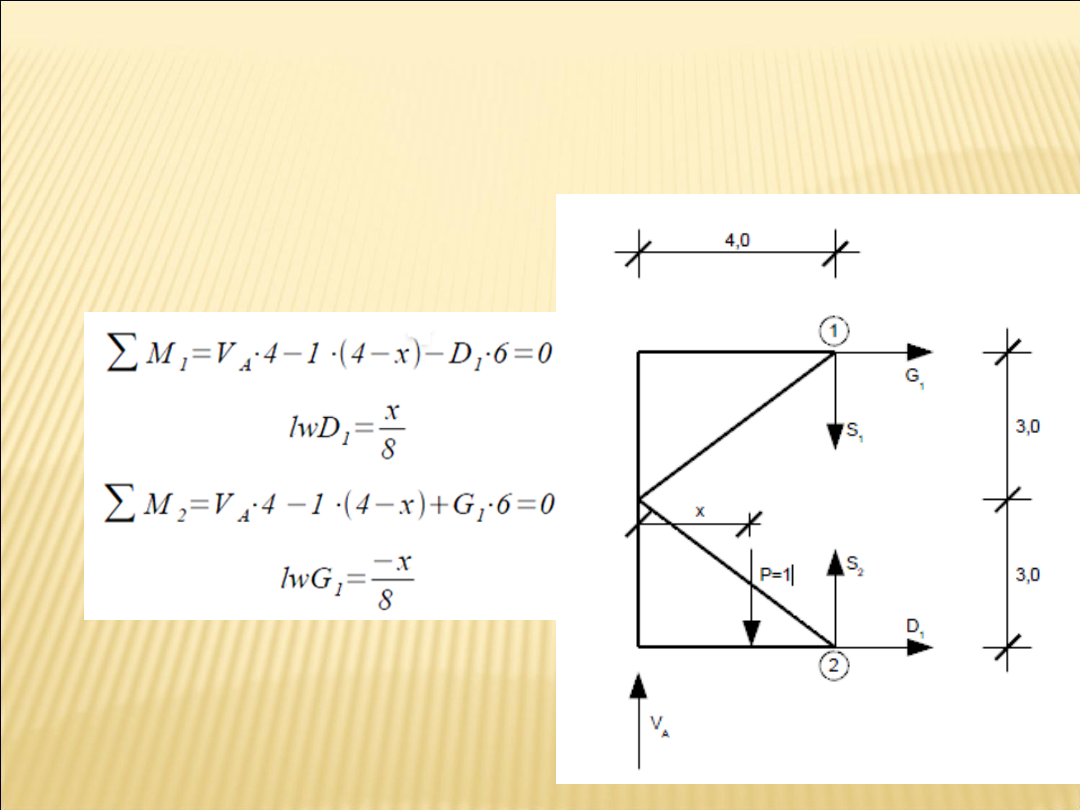
Linie wpływu sił wewnętrznych w kratownicy można
wyliczyć z równań równowagi stosując przecięcie przez 3
pręty kratowe ,dla wyciętego fragmentu kratownicy.

Linie wpływu prętów D1 oraz G1:
• x∈ 0 ; 4

〈

〉

17

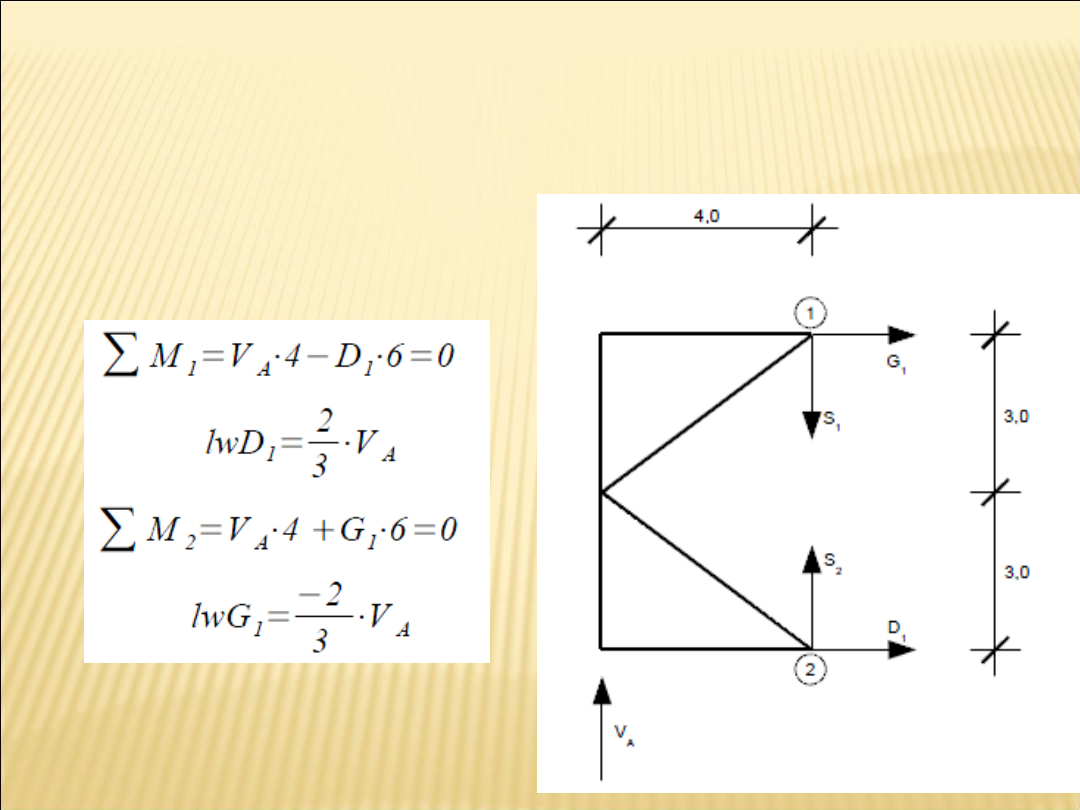
Równania równowagi można zapisywać zarówno dla
części po której porusza się siła jednostkowa jak i dla
pozostałego fragmentu układu.

• x∈ 8 ; 16

〈

〉

18

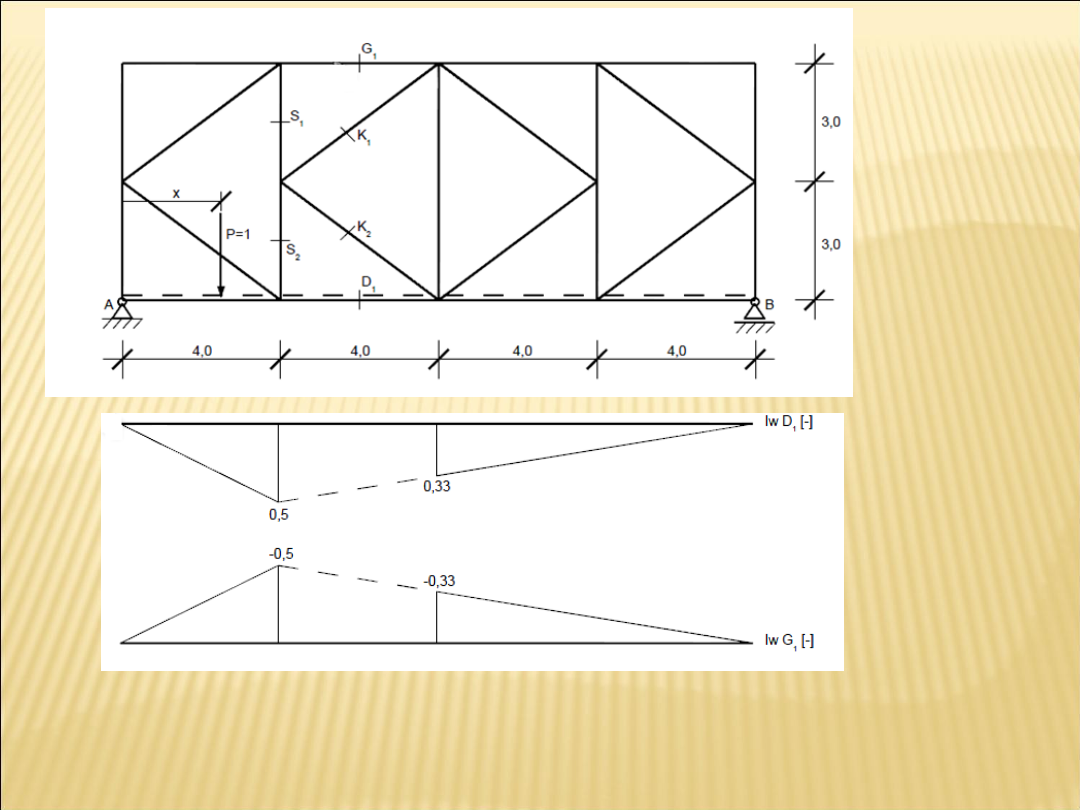
Dlatego łączymy punkty
charakterystyczne
po jego obu stronach linią przerywaną.

W miejscu przekroju nie znamy
przebiegu linii wpływu.

19

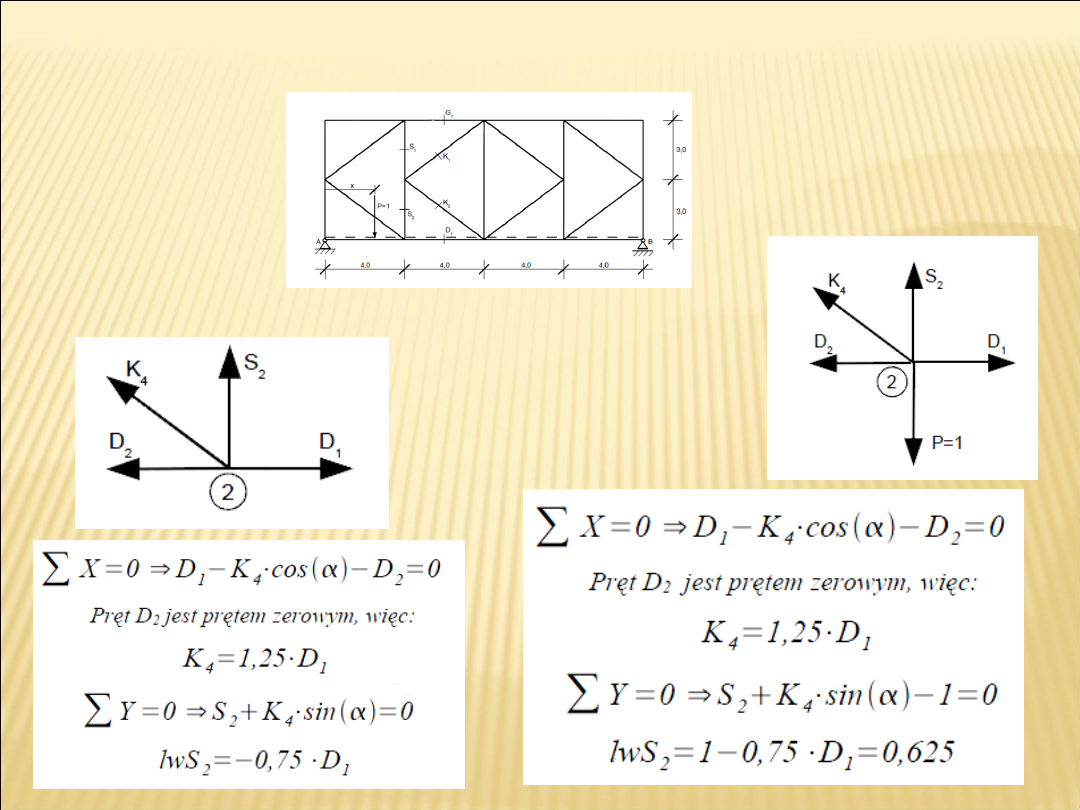
Linię wpływu w pręcie S2 wyznaczamy przez myślowe wycięcie węzła

2

:

• gdy poruszająca sie
siła znajduje się
dokładnie w węźle 2

• gdy
poruszająca
sie siła
znajduje się
poza węzłem
2

20

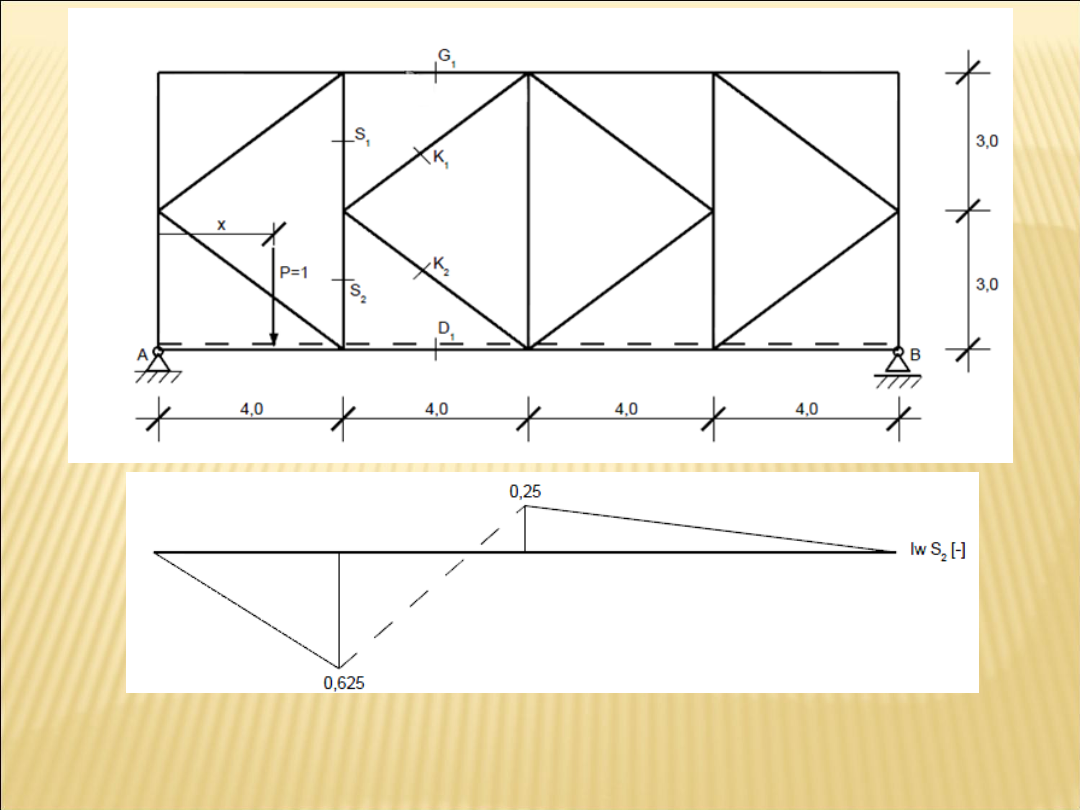
Linia wpływu siły w pręcie S

2

21

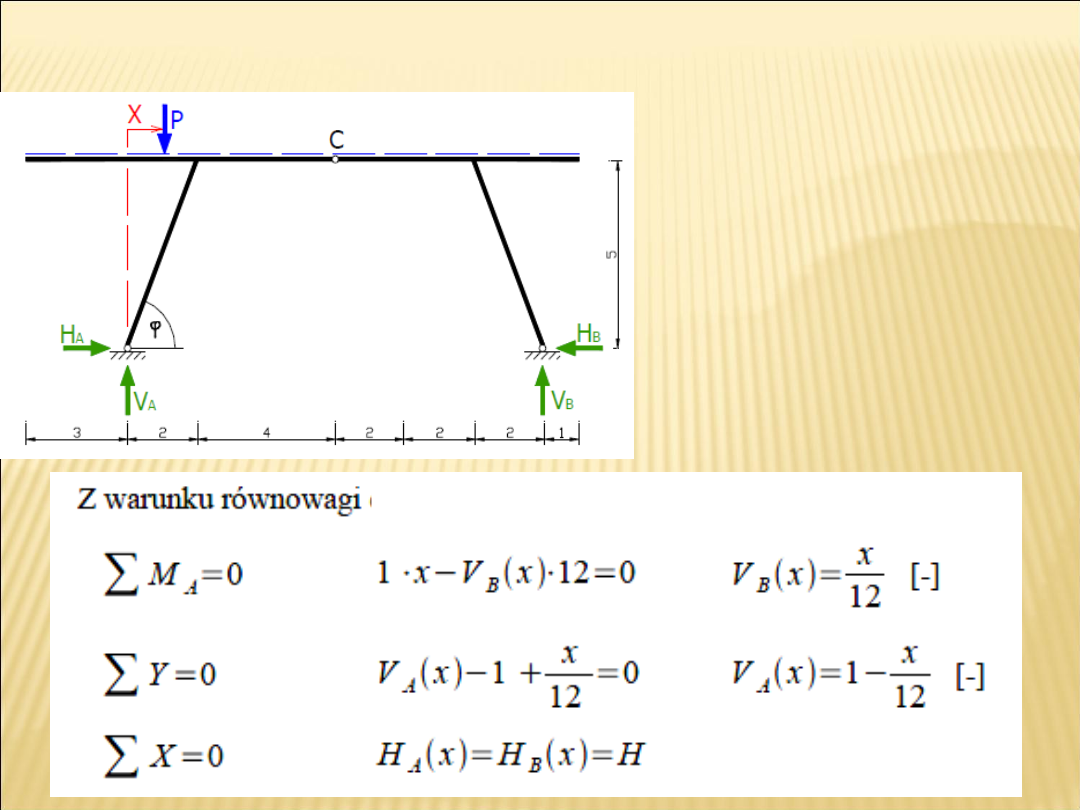
Ramy

Dziedzina współrzędnej:
X ∈ −3 ;13

〈

〉

Obliczenia należy zacząć
od przyjęcia
współrzędnej x
określającej położenie
jednostkowej siły P [-]

22

Z warunku równowagi dla
prawej części ramy gdy X ∈ −3 ;

〈

6 〉

Z warunku równowagi
dla
lewej części ramy gdy
X ∈ 6 ;13

〈

〉

23

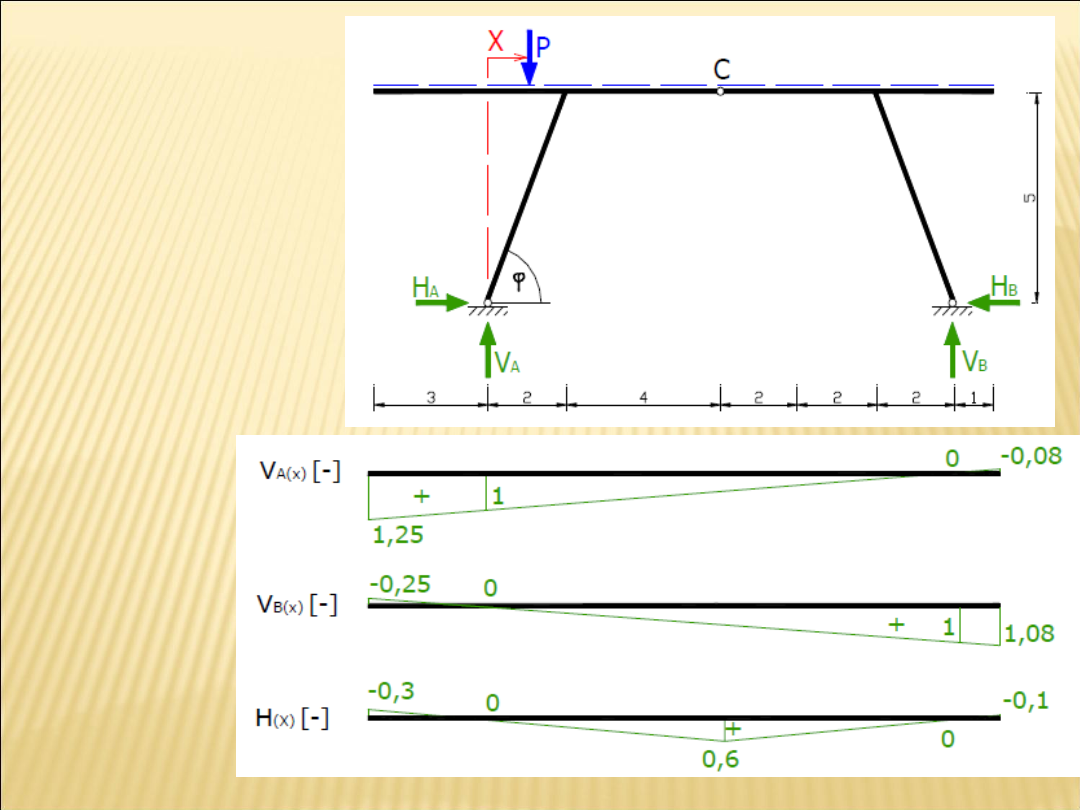
Linie wpływu
reakcji
podporowych

24

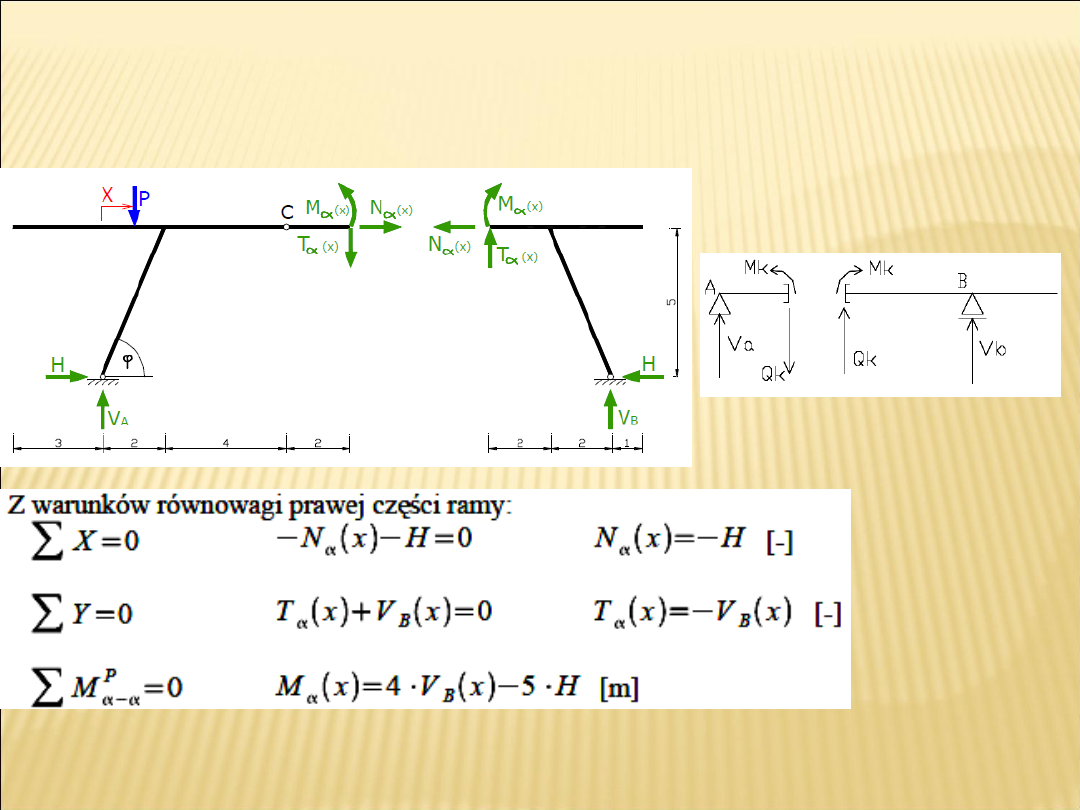
Obliczenie linii wpływu sił przekrojowych

Rozważamy dwa przypadki położenia siły: po lewej lub prawej stronie przekroju.
W obu przypadkach możemy zapisywać równania równowagi dla obu
części ramy.

Obliczamy funkcję linii wpływu sił przekrojowych
korzystając ze znanych reakcji podporowych.

Dodatnie zwroty sił:

25

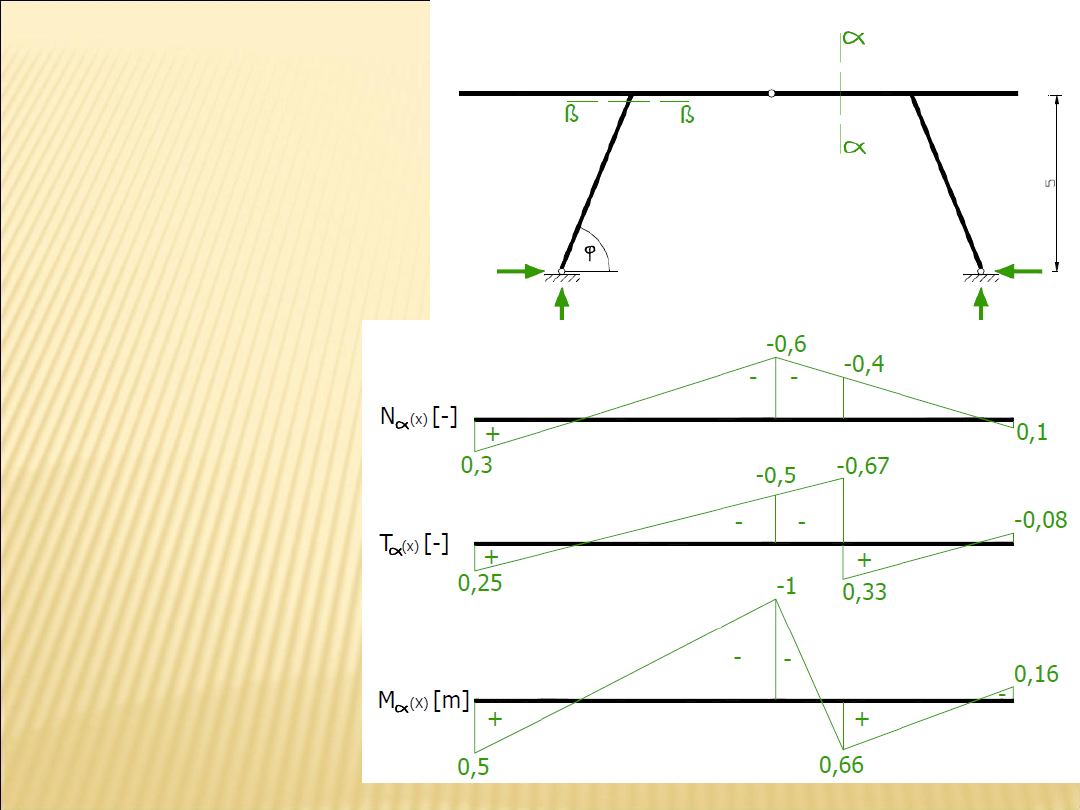
Linie wpływu dla
sił przekrojowych
Przekrój α - α

Wszystkie
omawiane
dotychczas zasady
mają zastosowanie
także w układach
ramowych.
Występuje skok na
linii wpływu sił
tnących, a także
załamanie na linii
wpływu momentu.

26

Linie wpływu ustrojów statycznie
wyznaczalnych ograniczone są
łamanymi liniami prostymi, których
równania są łatwe do
wyprowadzenia .

Natomiast linie wpływu ustrojów
statycznie niewyznaczalnych ( w
tym belek ciągłych) ograniczone są
krzywymi wyższego rzędu i z tego
względu do ich określenia stosuje się
metodę „dyskretną „ obliczając
kolejne rzędne o gęstości zależnej od
potrzeb i wymaganej dokładności.
Sposób ten jest dość mozolny należy
bowiem rozwiązać tyle schematów ile
rzędnych mamy obliczyć

27

10*2

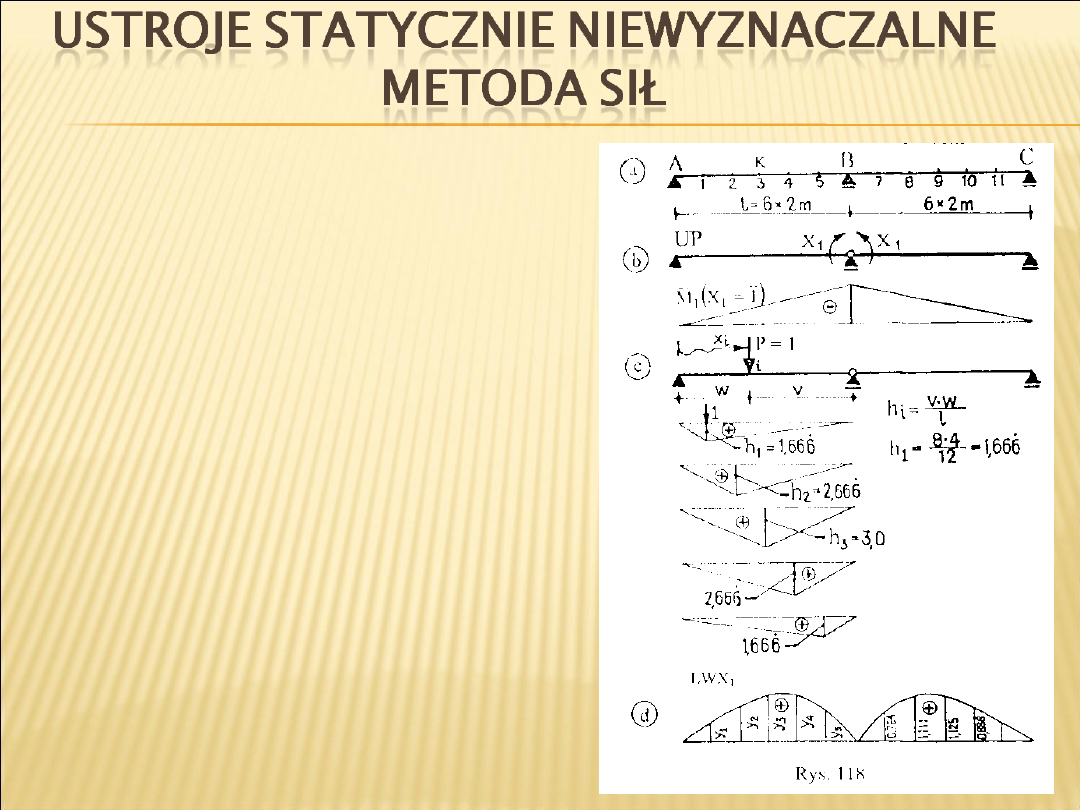
PRZYKŁAD
a –temat
b –UP z niewiadoma hiperstatyczną ,
wykres momentu zginającego dla
X

1

=1

c –obciążenie przemieszczającej się
siły jednostkowej (stan P) i wykresy
momentów zginających dla siły
znajdującej się w punktach od1-5
d-LWX

1

W pierwszej kolejności sporządza się
LWX1 (czyli LWM

B

), a korzystając z

niej oblicza się rzędne LW reakcji, LW
momentu zginającego i LW siły
poprzecznej.
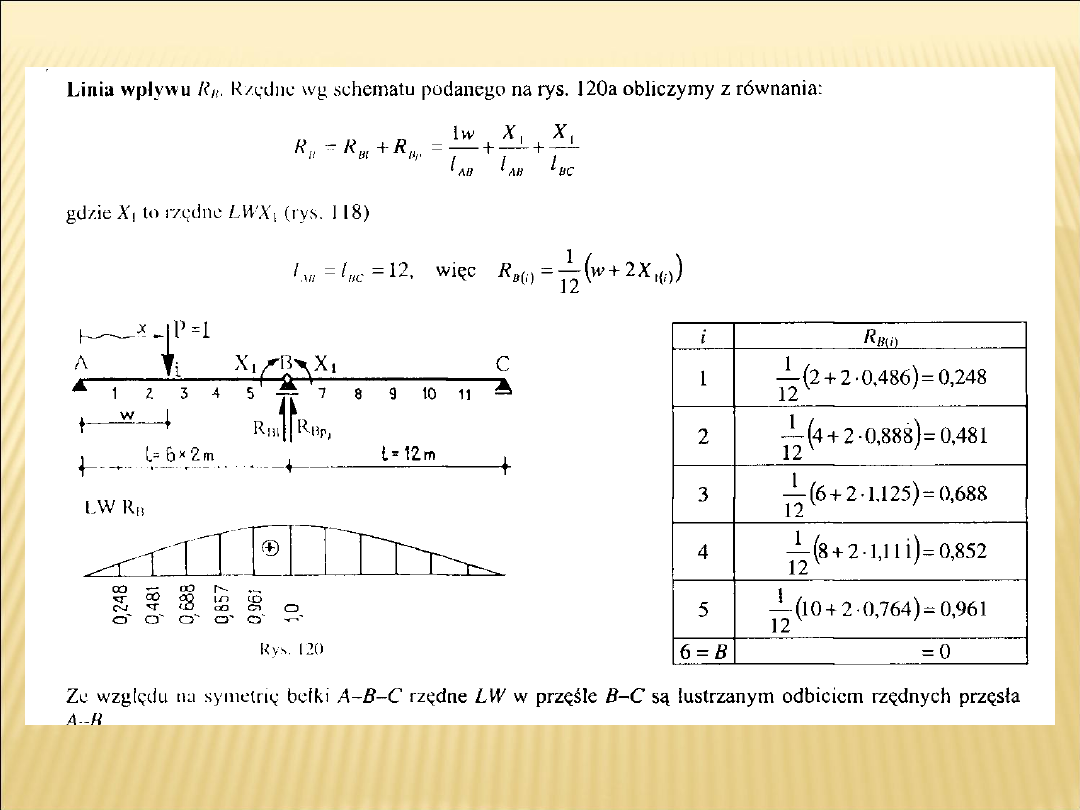
LWX1-rzędne LW oblicza się
korzystając z równania kanonicznego

EI=const upraszcza się w
obliczeniach i zostaje
pominięte

EI= const

28

10*2

Dla każdego usytuowania siły P=1
w kolejnych punktach od 1-5
obliczono Δ

1p(i)

korzystając z wzoru

całki graficznej

29

10*2

30

31

1

32

M

33

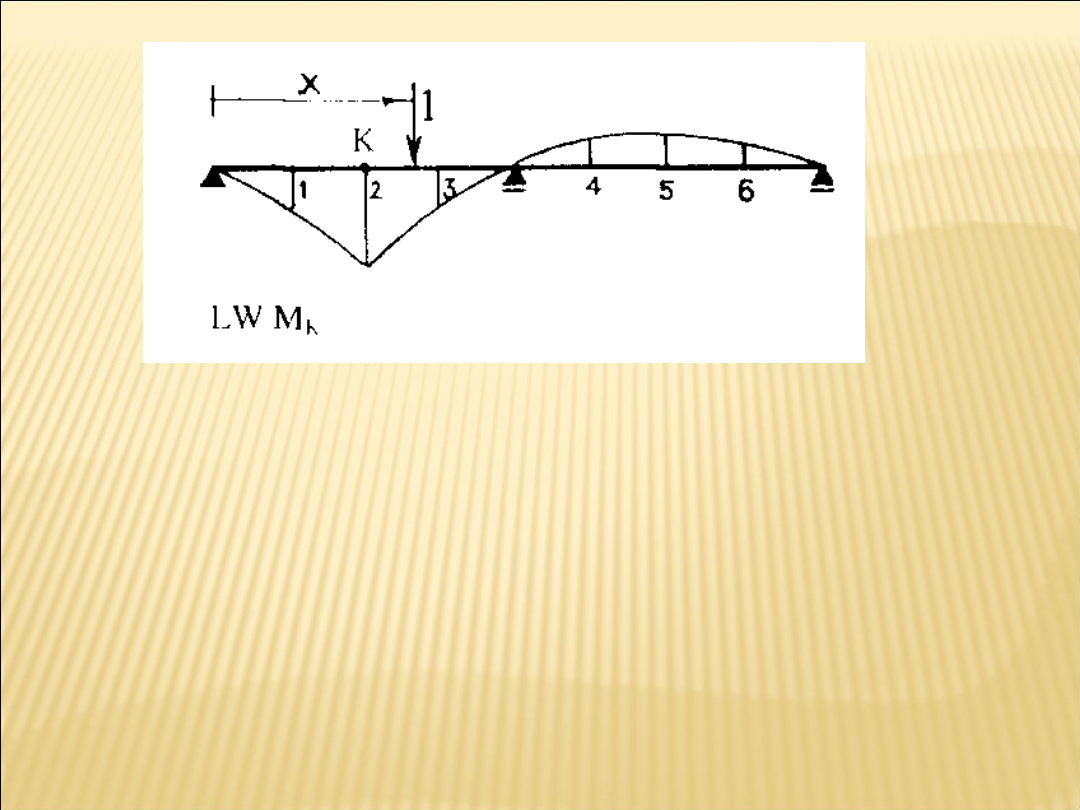
a –temat

Wszystkie rzędne wykresu linii wpływu podają wielkości momentu
zginającego w punkcie K, wywołanego działaniem jednostkowej
siły
sytuowanej w kolejnych punktach belki.
Przykładowo : rzędna y

1

jest wielkością momentu zginającego w

punkcie K wywołanego siła jednostkową działającą w punkcie 1,
rzędne y2,y3 itd. To wielkości momentu zginającego w punkcie K ,
wywołanego działaniem jednostkowej siły w punktach 2,3 itd.
Podobnie jest z liniami wpływu reakcji, siły poprzecznej , a w
pewnych przypadkach sił podłużnych ( w belkach ukośnych łukach
lub ramach)

34

Linie wpływu szczególnie mają znaczenie przy wyznaczaniu
obwiedni sił przekrojowych (momentów, sił tnących, sił
osiowych).

Zastosowanie linii wpływu

Znajomość linii wpływu wielkości statycznej „ Z „pozwala w
łatwy sposób wyznaczyć wielkość „ Z „ od danego programu
obciążenia.

Linie wpływu wykorzystuje się głównie przy projektowaniu
mostów ,belek podsuwnicowych i innych konstrukcji , w których
mamy do czynienia z obciążeniami ruchomymi .

W obciążeniu zmiennym wyróżniamy siły skupione i obciążenie
rozłożone.
Częstym zadaniem jest wyznaczenie wartości ekstremalnych
wielkości „Z „ , a więc Z

max

i Z

min

.

35

DZIĘKUJĘ ZA UWAGĘ

LITERATURA :

[1] -

[2] -

[3] -

[4] -

Dyląg , Filip , Niemiec , Mechanika budowli , t. 1, 2 PWN, Warszawa 1989.

Paluch M. Podstawy Mechaniki Budowli, Wyd. K.G.B. i G. AGH, Kraków
2003

Bodnar A. Wytrzymałość materiałów Wyd. PK. Kraków 2003

Bogusz Jerzy Metoda sił , wyd. 2 Wyd. PK Kraków 2004

36