TWIERDZENIE

COSINUSÓW

W dowolnym trójkącie kwadrat dowolnego

boku równa się sumie kwadratów dwóch

pozostałych boków pomniejszonej o

podwojony iloczyn tych boków

i cosinusa kąta zawartego między nimi.

C

B

A

α

γ

β

a

c

b

Oznaczenia trójkąta w rozwiązywanych zadaniach są takie
same: naprzeciw wierzchołka A jest bok długości a; naprzeciw
wierzchołka B bok długości b; naprzeciw wierzchołka C jest bok
długości c.

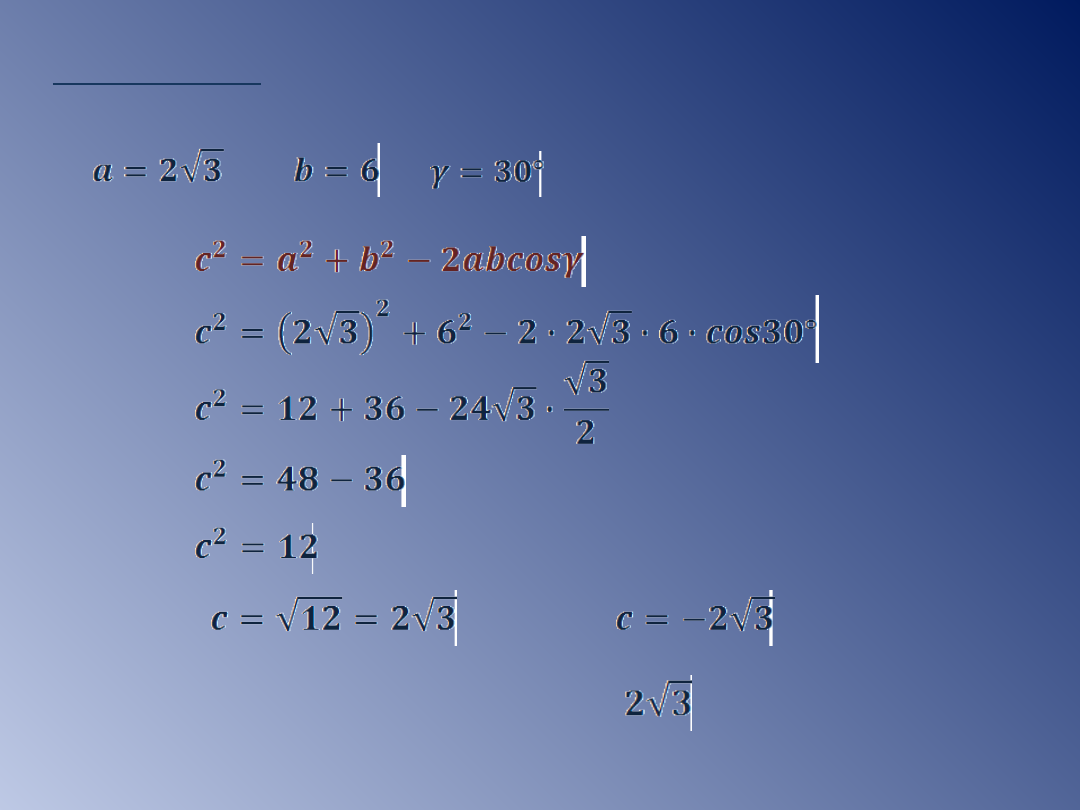
Przykład 1.

Oblicz długość nieznanego boku w trójkącie ABC
jeżeli:
a)

lub - odpada

Długość nieznanego boku równa się

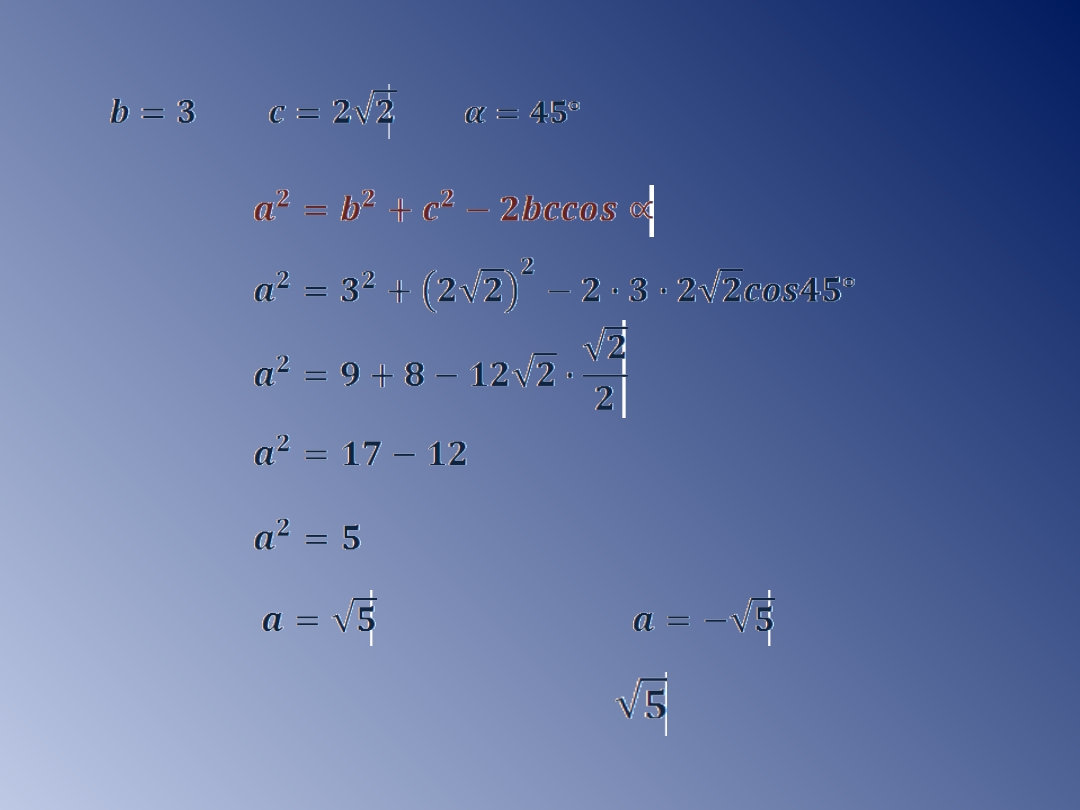
b)

lub - odpada

Długość nieznanego boku równa się

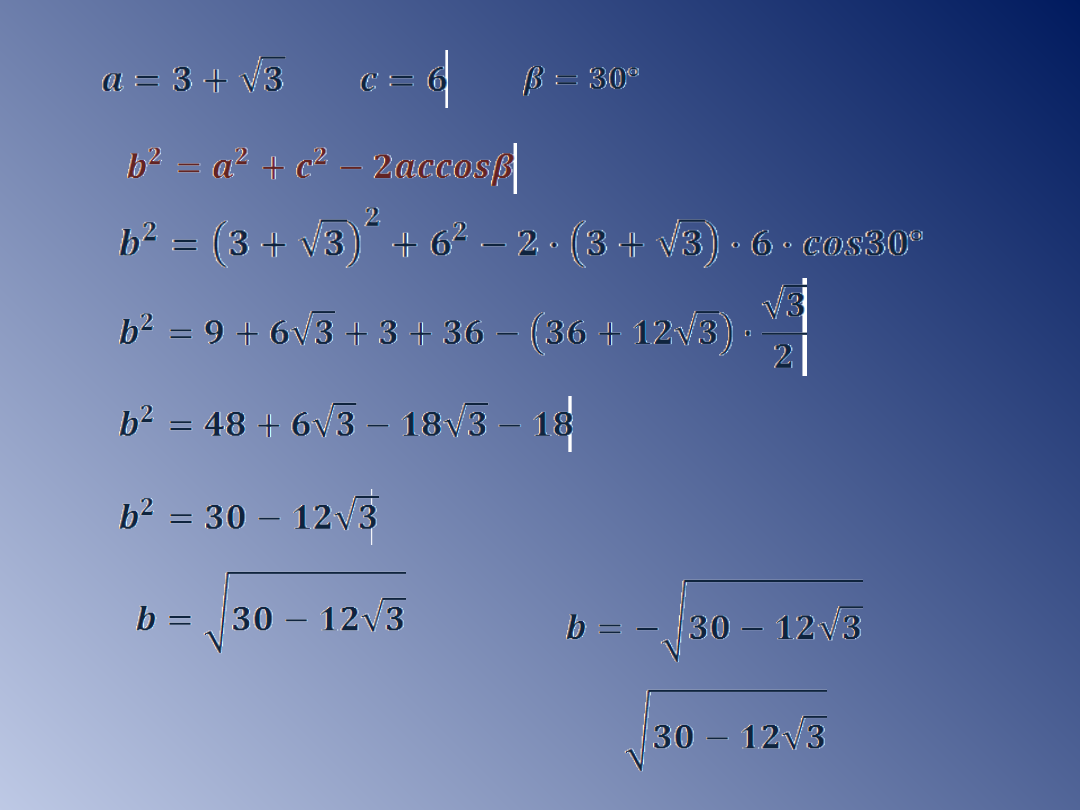
c)

lub - odpada

Długość nieznanego boku równa się

Przykład 2.

Wyznacz miary kątów trójkąta, wiedząc, że:
a=10cm, b=8cm, c=6cm.

Obliczamy miarę kąta zawartego między bokami b i c.

Obliczamy miarę kąta zawartego między bokami a i c.

Suma miar kątów wewnętrznych w trójkącie wynosi 180°.
Obliczamy miarę trzeciego kąta w trójkącie.

Odp: Miary kątów wewnętrznych w trójkącie wynoszą: 90°,
53°, 37°.

Przykład 3.

Wierzchołki trójkąta ABC mają współrzędne: A=(-
2,3) B=(1,0) C=(6,3). Wyznacz długości boków i
miary kątów wewnętrznych w trójkącie ABC.

A

B

C

c

b

a

Obliczamy długości boków trójkąta ABC,
wykorzystując wzór na długość odcinka.

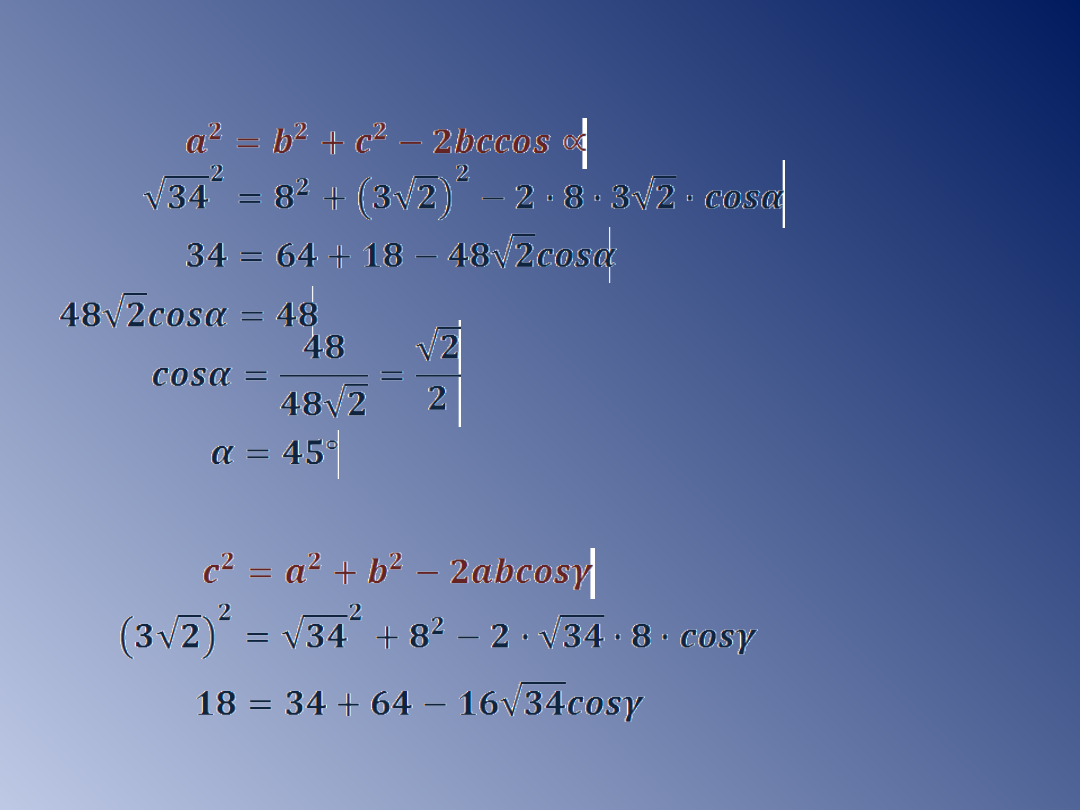
Wykorzystując twierdzenie cosinusów wyznaczamy miary kątów
wewnętrznych w trójkącie.

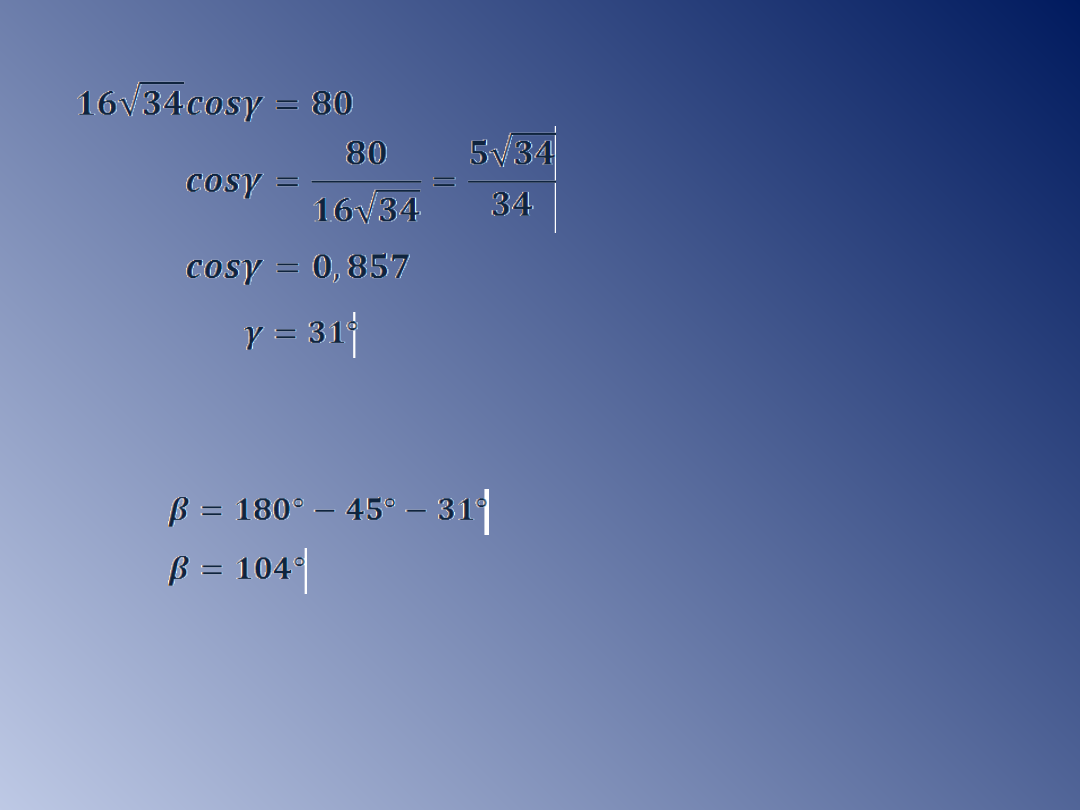
Suma miar kątów wewnętrznych w trójkącie wynosi 180°.
Obliczamy miarę trzeciego kąta w trójkącie.

Odp: Miary kątów wewnętrznych w trójkącie
ABC
wynoszą: 45°, 104°, 31°.

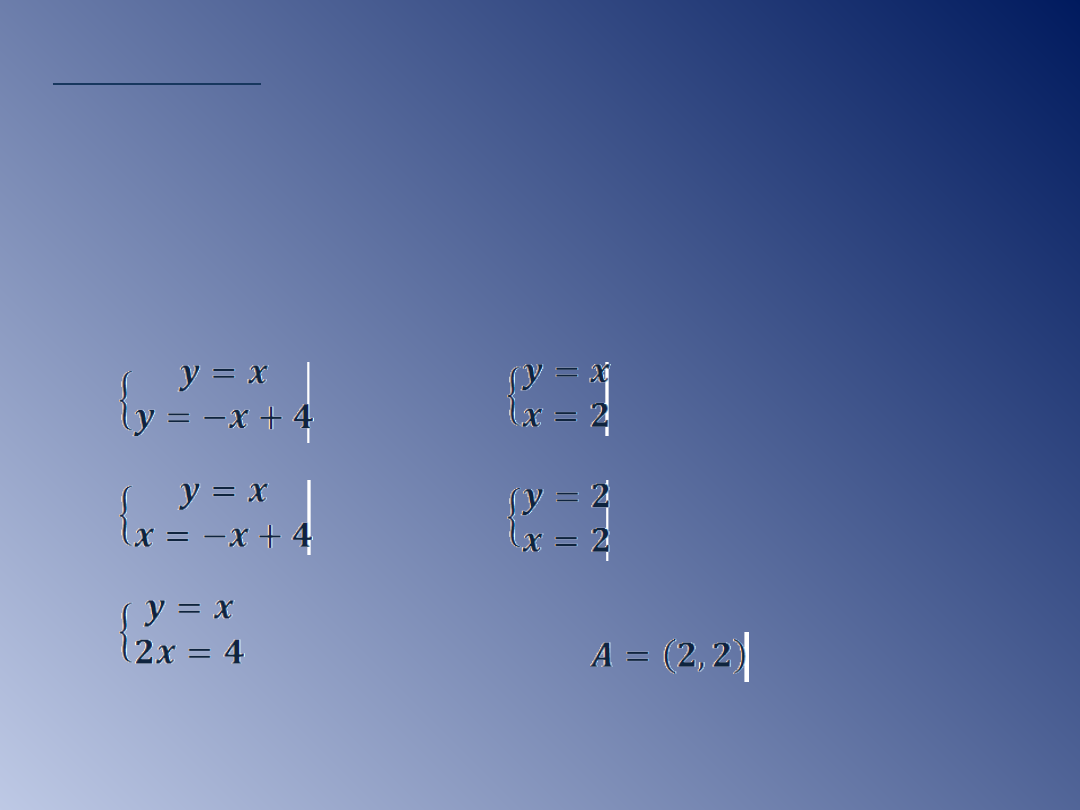
Przykład 4.

Znajdź kąt między prostymi k i l o równaniach:
k: y=x
l: y=-x+4

Wyznaczamy współrzędne punktu wspólnego obydwu prostych.
Tworzymy układ równań:

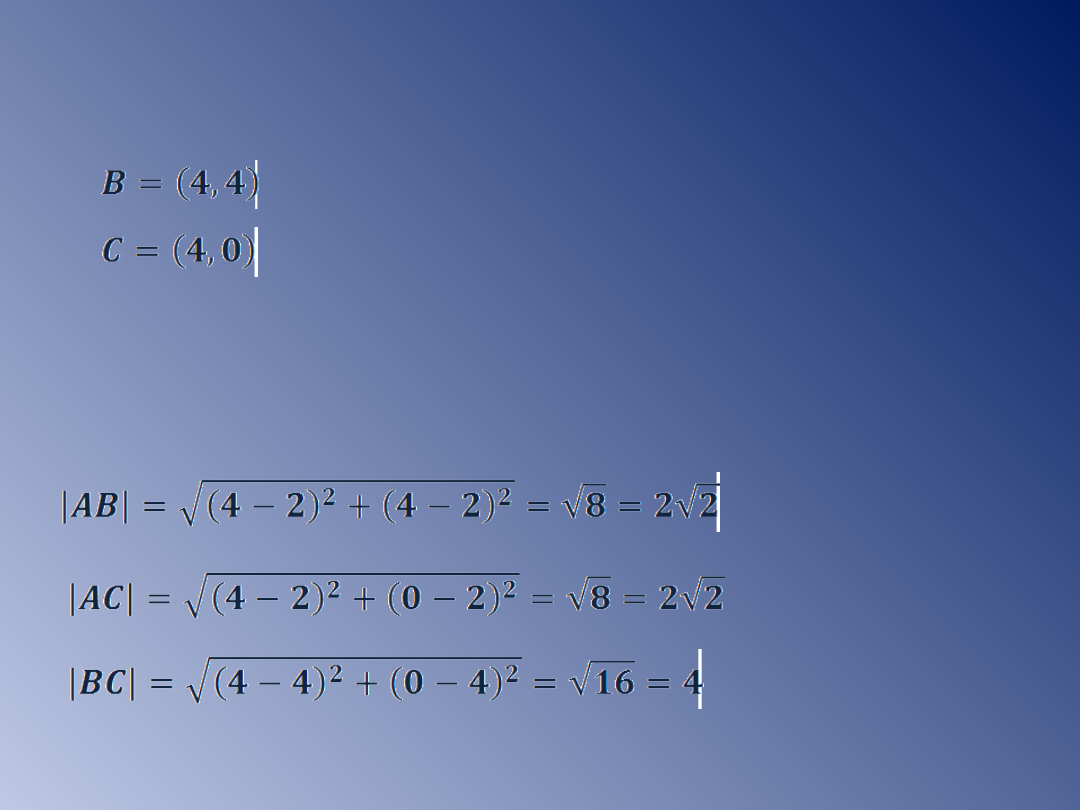
Wybieram dowolne dwa punkty – jeden należący do jednej
prostej, drugi należący do drugiej prostej.

Łącząc te punkty otrzymujemy trójkąt ABC, w którym kąt
wewnętrzny α jest jednocześnie kątem między prostymi k i l.
Obliczam długości boków trójkąta ABC.

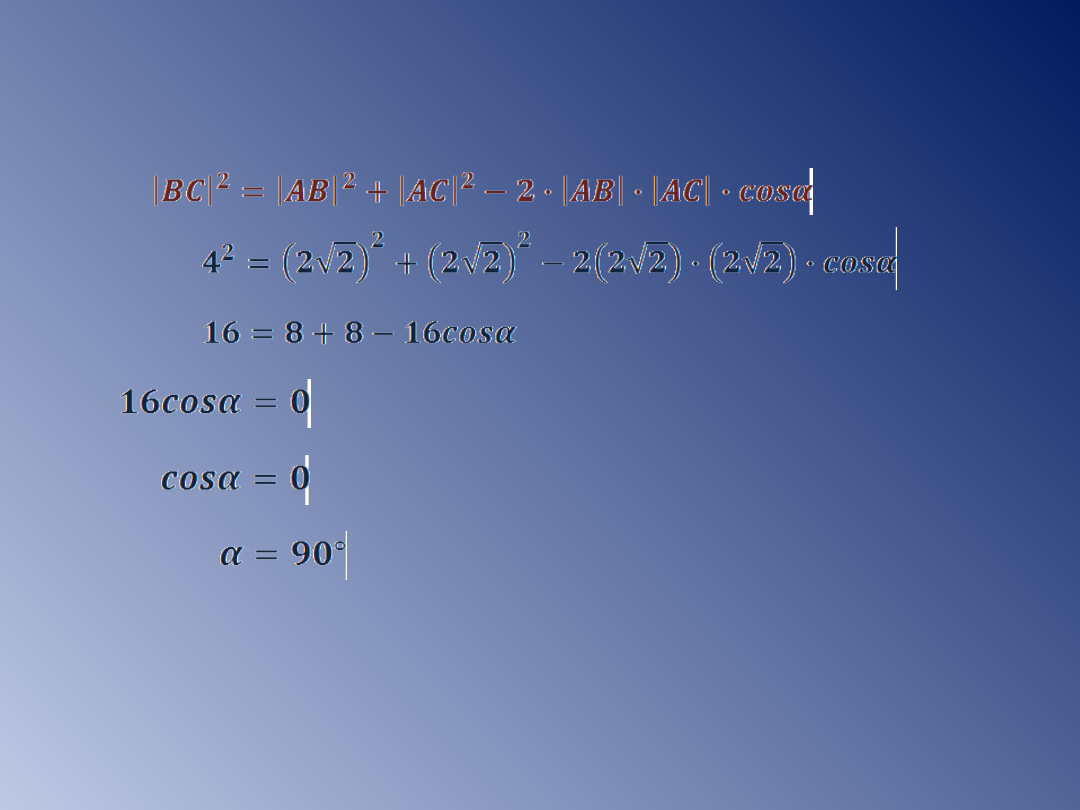
Wykorzystując twierdzenie cosinusów wyznaczamy miarę kąta
przy wierzchołku A.

Odp: Kąt między prostymi ma miarę 90˚.