©M

Figury w układzie
współrzędnych.

© M

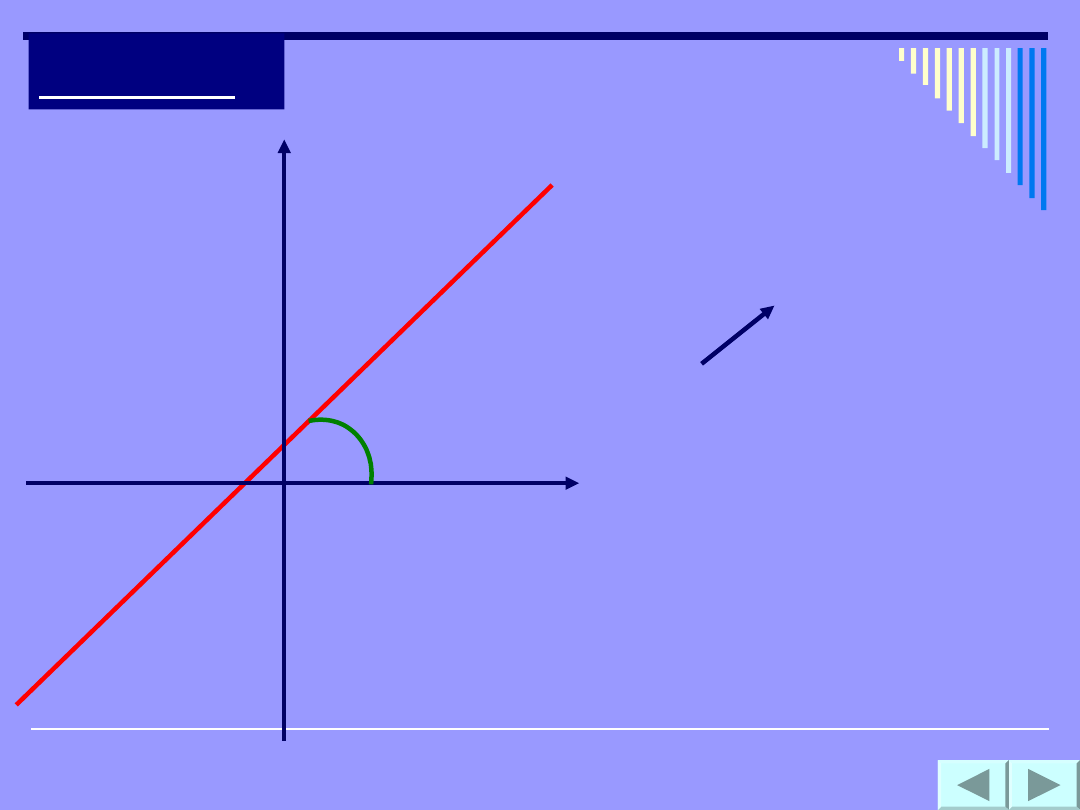
Prosta

x

y

1.Postać
kierunkowa

y = ax + b

współczynnik kierunkowy

a=tg





2.Postać ogólna

Ax + By + C =
0

gdzie a

2

+b

2



0

© M

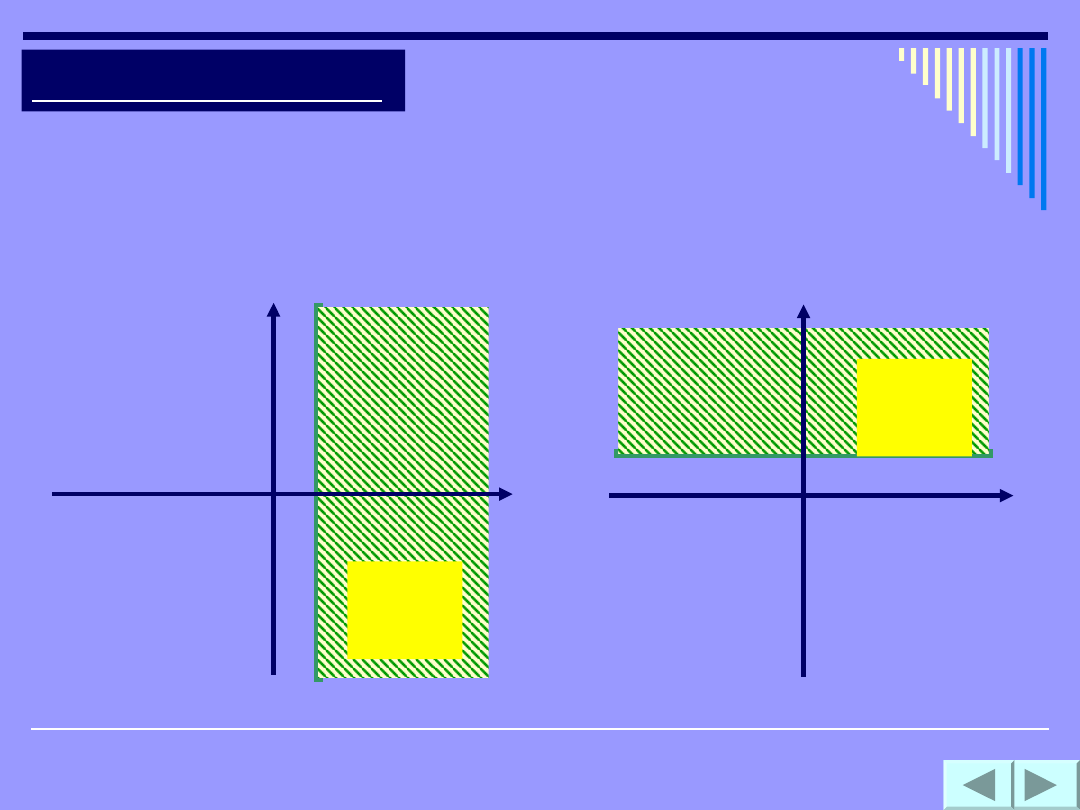
Jeżeli krawędź półpłaszczyzny jest
równoległa do jednej z osi to opisuje ją
jedna z czterech nierówności.

Półpłaszczyzna

x

y

x

y

półpłaszczyzna
domknięta

półpłaszczyzna
domknięta

x 

a

x=
a

y =
b

y 

b

© M

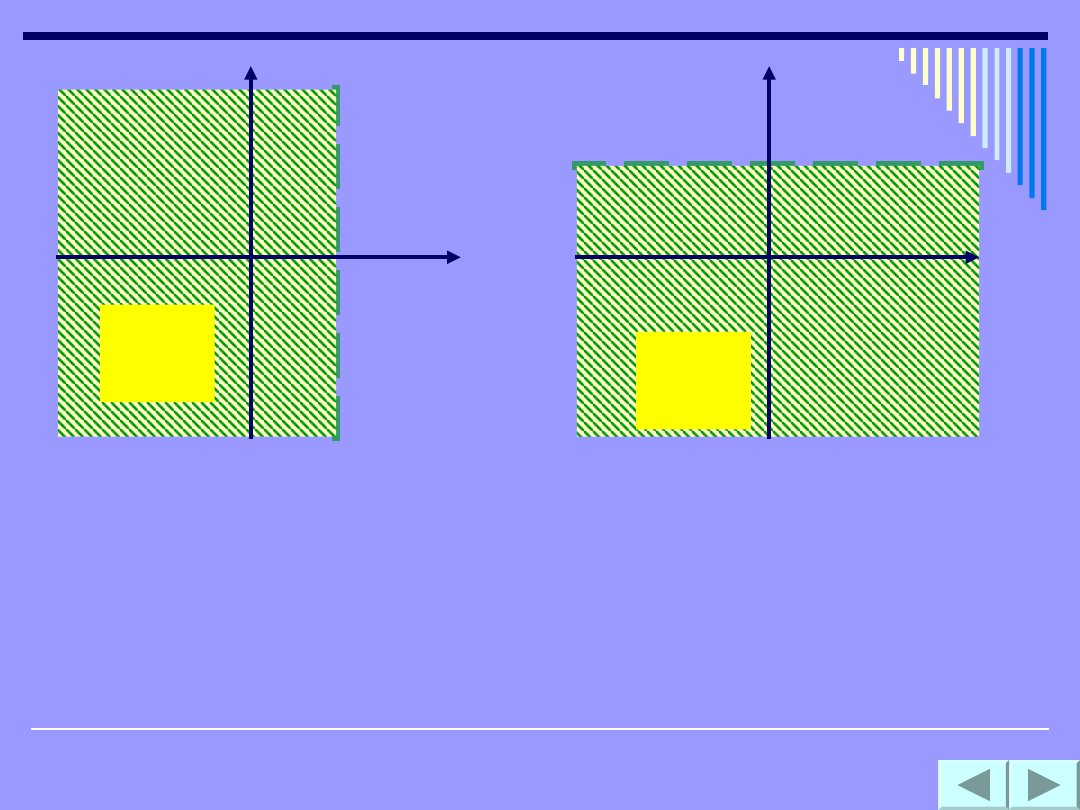
x

y

x

y

półpłaszczyzna otwarta

półpłaszczyzna otwarta

!!!

zwracaj zawsze uwagę na znak nierówności,

jeżeli nierówność jest słaba (



lub



) to

półpłaszczyzna jest domknięta, natomiast
nierówność mocna (< lub >) daje nam
półpłaszczyznę otwartą.

x = a

y =
b

x <
a

y <
b

© M

x

y

x

y

y=

3/

4x

+1

y

=

x

-1

y  x-

1

y=

3/

4x

+1

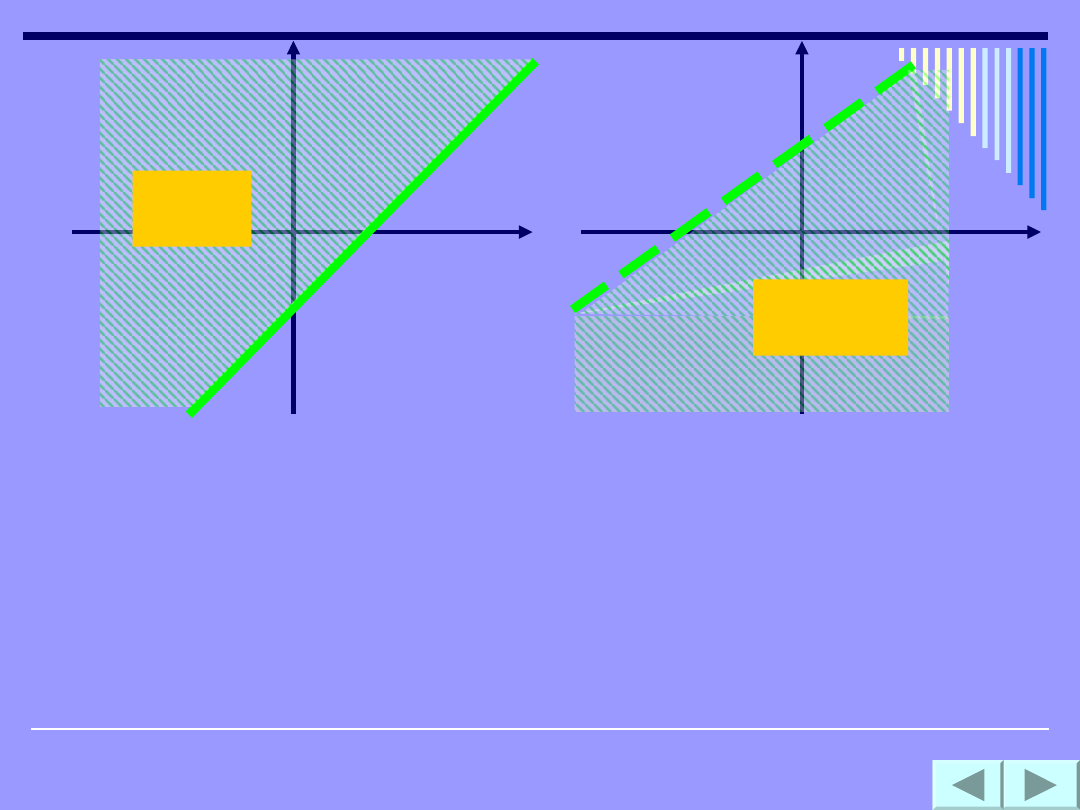
Prosta o równaniu Ax+By+C=0 jest wspólnym
brzegiem dwóch półpłaszczyzn domkniętych.
Jedną z tych półpłaszczyzn opisuje nierówność
Ax +By +C



0, a drugą – nierówność Ax+By

+C



0. Nierówności

Ax + By + C < 0,

Ax + By +C

> 0 opisują półpłaszczyzny otwarte.

Aby zaznaczyć właściwą półpłaszczyznę najwygodniej
sprowadzić prostą do postaci kierunkowej.

y <

3/4x+1

© M

y=

-x

+4

x

y

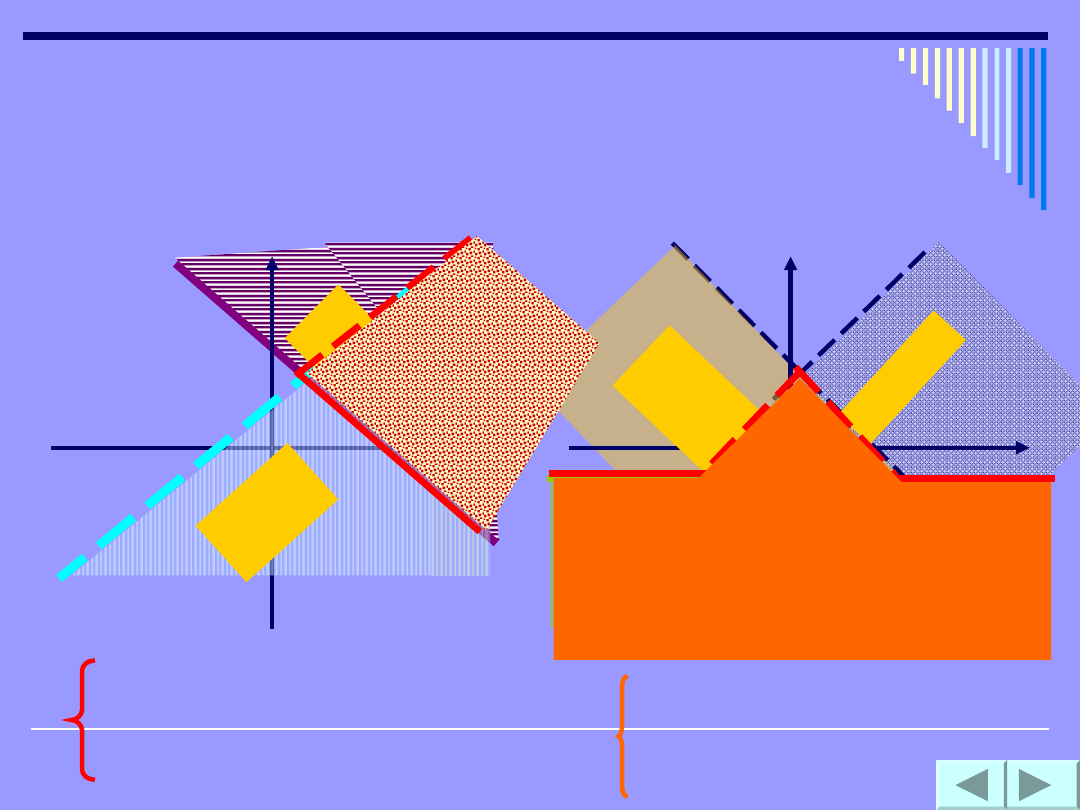
Jeśli chcemy opisać część wspólną pewnych
podzbiorów płaszczyzny, możemy to zrobić za
pomocą koniunkcji równań lub nierówności. Za
pomocą alternatywy możemy opisać sumę
zbiorów.

przykłady

y  -x

+ 4

y < x+2

x

y

y

=x

+2

y < -
x+2

y < x+2

lub y 

-1

y<

x+

2

y 

-x

+

4

y <

- x

+

2

y

<

x

+

2

y  -1

© M

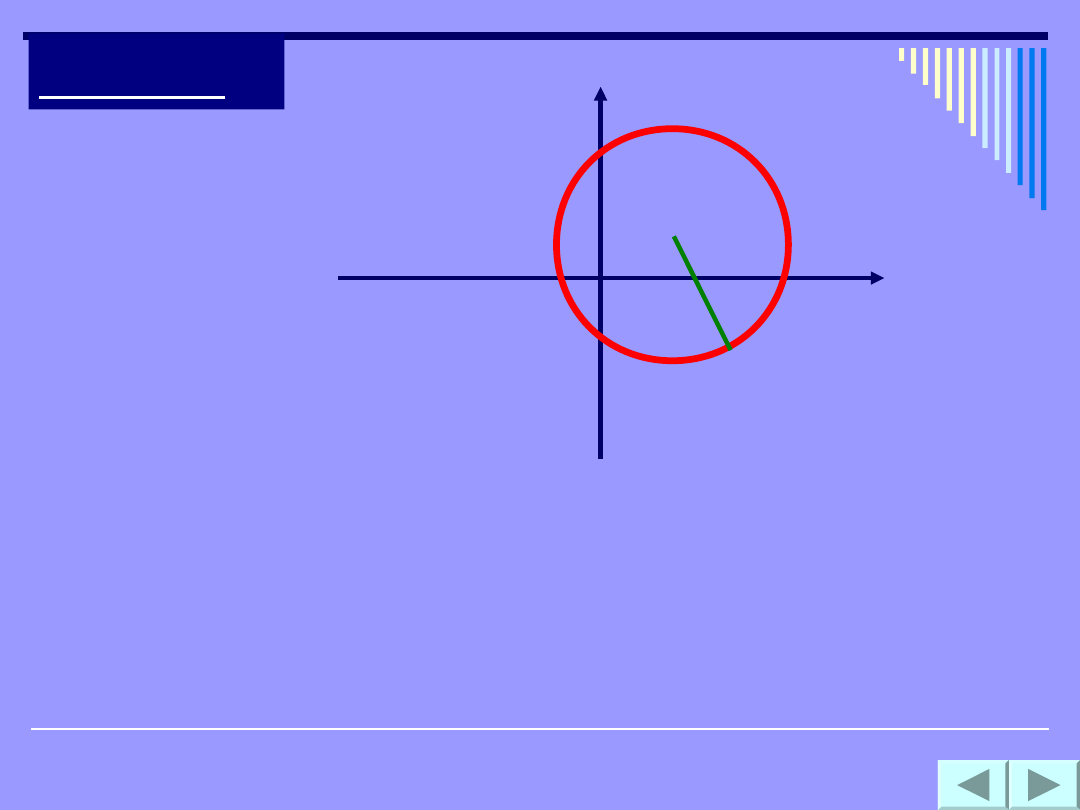
Okrąg

x

y

Równanie

(x - a)

2

+ (y - b)

2

= r

2

opisuje na płaszczyźnie kartezjańskiej
okrąg o środku S(a ,b) i promieniu r.

.

.

S(a,b)

r

.

P(x,y)

© M

Równanie ogólne okręgu

x

2

+ y

2

- 2ax - 2 by + c = 0

Przykład

Znaleźć współrzędne środka i długość promienia

okręgu danego wzorem

x

2

– 4x + y

2

+ 2y - 20 = 0

Sprowadzimy równanie do postaci

(x - a)

2

+ (y - b)

2

= r

2

© M

Dopełniamy w tym celu wyrażenia
po lewej stronie równania do
kwadratów.

Do wyrażenia x

2

– 4x

trzeba dodać 4,

by uzyskać (x -2 )

2

.

Z kolei

do y

2

+2 y należy dodać 1

, by

otrzymać (y + 1)

2.

Skoro do lewej

strony równania dodaliśmy 4 i 1 to do
prawej również musimy je dodać.

x

2

– 4x + 4 + y

2

+ 2 y +1- 20 =

4 + 1

(x – 2 )

2

+ ( y + 1)

2

= 5 + 20

(x – 2 )

2

+ ( y + 1)

2

=

25

Jest to równanie okręgu o środku S(2,-1)

i promieniu 5.

© M

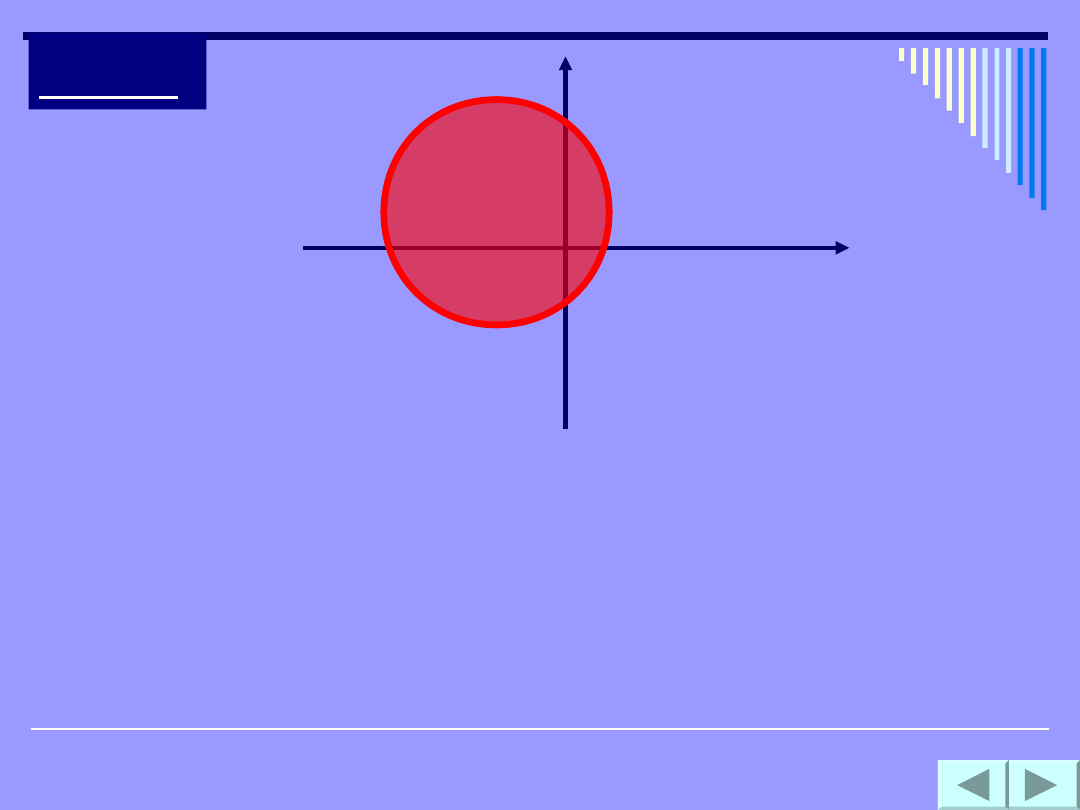
Koło

x

y

Nierówność

(x - a)

2

+(y - b)

2



r

2

opisuje na płaszczyźnie
kartezjańskiej koło o środku S(a,b)
i promieniu r.

.

S(a,b)

© M

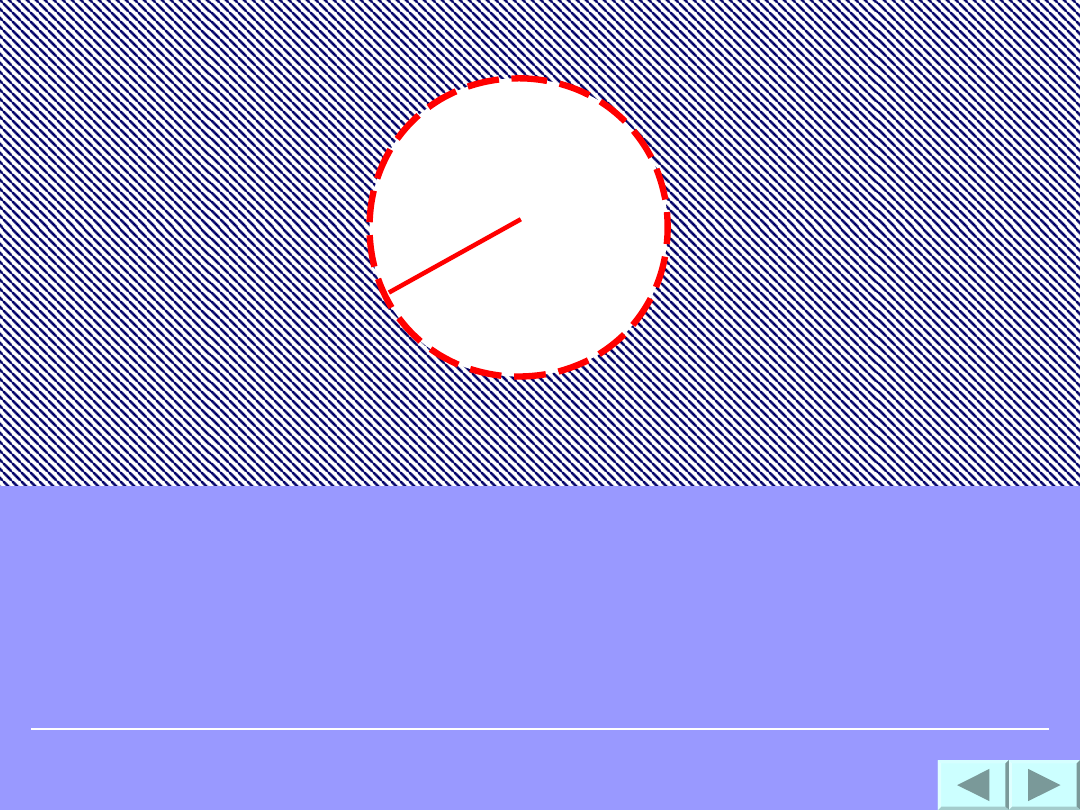
Nierówność

(x - a)

2

+(y - b)

2

> r

2

opisuje na płaszczyźnie kartezjańskiej zbiór
punktów leżących na zewnątrz koła o
środku S(a,b) i promieniu r.

.

S(a,b)

r

© M

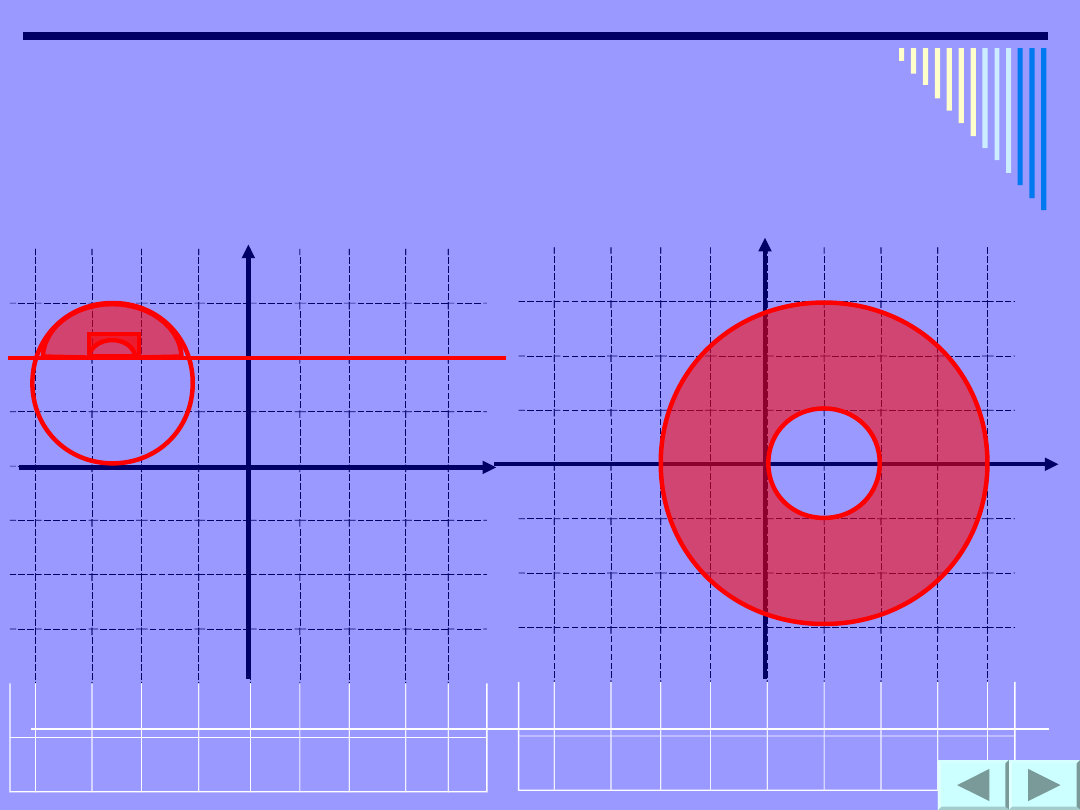
x

y

x

y

1

1

Zapisz, jakie warunki spełniają współrzędne
punktów należących do zaznaczonych
obszarów

zad1

zad2

1

1

© M

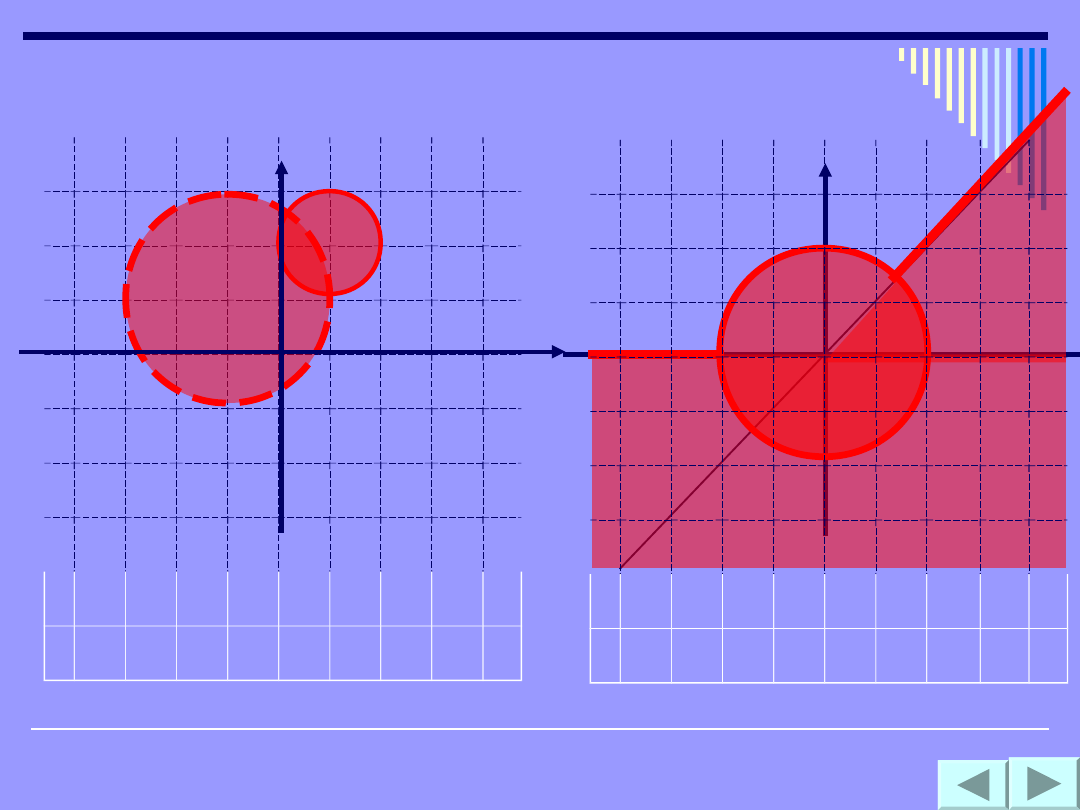
x

y

Zad3

Zad4

x

y

1

1

1

1

1

1

© M

Rozwiązania

Zad.1

y  2
(x + 2,5)

2

+ ( y - 1,5)

2

= 1,5

Zad.2

Zad.3

Zad.4

( x – 1 )

2

+ ( y – 1 )

2

 3

( x – 1 )

2

+ ( y – 1 )

2

 1

( x + 1 )

2

+ ( y – 1 )

2

< 2 lub ( x - 1 )

2

+

( y – 2 )

2

 1

x

2

+ y

2

 9 lub y  x lub y  0

© M

© M