Figury w układzie współrzędnych

Wiemy już, w jaki sposób przedstawiamy graficznie prostą w układzie współrzędnych. Dziś zajmiemy się prezentacją graficzną rozwiązania nierówności z dwiema niewiadomymi w układzie współrzędnych. Rozwiązaniem takiej nierówności nazywamy każdą parę liczb spełniających nierówność. Obrazem graficznym (wykresem) zbioru rozwiązań nierówności liniowej z dwiema niewiadomymi jest półpłaszczyzna o krawędzi określonej równaniem Ax + By + C = 0  (wraz z tą krawędzią, jeśli nierówność jest nieostra, lub bez krawędzi, jeśli nierówność jest ostra).

Przykładowe obrazy graficzne zbiorów rozwiązań nierówności liniowych z dwiema niewiadomymi przedstawiają rysunki:

 

W jaki sposób tworzymy taki wykres?

Przykład 1

Zaznacz rozwiązanie nierówności -x + y +2 > 0 w układzie współrzędnych.

Rozwiązanie

Przekształcamy daną nierówność do postaci, w której po jednej stronie znaku nierówności znajduje się tylko y, a po drugiej wszystkie pozostałe wyrażenia

-x + y +2 > 0

y > x - 2

Następnie „zamieniamy” otrzymaną nierówność na równanie

y = x - 2

i wykreślamy prostą opisaną otrzymanym równaniem.

Aby narysować prostą wybieramy dwie wartości x , np. x = 2 i x = 5, i wyznaczamy drugie współrzędne punktów (y)

x = 2 i x = 5

y = 2 - 2 y = 5 - 2

y = 0 y = 3

Otrzymane punkty (2,0) i (5, 3) zaznaczamy w układzie współrzędnych i rysujemy prostą.

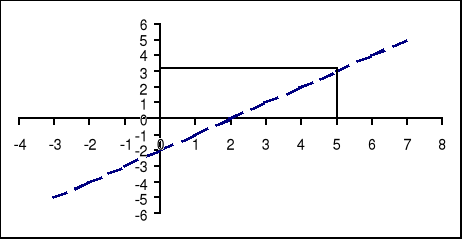
Kolejny krok to zaznaczenie tej części płaszczyzny, której punkty spełniają nierówność y > x - 2.

Rozwiązaniem tej nierówności jest więc zbiór par liczb (x, y) takich, że liczba y jest większa od liczby x. W naszym przypadku y = x - 2, więc x-2 ma być większe od x. Wybieramy np. punkt leżący poniżej narysowanej prostej o współrzędnych (7, -3) i sprawdzamy, czy jego współrzędne spełniają powyższy warunek,

tzn. x = 7 i -3 > 7 - 2

x = 7 i -3 >5.

Współrzędne tego punktu nie spełniają danego warunku. Podobnie będzie dla wszystkich punktów położonych poniżej narysowanej prostej.

W podobny sposób sprawdzamy jeden z punktów leżących powyżej prostej, np. (1, 5). Współrzędne tego punktu spełniają warunek. Wybierając kilka innych punktów również otrzymujemy nierówności prawdziwe. Zatem rozwiązaniem nierówności y > x - 2 jest obszar położony powyżej naszej prostej y = x - 2.

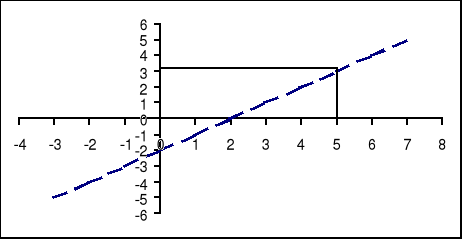
W szczególnych przypadkach nierówność z dwiema zmiennymi może stać się nierównością z jedną zmienną. Jest tak wtedy, gdy współczynniki przy zmiennych x lub y są równe zero. Na przykład, nierówność y > 0x + 2 przyjmuje postać y > 2, zaś nierówność 0y > x - 3 przyjmuje postać 3> x. W takich przypadkach rysowane proste są równoległe odpowiednio do osi Ox i Oy.

Przykład 2

Zaznacz rozwiązanie poniższych nierówności w układzie współrzędnych:

1. y > -3

2. x ≤ 2

Rozwiązanie

1. y > -3

Przekształcam nierówność w równanie y = - 3. W tym równaniu współczynnik przy zmiennej x jest równy 0, zatem niezależnie od wartości tej zmiennej, y zawsze będzie równy 3 (dla każdego punktu należącego do tej prostej, przy dowolnej wartości pierwszej współrzędnej z osi Ox, druga współrzędna będzie równa 3). Otrzymujemy zatem prostą równoległą do osi Ox.

y

x

-1

-2

-3 y = -3

Ponieważ mamy zaznaczyć rozwiązanie nierówności y > -3, więc rozwiązaniem są wszystkie te punkty płaszczyzny, dla których druga współrzędna jest większa od -3. Punktu te znajdują się powyżej zaznaczonej prostej. Ponieważ nierówność jest ostra, więc punkty leżące na prostej nie spełniają tej nierówności i dlatego prostą zaznaczamy linia przerywaną.

y

x

-1

-2

-3 y = -3

2. x ≤ 2

x = 2

W tym przypadku wartość x jest stała, a zmienia się wartość drugiej współrzędnej punktów. Otrzymujemy wówczas prostą równoległą do osi Oy.

y

2 x

Ponieważ rozwiązanie są wszystkie punkty płaszczyzny, których współrzędne spełniają nierówność x ≤ 2, zatem rozwiązaniem jest półpłaszczyzna złożona z punktów których pierwsza współrzędna jest mniejsza bądź równa 2 (stąd linia ciągła prostej)

y x = 2

2 x

Jeśli dwie nierówności, w których występuje ta sama zmienna połączymy w układ, wówczas rozwiązaniem układu są wszystkie punkty spełniające równocześnie obie nierówności, czyli część wspólna obu półpłaszczyzn.

Przykład 3

Zaznacz w układzie współrzędnych obszar opisany w następujący sposób: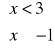

Rozwiązanie

W układzie występuje tylko jedna zmienna. Rozwiązaniem układu są wszystkie punkty, których pierwsza współrzędna jest jednocześnie mniejsza od 3 i większa lub równa -1. Można więc go zapisać w następującej postaci -1 ≤ x < 3. Postępując zatem podobnie jak w poprzednim przykładzie zaznaczamy odpowiednie proste i półpłaszczyzny w jednym układzie współrzędnych. Rozwiązaniem jest ta część płaszczyzny, która jednocześnie należ y do rozwiązania jednej i drugiej nierówności. W układzie współrzędnych, jako rozwiązanie, dostajemy pas pomiędzy prostą x = -1 (wraz z ta prostą) i prostą x = 3.

y

-1 1 2 3 x

Uwaga!

Gdy w nierównościach występuje tylko zmienna y, otrzymujemy pas równoległy do osi Ox.

Gdy układ zbudowany jest z nierówności (dwóch lub więcej), w których występują dwie zmienne, wówczas postępujemy tak jak w przykładzie 1, a wszystkie rozwiązania zaznaczamy w jednym układzie współrzędnych.

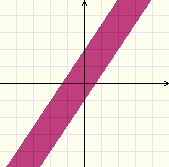
np.

lub łączymy metody z kilku przykładów

5

-5 5

-5

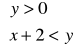
Rozwiązaniem jest ta część płaszczyzny, w której pokrywa się kolor pomarańczowy i zielony (czerwone bazgroły pomiędzy linią niebieską i czarną).

W powyższych przypadkach mieliśmy do czynienia z układem będącym koniunkcją nierówności. Bywa jednak tak, że mamy znaleźć rozwiązanie alternatywy nierówności liniowych. Rozwiązaniem takiego układu są wszystkie punkty spełniające jedną, drugą (lub trzecią) nierówność, czyli suma wszystkich półpłaszczyzn.

Przykład 4

Zaznacz w układzie współrzędnych obszar opisany następująco: -1 ≤ x < 2 lub -2 < y ≤ 2.

Rozwiązanie

W jednym układzie współrzędnych zaznaczamy rozwiązania podanych nierówności. Rozwiązaniem tej alternatywy jest cały „pas” powstały z nierówności ze zmienną x i cały „pas” powstały z nierówności ze zmienną y.

Jeżeli dany mamy opis graficzny układu nierówności, a określić mamy właśnie składniki tego układu, najpierw znajdujemy równania prostych ograniczających zaznaczony obszar, przekształcamy je w odpowiednie nierówności i zapisujemy w postaci koniunkcji nierówności lub ich alternatywy (w zależności od warunków jakie spełniają punkty zaznaczonego obszaru).

Przykład 5

Podaj nierówności opisujące poniższy obszar

Rozwiązanie

Ponieważ żadna z prostych ograniczających ten obszar (biały) nie jest równoległa do osi układu współrzędnych, więc mają one równania postaci y = ax + b.

Pierwsza prosta przecina oś y w punkcie (0,-3). Zatem przyjmuje ona postać y = ax - 3. Jej miejscem zerowym jest x = -3. Zatem współrzędne punktu (-3,0) muszą spełniać jej równanie,

tzn. 0 = a⋅ (-3) -3, skąd otrzymujemy a = -1. Mamy więc równanie pierwszej prostej y = -x - 3.

W celu wyznaczenie drugiego równania postępujemy analogicznie. Prosta przecina os y w punkcie (0,3), a miejscem zerowym jest x = 3. Stąd y = ax + 3 i 0 = a⋅ 3 +3. Zatem a = -1, a nasza prosta ma równanie postaci y = -x + 3.

Ponieważ przedstawiony obszar to pas między tymi prostymi, więc jest on prezentacją koniunkcji następujących nierówności y > -x - 3 (zamalowano obszar powyżej prostej) i y < - x + 3 (zamalowano obszar poniżej prostej). Zatem szukany układ to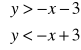
.

Ćwiczenie 1

Rozwiąż zadania:1- 4 str. 151 z podręcznika.

---