ALGORYTMY POSZUKIWANIA I

PORZĄDKOWANIA

ELEMENTY JĘZYKA PROGRAMOWANIA

Maciej M. Sysło

Uniwersytet Wrocławski

Uniwersytet UMK w Toruniu

[e-mail]

2

informatyka +

Algorytm, algorytmika

Algorytm

– opis rozwiązania krok po kroku

postawionego problemu lub sposobu
osiągnięcia jakiegoś celu

Pierwszy algorytm –

algorytm Euklidesa

300 p.n.e

algorytm

od

Muhammad

ibn Musa al-Chorezmi

IX w.

Algorytmika

– dziedzina zajmująca się algorytmami i

ich własnościami

informatyka +

3

Na str. 3-7 są zamieszczone
uwagi wstępne na temat
algorytmiki. Można je pominąć
i wrócić później.

Algorytmy a informatyka

Informatyka –

jedna z definicji:

dziedzina wiedzy i

działalności zajmująca się algorytmami

Czy zajmuje się też

algorytmami kulinarnymi?

Donald E. Knuth:

Mówi się często, że człowiek dotąd nie zrozumie czegoś,

zanim nie nauczy tego – kogoś innego.

W rzeczywistości,

człowiek nie zrozumie czegoś (

algorytmu

) naprawdę,

zanim nie zdoła nauczyć tego – komputera.

Ralf Gomory (IBM):

Najlepszym sposobem przyspieszania komputerów

jest obarczanie ich mniejszą liczbą działań (

szybszymi

algorytmami

)

informatyka +

4

Algorytmiczne rozwiązywanie problemu

Dla problemu – chcemy otrzymać rozwiązanie
komputerowe, które jest:

•

zrozumiałe

dla każdego, kto zna problemu

• poprawne

, czyli spełnia specyfikację (opis) problemu

• efektywne

, czyli nie marnuje czasu i pamięci

Metoda rozwiązywania:

•

analiza

sytuacji problemowej

•

sporządzenie

specyfikacji

: wykaz danych, wyników i relacji

• projekt

rozwiązania

•

komputerowa realizacja rozwiązania –

implementacja

• testowanie poprawności

rozwiązania

•

dokumentacja

i

prezentacja

rozwiązania

informatyka +

5

Rozwiązywanie problemów z pomocą
komputerów

Objaśnienie dwóch terminów:

Problem

:

•problem, gdy nie podano nam, jak należy go rozwiązać, ale wiemy
wystarczająco, by poradzić sobie z nim
•a więc, problem jest dla każdego

nie tylko dla orłów

Programowanie

:

•komputery wykonują tylko programy
•cokolwiek uruchamiamy na komputerze: Google, dokument w
Word, arkusz w Excel, naciśnięcie klawisza – jest programem
•każdy widoczny i niewidoczny efekt działania komputera to wynik
działania jakiegoś programu

Konkluzja:

powinniśmy

lepiej poznać programowanie

komputerów

informatyka +

6

Myślenie algorytmiczne
Myślenie komputacyjne
(ang. computational thinking)

informatyka +

7

Reklama firmy

IBM z 1924 roku

Komputer to

maszyna do myślenia

!!!

Poszukiwanie, porządkowanie,
elementy programowania
PLAN

• Rozgrzewka (warm-up) – kilka krótkich programów
• Przeszukiwanie zbioru – Min i Max: schematy

blokowe, pierwsze programy, złożoność algorytmu,

• Kompletowanie podium zwycięzców turnieju
• Jednoczesne znajdowanie najmniejszego i

największego elementu

• Porządkowanie przez wybór – iteracja algorytmu
• Porządkowanie przez zliczanie
• Poszukiwanie informacji w zbiorach

nieuporządkowanych i uporządkowanych

• Dziel i zwyciężaj, rekurencja: sortowanie przez

scalanie i sortowanie szybkie

informatyka +

8

Rozgrzewka przy komputerach

Rozgrzewka (warm-up)

– kilka krótkich programów:

• obliczanie pole trójkąta
• dodatkowo sprawdzanie, czy dane są dobre –

warunek

• obliczanie pola trójkąta dla ciągu danych –

iteracja

i

tablice

Ciekawe zadanie

dotyczące trójkątów:

Dane:

ciąg (bardzo długi) liczb

Odpowiedź:

czy z każdej trójki liczb z tego ciągu można

zbudować trójkąt?

Wskazówka:

istnieje rozwiązanie, w którym nie trzeba

sprawdzać warunku trójkąta dla każdej trójki liczb

informatyka +

9

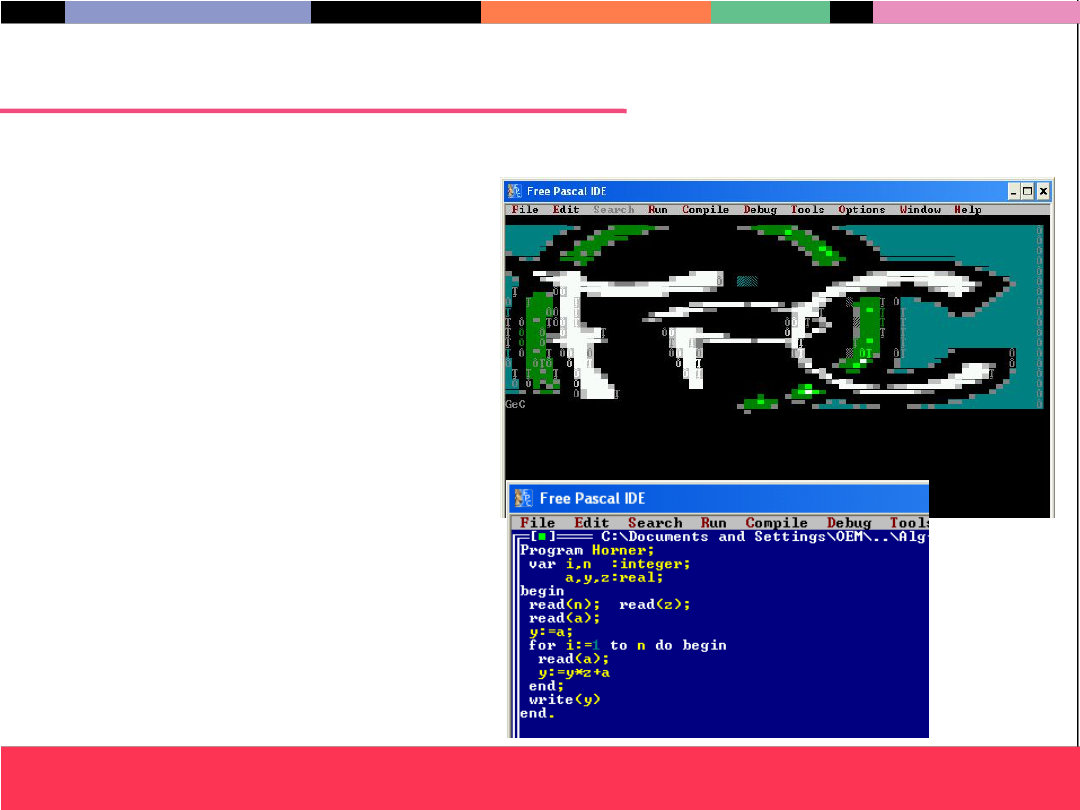
Warsztaty
Algorytm, język programowania, komputer

informatyka +

10

Proces komputerowej
realizacji algorytmu:

•Opis algorytmu – słowny
•Zapis w języku
programowania (Pascal, C++)
•Kompilacja –
przetłumaczenie na język
zrozumiały przez komputer
•Wykonanie
•Testowanie
•Dokumentacja

Znajdowanie elementu w zbiorze

Znajdź element w zbiorze:

• najwyższego ucznia

w swojej klasie –

metoda spaghetti

• jak zmieni się Twój algorytm, jeśli chciałbyś znaleźć w klasie

najniższego ucznia

• znajdź w swojej klasie ucznia, któremu droga do szkoły zabiera

najwięcej czasu

• znajdź

najstarszego

(lub

najmłodszego

) ucznia w swojej szkole

• znajdź

największą kartę

w potasowanej talii kart

• znajdź

najlepszego tenisistę

w swojej klasie – nie ma remisów

• znajdź

najlepszego gracza w warcaby

w swojej klasie –

możliwe są

remisy

Podstawowa operacja –

porównanie

:

• dwóch liczb lub kombinacji liczb (data, karty):

czy x < y ?

• dwóch zawodników:

rozegranie meczu

informatyka +

11

Specyfikacja problemu

Specyfikacja problemu

– dokładne opisanie problemu

Problem Min

– Znajdowanie najmniejszego elementu w zbiorze

Dane:

Liczba naturalna n i zbiór n liczb dany w ciągu x

1

, x

2

, ..., x

n

Wynik:

Najmniejsza wśród liczb x

1

, x

2

, ..., x

n

– oznaczmy ją

min

Metoda rozwiązania:

przeszukiwanie liniowe –

od lewej do prawej

Algorytm Min

– Znajdowanie najmniejszego elementu w zbiorze

Krok 1.

Przyjmij za min pierwszy element w zbiorze (w ciągu),

czyli przypisz min := x

1

.

Krok 2.

Dla kolejnych elementów x

i

, gdzie i = 2, 3, ..., n,

jeśli min > x

i

, to przypisz min := x

i

.

Algorytm Max

– prosta modyfikacja: zamiana > na <

Wyznaczanie

imin

– indeksu elementu o wartości

min

informatyka +

12

imin

:= 1

imin

:=

i

Algorytm Min – demo

Demonstracja przeszukiwania od lewej do prawej:

informatyka +

13

(Zgrubny) schemat blokowy algorytmu Min

informatyka +

14

Instrukcja iteracyjna

Instrukcje

warunkowe:

rozgałęzienia

algorytmu

Ada Augusta,

córka Byrona,

uznawana powszechnie za pierwszą
programistkę komputerów,
przełomowe znaczenie

maszyny

analitycznej Ch. Babbage’a

,

pierwowzoru dzisiejszych
komputerów, upatrywała właśnie „

w

możliwości wielokrotnego
wykonywania przez nią danego ciągu
instrukcji, z liczbą powtórzeń z góry
zadaną lub zależną od wyników
obliczeń

”, a więc w

iteracji

.

Krok
1:

Krok
2:

min ← pierwszy
element
ze zbioru A

Czy porównano

wszystkie elementy ze

zbioru A ?

Nie

min >
x ?

Tak

x ← kolejny
element
ze zbioru A

Tak

min ←
x

Nie

Koniec

algorytmu

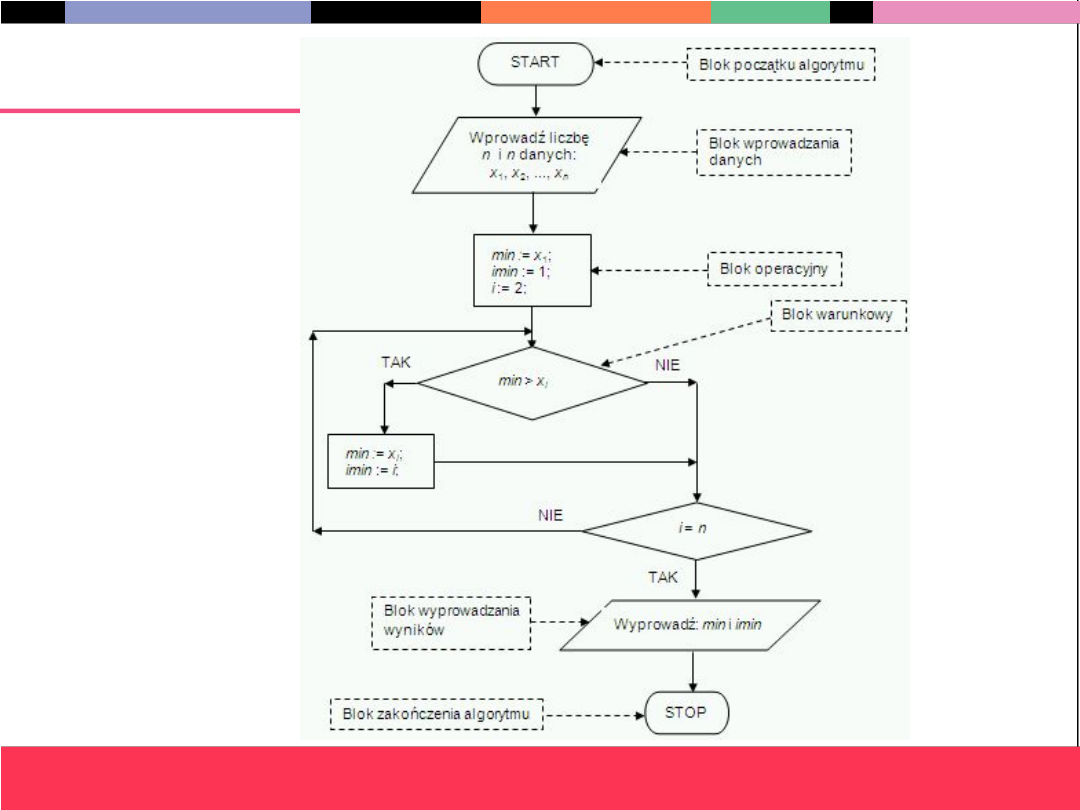
Pełny
schemat
blokowy
algorytmu
Min

informatyka +

15

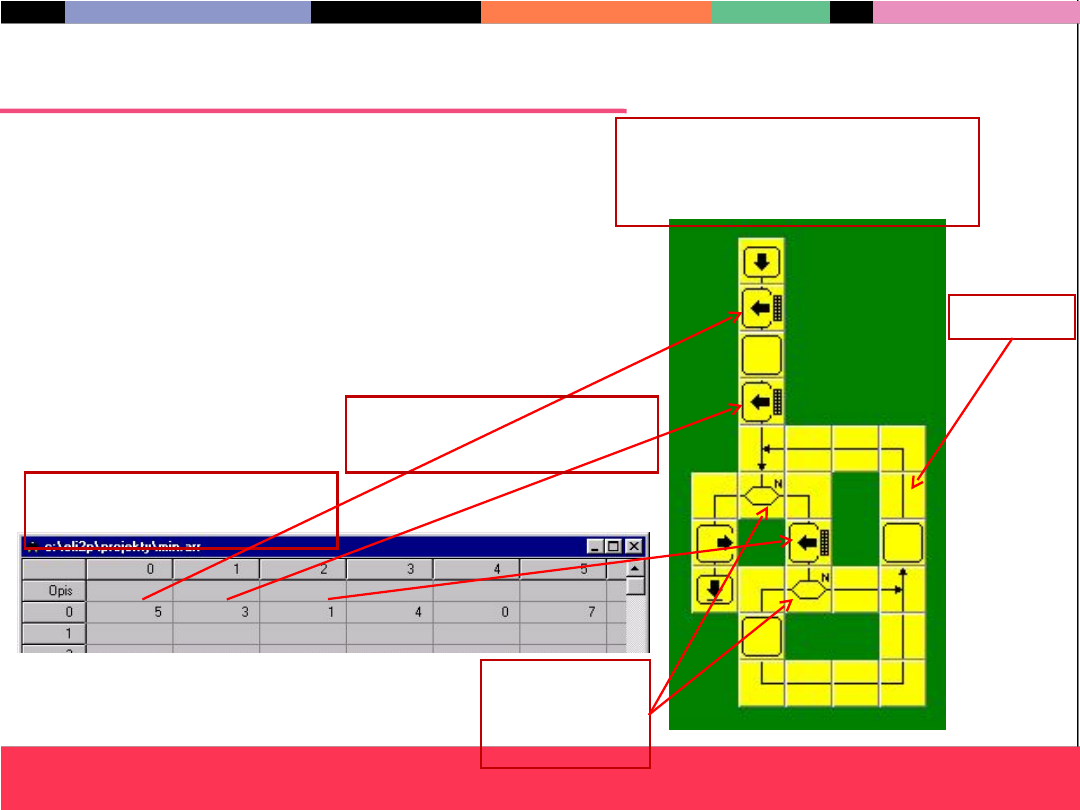
Skomputeryzowany schemat blokowy

informatyka +

16

Schemat blokowy
wykonany w programie
ELI

Ciąg (tablica) z
danymi

Bloki
warunkow
e

Iteracja

Wprowadzanie
danych

Algorytm Min w postaci programu

Program w języku Pascal

program Min;
var i,imin,min,n,x:integer;
begin
read(n);
read(x); min:=x; imin:=1;
for i:=2 to n do begin
read(x);
if min > x then begin
min:=x; imin:=i
end

end;
write(imin,min)
end.

informatyka +

17

nazwa programu
deklaracje, typy

zmiennych

blok programu –

początek

czytaj n
czytaj pierwszy element
iteracja

od 2 do n

czytaj kolejny element

instrukcja warunkowa

popraw min
instrukcja war. – koniec

iteracja – koniec
pisz wynik
blok programu – koniec

Pracochłonność algorytmu Min

• Porównanie

– podstawowa operacja w algorytmie Min.

•Pracochłonność (złożoność obliczeniowa) algorytmu

–

liczba podstawowych operacji wykonywanych przez
algorytm.

• Pytanie:

Ile porównań wykonuje algorytm Min?

• Odpowiedź:

o jedno mniej niż jest elementów, czyli

n

– 1

Pytania:

•

Czy można szybciej?

• Czy istnieje szybszy algorytm znajdowania min?
•A może

metoda pucharowa

wyłaniania zwycięzcy w turnieju

jest szybsza?

informatyka +

18

Wyłanianie najlepszego zawodnika w turnieju
czyli inny sposób znajdowania max (lub min)

informatyka +

19

Barte
k

Rome
k

Bolek

Witek Tome

k

Zene
k

Tolek

Felek

Barte
k

Witek

Tome
k

Tolek

Barte
k

Tome
k

Tome
k

Porównania –
mecze

Ośmiu zawodników: 7

meczy

n zawodników: n – 1 meczy

a więc nie jest szybsza

A może mamy algorytm najlepszy?

Podsumowanie:

Mamy dwa algorytmy znajdowania min lub max:
•

przeszukiwanie liniowe

• rozegranie turnieju

które na zbiorze n elementów wykonują n – 1 porównań

Może nie ma szybszego algorytmu?

TAK! Hugo Steinhaus

tak to uzasadnił:

Jeśli Tomek jest zwycięzcą turnieju, w którym startuje n
zawodników, to każdy inny spośród n – 1 zawodników musiał
przegrać przynajmniej raz, a zatem rozegrano przynajmniej n –
1 meczy. Zatem każdy algorytm musi wykonać przynajmniej n
– 1 porównań, czyli nasze algorytmy są najszybsze –

są

optymalne.

informatyka +

20

A jak znaleźć drugiego najlepszego
zawodnika w turnieju?

informatyka +

21

Barte
k

Rome
k

Bolek

Witek Tome

k

Zene
k

Tolek

Felek

Barte
k

Witek

Tome
k

Tolek

Barte
k

Tome
k

Tome
k

Czy jest nim

Bartek?

Bo przegrał z
Tomkiem?

Ale Bartek nie
grał z drugą
połową!

???

???

Tylko dwa
dodatkowe
mecze!

3 1 2 2 5 3 4 8 2 5

Jednoczesne znajdowanie min i max

informatyka +

22

Obserwacja:

jeśli x  y, to x kandydatem na min, a y kandydatem na

max

Algorytm „dziel i zwyciężaj”:

Krok 1. Podział

na kandydatów na min i kandydatów na

max

Kandydaci na
max

Kandydaci na
min

max =
8

min = 1

Krok 2.

Znajdź min i max

Liczba porównań:

•

algorytm

naiwny

: n – 1 (min) + n – 2 (max) = 2n – 3

• algorytm

dziel i zwyciężaj

: n/2(podział)+ (n/2–1)(min) + (n/2–1)

(max)

ok. 3n/2 – 2 – jest to

algorytm optymalny

Porównania
parami

3

↑

3 ? 1

↓

1

2

↑

2 ? 2

↓

2

5

↑

5 ? 3

↓

3

8

↑

4 ? 8

↓

4

5

↑

2 ? 5

↓

2

Problem porządkowania (sortowania)

Problem porządkowania (sortowania)

Dane:

Liczba naturalna n i ciąg n liczb x

1

, x

2

, ..., x

n

Wynik:

Uporządkowanie tego ciągu liczb od najmniejszej do

największej

Algorytm: porządkowanie przez wybór – Selection Sort

Idea:

najmniejszy wśród nieuporządkowanych daj na

początek

Krok 1.

Dla i = 1, 2, ..., n – 1 wykonaj kroki 2 i 3, a następnie

zakończ algorytm

Krok 2.

Znajdź k takie, że x

k

jest najmniejszym elementem w

ciągu x

i

, ..., x

n

Krok 3.

Zamień miejscami elementy x

i

oraz x

k

informatyka +

23

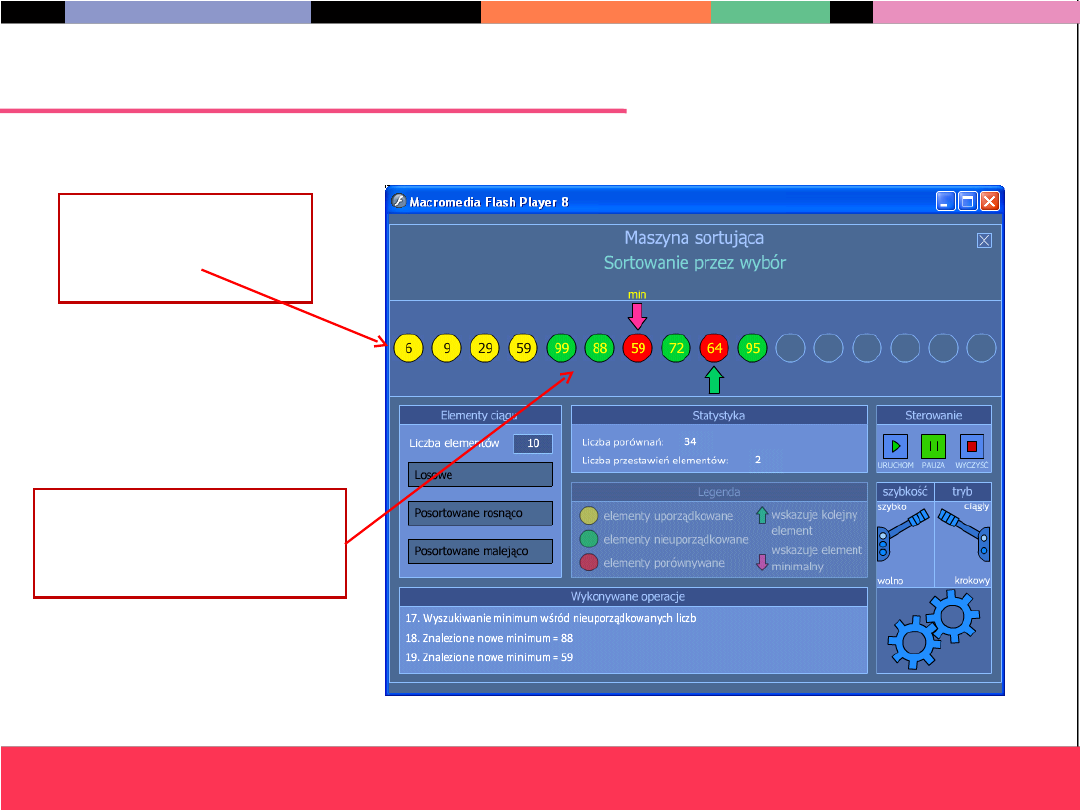
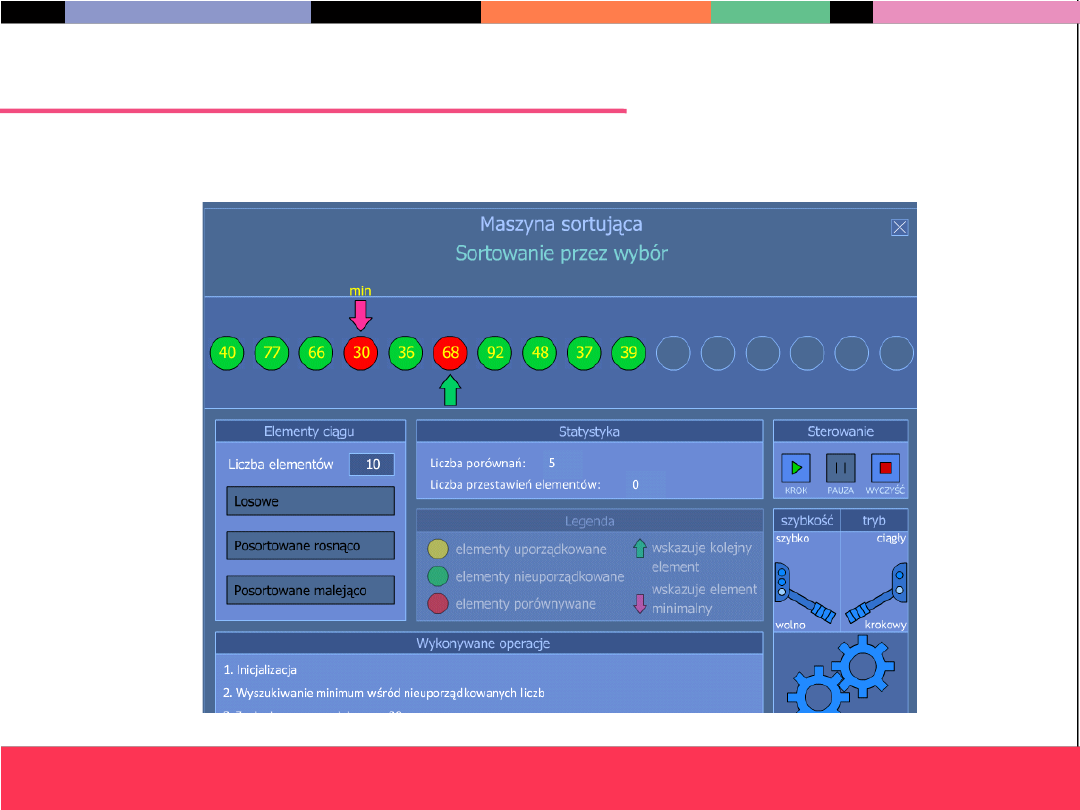
Porządkowanie przez wybór – demo (1)

informatyka +

24

Żółte – podciąg
już
uporządkowany

Zielone i czerwone –
podciąg
porządkowany

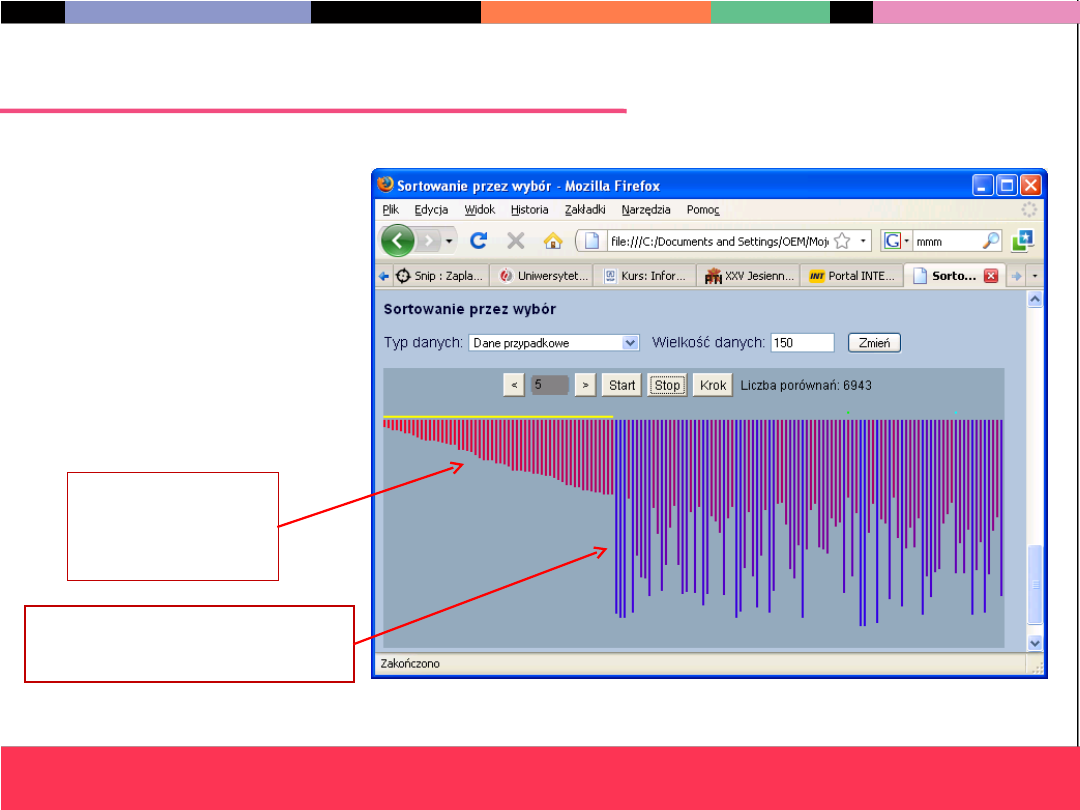
Porządkowanie przez wybór – demo (2)

informatyka +

25

Podciąg już
uporządkowa
ny

Podciąg
porządkowany

Złożoność porządkowania przez wybór

Liczba

zamian

elementów w kolejnych krokach:

1 + 1 + 1 + … + 1 = n – 1

Liczba

porównań

w kolejnych krokach:

(n – 1) + (n – 2) + (n – 3) + … + 3 + 2 + 1 = ?

informatyka +

26

5













4













3













2













1













Przykład

n = 6

6 =
n

5 = n –
1

Pole prostokąta: 5 x 6

Suma = pole czarnych

diamentów:

5 x 6

2

Ogólnie suma:

(n – 1) x n

2

Liczby trójkątne

Porządkowanie przez zliczanie

Problem porządkowania niewielkich liczb

Dane:

Liczba naturalna n i ciąg n liczb całkowitych x

1

, x

2

, ..., x

n,

należących do przedziału [1..M] – na ogół n < M.

Wynik:

Uporządkowanie tego ciągu liczb od najmniejszej do

największej

Algorytm. Porządkowanie przez zliczanie – CountingSort

Idea:

Liczymy, ile jest konkretnych liczb w ciągu

Krok 1.

Dla i = 1, 2, ..., M: c

i

= 0 zerowanie liczników.

Krok 2.

Dla i = 1, 2, ..., n: zwiększ c

k

o 1, gdzie k = x

i

.

Krok 3.

Dla i = 1, 2, ..., M: na kolejnych c

i

pozycjach w ciągu x

umieść element i.

Liczba operacji

– proporcjonalna do n + M.

informatyka +

27

Poszukiwanie elementu w zbiorze

Problem poszukiwania elementu w zbiorze

Dane:

Zbiór elementów w postaci ciągu n liczb x

1

, x

2

, ..., x

n

.

Wyróżniony element y

Wynik:

Jeśli y należy do tego zbioru, to podaj jego miejsce

(indeks) w ciągu, a w przeciwnym razie – sygnalizuj brak
takiego elementu w zbiorze

Dwa przypadki:

• Nieuporządkowany

ciąg liczb x

1

, x

2

, ..., x

n

• Uporządkowany

ciąg liczb x

1

, x

2

, ..., x

n

Nasz cel:

Jakie są

korzyści z uporządkowania

?

Jak

utrzymywać porządek

wśród informacji?

informatyka +

28

– wstaw y do ciągu

Poszukiwania w zbiorze nieuporządkowanym

Algorytm – Poszukiwanie liniowe

Krok 1.

Dla i = 1, 2, ..., n, jeśli x

i

= y, to przejdź do kroku 3.

Krok 2.

Komunikat: W ciągu danych nie ma elementu

równego y. Zakończ algorytm: –

wynik: –1

Krok 3.

Element równy y znajduje się na miejscu i w ciągu

danych. Zakończ algorytm:

wynik: i

begin
i:=1;
while (x[i]<>y) and (i<n) do i:=i+1;
if x[i]=y then PrzeszukiwanieLiniowe:=i
else PrzeszukiwanieLiniowe:=-1
end

informatyka +

29

Pewna
niedogodność –
sprawdzanie, czy
koniec ciągu.

Poszukiwania w zbiorze nieuporządkowanym
z wartownikiem

Algorytm – Poszukiwanie liniowe z wartownikiem

Takie same kroki algorytmu

inna implementacja

, czyli

komputerowa realizacja:

na końcu ciągu:

x

1

x

2

x

3

x

4

… x

n

begin
i:=1;
x[n+1]:=y;
while x[i]<>y do i:=i+1;
if i<=n then PrzeszukiwanieLinioweWartownik:=i
else PrzeszukiwanieLinioweWartownik:=-1
end

informatyka +

30

wstawiamy
wartownika – pilnuje
końca ciągu

x

n+1

Nie ma sprawdzania, czy
koniec ciągu, bo
przeszukiwanie zawsze
zatrzyma się na elemencie y.

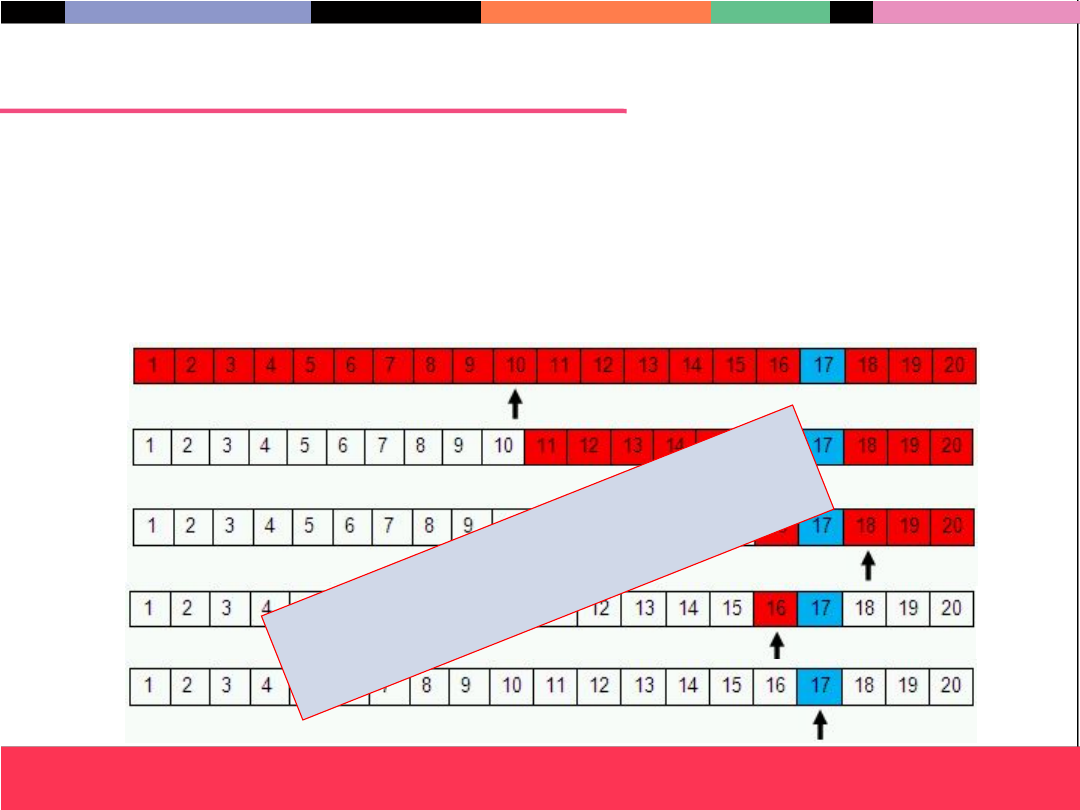
Poszukiwanie w zbiorze uporządkowanym
Zabawa w zgadywanie liczby

informatyka +

31

Zgadywana liczba:

17

w przedziale [1 : 20]

Metoda:

połowienia przedziału

Kolejne kroki:

strzałka wskazuje wybór;

kolor czerwony

– ciąg do przeszukania:

5 p

oró

wn

ań

zam

ias

t

20

!!!

Poszukiwanie przez połowienie

w ciągu uporządkowanym

function PrzeszukiwanieBinarne(x:tablicax; k,l:integer;

y:integer):integer;

{Przeszukiwanie binarne ciagu x[k..l] w poszukiwaniu

elementu y.}

var Lewy,Prawy,Srodek:integer;
begin
Lewy:=k; Prawy:=l;
while Lewy<=Prawy do begin
Srodek:=(Lewy+Prawy) div 2;
if x[Srodek]=y then begin
PrzeszukiwanieBinarne:=Srodek; exit
end; {element y nalezy do przeszukiwanego ciagu}
if x[Srodek]<y then Lewy:=Srodek+1
else Prawy:=Srodek-1
end;
PrzeszukiwanieBinarne:=-1
end

informatyka +

32

Połowienie
przedziału

Początkowe końce
przedziału

Zmiana końców
przedziału

y nie należy do
przeszukiwanego
przedziału

y należy do
przedziału

Dane:

Uporządkowany ciąg liczb w tablicy x[k..l]

oraz element y

Wynik:

Miejsce dla y w ciągu x[k..l] takie, aby po

wstawieniu y ciąg nadal był uporządkowany

Algorytm:

y wstawiamy do przeszukiwanego ciągu w to

miejsce, gdzie algorytm poszukiwania kończy
działanie, a więc tam, gdzie jest y (jeśli y jest już
w ciągu), albo gdzie powinien być.

informatyka +

33

Umieszczanie przez połowienie

w ciągu uporządkowanym

Liczba kroków w algorytmie połowienia:

Ile razy należy przepołowić ciąg o danej długości, aby znaleźć
element lub miejsce dla niego?

Przykład dla

n = 1200

Kolejne długości ciągu:

1200, 600, 300, 150, 75, 38, 19, 10, 5, 3, 2, 1

11

razy dzielono ciąg o długości 1200, by pozostał 1 element

Liczba porównań w algorytmach poszukiwania dla n =
1200:

• przez połowienie 11

• liniowy

1200

informatyka +

34

Poszukiwanie przez połowienie –
złożoność

Porównaj, jaka jest

potęga

uporządkowania !!!

Dla

n = 1200

liczba porównań w algorytmie połowienia

wyniosła

11

Pytania:

•Jak liczba porównań zależy od n?
•Jak dobry jest to algorytm?

Liczba porównań dla różnych n:

informatyka +

35

Poszukiwanie przez połowienie
złożoność – dla orłów

n liczba
porównań

100

7

1000

10

10000

14

100000

17

1000000

20

10000000

24

ok.log

2

n

Funkcja logarytm

,

bardzo ważna w
algorytmice

logarytm

to anagram od

algorytm

Algorytm poszukiwania
przez połowienie jest
optymalny, czyli
najszybciej przeszukuje
zbiory uporządkowane.

Jednoczesne znajdowanie min i max

pełny algorytm dziel i zwyciężaj

informatyka +

36

Algorytm Min-i-Max-Rek

(Z,min,max)

Dane:

Zbiór liczb Z

Wyniki:

min – najmniejszy element w zbiorze

Z

max – największy element w zbiorze Z

Krok 1.

Jeśli Z = {a}, to min := a; max := a

Jeśli Z = {a, b}, to min := min {a, b}; max := max

{a, b}

Krok 2.

Gdy Z ma więcej niż dwa elementy, to:

2a.

Podziel zbiór Z na dwa podzbiory Z

1

i Z

2

2b.

Min-i-Max-Rek

(Z

1

,min

1

,max

1

)

2c.

Min-i-Max-Rek

(Z

2

,min

2

,max

2

)

2d.

min := min {min

1

, min

2

}; max := max {max

1

,

max

2

}

Rekurencyjn
e wywołania
na
podzbiorach

Jednoczesne znajdowanie min i max

pełny algorytm dziel i zwyciężaj
DEMO

informatyka +

37

1 4 5 2 4 9 7

3

1 4 5 2

4 9 7 3

dziel

dziel

1 4

5 2

dziel

4 9

7 3

(1 ,4)

(2, 5)

(4, 9)

(3, 7)

(min,
max)

(1, 5)

(3, 9)

(1, 9)

Sortowanie przez scalanie – scalanie

informatyka +

38

Scalanie

– z dwóch uporządkowanych ciągów utwórz

jeden uporządkowany

Algorytm scalania. Scal.
Dane:

dwa ciągi uporządkowane

Wynik:

scalony ciąg uporządkowany

Krok:

do tworzonego ciągu pobieraj najmniejszy
element z czoła scalanych ciągów

1 3 5 7 10 12

1 2 6 9 11 15 17
20

1 3 5 7 10 12
1 2 6 9 11 15
17 20

Scalane ciągi

Scalani
e

1 1 2 3 5 6 7 9 10 11 12 15
17 20

Scalony
ciąg

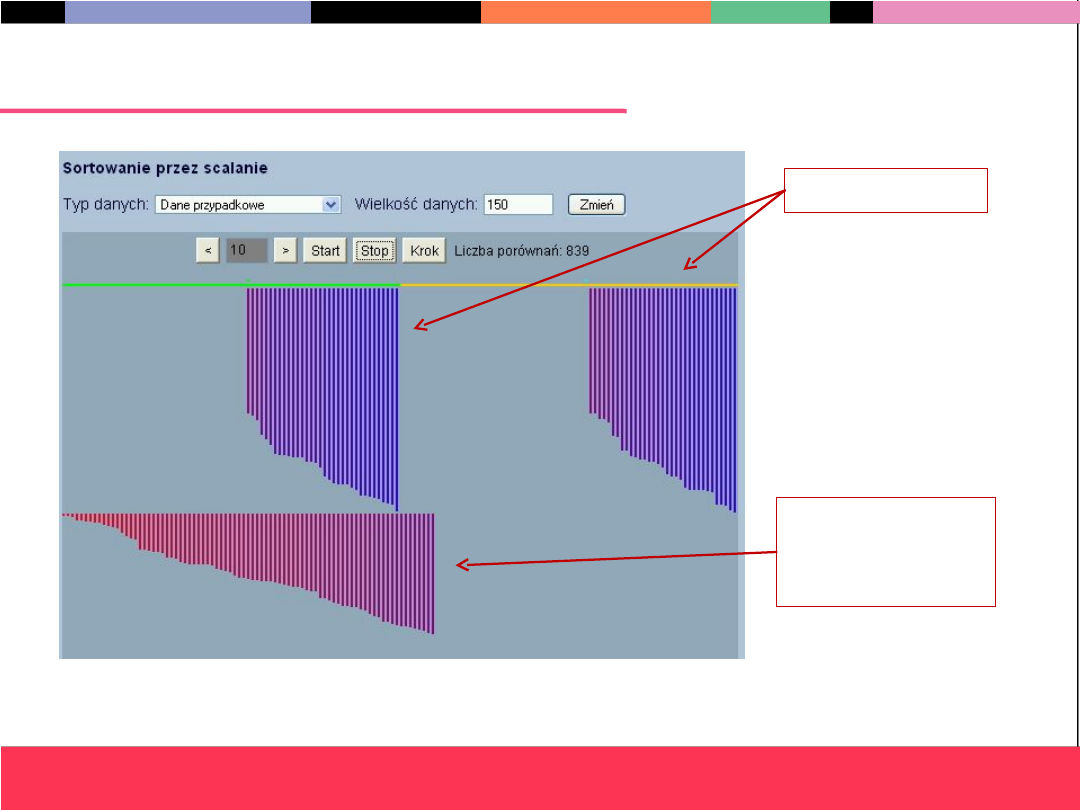
Sortowanie przez scalanie – scalanie

informatyka +

39

Scalane ciągi

Scalone ciągi,
w innym
miejscu

informatyka +

40

Algorytm porządkowania przez scalanie MergeSort

(l,p,x)

Dane:

Ciąg liczb x

l

, x

l+1

, …, x

p

Wynik:

Uporządkowanie tego ciągu liczb od najmniejszej

do największej.

Krok 1.

Jeśli l < p, to przyjmij s:=(l+p) div 2 i wykonaj trzy

następne kroki.

Krok 2.

MergeSort

(l,s,x) – sortowanie pierwszej połowy

ciągu

Krok 3. MergeSort

(s+1,p,x) – sortowanie drugiej połowy

ciągu

Krok 4.

Zastosuj algorytm

Scal

do ciągów (x

l

, …, x

s

) i (x

s+1

,

…, x

p

) i wynik umieść w ciągu (x

l

, …, x

p

).

Rekurencyjn
e wywołania
na
podciągach

Sortowanie przez scalanie – opis

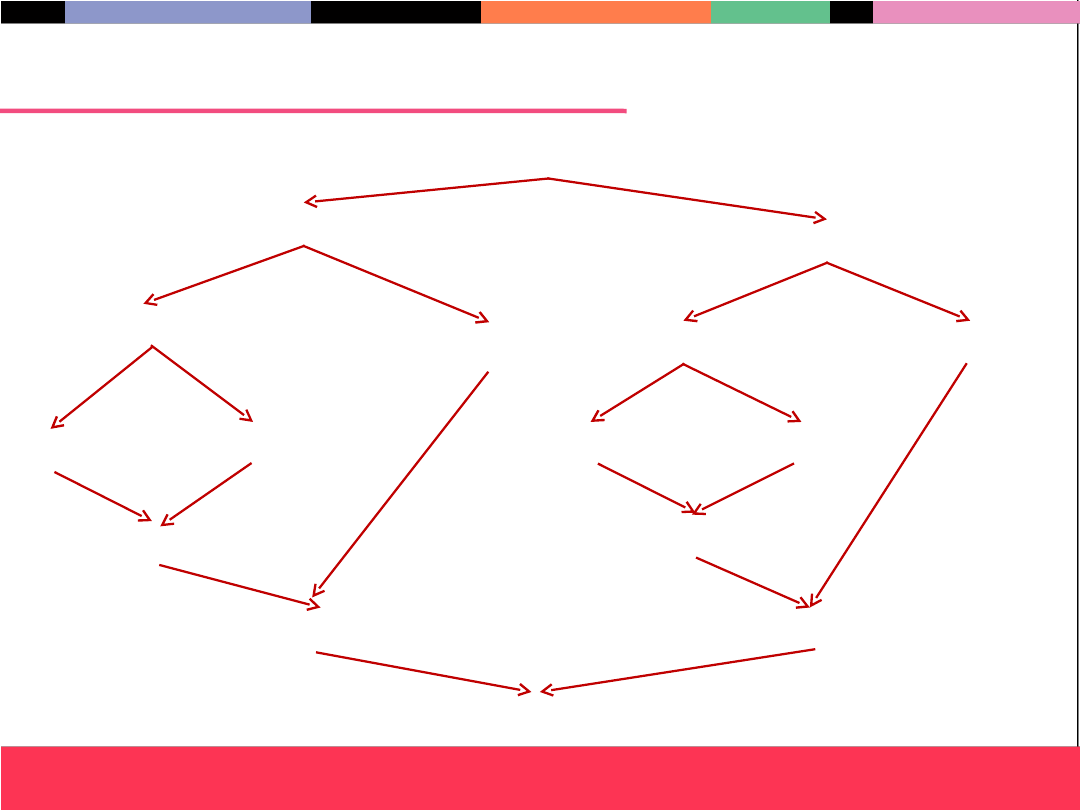
informatyka +

41

2 1 2 9 5 0

2 1 2

9 5 0

dziel

dziel

2 1

dziel

9

0

1 2

9 5

1 2 2

0 5 9

0 1 2 2 5

9

Sortowanie przez scalanie
DEMO

dziel

2

1

2

scal

scal

scal

scal

scal

5

dziel

5 9

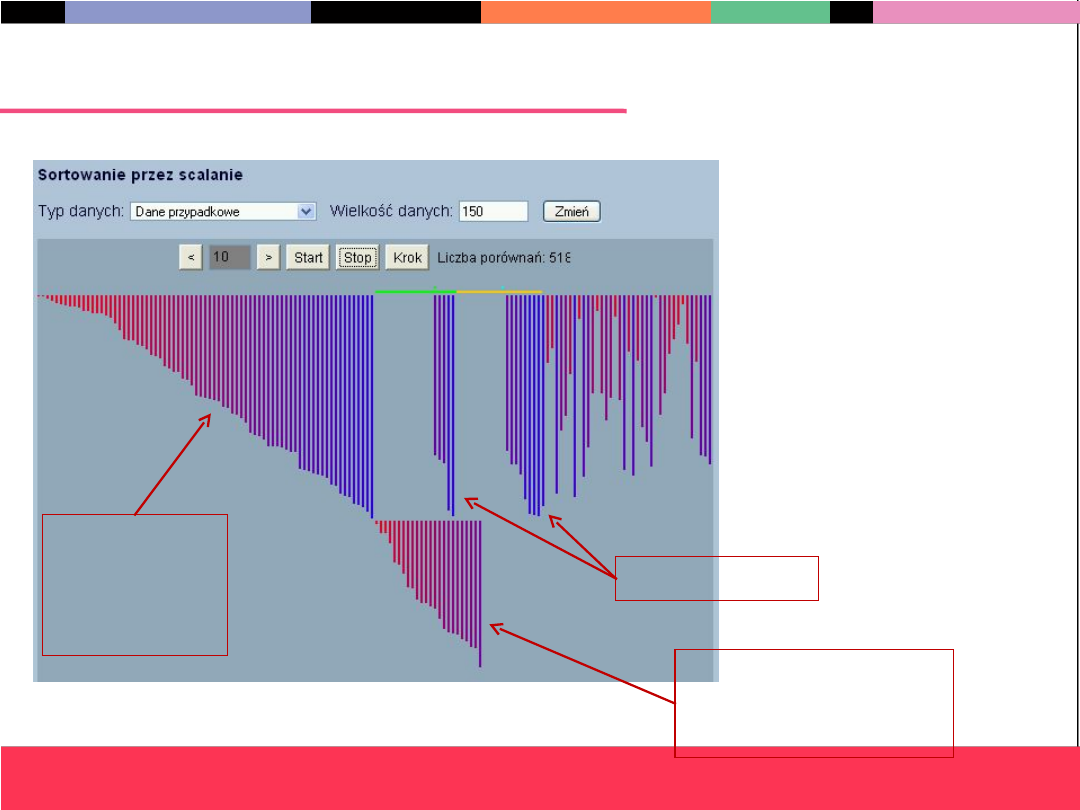
Sortowanie przez scalanie
DEMO

informatyka +

42

Scalane ciągi

Wynik scalania
dodatkowym
miejscu

Posortowan
a pierwsza
połowa
ciągu

Posortowana jest już
pierwsza połowa
ciągu i w trakcie
sortowania drugiej
połowy, scalane są
dwa podciągi z
pierwszej części
drugiej połowy,
uporządkowane
wcześniej
rekurencyjnie tą
samą metodą

informatyka +

43

Algorytm szybkiego sortowania QuickSort

(l,p,x)

Dane:

Ciąg liczb x

l

, x

l+1

, …, x

p

Wynik:

Uporządkowanie tego ciągu liczb od najmniejszej

do największej.

Krok 1.

Jeśli l < p, to przyjmij za element podziału v = x

l

i

podziel tym elementem dany ciąg. Oznacza to, że v
znajdzie się na pozycji elementu x

k

, dla pewnego k

spełniającego l ≤ k ≤ p, i elementy na lewo będą od niego
nie większe, a na prawo – nie mniejsze.

Wykonaj dwa następne kroki.

Krok 2.

QuickSort

(l,k–1,x) – sortowanie elementów na lewo

od v
Krok 3.

QuickSort

(k+1,p,x) – sortowanie elementów na

prawo od v

Rekurencyjn
e wywołania
na
podciągach

Sortowanie szybkie – opis

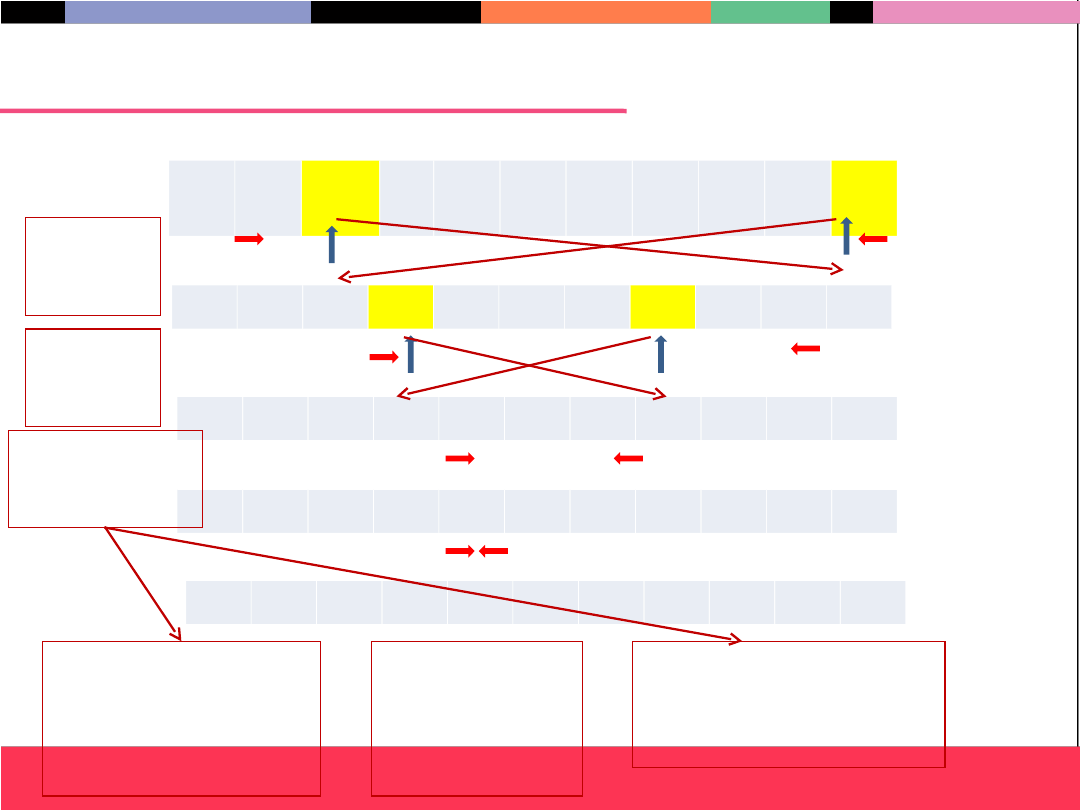
informatyka +

44

Sortowanie szybkie

DEMO

7

5

8

1

0

1

15

12

4

11

19

1

7

5

1

10

1

15 12

4

11 19

8

7

5

1

4

1

15 12 10 11 19

8

7

5

1

4

1

15 12 10 11 19

8

1

5

1

4

7

15 12 10 11 19

8

Na lewo od 7
elementy nie
większe od 7 –
porządkujemy

tak

samo

7 na swoim
miejscu w
ciągu
uporządkowany
m

Na prawo od 7
elementy nie mniejsze
od 7 – porządkujemy

tak samo

Rekurencyjne
wywołania na
podciągach

Zamiana
miejsca
mi

Zamiana
miejsca
mi

Pokrewne zajęcia w Projekcie Informatyka +

Wykład+Warsztaty (Wszechnica Poranna):

• Wprowadzenie do algorytmiki i programowania – wyszukiwanie

i porządkowanie informacji

• Proste rachunki wykonywane za pomocą komputera.
• Techniki algorytmiczne – przybliżone (heurystyczne) i dokładne.

Wykłady (Wszechnica Popołudniowa):

• Czy wszystko można policzyć na komputerze?
• Porządek wśród informacji kluczem do szybkiego wyszukiwania.
• Dlaczego możemy się czuć bezpieczni w sieci, czyli o

szyfrowaniu informacji.

• Znajdowanie najkrótszych dróg, najniższych drzew, najlepszych

małżeństw

informatyka +

45

Pokrewne zajęcia w Projekcie Informatyka +

Kursy (24 godz.) – Wszechnica na Kołach:

• Algorytmy poszukiwania i porządkowania. Elementy języka

programowania

• Różnorodne algorytmy obliczeń i ich komputerowe realizacje
• Grafy, algorytmy grafowe i ich komputerowe realizacje
 

Kursy (24 godz.) – Kuźnia Informatycznych Talentów – KIT dla Orłów:

• Przegląd podstawowych algorytmów
• Struktury danych i ich wykorzystanie
• Zaawansowane algorytmy

Tendencje – Wykłady 

• Algorytmy w Internecie, K. Diks
• Czy P = NP, czyli jak wygrać milion dolarów w Sudoku, J. Grytczuk
• Między przeszłością a przyszłość informatyki, M.M Sysło

informatyka +

46