Algorytmy sortowania

i przeszukiwania

Spis treści

1.

Sortowanie przez wstawianie - InsertSort

2.

Sortowanie przez wybór – SelectionSort

3.

Algorytm sortowania bąbelkowego

4.

Rekurencja

5.

Szybkie sortowanie - quicksort

Sortowanie przez wstawianie -
InsertSort

3

4

7

6

8

1

Karty posortowane

Karty do posortowania

Metoda sortowania przez wstawianie używana jest najczęściej
przez
osoby grające w karty.
Polega ona na założeniu, że w danym momencie w ręku trzymamy
jednocześnie karty posortowane i nieposortowane.
W celu realizacji zadania porządkowania należy pobrać ze sterty
kart do posortowania kartę i wstawienia jej na odpowiednie
miejsce w obszarze
kart posortowanych.

Sortowanie przez wstawianie -
InsertSort

Dane:

n - liczba elementów w sortowanym zbiorze, d[ ] – zbiór,

który będzie sortowany.

Wynik:

Uporządkowany zbiór d[ ]

Algorytm: porządkowanie przez wstawianie– InsertSort

Krok 1.

Dla i = 1, 2, ..., n – 1 wykonaj kroki 2 … 4, a następnie

zakończ algorytm

Krok 2.

x ← d[j];  i ← j + 1

Krok 3.

Dopóki ( i ≤ n )  ∧  ( x > d[i] ): wykonuj d[i - 1] ← d[i]; 

i ← i + 1

Krok 4

d[i - 1] ← x

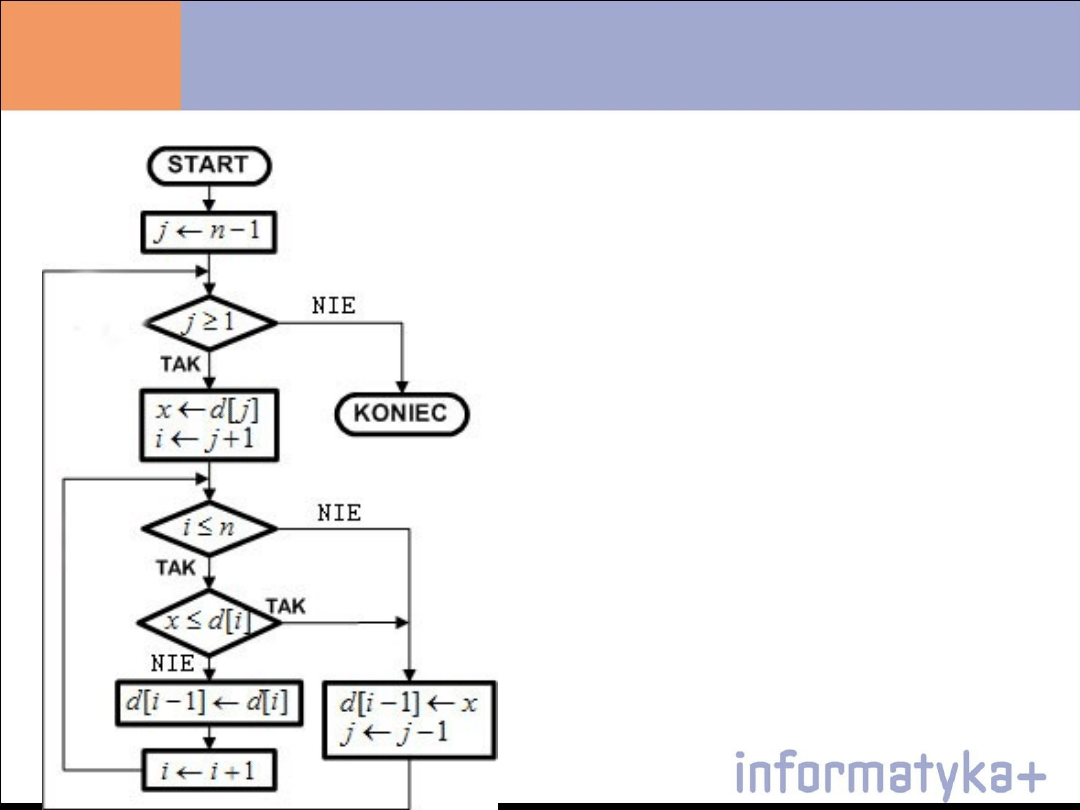
Sortowanie przez wstawianie -
InsertSort

for(j = n - 2; j >= 0; j--)
{
x = d[j];
i = j + 1;
while((i < n) && (x >
d[i]))
{
d[i - 1] = d[i];
i++;
}
d[i - 1] = x;
}

Sortowanie przez wstawianie -
InsertSort

Wnioski:

- algorytm ten jest bardzo kosztownym algorytmem

(klasa złożoności obliczeniowej – O(N

2

)

- nie nadaje się do porządkowania dużych zbiorów

- postać algorytmu przejrzysta

- algorytm krótki

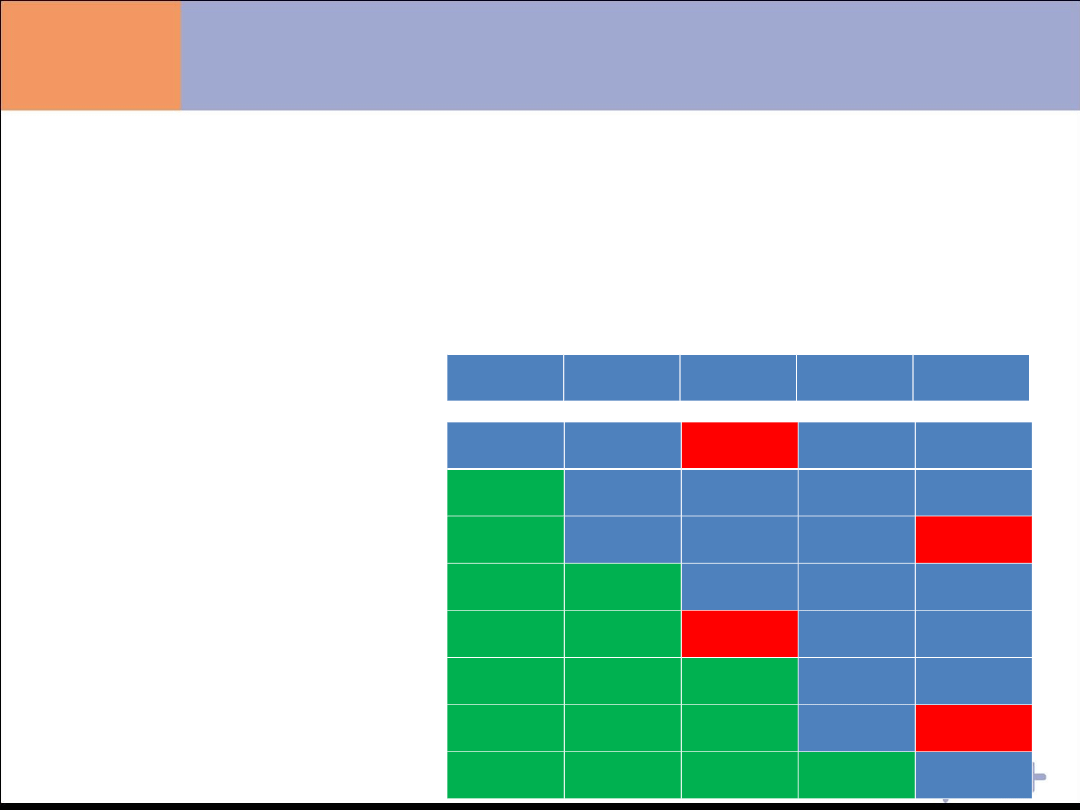
Sortowanie przez wybór - SelectionSort

Metoda porządkowania przez wybór polega na porządkowaniu
zbioru
w sposób rosnący tzn. element najmniejszy powinien znaleźć się
na pierwszej pozycji. Metoda ta polega na znalezieniu w zbiorze
elementu najmniejszego i wymienieniu go z elementem na
czytanej pozycji zbioru aż do całkowitego jego uporządkowania.

Zbiór nieuporządkowany

4

7

2

9

3

4

7

2

9

3

2

7

4

9

3

2

7

4

9

3

2

3

4

9

7

2

3

4

9

7

2

3

4

9

7

2

3

4

9

7

2

3

4

7

9

Etapy porządkowania

Sortowanie przez wybór - SelectionSort

Dane:

n - liczba elementów zbioru,

d[ ] – zbiór sortowany. Elementy zbioru mają indeksy od
1 do n.

Wynik:

Uporządkowany zbiór d[ ]

Algorytm: porządkowanie przez wybór – Selection Sort

Idea:

najmniejszy wśród nieuporządkowanych daj na początek

Krok 1.

Dla j = 1, 2, ..., n - 1: wykonuj Krok 1 ...Krok 4, a

następnie zakończ algorytm

Krok 2.

p

min

← j

Krok 3.

Dla i = j + 1,  j + 2, ..., n: jeśli d[i] < d[p

min

], to p

min

← i

Krok 4.

d[j] ↔ d[p

min

]

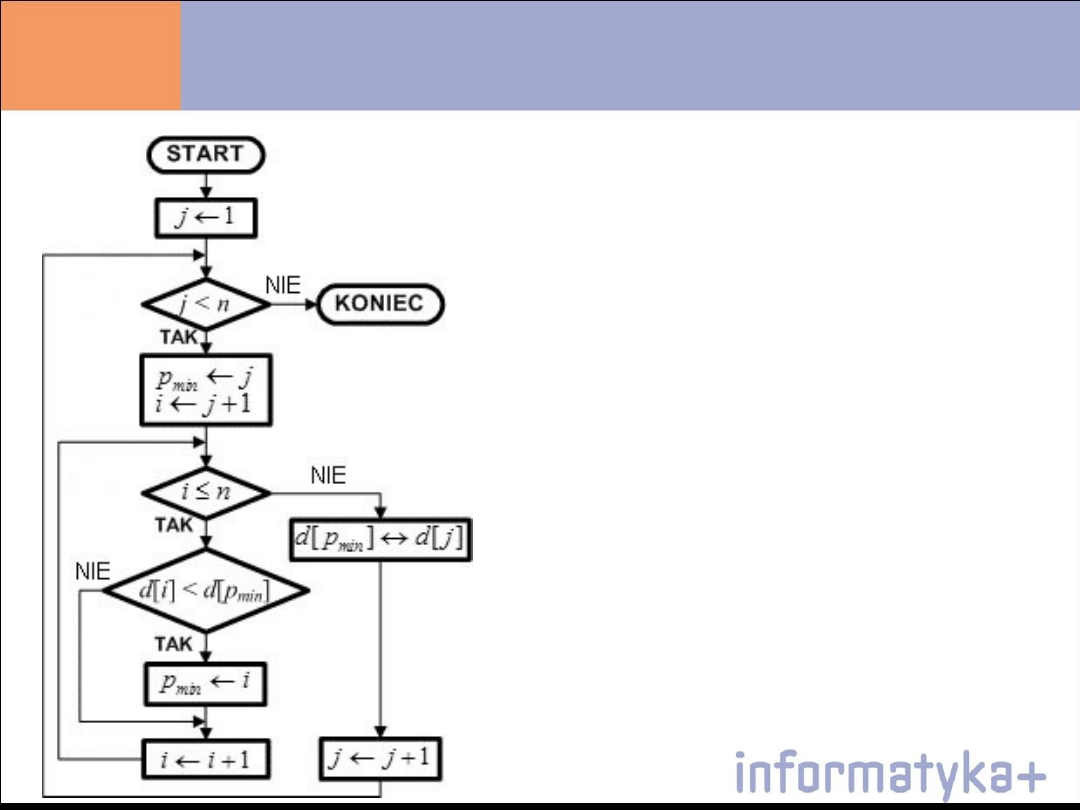
Sortowanie przez wybór - SelectionSort

for(j = 0; j < N - 1; j++)
{
pmin = j;
for(i = j + 1; i < N; i++)
{
if(d[i] < d[pmin]) pmin
= i;
}
swap(d[pmin], d[j]);
}

Sortowanie przez wybór - SelectionSort

Wnioski:

- algorytm ten jest bardzo kosztownym algorytmem

(klasa złożoności obliczeniowej – O(N

2

)

- nie nadaje się do porządkowania dużych zbiorów

- wykonuje taką samą ilość operacji porównania dla
zbiorów częściowo uporządkowanych jak i dla zbiorów
nieuporządkowanych

- algorytm przejrzysty, zwięzły

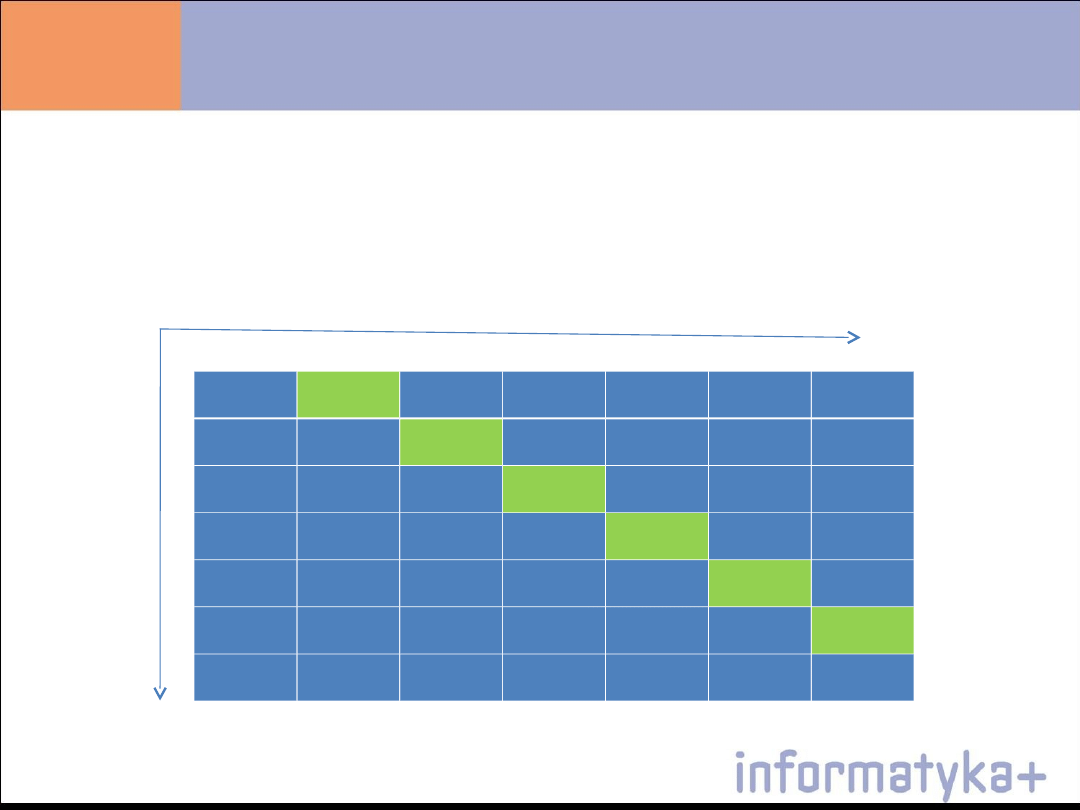
Algorytm sortowania bąbelkowego

Metoda porządkowania bąbelkowego swoją nazwę wzięła od
pęcherzyków powietrza ulatujących w górę tuby wypełnionej
wodą. Metoda ta polega na analizowaniu dwóch sąsiadujących
ze sobą elementów, jeśli nie są one uporządkowane następuje
ich zamiana.

40

2

2

2

2

2

2

2

40

4

4

4

4

4

39

4

40

6

6

6

6

6

39

6

40

18

18

18

18

6

39

18

40

20

20

4

18

18

39

20

40

39

20

20

20

20

39

39

40

Indeks tablicy

Etapy

Algorytm sortowania bąbelkowego

Dane:

n - liczba elementów zbioru,

d[ ] – zbiór sortowany. Elementy zbioru mają indeksy od
1 do n.

Wynik:

Uporządkowany zbiór d[ ]

Algorytm: porządkowanie bąbelkowe

Krok 1.

Dla j = n - 1, n - 2, ..., 1: wykonuj K02...K04, zakończ

algorytm

Krok 2.

p ← 1

Krok 3.

Dla i = 1, 2, ..., j: jeśli d[i] > d[i + 1], to d[i] ↔ d[i + 1]; 

p ← 0

Krok 4.

Jeśli p = 1, to zakończ

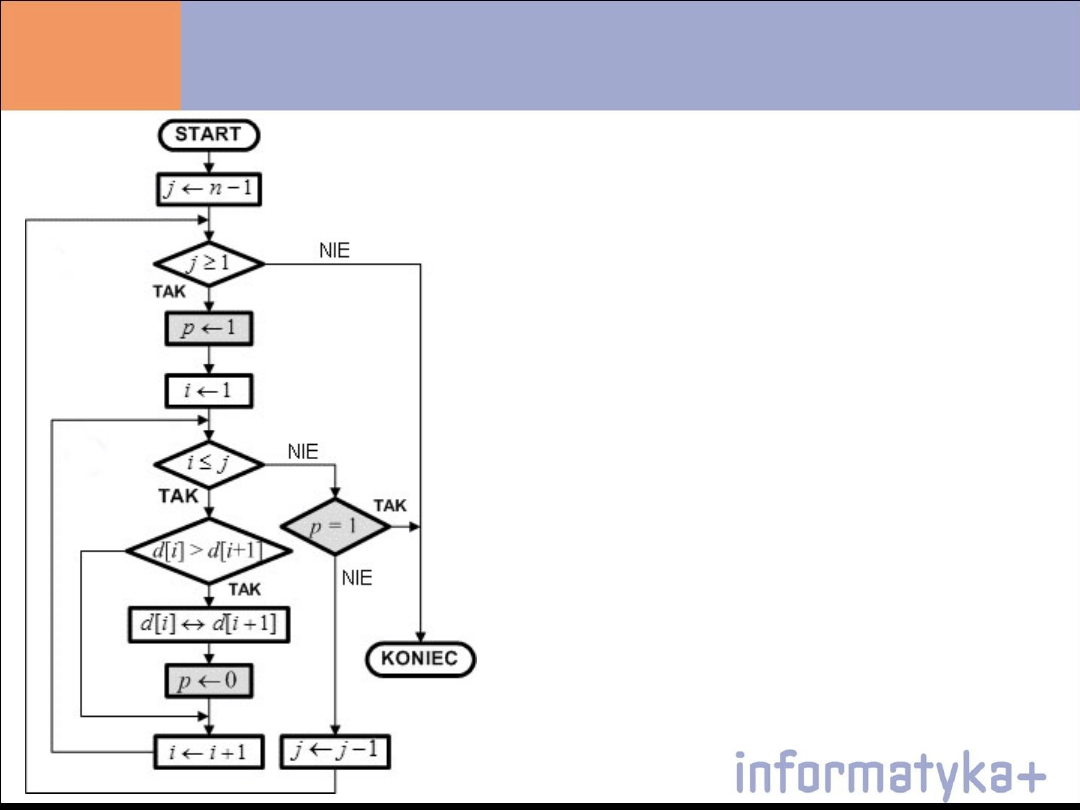
Algorytm sortowania bąbelkowego

for(j = N - 1; j > 0; j--)
{
p = 1;
for(i = 0; i < j; i++)
{
if(d[i] > d[i + 1])
{
swap(d[i],
d[i + 1]); p = 0;
}
}
if(p) break;
}

Algorytm sortowania bąbelkowego

Wnioski:

- algorytm ten jest bardzo kosztownym algorytmem

(klasa złożoności obliczeniowej – O(N

2

)

- bardzo prosta i zrozumiała struktura zapisu

- dość często zdarzają się puste przebiegi (brak
wykonania wymiany jeżeli elementu są
uporządkowane)

Rekurencja

Rekurencja - jest modą programowania polegająca na

wywoływaniu funkcji programu przez samą siebie .

Przykład:

long int silnia(int x)
{
if (x==0)
{
return 1;
}
else
{
return x * silnia(x-1);
}
}

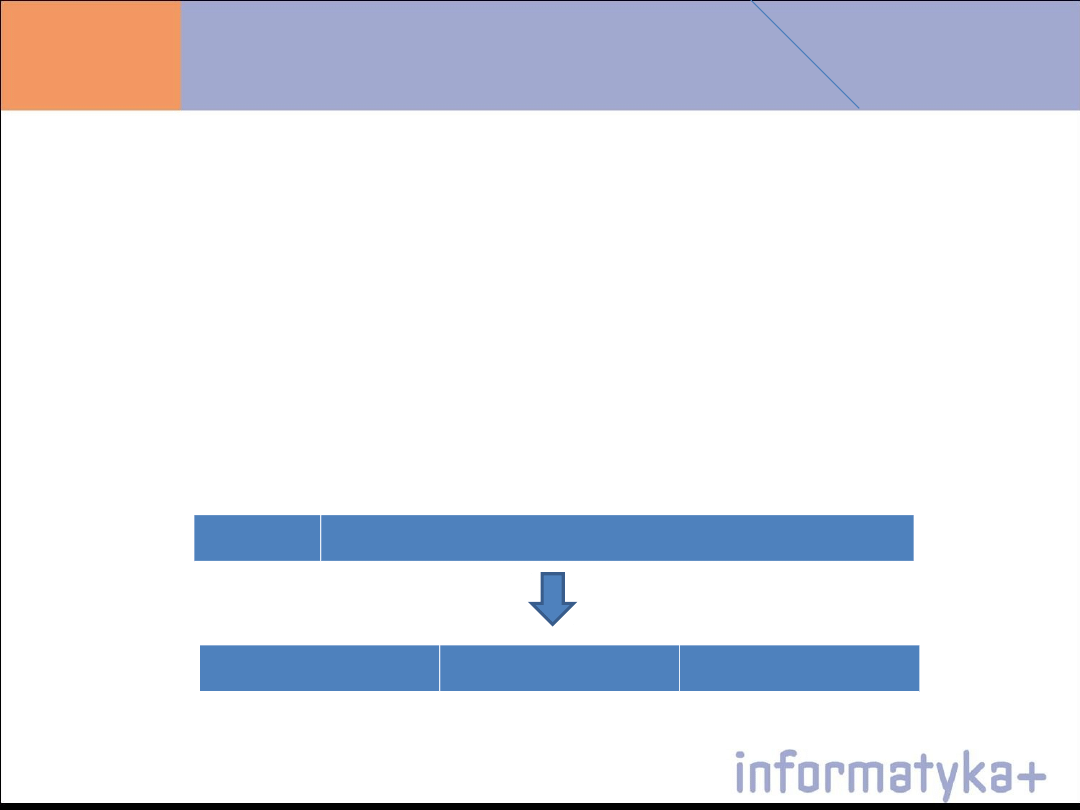
Szybkie sortowanie - quicksort

Algorytm ten jak sama nazwa wskazuje, poprzez odpowiednią
dekompozycję osiągnął znaczny zysk w szybkości
porządkowania zbiorów.
Metoda szybkiego sortowania podzielona została na dwie części:

• część służąca do właściwego sortowania polegająca na
wywoływaniu samej siebie

• część odpowiadająca za rozdzielenie elementów tablicy
wartości osiowej podziału

P

< P

P

>= P

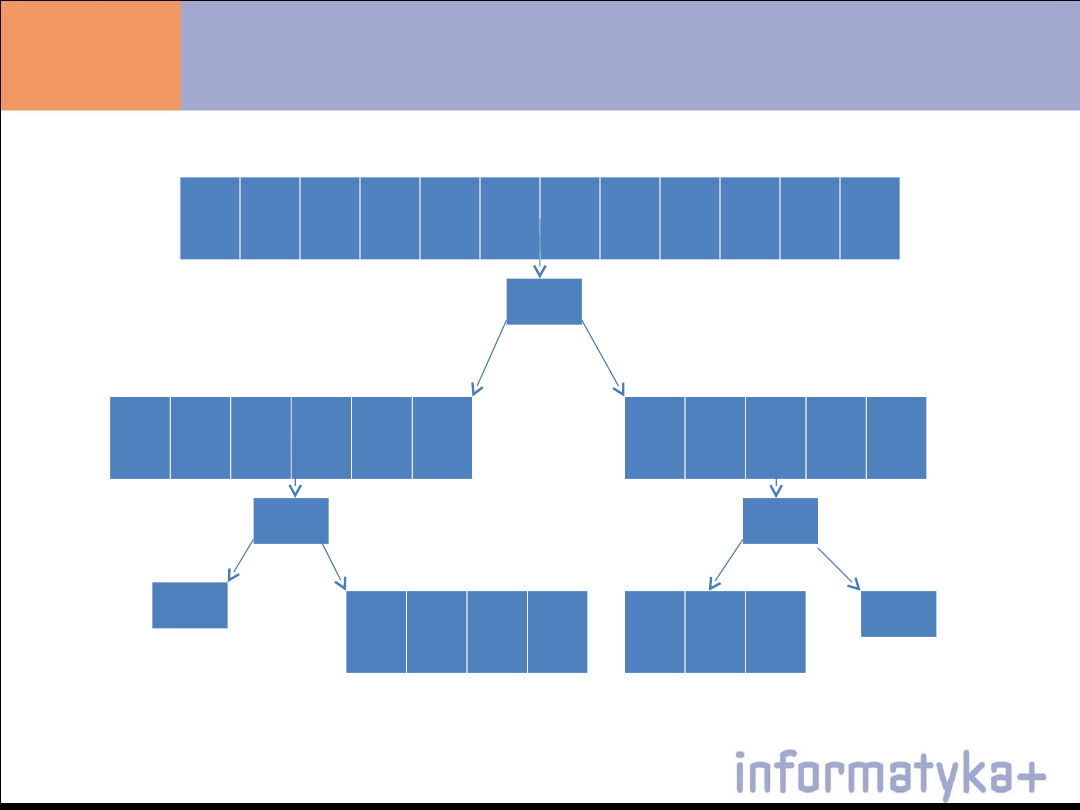
Szybkie sortowanie - quicksort

2
9

4
0

2

1

6

1
8

2
0

3
2

2
3

3
4

3
9

4
1

29

2

1

6

1

8

2

0

2

3

4

0

3

2

3

4

3

9

4

1

2

1

6

1
8

2
0

2
3

40

3
2

3
4

3
9

41

Szybkie sortowanie - quicksort

Oznaczenia:

left – lewy skrajny element
right – prawy skrajny element
p – wartość osiowa
i – zmienna sterująca pętlą
m – poszukiwany indeks komórki tablicy, w

której
umieszczamy element osiowy

Szybkie sortowanie - quicksort

void qsort(int* d, int left, int right)
{
if (left < right)
{
int m = left;
for(int i = left+1; i <= right; i++)
if (d[i] < d[left]) swap(d[++m],d[i]);
swap(d[left], d[m]);
qsort(d, left, m-1);
qsort(d, m+1, right);
}
}

Szybkie sortowanie - quicksort

Wnioski:

- dzięki zastosowaniu metody programowania „dziel
i zwyciężaj” algorytm w optymalnie krótkim czasie

realizuje

zadanie porządkowania zbiory

(klasa złożoności obliczeniowej – O(N log N)