
Mechanika płynów
II rok
Inżynieria Środowiska
Wykład nr 4
Marcin Widomski
dr inż.
p. 309
tel. wew. 4183 – z portierni
tel. 0-8153844183
M.Widomski@wis.pol.lublin.pl

KINEMATYKA PŁYNÓW

Kinematyka płynów
Kinematyka płynów
• Opis i analiza ruchu płynów bez wnikania w
przyczyny powodujące ruch, tzn. bez wnikania w istotę
działania sił.
• Wszystkie rozważania są związane z elementem
płynu.
• Ruch płynu określony jest wtedy, gdy znane są
prędkości wszystkich elementów płynu, tzn. znane jest
w pełni pole prędkości.
Znane są dwie metody badania ruchu płynów:
• Metoda Lagrange’a
• Metoda Eulera

Kinematyka płynów
Metoda Lagrange’a
Metoda Lagrange’a, inaczej analiza wędrowna,
polega na badaniu ruchu wybranego elementu
płynu po jego torze.
Metoda Lagrange’a opisuje zatem zmianę różnych
wielkości hydrodynamicznych zachodzącą podczas
przepływu indywidualnie dla każdego elementu
płynu; w metodzie tej bada się ich historię.
Jeżeli w chwili t
0
element płynu zajmuje położenie
określone promieniem – wektorem r
0
(x
0
, y
0
, z
0
), to
z czasem położenie to będzie ulegało zmianie.
Podobnie będą się zmieniały inne parametry
związane z wybranym elementem płynu.

Kinematyka płynów
Metoda Lagrange’a
W dowolnej chwili t współrzędne wybranego elementu płynu w
układzie kartezjańskim będą zależne od lokalizacji
początkowej oraz upływającego czasu.
W takim przypadku wektor prędkości można opisać jako:

Kinematyka płynów
Metoda Lagrange’a
Przyspieszenie zaś wyznaczymy różniczkując równanie
prędkości względem czasu.
Z metodą Lagrange’a jest związane pojęcie powierzchni płynnej, czyli
dowolnej
(otwartej lub zamkniętej) powierzchni ruchomej, utworzonej z tych samych
poruszających się elementów płynu, traktowanych jako punkty materialne.
Obszar ograniczony zamkniętą powierzchnią płynną jest nazywany obszarem
płynnym.

Kinematyka płynów
Metoda Eulera
Metoda Eulera, inaczej analiza lokalna, polega na
badaniu ruchu kolejnych elementów płynu
przepływających przez nieruchomy, zlokalizowany,
określony współrzędnymi x, y, z punkt.
Czyli w stałym układzie współrzędnych wydziela się
pewien obszar wypełniony płynem i bada się
zmianę wielkości charakteryzujących przepływ w
zadanym punkcie. W metodzie tej rozpatruje się
więc
zmianę
wielkości
charakteryzujących
przepływ w zależności od czasu t i od położenia
punktu.
Np.

Kinematyka płynów
Metoda Eulera
Pole prędkości opisuje następująca funkcja:
Analogicznie wyznaczamy przyspieszenie.
Kinematyka płynów
Metoda Eulera
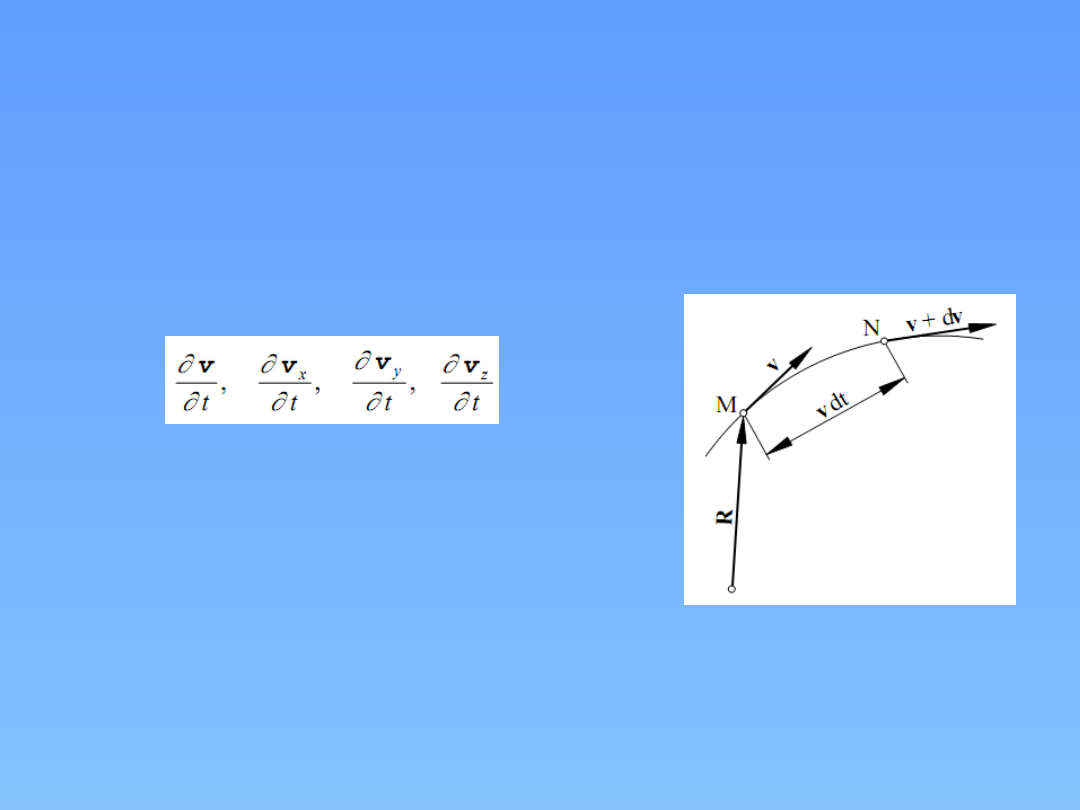
Zmianę prędkości elementów przepływających w
czasie przez punkt M z prędkością v (x, y, z, t)
określają
pochodne
cząstkowe
prędkości
względem czasu t:
Są to zmiany lokalne prędkości w
czasie i dlatego te pochodne nazywa
się pochodnymi lokalnymi lub
miejscowymi.

Kinematyka płynów
Metoda Eulera
Zmianę prędkości elementów przepływających w
czasie przez punkt M po czasie dt opiszemy więc
jako:
Zaś przyspieszenie:

Kinematyka płynów
Metoda Eulera
Powyższe
można
przedstawić
w
postaci
operatorowej:
Gdzie: ∇ - operator różniczkowy Hamiltona.
Finalnie, współrzędne wektora przyspieszenia a
można przedstawić jako:
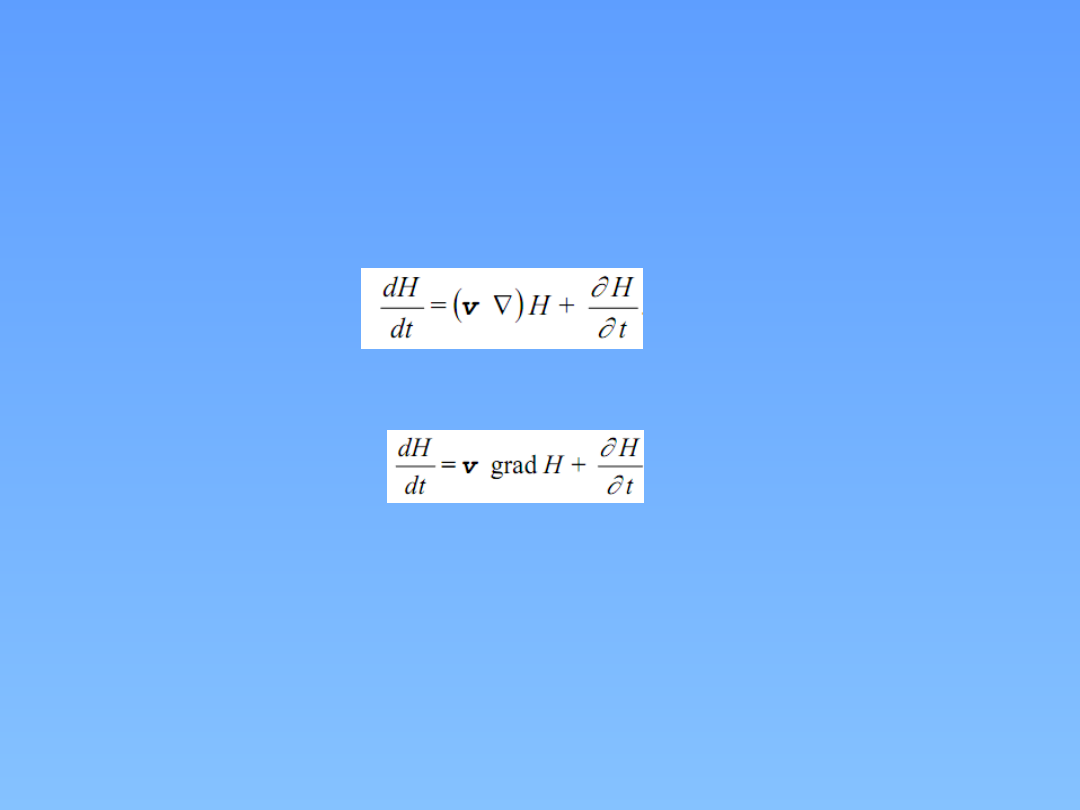
Przyśpieszenie a jest pochodną zupełną prędkości względem
czasu
dv/dt. Pochodna ta jest nazywana pochodną substancjalną i jest
sumą pochodnej konwekcyjnej i lokalnej.
W przypadku zmiennych skalarnych pochodna substancjalna
przyjmie postać:
Kinematyka płynów
Metoda Eulera
Z metodą Eulera jest związane pojęcie powierzchni kontrolnej,
czyli otwartej lub zamkniętej nieruchomej powierzchni, utworzonej
przez te same nieruchome punkty przestrzeni. Obszar ograniczony
zamkniętą powierzchnią kontrolną nazywamy obszarem kontrolnym.

PODSTAWOWE POJĘCIA
KINEMATYKI PŁYNÓW

Podstawowe pojęcia kinematyki płynów
Pole fizyczne – obszar, w którym każdemu punktowi i w każdej
chwili czasu jest jednoznacznie przyporządkowana określona
wartość jakiejś wielkości fizycznej (parametru) – prędkość,
ciśnienie, gęstość itp.
Pole fizyczne może być:
• Ustalone i nieustalone,
• Jednorodne i niejednorodne,
• Ciągłe i nieciągłe,
• Źródłowe i bezźródłowe,
• Wirowe i bezwirowe,
• Jedno, dwu i trójwymiarowe.
Podstawowe pojęcia kinematyki płynów
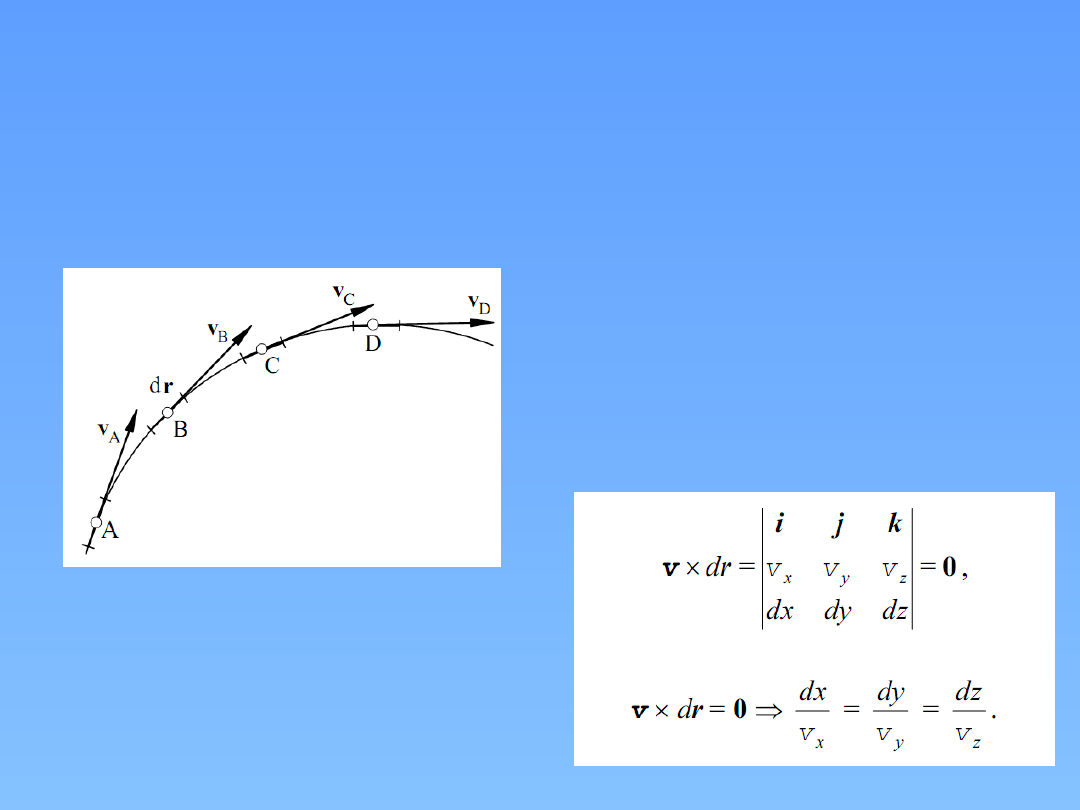
Linia prądu – linia pola wektorowego prędkości, czyli linia styczna
do wektorów prędkości różnych elementów płynu poruszających
się ruchem ustalonym.
Linia prądu i równanie
linii prądu.
Podstawowe pojęcia kinematyki płynów
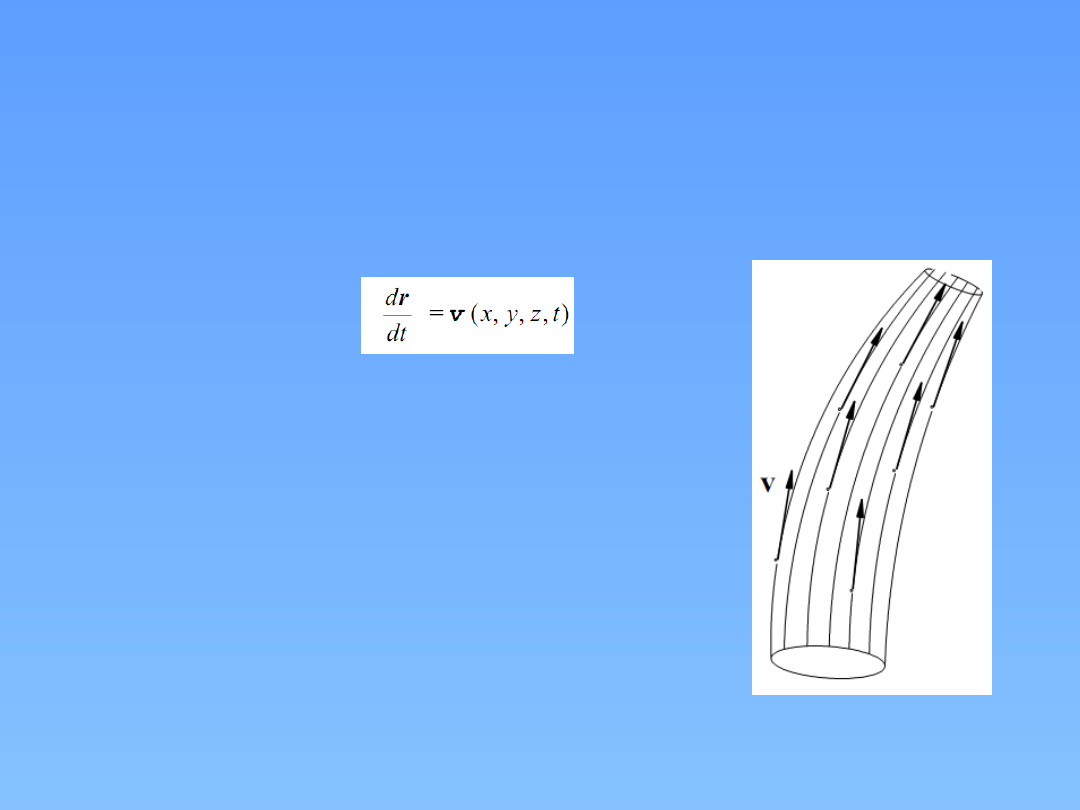
Tor elementu płynu – linia po której porusza się element płynu
czyli krzywa opisywana przez poruszający się element płynu.
W przepływach ustalonych tor elementu płynu pokrywa się z linią
prądu.
Rurka prądu – powierzchnia utworzona z linii prądu.
Struga - poruszający się płyn wypełniający rurkę prądu,
Inaczej, struga tobiór linii prądu wypełniających w sposób
ciągły rurkę prądu.
Struga elementarna - struga, której pole
przekroju poprzecznego jest nieskończenie małe.

STRUMIEŃ OBJĘTOŚCI
I STRUMIEŃ MASY

Strumień objętości i strumień masy
Strumień objętości q
V
(nazywany także objętościowym natężeniem
przepływu, oznaczany jako Q) jest to strumień wektora prędkości v
przechodzący przez powierzchnię A.
Jest to więc całka z iloczynu skalarnego wektora v i wektora
zorientowanego wycinka pola przekroju dA.
Inna definicja to: miara ilości płynu, substancji, mieszaniny,
przepływającego przez wyodrębnioną przestrzeń, obszar lub
poprzeczny przekrój w jednostce czasu
dt
dV
Q
/
dV – elementarna objętość [m
3
], dt –
jednostkowy czas [s]

Strumień objętości i strumień masy
Strumień masy q
V
(nazywany także masowym natężeniem przepływu,
oznaczany jako G lub ) jest to strumień uwzględniający gęstość
przepływającej cieczy.
Inna definicja to: miara masy płynu, substancji, mieszaniny,
przepływającego przez wyodrębnioną przestrzeń, obszar lub
poprzeczny przekrój w jednostce czasu
dt
dm
G
/
dm – elementarna masa [m
3
], dt –
jednostkowy czas [s]

RÓWNANIE CIĄGŁOŚCI
PRZEPŁYWU

Równanie ciągłości przepływu
Równanie ciągłości przepływu wyraża prawo zachowania masy
(niezniszczlności materii).
Zgodnie z zasadą zachowania masy, w żadnym punkcie pola masa nie
może się
tworzyć ani znikać.
W płynie nieściśliwym ( ρ = const) tylko takie pole prędkości będzie
spełniało tę zasadę, w którym w każdej chwili do obszaru ograniczonego
powierzchnią kontrolną będzie wpływało tyle płynu, ile w tej samej chwili
wypływa.

Równanie ciągłości przepływu
W przestrzeni wypełnionej poruszającym się płynem wyodrębnijmy
obszar o objętości V ograniczony powierzchnią kontrolną A o normalnej
zewnętrznej n w punkcie M.
Zmiana masy w
objętości V może być
wywołana:
• dopływem poprzez
ścianę powierzchni
kontrolnej,
• lokalną zmianą
gęstości.
W czasie dt przez powierzchnię A
przepłynie następujący strumień:
Przyrost masy wywołany zmianą
gęstości można opisać jako:

Równanie ciągłości przepływu
Zgodnie z prawem zachowania masy, masa nie może powstawać
ani zanikać w obszarze kontrolnym, dlatego bilans dopływu i
przyrostu masy musi być równy zeru.
Całkowa postać równania ciągłości
(zachowania masy).
Drugi składnik sumy można zapisać jako:
div - dywergencja (albo rozbieżność, źródłowość) pola wektorowego - operator różniczkowy
przyporządkowujący trójwymiarowemu polu wektorowemu pole skalarne będące formalnym
iloczynem skalarnym operatora nabla z polem.

Równanie ciągłości przepływu
Podstawiając otrzymamy:
Ponieważ funkcja podcałkowa musi być równa zeru więc:
Otrzymaliśmy w ten sposób różniczkowe równanie ciągłości
przepływu.

RÓWNANIE CIĄGŁOŚCI PRZEPŁYWU
W RUCHU JEDNOWYMIAROWYM
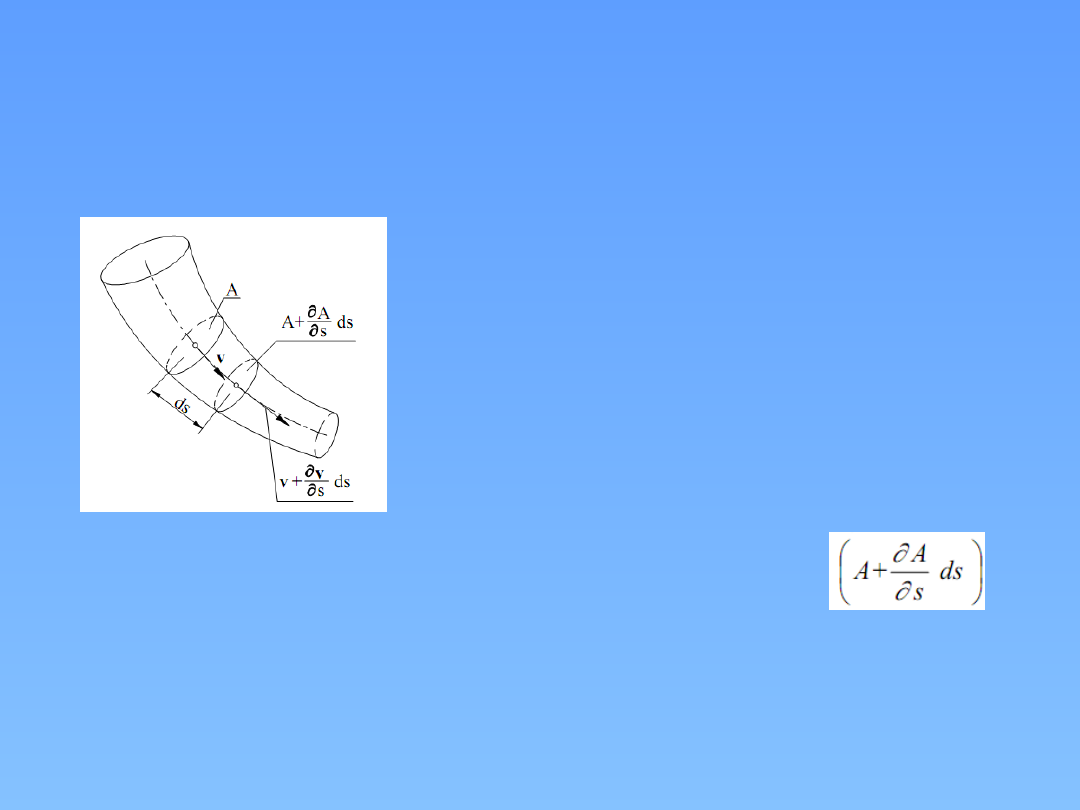
Równanie ciągłości przepływu w ruchu
jednorodnym
Przeanalizujemy prawo zachowania masy dla objętości kontrolnej
strugi zamkniętej pomiędzy dwoma przekrojami.
W obrębie założonego elementu
płynu
o podstawie A i wysokości ds
prędkości podczas przejścia od
przekroju A do przekroju sąsiedniego
zmieniają się tylko w kierunku ds.
Oznacza to, że prędkość v zależy
tylko od jednego wymiaru, a ruch taki
nazywa
się przepływem
jednowymiarowym.
Musimy teraz porównać masy przepływające przez przekroje A i

Równanie ciągłości przepływu w ruchu
jednorodnym
Masa wypływająca z przekroju o polu A z prędkością v wyniesie:
Masa wypływająca z przekroju o polu
z prędkością
Różnica mas płynu wpływającego do i wypływającego z elementu
płynu, równa przyrostowi masy w czasie dt wyniesie:

Równanie ciągłości przepływu w ruchu
jednorodnym
Powyższe równanie można uprościć do postaci:
Dla płynu nieściśliwego (ρ = const) równanie to przybiera postać
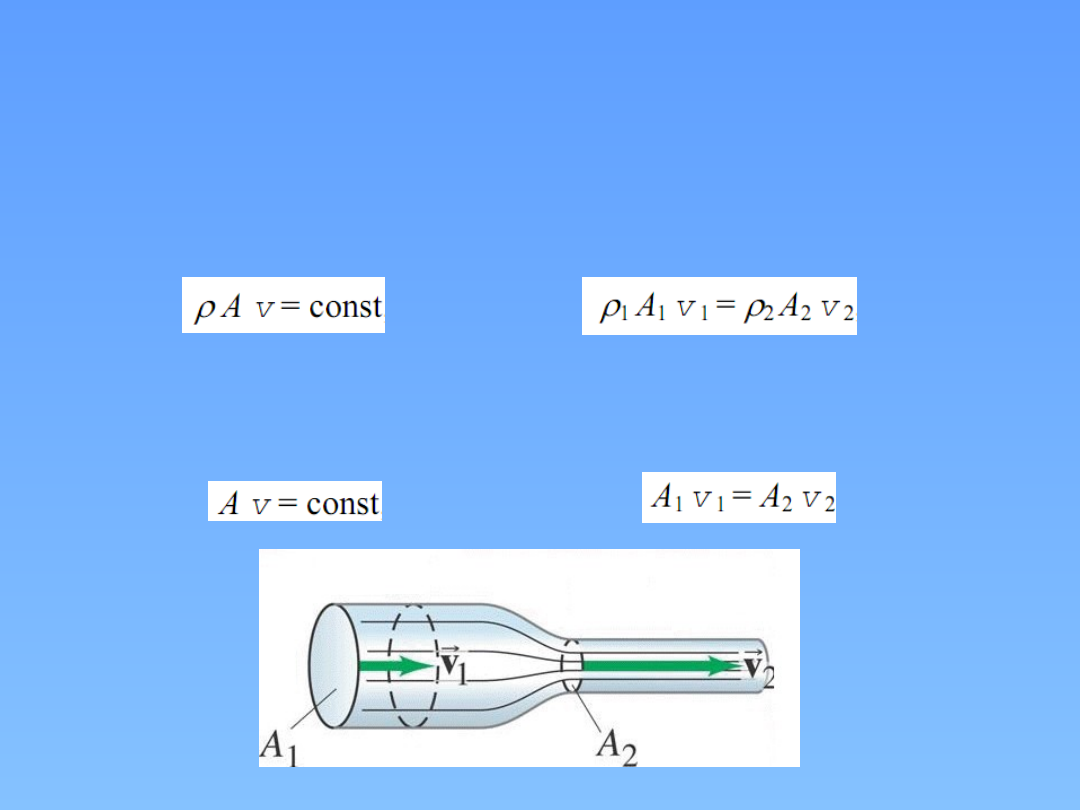
Równanie ciągłości przepływu w ruchu
jednorodnym
Najczęściej wykorzystywane w praktyce formy równania ciągłości
Ruch ustalony, płyn ściśliwy
Ruch ustalony, płyn nieściśliwy
Document Outline
- Slide 1
- Kinematyka PŁYNÓW
- Kinematyka płynów
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
Wyszukiwarka
Podobne podstrony:
Wykład nr 4
Wykład nr 7
WYKŁAD NR 3 KB2 PŁYTY WIELOKIERUNKOWO ZBROJONE
Wykład nr 5 podstawy decyzji producenta
Hydrologia Wyklad nr 11
wykład+nr+8+ +Obróbki+powierzchniowe
Ochrona Środowiska wykład Nr 1 z dnia 27 streszczenie, ochrona środowiska(1)
MP 1, Semesr 4, MP, Wykłady
Wykład nr 1, materiał♫y z pedagogiki
Biochemia wykład nr 3 kopia
STANDARDY Wyklad nr 2
Wykład nr 7
Prawo karne wykład nr 3 z dn ) 10 2011
MSG wykład nr 6
BO II stacjonarne wykład nr 09
AUDYT WEWNĘTRZNY Z DNIA 26 LUTY 2011 WYKŁAD NR 1
Farma wyklad nr 3 18, Farma, farma 4 rok, prezentacjezcukrzycyiwykladyzfarmy
wykład nr 5, prawo karne i prawo wykroczeń
więcej podobnych podstron