Statystyka

Zajęcia 2

Opis statystyczny (cz.1)

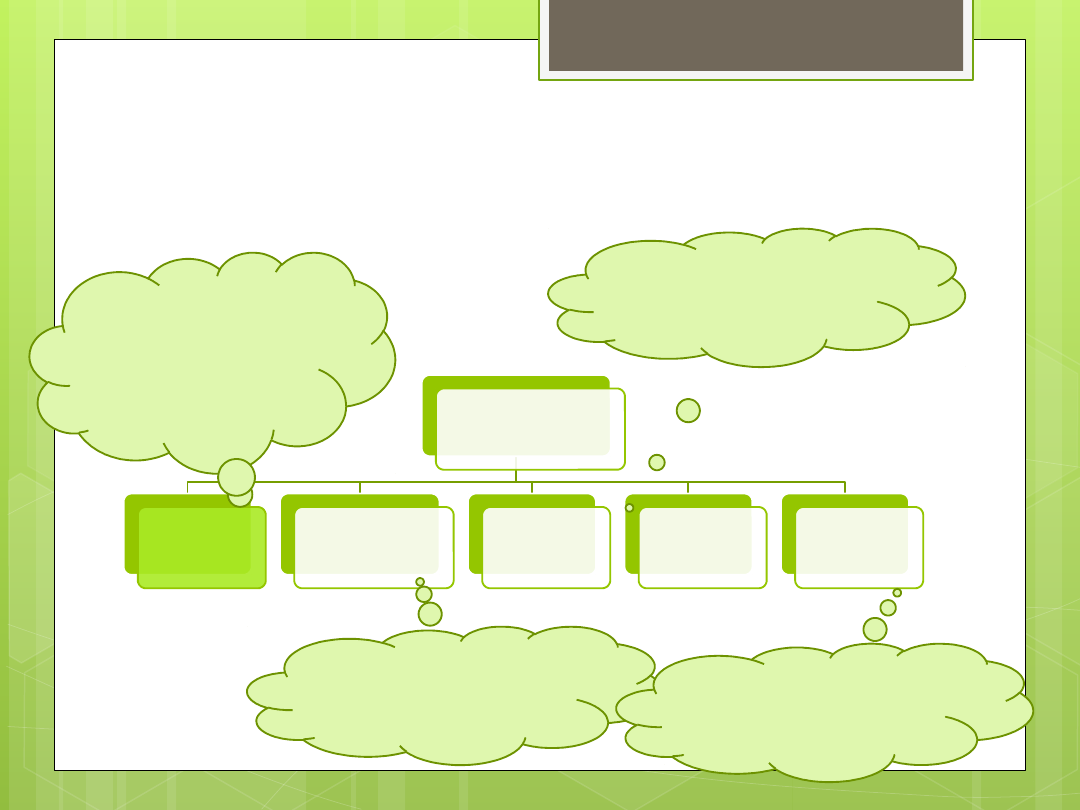
Opis statystyczny

OPIS

STATYSTYCZNY

Miara

tendencji

centralnej

Miara

rozproszenia

Miara

asymetrii

Miara

kurtozy

Miara

pozycyjna

(kwantyle

)

Pozwalają

opisać miejsce

największej

koncentracji

wyników

Mierzą

zróżnicowanie/

rozrzut danych

Pozwalają opisać

kształt rozkładu

danych

Pozwalają dzielić

dane na określone

części

Ile waży Bonifacy ?

Miary tendencji centralnej



Średnia arytmetyczna



Mediana – wynik środkowy



Dominanta (moda, modalna) –
najczęściej występujący wynik

Ćwiczenie 1



Oblicz medianę i średnią arytmetyczną

a)

70, 65, 62, 61, 67

b)

62, 65, 66, 60, 72

Opis statystyczny

OPIS

STATYSTYCZNY

Miara

tendencji

centralnej

Miara

rozproszenia

Miara

asymetrii

Miara

kurtozy

Miara

pozycyjna

(kwantyle

)

s

2

Miary rozproszenia



Rozstęp

V = X

max

– X

min



Odchylenie przeciętne - przeciętna odległość pomiarów od średniej
arytmetycznej



Wariancja – przeciętna kwadratowa odległość pomiarów od średniej
arytmetycznej



Odchylenie standardowe

Sp

n-1

Ćwiczenie 2

Grupa 50 studentów rozwiązywała test
składający się z 31 zadań, o wartości 1 pkt
każde. Poniżej przedstawione zostały wyniki
studentów. Oblicz miary tendencji centralnej i
miary rozproszenia wyników studentów.

27,15,5,26,14,14,15,22,23,16,19,20,10,14,17,1
8,23,25,26,30,2,4,16,17,12,9,13,14,16,20,21,1
7,17,14,19,12,13,18,16,12,5,8,10,16,18,19,22,
12,23,16

Ćwiczenie 2



Dane uporządkowane

2,4,5,5,8,9,10,10,12,12,12,12,13,13,14,14,14,14,
14,15,15,16,16,16,16,16,16,17,17,17,17,18,18,18,
19,19,19,20,20,21,22,22,23,23,23,25,26,26,27,30



Średnia arytmetyczna

x= 810/50 = 16,2

Ćwiczenie 2



Tworzymy przedziały klasowe



Ile powinno być klas?

Rozpiętość

(R)

Interwał

(h)

Liczba

klas

(R/h)

Liczba klas

zaokrąglon

a do góry

28

:

1

=

28,00

28

28

:

2

=

14,00

14

28

:

3

=

9,33

10

28

:

4

=

7,00

7

Szereg rozdzielczy:

• Porządkujemy dane

• Redukujemy nadmiar

informacji

Szereg rozdzielczy (część
1)

j

(x

dj

; x

gj

> f

j

1

(1,5;

4,5>

2

2

(4,5;

7,5>

2

3
4
5
6
7
8
9
10
k= 10

h= 3

n=…

Dokładne

granice sięgają

+/- 0,5 dalej !!!

Szereg rozdzielczy (część
2)

j

(x

dj

; x

gj

>

f

j

x

j

1

(1,5; 4,5>

2

3

2

(4,5; 7,5>

2

6

3

(7,5; 10,5>

4

4

(10,5;

13,5>

6

5

(13,5;

16,5>

13

6

(16,5;

19,5>

10

7

(19,5;

22,5>

5

8

(22,5;

25,5>

4

9

(25,5;

28,5>

3

10

(28,5;

31,5>

1

k=

10

h=3

n=50

Środek j-tego

przedziału – wartość

reprezentująca ten

przedział

Szereg rozdzielczy (część
3)

j

(x

dj

; x

gj

>

f

j

x

j

x

j *

f

j

1

(1,5; 4,5>

2

3

6

2

(4,5; 7,5>

2

6

12

3

(7,5; 10,5>

4

9

4

(10,5;

13,5>

6

12

5

(13,5;

16,5>

13

15

6

(16,5;

19,5>

10

18

7

(19,5;

22,5>

5

21

8

(22,5;

25,5>

4

24

9

(25,5;

28,5>

3

27

10

(28,5;

31,5>

1

30

k=

10

h=3

n=5

0

f

j

j

j

k

Szereg rozdzielczy (część
4)

j

(x

dj

; x

gj

>

f

j

x

j

x

j *

f

j

1

(1,5; 4,5>

2

3

6

2

(4,5; 7,5>

2

6

12

3

(7,5; 10,5>

4

9

36

4

(10,5; 13,5> 6

12

72

5

(13,5; 16,5> 13

15

195

6

(16,5; 19,5> 10

18

180

7

(19,5; 22,5> 5

21

105

8

(22,5; 25,5> 4

24

96

9

(25,5; 28,5> 3

27

81

10

(28,5; 31,5> 1

30

30

k=

10

h=3

n=5

0

Suma=81

3

f

j

j

j

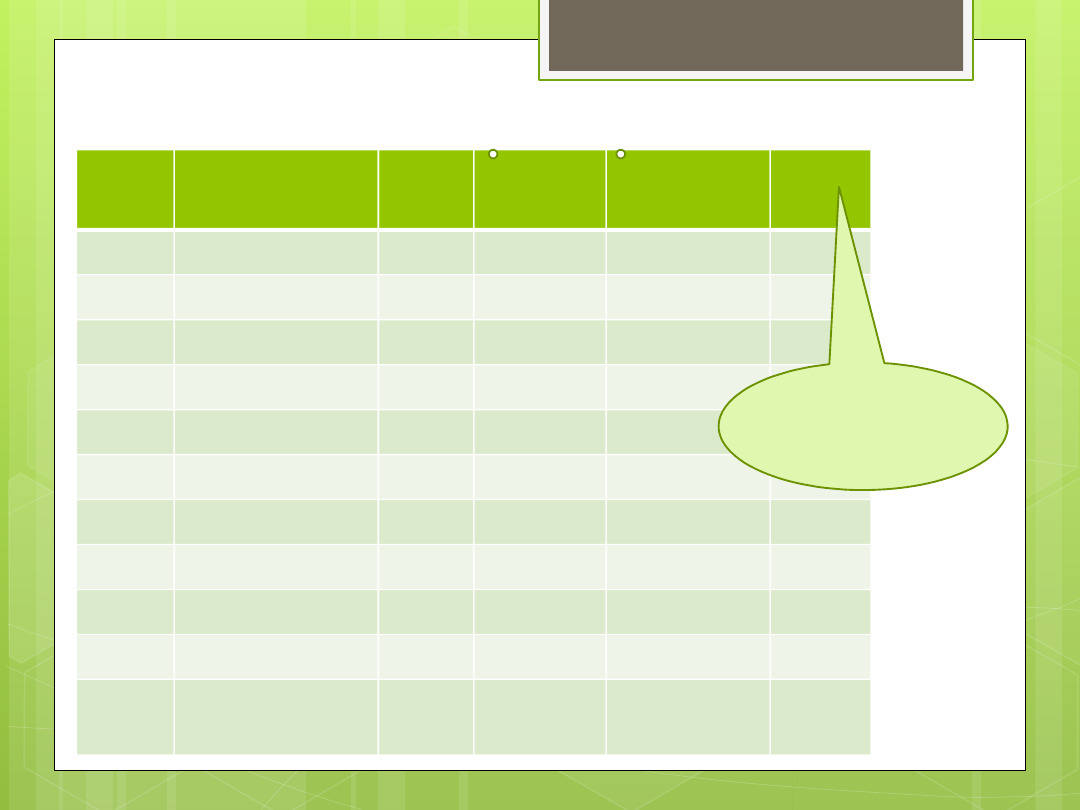
Szereg rozdzielczy (część
5)

me= xd

j

+

(n/2 – fc

j

– 1)

f

j

* h

j

j

(x

dj

; x

gj

>

f

j

x

j

x

j *

f

j

f

cj

1

(1,5; 4,5>

2

3

6

2

2

(4,5; 7,5>

2

6

12

4

3

(7,5; 10,5>

4

9

36

8

4

(10,5; 13,5>

6

12

72

5

(13,5; 16,5>

13

15

195

6

(16,5; 19,5>

10

18

180

7

(19,5; 22,5>

5

21

105

8

(22,5; 25,5>

4

24

96

9

(25,5; 28,5>

3

27

81

10

(28,5; 31,5>

1

30

30

k=

10

h=3

n=5

0

Suma=81

3

Liczebność

skumulowan

a j-tej klasy

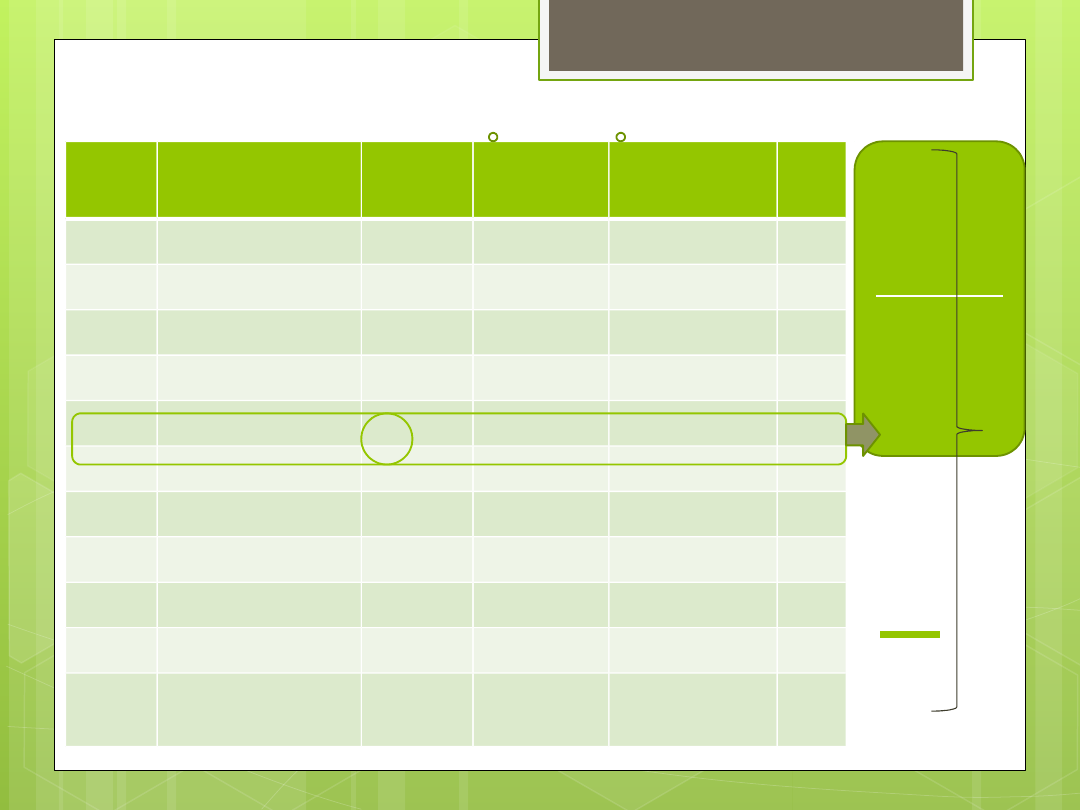
Szereg rozdzielczy (część
6)

j

(x

dj

; x

gj

>

f

j

x

j

x

j *

f

j

f

cj

1

(1,5; 4,5>

2

3

6

2

2

(4,5; 7,5>

2

6

12

4

3

(7,5; 10,5>

4

9

36

8

4

(10,5; 13,5>

6

12

72

14

5

(13,5; 16,5>

13

15

195

27

6

(16,5; 19,5>

10

18

180

37

7

(19,5; 22,5>

5

21

105

42

8

(22,5; 25,5>

4

24

96

46

9

(25,5; 28,5>

3

27

81

49

10

(28,5; 31,5>

1

30

30

50

k=

10

h=3

n=50

Suma=81

3

Mediana:

połowa

obserwacji

poniżej i

połowa

powyżej

1
2
3
4
5
6
7
8
9
1

0
1

1
1

2
1

3

3 p-kty

Szereg rozdzielczy (część
3)

j

(x

dj

; x

gj

>

f

j

x

j

x

j *

f

j

f

cj

1

(1,5; 4,5>

2

3

6

2

2

(4,5; 7,5>

2

6

12

4

3

(7,5; 10,5>

4

9

36

8

4

(10,5; 13,5> 6

12

72

14

5

(13,5; 16,5> 13

15

195

27

6

(16,5; 19,5> 10

18

180

37

7

(19,5; 22,5> 5

21

105

42

8

(22,5; 25,5> 4

24

96

46

9

(25,5; 28,5> 3

27

81

49

10

(28,5; 31,5> 1

30

30

50

k=

10

h=3

n=50

Suma=81

3

(n/2 – fc

j

– 1

)

f

j

* h

j

me= xd

j

+