Analiza kowariancji

Metodologia ze statystyką

Kurs zaawansowany

Wykład 07

dr Rafał Albiński

Rodzaje schematów badawczych

• Schemat między osobami

– Kilka niezależnych grup, może

być więcej niż jedna zmienna
grupująca

• Powtarzane pomiary

– Kilka pomiarów dokonanych

na tych samych osobach
badanych

• Schemat mieszany

– Co najmniej jedna zmienna

grupująca plus powtarzany
pomiar

Jeszcze jedna metoda oparta o

analizę wariancji

• ANALIZA KOWARIANCJI

– To swego rodzaju dodatek do

standarodowej jednoczynnikowej
ANOVY w schemacie międzyosobami
(międzygrupowym)

• Dzięki tej metodzie możemy kontrolować

wpływ zmiennych, które – choć nie podlegają
naszej manipulacji – to mają wpływ na
zmienną zależną.

• Takie zmienne nazywamy kowariantami

(wspózmiennymi)

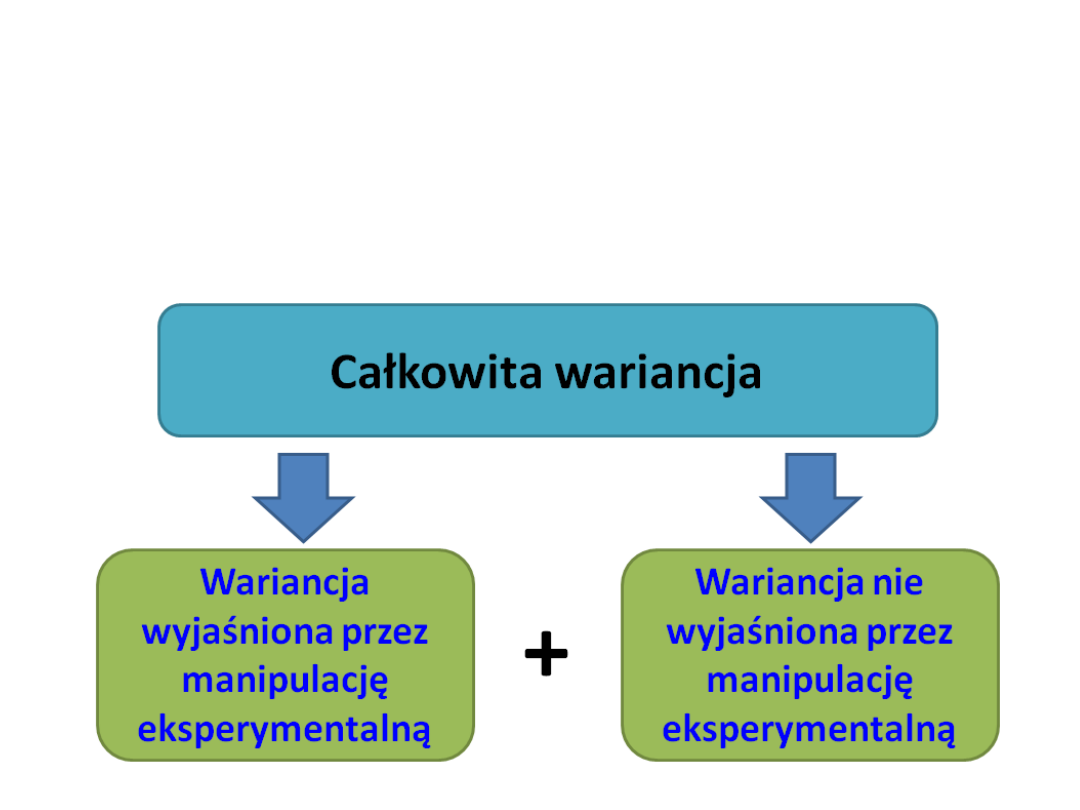
Całkowita wariancja

Wariancja

wyjaśniona

przez

manipulację

eksperymenta

lną

Wariancja nie

wyjaśniona

przez

manipulację

eksperymenta

lną

+

BŁĄD

Po co używamy kowariantów?

• Aby zredukować wariancję błędu

– Przy użyciu kowariantów (współzmiennych)

staramy się wyjaśnić część wariancji błędu. Jeżeli
się nam to uda, to będziemy lepiej w stanie ocenić
efekt naszej manipulacji (zmiennej niezależnej).

• Eliminacja zmiennych ubocznych

– Różne zmienne, których np. oryginalnie nie

planowaliśmy mierzyć mogą wpływać na efekty
naszych badań. Jeżeli uda nam się te zmienne
zidentyfikować i zmierzyć ANCOVA może usunąc
ich zakłócający wpływ na wyniki badania.

Założenia

• W zasadzie

ANCOVA ma ten
sam zestaw założeń
co ANOVA – z
niewielkimi
dodatkami 

• Najpierw

obejrzyjmy
założenia dzielone
przez obie metody.

ANOVA - założenia

• Niezależne grupy
• Zmienna zależna mierzona co

najmniej na skali przedziałowej

• Równoliczne grupy

– Lub przynajmniej takie, które nie różnią

się istotnie pod względem liczebności

– Test chi-kwadrat

• Normalny rozkład zmiennej

zależnej w każdej z grup

– test Kołmogorowa-Smirnowa (n > 100)
– test Shapiro-Wilk a(n < 100)

• Homogeniczność wariancji

– Test Levene’a

ANCOVA – dodatkowe założenia

• Niezależność kowariantu i

manipulacji
eksperymentalnej (warunku
badania)

• Homogeniczność relacji

zmiennej zależnej i
kowariantu (współzmiennej)

Tudzież: homogeniczność

nachylenia linii regresji
(homogeneity of the regression
slopes)

ANCOVA – dodatkowe założenia

• Niezależność kowariantu i

manipulacji eksperymentalnej
(warunku badania/zmienne
niezależnej) – kowariant i zmienna
niezależna

– Jak wspomniano, jeden ze sposobów użycia

ANCOVY zakłada zredukowanie wariancji
błędu dzięki włączeniu kowariantów do
analiz.

– Jednak żeby to było możliwe, kowariant musi

być niezależny od warunku
badawczego/zmiennej niezależnej (np. grupa
kontrola, grupa eksperymentalna 1, grupa
eksperymentalna 2).

– Ten warunek ogranicza nieco liczbę sytuacji,

w których możemy użyć analizy kowariancji.

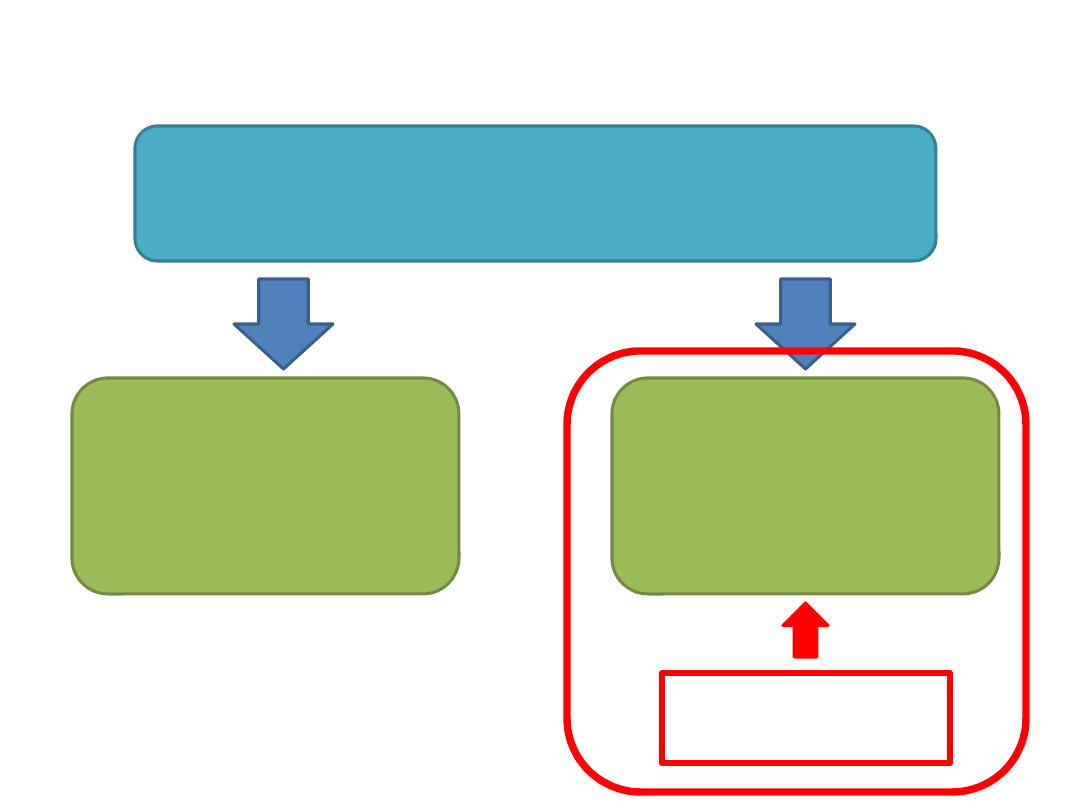
Kiedy używać analizy

kowariancji?

• Punkt odniesienia: typowa jednoczynnikowa

ANOVA (w schemacie międzygrupowym)

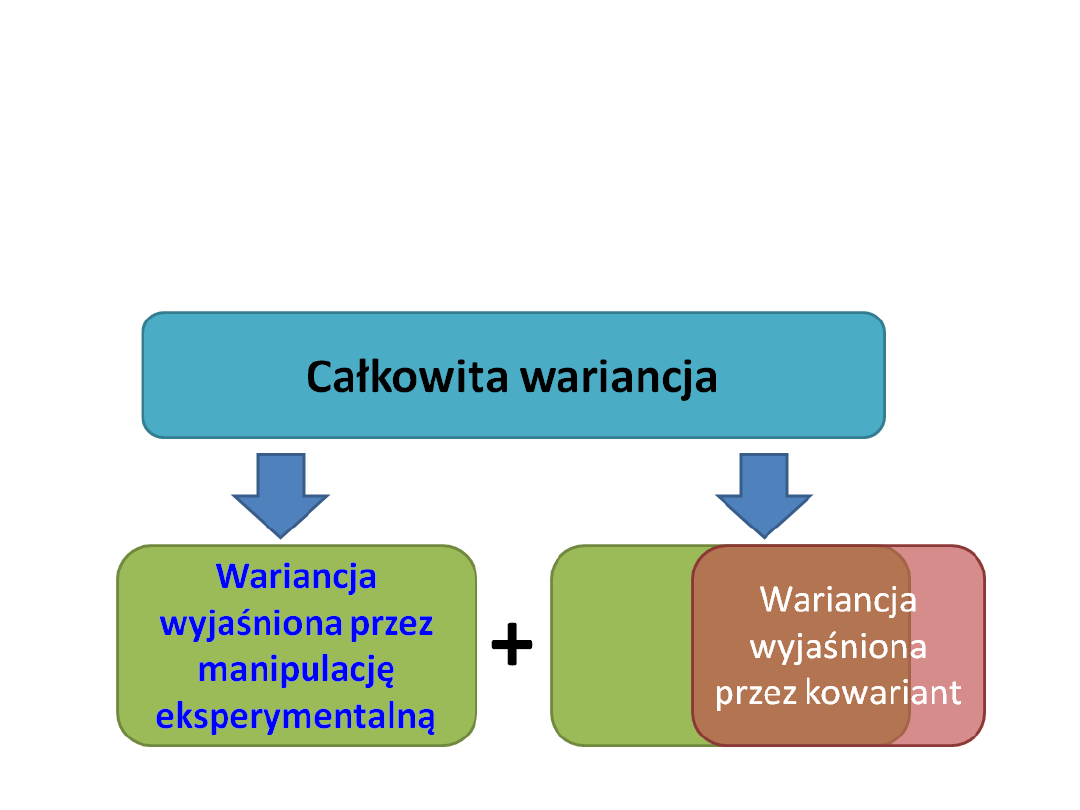
Kiedy używać analizy

kowariancji?

• Idealne warunki użycia analizy kowariancji

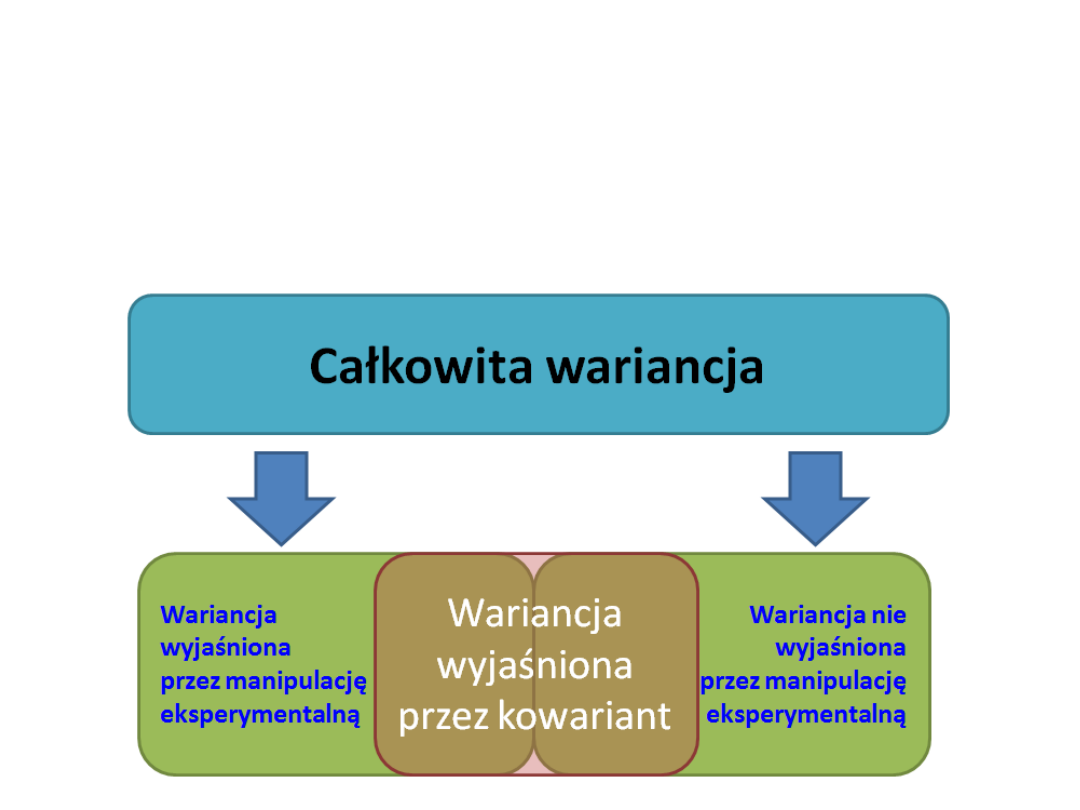
Kiedy używać analizy

kowariancji?

• Błędne użycie ANCOVY

Problem lęku i depresji

• Wyniki badań pokazują zazwyczaj,

że depresja i lęk są ze sobą
skorelowane

• Jeżeli chcemy porównać poziom

wykonania jakiegoś zadania przez
osoby lękowe i nie lękowe,
możemy odczuwać pokusę, żeby
dodać depresję jako kowariant

• Ale to kiepski pomysł, właśnie

dlatego, że depresja i lęk są
skorelowane (złamane będzie
założenie o niezależności
kowariantu od zmiennej
niezależnej/warunku badania)!

Problem lęku i depresji

• Dodanie depresji jako

kowariantu nie da nam
„czystego” efektu lęku!

• W rzeczywistości dodanie depresji

jako kowariantu zredukuje nasz
efekt, gdyż w rezultacie „zajmie”
część wariancji, którą można by
przypisać naszej
manipulacji/zmiennej niezależnej.

• Badacze często ignorują ten problem

.

• Później zobaczymy jak sprawdzić

założenie o niezależności kowariantu
i zmiennej niezależnej.

ANCOVA – dodatkowe założenia

• Homogeniczność relacji zmiennej

zależnej i kowariantu

– Używając ANCOVY patrzymy na relację

zmiennej zależnej i kowariantu.

– Zakładamy, że relacja tych dwóch zmiennych

jest jednakowa niezależnie od grupy
badawczej.

– Np. jeżeli w jednej z trzech grup w badaniu

jest dodatnia korelacja kowariantu i zmiennej
zależnej, to oczekujemy, że podobna relacja
(tj. pozytywna) pojawi się także w
pozostałych dwóch grupach.

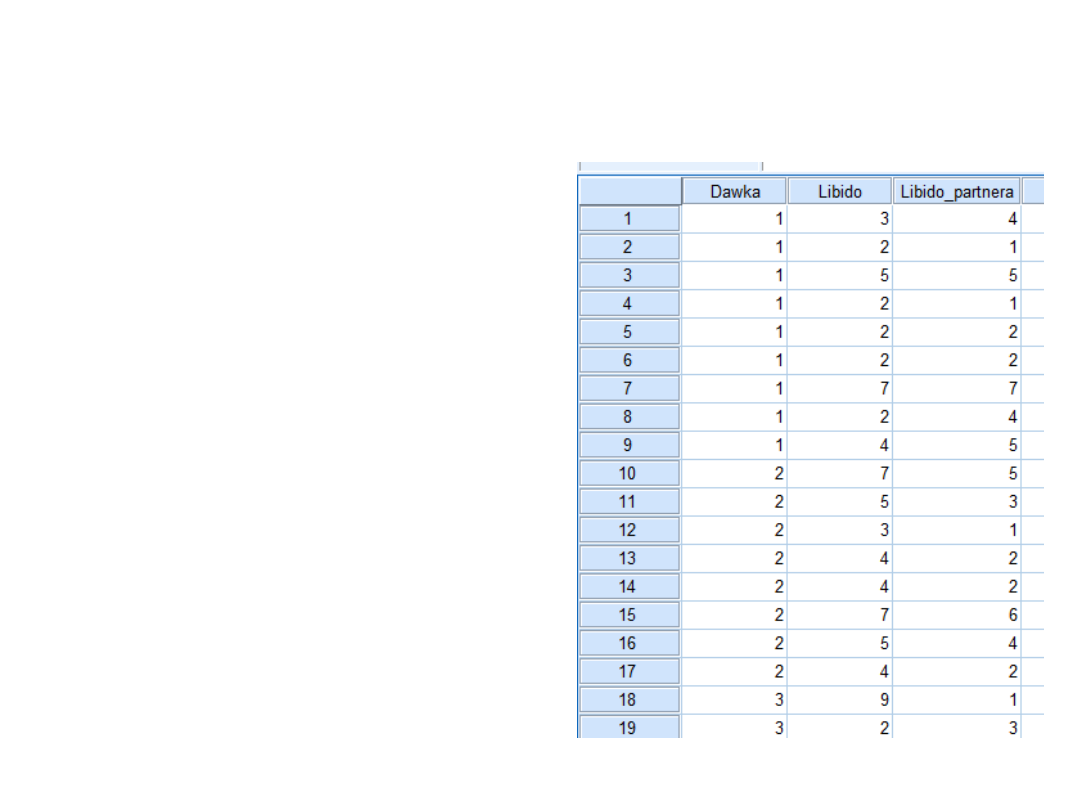
Przykład z Viagrą raz jeszcze

• Plik stworzony

przez Andy’ego
Fielda

– Zmienna

niezależna: dawka
(placebo, niska dawka,
wysoka dawka)

– Zmienna zależna:

libido (1-10)

– Kowariant: libido

partnerki (1-10)

Na początek – nowe założenie nr

1

• Testowanie niezależności

kowariantu i zmiennej niezależnej

– Kowariant: libido partnerki
– Chcemy sprawdzić, czy libido

partnerek jest podobne dla każdego
poziomu zmiennej niezależnej (tj.
dawki Viagry)

– Potrzebujemy dodatkowej analizy

wariancji

• Zmienna niezależna: dawka
• Zmienna zależna: libido partnerki

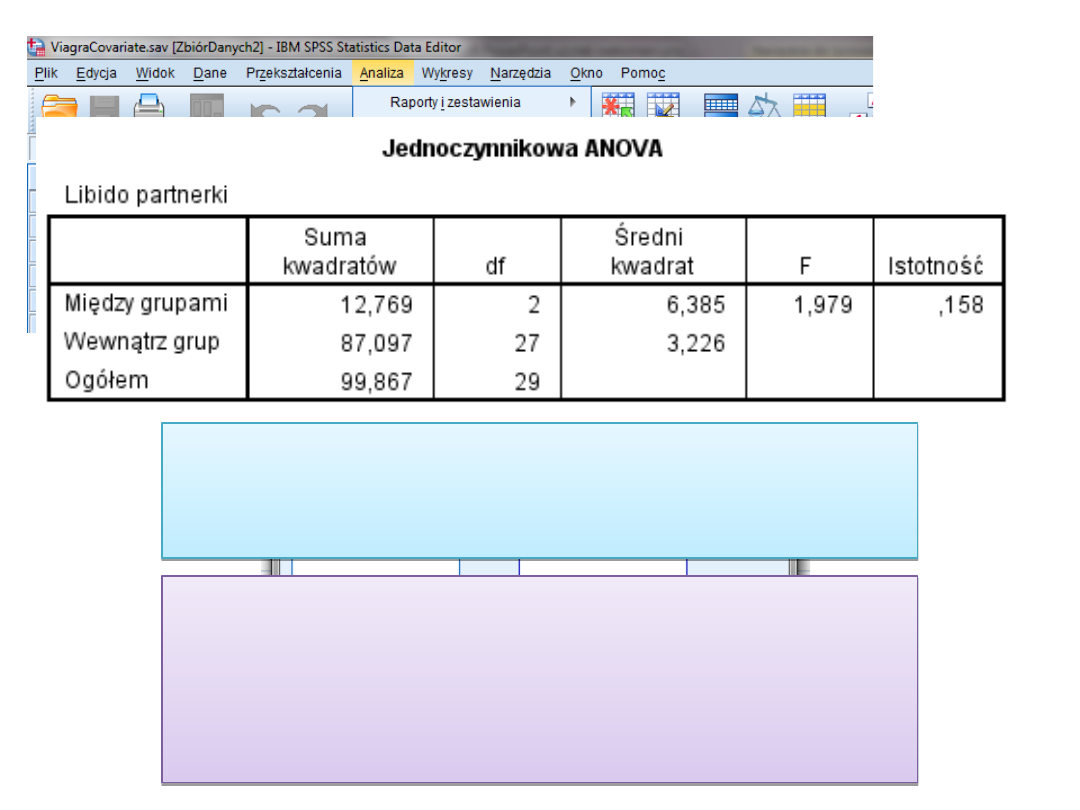
F (2,27) = 1,98; p

= 0,158

F (2,27) = 1,98; p

= 0,158

Nie ma istotny statystycznie

różnic w libido partnerek

pomiędzy trzema

porównywanymi grupami

Nie ma istotny statystycznie

różnic w libido partnerek

pomiędzy trzema

porównywanymi grupami

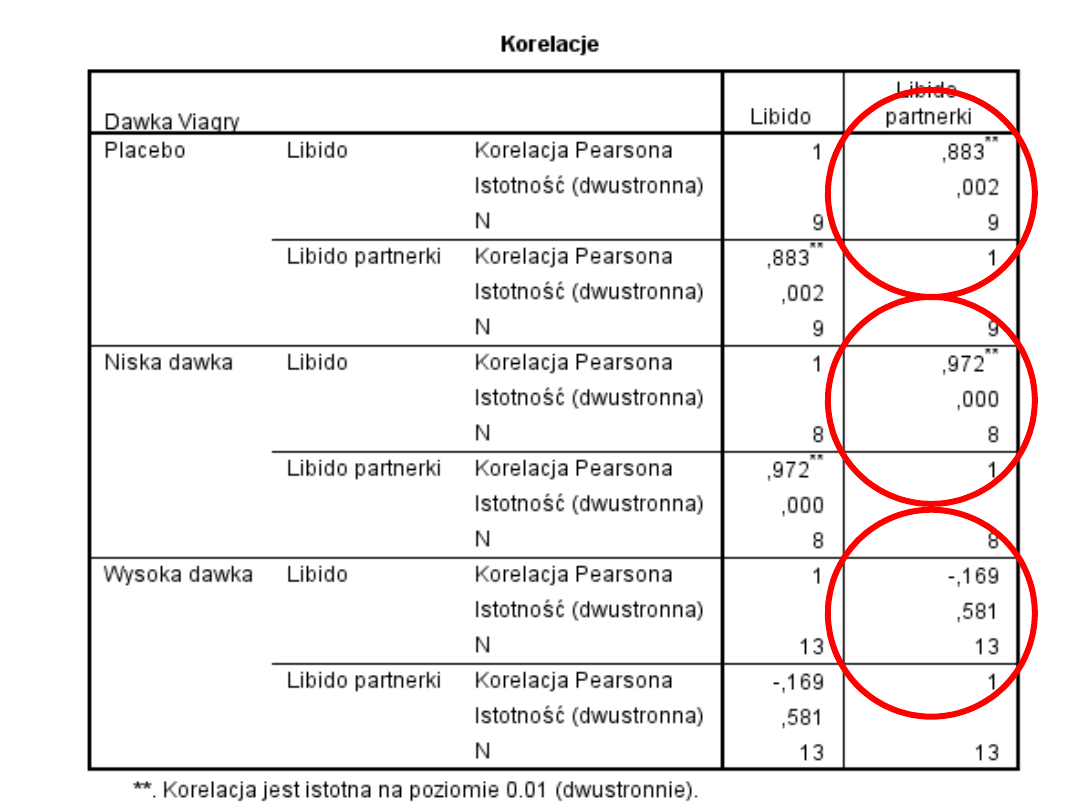
Na początek – nowe

założenie nr 2

Homogeniczność relacji zmiennej zależnej i
kowariantu

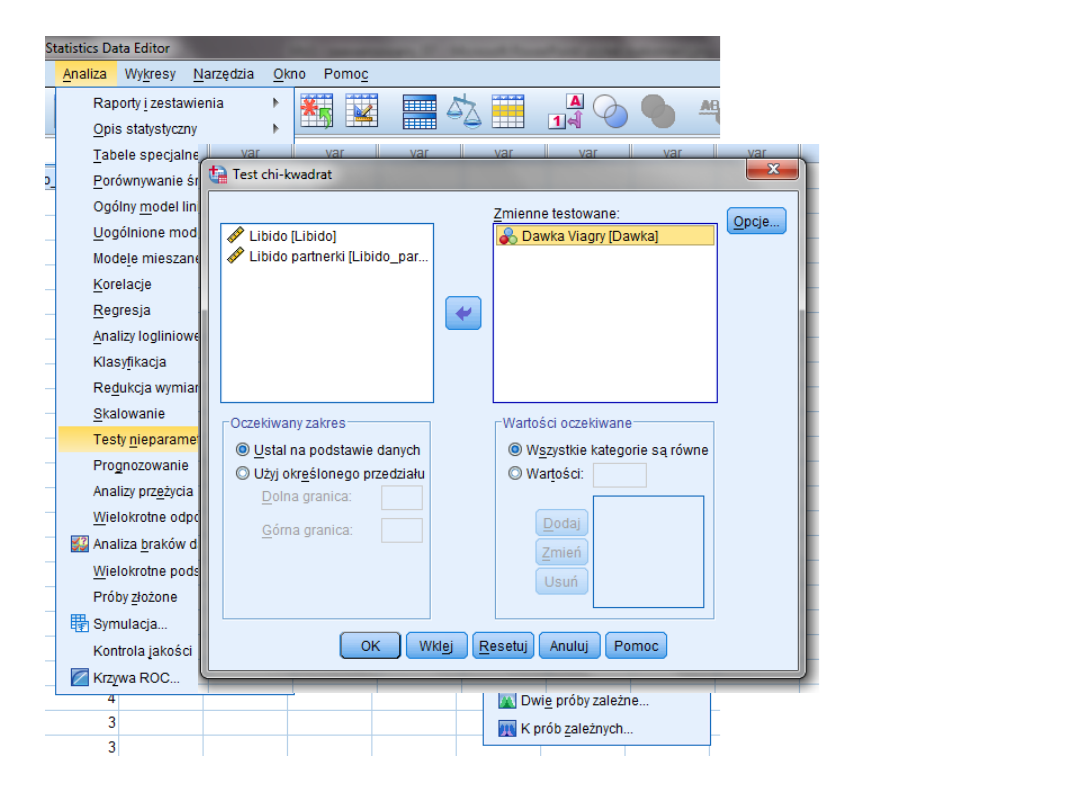
A co z równolicznością

grup?

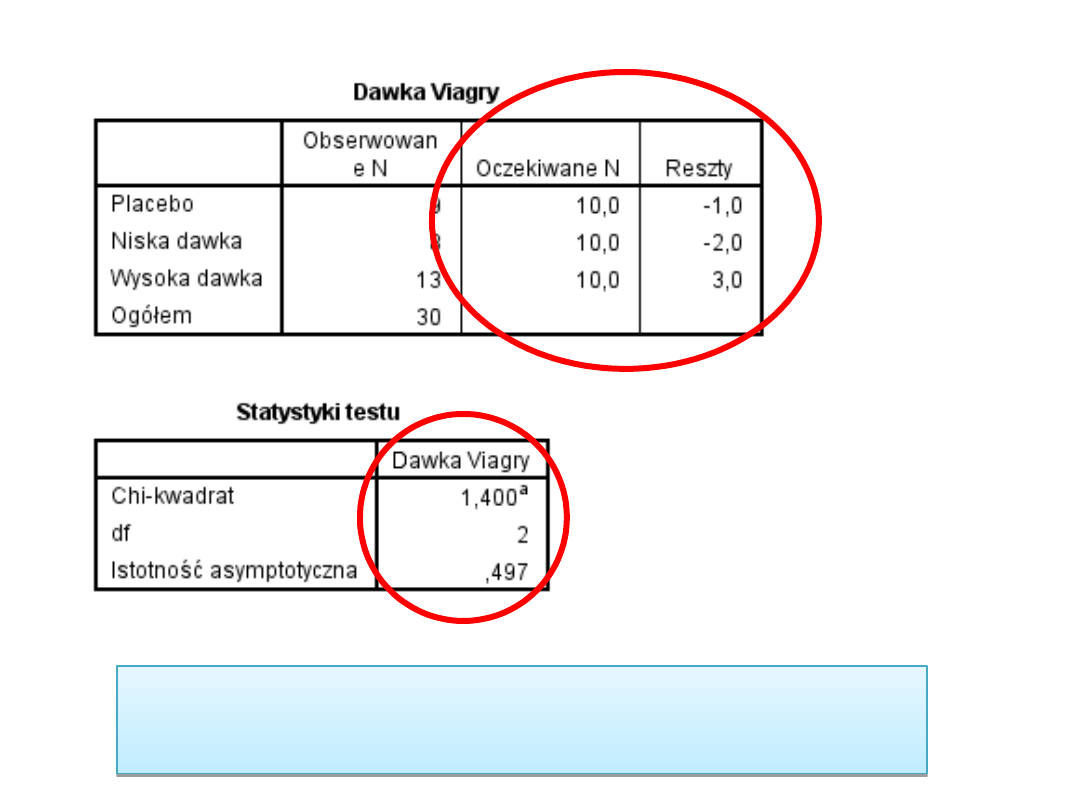
χ

2

(2) = 1,4; p =

0,497

χ

2

(2) = 1,4; p =

0,497

Warto by też
sprawdzić
założenie o
normalności
rozkładów
zmiennej
zależnej…
Ale to możecie
sprawdzić w
materiałach z
poprzednich
wykładów

ANCOVA => ANOVA (???)

Co by się stało, gdyby nie było kowariantu?

F (2,27) = 2,42; p

= 0,108

F (2,27) = 2,42; p

= 0,108

Wykonajmy w końcu ANCOVĘ 

Wykonajmy w końcu ANCOVĘ 

ANCOVA – główne wyniki

Współzmienna pozwala w sposób istotny

statystycznie przewidywać zmienną

zależną (p < 0,05) – libido badanych i libido

ich partnerek są ze sobą istotnie

powiązane.

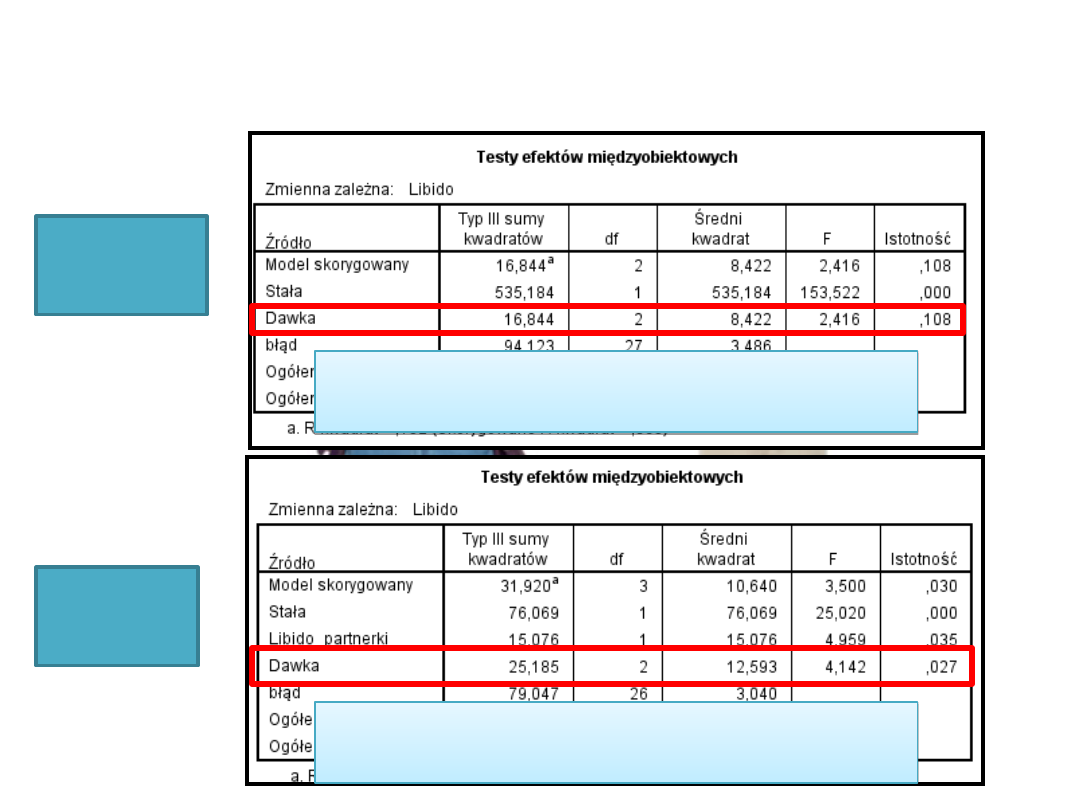
Co z naszą manipulacją (dawka Viagry)?

PRZE

D

PO

F (2,27) = 2,42; p =

0,108

F (2,27) = 2,42; p =

0,108

F (2,26) = 4,14; p <

0,05

F (2,26) = 4,14; p <

0,05

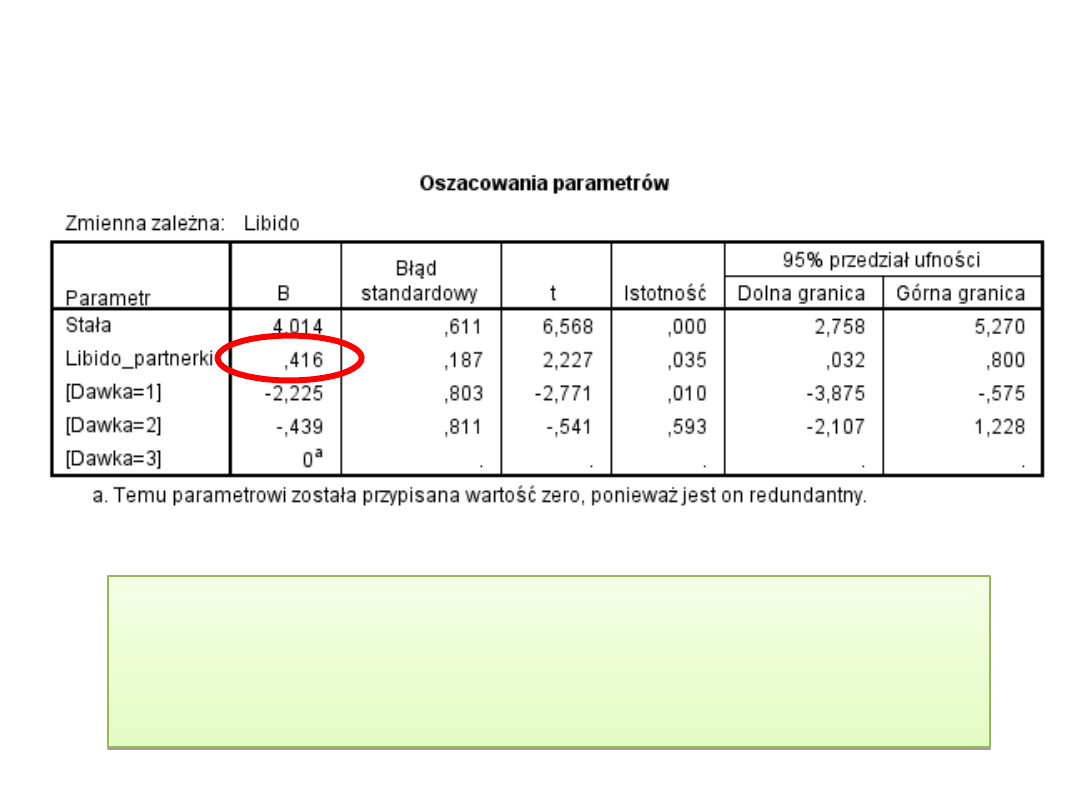
Kowariant

(współzmienna)

Jeżeli libido partnerki wzrośnie o jedną jednostkę,

wtedy libido partnera (tj. naszych badanych)

wzrośnie o 0,416 jednostki (nie ma tu jednak

zależności przyczynowo skutkowej)

Jeżeli libido partnerki wzrośnie o jedną jednostkę,

wtedy libido partnera (tj. naszych badanych)

wzrośnie o 0,416 jednostki (nie ma tu jednak

zależności przyczynowo skutkowej)

Testy post-hoc i

kontrasty…

• …wykonujemy w taki sam sposób,

jak to było pokazane na
wcześniejszych wykładach.

• DOŚĆ KONTRASTÓW I TESTÓW

POST HOC! 

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

DOŚĆ!!!

I to tyle w tym

temacie…