DZIESIĘTNY SYSTEM LICZBOWY
Do zapisu dowolnej liczby system wykorzystuje dziesięć
symboli (cyfr):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Dowolną liczbę w systemie dziesiętnym możemy przedstawić
jako następująca sumę:
(a
n-1
...a
1
a
0
)
(10)
= a
n-1
*10
(n-1)
+...+ a
1
*10
1
+ a
0
*10
0
=
gdzie: i - numer pozycji w liczbie,
a
i
- dowolna z cyfr od 0 do 9,
n - ilość cyfr (pozycji) w liczbie
Przykład:
424
(10)
= 4*10
2
+ 2*10
1
+ 5*10
0
pozycja jedynek
(0)
pozycja dziesiątek
(1)
pozycja setek (2)
1
n
0
i
i
i
10
a
DWÓJKOWY SYSTEM LICZBOWY
Do zapisu dowolnej liczby system wykorzystuje dwa
symbole (cyfry):
0, 1
Dowolną liczbę w systemie dwójkowym możemy
przedstawić jako następująca sumę:
(a
n-1
...a
1
a
0
)
B
= a
n-1
*2
(n-1)
+...+ a
1
*2
1
+ a
0
*2
0
=
gdzie: i - numer pozycji w liczbie,
a
i
- dowolna z cyfr (0 lub 1),
n - ilość cyfr (pozycji) w liczbie
Przykład:
10100
B
= 1*2
4
+ 0*2
3
+ 1*2
2
+ 0*2
1
+ 0*2
0
1
n
0
i
i
i
2
a
HEKSADECYMALNY
(SZESNASTKOWY) SYSTEM
LICZBOWY
Do zapisu dowolnej liczby system wykorzystuje szesnaście
symboli (cyfr i liter):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Dowolną liczbę w systemie heksadecymalnym możemy
przedstawić jako następująca sumę:
(a
n-1
...a
1
a
0
)
H
= a
n-1
*16
(n-1)
+...+ a
1
*16
1
+ a
0
*16
0
=
gdzie: i - numer pozycji w liczbie,
a
i
- dowolna cyfra heksadecymalna,
n - ilość cyfr (pozycji) w liczbie
Przykład:
1C2
H
= 1*16
2
+ C*16
1
+ 2*16
0
Bardzo łatwa konwersja pomiędzy zapisem dwójkowym i
szestnastkowym:
7 𝐴� 3
�
=0111
′
1010
′
1100
′
0011
1
n
0
i
i
i
16
a
INFORMACJA CYFROWA
W słowach cyfrowych wyróżnia się najstarszą i najmłodszą pozycję,
tj.
bit najbardziej znaczący
zwany najstarszym (ang.
MSB
- Most
Significant Bit)
oraz
bit najmniej znaczący
zwany najmłodszym (ang.
LSB
- Least
Significant Bit)
a
n-1
......................... a
0
MSB
LSB
Analogicznie możemy mówić o starszym i
najmłodszym bajcie lub o starszej lub młodszej
tetradzie
KODOWANIE
Zbiorem
kodowanym może
być zbiór
dowolnych
obiektów (cyfr,
liter, symboli
graficznych,
stanów
logicznych,
poleceń do
wykonania itp.)
Kodowaniem
nazywamy przyporządkowanie poszczególnym
obiektom zbioru kodowanego odpowiadających im
elementów zwanych słowami kodowymi, przy czym każdemu
słowu kodowemu musi odpowiadać dokładnie jeden element
kodowany
Kodowaniem
nazywamy przyporządkowanie poszczególnym
obiektom zbioru kodowanego odpowiadających im
elementów zwanych słowami kodowymi, przy czym każdemu
słowu kodowemu musi odpowiadać dokładnie jeden element
kodowany
A
B
C
010
111
100
001
Proces kodowania może
być opisem słownym,
wzorem (zależnością
matematyczną), tabelą
kodową itp.
Kodem liczbowym nazywamy taki kod, który liczbom dowolnego
systemu będzie przyporządkowywał słowa kodowe w postaci
zero-jedynkowej (binarnej)
Kodem liczbowym nazywamy taki kod, który liczbom dowolnego
systemu będzie przyporządkowywał słowa kodowe w postaci
zero-jedynkowej (binarnej)
KODOWANIE LICZB I TEKSTÓW
Kody binarne
kod naturalny NKB
kod BCD
kod Gray’a
inne kody
Kodowanie znaków (tekstów)
2
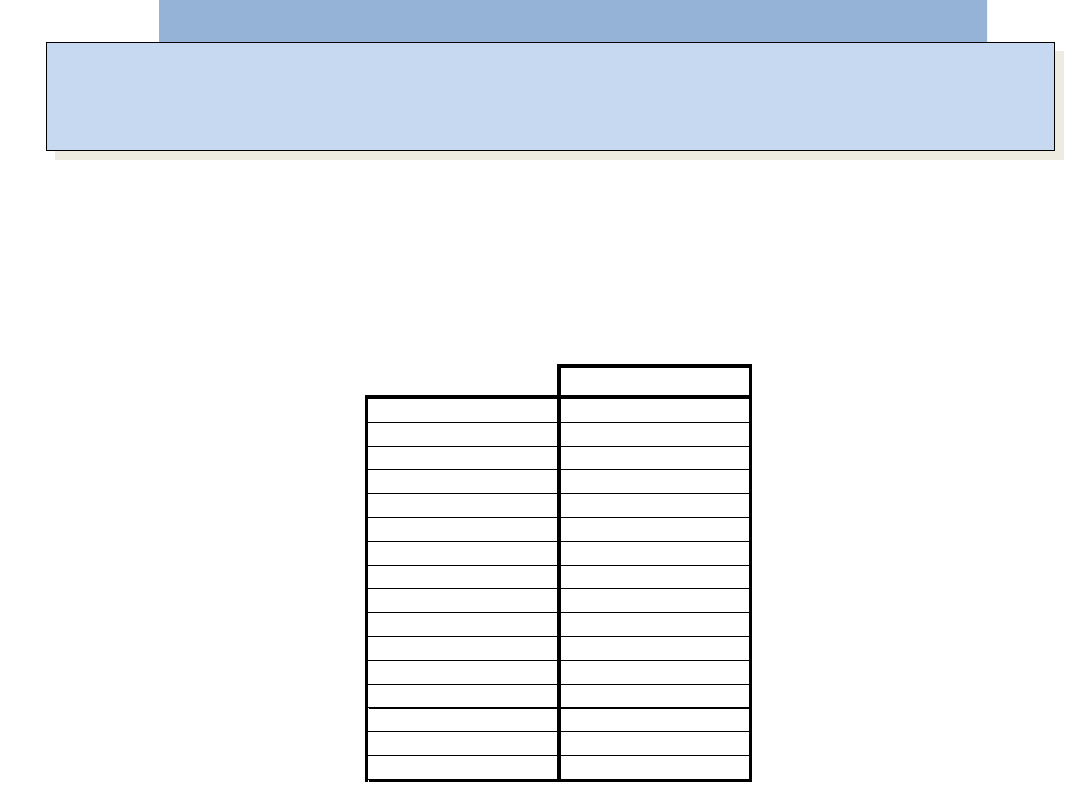
NATURALNY KOD BINARNY (NKB)
Jeżeli dowolnej liczbie dziesiętnej przyporządkujemy
odpowiadająca jej liczbę binarną, to otrzymamy naturalny
kod binarny (NKB)
Jeżeli dowolnej liczbie dziesiętnej przyporządkujemy
odpowiadająca jej liczbę binarną, to otrzymamy naturalny
kod binarny (NKB)
Minimalna długość
k
słowa binarnego reprezentującego liczbę
dziesiętną
A
musi spełniać warunek:
Oznacza to, że aby zakodować liczbę dziesiętną w zakresie 0-15
wystarczy wykorzystać jedną tetradę (długość słowa kodowego
k=4) gdyż
1
2A
2
A
k
31
2
15
4
NKB
0
0000
1
0001
2
0010
3
0011
4
0100
5
0101
6
0110
7
0111
8
1000
9
1001
10
1010
11
1011
12
1100
13
1101
14
1110
15
1111
KOD PROSTY BCD
Gdy w systemie wygodnie jest operować liczbami dziesiętnymi
stosowany jest kod BCD. Liczba terad kodu BCD jest bowiem
równa liczbie pozycji dziesiętnych reprezentowanej liczby. Np.
dziesiętna liczba 6-pozycyjna (000000-999999) jest kodowana
na 24 bitach
Konstrukcja:
• każdej cyfrze dziesiętnej przyporządkowujemy czterocyfrową
liczbę dwójkową w kodzie NKB
*)
;
• słowo kodowe w kodzie prostym BCD otrzymujemy zapisując
każdą cyfrę liczby dziesiętnej w postaci tetrady binarnej
463
D
=
0100’0110’0011
BCD
67
D
= 0110’0111
BCD
KODOWANIE ZNAKÓW
Początki:
• Harald C. M. Morse (kropka - kreska - ....);
• Anatol de Baudot (dalekopis);
• w pierwszych maszynach cyfrowych - kod dalekopisowy
5-bitowy, a potem 8-bitowy (EBCDIC);
W 1977 roku kiedy to ANSI (American National Standards
Institute) zatwierdził kod ASCII (The American Standard Code for
Information Interchange).
Jest to 7-bitowy kod (8 bit do kontroli parzystości),
definiujący 128-elementowy zestaw znaków (character
set) o wartościach kodowych od 0 do 127. Zestaw
zawiera litery łacińskie (duże i małe), cyfry i znaki
interpunkcji
oraz
różne
znaki
specjalne.
Międzynarodowa Organizacja Standaryzacji - ISO,
nadała amerykańskiemu systemowi kodowania status
standardu międzynarodowego oznaczonego jako ISO
646.
Kod ASCII rozszerzony wprowadza dodatkowe 128 znaków
wykorzystując mało używany bit parzystości:
IBM wprowadza
• Code Page 474 dla USA
• Code Page 852 dla Europy Wschodniej
KODOWANIE ZNAKÓW
kod ASCII
8
Bit kontroli parzystości
7
0
0
0
0
1
1
1
1
6
0
0
1
1
0
0
1
1
Numery bitów słowa
5
0
1
0
1
0
1
0
1
4
3
2
1
0
0
0
0
NUL DEL
SP
0
@
P
‘
p
0
0
0
1
SOH DC1
!
1
A
Q
a
q
0
0
1
0
STX DC2
„
2
B
R
b
r
0
0
1
1
ETX DC3
3
C
S
c
s
0
1
0
0
EOT DC4
$
4
D
T
d
t
0
1
0
1
ENQ NAK
%
5
E
U
e
u
0
1
1
0
ACK SYN
&
6
F
V
f
v
0
1
1
1
BEL
ETB
`
7
G
W
g
w
1
0
0
0
BS
CAN
(
8
H
X
h
x
1
0
0
1
HT
EM
)
9
I
Y
i
y
1
0
1
0
LF
SUB
*
:
J
Z
j
z
1
0
1
1
VT
ESC
+
;
K
[
k
{
1
1
0
0
FF
FS
,
<
L
\
l
|
1
1
0
1
CR
GS
-
=
M
]
m
}
1
1
1
0
SO
RS
.
>
N
n
~
1
1
1
1
SI
US
/
?
O
o
DEL
Document Outline