Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

1 

 

 

Zasada  włączeń  i  wyłączeń  (tylko  zbiory 
skończone): 



 

 dla dwóch zbiorów: 

                              



 

 dla trzech zbiorów: 

                                

                                          

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

2 

 

 



 

 dla   zbiorów: 

     

 

       

 

        

 

   

 

 

 

       

   

 

   

 

   

  

 

  

 

   

 

   

 

       

 

           

     

    

 

  

 

   

 

       

 

  

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

3 

 

 

Przykład: 

Ile  jest  liczb  całkowitych  w  zbiorze  {1,  2,  3,  …, 
3000}, które są podzielne przez 9 lub 11 lub 13? 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

4 

 

 

Dla zbiorów rozłącznych: 

     

 

       

 

 

 

   

 

   

 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

5 

 

 

Prawo mnożenia (tylko zbiory skończone): 

  

 

   

 

       

 

      

 

      

 

          

 

  

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

6 

 

 

Przykład: 

Niech                        .  Ile  słów  co  najwyżej 
5-literowych można zbudować z tego alfabetu? 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

7 

 

 

Przykład: 

                                       

               

 

   

 

   

 

                     

                                   

 

                  

 

  

                

           =? 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

8 

 

 

Niech 

dany 

będzie 

zbiór 

 

 

 

złożony 

z   elementów. 
 -elementową 

(     ) 

wariacją 

bez 

powtórzeń  

 

 

 ze zbioru  

 

 nazywamy każdy  -

elementowy  ciąg  utworzony  z  elementów 
zbioru   

 

  taki,  że  elementy  w  tym  ciągu  nie 

mogą się powtarzać. 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

9 

 

 

Liczba wszystkich  -elementowych wariacji bez 
powtórzeń ze zbioru  

 

 wyraża się wzorem: 

  

 

 

   

  

        

                                

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

10 

 

 

Jeśli         to  wariację  bez  powtórzeń 
nazywamy permutacją  

 

 zbioru  

 

. 

Czyli: 

 

 

   

 

 

 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

11 

 

 

Liczba  wszystkich  permutacji  zbioru   

 

  wyraża 

się wzorem: 

  

 

      

 

 

   

  

        

 

  

  

     

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

12 

 

 

 -elementową  wariacją  z  powtórzeniami   

 

 

 

ze  zbioru   

 

  nazywamy  każdy   -elementowy 

ciąg utworzony z elementów zbioru  

 

 taki, że 

elementy w tym ciągu mogą się powtarzać. 

 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

13 

 

 

Liczba  wszystkich   -elementowych  wariacji 
z powtórzeniami  ze  zbioru   

 

  wyraża  się 

wzorem: 

  

 

 

     

 

 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

14 

 

 
 -elementową  (     )  kombinacją  bez 
powtórzeń  

 

 

 ze zbioru  

 

 nazywamy każdy  -

elementowy  podzbiór  utworzony  z  elementów 
zbioru   

 

.  Skoro  podzbiór,  to  elementy  nie 

mogą się powtarzać. 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

15 

 

 

Liczba  wszystkich   -elementowych  kombinacji 
bez  powtórzeń  ze  zbioru   

 

  wyraża  się 

wzorem: 

  

 

 

     

 

    

  

           

 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

16 

 

 



 

   

 

 

      

 

   

  



 

   

 

 

      (zbiór pusty) 



 

   

 

 

      (cały zbiór) 



 

   

 

 

      

 

   

      

 



 

   

 

 

      

 

 

      

 

  

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

17 

 

 
 -elementową  kombinacją  z  powtórzeniami 
 

 

 

  ze  zbioru   

 

  nazywamy  każdy   -

elementowy 

wielozbiór 

utworzony 

z elementów  zbioru   

 

.  Skoro  wielozbiór,  to 

elementy mogą się powtarzać. 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

18 

 

 

Liczba  wszystkich   -elementowych  kombinacji 
z powtórzeniami  ze  zbioru   

 

  wyraża  się 

wzorem: 

  

 

 

              

 

   

            

           

 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

19 

 

 

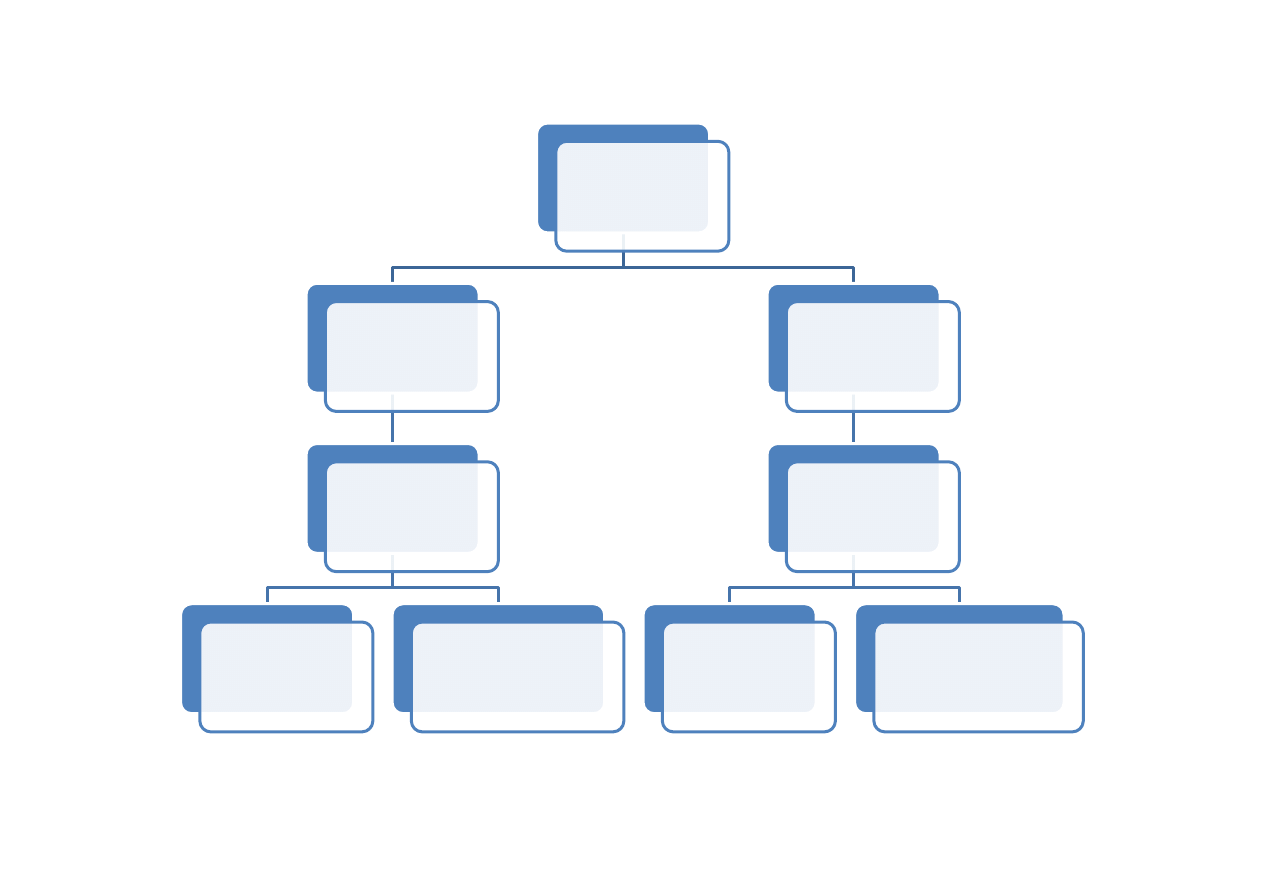
Czy liczy się 

kolejność? 

Nie 

Kombinacje 

Czy są 

powtórzenia? 

Nie 

Kombinacje 

bez powtórzeń 

Tak 

Kombinacje 

z powtórzeniami 

Tak 

Wariacje 

Czy są 

powtórzenia? 

Nie 

Wariacje 

bez powtórzeń 

Tak 

Wariacje 

z powtórzeniami 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

20 

 

 

Przykład: 

Pięć  samochodów  wjechało  na  parking,  na 
którym jest 13 wolnych miejsc. Na ile sposobów 
mogą zaparkować? 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

21 

 

 

Przykład: 

Pięć 

identycznych 

(nierozróżnialnych) 

samochodów  wjechało  na  parking,  na  którym 
jest 13  wolnych miejsc. Na ile sposobów mogą 
zaparkować? 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

22 

 

 

Przykład: 

Na  ile  sposobów  można  wyciągnąć  bez 
zwracania  osiem  kart  z  talii  52  kart,  wśród 
których  będą  dokładnie  cztery  piki,  jeden  trefl 
i dwa kiery? 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

23 

 

 

Przykład: 

Na  ile  sposobów  można  wyciągnąć  ze 
zwracaniem  osiem  kart  z  talii  52  kart,  wśród 
których będą cztery piki, jeden trefl i dwa kiery? 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

24 

 

 

Przykład: 

Na  ile  sposobów  można  ułożyć  sześć 
ponumerowanych 

kul 

w 

dziewięciu 

pojemnikach? 

 

 

Matematyka Dyskretna – wykład 4 

dr Marcin Raniszewski 

25 

 

 

Przykład: 

Na 

ile 

sposobów 

można 

utworzyć 

siedmiocyfrową  liczbę  o  różnych  cyfrach,  tak 
aby miała dokładnie trzy cyfry parzyste i cztery 
cyfry nieparzyste?