
Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
1
Twierdzenie o indukcji dla tezy :
Jeżeli:
krok 1: teza jest prawdziwa dla ;
krok 2: dla dowolnego prawdziwa jest
implikacja: ;
to teza jest prawdziwa dla .

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
2
Twierdzenie o indukcji dla tezy
:
Jeżeli:
krok 1: teza jest prawdziwa dla
;
krok 2: dla dowolnego
prawdziwa jest
implikacja: ;
to teza jest prawdziwa dla
.
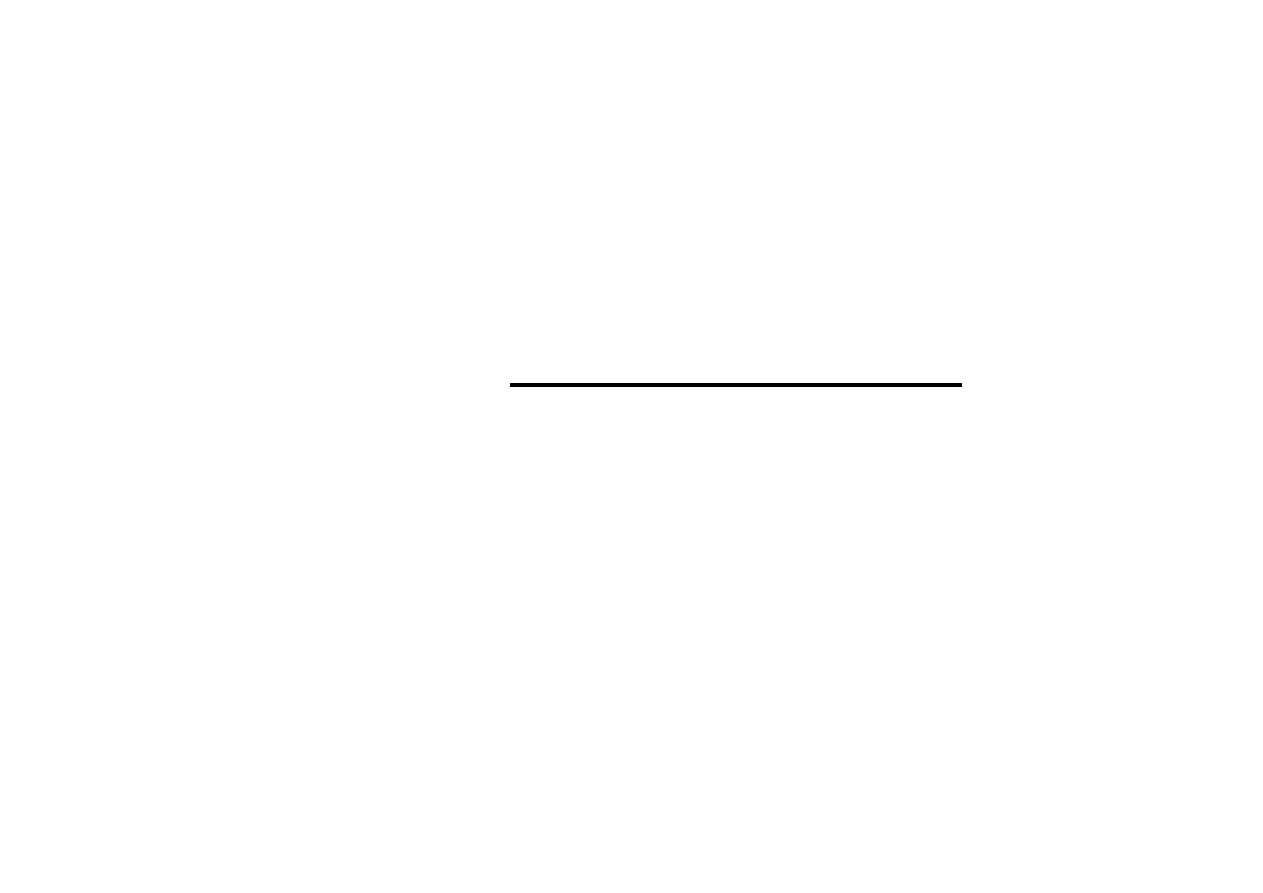
Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
3
Udowodnić indukcyjnie:
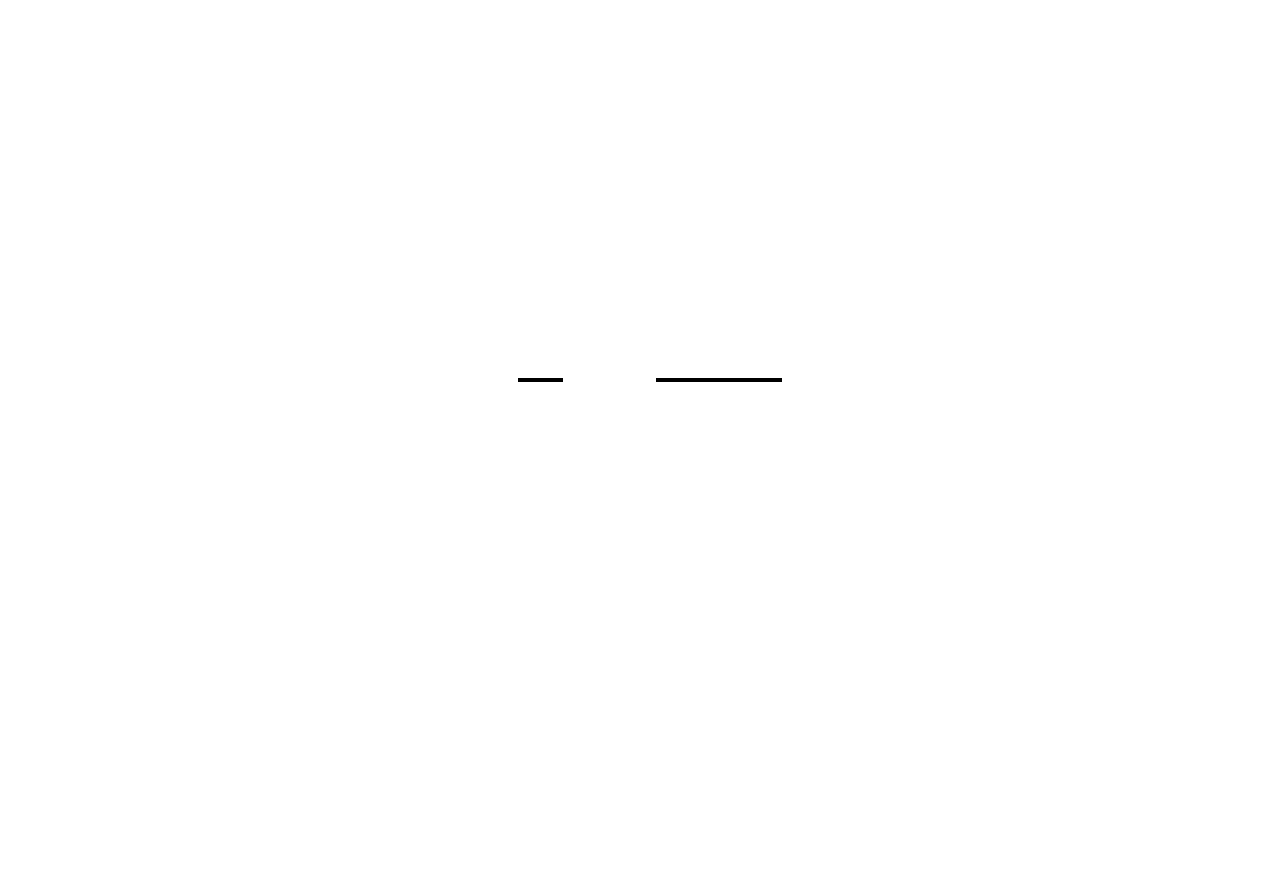
Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
4
Udowodnić indukcyjnie:

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
5
Silnia:
,
gdzie: .
Dodatkowo określamy:

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
6
Dla :
Dla :

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
7
Symbol Newtona:
gdzie: , .

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
8
1.
2.
3.
4.

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
9
5.
6.

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
10
Dwumian Newtona:
czyli:

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
11
Dwumian Newtona (przypadek dla ):

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
12
Trójkąt Pascala:

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
13
Udowodnić indukcyjnie:

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
14
Udowodnić indukcyjnie:

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
15
Udowodnić indukcyjnie:

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
16
Udowodnić indukcyjnie:

Matematyka Dyskretna – wykład 3
dr Marcin Raniszewski
17
Udowodnić indukcyjnie:
Wyszukiwarka
Podobne podstrony:
MD wykl 06 id 290158 Nieznany
MD wykl 08 id 290160 Nieznany
MD wykl 07 id 290159 Nieznany
MD cw 03 id 290124 Nieznany
MD wykl 10 id 290163 Nieznany
MD wykl 06 id 290158 Nieznany
LsciA gi z wykL,adAlw id 10118 Nieznany
Konserwacja 2014 03 id 245321 Nieznany
ais 03 id 53431 Nieznany (2)
Chemia 03 id 557778 Nieznany
mat fiz 2007 12 03 id 282357 Nieznany
Module 03 id 305940 Nieznany
MD cw 08 id 290129 Nieznany
MD cw 02 id 290123 Nieznany
III CZP 43 03 id 210280 Nieznany
MD cw 04 id 290125 Nieznany
MD cw 12 id 290134 Nieznany
AG 03 id 52753 Nieznany
kurs ZERO OSN wiczenie 03 id 25 Nieznany
więcej podobnych podstron