
Automatyka i sterowanie
Krzysztof Marzjan

Stabilność układów automatycznej regulacji.
UAR jest stabilny wtedy i tylko wtedy gdy pierwiastki równania charakterystycznego leżą w lewej
półpłaszczyźnie zmiennej zespolonej.
0
)
(
)
(
)
(
)
(
=
⇒
=
s
M
s
M
s
L
s
G
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
=
−
=
⇒
+
=
+
=
A
sI
det
s
M
t
Du
t
Cx
t
y
t
Bu
t
Ax
t
x
dt
d
Przyjmujemy:
2
Automatyka i sterowanie – stabilność układów ciągłych
0
1
2
2
2
2
1
1
)
(
a
s
a
s
a
s
a
s
a
s
a
s
M
n
n
n
n
n
n
+
+
+
+
+
+
=
−
−
−
−
K
Kryteria algebraiczne
Kryterium Hurwitz’a
Warunek konieczny
Wszystkie współczynniki równania charakterystycznego istnieją i są dodatnie.
Warunek wystarczający
Budujemy wyznacznik
0
2
1
0
4
3
2
2
3
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
a
a
a
a
a
a
a
a
a
a
a
n
n
n
n
n
L
L
K
M
M
M
O
M
M
L
L
−
−
−
=
∆
3
Automatyka i sterowanie – stabilność układów ciągłych
współczynniki równania charakterystycznego
zwiększanie indeksu
zmniejszanie indeksu

Wyznacznik
n
∆
oraz wszystkie podwyznaczniki główne
1
,
2
,
1
−
=
∆
n
i
i
K
są dodatnie:
1
1
−
=
∆
n
a
2
3
1
2
−
−
−
=
∆
n
n
n
n
a
a
a
a
L
5
6
7
2
3
4
1
3
0
−
−
−
−
−
−
−
=
∆
n
n
n
n
n
n
n
n
a
a
a
a
a
a
a
a
warto zauważyć, że jeżeli warunek konieczny jest spełniony to wystarczy obliczyć wyznaczniki od
2
∆
do
1
−
∆
n
, bo
4
Automatyka i sterowanie – stabilność układów ciągłych
1
0
−
∆
=
∆
n
n
a

Kryterium Routh’a
Warunek konieczny
Wszystkie współczynniki równania charakterystycznego istnieją i są dodatnie.
Warunek wystarczający
Budujemy tablicę
1
1
2
1
2
3
3
2
1
2
1
2
3
3
2
1
0
2
4
5
3
1
1
3
5
4
2
0
1
3
2
1
z
w
c
c
c
c
c
n
b
b
b
b
b
n
a
a
a
a
a
a
n
a
a
a
a
a
a
n
n
n
n
n
n
n
n
n
n
n
M
M
L
L
L
L
−
−
−
−
−
−
−
−
−
−
−
−
5
Automatyka i sterowanie – stabilność układów ciągłych
współczynniki
równania
charakterystycznego
n - nieparzyste
wielkości
obliczane
numer
wiersza

6
Automatyka i sterowanie – stabilność układów ciągłych
1
1
2
2
2
3
2
1
2
2
2
3
2
1
1
3
5
3
1
0
2
4
4
2
0
1
3
2
0
1
z
w
c
c
c
c
c
n
b
b
b
b
b
n
a
a
a
a
a
n
a
a
a
a
a
a
n
n
n
n
n
n
n
n
n
n
n
M
M
L
L
L
L
−
−
−
−
−
−
−
−
−
−
współczynniki
równania
charakterystycznego
n - parzyste
wielkości
obliczane
numer
wiersza

7
Automatyka i sterowanie – stabilność układów ciągłych
1
3
1
2
1
−
−
−
−
−
=
n
n
n
n
n
a
a
a
a
a
b
L
1
5
1
4
2
−
−
−
−
−
=
n
n
n
n
n
a
a
a
a
a
b
0
1
1
0
2
1
0
1
1
2
1
0
a
a
a
a
a
b
lub
a
a
a
a
a
b
n
n
n
n
n
n
n
n
=
−
=
−
=
−
−
−
−
−

1
2
1
3
1
1
b
b
b
a
a
c
n
n
−
=
−
−
L
1
3
1
5
1
2
b
b
b
a
a
c
n
n
−
=
−
−
Układ jest stabilny jeżeli w pierwszej kolumnie tablicy Routh’a wszystkie współczynniki są dodatnie.
8
Automatyka i sterowanie – stabilność układów ciągłych
Ilość zmian znaku w tej kolumnie jest równa liczbie pierwiastków w prawej półpłaszczyźnie.

Kryterium Nyquista
Układ otwarty o transmitancji operatorowej
)
(
)
)(
(
)
(
,
)
(
)
(
)
(
0
02
01
0
0
0
0
n
s
s
s
s
s
s
s
M
s
M
s
L
s
G
−
−
−
=
=
L
i transmitancji widmowej
ω
ω
j
s
s
G
j
G
=
=
)
(
)
(
0
0
daje układ zamknięty o transmitancji
)
(
)
)(
(
)
(
,
)
(
)
(
)
(
)
(
)
(
)
(
2
1
0
0
0
0
n
s
s
s
s
s
s
s
M
s
M
s
L
s
M
s
L
s
L
s
G
−
−
−
=
=
+
=
L
Twierdzenie
Jeżeli M
0
(s) ma k pierwiastków w prawej i n-k lewej półpłaszczyżnie zmiennej zespolonej (nie ma pierwiastków na
osi liczb urojonych), to M(s) ma n pierwiastków w lewej półpłaszczyźnie wtedy i tylko wtedy gdy:
{
}
{
}
π
ω
π
ω
ω
ω
k
j
G
arg
k
j
G
arg
=
+
∆
⇔
=
+
∆
∞
<
<
∞
<
<
∞
−
)
(
1
2
)
(
1
0
0
0
9
Automatyka i sterowanie – stabilność układów ciągłych
(charakterystyka amplitudowo – fazowa układu otwartego
)
(
0
ω
j
G
obejmuje w kierunku dodatnim punkt (-1, j0) k
razy).

Dowód
)
(
)
(
)
(
1
0
0
s
M
s
M
s
G
=
+
{
}
{
}
{
}
{
}
{
}
π
π
π
π
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
k
k
k
n
n
s
j
arg
s
j
arg
j
M
arg
j
M
arg
j
G
arg
n
i
i
n
i
i
2
]
)
[(
)
(
)
(
)
(
1
1
0
1
0
0
=
−
−
−
=
−
∆
−
−
∆
=
=
∆
−
∆
=
+
∆
∑
∑
=
∞
<
<
∞
−
=
∞
<
<
∞
−
∞
<
<
∞
−
∞
<
<
∞
−
∞
<
<
∞
−
{
}
π
ω
ω
=
−
∆
∞
<
<
∞
−
i
s
j
arg
{
}
π
ω
ω
−
=
−
∆
∞
<
<
∞
−
i
s
j
arg
10
Automatyka i sterowanie – stabilność układów ciągłych
s
i
jω
Re
Im
jω-s
i
s
i
jω
Re
Im
jω-s
i
11
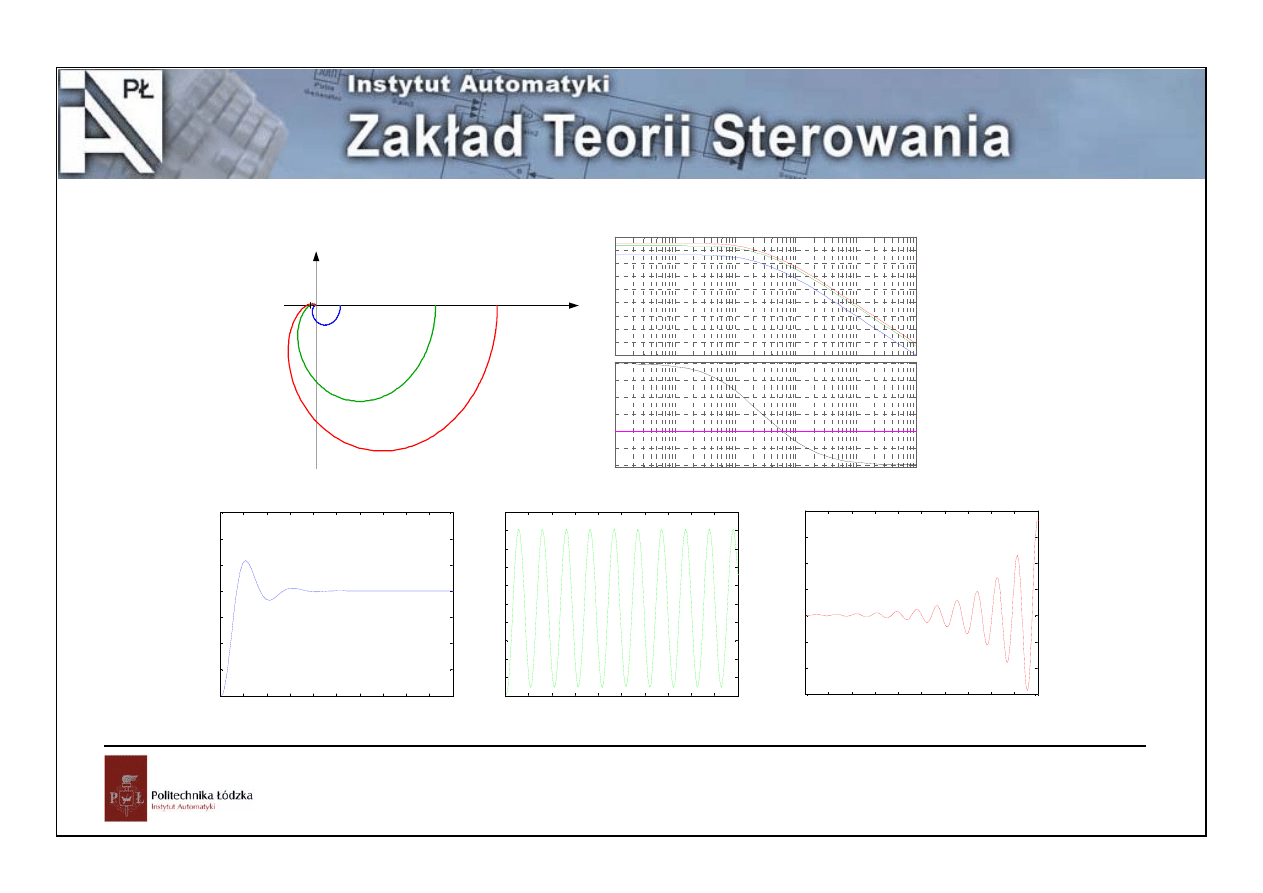
Automatyka i sterowanie – stabilność układów ciągłych
{
}
)
(
0
ω
j
G
Re
{
}
)
(
0
ω
j
G
m
I
(-1,j0)
)
(
ω
ϕ
20log(1)=0
ω
-180
0
)
(
ω
L
ω
2
)
(
1
)
(
1
1
2
π
ω
ϕ
ω
π
−
=
=
=
−
−
A
e
j
12
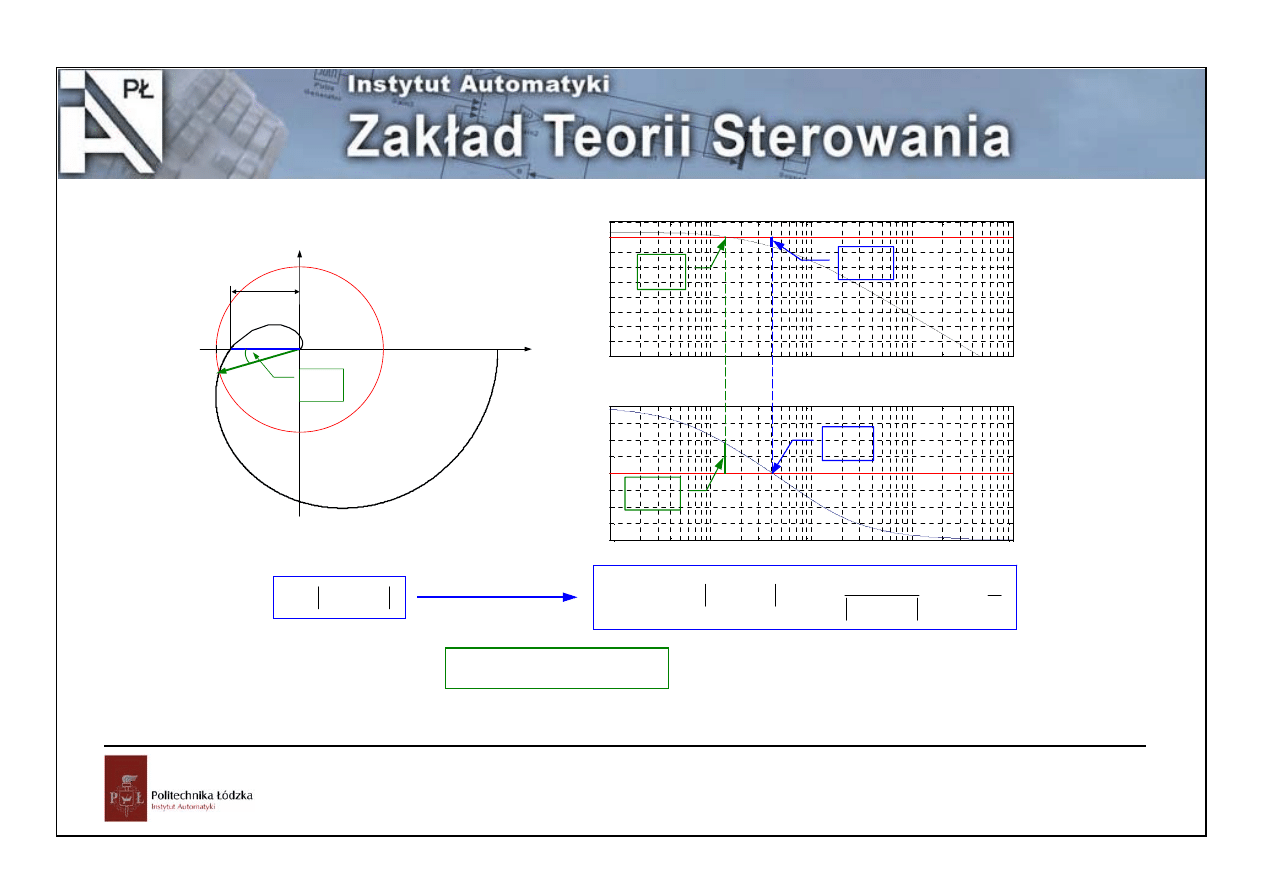
Automatyka i sterowanie – stabilność układów ciągłych
-140
-120
-100
-80
-60
-40
-20
0
20
40
10
-2
10
-1
10
0
10
1
10
2
10
3
-270
-225
-180
-135
-90
-45
0
Bode Diagram
Frequency (rad/sec)
{
}
)
(
0
ω
j
G
Re
{
}
)
(
0
ω
j
G
m
I
stabilny
na granicy
stabilności
niestabilny
0
1
2
3
4
5
6
7
8
9
10
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0
1
2
3
4
5
6
7
8
9
10
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
1
2
3
4
5
6
7
8
9
10
-150
-100
-50
0
50
100
150
200
13
Automatyka i sterowanie – stabilność układów ciągłych
Re{G(jω)}
Im{G(jω)}
k
)
0
,
1
(
j
−
d
∆φ
10
-2
10
-1
10
0
10
1
10
2
-160
-140
-120
-100
-80
-60
-40
-20
0
20
charakterystyka amplitudowo-czestotliwosciowa
10
-2
10
-1
10
0
10
1
10
2
-360
-315
-270
-225
-180
-135
-90
-45
0
charakterystyka amplitudowo-czestotliwosciowa
∆φ
∆L
)
(
0
π
ω
−
=
j
G
d
d
log
j
G
log
j
G
log
L
1
20
)
(
1
20
)
(
20
0
0
=
=
−
=
∆
−
−
π
π
ω
ω
)]
(
[
180
1
0
0
ω
ϕ
j
G
arg
+
=
∆
π
ω
−
1
ω
Document Outline
Wyszukiwarka
Podobne podstrony:
Konserwacja 2014 03 id 245321 Nieznany
Chemia 03 id 557778 Nieznany
ais 01 id 53429 Nieznany (2)
mat fiz 2007 12 03 id 282357 Nieznany
ais 04 id 53433 Nieznany (2)
ais d05 id 53449 Nieznany (2)
ais d01 id 53441 Nieznany (2)
ais d03 id 53445 Nieznany (2)
Module 03 id 305940 Nieznany
III CZP 43 03 id 210280 Nieznany
ais 07 id 53437 Nieznany (2)
AG 03 id 52753 Nieznany
kurs ZERO OSN wiczenie 03 id 25 Nieznany
Neurofizjologia Wyklad 03 id 31 Nieznany
Cw 03 id 122508 Nieznany
lab pwsp 03 id 258617 Nieznany
LAB 03 id 258787 Nieznany
fbuzf 03 id 168997 Nieznany
więcej podobnych podstron