"Stworzenie Sztucznej Inteligencji
było marzeniem ludzkości od chwili
narodzin nauki"

Cytat z filmu "A.I."

INTELIGENCI
I

Wykład 15h

Dr hab. inż. Roman Stryczek

METODY

SZTUCZN
EJ

tematyka

• 1,2 – Definicja AI, przesłanki rozwoju, obszary zastosowania
• 3, – logika klasyczna, logika i zbiory rozmyte, wnioskowanie

rozmyte

• 4 – klasyczne języki sztucznej inteligencji PROLOG, LISP
• 5 – drzewa decyzyjne, wnioskowanie heurystyczne
• 6,7 – rozpoznawanie obrazów,
• 8, 9 - systemy uczące się, sieci neuronowe
• 10, 11 – techniki ewolucyjne (AG, PSO)
• 12– systemy hybrydowe
• 13 – sztuczne życie, automaty komórkowe
• 14 – inteligentne systemy wytwarzania

• Literatura:
•
• L. Rutkowski: Metody i Techniki Sztucznej Inteligencji.

PWN, 2005.

• M.J. Kasperski: Sztuczna inteligencja. Helion 2003.
• J. Chromiec, E. Strzemieczna: Sztuczna inteligencja.

Metody konstrukcji i analizy systemów eksperckich.
Akademicka Oficyna Wydawnicza. Warszawa 1994.

• Jan Mulawka: Systemy ekspertowe. WNT Warszawa

1996.

• E. Chwiałkowska: Sztuczna inteligencja w systemach

eksperckich. Zakład nauczania Informatyki „MIKOM”,
Warszawa 1991. Highfield: Granice złożoności.
Prószyński i S-ka, W-wa 1997.

•

L. Bolc, W. Borodziewicz, M. Wójcik: Podstawy przetwarzania informacji
niepewnej i niepełnej. PWN, Warszawa 1991.

•

W.M. Nazaretow, D.P. Kim T. Krupa: Techniczna imitacja intelektu. ESP/6,
WNT, Warszawa 1991.

•

C. Iwański, G. Szkatuła: Wybrane metody uczenia maszynowego dla
tworzenia reguł klasyfikacji obiektów.Instytut Badań Systemowych, Warszawa
1992.

•

R. Tadeusiewicz: Sieci neuronowe. Akademicka Oficyna Wydawnicza,
W-wa 93. http://winntbg.bg.agh.edu.pl/skrypty/0001/main.html

•

R. Tadeusiewicz – systemy wizyjne robotów przemysłowych. WNT, W-wa 92.

•

Paweł. Cichosz: Systemy uczące się. WNT, W-wa 2000.

•

R.Tadeusiewicz, P.Korohoda: Komputerowa analiza i przetwarzanie
obrazów .WFPT, Kraków 97.

•

R.Tadeusiewicz, M. Faliński: Rozpoznawanie obrazów,

http://winntbg.bg.agh.edu.pl/skrypty/5/

•

Korbicz, Kościelny, Kowalczuk, Cholewa: Diagnostyka Procesów, Modele,
Metody sztucznej inteligencji, zastosowania, WNT 2002.

•

Antoni Niederliński: Regułowe systemy ekspertowe.

•

Peter Coveney, Roger

•

http://sound.eti.pg.gda.pl/rekonstrukcja/sztuczna_inteligencja.
html

•

http://k0pper.republika.pl/

•

http://gimnr1olkusz.republika.pl/ai.htm

•

http://www.zasada.ps.pl/Ai.html

•

http://republika.pl/edward_ch/

•

http://www.phys.uni.torun.pl/~duch/neural.html

•

http://cgm.cs.mcgill.ca/~godfried/teaching/pr-
web.html#nearest

•

http://wombat.ict.pwr.wroc.pl/nauczanie/prezentacja/flash/ag/in
tro.swf

•

http://panda.bg.univ.gda.pl/~sielim/genetic/

•

http://www.visual-prolog.com

DEFINICJE

•

Inteligencja:

•

(filozoficzna) zdolność umysłu do efektywnego ujmowania - dzięki
posługiwaniu się pamięcią, wyobraźnią, świadomością i
podświadomością, intuicją, abstrakcją i przeżywaniem stanów
emocjonalnych - zagadnień zarówno praktycznych jak i teoretycznych;

•

(wg słownika Webstera) zdolność uczenia się i rozumienia zjawisk
poprzez doświadczenie, zdolność zdobywania wiedzy i wykorzystania
jej w celu szybkiego i efektywnego reagowania na nowe sytuacje;
zdolność rozumowania w celu efektywnego rozwiązywania
problemów.

(wg słownika Webstera)

zdolność  uczenia  się  i  rozumienia  zjawisk  poprzez
doświadczenie,  zdolność  zdobywania  wiedzy  i
wykorzystania  jej  w  celu  szybkiego  i  efektywnego
reagowania na nowe sytuacje; zdolność rozumowania
w celu efektywnego rozwiązywania problemów.

(wg słownika Webstera)

Definicje
Inżynieria wiedzy
- systemy związane z pozyskiwaniem, gromadzeniem i
przetwarzaniem wiedzy

(filozoficzna)

zdolność umysłu do efektywnego ujmowania - dzięki
posługiwaniu

się

pamięcią,

wyobraźnią,

świadomością

podświadomością,

intuicją,

abstrakcją i przeżywaniem stanów emocjonalnych -
zagadnień zarówno praktycznych jak i teoretycznych;

Inteligencja: zdolności umysłowe człowieka
(Cyceron);

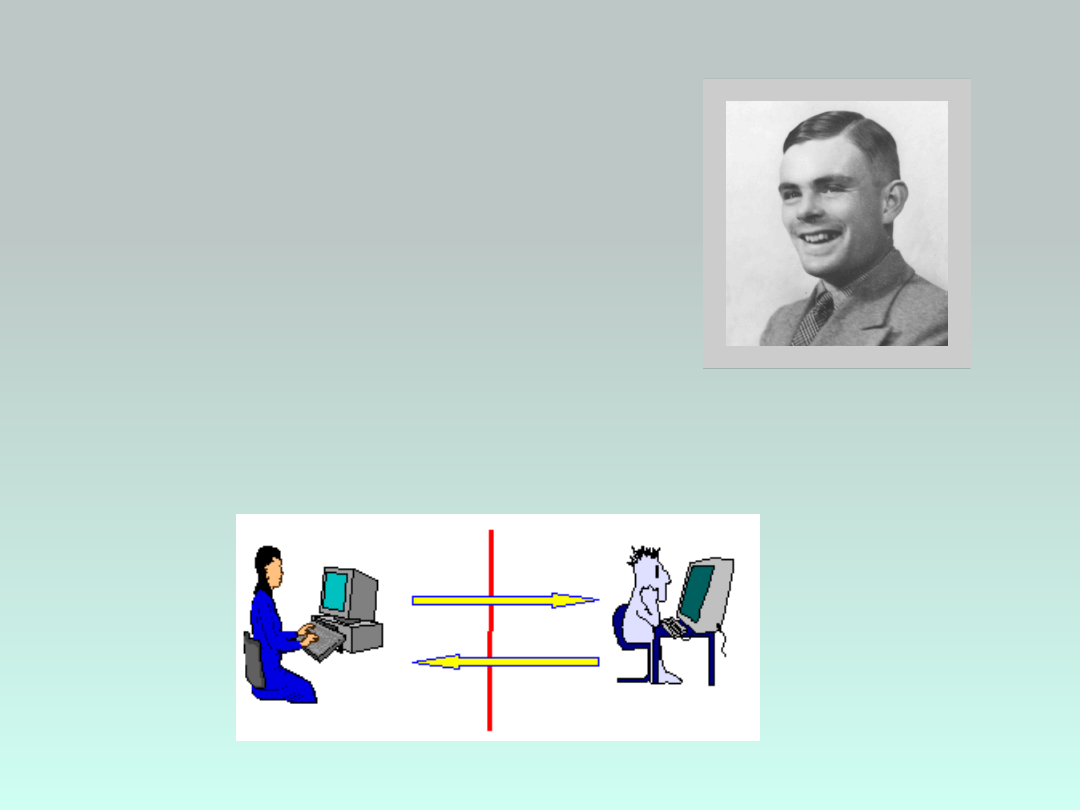
Test Turinga

(1950)

Alan Turing (1912-
1954)

- Sposób określania zdolności
maszyny do posługiwania się
językiem naturalnym i
pośrednio mającym dowodzić
opanowania przez nią
umiejętności myślenia w
sposób podobny do ludzkiego

definicje sztucznej
inteligencji

Nauka o maszynach realizujących
zadania,

które

wymagają

inteligencji

wówczas,

gdy

są

wykonywane przez człowieka (M.
Minsky) .

Dziedzina  informatyki  dotycząca
metod  i  technik  wnioskowania
symbolicznego  przez  komputer
oraz  symbolicznej  reprezentacji
wiedzy

stosowanej

podczas

takiego

wnioskowania

(E.

Feigenbaum).

Jest to interdyscyplinarna dziedzina nauki,
zajmująca

się

metodami

wyciągania

zadowalających  pod  względem  poprawności
wniosków  na  podstawie  niepełnej  i  niepewnej
informacji  oraz  nieugruntowanej  wiedzy.
[R.S.]

Logika

rozmyta

Logika

rozmyta

Psychologia

Matematyka

Neurofizjologi

Lingwistyka

Filozofia

Informatyk

Elektronika

Antropologi

Robotyka

Systemy

ekspertowe

Systemy

ekspertowe

Systemy wizyjne

Procesy

percepcji

Procesy

percepcji

Przetwarzania

języka

Przetwarzania

języka

Rozpoznawanie

obrazów

Rozpoznawanie

obrazów

Algorytmy

ewolucyjne

Algorytmy

ewolucyjne

Sieci neuronowe

Wnioskowanie

heurystyczne

Wnioskowanie

heurystyczne

Teoria gier

Automaty komórkowe

Techniki

ewolucyjne

Techniki

ewolucyjne

Inteligencj

a Roju

Inteligencj

a Roju

ACO

Pod-dziedziny sztucznej inteligencji:

• rozwiązywanie problemów i strategie przeszukiwań;
• teoria gier;
• rozumowanie logiczne, automatyczne dowodzenie

twierdzeń;

• systemy ekspertowe;
• robotyka (inteligentne połączenie pomiędzy percepcją a

akcją);

• procesy percepcji (wizja, słuch, dotyk, mowa);
• uczenie się maszyn;
• wyszukiwanie informacji (inteligentne bazy danych);
• programowanie automatyczne;
• analiza scen;
• specjalistyczne stacje robocze;
• systemy hybrydowe (połączenie tradycyjnych systemów

ekspertowych, systemów uczących się, sztucznych sieci
neuronowych oraz algorytmów ewolucyjnych

• Itp.

Najważniejsze osiągnięcia w

rozwoju AI

- lata przed II wojną światową (prehistoria):
•

logika formalna

•

psychologia poznawcza

•

1945 ENIAC (Electronic Numerical Integrator and Computer) – 333
mnożeń na minutę (17 468 lamp, 70000 oporników, 10 000
kondensatorów, 1500 przekaźników i 6000 przełączników) – waga 30
ton

- lata powojenne (1945-1954)
•

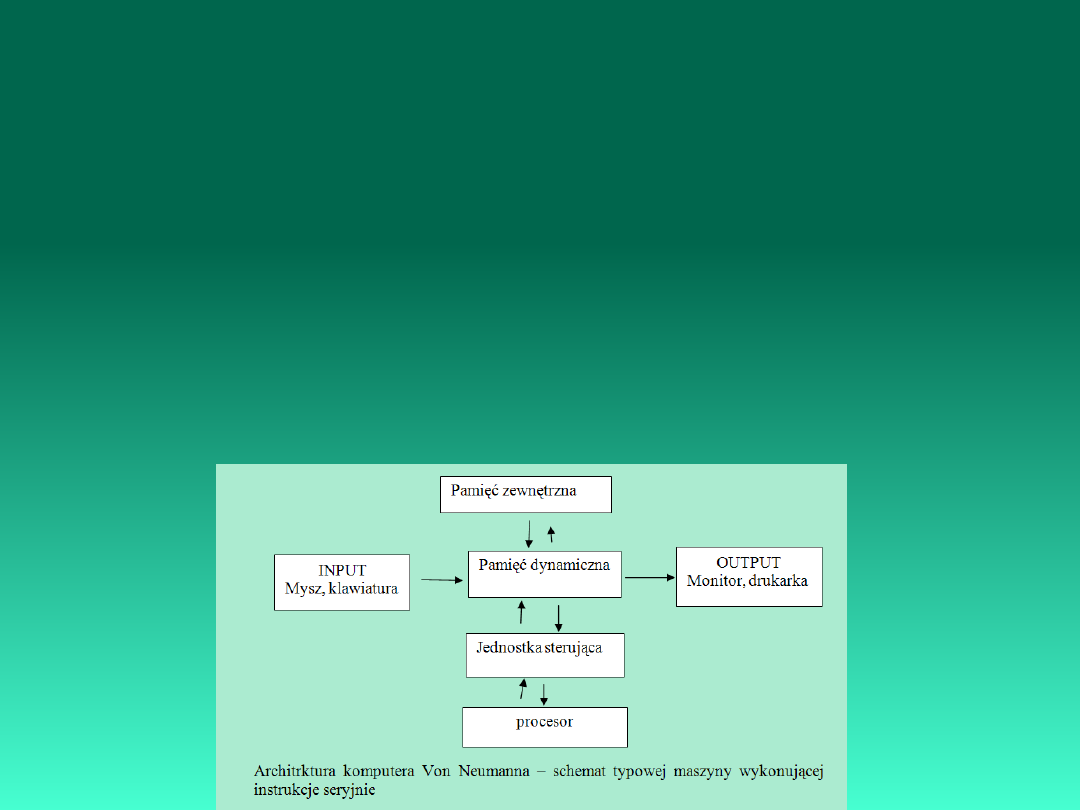
John von Neumann (1908-1958) (prace na bombą jądrową
(przebiegiem implozji), pionierskie metody numerycznego
rozwiązywania równań hydrodynamicznych, szeregowa architektura
komputera) – pierwszy EDVAC (52 rok)

Najważniejsze osiągnięcia w

rozwoju AI

•

Alan Turing (1912 –1954) (metody krypto-analityczne - Enigma,
uniwersalna maszyna Turinga, abstrakcyjna maszyna potrafiąca
wykonać dowolny algorytm – teoretyczny schemat komputera)
(projekt ACE – Automatic Computing Engin)

•

1948 powstanie MARK1 (Menchester) – pierwszy programowalny
komputer cyfrowy

•

Stanisław Ulam (automaty komórkowe)

•

- powstanie komputerów

•

- rozwój cybernetyki

- 1955-1960: (średniowiecze)
•

- rozpoczęcie badań nad sztuczną inteligencją

•

- rozwój komputerów

•

- LISP

•

sformułowanie programu ogólnego rozwiązywania problemów
(General Problem Solver)

•

PERCEPTRON (Frank Rosenblatt)

Najważniejsze osiągnięcia w

rozwoju AI

- 1961-1970: (wiek rozumowania)
•

GOFAI

•

heurystyki (prace Newell’a i Simon’a nad przeszukiwaniem
przestrzeni rozwiązań)

•

robotyka

•

1965 DENDRAL (Uniwersytet Stanford -Edward Feigenbaum) –
określał strukturę cząsteczki na podstawie na podstawie odczytu
spektografu masowego, zrealizowany w LISP’ie;

•

programy do gry w szachy

•

logika rozmyta (Lotfi Zadeh 1965)

- 1971-1980: (okres romantyczny)
•

porażka GOFAI (Piotr zobaczył komputer na wystawie sklepu i chce
go kupić)

•

systemy oparte na bazach wiedzy

•

MYCIN, EMYCIN

•

MYCIN - system interacyjny, diagnozujący infekcje bakteryjne i
polecający stosowną terapię antybiotykową. Umiejętnie i proawidłowo
stawia diagnozy w przypadku gdy brak jest kompletnych czy pewnych
danych. System ten jest uznawany za pierwszy i jak dotąd
najpopularniejszy system ekspertowy. Został zaprojektowany przez
Edwarda Shortlife'a z Uniwersytetu Stanforda w połowie lat 70-tych.

•

Prolog(72)

•

John Holland algorytmy genetyczne(75)

Najważniejsze osiągnięcia w

rozwoju AI

- po 1981-1985:
•

PROSPECTOR

•

nie zrealizowany japoński projekt komputera 5 generacji

- 1986-1990: (okres oświecenia)
•

rozwój sieci neuronowych

•

rozwój algorytmów genetycznych

- lata 90/XX w.
•

pojawienie się pierwszych inteligentnych urządzeń powszechnego
użytku

•

pojawienie się systemów hybrydowych

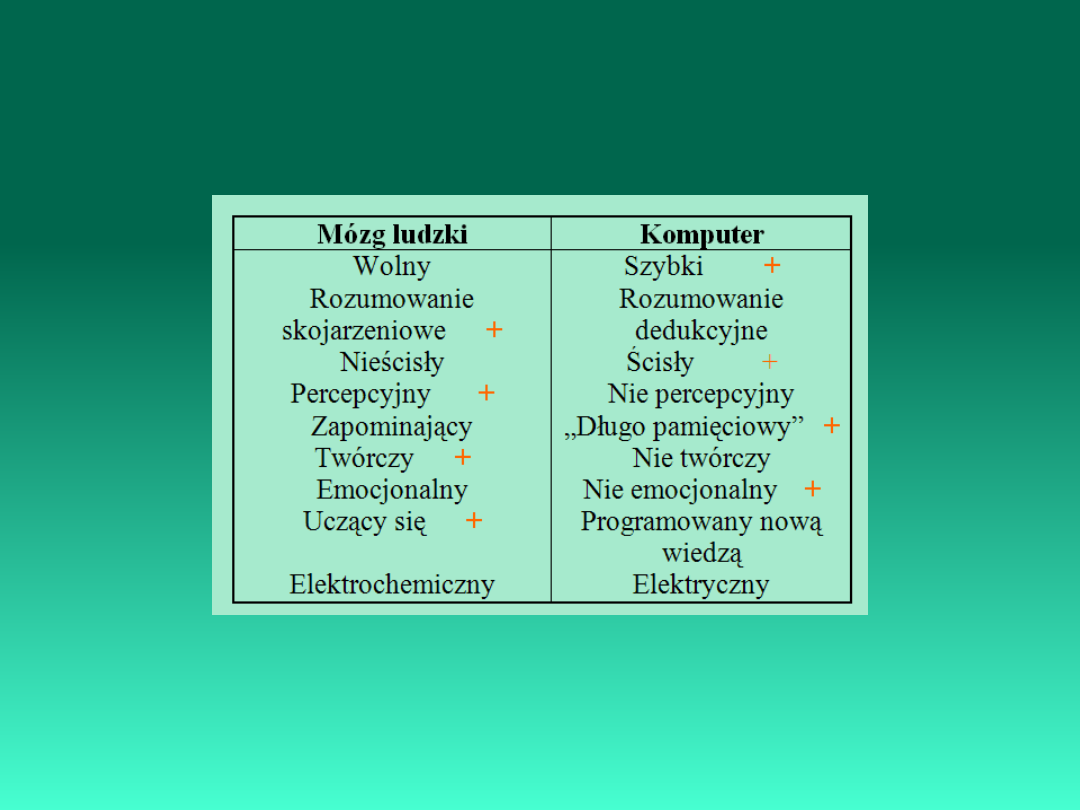
Porównanie mózgu ludzkiego i

komputera.

Zbiory rozmyte (Logika

rozmyta)

• W praktyce większość przypadków podejmowania decyzji

w procesie planowania lub zarządzania odbywa się w
warunkach pewnej nieokreśloności. Nieokreśloność
uwarunkowaną czynnikami przypadkowymi nazywamy
nieokreślonością losową lub stochastyczną. W celu
podejmowania decyzji w warunkach nieokreśloności
stochastycznej wykorzystywana jest teoria
prawdopodobieństwa.

• Innym typem nieokreśloności jest nieokreśloność

spowodowana niedokładnością (rozmytością,
nieostrością) celu i/lub ograniczeń. Do tego typu
nieokreśloności zaliczmy także niedokładność
lingwistyczną.
W celu formalizacji zadań podejmowania decyzji z
niedokładnym celem i/lub niedokładnym ograniczeniem lub
też w celu zbudowania modelu matematycznego systemów,
w którym istnieje lingwistyczna nieokreśloność –
opracowano teorię zbiorów rozmytych.

Lotfi A. Zadeh

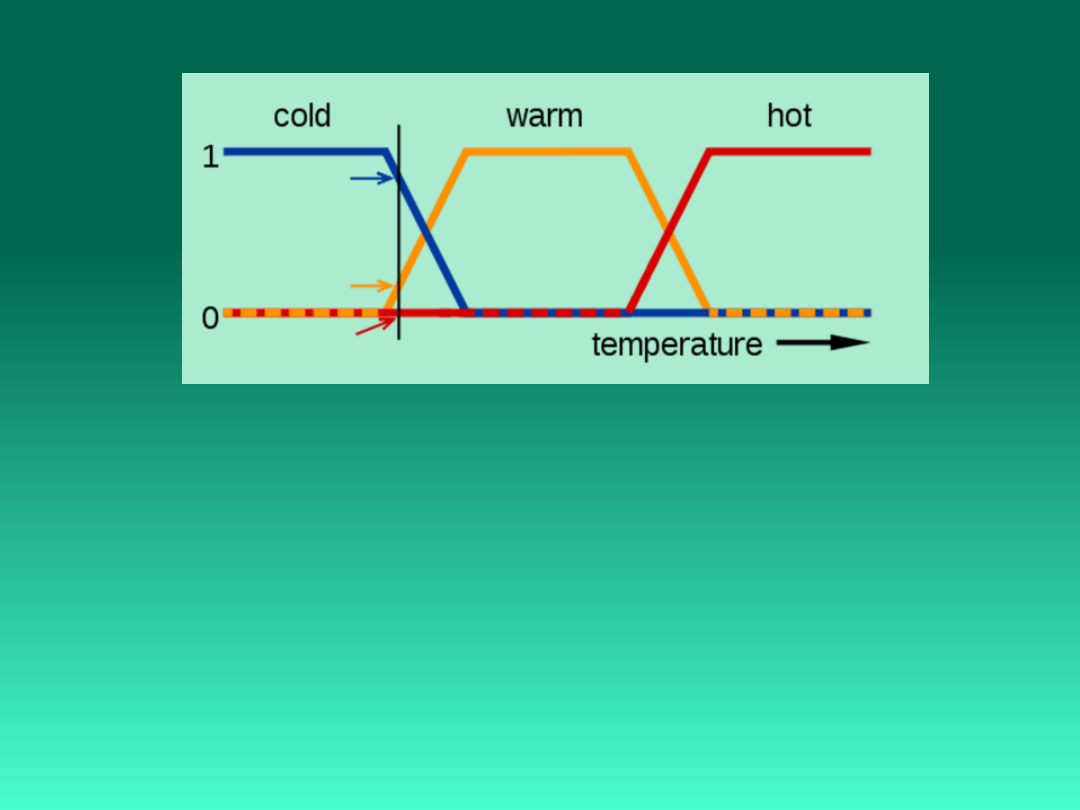
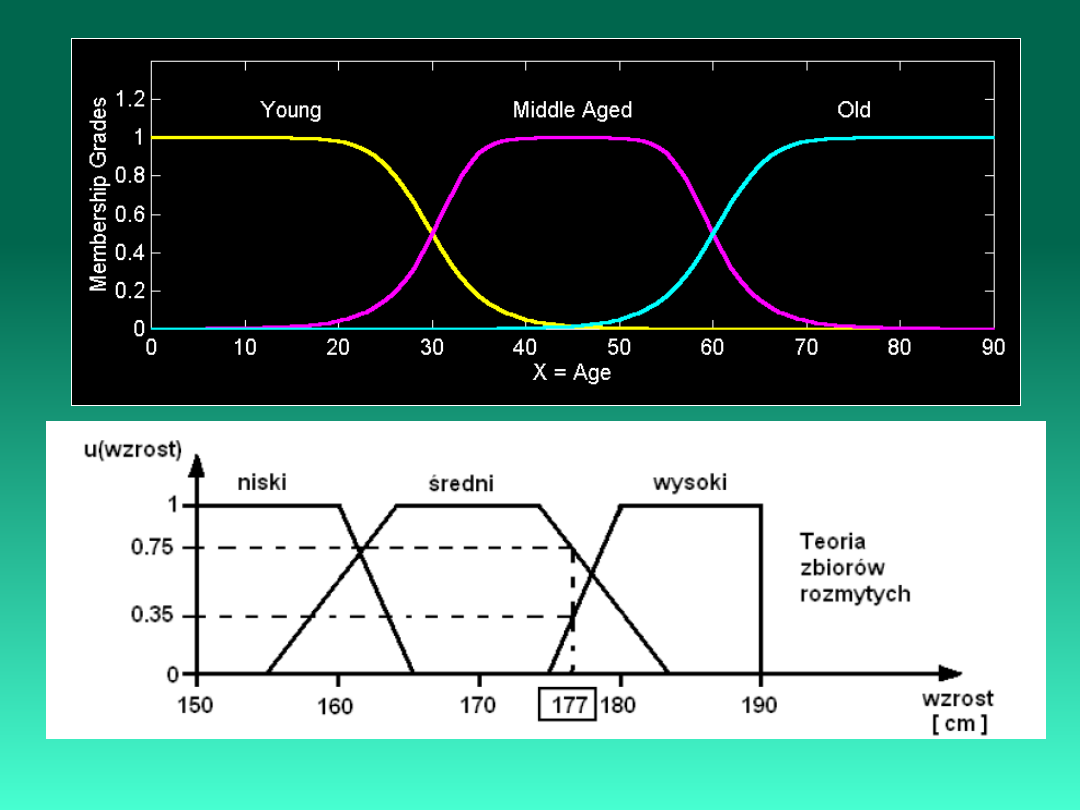
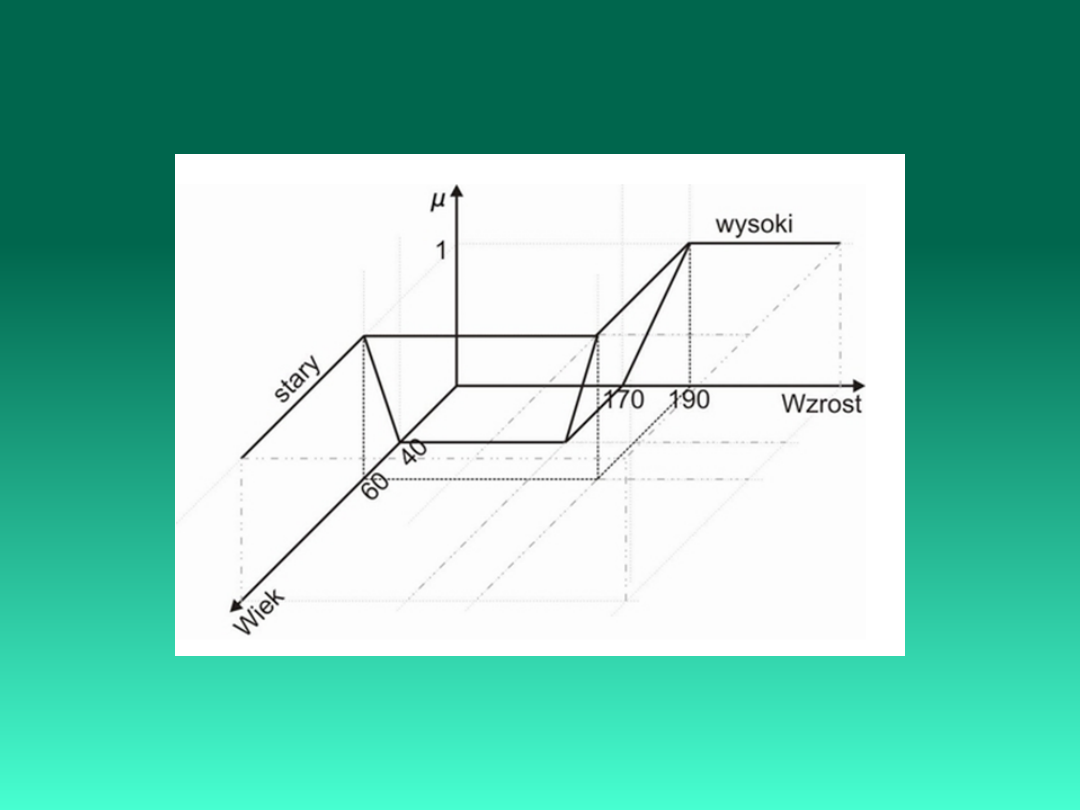
Funkcje Przynależności

(x)

Singleton: (a,1) i (b,0.5)

(x)

a b

Trójkątna: <a,b,c>

(

)

; , ,

max min

x a c x

T x a b c

b a c b

�

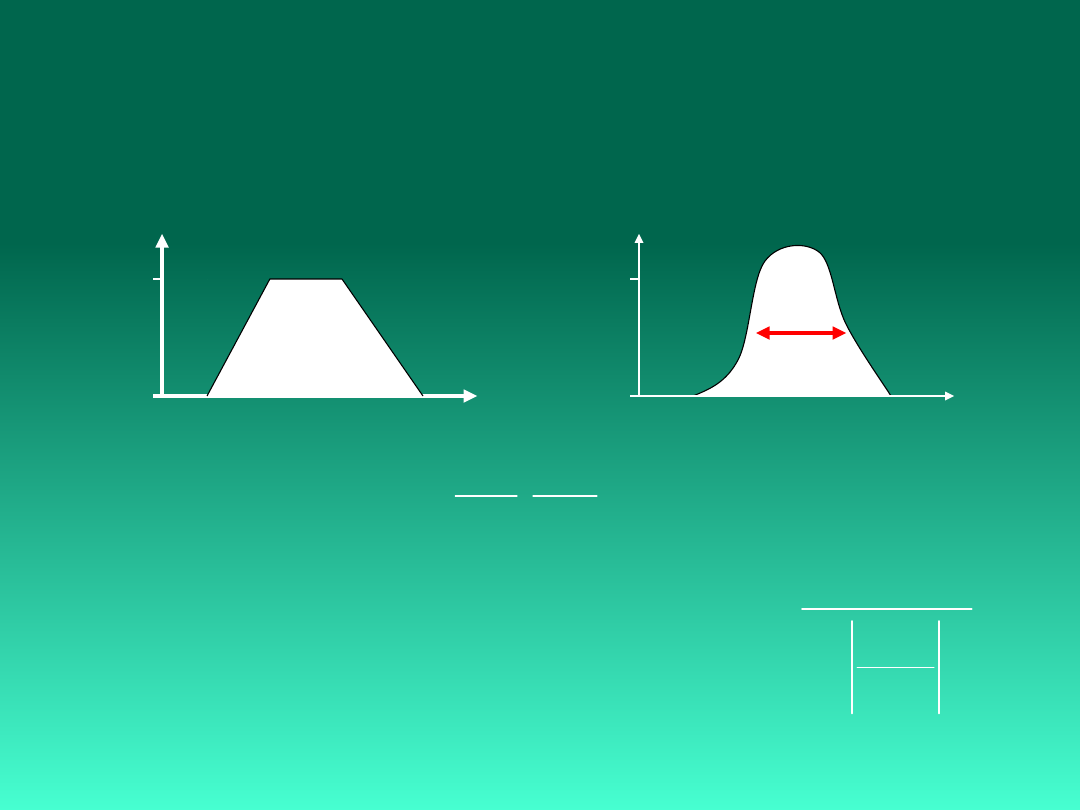
Typy Funkcji

Przynależności

(x)

a b

Trapezoid: <a,b,c,d>

(x)

Gaus/Bell: N(m,s)

(

)

; , , ,

max min

,1 ,0

x a d x

Trap x a b c d

b a d c

�

(

)

(

)

;

x a

G x a

(

)

; ,

B x a b

x a

Przykłady rozmytych

relacji

X = { deszczowo, pochmurnie, słonecznie }

Y = { opalanie, wrotki, kamping, lektura }

deszczowo

pochmurni
e

słonecznie

X/Y opalanie wrotki kamping
lektura

0.0

0.2

0.0

1.0

0.0

0.8

0.3

1.0

0.2

0.7

0.0

Reguły rozmyte

Wiedzę potoczną można często zapisać w
naturalny sposób za pomocą reguł rozmytych.

Jeśli zm. lingw-1 = term-1 i zm. lingw-2 = term-
2
to zm. lingw-3 = term-3

Jeśli Temperatura = zimno i cena ogrzewania
= niska
to ogrzewanie = mocno

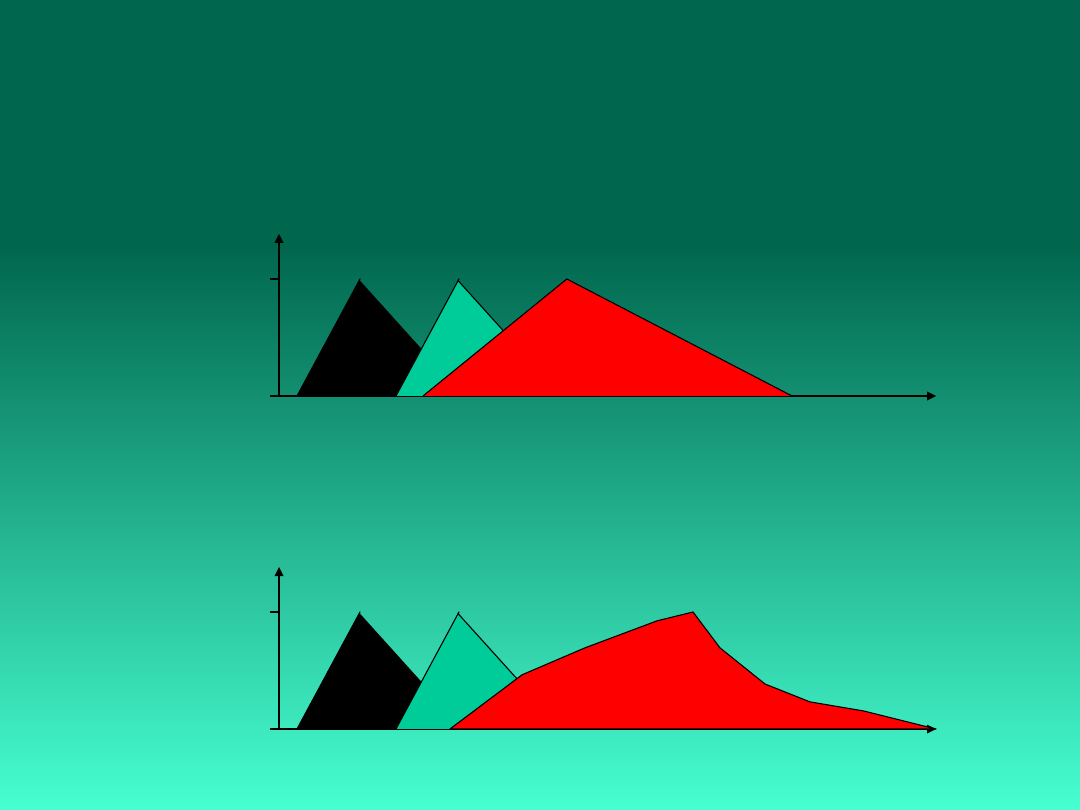
Operacje na liczbach

rozmytych

Operacje na liczbach

rozmytych

Dodawanie:



A+B

(x) = max{

(y), 

(z) | x = y+z}

(x)



(y) 

(z) 

A+B

(x)

Iloczyn: 

AB

(x) = min{

(y), 

(z) | x = y



(x)



(y) 

(z)



AB

(x)

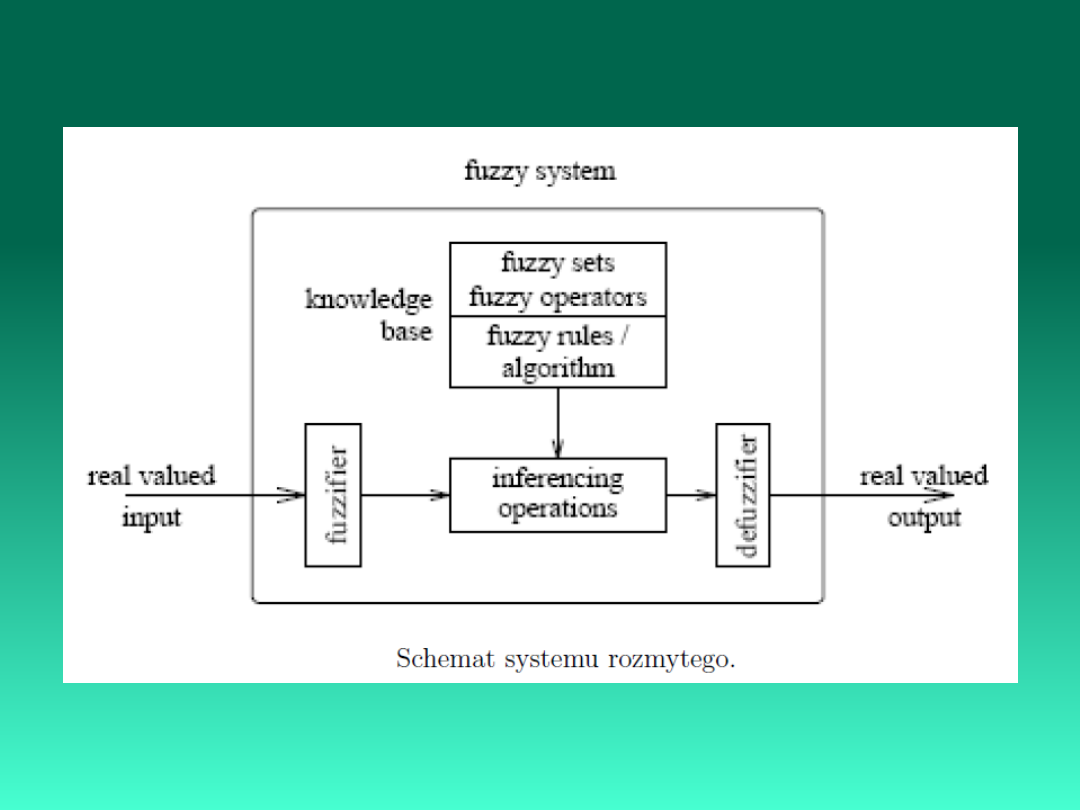
Zastosowania logiki

rozmytej

Inteligentne bazy wiedzy.

Wszędzie tam, gdzie trudno jest utworzyć

matematyczny model ale daje się opisać sytuację

w sposób jakościowy, za pomocą reguł

rozmytych.

Kontrolery rozmyte: ABS, aut. wycieraczki

„Inteligentne” lodówki, pralki, opiekacze do
grzanek, aparaty fotograficzne.
Tam gdzie nieprecyzyjny język daje się przełożyć
na reguły rozmyte.
Wiele zastosowań przemysłowych, głównie
dotyczących kontroli procesów.

Narzędzia AI

Języki AI

Development tools

LISP

PROLOG

EMYCIN (Van Melle et al., 1979)

KEE

KES

Knowledge Craft

Personal Consultant

Prolog

(od

francuskiego

Programmation

Logique) jest to jeden z najpopularniejszych języków
programowania logicznego. Prolog jest językiem
ogólnego

zastosowania,

szczególnie

dobrze

sprawdzającym się w programach związanych ze
sztuczną inteligencją. Prolog w przeciwieństwie do
większości

popularnych

języków

jest

językiem

deklaratywnym.
Program w Prologu składa się z faktów oraz reguł
wnioskowania. Aby go uruchomić należy wprowadzić
odpowiednie zapytanie.
Prolog został stworzcony w 1971 roku przez

Prolog opiera się o rachunek predykatowy, jednak
ogranicza się tylko do

klauzul Horna

. Istnieją jednak

wbudowane predykaty wyższego rzędu.

Przykład :

Predicates

n_silnia(Integer,Real)

Clauses

n_silnia(0,1):-!.
n_silnia(N,W):-n_silnia(N-1,W0), W=N*W0.

Goal

n_silnia(10,W),write(W).

LISP

(ang. List Processing) –

język programowania

wysokiego poziomu przeznaczony do przetwarzaniu typu lista. Lisp
został wymyślony przez

Johna McCarthy'ego

w 1958 podczas jego

pobytu na

MIT

. Stosowany jest do analizy tekstów, obliczeń

symbolicznych

(nienumerycznych)

logicznych,

sztucznej

inteligencji.

Podstawową strukturą danych w Lispie jest lista;
Kod źródłowy programów w Lispie składa się z list.

; marszruta
(command  "_color" "_red")
(setq lista (open   "c:\\CAPP\\lista" "r"))
(setq blok (read-line lista))
(setq x0 (atof (substr blok 1 10)))
(setq y0 (atof (substr blok 11)))
(while (/= blok nil)
    (progn

(setq blok (read-line lista))
(setq x (atof (substr blok 1 10)))
(setq y (atof (substr blok 11)))
(command "_line" (list x0 y0) (list x y) "")
(setq x0 x y0 y)

)
)
(close lista)

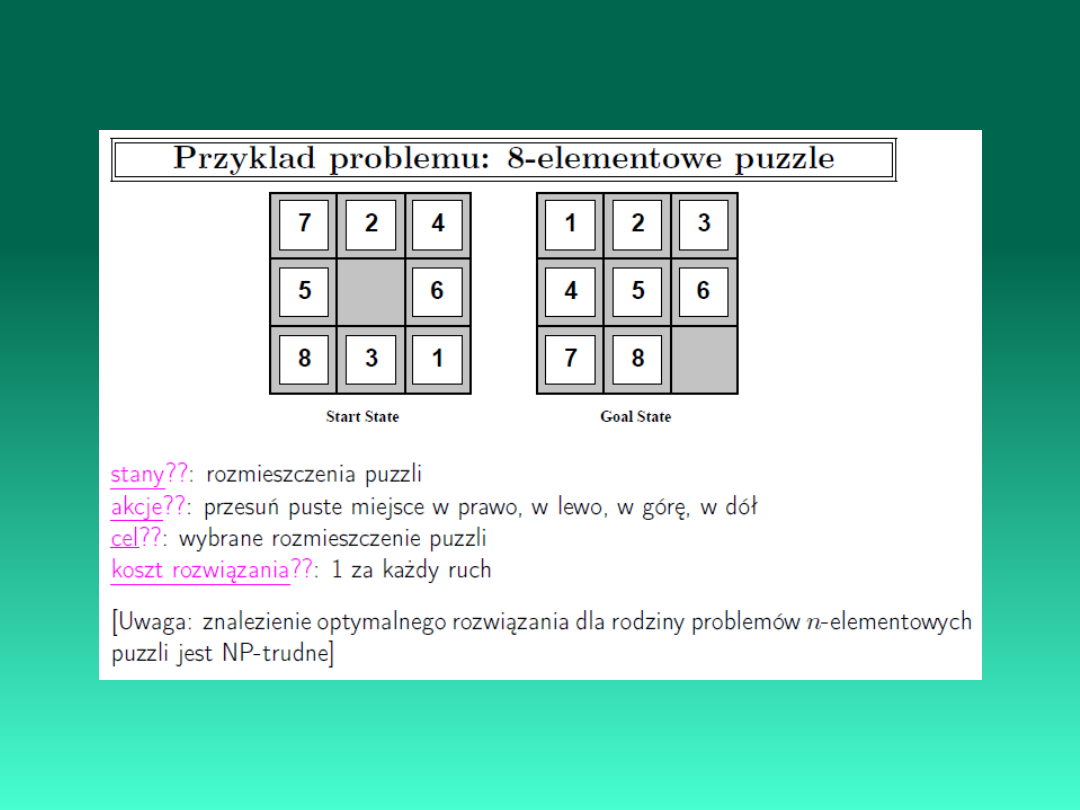
Rozwiązywanie zadań - poprzez analizę

przestrzeni stanów

Praca Feigenbauma i Feldmana opublikowana w 1963
roku. wprowadza pojęcie przeszukiwanie przestrzeni
stanów (ang. state space search).

Reprezentacja problemu:

stany

: reprezentują opisy różnych stanów świata

rzeczywistego

akcje

: reprezentują działania zmieniające bieżący stan

koszt akcji

( 0): reprezentuje koszt związany z

wykonaniem akcji

Sformułowanie problemu

stan początkowy

: początkowy stan przed

rozwiązaniem problemu

cel:

stan docelowy lub formuła oceniająca, czy dany

stan spełnia cel

rozwiązanie

: ciąg akcji prowadzący od stanu

początkowego do celu
koszt rozwiązania: funkcja oceny kosztu rozwiązania
równa sumie
kosztów poszczególnych akcji występujących w
rozwiązaniu

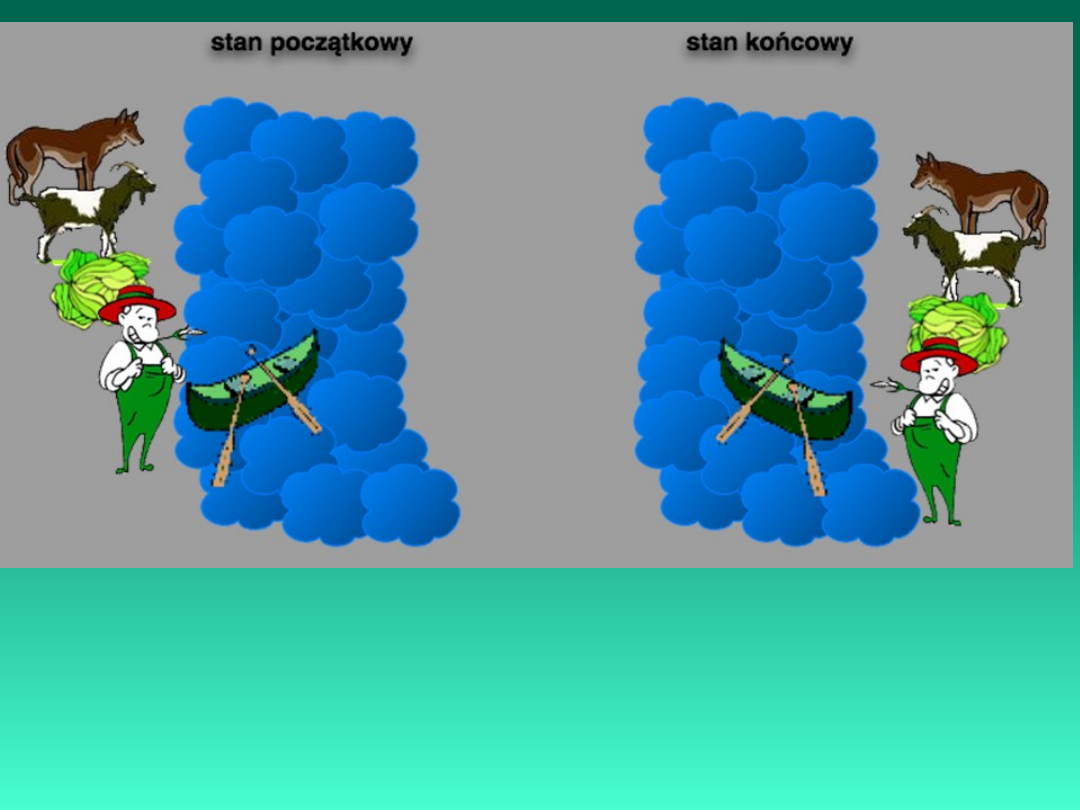
Powyższe zadanie jest klasycznym przykładem
problemu, w którym poszukujemy ciągu operacji
jakie przekształcą pewien stan początkowy w stan
końcowy.

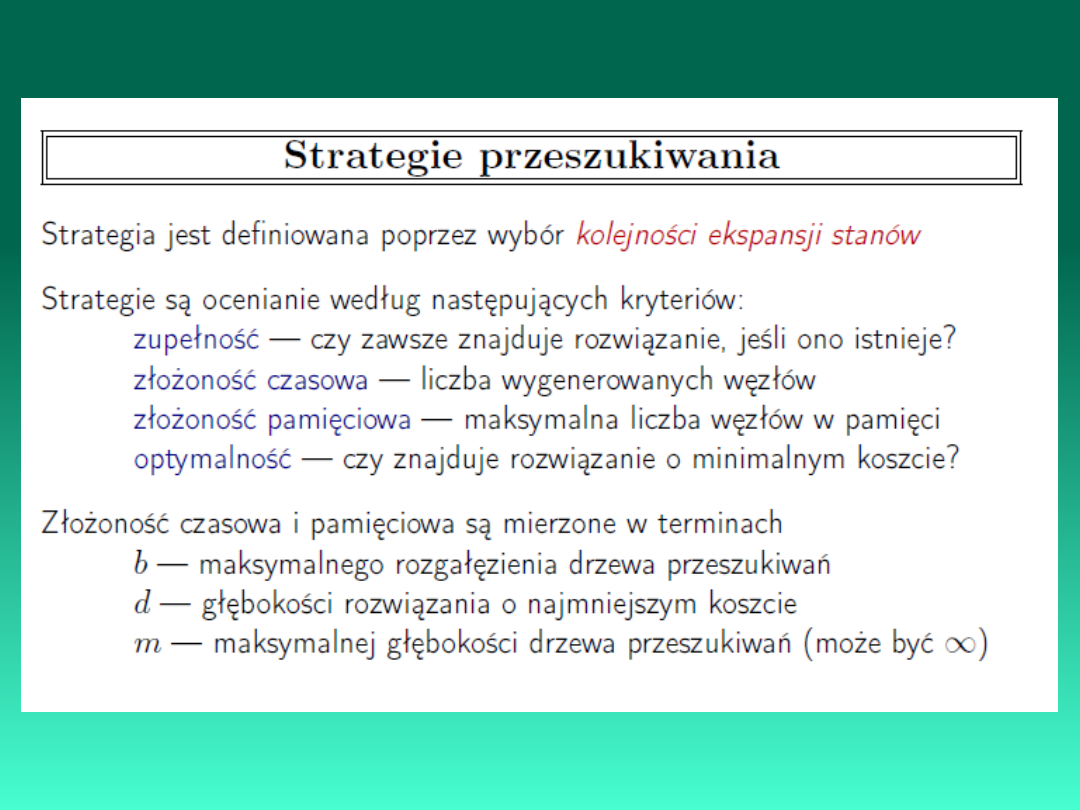
Najprostszą formą przeszukiwania przestrzeni stanów jest algorytm określany
jako generuj i testuj.

Przykład:
% Program naczynia generuje stany bez powtórzeń
%trace
Database

s(Integer,Integer)

Predicates
nondeterm run

d(Integer,Integer,Integer,Integer)

Clauses

run:-s(X,Y),d(X,Y,7,Y).

%napelnienie A

run:-s(X,Y),d(X,Y,0,Y).

%wylanie A

run:-s(X,Y),D=7-X,D>=Y,X1=X+Y,d(X,Y,X1,0).

%przelanie B do A

run:-s(X,Y),D=7-X,D<Y,Y1=Y-D,d(X,Y,7,Y1). %uzupelnienie A
run:-s(X,Y),d(X,Y,X,5).

%napelnienie B

run:-s(X,Y),d(X,Y,X,0).

%wylanie B

run:-s(X,Y),D=5-Y,D>=X,Y1=Y+X,d(X,Y,0,Y1).

%przelanie A do B

run:-s(X,Y),D=5-Y,D<X,X1=X-D,d(X,Y,X1,5). %uzupelnienie B
run:-!,run.

d(_,_,X,Y):-s(X,Y),!,fail.
d(X0,Y0,X,Y):-assert(s(X,Y)),write(X0,",",Y0," > ",X,",",Y),nl,

X=4,write("--------------"),nl,readchar(_).

Goal

assert(s(0,0)),
run,fail.

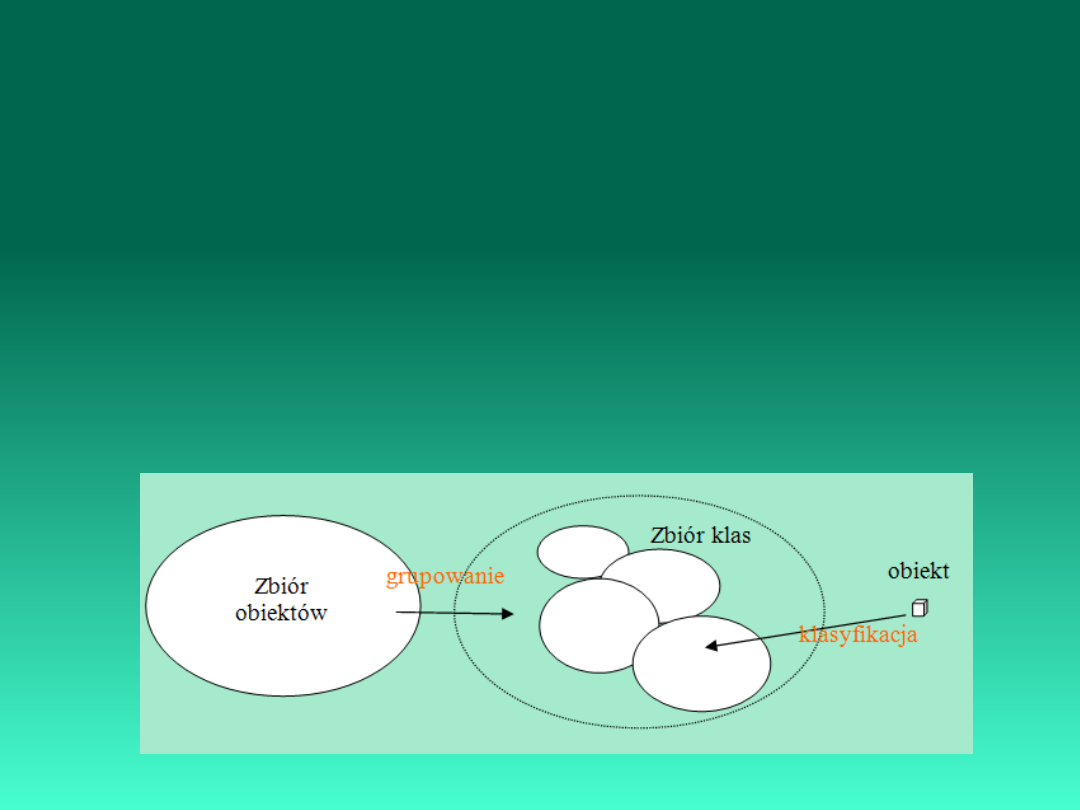
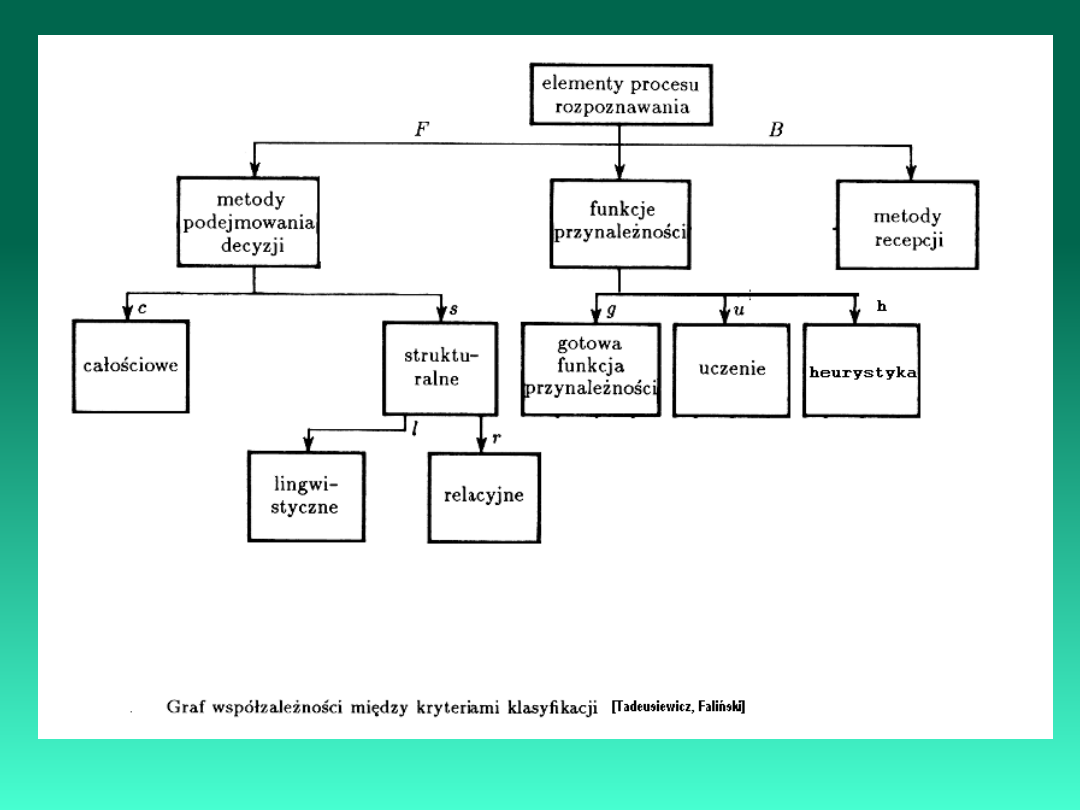
Rozpoznawanie obrazów

W zadaniu rozpoznawania obrazów chodzi o rozpoznawanie

przynależności  rozmaitego  typu  obiektów  (lub  zjawisk)  do
pewnych klas. Rozpoznawanie to ma być prowadzone w sytuacji
braku  apriorycznej  informacji  na  temat  reguł  przynależności
obiektów  do  pewnych  klas,  a  jedyna  informacja  możliwa  do
wykorzystania  przez  algorytm  lub  maszynę  rozpoznającą  jest
zawarta  w  ciągu  uczącym,  złożonym  z  obiektów,  dla  których
znana jest prawidłowa klasyfikacja.

Rozpoznawanie obrazów obejmuje dwa komplementarne w

stosunku do siebie zadania: grupowanie (klasteryzacja, analiza
skupień) i klasyfikację.

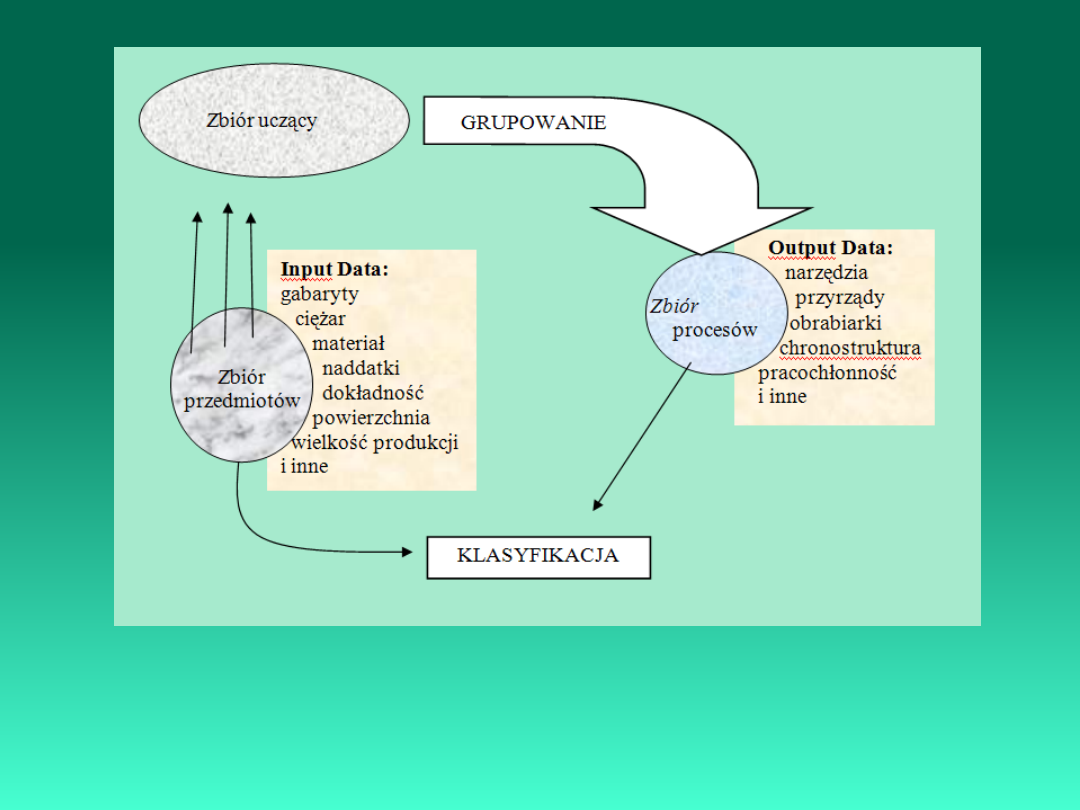
Schemat rozpoznawania obrazów na przykładzie klasyfikacji przedmiot  proces obróbki

Niektóre zastosowania metody rozpoznawania
obrazów:

•rozpoznawanie mowy, pisma, znaków,

•analiza topograficznych zdjęć lotniczych,

•rozpoznawanie złóż surowców mineralnych,

•opisywanie elektrokardiogramów,

•prognozowanie zachowania się giełd finansowych,

•diagnostyka układów elektronicznych,

•badania psychiatryczne,

•prognozowanie sprzedaży,

•interpretacja badań biologicznych, medycznych,

•prognozy cen,

•planowanie remontów maszyn,

•typowanie na wyścigach konnych,

•selekcja celów śledztwa,

•dobór pracowników.

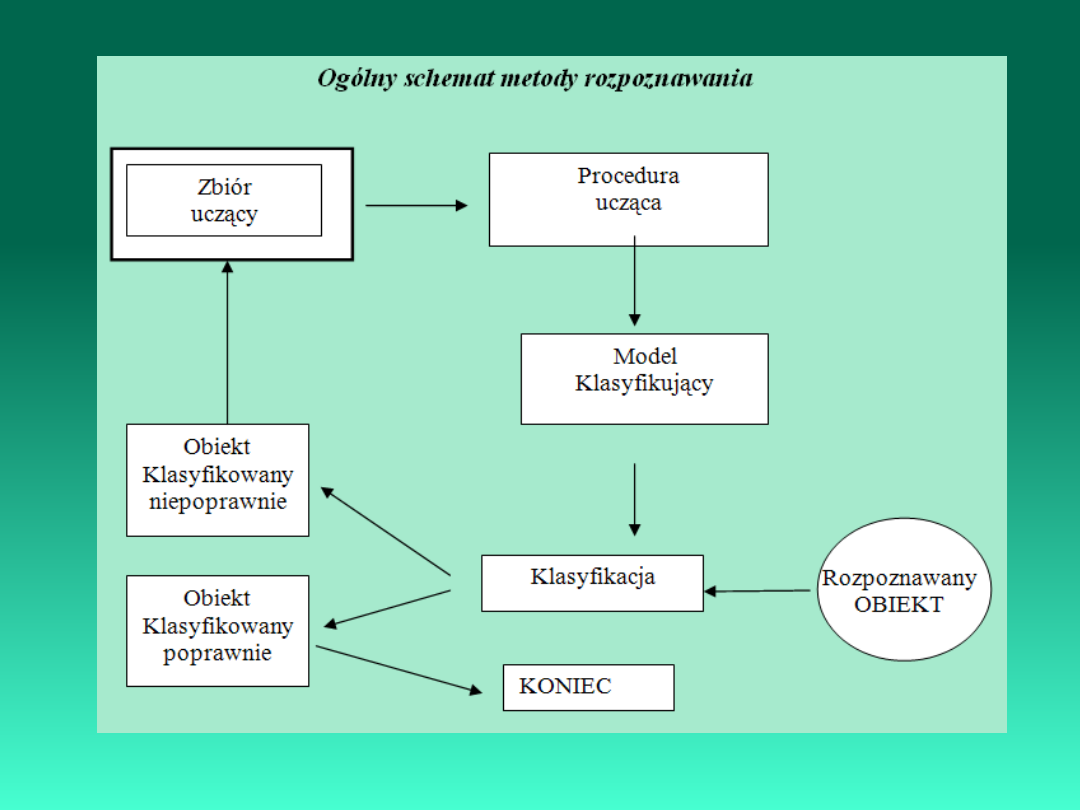
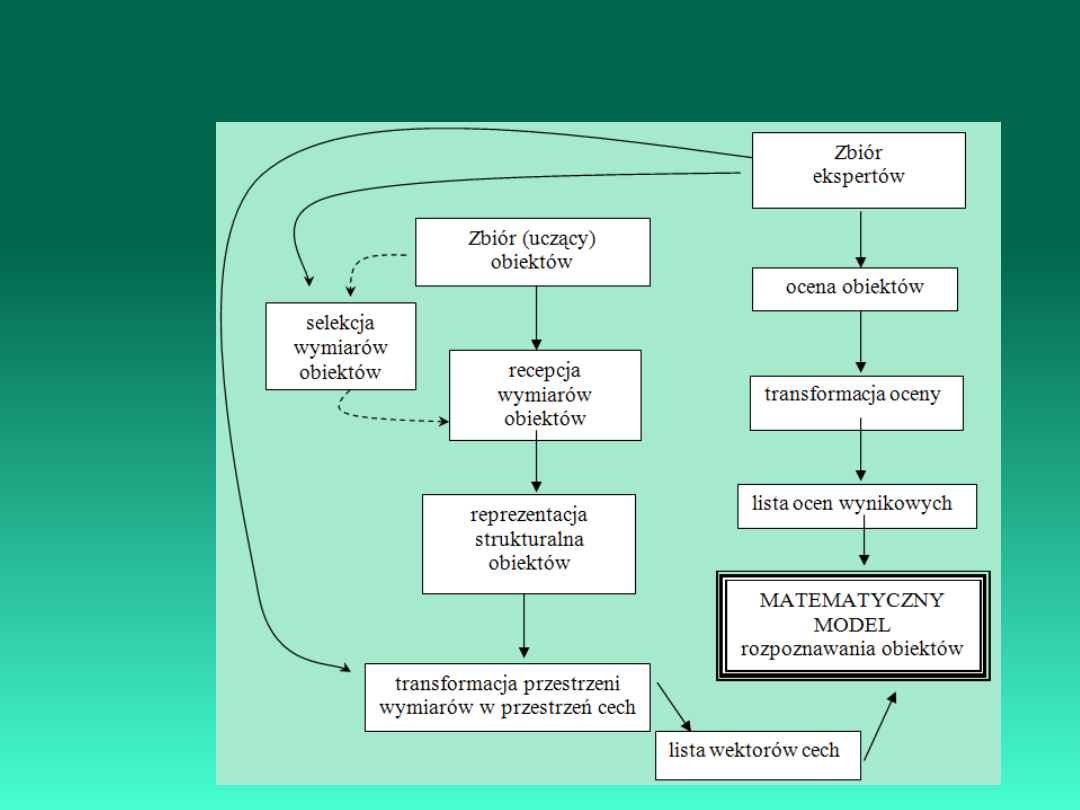
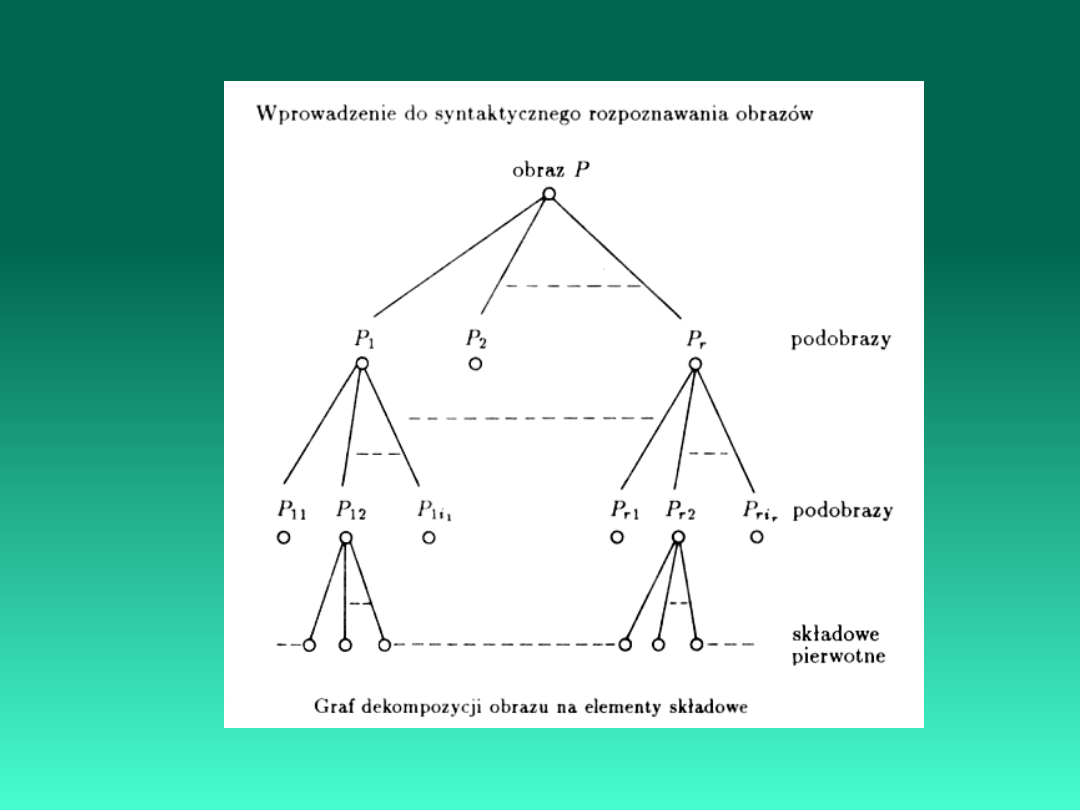
Automatyzacja percepcji (odczytania) wiedzy w obszarze przedmiotowym
jest realizowana zgodnie z modelem percepcji wiedzy:

Klasyfikacja metod rozpoznawania

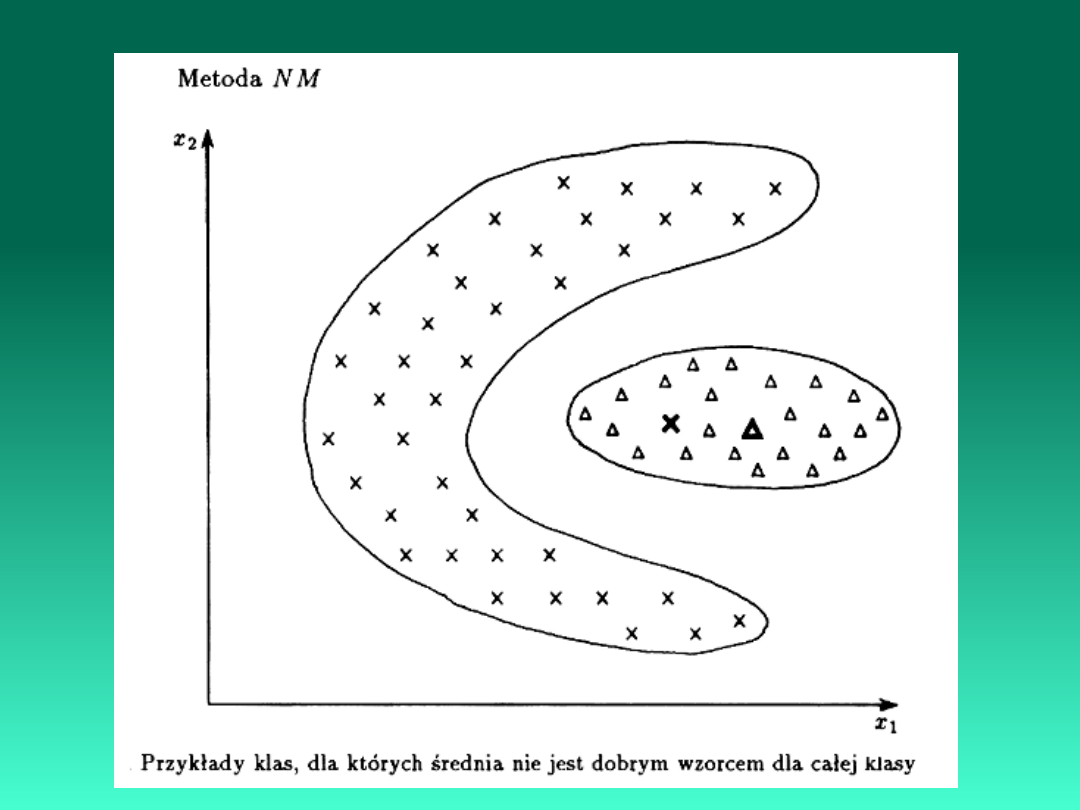
1. Metody minimalno-odległościowe
2. Metody wzorców
3. Metody aproksymacyjne
4. Metody probabilistyczne
5. Metody funkcji potencjalnych
6. Sieci neuronowe
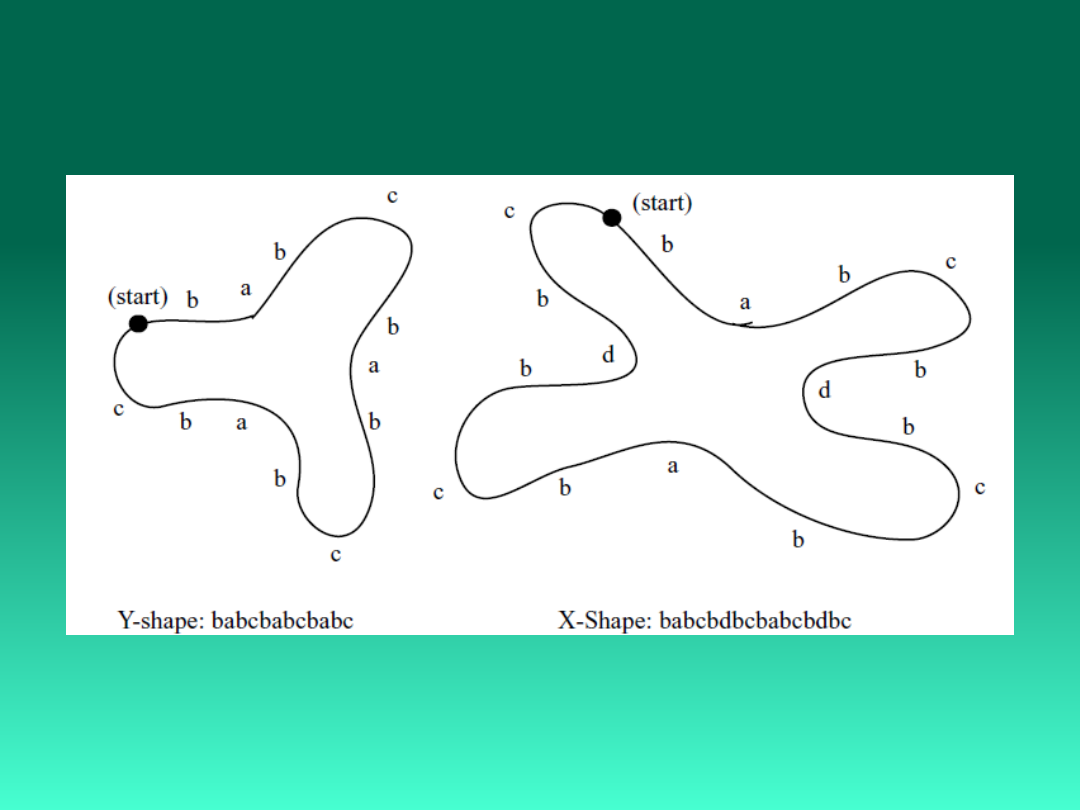
7. Metody syntaktycznego
rozpoznawania obrazów
8 Metody ciągowe
9 Metody drzewowe
10 Metody grafowe

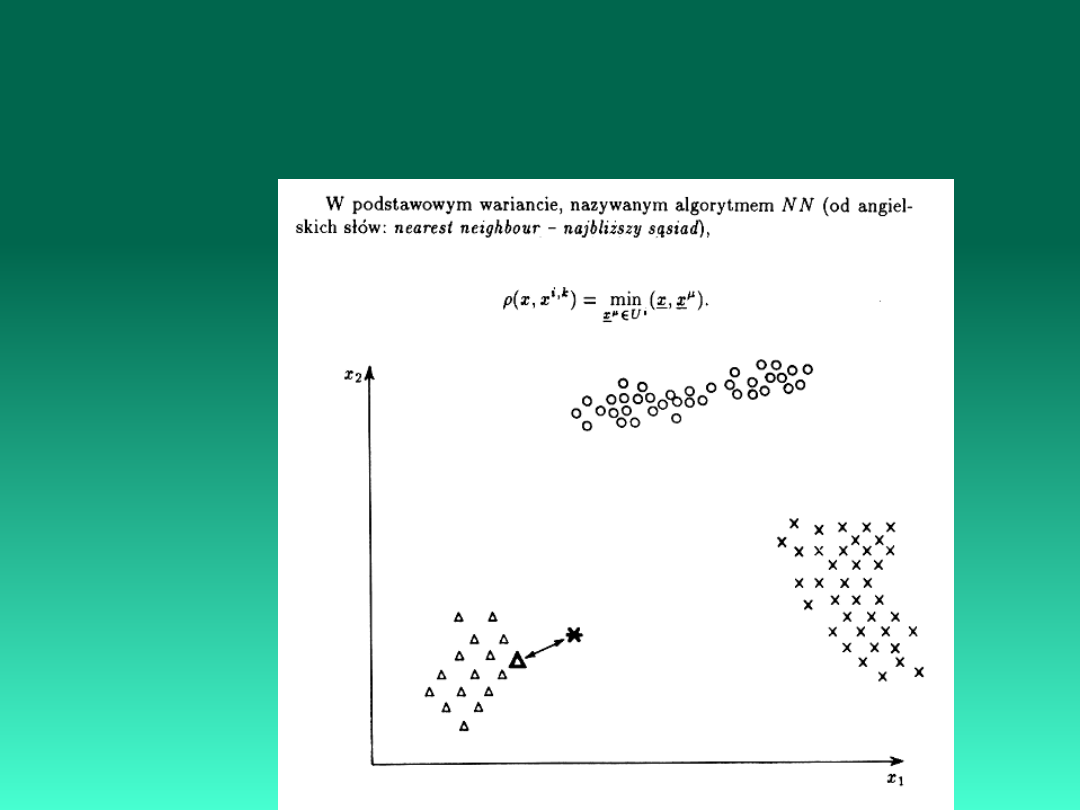
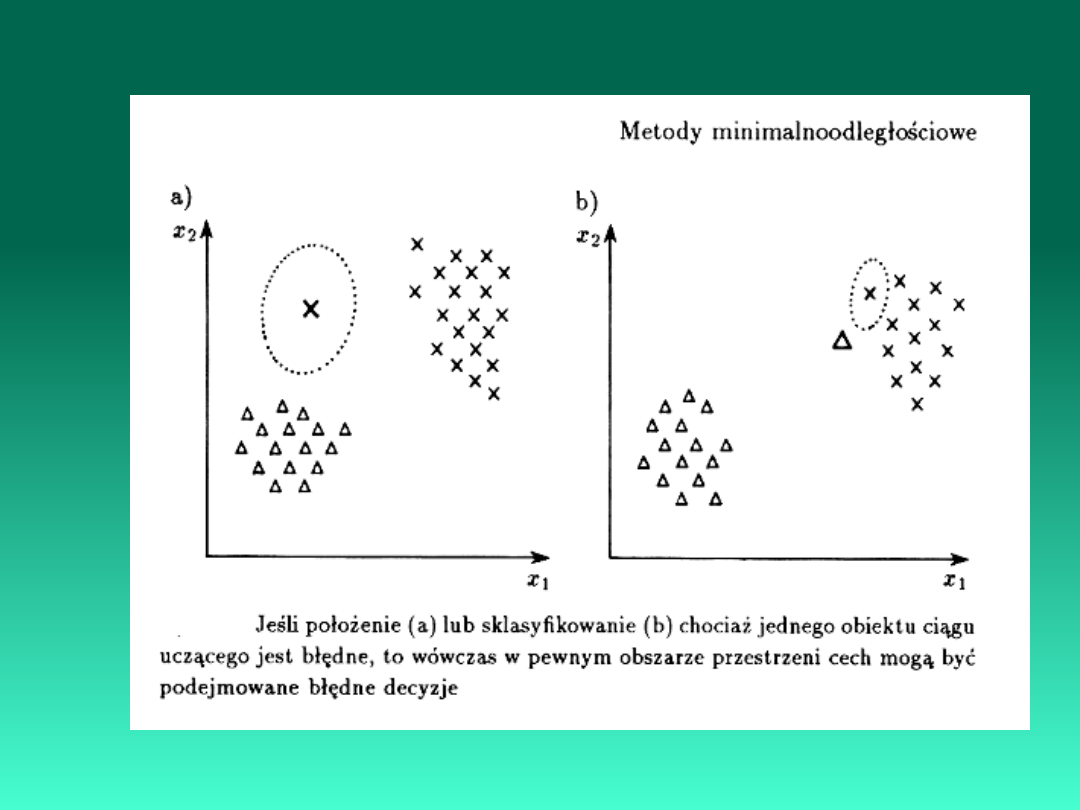
Metody minimalnoodległościowe są oparte na przesłankach
związanych z geometrią przestrzeni cech. Jeśli punkty, odpowiadające
obiektom różnych klas grupują się w
formie wyraźnych skupisk, to wówczas możliwe jest i celowe posłużenie
się pojęciem
odległości przy podejmowaniu decyzji.

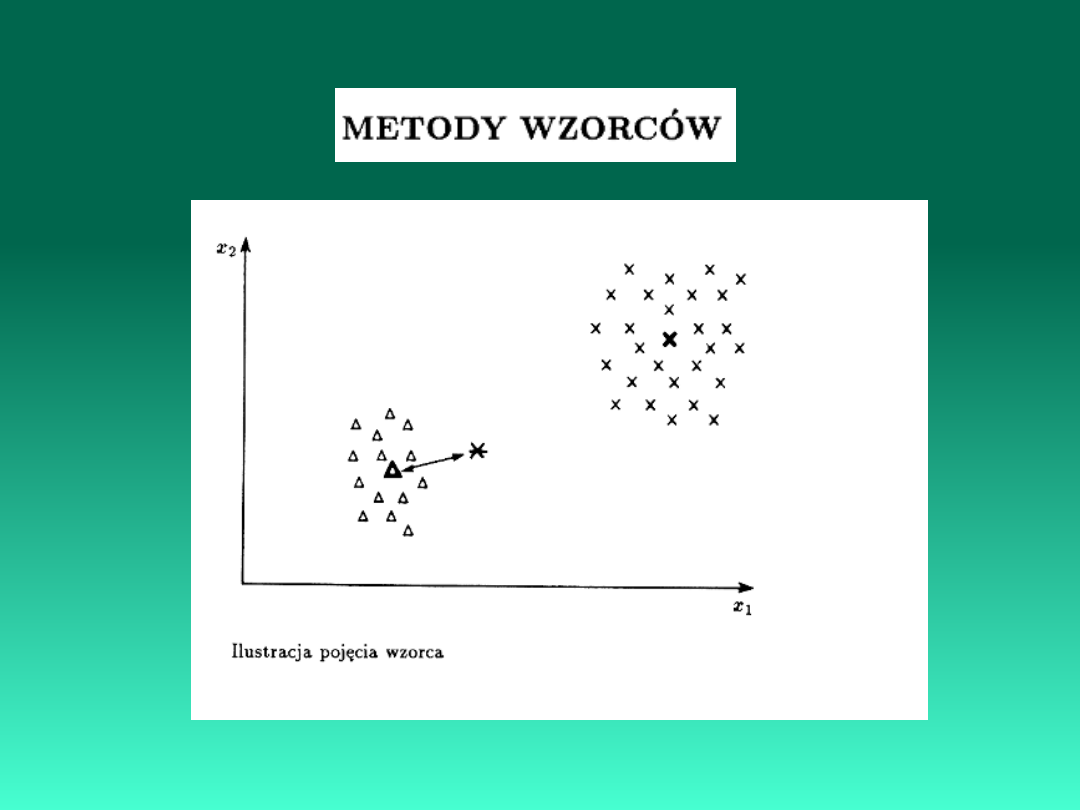
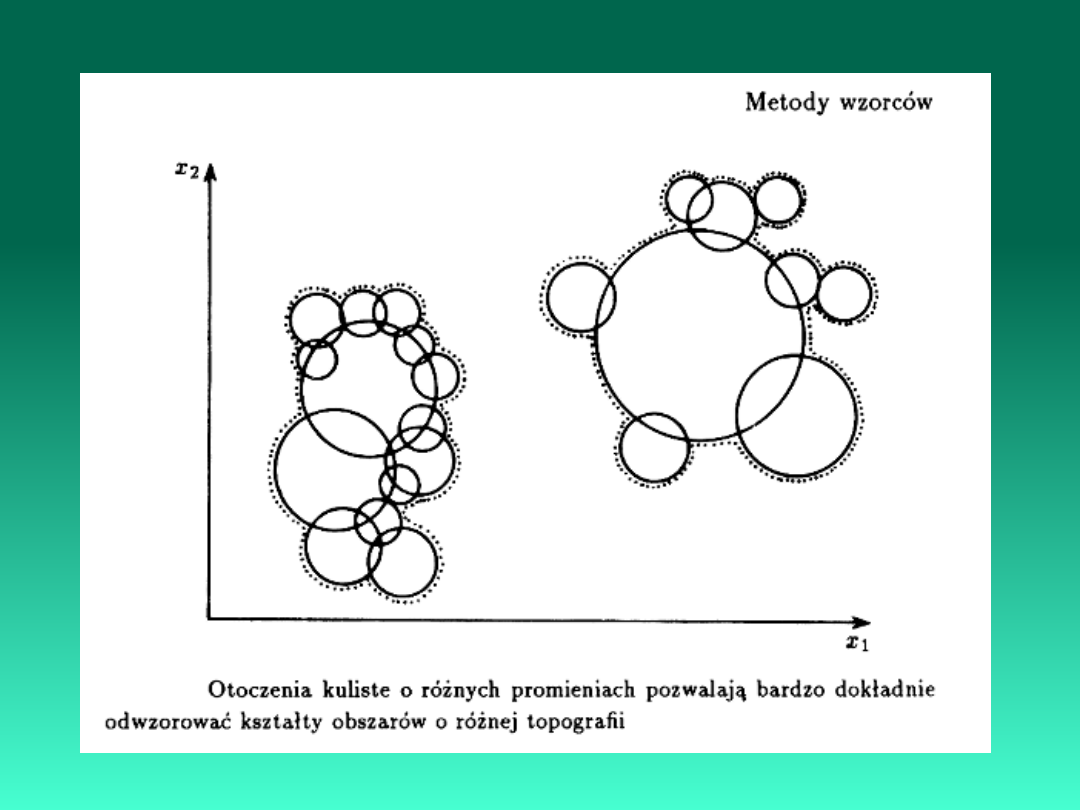
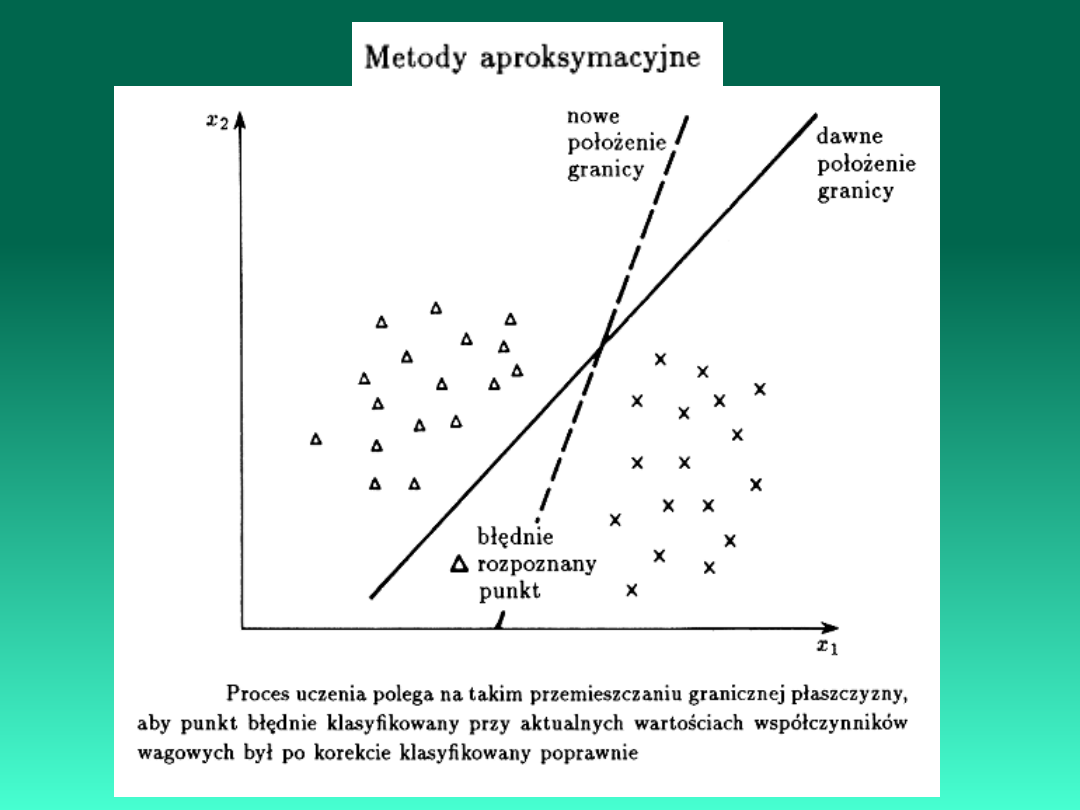
Rozpoznawanie kształtów

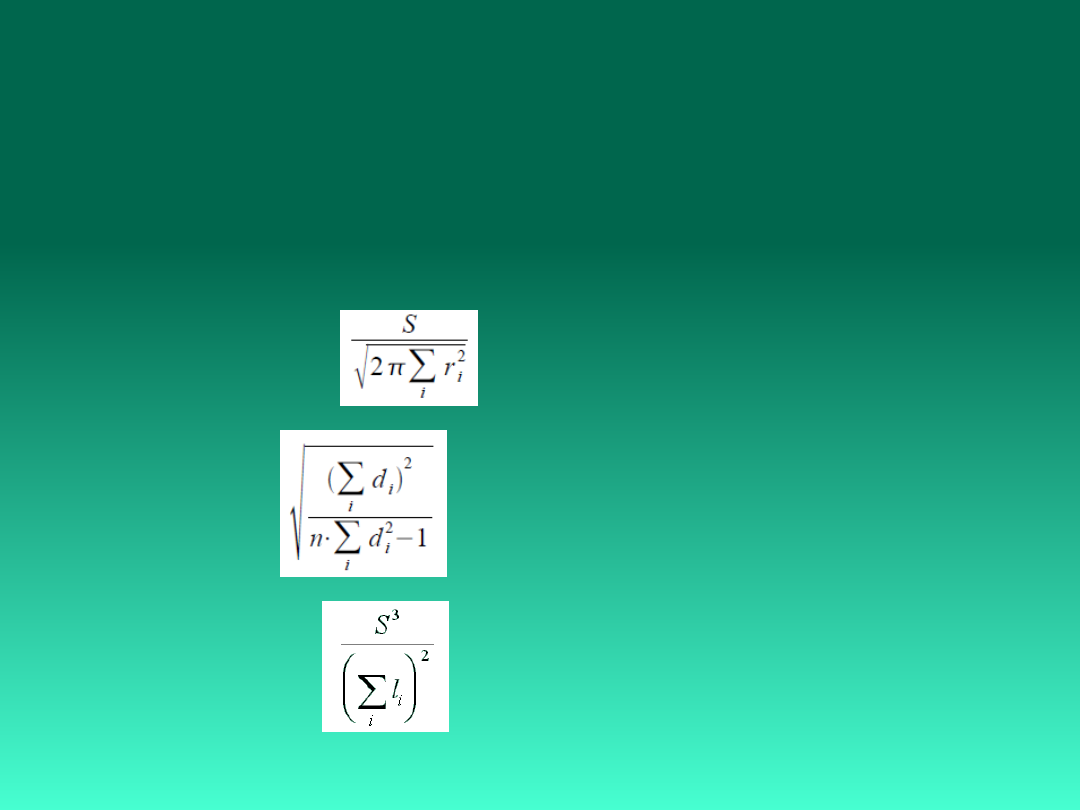
Współczynniki kształtu

Compactness - stosunek pola obiektu do pola
najmniejszego

prostokąta w jakim się obiekt mieści;

Rmin/Rmax - pierwiastek stosunku minimalnej odległości
konturu od środka ciężkości do maksymalnej odległości
konturu

od środka ciężkości;

Blaira - Blissa –

gdzie: S

- pole powierzchni obiektu,

ri - odległość piksela obrazu

od środka ciężkości,

i - numer piksela obiektu.

Haralicka –

di - odległość piksela konturu

od środka ciężkości,

n – liczba pikseli konturu.

Danielssona -

li - minimalna odległość piksela obiektu

od konturu obiektu.

Wyznaczanie szkieletu

Sieci

neuronowe

Sieci

neuronowe

TECHNIKI
EWOLUCYJNE

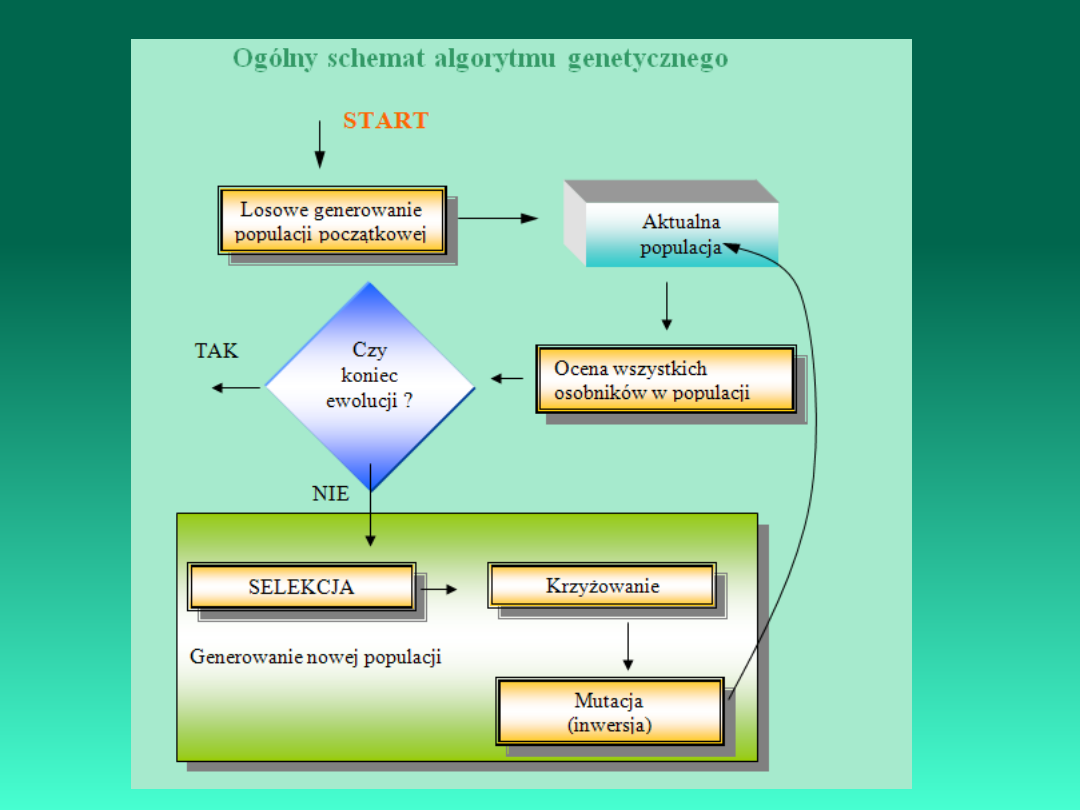
Algorytmy  ewolucyjne  (ang.  Evolutionary  algorithms
(EAs))    są  stochastyczną  techniką  optymalizacji
bazującą na zasadach naturalnej ewolucji.
Jedną z podstawowych zasad ewolucji jest zwiększenie
szans  na  przeżycie  osobnika  (populacji)  lub  jego
potomka.
Celem badań  nad EAs jest:

- Wyjaśnić

istotę

procesów

adaptacyjnych,

występujących w świecie natury;

- Stworzyć oprogramowanie, które odtwarzałoby

podstawowe

mechanizmy

rządzące

systemami

biologicznymi.

Cechy EAs:

- łatwo je implementować na komputerach

równoległych,

- nie zależy w nich na rozwiązaniach optymalnych,

lecz bliskich optymalnemu,

- są stosowane wówczas gdy techniki tradycyjne nie

wystarczą.

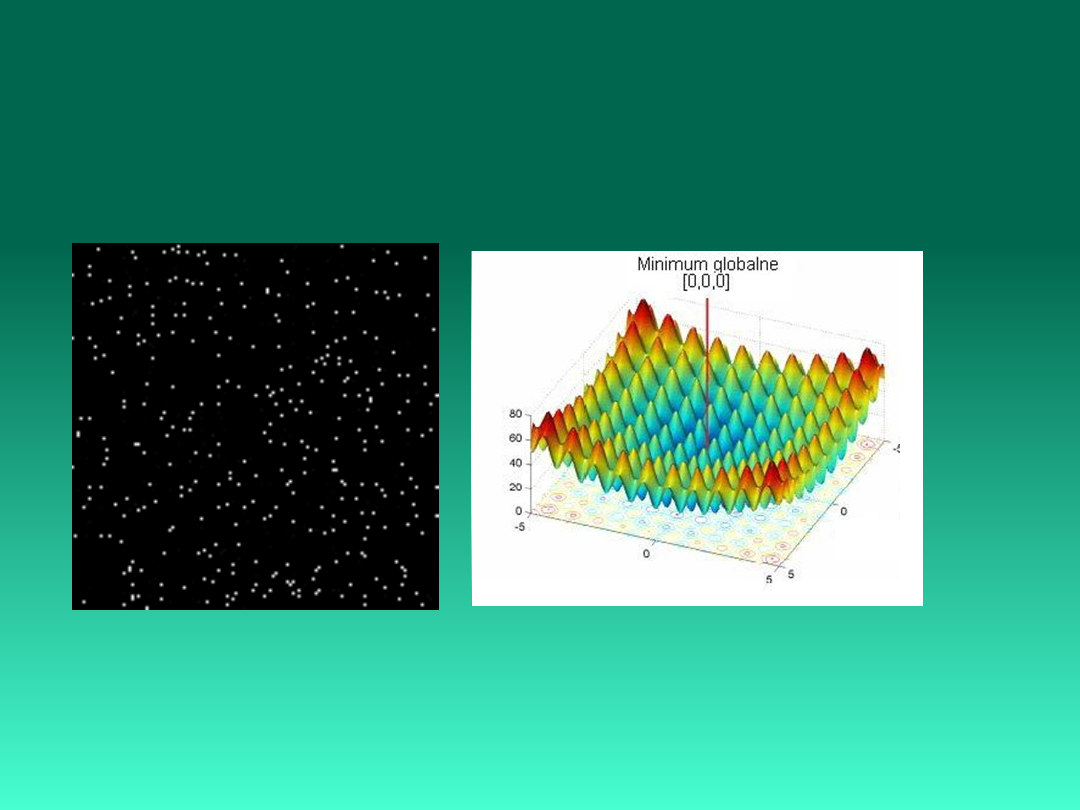
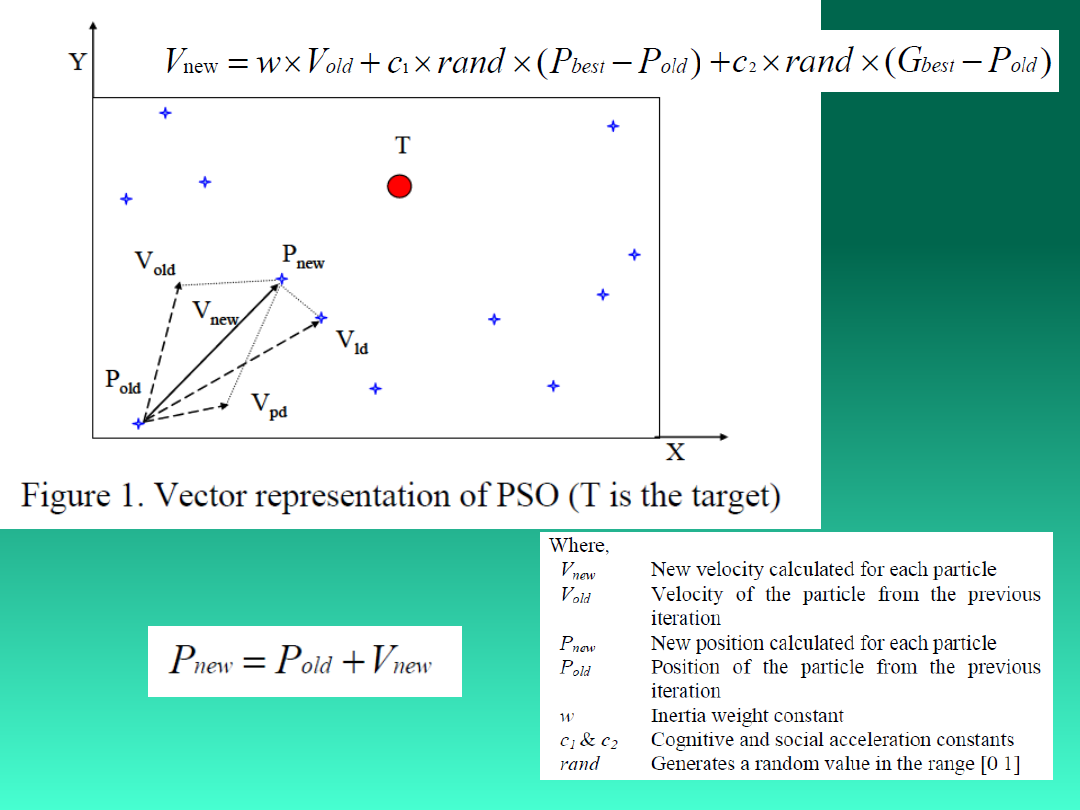
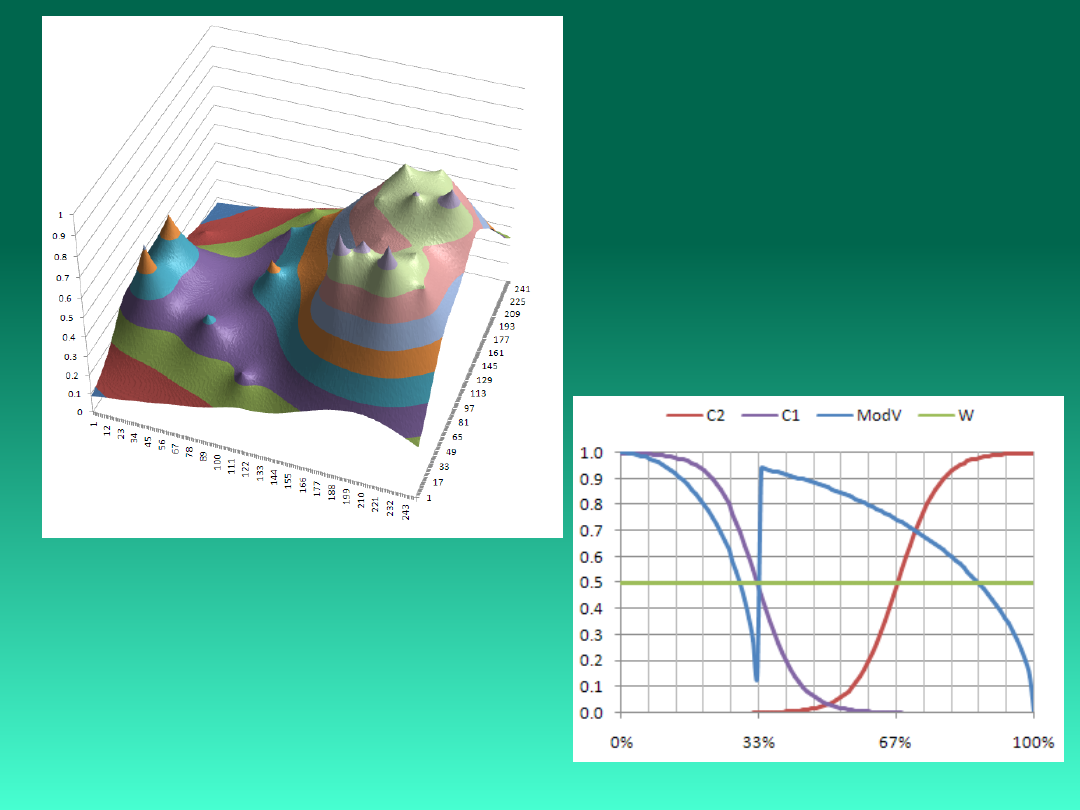
Metoda optymalizacji rojem cząstek

PSO - Particle Swarm Optimization

Particle swarm optimization (PSO) is a parallel population-based
computation technique proposed by Kennedy and Eberhart
(Eberhart and Kennedy, 1995;

20.01.2011

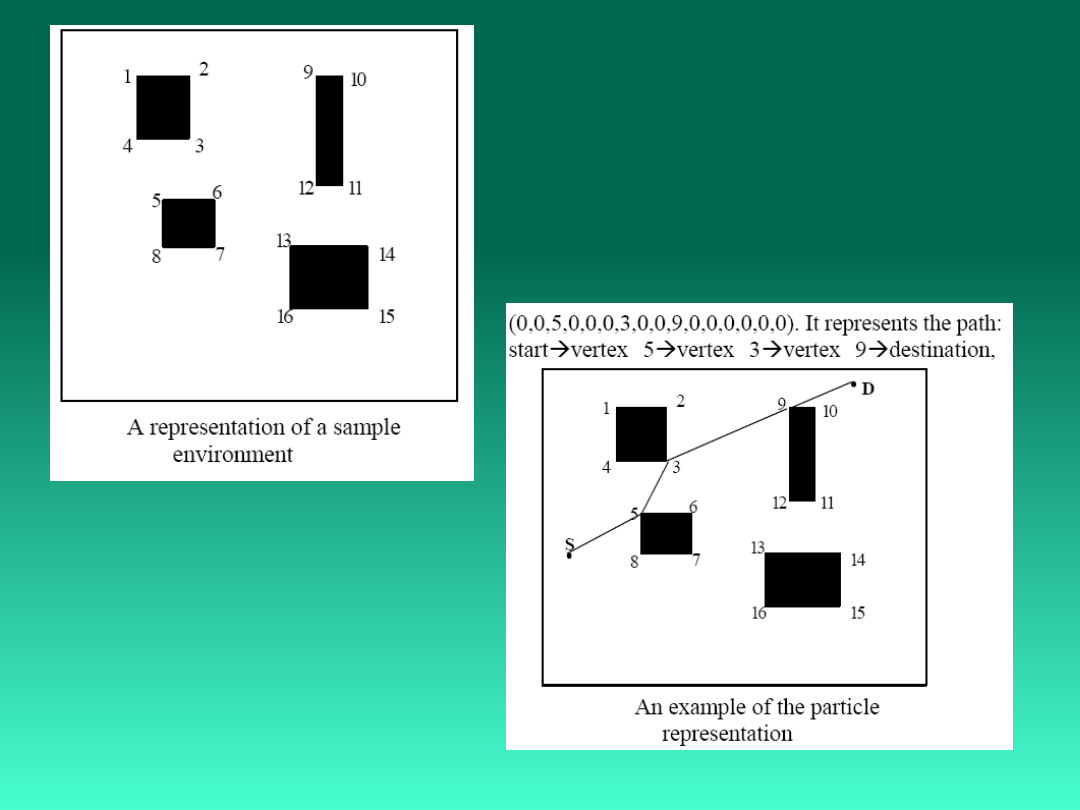
Konfiguracja zautomatyzowanych gniazd
obróbkowych

Manufacturing Cell Formation Problems

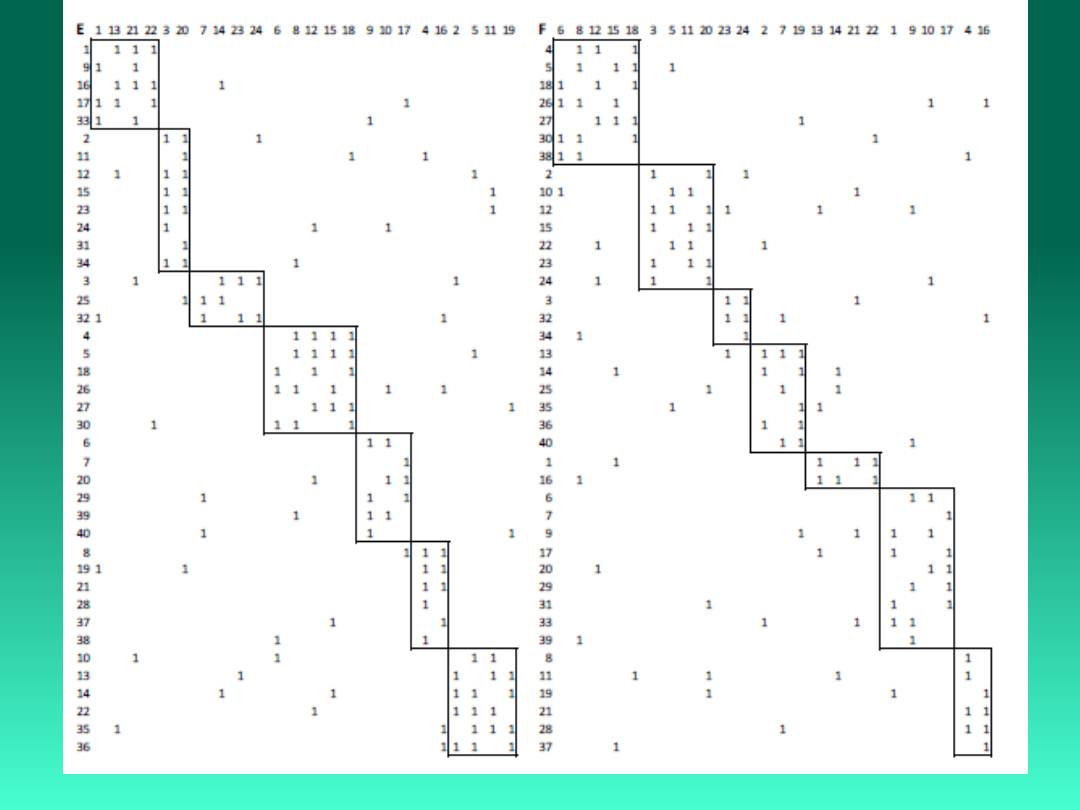
The  chromosome  representation  consists  of
three  sections:  one  representing  the  number  of
cells  to  be  formed,  one  representing  the  parts,
one representing the machines. The first section
contains only one gene. The second and the third
sections  contain  m  (number  of  the  machines)
and  n  (the  number  of  the  parts)  genes
respectively.  All  genes  in  the  chromosome  have
values  between  0  and  0.99  and  the  genes  in
second  and  third  sections  are  decoded  by  using
the  number  of  cells  (c)  which  is  determined  by
the first gene. For example, a solution for the 6-
machines,  6-parts  problem  can  be  represented
as  the  chromosome  is  given  in  Fig.2.  Since  this
example  contains  6  machines,  the  maximum  c
can  be  6  so  the  range  [0  ,  1)  is  divided  into  6
equal ranges as given below.

Initial population. Initial population is constructed by generating
random numbers in range [0,1) for each genes in the
chromosomes of the initial population.

Życie jest to możliwość trwania (reprodukcji i
ewolucji) bardzo nieprawdopodobnych
uporządkowanych stanów materii (Erwin
Schrődinger).

Żywy jest ten kto (Ellen Thro):
• Istnieje w przestrzeni i w czasie.
• Rozmnaża się.
• Przechowuje informację o samym sobie.
• Oddziałuje z otoczeniem.
• Składa się z niezależnych części.
• Wykazuje stabilność przy zmiennych warunkach

środowiska.

• Ewoluuje.
• Rośnie lub rozszerza się.
• Może przetwarzać materię na energię (posiada

metabolizm).

Sztuczne życie: dziedzina badań zajmująca się modelowaniem
i  symulacją  zjawiska  życia  w  szczególności  modelowaniem
żywych  organizmów  w  różnych  środowiskach  (komputerach,
układach  elektronicznych  lub  chemicznych),  w  celu  odkrycia
istoty  i  uniwersalnych  cech  „życia”  jakie  znamy  i  jakie
gdziekolwiek mogłoby zaistnieć.

Bóg zawarł w prawach Natury tajemną
sztukę, tak aby chaos przemienił się w
doskonały system świata (Immanuel Kant).

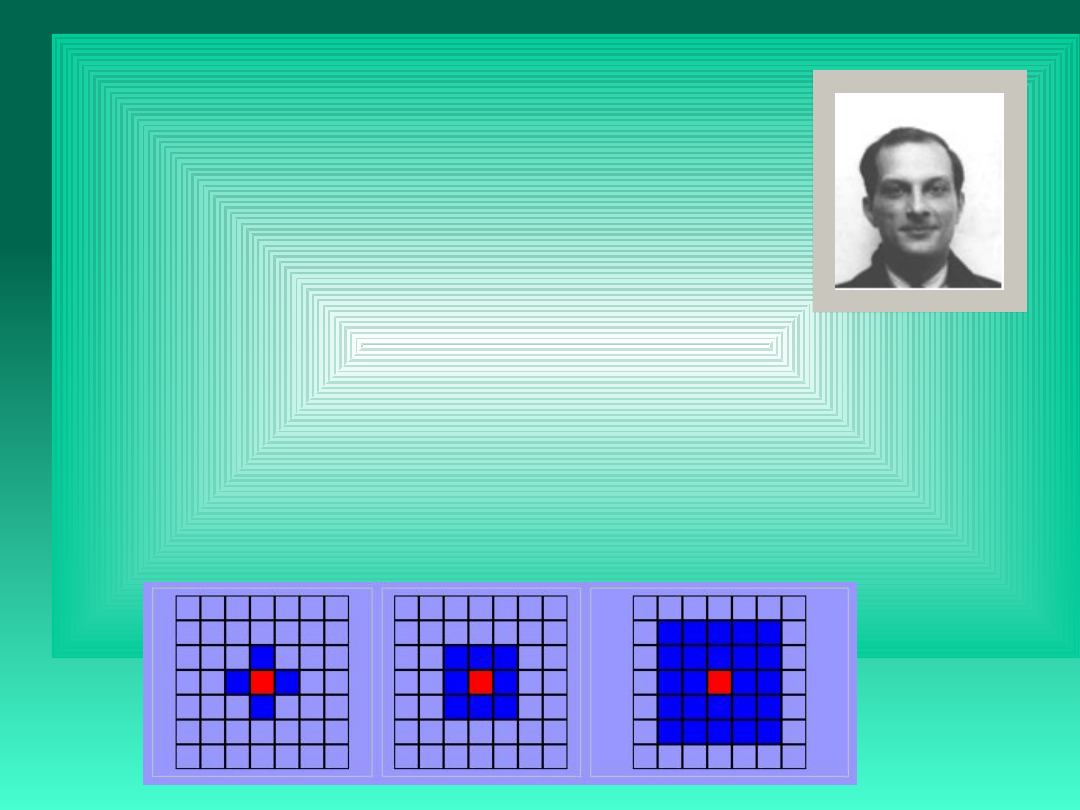
Automat komórkowy jest matematycznym, równoległym
modelem obliczeniowym
i charakteryzuje się:
• zbiorem C komórek c

, tworzących regularną sieć

w n - wymiarowej przestrzeni;
• zbiorem S stanów s

pojedynczych komórek,

zawierającym k

elementów;

• regułami F określających stan komórki w chwili t+1 w zależności od jej

stanu
w chwili t oraz stanu komórek ją otaczających.

(t+1) = F(s

(t), {s

(t)}),

j  O(i)

gdzie O(i) jest otoczeniem i-tej komórki.

otoczenie von Neumann’a otoczenie Moore’a rozszerzone otoczenie Moore’a

Skąd bierze się złożoność automatów komórkowych ?

Weźmy pod uwagę:

• automat jednowymiarowy;

• o promień sąsiedztwa = 1;

• dwustanowy (1,0);

| X | X

111 110 101 100 011 010 001 000

1 0 1 1 0 1 0 0

(2,1) 

= 256 automatów

(liczba stanów, promień sąsiedztwa)

(2,2)  2

= 4294967300 automatów

(3,1)  3

 7.6 x 10

automatów

(4,1)  4

 3.4 x 10

automatów

Zastosowania automatów komórkowych:

modelowanie i symulacja zjawisk fizycznych i biologicznych takich
jak:

- przepływy cieczy,
- formowanie się galaktyk,
- trzęsienia Ziemi,
- formowanie się struktur geologicznych,
- proces uwadniania cementu i starzenia betonu,
- procesy krystalizacji,
- modelowanie zachowania się lawiny śnieżnej
- generowanie i obróbka obrazów rastrowych,
- generowanie efektów kinowych i inne.

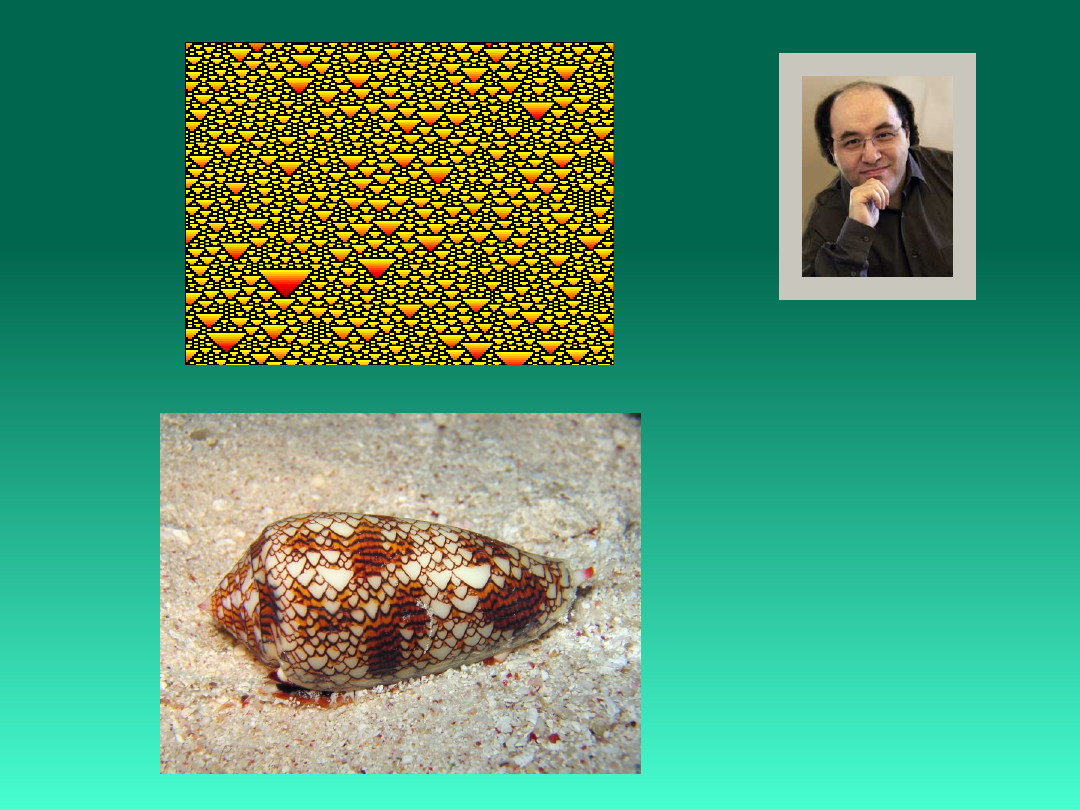
Stephen
Wolfram

Przykład: metoda generowania przedstawiciela

syntetycznego

Fragment powierzchni roboczej walca bruzdowego

Dziękuję za uwagę

Ask not what mathematics can do for biology.
Ask what biology can do for Mathematics.

Stan Ulam

Document Outline

Slide 1
Slide 2
tematyka
Slide 4
Slide 5
Slide 6
DEFINICJE
Slide 8
Slide 9
Slide 10
Slide 11
Pod-dziedziny sztucznej inteligencji:
Najważniejsze osiągnięcia w rozwoju AI
Najważniejsze osiągnięcia w rozwoju AI
Najważniejsze osiągnięcia w rozwoju AI
Najważniejsze osiągnięcia w rozwoju AI
Porównanie mózgu ludzkiego i komputera.
Zbiory rozmyte (Logika rozmyta)
Slide 19
Slide 20
Slide 21
Slide 22
Funkcje Przynależności
Typy Funkcji Przynależności
Slide 25
Przykłady rozmytych relacji
Reguły rozmyte
Operacje na liczbach rozmytych
Slide 29
Zastosowania logiki rozmytej
Narzędzia AI
Slide 32
Slide 33
Slide 34
Slide 35
Slide 36
Slide 37
Slide 38
Slide 39
Slide 40
Slide 41
Slide 42
Slide 43
Slide 44
Slide 45
Slide 46
Slide 47
Slide 48
Slide 49
Slide 50
Slide 51
Slide 52
Slide 53
Slide 54
Slide 55
Slide 56
Slide 57
Slide 58
Slide 59
Slide 60
Slide 61
Slide 62
Slide 63
Slide 64
Slide 65
Slide 66
Slide 67
Slide 68
Slide 69
Slide 70
Slide 71
Slide 72
Slide 73
Slide 74
Slide 75
Slide 76
Slide 77
Slide 78
Slide 79
Slide 80
Slide 81
Slide 82
Slide 83
Slide 84
Slide 85