Nieliniowe

właściwości

optyczne

Zbigniew Chałupka

Optyka nieliniowa



Jest to dział nauki zajmujący się badaniem właściwości układów
nieliniowo zależących od natężenia fali padającej.



Aby móc obserwować własności nieliniowe należy stosować światło
o wysokim natężeniu tak jak np. generowane za pomocą laserów
rubinowych.

Polaryzacja indukowana



Polaryzację indukowaną (P) możemy zapisać jako szereg potęgowy
pola elektrycznego (E):

χ- liniowa podatność magnetyczna



 

Pole elektryczne



Pole elektryczne związane ze światłem padającym jest zależnością
sinusoidalną:



Podstawiając E za wyrażenia P otrzymujemy szereg potęgowy w
relacji zależnej od:



 

Pole elektryczne



Drugie wyrażenie zawiera składową polaryzacji pola E:

)



Intensywność światła zależna jest od wielkości d- drugiego
współczynnika w szeregu



 

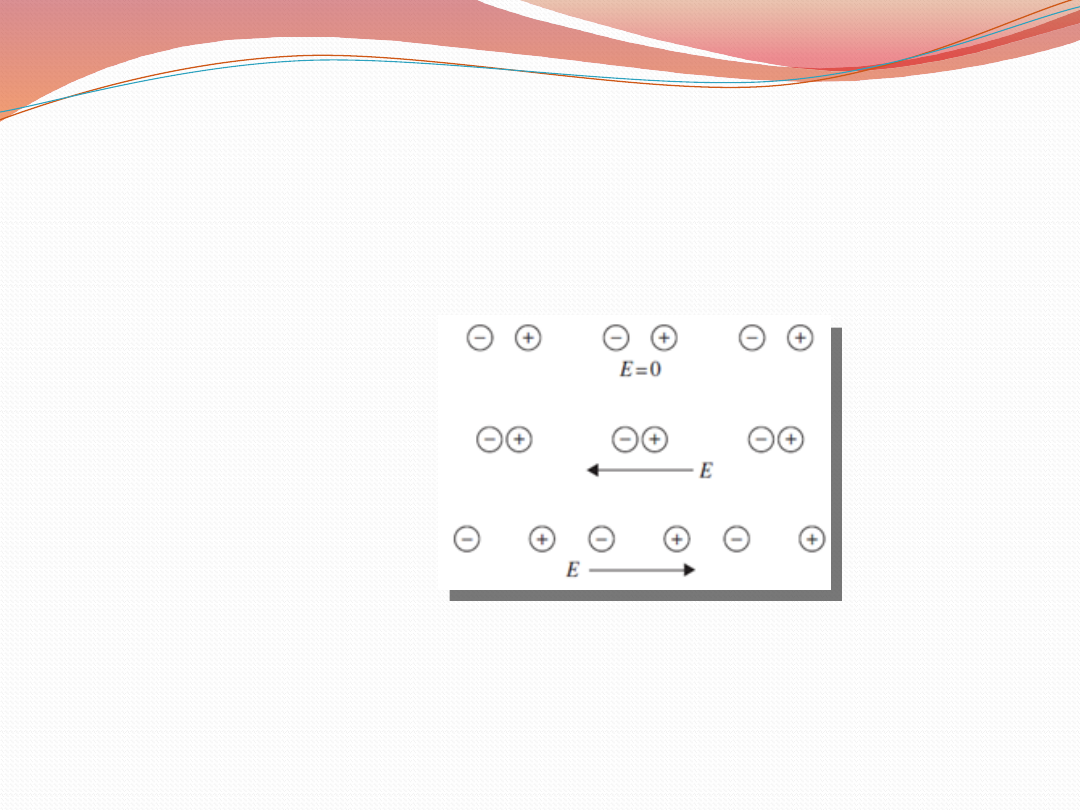
Struktura a właściwości



Symetria kryształów – najważniejszy czynnik determinujący
obecność efektów drugiego rzędu

Jednowymiarowy polarny
łańcuch w polu skierowanym
w lewo i w prawo pokazujący
pochodzenie nieliniowych
własności optycznych



Kryształy centrosymetryczne są nieprzydatne w generowaniu
drugiej harmonicznej

Struktura a właściwości



Generowanie drugiej harmonicznej jest dobrym eksperymentem na
obecność środka inwersji- silny sygnał jest dowodem na brak
środka symetrii!



Kryształy LiO

3

oraz HIO

3

zawierają oktaedry IO

6

są one

obiecującymi kryształami nieliniowymi, ponieważ owe oktaedry
posiadają trwałe zaburzenia spowodowane niezwiązanymi
elektronami.

Struktura a właściwości



Najlepsze związki do generowania drugiej harmonicznej posiadają
duże współczynniki załamania światła.



Współczynniki te są proporcjonalne do:



Tytaniany i niobiany są doskonałymi materiałami nieliniowymi.



 

Nieliniowe właściwości optyczne



Są charakteryzowane za pomocą polaryzacji rozpisanej w szereg
potęgowy:

χ

ij-

podatność elektryczna powiązana z przenikalnością optyczną

definiowana jako:

χ

ijk-

czynnik odpowiedzialny za generowanie drugiej harmonicznej

(SHG)
χ

ijkl-

tensor czwartego rzędu odpowiedzialny za generowanie trzeciej

harmonicznej (THG)



 

Nieliniowe właściwości optyczne



Relację tensorową można zapisać jako funkcję częstotliwości, ω:



Po uwzględnieniu czasu otrzymujemy:

E

0

- amplituda fali

φ- różnica fazowa pomiędzy dwoma przemieszczającymi się polami



 

Nieliniowe właściwości optyczne



Wynik dwóch pól można zapisach jako sumę i różnicę
częstotliwości:



Wynika z tego, iż tensor III rzędu jest niezerowy tylko w dwóch
przypadkach:

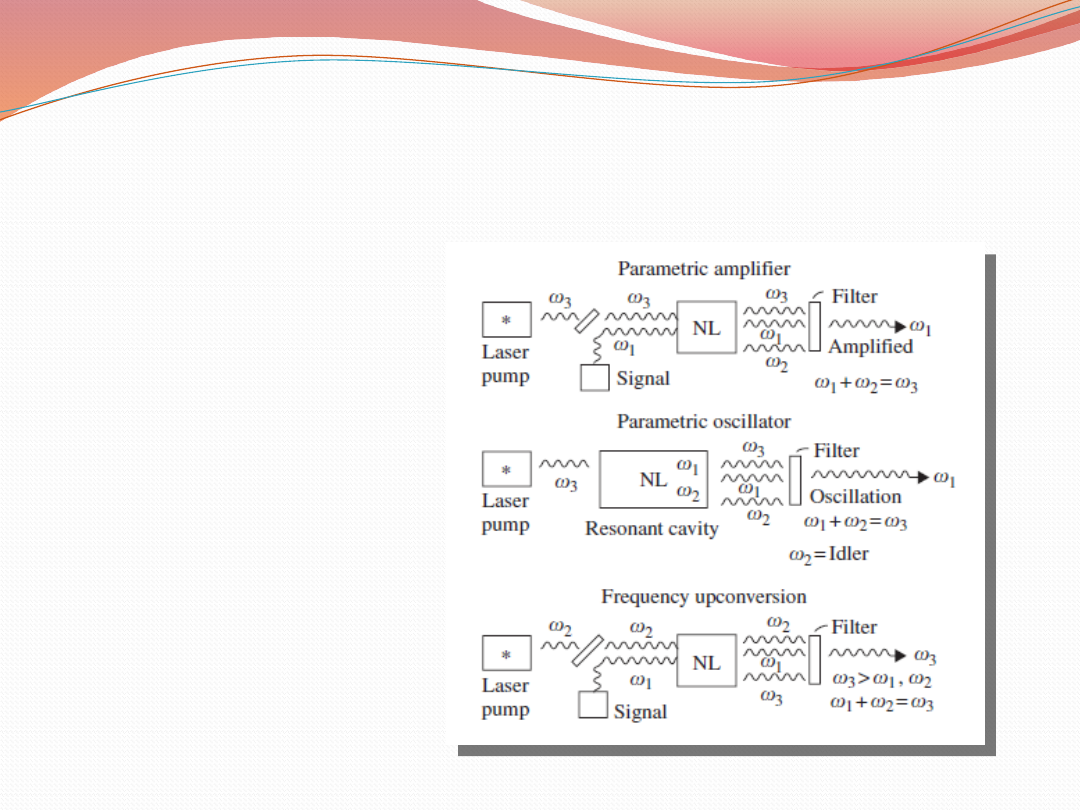
Nieliniowe właściwości optyczne



Przykłady nieliniowości w
kryształach-
wykorzystanie:

1.

Wzmacniacz
parametryczny

2.

Oscylator parametryczny

3.

Konwerter częstotliwości
sygnału

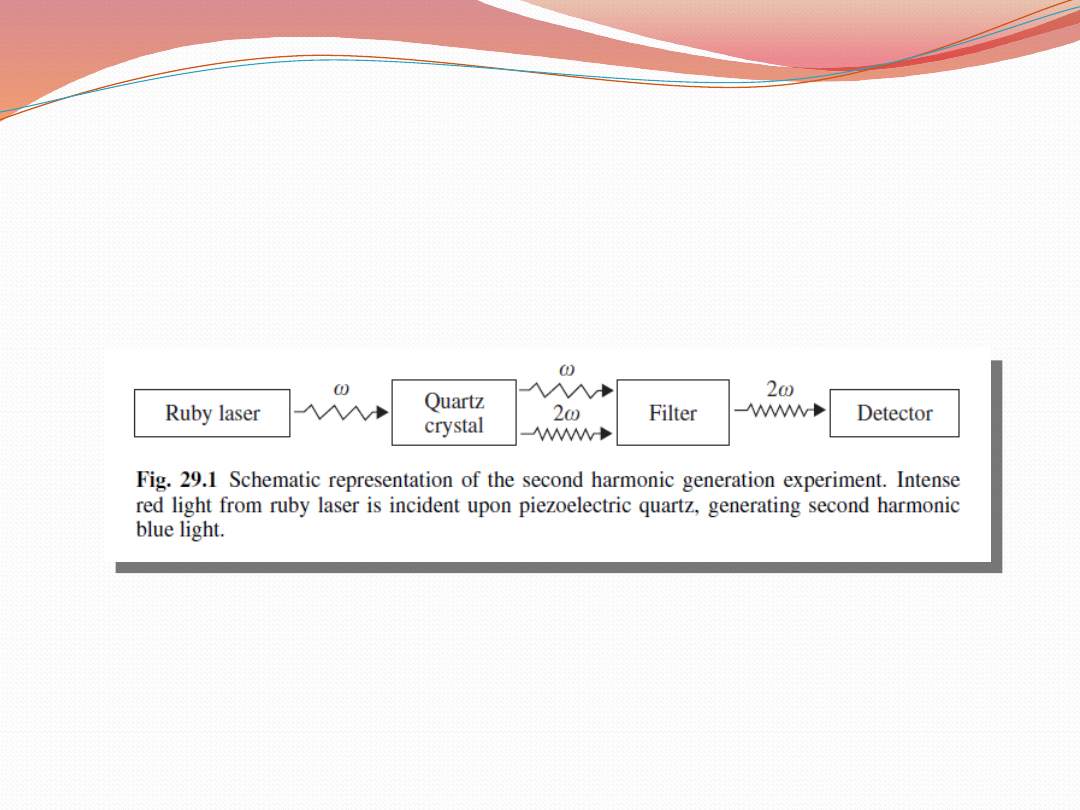
Generowanie drugiej

harmonicznej(SHG)

Np. za pomocą lasera rubinowego

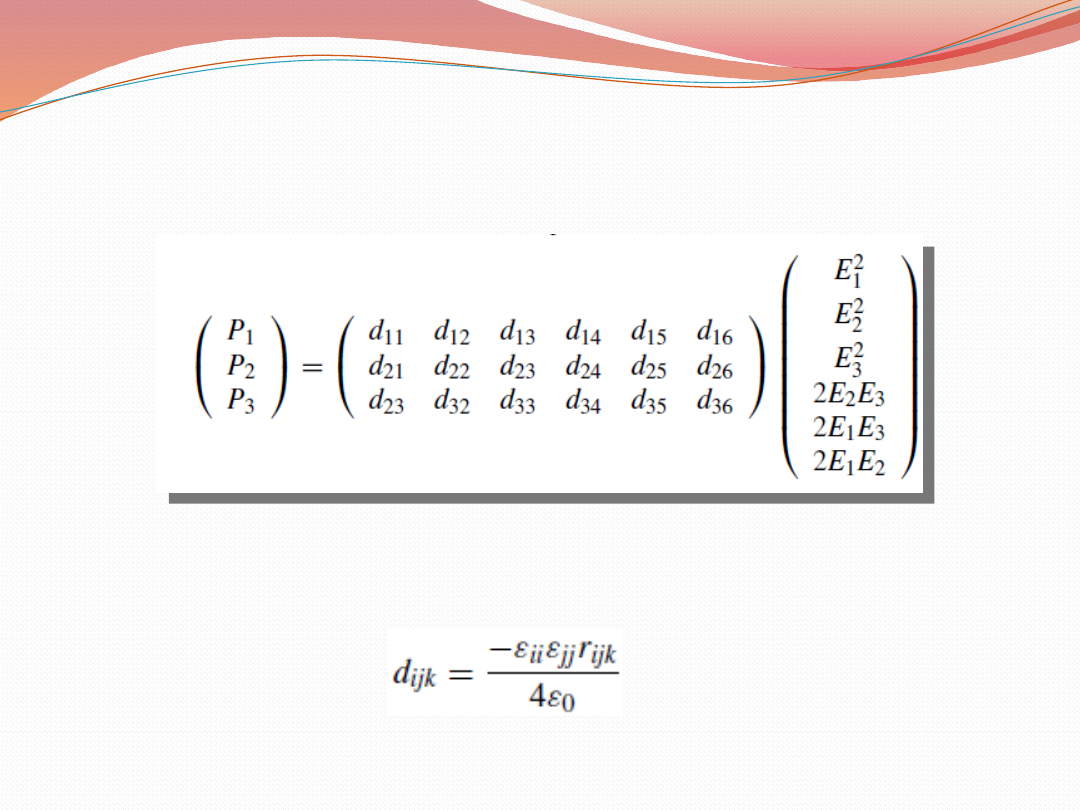
Polaryzacja nieliniowa- macierz

Zachodzi relacja pomiędzy współczynnikiem SHG a liniowym
współczynnikiem elektro- optycznym (r

ijk

):

Tabela wartości nieliniowych współczynników

mierzonych w jednostce 10

-23

F/N

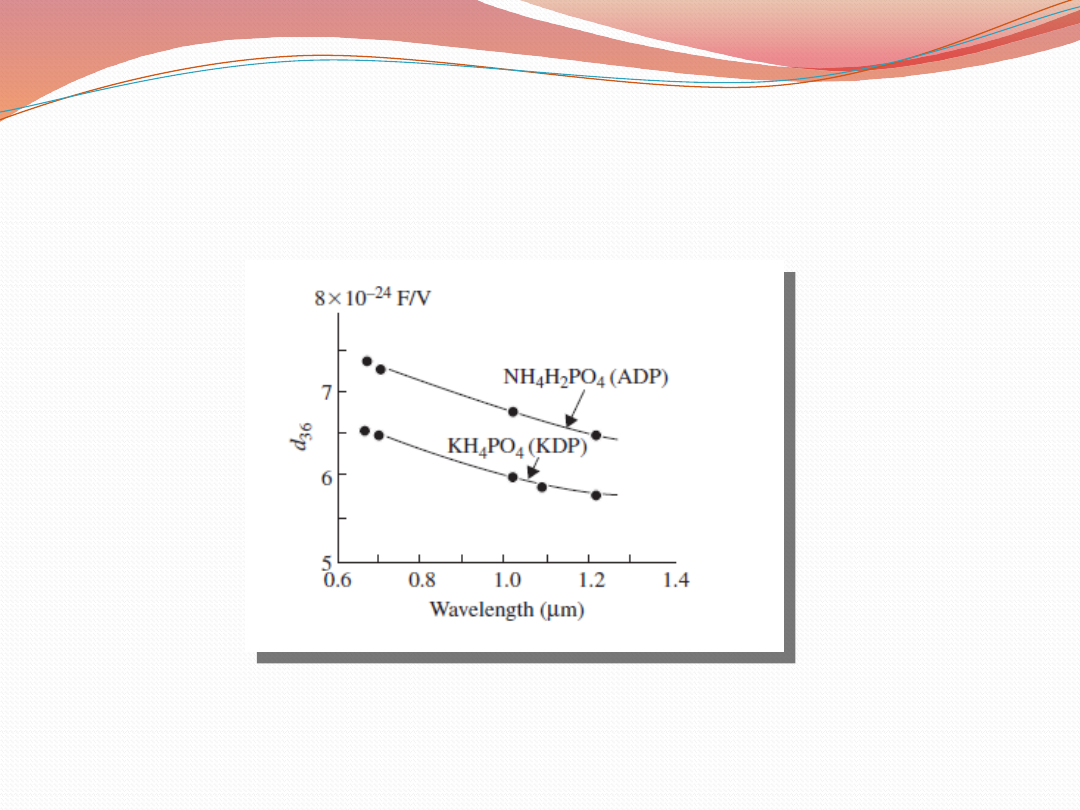
Nieliniowe własności optyczne

Dyspersja współczynnika d

36

dla ADP

oraz KDP

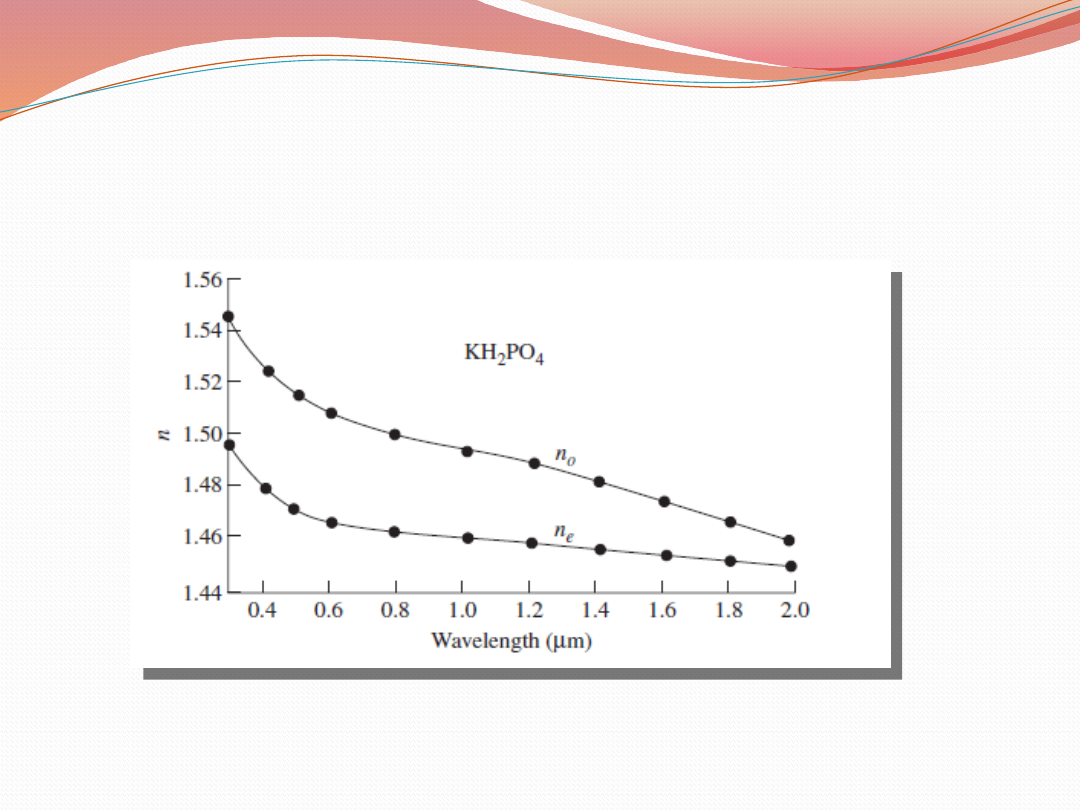
Nieliniowe własności optyczne

Optyczna dyspersja w tetragonalnym KDP-

diwodorofosforanie potasu

Dopasowywanie fazy



Interferencja jest wymagana jeśli chcemy wygenerować drugą
harmoniczną z dużą efektywnością



Wykorzystujemy zjawisko dwójłomności; dwie fale podróżują z tą
samą prędkością jeżeli ich współczynniki załamania są równe:

n(2ω) = n(ω)

Dopasowywanie fazy



Jeśli fala układa się pod kątem θ zgodnie z osią Z

3

to współczynnik

refrakcji można opisać wzorem:



Zakładając, że:

θ

m

- kąt dopasowania fazy

Dopasowywanie fazy



Otrzymujemy fazę dopasowania θ

m

:



Ostatecznie rozwiązanie dla θ

m

:

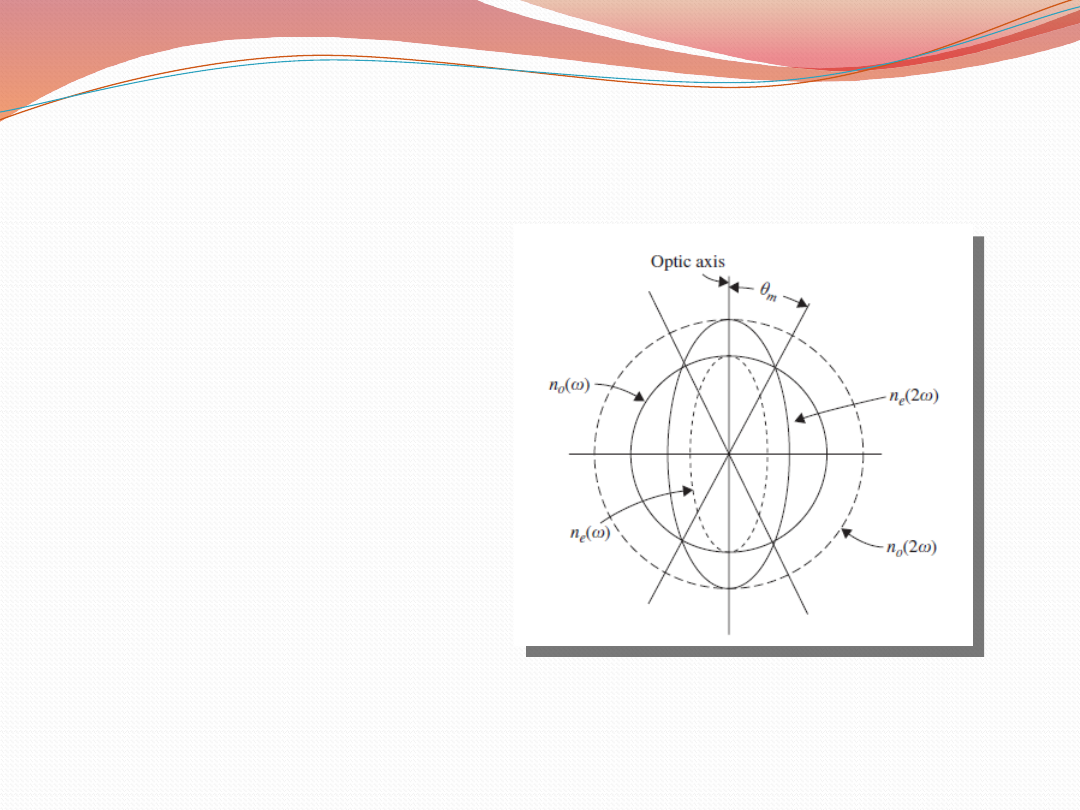
Elipsoidy współczynników refrakcji

Elipsoidy
współczynników
refrakcji dla fal
podstawowych (ω) i
harmonicznych (2 ω)
w jednoosiowym
ujemnym
(n

o

<

n

e

)

krysztale

KDP

Dopasowywanie w fazie jest możliwe tylko dla kryształów
z niską dyspersją i względnie dużą dwójłomnością

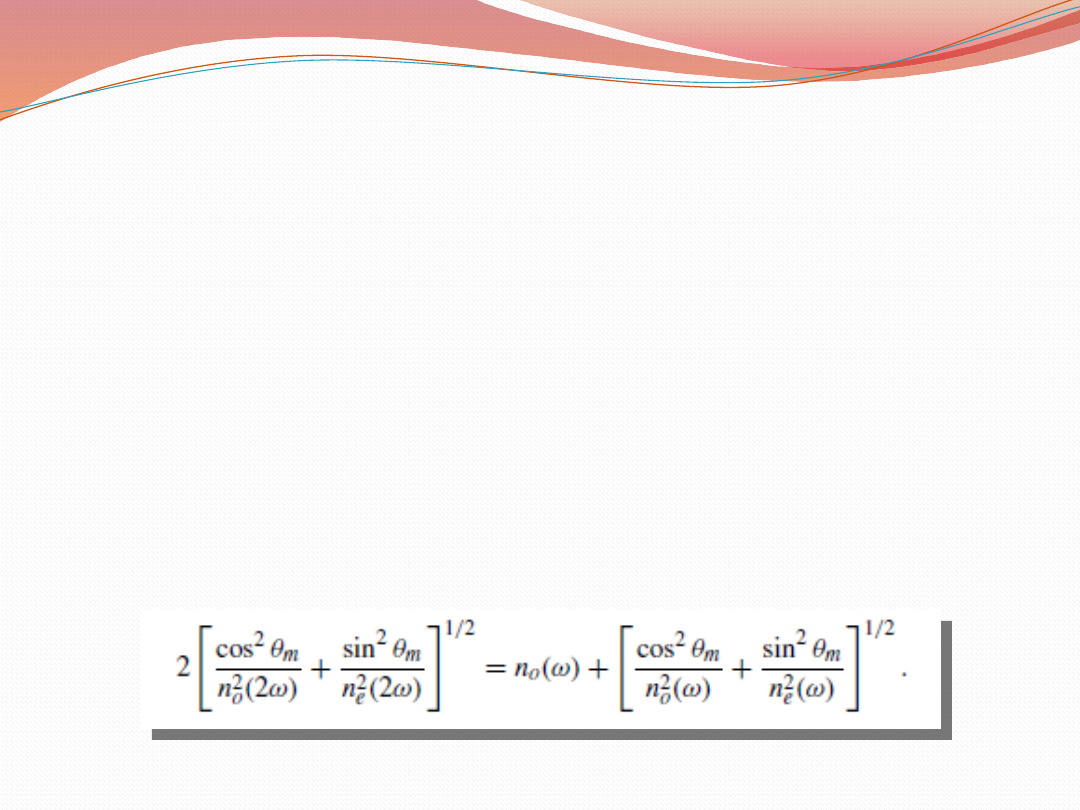
Dopasowywanie fazy



Warunki dopasowania fazy dla kryształów KDP:

(2ω, ω, ω) = (e, o, o) lub (2ω, ω, ω) = (e, o, e)



Dla dopasowania fazy (e, o, e) w krysztale KDP

wartość krytyczna kąta opisywana jest równaniem:

KDP- a nieliniowe własności

optyczne



KDP grupa punktowa



Nieliniowe współczynniki optyczne występujące w KDP to: oraz



 

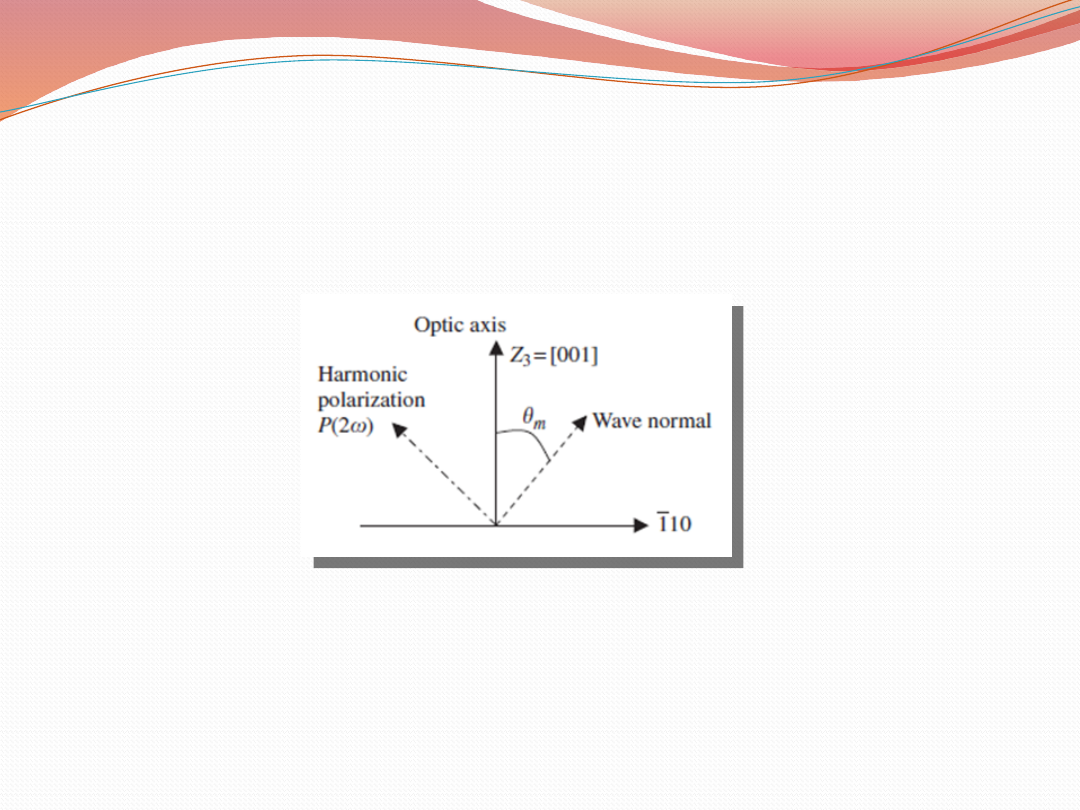
Dopasowanie fazowe- KDP

Kierunki dopasowania fazowego dla normalnej i
harmonicznej fali polaryzacji dla kryształu KDP.
Podstawowa polaryzacja jest prostopadła w
kierunku [110] do czterech przedstawionych
wektorów.

Związki stosowane w optyce

nieliniowej



KDP



Siarczki i selenki należące do grupy punktowej



Kryształy LiNbO

3

i Ag

3

AsS

3

(proustyt) należące do grupy punktowej



tellurki



 

Rys. 1 Proustyt

Generowanie trzeciej harmonicznej

(THG)

- tensor polarny czwartego rzędu występuje we
wszystkich 32 grupach symetrii oraz i
wszystkich 7 grupach Curie

 

Zachodzi relacja:

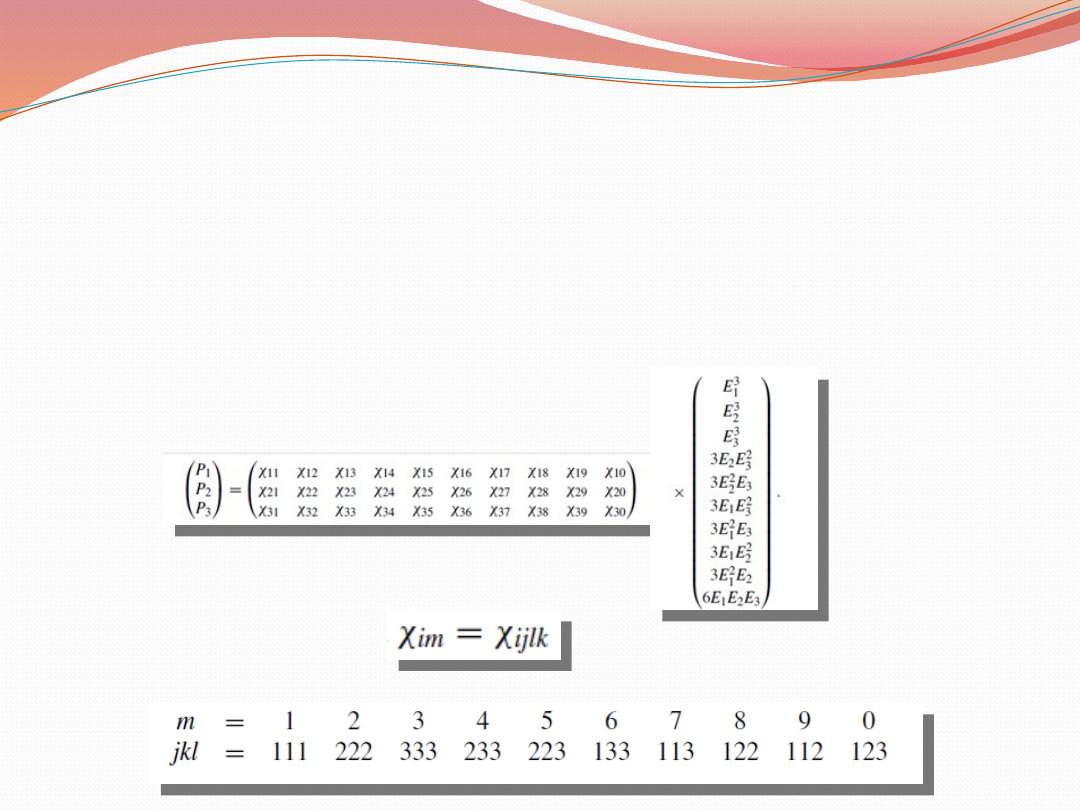
Generowanie trzeciej harmonicznej

(THG)



Dzięki zastosowaniu wcześniejszej relacji

jesteśmy w stanie uprościć macierz z 81 do 30
współczynników:

Generowanie trzeciej harmonicznej

(THG)



Uwzględniając dodatkowo prawo Neumanna dochodzi do redukcji
ilości współczynników z 30 do 9, natomiast przybliżenie
Kleinmanna powoduje redukcję z 30 do 15 współczynników.

Wpływ symetrii na generowanie trzeciej harmonicznej.

• Liczby przedstawiają liczbę niezerowych

współczynników macierzy.

• W nawiasach podano ilość niezależnych

współczynników macierzy.

Generowanie trzeciej harmonicznej
(THG)

Współczynniki trzeciego rzędu dla cieczy, szkieł i kryształów
kubicznych

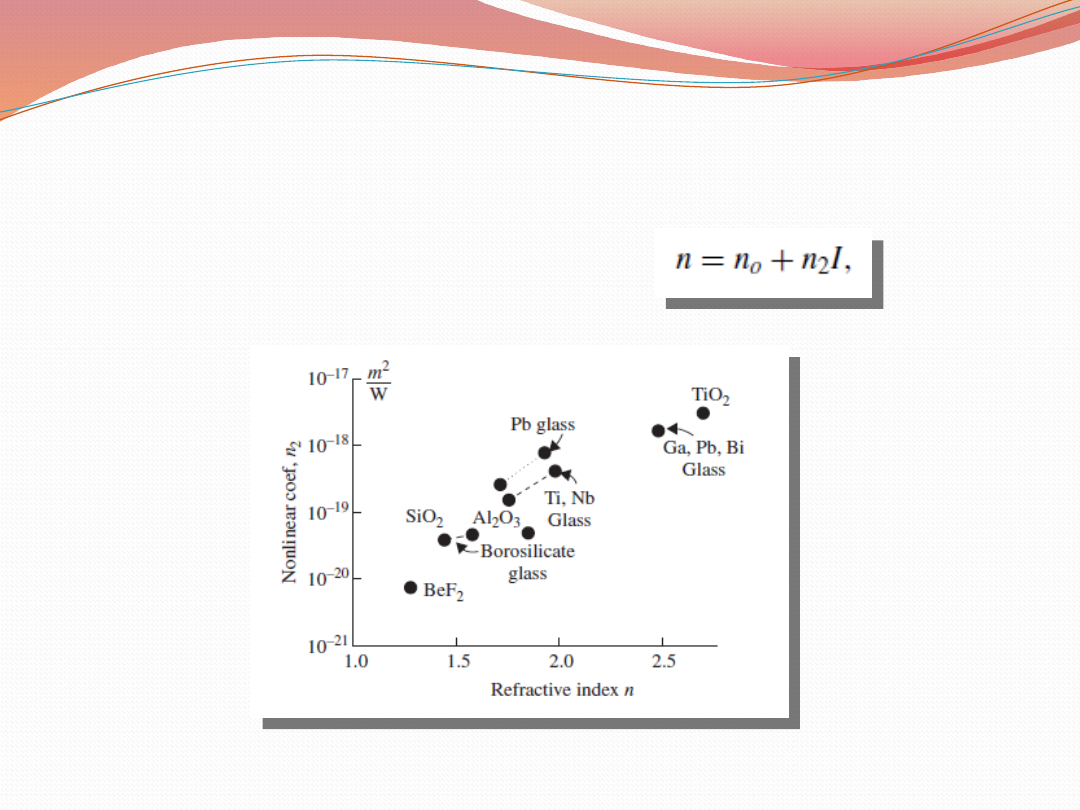
Generowanie trzeciej harmonicznej
(THG)

Krzemionka i inne szkła optyczne – wykorzystanie w systemach
komunikacji optycznej

Zmiana współczynnika refrakcji dla szkieł
zachodzi zgodnie z relacją:

I- natężenie wiązki światła [W/m

2

]

n

2

- nieliniowy współczynnik optyczny

Generowanie trzeciej harmonicznej
(THG)



Trzy możliwości dla THG:

(3ω, ω, ω, ω) = (e, o, o, o),
(e, o, o, e), oraz (e, o, e, e)



Dla dopasowania fazy (e, o, o, o) wartość kąta opisywana jest
równaniem:

Wykorzystanie właściwości

nieliniowych trzeciego rzędu



Przetwarzanie fal elektromagnetycznych w czasie rzeczywistym



Transmisja obrazu



Kompresja impulsów



Przetwarzanie obrazów w optycznych systemach komunikacyjnych

Badanie nieliniowych właściwości

oraz pierścieni dyfrakcji w

węglowych nanorurkach



Badaniu poddano węglowe nanorurki jednościenne (SWNT- single-
wall carbon nanotubes) oraz wielościenne (MWNT- multi- wall
carbon nanotubes) rozpuszczone w 1,2- dichlorobenzenie. Nanorurki
jednościenne były dodoatkowo domieszkowane poli propiolanem
etylu.



Próbki oświetlano za pomocą lasera o mocy 26 mW generującego
fale o długości 635 nm.



Eksperyment wykazał, że jednościenne nanorurki charakteryzują się
wyższymi współczynnikami nieliniowymi niż nanorurki wielościenne.

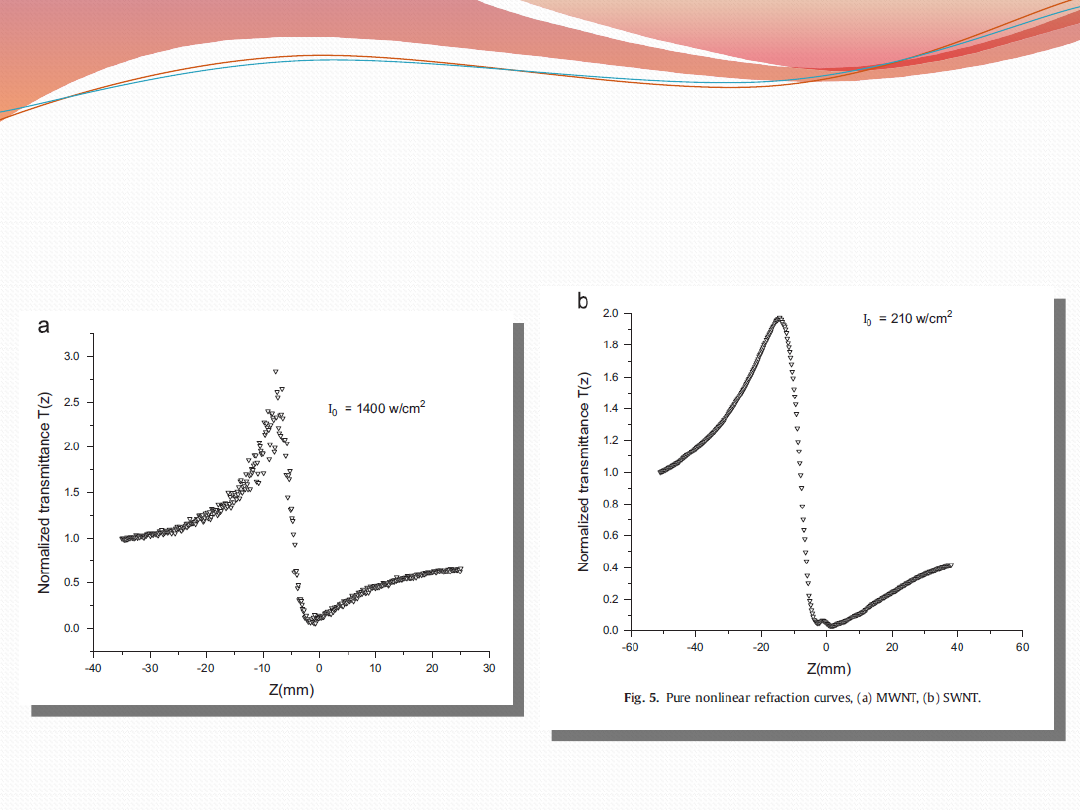
Krzywe nieliniowej refrakcji

Nieliniowe współczynniki refrakcji

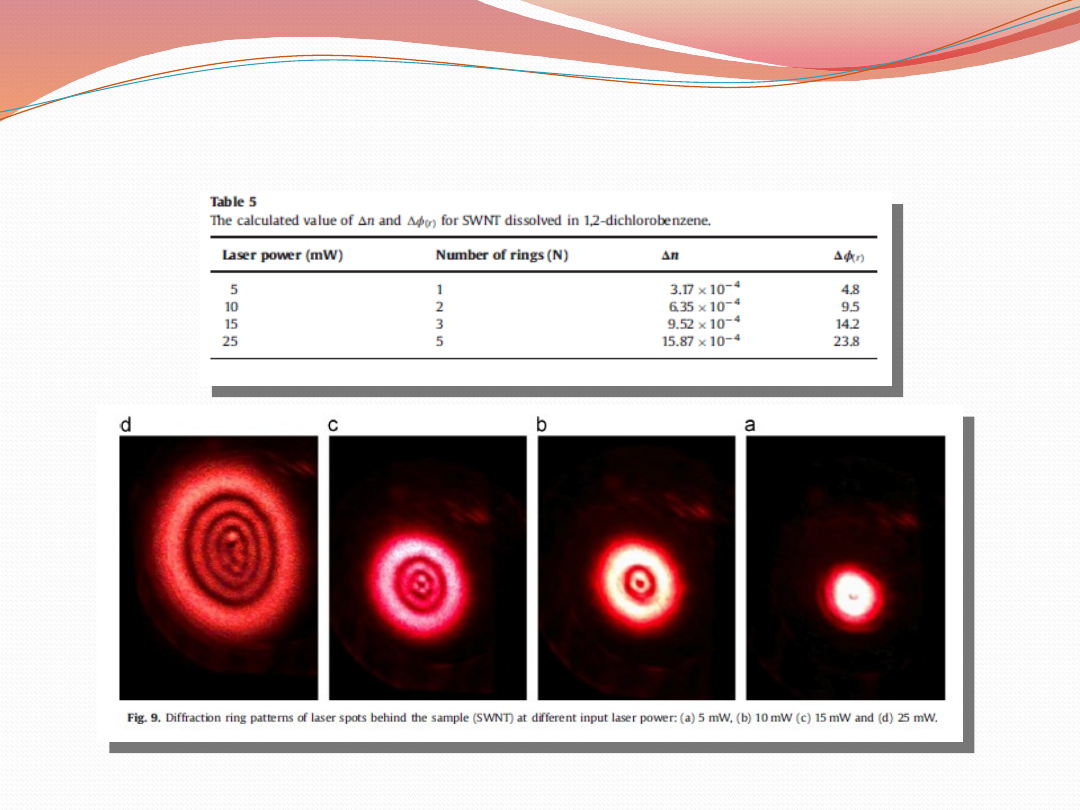
Pierścienie dyfrakcji w węglowych
nanorurkach

Generowane za pomocą lasera o różnej mocy pierścienie dyfrakcyjne
widoczne dla SWNT

Źródła



Properties of materials, Robert E. Newnham, 313- 324



Investigation of optical nonlinearity and diffraction ring patterns of
carbon nanotubes

M.D. Zidan , A.W.Allaf, M.B.Alsous, A.Allahham

Dziękuję

za uwagę;)