Metodologia ze statystyką:

kurs podstawowy

wykład 5



Eksperyment jednozmiennowy z

powtarzaniem pomiarów na więcej niż

dwóch poziomach. Jednoczynnikowa

analiza wariancji dla prób zależnych.

Porównania planowane i porównania post

hoc.



Współczynniki korelacji. Związek miedzy

współczynnikiem korelacji a testem t-

Studenta. Interpretacja współczynnika

korelacji w kategoriach procentu wariancji

wspólnej. Badania korelacyjne a

korelacyjna analiza danych. Test chi-

kwadrat i wprowadzenie to testów

nieparametrycznych.

Eksperyment jednozmiennowy

z powtarzaniem pomiarów na

więcej niż dwóch poziomach



Te same odmiany co w przypadku
dwóch poziomów



Te same mocne i słabe strony co w
przypadku dwóch poziomów

PRZYPOMNIENIE

Eksperyment jednozmiennowy

z powtarzaniem pomiarów:

Odmiany



Poziom zmiennej niezależnej manipulowany

losowo wewnątrz osób (np ocena bodzców

znanych i nieznanych prezentowanych w losowej

kolejności)



Counterbalansing-zrównoważenie między

osobami (np dla jednej połowy badanych najpierw

frustracja a dla drugiej połowy najpierw brak

frustracje)



Matching czyli dobór parami (dla każdej osoby z

grupy eksperymentalnej pomiar jest

„powtórzony” na jak najbardziej podobnej do

niej osobie z grupy kontrolnej)

PRZYPOMNIENIE

Mocne strony badań z

powtarzanymi pomiarami



Zmniejszenie lub wyeliminowanie
wariancji błędu spowodowanej
różnicami indywidualnymi.



W rezultacie wzrost mocy testu
statystycznego (zmniejszenie ryzyka
błędu drugiego rodzaju)

PRZYPOMNIENIE

Słabe strony badań z powtarzanymi

pomiarami: kolejność losowa lub

counterbalansing



Trudna do zastosowania gdy efekt
manipulacji jest długotrwały



Zwiększone prawdopodobieństwo
odgadnięcia hipotezy

PRZYPOMNIENIE

Słabe strony badań z powtarzanymi

pomiarami: Matching



Pracochłonna dla badacza



Arbitralność kryteriów doboru par

Eksperyment jednozmiennowy

z powtarzaniem pomiarów na

więcej niż dwóch poziomach:

Analiza



Jednoczynnikowa analiza
wariancji dla prób zależnych

Analiza wariancji z powtarzanymi

pomiarami: dwie odmiany



Multivariate solution (Testy

wielu zmiennych)



Univariate solution (Testy

efektów

wewnątrzobiektowych)



W przypadku gdy zmienna

ma tylko dwa poziomy wyniki

takie same

Porównania planowane



Z góry ustalone



Często używa sie testu t



Zwykle stosuje sie je po stwierdzeniu
istotnego F



Alternatywa dla analizy wariancji?

Porównania post hoc



Wszystko ze wszystkim



Zwykle stosuje sie je po stwierdzeniu
istotnego F



Alternatywa dla analizy wariancji?

Porównania post hoc



Istnieje wiele testów post hoc. Najczęściej
używane to test LSD, test Tukey’a, test
Scheffe, test Bonferroniego i test Duncana.



Test Duncana jest szczególnie liberalny i
może prowadzić do błędu 1 rodzaju.



Test LSD jest także bardzo liberalny ale
stosuje sie go zwykle jedynie w przypadku
3 grup.



Test Scheffe jest szczególnie
konserwatywny.

Test t a test F



W przypadku dwóch grup

F=t

2

Wyniki standardowe

(standaryzowane) – wartości “z”

  z

i

= (x

i

– M)/SD

  M – średnia (mean)
SD – odchylenie standardowe

(standard deviation)

wartość standaryzowana (“z”)

danego wyniku “x” = wynik surowy
(x

i

) minus średnia (M) dzielone przez

odchylenie standardowe (SD)

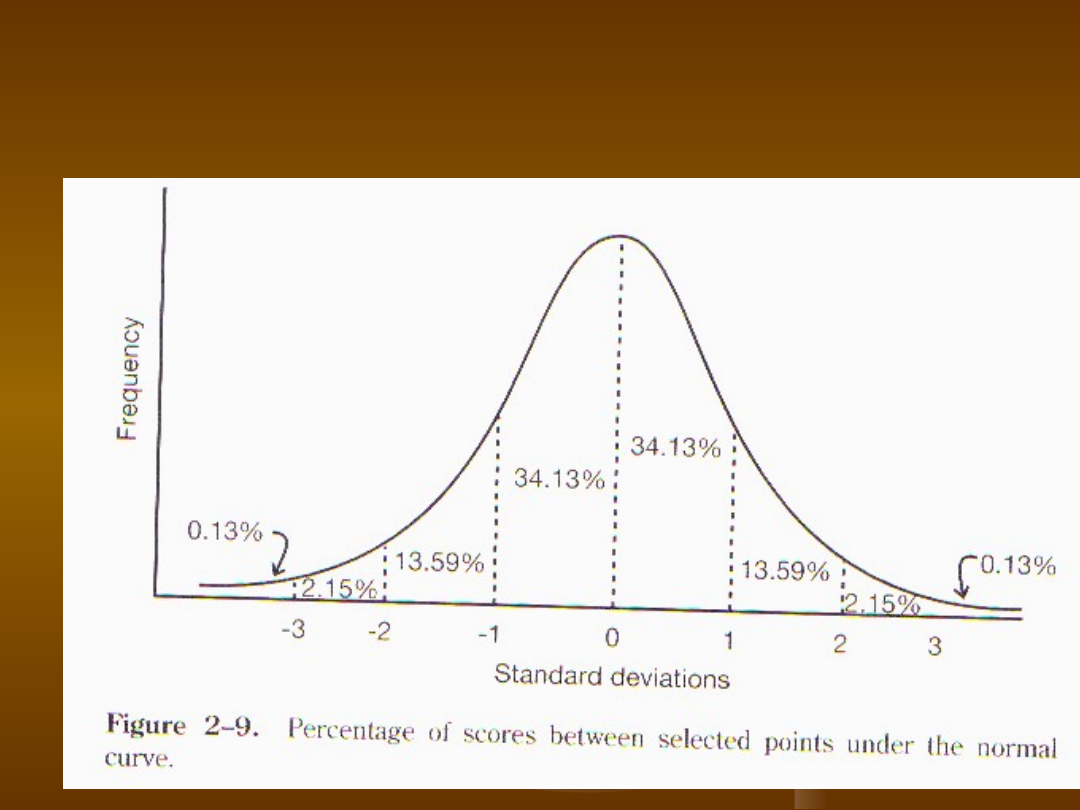
Procenty wyników pod krzywą

normalną (M=0; SD=1)

Właściwości wyników standardowych

“z”

   średnia wyników „z” = 0; wariancja = 1
 
  wyniki surowe bliskie średniej M dają

wyniki „z” bliskie wartości “0”,

wyniki dokładnie równe średniej są

równe zeru.

     wyniki surowe mniejsze od średniej M

dają ujemne wartości „z „

   wyniki surowe większe od średniej M

daja dodatnie wartości „z”

Standardyzacja umożliwia porównania na tle

grupy

Anna i Marek zdawali egzamin z

Metodologii ze Statystyką u różnych
profesorów. Anna otrzymała ocenę 5
z egzaminu (średnia ocen w jej
grupie 4,5; odchylenie standardowe
ocen 2). Marek otrzymał ocenę 3,5 z
egzaminu (średnia ocen w jego
grupie 2,5; odchylenie standardowe
ocen 1). Który ze studentów wypadł
lepiej na tle swojej grupy?

Standardyzacja umożliwia porównania na tle

grupy

Ania: x=5,0 (M= 4,5; S=2);
z=(5,0-4,5) /2 = 0,25
Marek x= 3,5 (M= 2,5; S=1);
z=(3,5-2,5)/1 = 1,00

Standardyzacja umożliwia porównania na tle

grupy

Tomek: x=3,0 (M= 4,0; S=1,0);
z=(3,0-4,0) /1 = -1,0
Krysia: x= 3,5 (M= 4,5; S=2);
z=(3,5-4,5)/2 = -0,50

Korelacja



miara statystyczna określająca

siłę związku między zmiennymi,

mieszcząca się w graniach (-1, 1)

Korelacja dodatnia

wzrostowi jednej zmiennej np.

stopnie towarzyszy wzrost
innej

zmiennej

np.

samoocena

Korelacja ujemna

wzrostowi jednej zmiennej

np.

stopnie

towarzyszy

spadek innej zmiennej np.
nadużywanie alkoholu

Brak korelacji

Zmienne

sa

ze

soba

niepowiązane np. stopnie a
numer buta,

współczynnik korelacji jest

bliski zera (nieistotny)

Związek krzywoliniowy



Np. związek między pobudzeniem a
poziomem wykonania zadania: w
miarę wzrostu pobudzenia wykonanie
jest coraz lepsze, osiąga maksimum
po czy zaczyna się pogarszać



Współczynnik korelacji (liniowej)
będzie bliski zera (nieistotny)

Obliczanie współczynnika

korelacji r Pearsona



r =  ZX ZY / N



r - współczynnik korelacji Pearsona



ZX - wartość z dla każdego
przypadku dla zmiennej x



ZY - wartość z dla każdego
przypadku dla zmiennej y



N - liczba przypadków (liczba par
obserwacji)

Istotność statystyczna

współczynnika korelacji



Ten sam współczynnik korelacji może
być lub nie być statystycznie istotny
w zależności od wielkości próby (od
ilości par obserwacji)



Im większa próba tym bardziej
istotny dany współczynnik korelacji



Poziom istotności odczytujemy z
tabeli w podręczniku statystyki lub z
wydruku SPSS

Korelacja a rodzaj skali

pomiarowej



r Pearsona zakłada pomiar obu

zmiennych na skali przedziałowej



Gdy jedna zmienna jest na skali

nominalnej i jest dychotomiczna

(płeć) wyniki takie same jak przy

teście t



współczynnik korelacji rang

Spermana zakłada pomiar na skali

porządkowej



Chi kwadrat zakłada pomiar obu

zmiennych na skali nominalnej

Korelacja a trafność

wewnętrzna



badanie korelacyjne vs.
eksperyment



analiza korelacyjna vs.
porownanie grup

Współczynnik determinacji

r

2

proporcja zmienności jednej zmiennej

dająca się przewidzieć na podstawie
informacji o poziomie drugiej
zmiennej

r

2

x 100 = procent wariancji

wspólnej

IQ a średnia ocen



Współczynnik korelacji między
ocenami a ilorazem inteligencji
r=0,50. W jakiej mierze da sie
przewidzieć średnią ocen na
podstawie IQ (lub odwrotnie)



r

2=

0,50

2

=0,25



25% wspólnej wariancji

Badanie zależności między

dwiema zmiennymi

mierzonymi na skali

nominalnej: test Chi-kwadrat

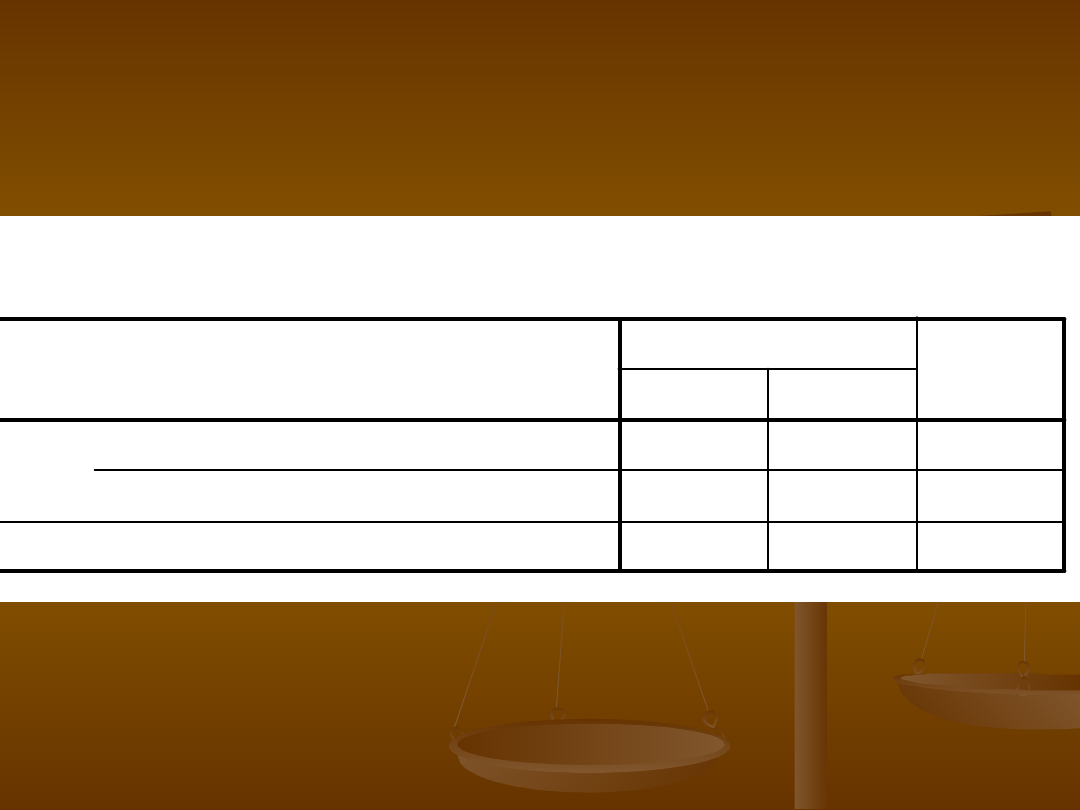
Czy istnieje zależność między

płcią a wyborem miejsca w

klasie

Tabela krzyżowa PLEC * MIEJSCE

26

20

46

12

35

47

38

55

93

Liczebność
Liczebność
Liczebność

kobieta
mezczyzna

PLEC

Ogółem

przod

tyl

MIEJSCE

Ogółem



Aby sprawdzić czy uzyskany patern
wyników nie powstał przez przypadek (czy
jest statystycznie istotny) stosujemy test
Chi-kwadrat

Informacje konieczne do

obliczenia wartości Chi-

kwadrat



fo - liczebności
zaobserwowane (dla każdej
kratki tabeli)

Liczebności zaobserwowane a

liczebności oczekiwane



fo - liczebności

zaobserwowane: ile obserwacji

(ile osób) znalazło się w każdej z

czterech kratek tabeli



fe - liczebności oczekiwane: ile

obserwacji (ile osób) powinno się

było znaleźć w każdej z czterech

kratek tabeli gdyby zmienne płeć

i wybór miejsca były od siebie

niezależne

Obliczanie liczebności

oczekiwanych f

e



Liczebność wiersza / Całkowita
liczebność x Liczebność kolumny



Np. Oczekiwana liczebność kobiet
siedzących z przodu to



ilość kobiet / ilość studentów x ilość
studentów siedzących z przodu

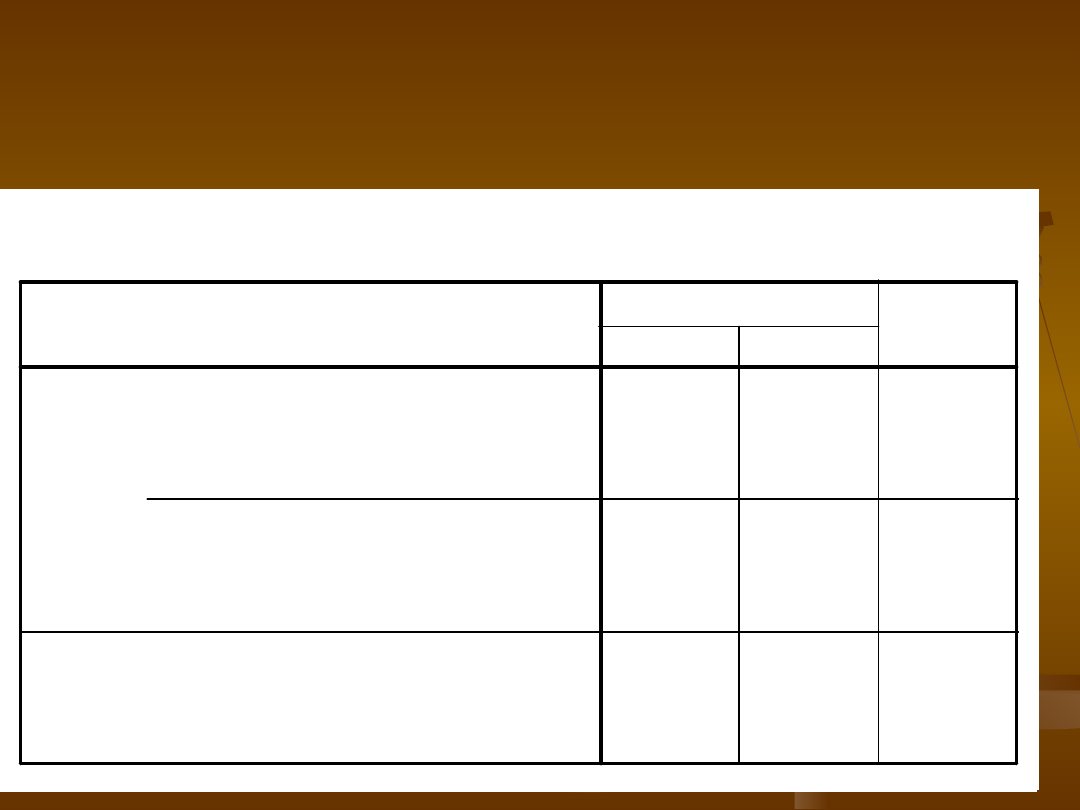
Liczebności zaobserwowane i

liczebności oczekiwane

Tabela krzyżowa PLEC * MIEJSCE

26

20

46

18,8

27,2

46,0

12

35

47

19,2

27,8

47,0

38

55

93

38,0

55,0

93,0

Liczebność
Liczebność
oczekiwana
Liczebność
Liczebność
oczekiwana
Liczebność
Liczebność
oczekiwana

kobieta

mezczyzna

PLEC

Ogółem

przod

tyl

MIEJSCE

Ogółem

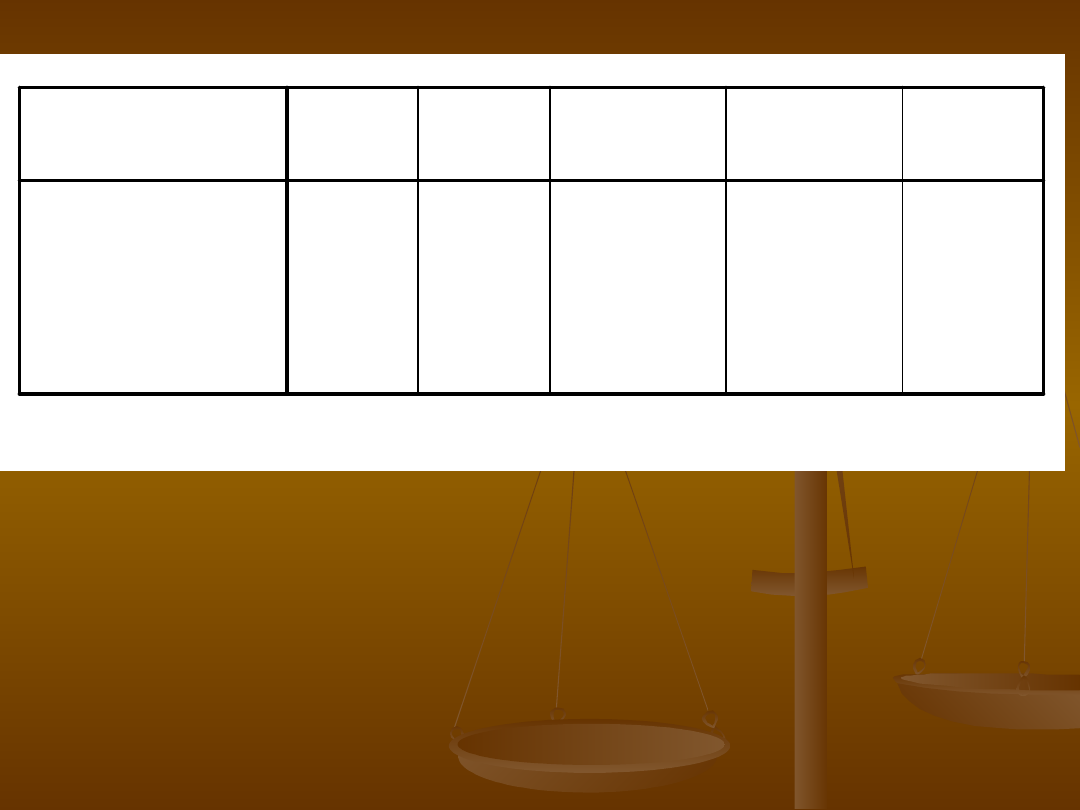
Płeć a wybór miejsca w klasie: Wyniki

obliczeń

Te s ty Chi-kw a dra t

9,239

b

1

,002

8,001

1

,005

9,414

1

,002

,003

,002

9,140

1

,003

93

Ch i-kwad rat
Pearsona
Poprawka na
ciąg łoś ć

a

Iloraz wiaryg od noś ci
Dokład ny tes t
Fis hera
Test związku
liniowego
N Ważn ych
obserwacji

Wartoś ć

d f

Istotn ość

asymp totycz

n a

(d wus tronn

a)

Istotnoś ć

d okładna

(dwu stron n

a)

Is totność

dokład na

(jed nostr

on na)

Ob liczone wyłączn ie d la tabeli 2x2.

a.

,0% komórek (0) ma liczebn oś ć oczekiwaną mn iejs zą niż 5. Min imaln a liczeb noś ć
oczekiwan a wyn osi 18,80.

b.



Sprawdzić czy ilość ważnych obserwacji jest co najmniej

20, jeśli tak można użyć testu Chi-kwadrat



Gdyby ilość obserwacji była niższa niż 20, należałoby

użyć dokładnego testu Fishera



Uwaga: Podejście tradycyjne zezwala na użycie test

Chi-kwadrat jedynie gdy żadna z liczebności

oczekiwanych nie jest niższa niż 5, nawet gdy całkowita

ilość ważnych obserwacji jest wyższa niż 20

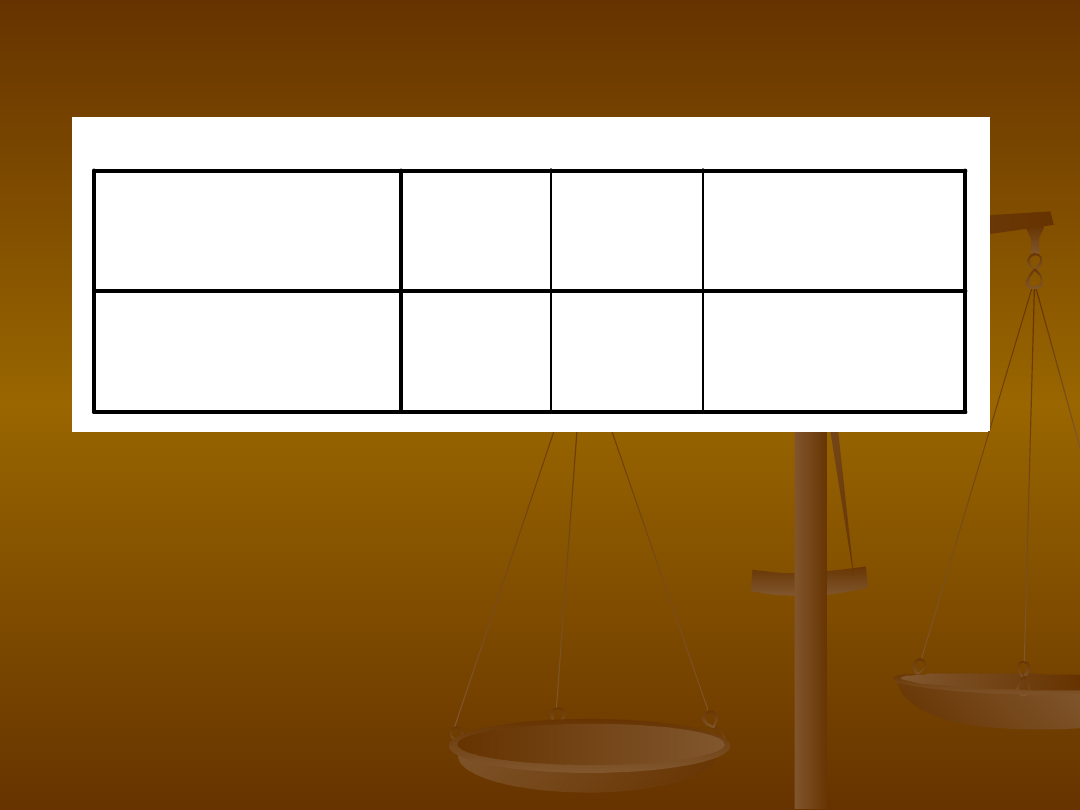
Ważne elementy poprzedniej

tabeli

Testy Chi-kwadrat

9,239

1

,002

93

Chi-kwadrat
Pearsona
N Ważnych
obserwacji

Wartość

df

Istotność

asymptotyczna

(dwustronna)

Odczytać poziom istotności dla testu Chi-

kwadrat



Jeśli istotność niższa niż 0,05 to znaczy, że
zależność między płcią studenta w
wyborem miejsca w klasie jest istotna
(mało prawdopodobne by pojawiła się
przez przypadek)

Informacje konieczne do

obliczenia wartości Chi-

kwadrat



fo - liczebności
zaobserwowane (dla każdej
kratki tabeli)

Liczebności zaobserwowane a

liczebności oczekiwane



fo - liczebności

zaobserwowane: ile obserwacji

(ile osób) znalazło się w każdej z

czterech kratek tabeli



fe - liczebności oczekiwane: ile

obserwacji (ile osób) powinno się

było znaleźć w każdej z czterech

kratek tabeli gdyby zmienne płeć

i wybór miejsca były od siebie

niezależne

Obliczanie liczebności

oczekiwanych f

e



Liczebność wiersza / Całkowita
liczebność x Liczebność kolumny



Np. Oczekiwana liczebność kobiet
siedzących z przodu to



ilość kobiet / ilość studentów x ilość
studentów siedzących z przodu

Czy jest istotny związek w

populacji?

Obliczanie Chi-kwadrat



2 - wartość statystyki Chi-kwadrat



fo - liczebność zaobserwowana



fe - liczebność oczekiwana



2 może się wahać od 0 do

nieskończoności



Poziom istotności odczytać można z tabeli

istotności lub z wydruku SPSS



2

=  (f

o

– f

e

)

2

/ f

e

Obliczanie Chi - kwadrat:

Sekret dla leniwych



Dla tabel 2 x 2 kwadraty różnicy

(fo – fe)

2

są takie same w każdej

kratce tabeli



2

=  (f

o

– f

e

)

2

/ f

e

Stopnie swobody dla testu Chi-

kwadrat



Przy odczytywaniu z tabeli

istotności potrzebna informacja o

ilości stopni swobody (df)



Df to iloczyn ilości wierszy – 1

oraz ilości kolumn – 1 w tabeli

danych dla których obliczono

Chi-kwadrat



W naszym przypadku df = (2-1) x

(2-1) = 1

Jak silny jest związek?

Obliczanie współczynnika

korelacji Phi dla tabeli 2x2



 - wartość statystyki Phi





2

- wartość statystyki Chi-

kwadrat



N - liczebność próby



 może się wahać od 0 do 1

 = (

2

/N)

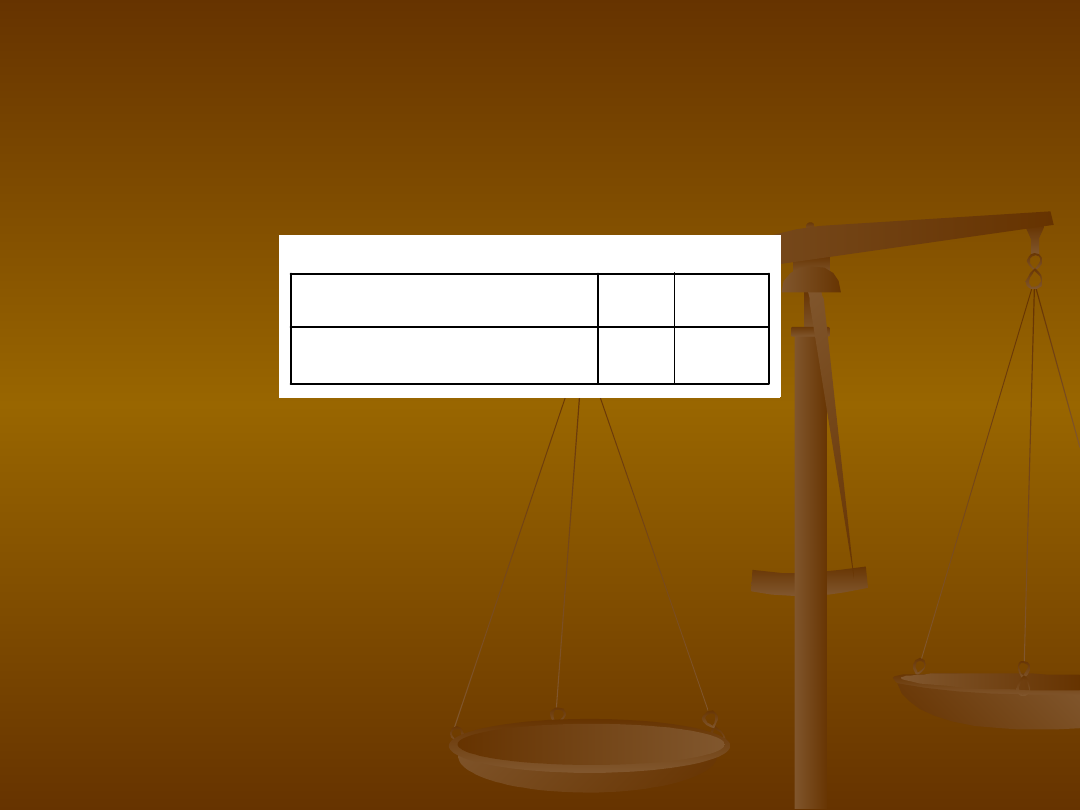
Płeć a wybór miejsca w klasie:

Współczynnik siły związku Phi

Miary symetryczne

,315

,002

,315

,002

93

Phi
V Kramera

Nominalna przez
Nominalna

N Ważnych obserwacji

Wartość

Istotność

przybliżona



Współczynnik Phi interpretować można podobnie
jak r Pearsona i obliczyć współczynnik
determinacji



0,315

2

=0,09



Wybór miejsca w klasie związany jest z płcią w
sposób istotny ale bardzo nieznaczny

Czy mnie jeszcze pamiętasz?



Demonstracja „Związek miedzy
wynikiem rozmowy kwalifikacyjnej z
kandydatem do pracy a późniejszą
jakością pracy”



Czy obliczenia statystyczne da się
zastąpić statystyczną intuicją?

Pytanie:



Czy ogólne wrażenie z rozmowy
wstępnej z kandydatem do pracy
pomaga przewidzieć późniejszą
jakość pracy kandydata?

Kandydat 1

Wynik rozmowy

wstępnej

Jakość pracy

Pozytywny (+)

Wysoka (+)

Czy dane 20 kandydatów wskazują, że

warto używać wyników rozmowy

kwalifikacyjnej przy przyjmowaniu do

pracy?



Jak silny związek?



0,0 – zupełny brak

związku



0,2 - słaby związek



0,5 – średni związek



0,8 – silny związek



1,0 – pełny związek

Jak silny związek?



Pozytywny wynik

rozmowy:



N=16



Prawd. że będą dobrze

pracować 12:16=0,75



Negatywny wynik

rozmowy:



N=4



Prawd. że będą dobrze

pracować 3:4=0,75



Wniosek:

Brak związku!

(Korelacja

pozorna)

Rozmowa

+

Rozmowa

-

Praca

+

12

3

Praca

-

4

1

Korelacja pozorna



Spostrzeganie związku miedzy
zmiennymi gdy w rzeczywistości
żaden związek nie zachodzi



Występuje szczególnie gdy w obrębie
każdej ze zmiennych jedna z
kategorii jest szczególnie liczna



Zapobieganie korelacjom pozornym:
obliczyć wskaźnik siły związku
(korelacji)

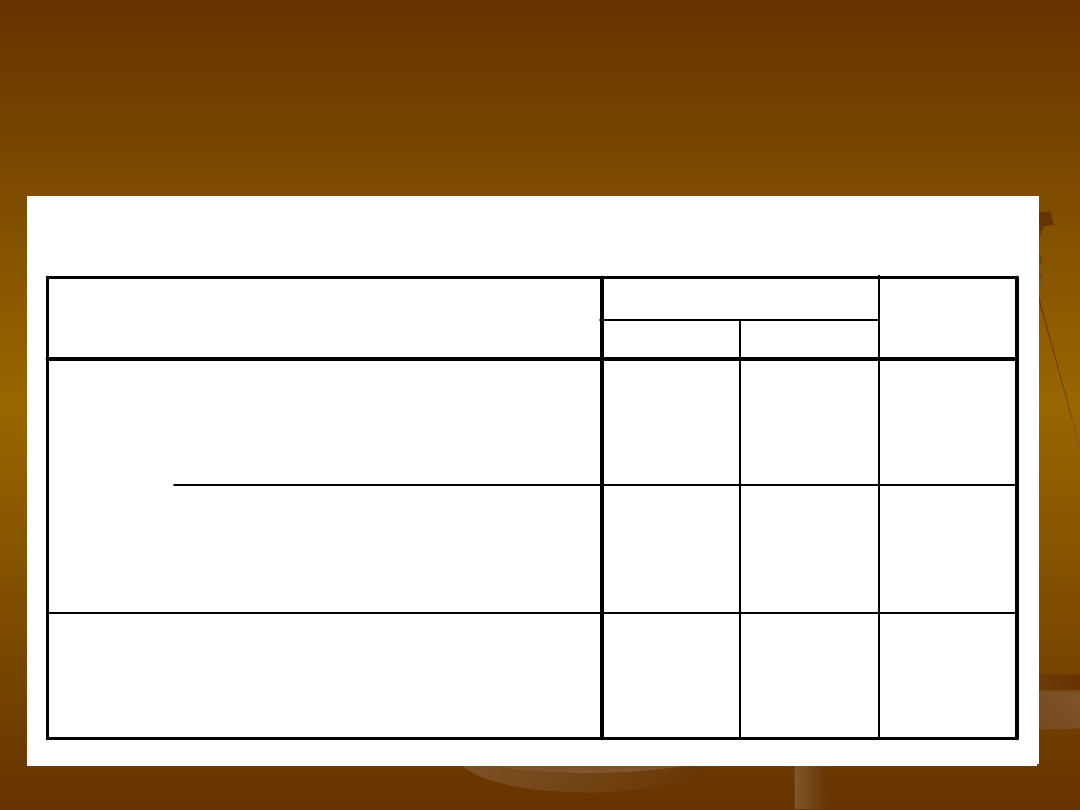
Tabela krzyżowa PRACA * ROZMOWA

1

4

5

1,0

4,0

5,0

3

12

15

3,0

12,0

15,0

4

16

20

4,0

16,0

20,0

Liczebność
Liczebność
oczekiwana
Liczebność
Liczebność
oczekiwana
Liczebność
Liczebność
oczekiwana

,00

1,00

PRACA

Ogółem

,00

1,00

ROZMOWA

Ogółem

Testy Chi-kwadrat

,000

b

1

1,000

,000

1

1,000

,000

1

1,000

1,000

,751

,000

1

1,000

20

Chi-kwadrat
Pearsona
Poprawka na
ciągłość

a

Iloraz wiarygodności
Dokładny test
Fishera
Test związku
liniowego
N Ważnych
obserwacji

Wartość

df

Istotność

asymptotyczn

a

(dwustronna)

Istotność

dokładna

(dwustronna)

Istotność

dokładna

(jednostronn

a)

Obliczone wyłącznie dla tabeli 2x2.

a.

75,0% komórek (3) ma liczebność oczekiwaną mniejszą niż 5. Minimalna liczebność
oczekiwana wynosi 1,00.

b.

Dokładny test Fishera



Bardziej konserwatywny niż test Chi –
kwadrat (może zwiększać
prawdopodobieństwo błędu drugiego
rodzaju)



Bardziej pracochłonne obliczenia



Powinien być używany zamiast testu Chi-
kwadrat gdy....



podejście tradycyjne: co najmniej jedna z
liczebności oczekiwanych jest niższa niż 5



podejście nowsze: całkowita liczebność jest
niższa niż 20

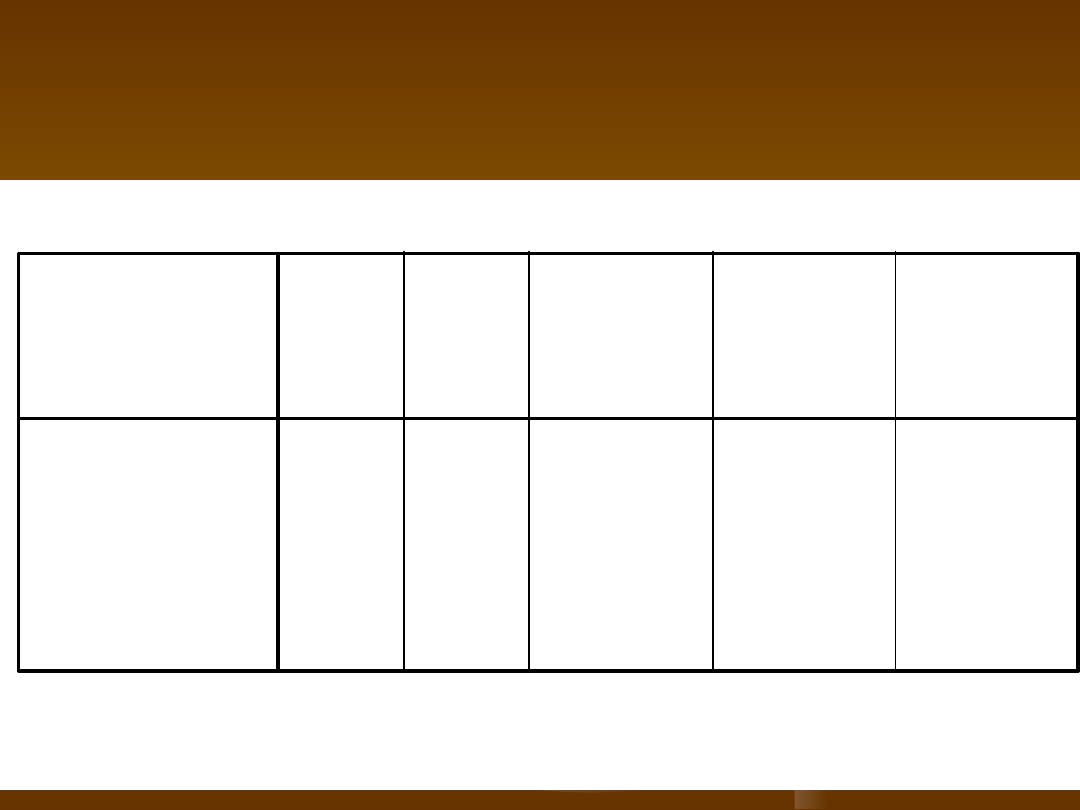
Testy Chi-kwadrat

,000

b

1

1,000

1,000

,751

20

Chi-kwadrat
Pearsona
Dokładny test
Fishera
N Ważnych
obserwacji

Wartość

df

Istotność

asymptotyczn

a

(dwustronna)

Istotność

dokładna

(dwustronna)

Istotność

dokładna

(jednostronn

a)

75,0% komórek (3) ma liczebność oczekiwaną mniejszą niż 5. Minimalna liczebność
oczekiwana wynosi 1,00.

b.

Nietypowe zastosowania testu

Chi - kwadrat



Może być używany zamiast testu Studenta dla

prób niezależnych (np. dzielimy badanych na 4

grupy w zależności od manipulacji

eksperymentalnej i od uzyskania w zmiennej

zależnej wyniku powyżej lub poniżej mediany)



Może być używany zamiast współczynnika

korelacji Pearsona (np. dzielimy badanych na 4

grupy w zależności od uzyskania wyników

powyżej lub poniżej mediany w każdej z dwóch

mierzonych zmiennych)



Zaletą takich zastosowań jest prostota, wadą jest

mniejsza moc testu (większe

prawdopodobieństwo błędu drugiego rodzaju)

Chi - kwadrat:

Informacje dodatkowe



Jest tzw. testem nieparametrycznym,
nie opiera się na założeniu o
normalności rozkładu



Może być używany do tabel
większych niż 2 x 2 (więcej niż dwa
poziomy zmiennej lub / i więcej niż
dwie zmienne)



Dane w poszczególnych kratkach
tabeli muszą być od siebie
niezależne!

Niektóre inne testy

nieparametryczne



Test U Manna-Whitney’a – podobny do
testu t Studenta dla prób niezależnych ale
zmienna zależna ma postać rang



Test Wilcoxona oraz test znaków - podobne
do testu t Studenta dla prób zależnych ale
zmienna zależna ma postać rang



Współczynnik korelacji rang Spearmana –
podobny do współczynnika korelacji
Pearsona ale obie zmienne mają postać
rang



W przeciwieństwie do testu Chi – kwadrat,
inne testy nieparametryczne są obecnie
stosunkowo rzadko używane



Testy nieparametryczne są z reguły
prostsze w użyciu



Mają zwykle niższą moc niż odpowiednie
testy parametryczne



Gdy odstępstwa od założeń testów
parametrycznych są bardzo znaczne,
testy nieparametryczne mogą mieć
wyższą moc niż odpowiednie testy
parametryczne