STANY MATERII
STANY MATERII
STANY SKUPIENIA
GAZOWY
CIEKŁY
STAŁY
GAZOWE STANY
MATERII
GAZOWE STANY
MATERII
CIEKŁE STANY MATERII
CIEKŁE STANY MATERII
STAŁE STANY MATERII
STAŁE STANY MATERII
STANY SKUPIENIA I FAZY MATERII
STANY SKUPIENIA to klasyfikacja form występowania materii z
MAKROSKOPOWEGO punktu widzenia
STANY SKUPIENIA
to klasyfikacja form występowania materii z
MAKROSKOPOWEGO
punktu widzenia
FAZY MATERII to klasyfikacja form jej występowania z
MIKROSKOPOWEGO punktu widzenia, czyli z punktu widzenia
struktur jakie tworzą atomy, jony lub cząsteczki.
FAZY MATERII
to klasyfikacja form jej występowania z
MIKROSKOPOWEGO
punktu widzenia, czyli z punktu widzenia
struktur jakie tworzą atomy, jony lub cząsteczki.
faza gazowa
– całkowity brak organizacji – cząsteczki (lub atomy)
mają pełną swobodę ruchu i nie występują między nimi żadne
oddziaływania oprócz odpychania w momencie zderzeń i
przyciągania grawitacyjnego energia cząsteczek nie jest zbyt duża i
dlatego ich zderzenia są sprężyste; w gazie mogą występować
przyciągania między cząsteczkami, lecz energia tych oddziaływań
jest mniejsza od energii kinetycznej cząsteczek
faza nadkrytyczna
– powstająca po przekroczeniu ciśnienia i
temperatury punktu krytycznego; faza ta posiada pośrednie
własności między cieczą a gazem
plazma
– jest to w zasadzie gaz, ale tworzony przez silnie
zjonizowane atomy/cząsteczki oraz elektrony ; plazmę można
wytwarzać w specjalnych urządzeniach, występuje ona także w
jądrach większości gwiazd; w plazmie cząsteczki mają na tyle dużą
energię, że zderzenia między cząsteczkami nie są sprężyste,
dochodzi do wzbudzenia lub jonizacji cząsteczek; plazma przewodzi
prąd elektryczny
Fazy gazowe
faza ciekła
– w fazie tej istnieje przyciąganie
międzycząsteczkowe powodujące, że cząsteczki pozostają
blisko siebie, ale zachowują swobodę ruchu; oddziaływania te
tworzą bliskozasięgowe i średniozasięgowe uporządkowanie w
cieczy lub w roztworach, przykładowo – oddziaływania
dipolowe (odpowiedzialne za hydratację jonów w roztworze),
siły Van der Waalsa oraz wiązania wodorowe; istnienie tych
oddziaływań powoduje powstawanie uporządkowanych
struktur cząsteczek w cieczach,
faza ciekła izotropowa
– w fazie tej nie występuje żadne
dalekozasięgowe uporządkowanie cząsteczek (podobnie jak w
gazach), choć mogą występować elementy uporządkowania
krótkozasięgowego (w obrębie kilku – kilkunastu cząsteczek)
faza nadciekła
– różni się od zwykłej cieczy tym, że jej lepkość
jest równa 0; Np. nadciekły hel
ciekłe kryształy
–ciecze, w których jednak istnieje częściowe
dalekozasięgowe uporządkowanie cząsteczek; obecnie
znanych jest kilkadziesiąt różnych faz ciekłokrystalicznych,
które różnią rodzajem tego dalekozasięgowego
uporządkowania
Fazy ciekłe
Fazy stałe
fazy stałe
– czyli takie, które nie płyną, tzn. pod
wpływem sił ścinających ulegają naprężeniom, a
przy większych pękają lub płyną (plastyczne):
faza krystaliczna
– w fazie tej cząsteczki są
"zablokowane" i tworzą trwałe sieci
kryształy plastyczne
– w fazie tej cząsteczki
są również zablokowane, ale mogą rotować
(obracać się) wokół własnych osi
kryształy condis
– w fazie tej cząsteczki nie
mogą się przemieszczać, ale mogą zmieniać w
dość szerokim zakresie swoją konformację
faza amorficzna
– w fazie tej cząsteczki nie
tworzą sieci krystalicznej, ale oddziaływania
między nimi są na tyle silne, że nie mogą się
one swobodnie przemieszczać względem siebie;
czasami fazę amorficzną nazywa się też
"superlepką" cieczą lub cieczą "zamrożoną
"
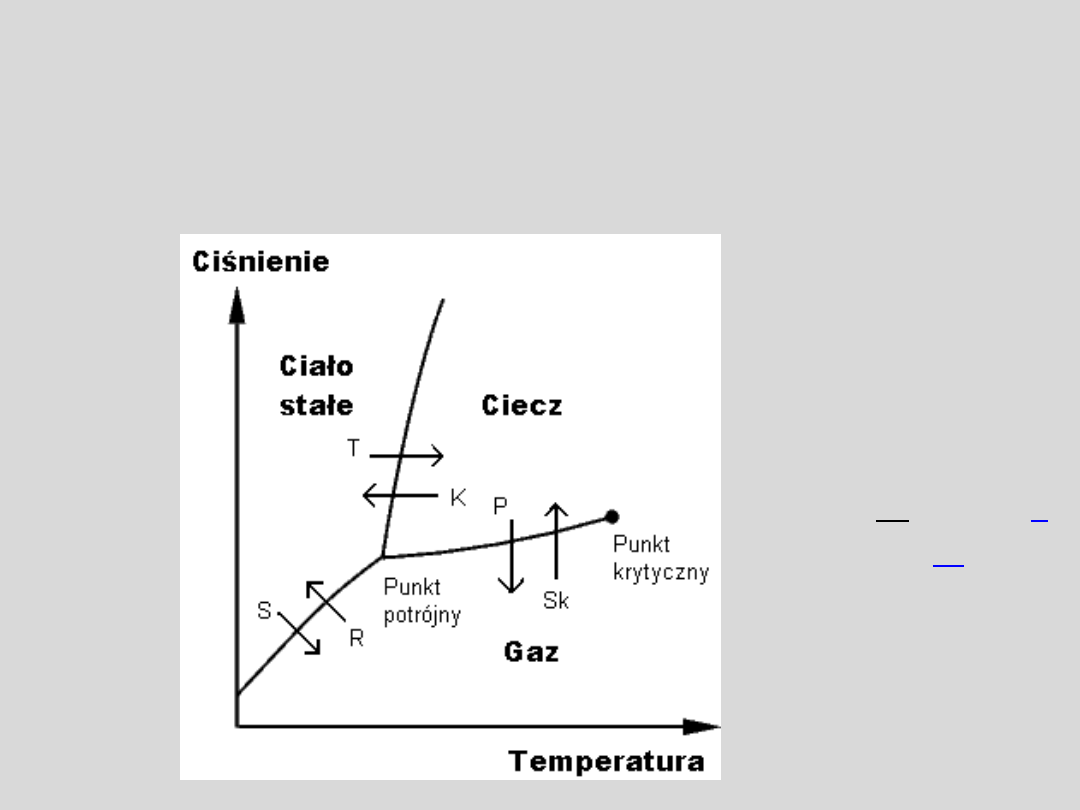
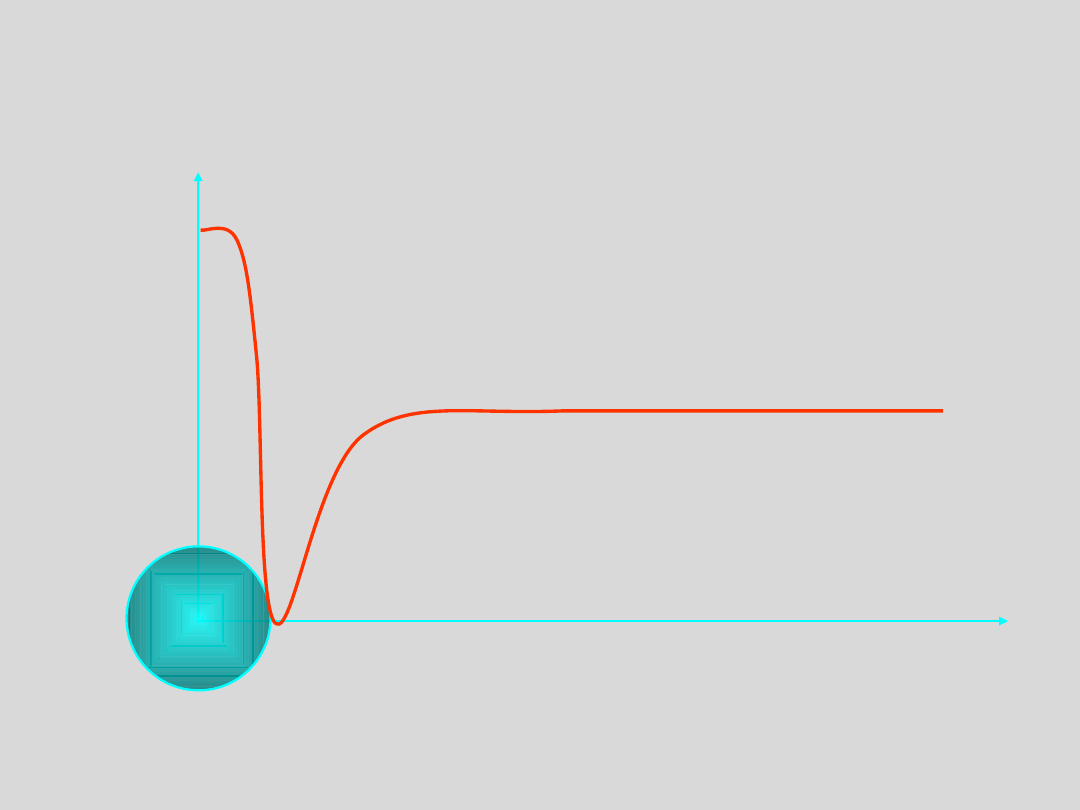
Przemiany fazowe
Przemiana fazowa
– przejście substancji z jednej
fazy (stanu skupienia) do drugiej.
T = 0,01°C (273,16
punkt potrójny wody
Przykład:
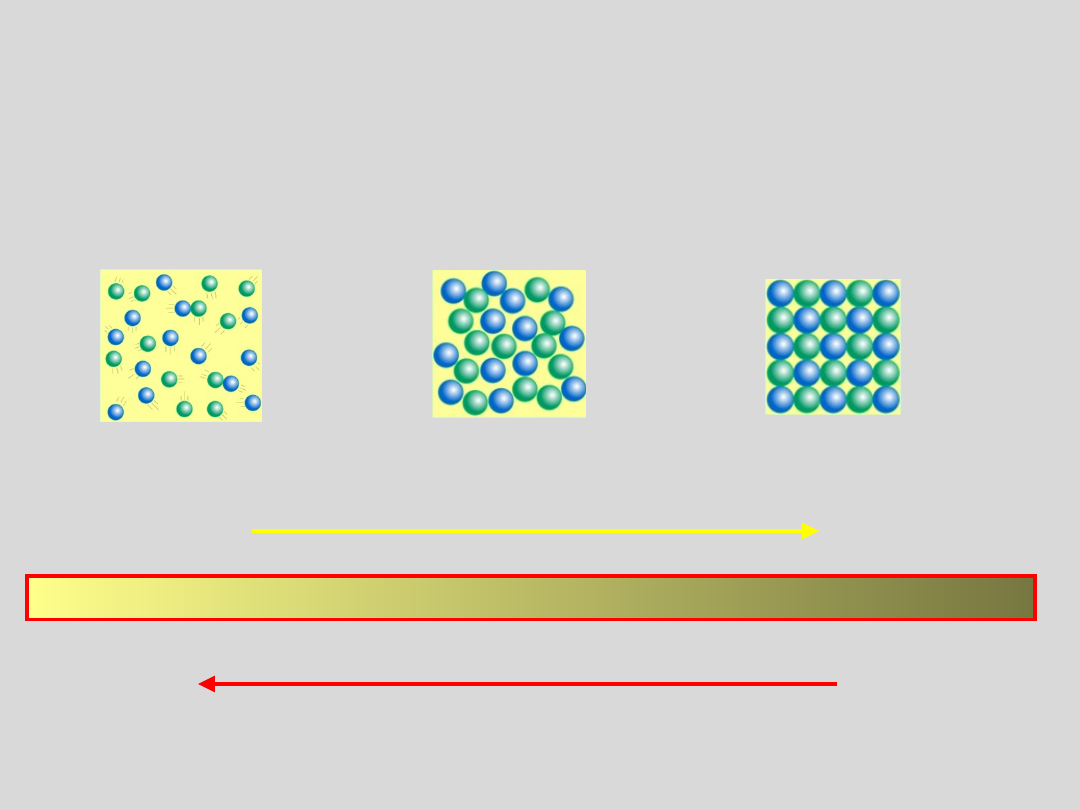
STAN GAZOWY STAN CIEKŁY STAN STAŁY
uporządkow
anie
temperatu
ra
STANY SKUPIENIA A UPORZĄDKOWANIE
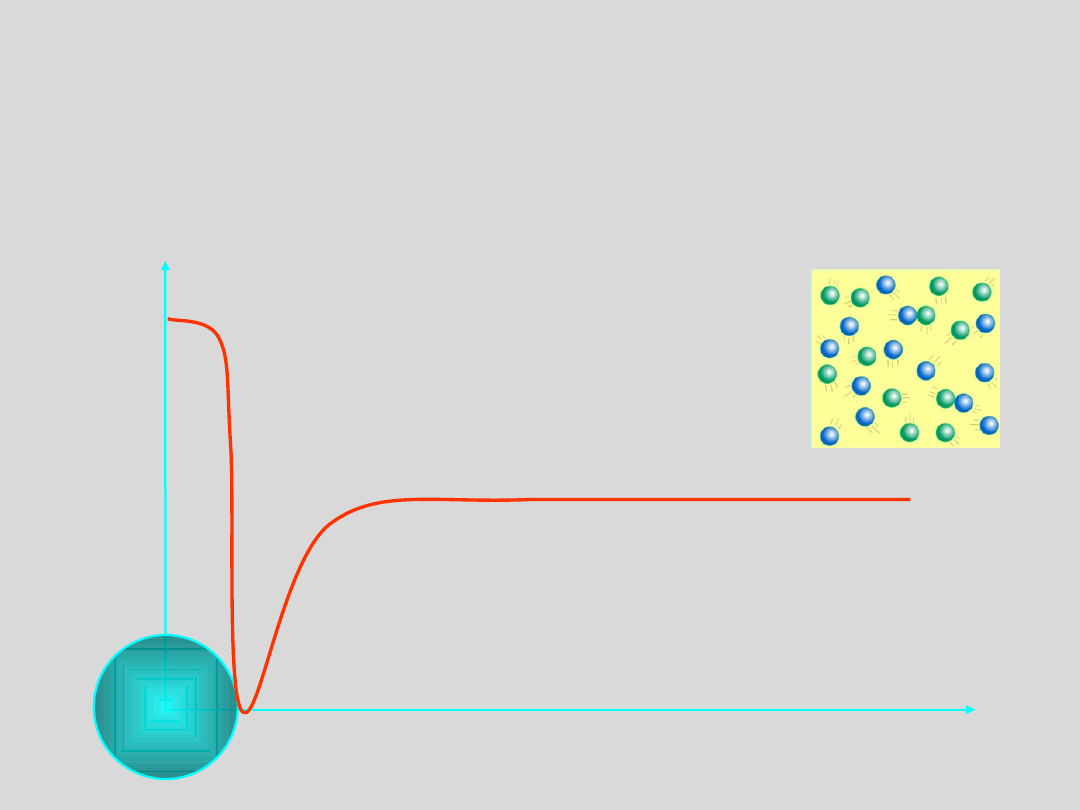
Uporządkowanie cząstek materii w poszczególnych stanach opisujemy
określając prawdopodobieństwo napotkania innych cząstek w
sąsiedztwie dowolnej wybranej cząstki co wyraża:
p
ra
w
d
o
p
o
d
o
b
ie
ń
st
w
o
n
a
p
o
tk
a
n
ia
c
zą
st
ki
odległość
gaz
właściwy
Uporządkowanie
FUNKCJA DYSTRYBUCJI
R. Boyle
R. Boyle
J. Dalton
J. Dalton
J. L. Gay-Lussac
J. L. Gay-Lussac
oddz
śr
kin
śr
E
E
PODSTAWOWE CECHY STANU GAZOWEGO
BRAK OBJĘTOŚCI
gaz przyjmuje objętość układu, w którym się
znajduje
BRAK KSZTAŁTU
gaz przyjmuje kształt układu, w którym się
znajduje
ŚREDNIA ENERGIA KINETYCZNA
obiektów tworzących gaz jest WIĘKSZA niż
energia oddziaływań pomiędzy nimi
założenia modelu:
GAZ DOSKONAŁY - MODEL
STANU GAZOWEGO
1. Cząsteczki są PUNKTAMI MATERIALNYMI, to znaczy
mają masę, ale nie mają wymiaru
2. Energia oddziaływań między cząsteczkami
wynosi 0, za wyjątkiem momentów zderzeń,
które są traktowane jako tzw. zderzenia
sprężyste
4. Cząsteczki znajdują się w ciągłym
chaotycznym ruchu
3. Zderzenia cząsteczek są doskonale sprężyste
Średnia energia kinetyczna
cząstek w gazie jest wprost
proporcjonalna do temperatury bezwzględnej:
kT
2
3
E
śr
A
N
R
k
k - stała Boltzmanna
*)
*) T [K] = t [°C] + 273,15
R - stała gazowa = 8.314
J·K
-1
mol
-1
N
A
- liczba Avogadro 6.02
·10
23
ZWIĄZEK POMIĘDZY ENERGIĄ
CZĄSTEK GAZU A
TEMPERATURĄ
k = 1,38·10
-23
J·K
-1
Zależność pomiędzy stałą Boltzmana k a stałą
gazową R:
A
śr
N
RT
E
2
3
ŚREDNIA PRĘDKOŚĆ CZĄSTEK
GAZU
kT
E
śr
2
3
2
2
śr
śr
mv
E
m
kT
v
śr
3
A
śr
mN
RT
m
kT
v
3
3
masa cząsteczkowa M
M
RT
v
śr
3
prędkość m/s
prędkość m/s
3
0
10
n
n
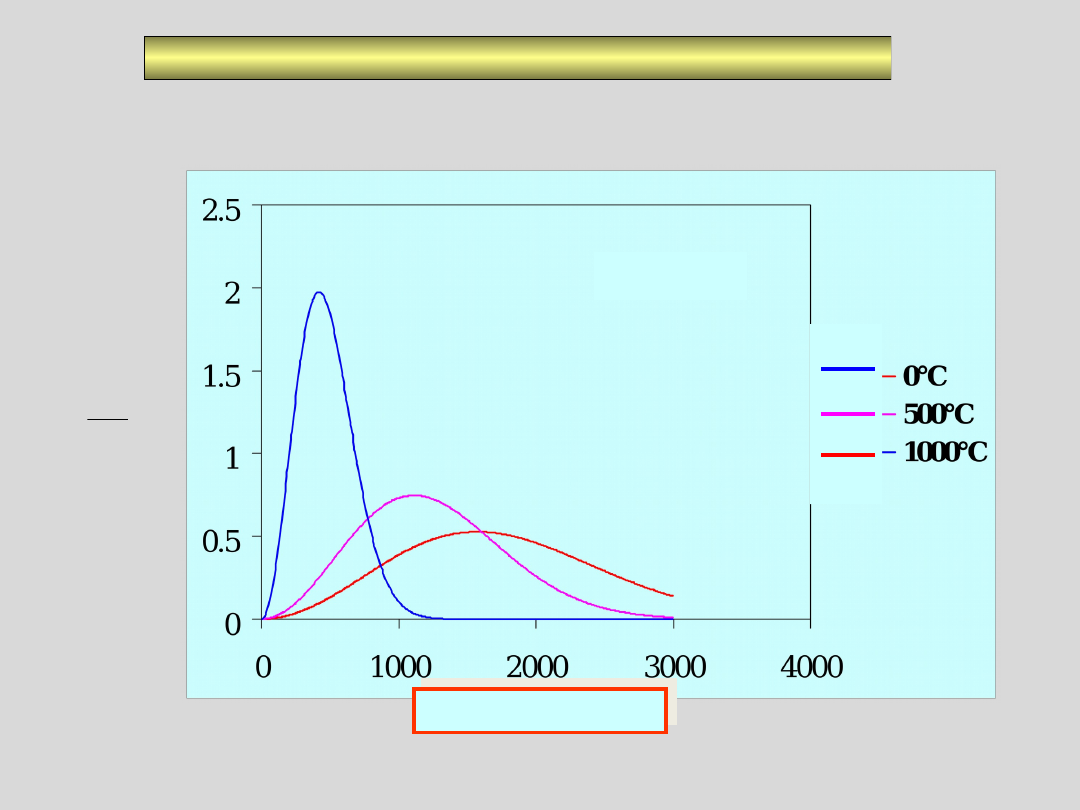
ROZKŁAD MAXWELLA-BOLTZMANNA
tlen O
2
v
i
i 1
(
) 6
3
0
10
n
n
prędkość m/s
25°C
0
4000
2
0
N
2
He
H
2
2000
ROZKŁAD PRĘDKOŚCI CZĄSTECZEK RÓŻNYCH GAZÓW W TEJ
SAMEJ TEMPERATURZE
...doświadczenia wykazały, że dla gazów spełnione jest równanie:
const
T
pV
..zatem dla 1 mola
gazu:
..zatem dla 1 mola
gazu:
R
T
pV
m
R = 8,3145 J mol
-1
K
-1
R = 8,3145 J mol
-1
K
-1
stała gazowa
stała gazowa
śr
2
pV
E
3
=
..jak pamiętamy Bernoulli wykazał:
R
T
pV
m
śr(m)
2
E
3
R
T
=
śr(m)
3
E
RT
2
=
dla 1 mola gazu doskonałego
dla 1 mola gazu doskonałego
m
(m)
śr
2
pV
E
3
=
śr
3
E
nRT
2
=
dla n moli gazu doskonałego
dla n moli gazu doskonałego
pV = nRT
RÓWNANIE CLAPEYRONA
ciśnienie: 101,325 kPa
temperatura: 0°C (273,15 K)
Objętość 1 mola gazu w warunkach normalnych:
R
T
pV
m
p
RT
V
m
R = 8,3145 J mol
-1
K
-1
R = 8,3145 J mol
-1
K
-1
l22,4 dm
3
WARUNKI NORMALNE - definicja
ciśnienie p, objętość V i temperatura T to PARAMETRY
STANU gazu
w szczególności jeżeli:
PRZEMIANA GAZOWA
to proces z udziałem gazu, w
którym co najmniej dwa z parametrów stanu ulegają
zmianie
PRZEMIANY GAZOWE
=
p
1
+
p
2
p
1
p
2
P
PRAWO DALTONA
PRAWO DALTONA
uporządkowanie
PLAZMA
GAZ WŁAŚCIWY
PARA
W
Y
S
O
K
O
-
T
E
M
P
E
R
A
T
U
R
O
W
A
N
IS
K
O
-T
E
M
P
E
R
A
T
U
R
O
W
A
N
IE
N
A
S
YC
O
N
A
N
A
S
YC
O
N
A
STANY MATERII W GRANICACH
GAZOWEGO STANU SKUPIENIA
GAZOWY STAN SKUPIENIA
25
Ją
dro
sło
ńca
Korona słoneczna
Synteza jądrowa
Wiatr
sło
ne
czny
PLAZMA GORĄCA
wysokotemperat
urowa
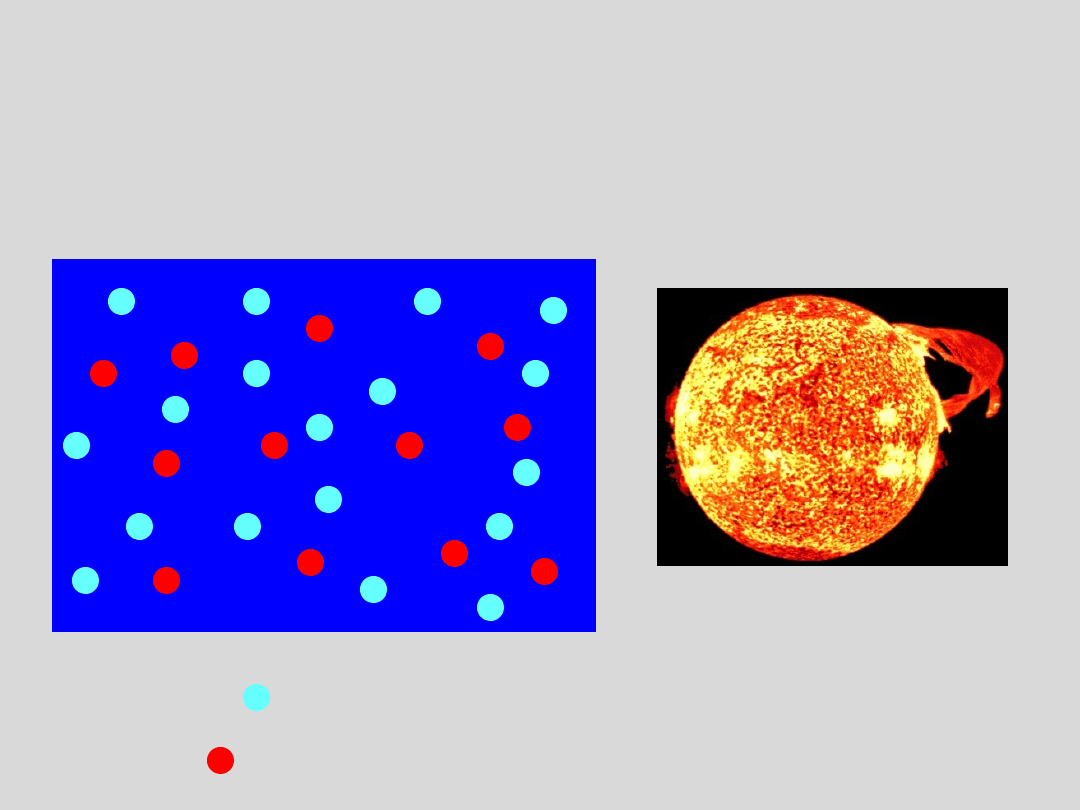
elektron
jądro
PLAZMA WYSOKOTEMPERATUROWA
W temperaturach > 10
5
-10
6
K
atomy ulegają całkowitej
jonizacji tworząc nieuporządkowany stan materii
złożony
z
jąder
i
elektronów
-
PLAZMĘ
WYSOKOTEMPERATUROWĄ
temperatura
w jądrze
słońca ~ 1.5·10
7
K
pV >
nRT
pV >
nRT
PLAZMA
WYSOKOTEMPERATUROWA
podstawowe właściwości
Występowanie
swobodnych ładunków
elektrycznych
o rozmiarach rzędu 10
-15
m
Silne oddziaływanie
elektrostatyczne i magnetyczne
pomiędzy składnikami
28
PLAZMA ZIMNA
niskotemperaturowa T 1000 – 10000K
PLAZMA ZIMNA
niskotemperaturowa T 1000 – 10000K
Zorza
polarna
Zorza
polarna
Wyładowani
a
atmosferycz
ne
Wyładowani
a
atmosferycz
ne
Wyładowani
a
elektryczne
Wyładowani
a
elektryczne
elektron
jon
dodatni
PLAZMA NISKOTEMPERATUROWA
W temperaturach > 10
3
K
atomy ulegają
częściowej
jonizacji
tworząc nieuporządkowany stan materii złożony z
jonów
dodatnich
i
elektronów:
PLAZMĘ
NISKOTEMPERATUROWĄ
pV > nRT
pV > nRT
PLAZMA
NISKOTEMPERATUROWA
podstawowe właściwości
Występowanie
swobodnych
ładunków
elektrycznych o rozmiarach rzędu 10
-10
m
(jony dodatnie)
i 10
-15
m
(elektrony)
Silne
oddziaływanie
elektrostatyczne
i
magnetyczne pomiędzy składnikami
Stopień jonizacji
31
•
Plazma jest opisywana za pomocą różnorodnych
parametrów, wśród których stopień jonizacji (stosunek
liczby elektronów do liczby pozostałych cząstek)
odgrywa rolę podstawową.
- stopień jonizacji
• Słabo zjonizowana plazma to taka, w której stopień jonizacji
wynosi mniej niż 10%. Z kolei, w plazmie silnie zjonizowanej
występują atomy pozbawione wielu swoich elektronów, co
prowadzi do dużej wartości stopnia jonizacji.
atom lub
cząsteczka
GAZ WŁAŚCIWY
W temperaturach od kilku do 1000-1500 K
atomy i
cząsteczki praktycznie
nie ulegają jonizacji
mogąc
tworzyć nieuporządkowany stan materii złożony z
obojętnych atomów lub cząsteczek -
GAZ
WŁAŚCIWY
pV
nRT
pV
nRT
GAZ WŁAŚCIWY
podstawowe właściwości
Występowanie
swobodnych atomów lub
cząsteczek
o rozmiarach rzędu 10
-10
m
Słabe
oddziaływania
elektrostatyczne
i
magnetyczne
pomiędzy
atomami
lub
cząsteczkami
p
ra
w
d
o
p
o
d
o
b
ie
ń
st
w
o
n
a
p
o
tk
a
n
ia
cz
ą
st
ki
odległoś
ć
Funkcja dystrybucji dla gazu właściwego
Brak struktury - cząsteczki przyjmują
RÓŻNE
wzajemne odległości, z
TAKIM
SAMYM
prawdopodobieństwem
Funkcja dystrybucji dla gazu
właściwego jest
izotropowa
oddz
śr
kin
śr
E
E
Pamiętajmy, że warunkiem
istnienia
stanu gazowego
jest:
Istnienie
silnych oddziaływań
w plazmie było
wynikiem obecności swobodnych ładunków
elektrycznych (dlatego plazma nie może istnieć
w niskich temperaturach)
Słabe oddziaływania
pomiędzy atomami i
cząsteczkami
gazów
właściwych
(co
umożliwia ich istnienie w stosunkowo niskich
temperaturach) są wynikiem istnienia
SIŁ
MIĘDZYCZĄSTECZKOWYCH
zwanych
siłami
Van der Waalsa
schematycznie:
atom m =
0
cząsteczka m
= 0
cząsteczka m >
0
+
-
SIŁY MIĘDZYCZĄSTECZKOWE
Gazy właściwe składają się z atomów, których
moment
dipolowy m = 0
,
lub z cząsteczek dla których
m > 0
F
2
F
1
F
4
F
3
rachunek wskazuje, że:
SIŁY
MIĘDZYCZĄSTECZKO
WE oddziaływania dipol
- dipol
F
1
+
F
2
>
F
3
+ F
4
SIŁY MIĘDZYCZĄSTECZKOWE
oddziaływania
dipol - indukowany dipol
duża
odległość
mała
odległość
indukowane
dipole
trwałe dipole
SIŁY MIĘDZYCZĄSTECZKOWE
siły
dyspersyjne (Londona)
W każdym atomie lub cząsteczce środki ładunku dodatniego i ujemnego
Q
s(+)
i Q
s(-)
wykonują ruch drgający wokół położenia równowagi, które jest
wspólne dla cząsteczek (i atomów) mających zerowy moment dipolowy
(m = 0)
Zatem każda cząsteczka, nawet taka, która ma m = 0, jest faktycznie
drgającym dipolem elektrycznym
W układzie drgających dipoli elektrycznych dochodzi do
powstawania identycznych sił przyciągających jak omówione
wcześniej oddziaływania dipol-dipol
siły Londona
siły Londona
SIŁY MIĘDZYCZĄSTECZKOWE siły Van der
Waalsa
SIŁY MIĘDZYCZĄSTECZKOWE siły Van der
Waalsa
oddziaływanie dipol -
dipol
oddziaływanie
dipol - indukowany dipol
oddziaływanie
dipol - indukowany dipol
siły dyspersyjne (Londona)
siły dyspersyjne (Londona)
7
1
d
~
F
mcz
d
F
mcz
PRAWA GAZOWE DLA GAZÓW RZECZYWISTYCH
pV nRT
Istnienie oddziaływań międzycząsteczkowych, jak i fakt posiadania
przez cząsteczki własnej objętości, staje się przyczyną odstępstw
zachowania gazów rzeczywistych od praw gazu doskonałego
Istnienie oddziaływań międzycząsteczkowych, jak i fakt posiadania
przez cząsteczki własnej objętości, staje się przyczyną odstępstw
zachowania gazów rzeczywistych od praw gazu doskonałego
Przybliżenie jest tym lepsze im średnie odległości cząsteczek gazu są
większe od średnic cząsteczek
Przybliżenie jest tym lepsze im średnie odległości cząsteczek gazu są
większe od średnic cząsteczek
zwykle:
p < 1 MPa T > T
k
*)
*)
T
k
- temperatura krytyczna
OBJĘTOŚCI MOLOWE GAZÓW
RZECZYWISTYCH
OBJĘTOŚCI MOLOWE GAZÓW
RZECZYWISTYCH
dla gazu doskonałego (0°C,
101,325 kPa):
V
m
= 22,414
dm
3
azot N
2
................................
22,401 dm
3
amoniak NH
3
....................... 22,089
dm
3
ditlenek siarki SO
2
...............
21,888 dm
3
siarkowodór H
2
S ..................
22,145 dm
3
azot N
2
................................
22,401 dm
3
amoniak NH
3
....................... 22,089
dm
3
ditlenek siarki SO
2
...............
21,888 dm
3
siarkowodór H
2
S ..................
22,145 dm
3
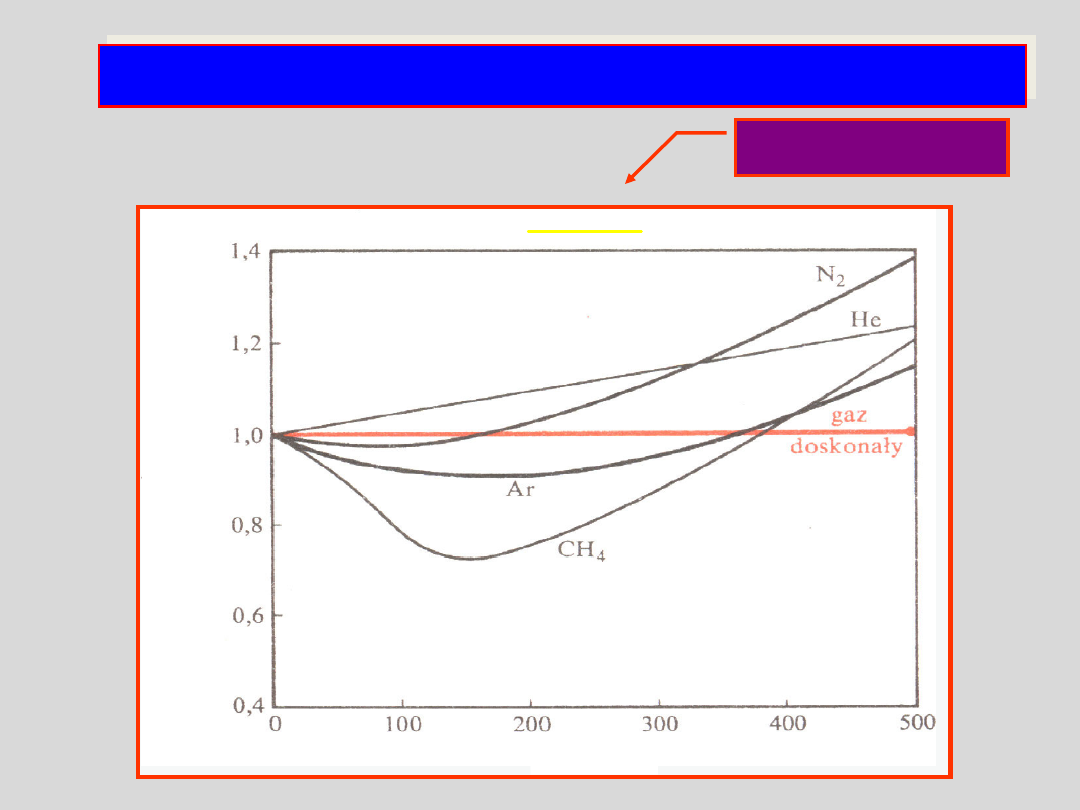
GAZY RZECZYWISTE
- współczynnik ściśliwości z
GAZY RZECZYWISTE
- współczynnik ściśliwości
z
z
p /atm
=
m
pV
z
RT
objętość
molowa
RÓWNANIA STANU GAZÓW
RZECZYWISTYCH
RÓWNANIA STANU GAZÓW
RZECZYWISTYCH
równanie Van der Waalsa dla n moli gazu:
nRT
nb
V
V
a
n
p
2
2
stałe a i b zależą od rodzaju gazu
równanie wirialne:
......
V
)
T
(
B
V
)
T
(
B
nRT
pV
2
2
1
1
Co dzieje się w gazie rzeczywistym, gdy
obniżamy jego temperaturę?
1) Średnia energia cząstek gazu maleje:
kT
E
śr
2
3
2) Energia oddziaływań międzycząsteczkowych praktycznie nie
zmienia się lub rośnie (gdy cząsteczki gazu mają różne od zera
momenty dipolowe)
w efekcie powyższego:
oddz
śr
kin
śr
E
E
oddz
śr
kin
śr
E
E
Zajrzyjmy do wnętrza gazu, w którym.....
oddz
śr
kin
śr
E
E
oddz
śr
kin
śr
E
E
Gdy sprężymy gaz, w którym...
oddz
śr
kin
śr
E
E
Gdy sprężymy gaz, w którym...
oddz
śr
kin
śr
E
E
podsumowując....
W gazie, w którym:
oddz
śr
kin
śr
E
E
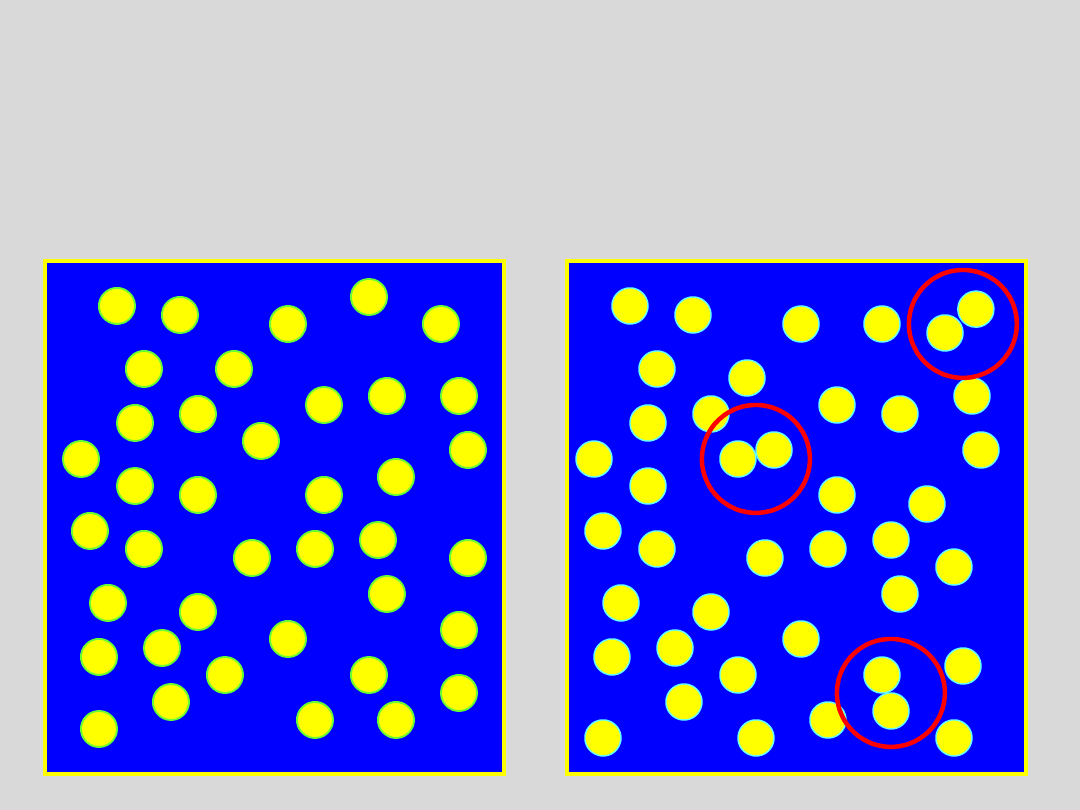
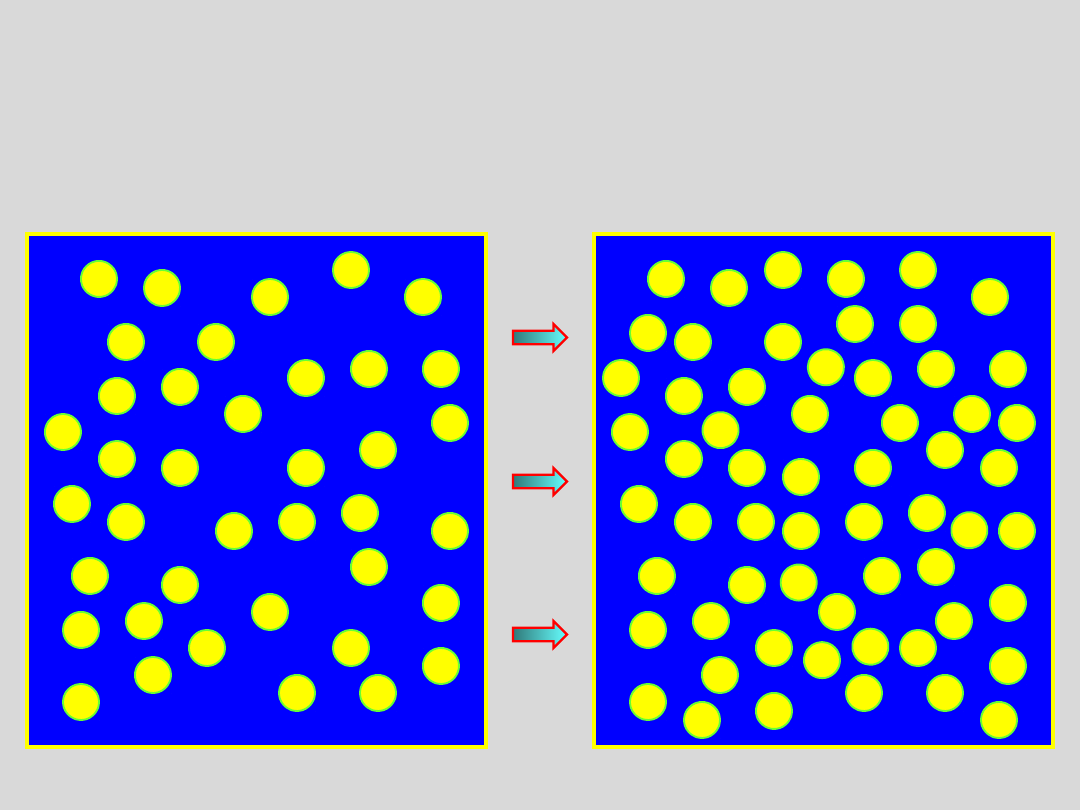
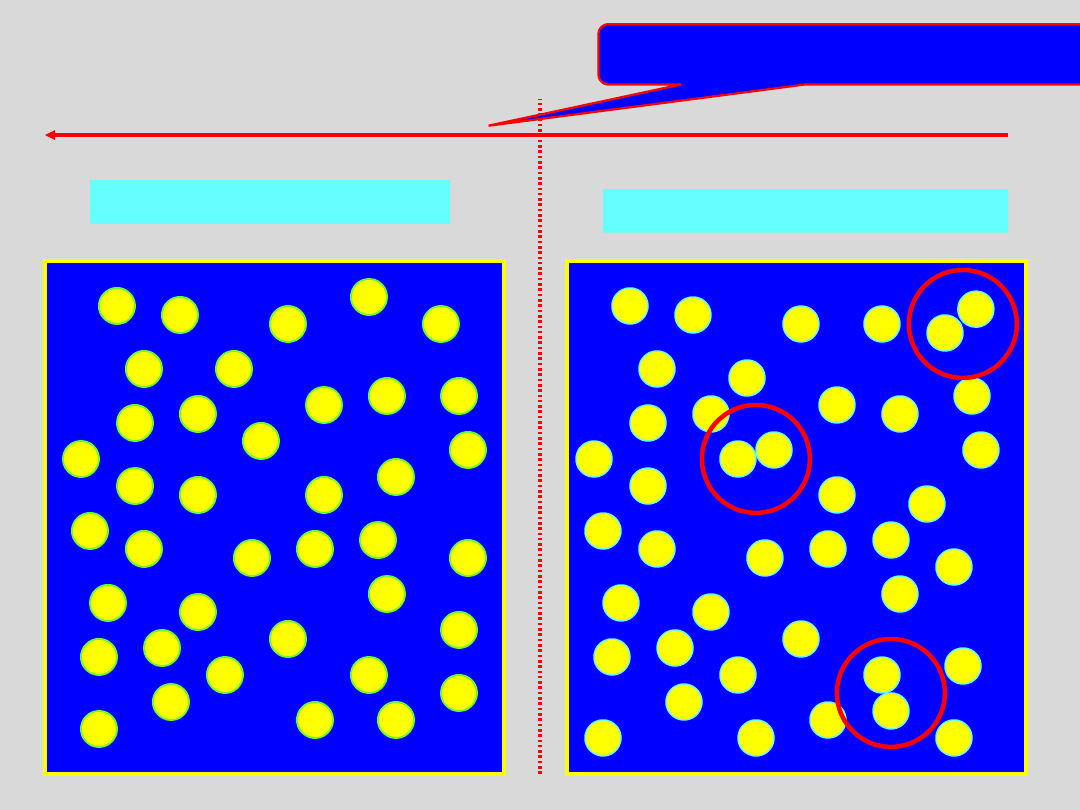
....cząsteczki nie tworzą agregatów, a sprężanie gazu prowadzi
wyłącznie do zmniejszania odległości miedzy cząsteczkami
W gazie, w którym:
oddz
śr
kin
śr
E
E
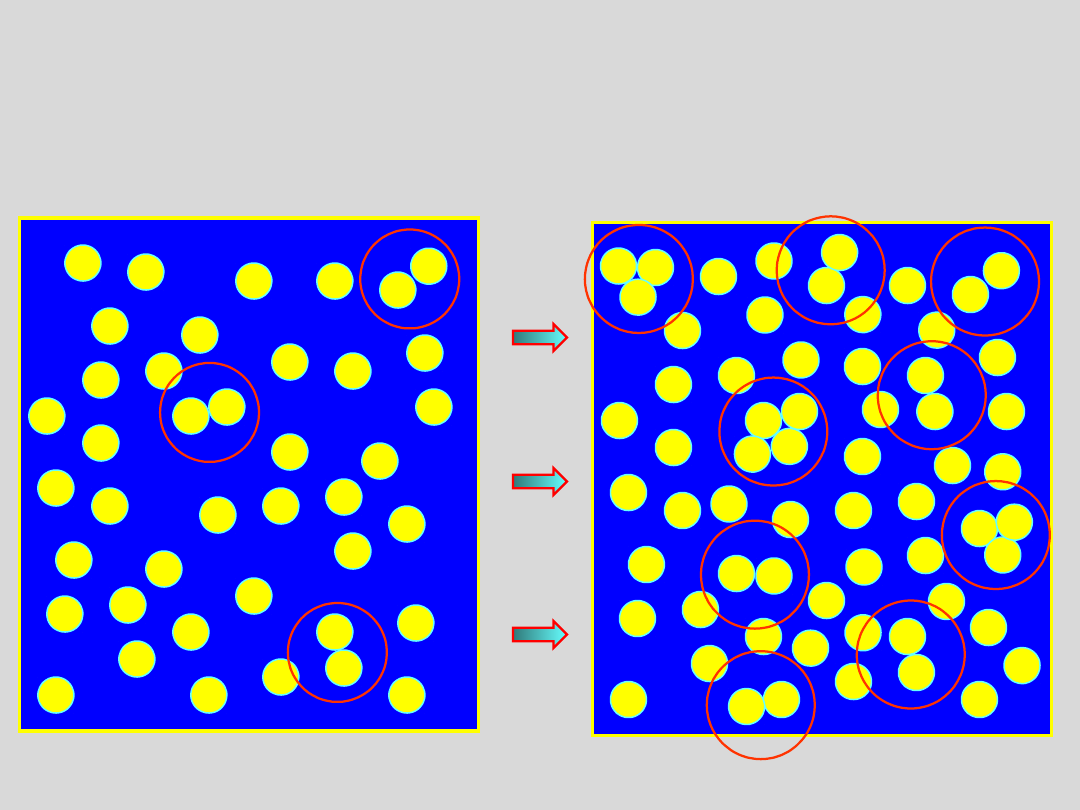
....obserwuje się tworzenie agregatów cząsteczek, a sprężanie gazu
prowadzi do zmniejszania odległości miedzy cząsteczkami oraz do
rozrostu agregatów
Zatem mamy dwa różne stany
materii....
oddz
śr
kin
śr
E
E
oddz
śr
kin
śr
E
E
temperatura
T
k
temperatura krytyczna
GAZ WŁAŚCIWY
PARA NIENASYCONA
PARA
NIENASYCONA
Jest to stan materii należący do gazowego stanu
skupienia, w którym możliwe jest tworzenie się
agregatów
cząsteczek
o
rozmiarach
nie
przekraczających pewnej wartości krytycznej
Jest to stan materii należący do gazowego stanu
skupienia, w którym możliwe jest tworzenie się
agregatów
cząsteczek
o
rozmiarach
nie
przekraczających pewnej wartości krytycznej
Granicę pomiędzy gazem a parą nienasyconą
wyznacza TEMPERATURA KRYTYCZNA T
k
temperatura
T
k
PARA NIENASYCONA
GAZ WŁAŚCIWY
TEMPERATURY
KRYTYCZNE
NH
3
132°C
O
2
-
119°C
Cl
2
144°C
N
2
-
147°C
He
-
268°C
CH
4
-82°C
H
2
O
374°C
H
2
S
100°C
Funkcja dystrybucji dla pary
nienasyconej
p
ra
w
d
o
p
o
d
o
b
ie
ń
st
w
o
n
a
p
o
tk
a
n
ia
c
zą
st
ki
odległość
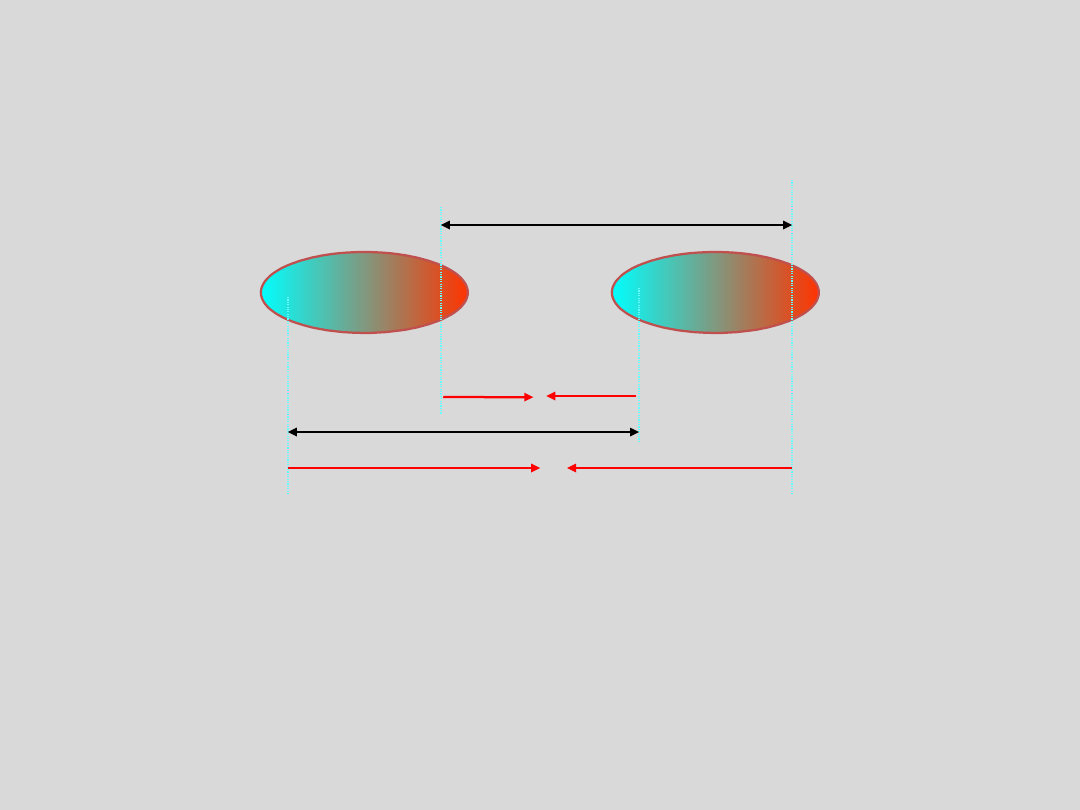
Zalążek
uporządkowania
–
pojawiają
się
odległości
międzycząsteczkowe (d
1
, d
2
), które
są uprzywilejowane w stosunku do
innych,
jednak
zasięg
uporządkowania jest niewielki
Funkcja dystrybucji dla pary
nienasyconej jest izotropowa
d
2
d
1
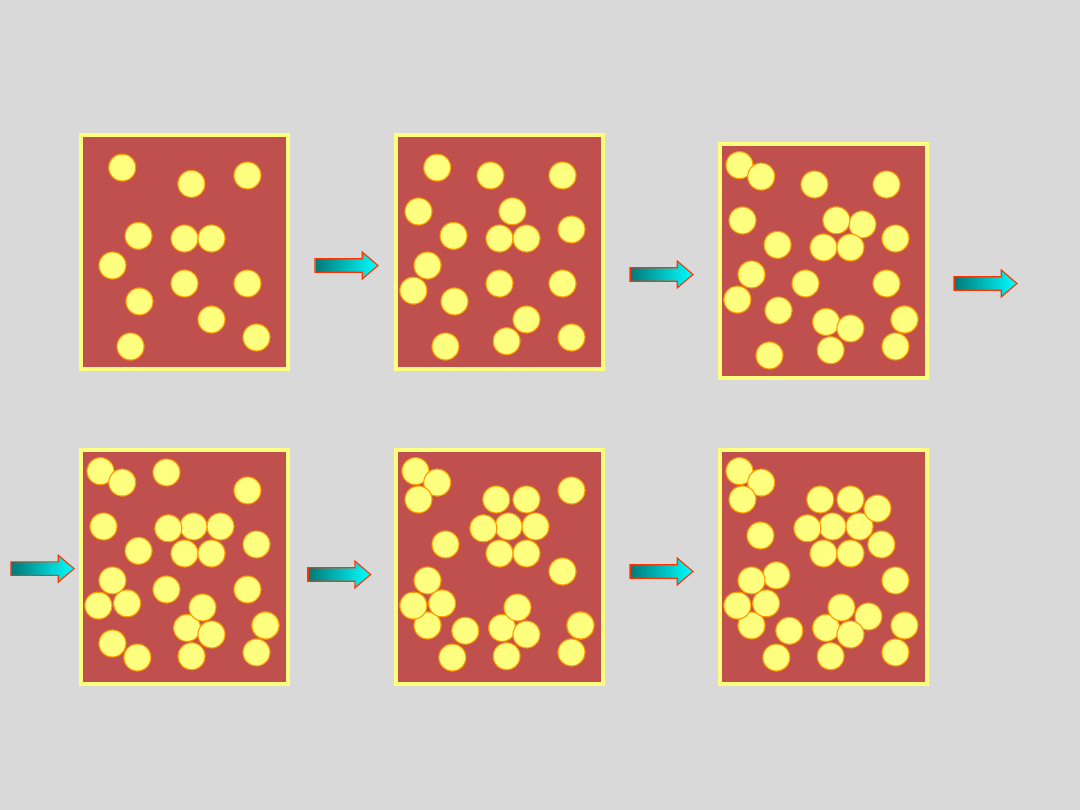
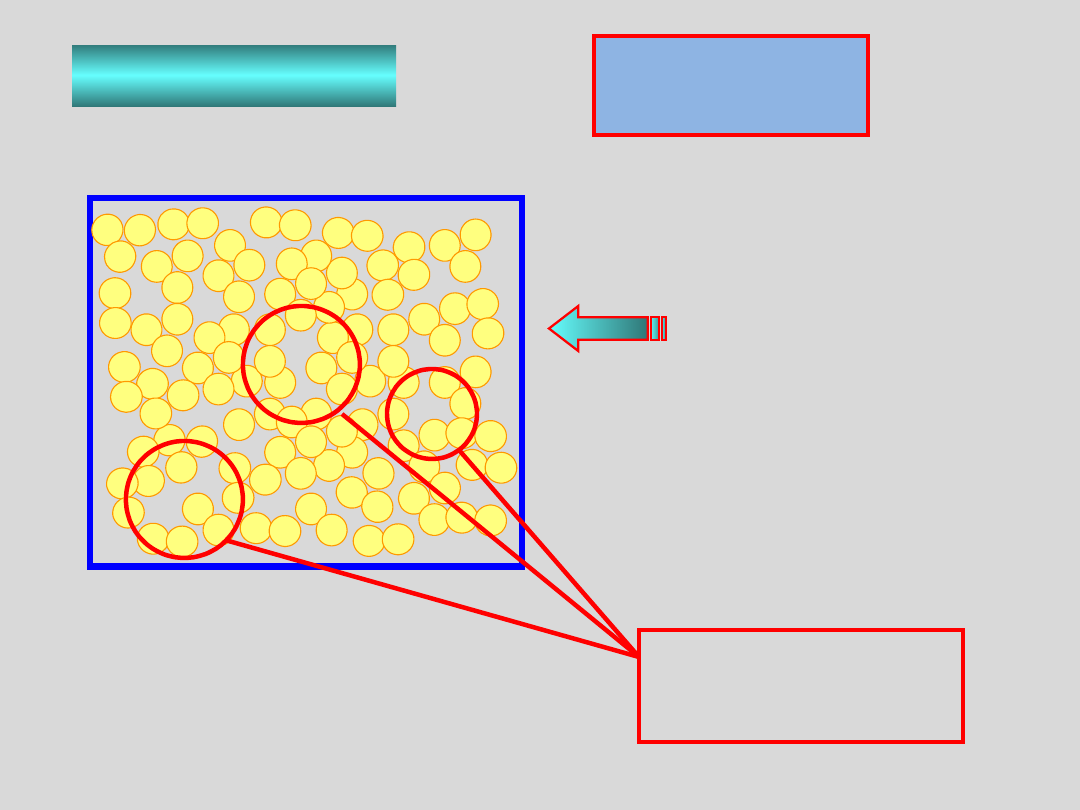
Zobaczmy jak zachowuje się para nienasycona przy
podwyższaniu ciśnienia lub przy obniżaniu temperatury
Przy obniżaniu temperatury lub podwyższaniu
ciśnienia pary nienasyconej wzrasta przeciętny
rozmiar agregatów cząsteczek
..agregaty takie tworzą się i rozpadają z szybkością
zależną od rodzaju cząsteczek, temperatury,
ciśnienia oraz rozmiarów agregatów (czyli od
liczby cząsteczek w agregacie),
ciśnienie
temperatur
a
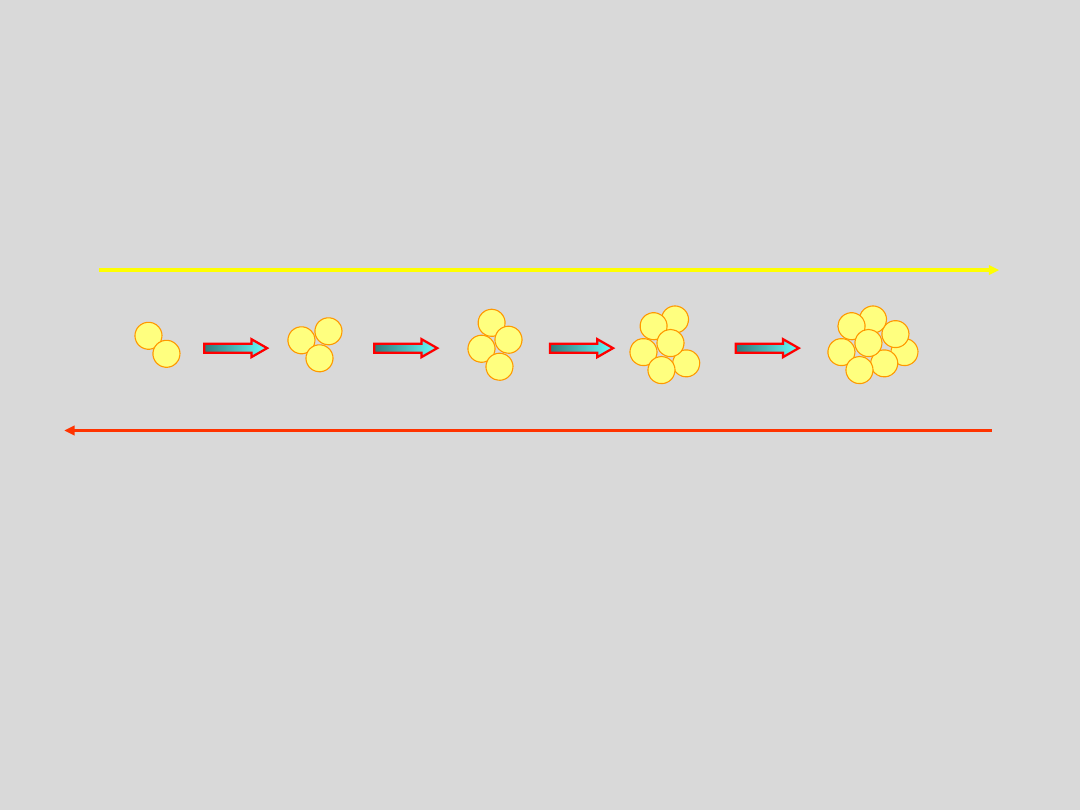
Dla każdej temperatury poniżej temperatury krytycznej T
K
istnieje takie ciśnienie p
k
, przy którym rozmiary agregatów
cząsteczek osiągają wartość krytyczną, to znaczy taką
począwszy od której, szybkość wzrostu v
wzr
agregatu przewyższa
szybkość jego rozpadu v
rozp
v
rozp
>
v
wzr
rozmiary agregatów są
MNIEJSZE niż rozmiary
krytyczne
v
rozp
<
v
wzr
rozmiary agregatów są
WIĘKSZE niż rozmiary
krytyczne
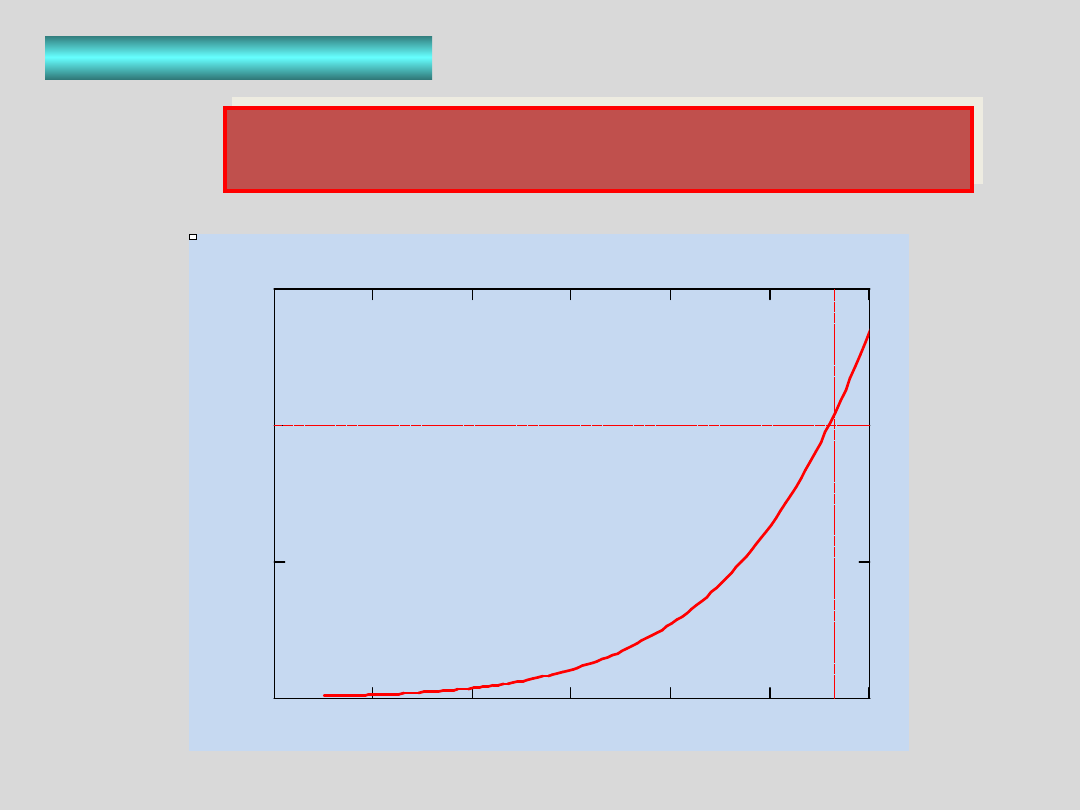
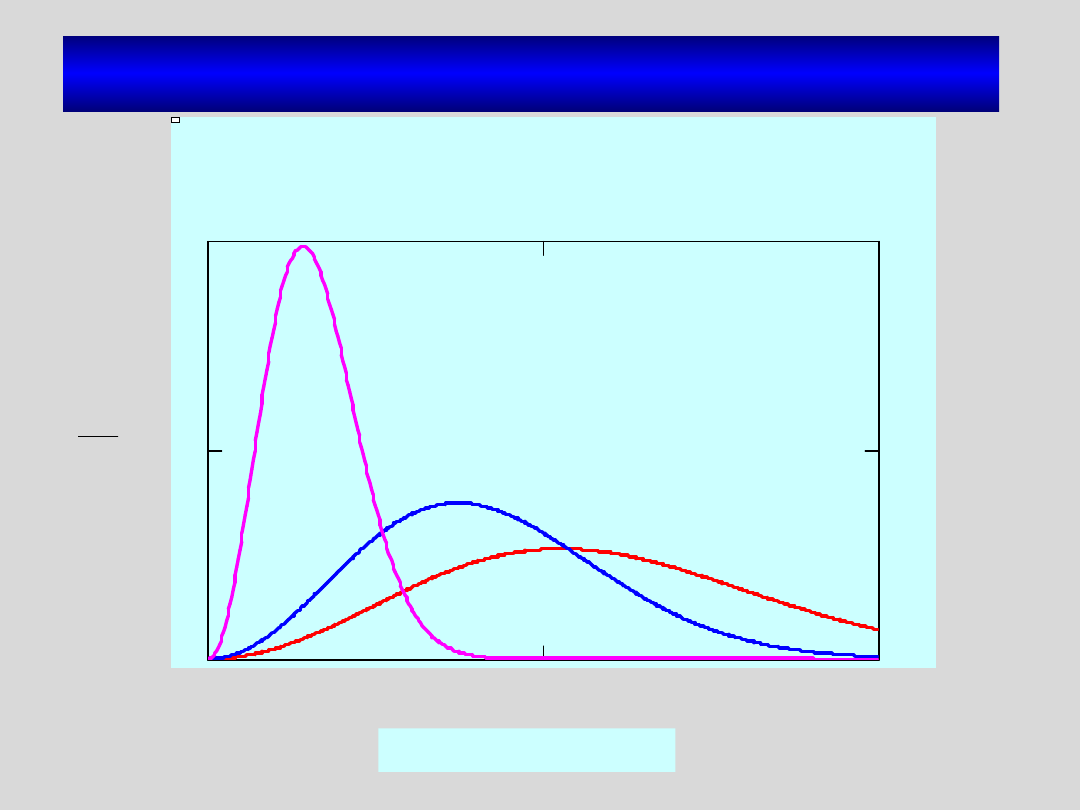
PARA NASYCONA
definicja:
para, która w danej temperaturze osiągnęła
maksymalne ciśnienie
para, która w danej temperaturze osiągnęła
maksymalne ciśnienie
a 1
260
280
300
320
340
360
380
0
0.5
1
1.5
temperatura /K
ci
œn
ie
ni
e
/a
tm
1
373
H
2
O
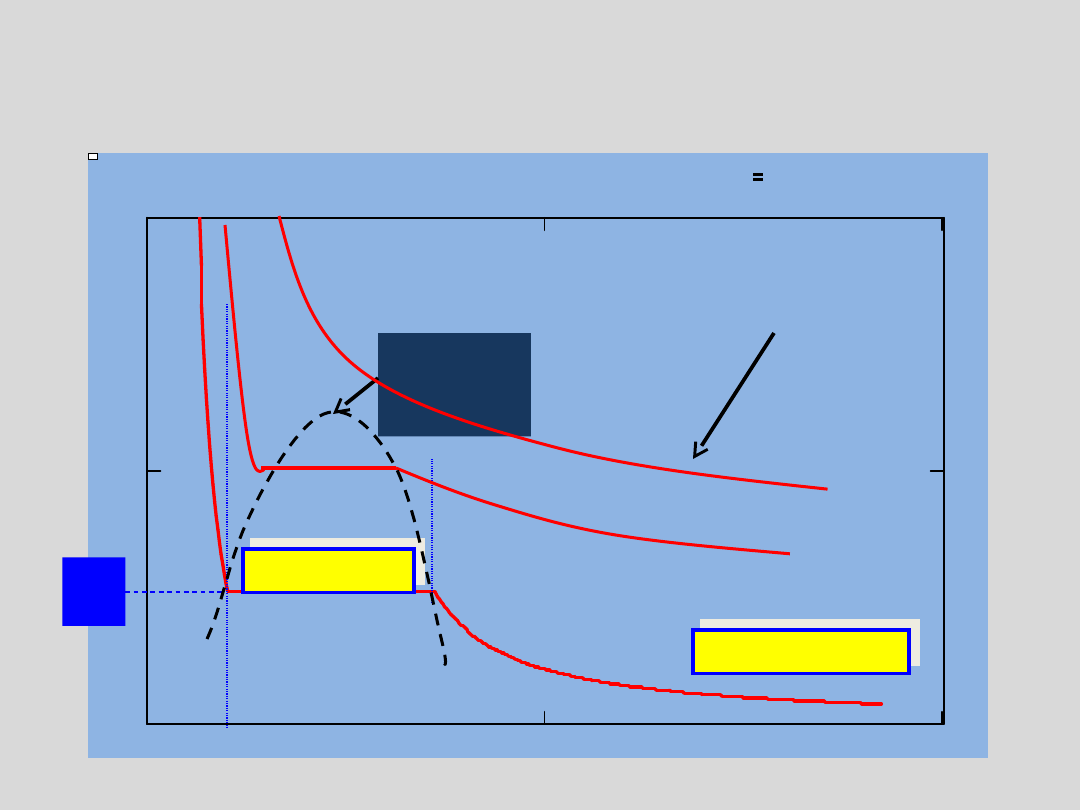
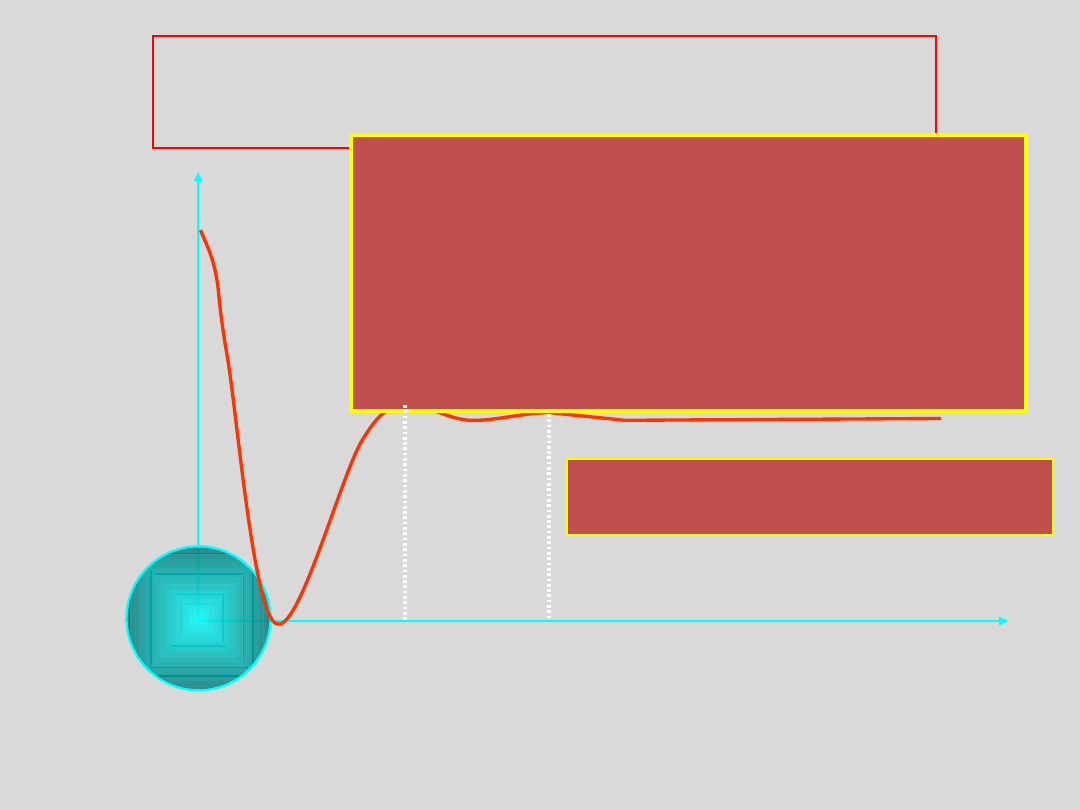
Rozważmy sytuację, w której para nienasycona o
temperaturze T < T
k
poddana jest sprężaniu...
a 1
objêtoœæ
ci
œn
ie
n
ie
p
k
para
nienasycona
para nasycona
ci
e
cz
pV = const
pV = const
p=const
p=const
Zależność p od V dla CO
2
w różnych temperaturach
20°
0°
T
kr
=
31°
prawo Boyle’a -
Mariotta
60°
PARAMETRY
KRYTYCZNE
p
k
V
k
T
k
OBJĘTOŚĆ KRYTYCZNA V
k
- objętość jednego mola gazu w
temperaturze krytycznej T
k
pod ciśnieniem krytycznym p
k
CIŚNIENIE KRYTYCZNE p
k
- ciśnienie pary nasyconej w temperaturze
krytycznej T
k
PARAMETRY KRYTYCZNE W RÓWNANIU
VAN DER WAALSA
PARAMETRY KRYTYCZNE W RÓWNANIU
VAN DER WAALSA
nRT
nb
V
V
a
n
p
2
2
2
3
27
8
27
=
=
=
k
k
k
V
b
a
p
b
a
T
bR
2
3
=
=
k k
k
a pV
V
b
gaz
a
atm·dm
2
·mol
-2
b
dm
3
·mol
-1
gaz
a
atm·dm
2
·mo
l
-2
b
dm
3
·mol
-1
NH
3
4,17
0,0514
H
2
0,2444 0,0266
N
2
1,39
0,0391
O
2
1,36
0,0318
Cl
2
6,493
0,0562
CO
2
11,62
0,0768
5
PRZYKŁADOWE WARTOŚCI PARAMETRÓW
a i b W RÓWNANIU VAN DER WAALSA
PRZYKŁADOWE WARTOŚCI PARAMETRÓW
a i b W RÓWNANIU VAN DER WAALSA
Funkcja dystrybucji dla pary nasyconej
p
ra
w
d
o
p
o
d
o
b
ie
ń
st
w
o
n
a
p
o
tk
a
n
ia
c
zą
st
ki
odległość
Zalążek uporządkowania – pojawiają się
odległości
międzycząsteczkowe,
które
są
wyraźnie uprzywilejowane w stosunku do
innych, jednak zasięg uporządkowania nie
przekracza 2 – 4 średnic cząsteczek
Funkcja dystrybucji dla pary
nasyconej jest izotropowa
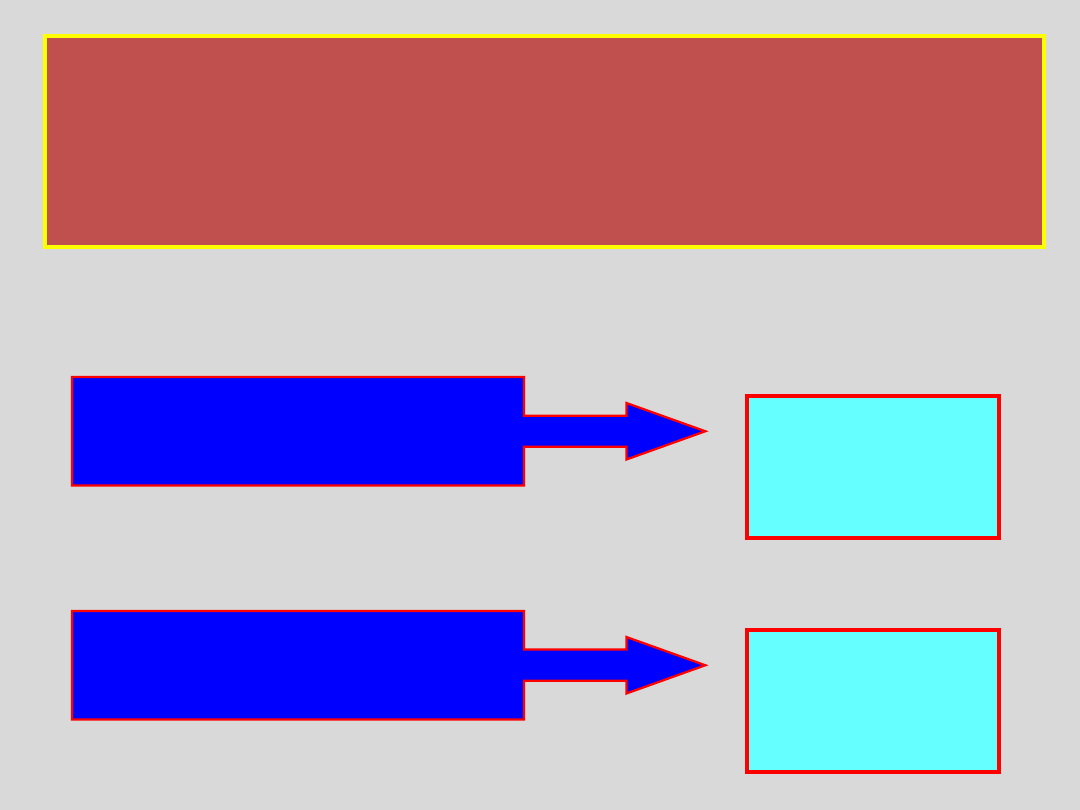
SKRAPLANIE GAZÓW
SKRAPLANIE GAZÓW
GAZ
GAZ
PARA NIENASYCONA
PARA NIENASYCONA
PARA NASYCONA
PARA NASYCONA
obniżenie
temperatu
ry
CIECZ
CIECZ
zmniejsze
nie
objętości
obniżenie
temperatu
ry
obniżenie
temperatu
ry
zmniejsze
nie
objętości
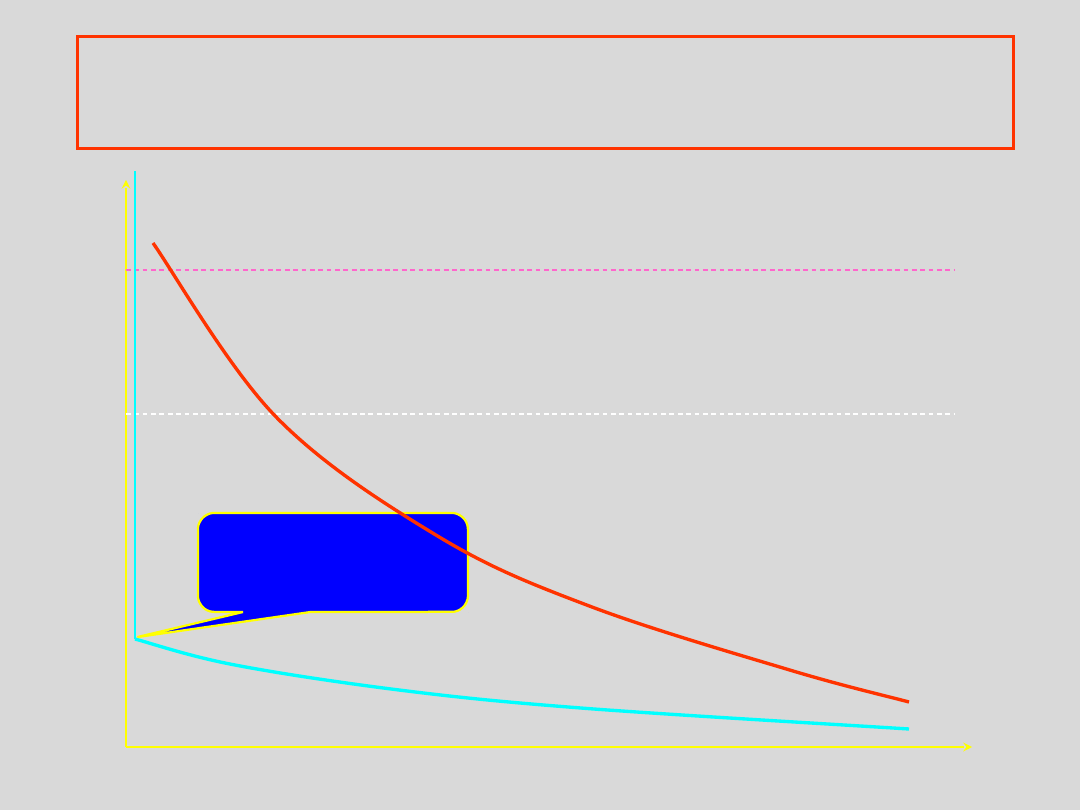
STAN GAZOWY STAN CIEKŁY STAN STAŁY
uporządkowanie
temperatura
podsumowanie
:
p
la
zm
a
w
y
so
ko
te
m
p
e
ra
tu
ro
w
a
p
la
zm
a
n
is
ko
te
m
p
e
ra
tu
ro
w
a
g
a
z
w
ła
śc
iw
y
p
a
ra
n
ie
n
a
sy
co
n
a
p
a
ra
n
a
sy
co
n
a
STAN CIEKŁY
<
oddz
śr
E
kin
śr
E
luki w
strukturze
ciecz zwykła
STAN CIEKŁY – FUNKCJA DYSTRYBUCJI
p
ra
w
d
o
p
o
d
o
b
ie
ń
st
w
o
odległość
Funkcja dystrybucji dla cieczy
zwykłych jest izotropowa
Blisko zasięgowe
uporządkowanie obejmuje 4 –
6 średnic cząsteczek
Blisko zasięgowe
uporządkowanie obejmuje 4 –
6 średnic cząsteczek
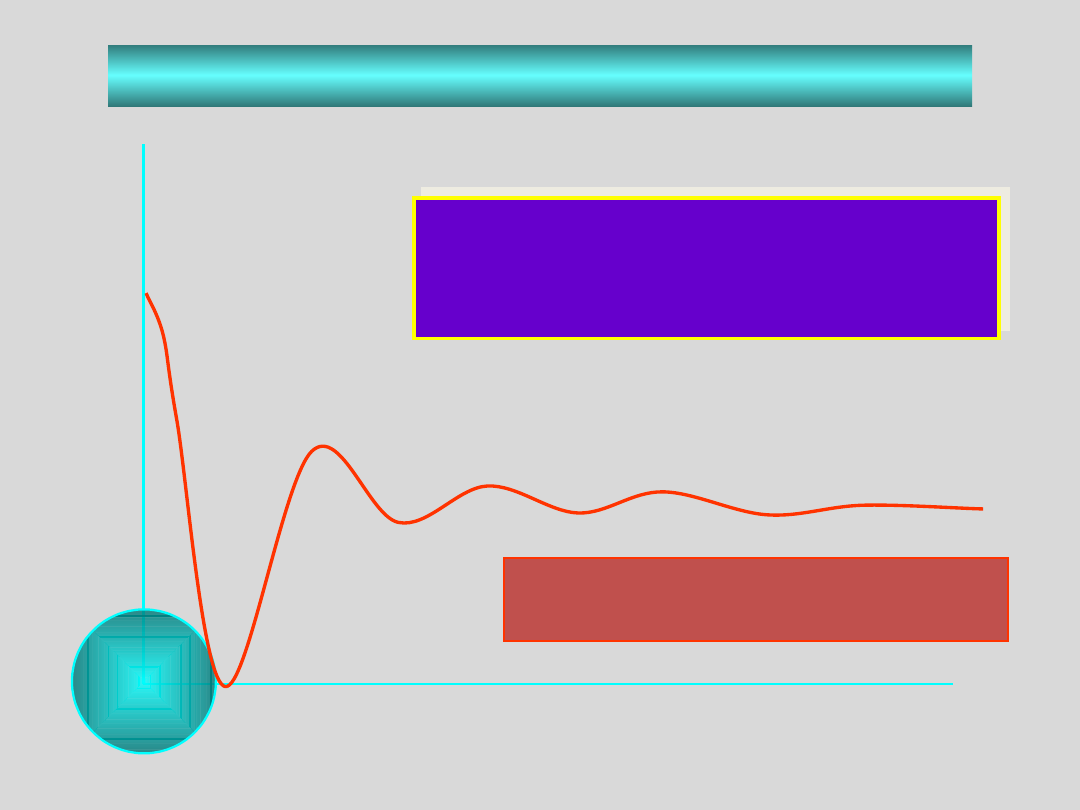
Podstawowe cechy stanu
ciekłego
Cząsteczki pomiędzy którymi działają znaczące siły znajdują się w
odległościach rzędu ich własnych rozmiarów
W cieczach obserwuje się tzw. blisko zasięgowe uporządkowanie
obejmujące kilka średnic cząsteczkowych
ściśliwość cieczy jest bardzo mała
powierzchnia cieczy ma szczególne cechy wynikające z istnienia SIŁ
NAPIĘCIA POWIERZCHNIOWEGO
SIŁY MIĘDZYCZĄSTECZKOWE W CIECZACH
SIŁY MIĘDZYCZĄSTECZKOWE W CIECZACH
oddziaływania dipol – dipol
oddziaływania dipol – indukowany dipol
siły dyspersyjne
siły Van der Waalsa
wiązanie
wodorowe
występujące wyłącznie w cieczach złożonych z cząsteczek
zawierających atomy wodoru oraz atomy:
azotu, tlenu lub fluoru
– silne wiązanie
fosforu, siarki, chloru, bromu lub jodu
– słabe wiązanie
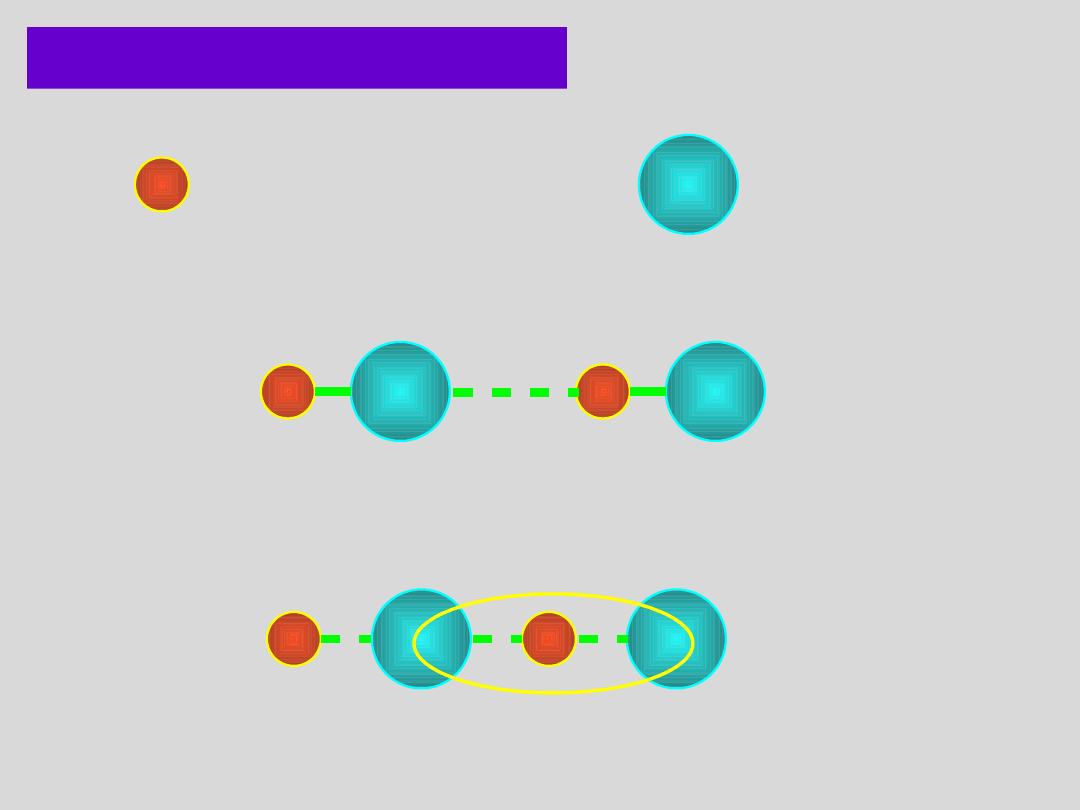
WIĄZANIE WODOROWE
wodór
fluor
etap I - zbliżanie
etap II – utworzenie wiązania wodorowego
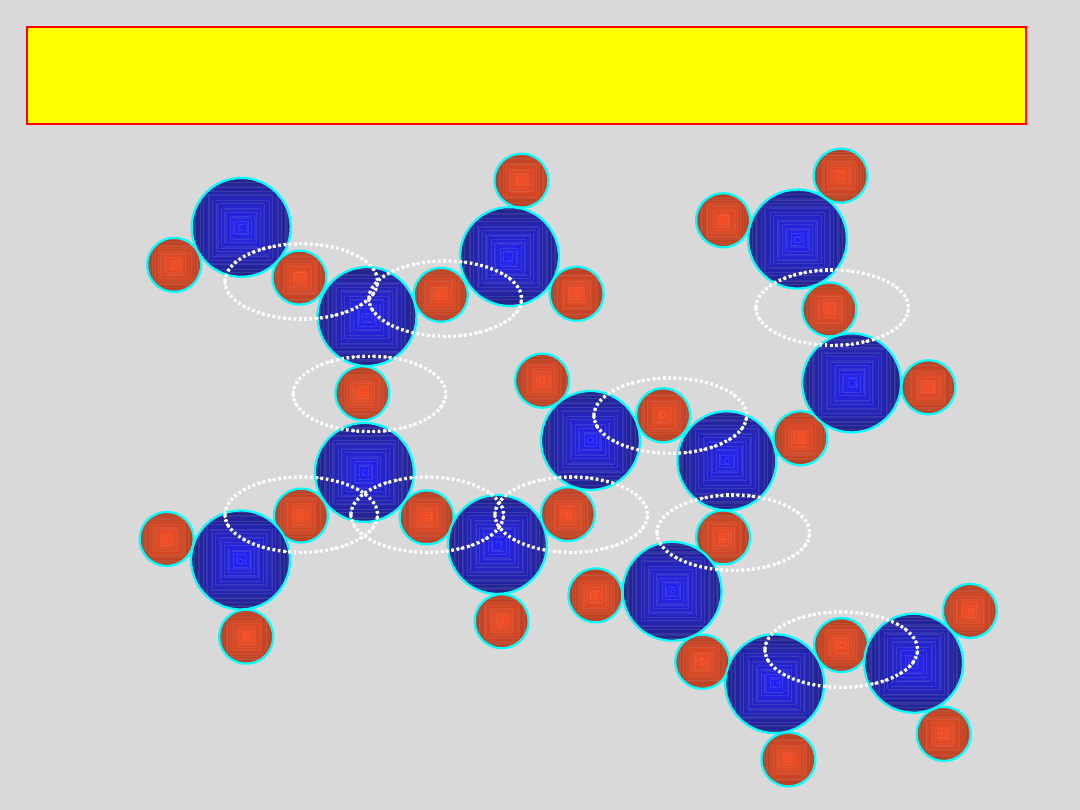
Struktura wody z uwidocznionymi wiązaniami
wodorowymi
O
H
H
ENERGIA WIĄZAŃ
WODOROWYCH
ENERGIA WIĄZAŃ
WODOROWYCH
siły
Van der Waalsa
siły
Van der Waalsa
wiązanie
wodorowe
wiązanie
wodorowe
wiązanie
chemiczne
wiązanie
chemiczne
<
<
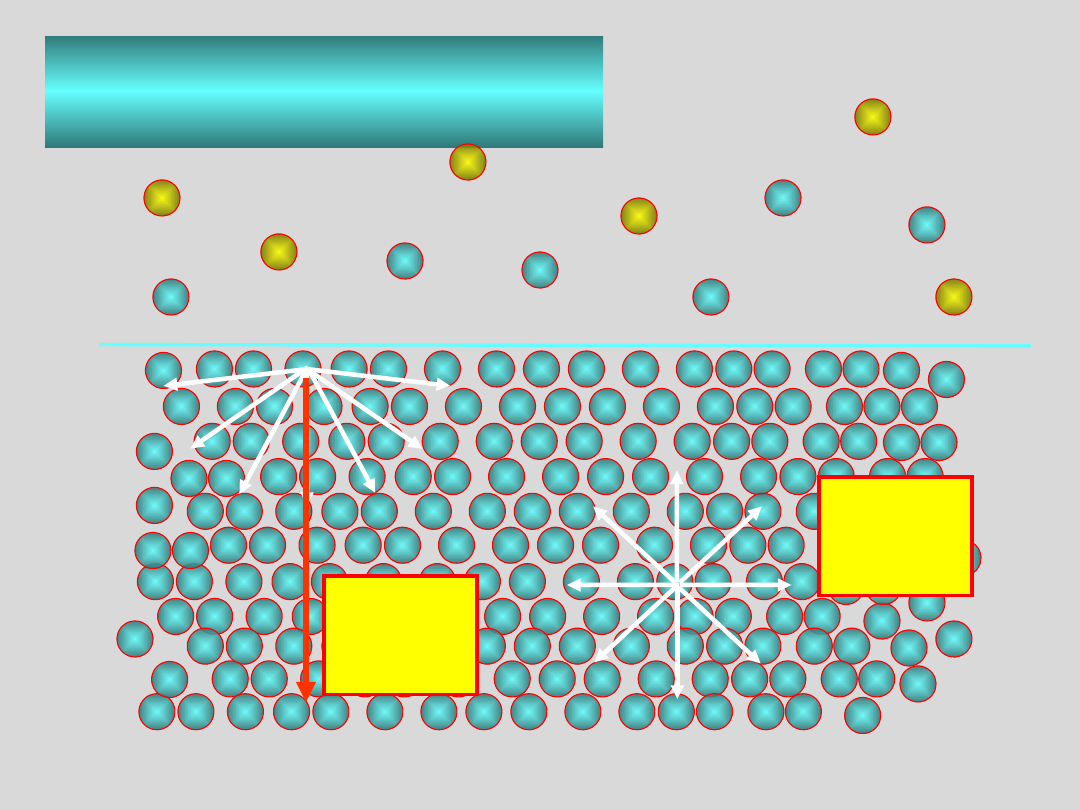
POWIERZCHNIA
CIECZY
F
w
>
0
F
w
=
0
ci
e
c
z
g
a
z
(p
a
ra
)
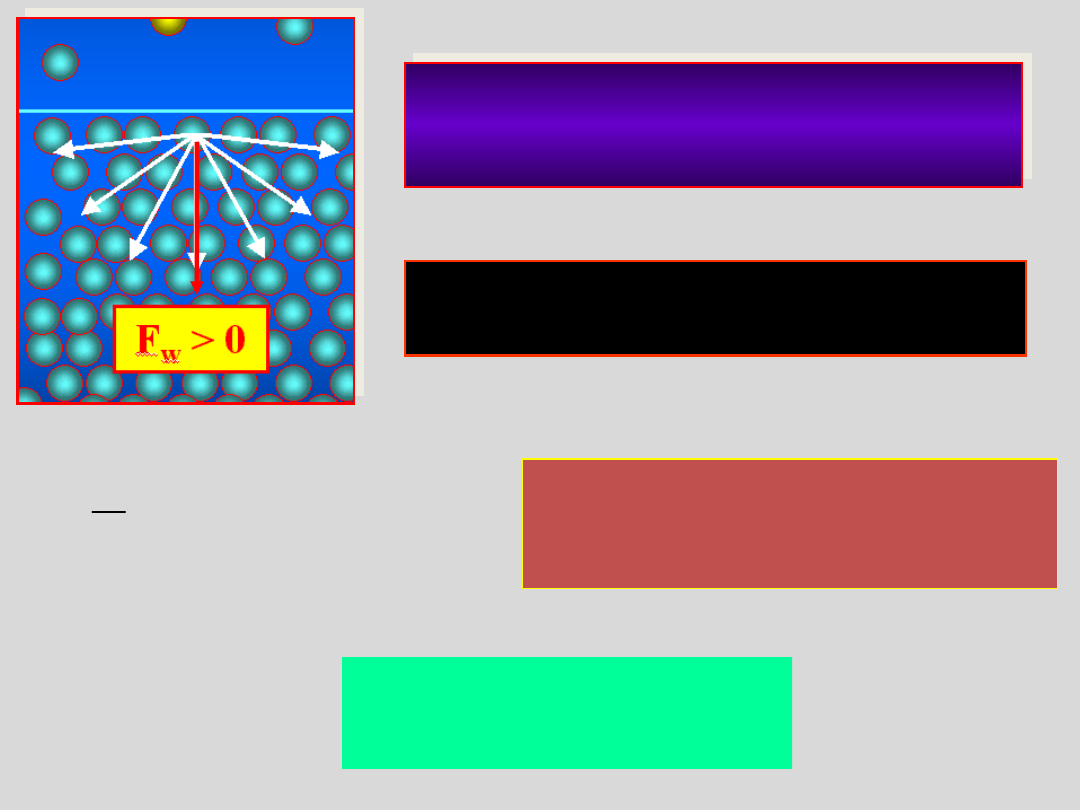
Zwiększenie
powierzchni
cieczy
wymaga zatem wykonania pracy L
przeciwko sile F
w
Zwiększenie
powierzchni
cieczy
wymaga zatem wykonania pracy
L
przeciwko sile
F
w
zdefiniujemy
NAPIĘCIE POWIERZCHNIOWE s
1
2
m
N
m
J
S
L
L – praca zużyta na
wytworzenie powierzchni S
cieczy
~10 < s < ~1500
mJ·m
-2
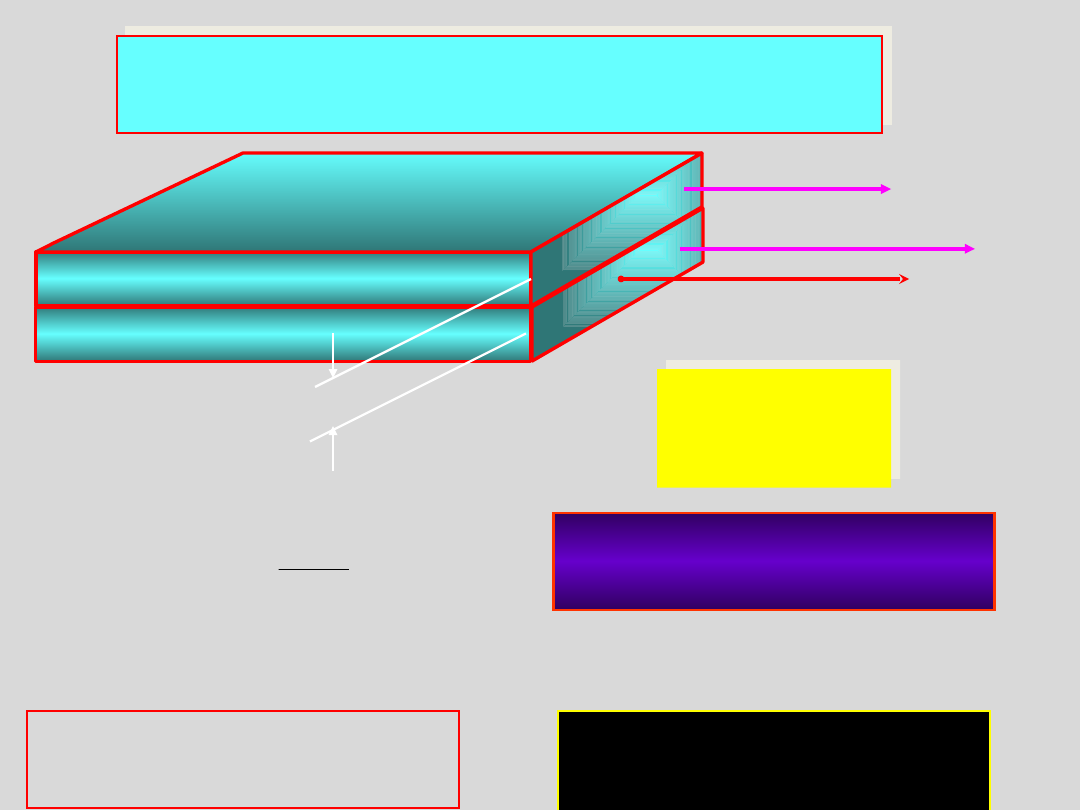
LEPKOŚĆ CIECZY (tarcie
wewnętrzne)
LEPKOŚĆ CIECZY (tarcie
wewnętrzne)
v
1
v
2
F
Dx
v
2
– v
1
=
Dv
v
2
– v
1
=
Dv
S
x
v
S
F
h – współczynnik
lepkości
jednostka (SI):
1N·s·m
-2
1 puaz = 0,1
N·s·m
-2
10
-4
< h < 10
13
N·s·m
-2
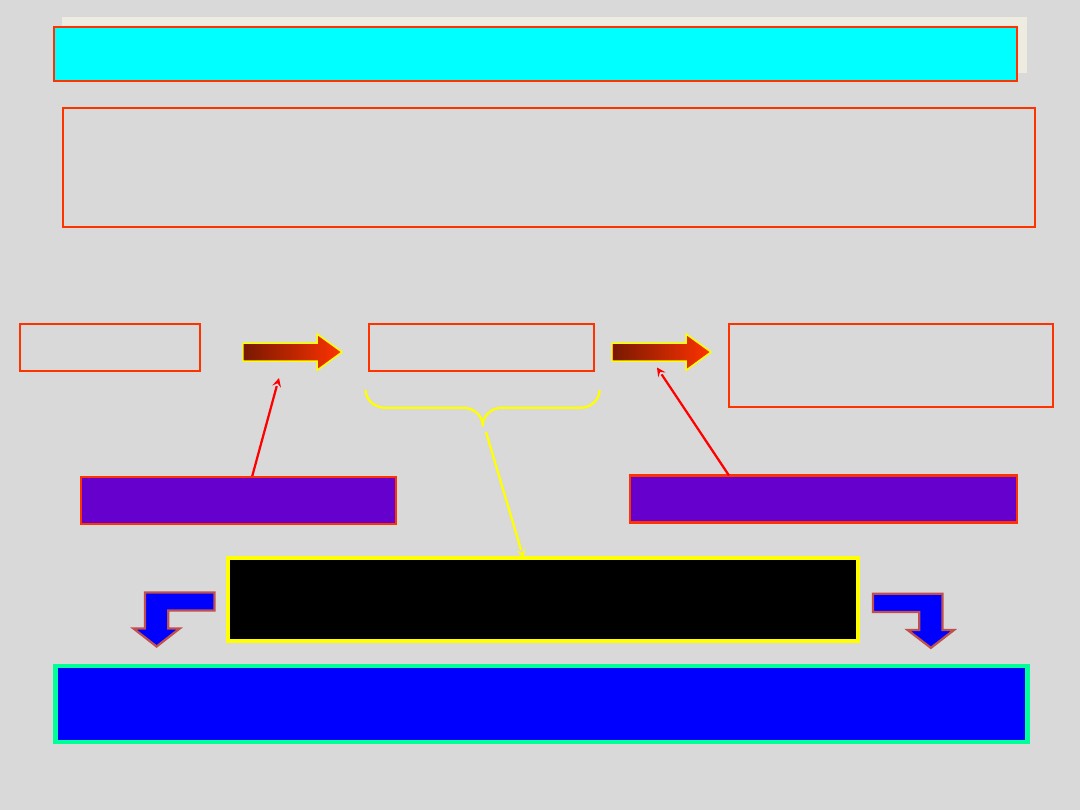
CIECZE ANIZOTROPOWE – CIEKŁE KRYSZTAŁY
CIECZE ANIZOTROPOWE – CIEKŁE KRYSZTAŁY
W trakcie topienia pewnych związków chemicznych o
cząsteczkach wydłużonych lub płaskich, posiadających duże
momenty dipolowe obserwuje się dwuetapowe topnienie:
kryształy
topnienie do fazy I
przemiana do fazy II
faza I – termotropowy ciekły
kryształ
mętna ciecz
I
przeźroczysta
ciecz
II
ciecz, dla której funkcja dystrybucji jest anizotropowa – różna dla
różnych kierunków w przestrzeni
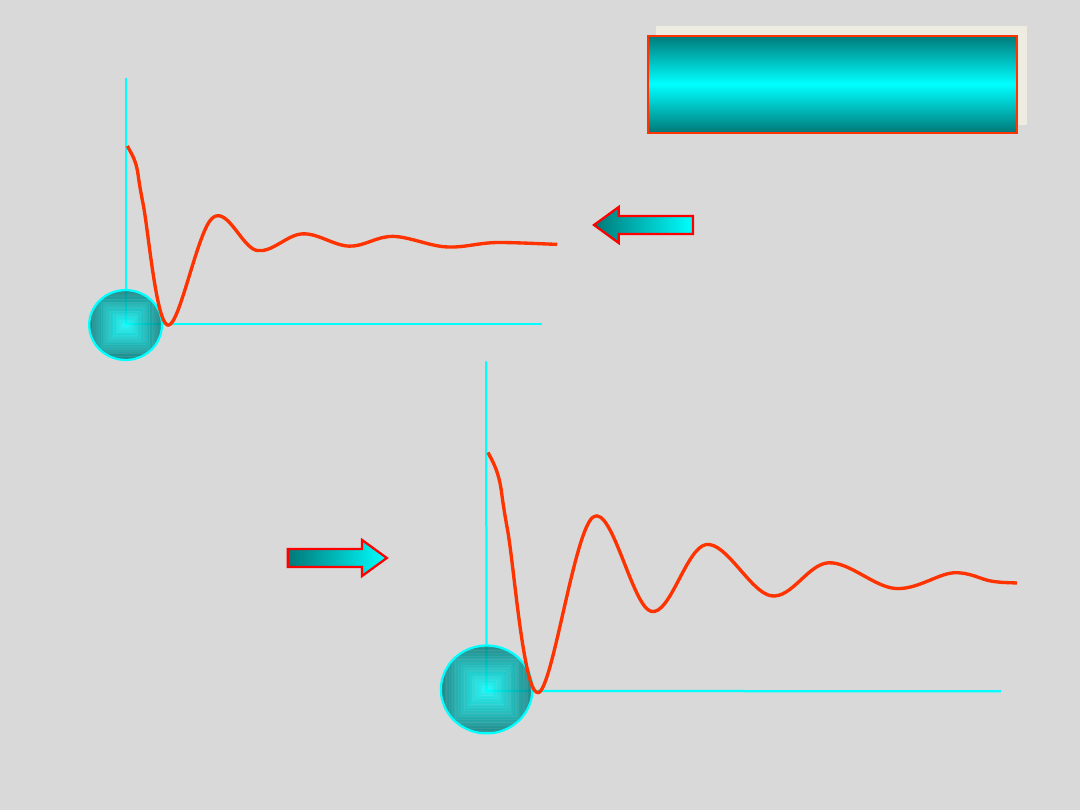
p
ra
w
d
o
p
o
d
o
b
ie
ń
st
w
o
odległość
odległość
p
ra
w
d
o
p
o
d
o
b
ie
ń
st
w
o
kierunek 1
kierunek 2
Ciecz
anizotropowa
Ciecz
anizotropowa
jak w „zwykłej
cieczy”
znacznie
lepsze
uporządkowani
e
STRUKTURY CIEKŁYCH
KRYSZTAŁÓW
STRUKTURY CIEKŁYCH
KRYSZTAŁÓW
faza
nematyczna
NEMATY
K
STRUKTURY CIEKŁYCH KRYSZTAŁÓW
STRUKTURY CIEKŁYCH KRYSZTAŁÓW
faza smektyczna
SMEKTY
K
STRUKTURY CIEKŁYCH KRYSZTAŁÓW
STRUKTURY CIEKŁYCH KRYSZTAŁÓW
faza
cholesterolowa
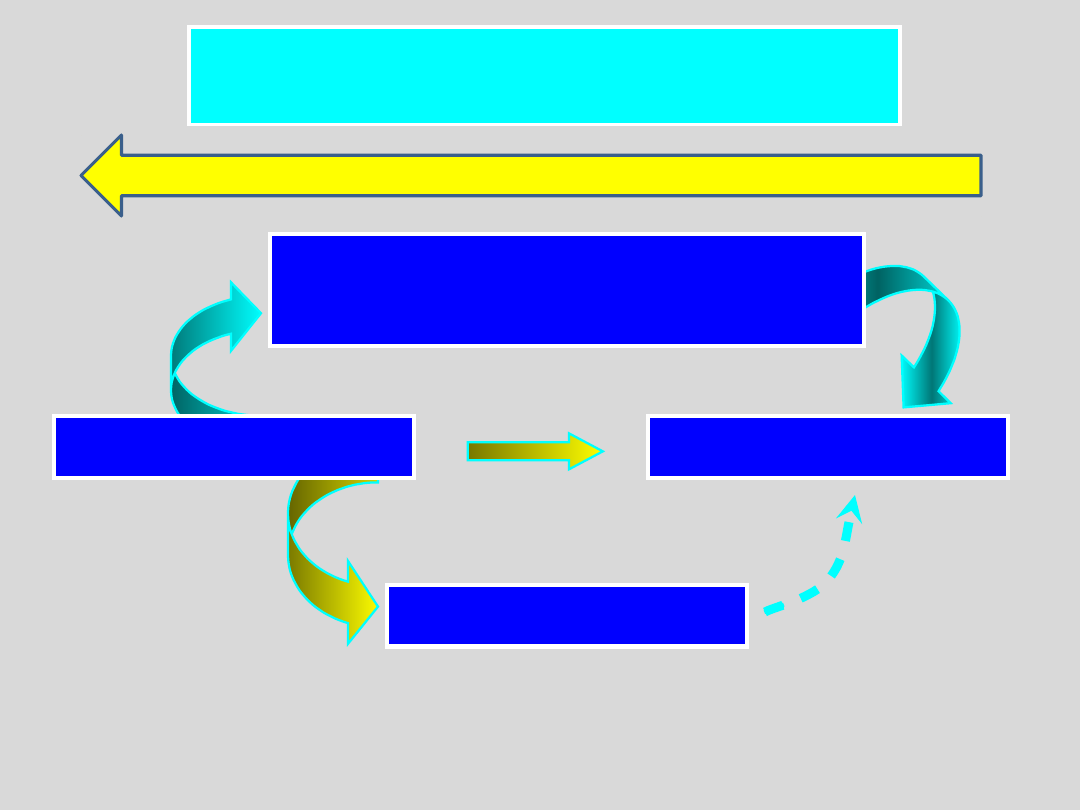
Drogi od stanu ciekłego do stanu
stałego
STAN CIEKŁY
STAN STAŁY
STAN
CIEKŁOKRYSTALICZNY
STAN SZKLISTY
temperatura
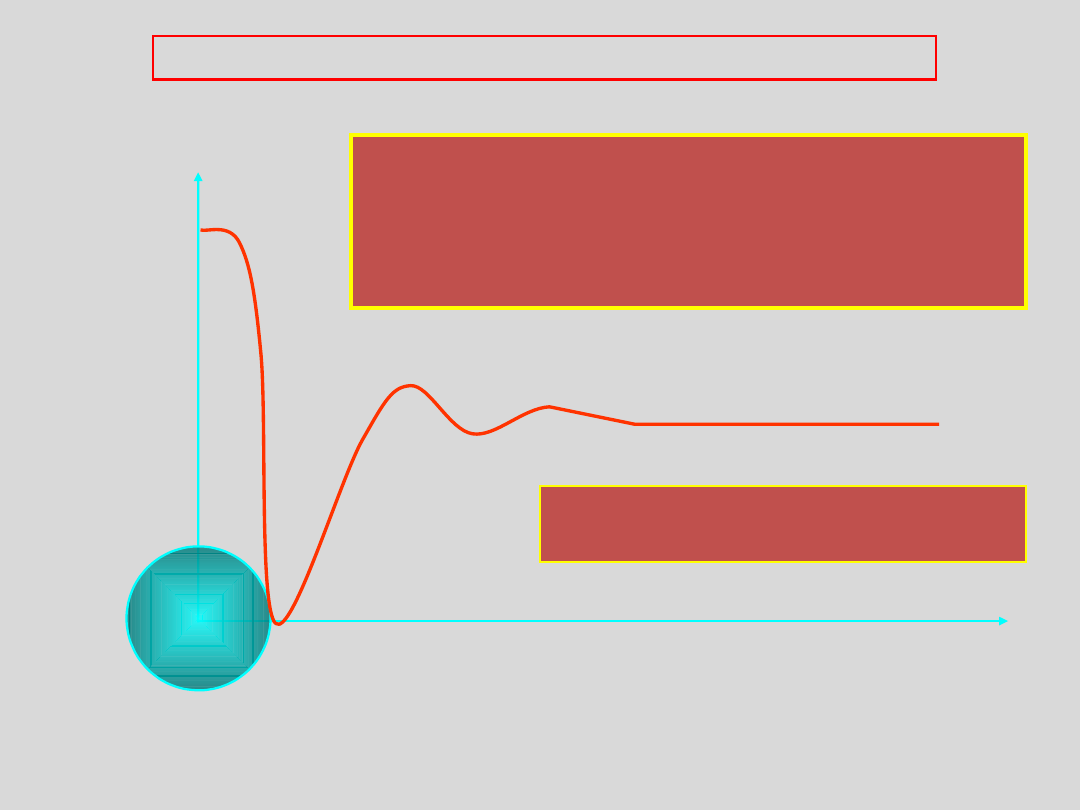
Przejście do stanu szklistego – zmiana
lepkości z temperaturą
10
0
10
12
10
3
10
6
10
9
stan plastyczny
sztywność
postaci
temperatura
h
temperatura
krzepnięcia
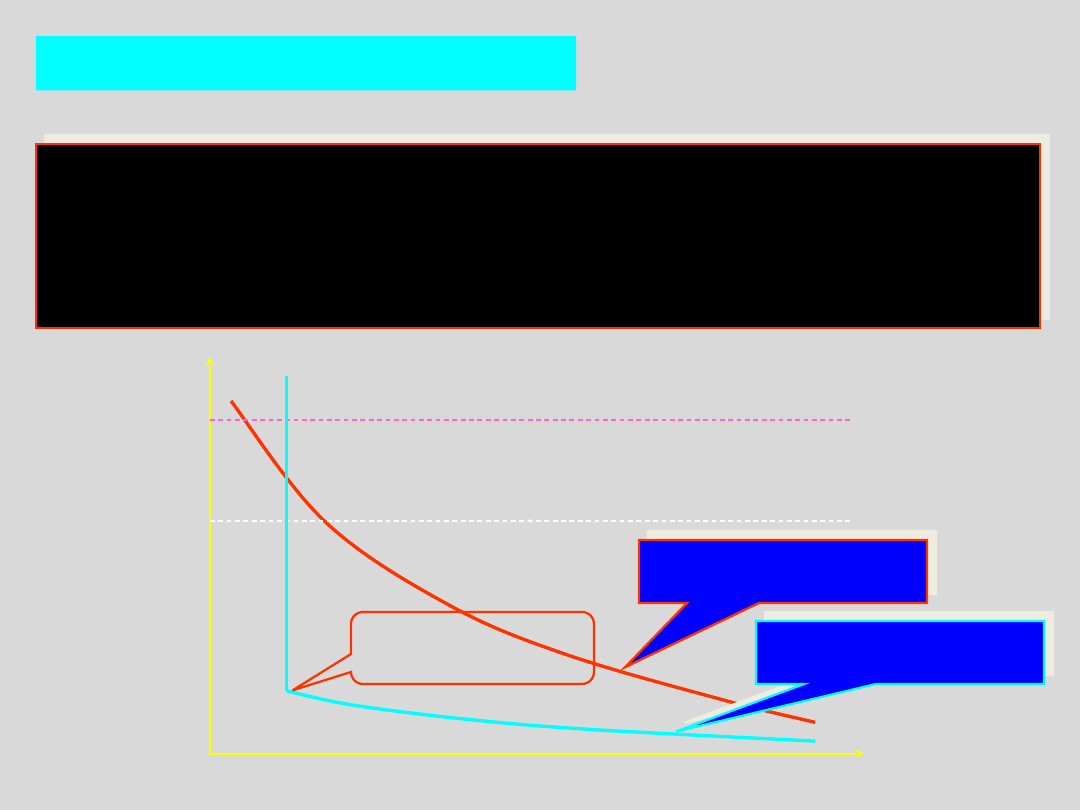
STAN SZKLISTY - definicja
SZKŁO jest substancją powstającą w wyniku ciągłego
przejścia przy ochładzaniu od stanu cieczy (lepkość
rzędu 1 N·s·m
-2
) do stanu w którym lepkość jest
większa od 10
12
N·s·m
-2
.
SZKŁO jest substancją powstającą w wyniku ciągłego
przejścia przy ochładzaniu od stanu cieczy (lepkość
rzędu 1 N·s·m
-2
) do stanu w którym lepkość jest
większa od 10
12
N·s·m
-2
.
10
0
10
12
10
3
10
6
10
9
stan plastyczny
stan szklisty lub stały
temperatura
h
temperatura
krzepnięcia
przejście w stan
szklisty
przejście w stan
szklisty
przejście w stan
stały
przejście w stan
stały
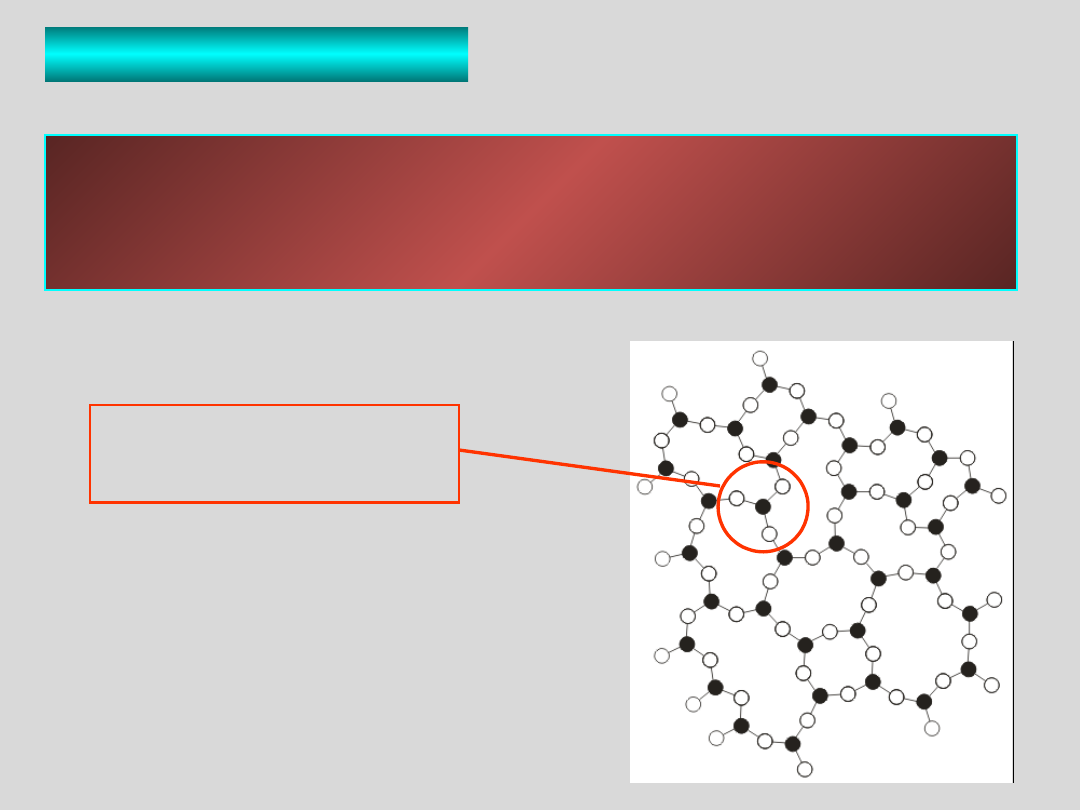
STRUKTURA SZKŁA
Struktura szkła przypomina strukturę cieczy, w której
„wyłączono” ruchy translacyjne (postępowe) składników.
Rezultatem jest utworzenie praktycznie nieuporządkowanej
struktury elementarnych składników szkła.
elementarny
składnik struktury
STAN STAŁY
CIAŁA KRYSTALICZNE
CIAŁA AMORFICZNE
RÓŻNE STRUKTURY
KRYSTALICZNE
SZKŁA
STAN
AMORFICZNY
STAN AMORFICZNY to stan materii cechujący się
brakiem uporządkowania (lub występowaniem
uporządkowania blisko zasięgowego), w którym
cząsteczki (atomy) zachowują swobodę ruchów
drgających, przy praktycznym braku swobody
ruchów postępowych.
STAN AMORFICZNY to stan materii cechujący się
brakiem uporządkowania (lub występowaniem
uporządkowania blisko zasięgowego), w którym
cząsteczki (atomy) zachowują swobodę ruchów
drgających, przy praktycznym braku swobody
ruchów postępowych.
Funkcja dystrybucji w tym stanie jest
izotropowa i analogiczna do funkcji
dystrybucji cieczy lub gazów
Stan krystaliczny
STAN KRYSTALICZNY
W STANIE KRYSTALICZNYM atomy, jony lub cząsteczki
są ułożone w periodyczny, trójwymiarowy wzór tzw.
KRYSZTAŁ
STRUKTURA KRYSZTAŁÓW
....
może być rozpatrywana z punktu
widzenia:
rozmieszczenia przestrzennego elementów
tworzących kryształ
rodzaju elementów tworzących
kryształ
rodzaju wiązań chemicznych
pomiędzy elementami tworzącymi
kryształ
podejście
geometryczne
podejście
geometryczne
podejście fizyczne
(chemiczne)
podejście fizyczne
(chemiczne)
SIEĆ PRZESTRZENNA
KRYSZTAŁÓW
Do opisu struktury geometrycznej kryształów
stosujemy pojęcie SIECI PRZESTRZENNEJ
Do opisu struktury geometrycznej kryształów
stosujemy pojęcie SIECI PRZESTRZENNEJ
SIEĆ PRZESTRZENNA
to zbiór punktów zwanych
WĘZŁAMI SIECI,
podających położenie środków masy
atomów, cząsteczek lub jonów tworzących kryształ
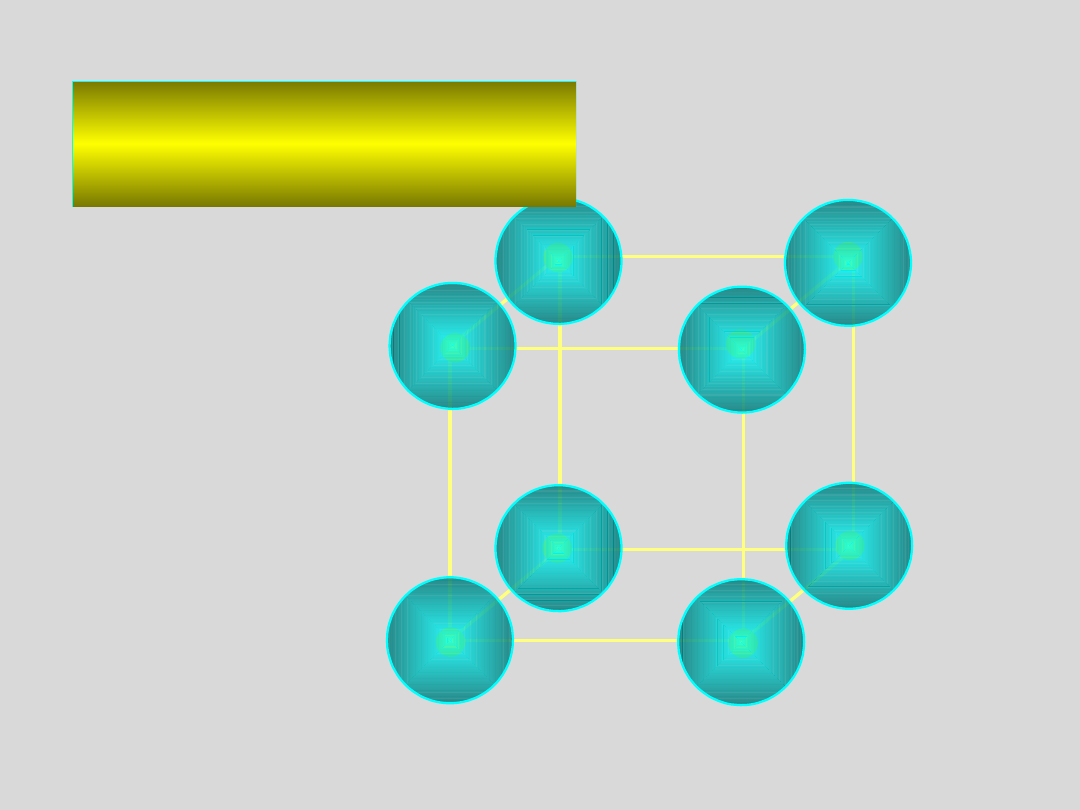
SIEĆ
PRZESTRZENNA
SYMETRIA KRYSZTAŁÓW
SYMETRIA KRYSZTAŁÓW
Opisem symetrii kryształów zajmuje się
KRYSTALOGRAFIA GEOMETRYCZNA
Pb
5
[Cl(VO
4
)
3
]
Pb
5
[Cl(VO
4
)
3
]
SiO
2
SiO
2
CaCO
3
CaCO
3
parametry sieciowe
parametry sieciowe
KOMÓRKA
ELEMENTARNA...
KOMÓRKA
ELEMENTARNA...
...to równoległościan stanowiący podstawowy, powtarzający się
okresowo w przestrzeni, element sieci przestrzennej
...to równoległościan stanowiący podstawowy, powtarzający się
okresowo w przestrzeni, element sieci przestrzennej
a
b
c
g
b
a
a, b, c
a, b, g
a, b, c
a, b, g
KOMÓRKA ELEMENTARNA
UKŁADY KRYSTALOGRAFICZNE
Szczegółowa analiza wykazała, że strukturę geometryczną
wszystkich kryształów, można odtworzyć przyjmując, że istnieją
4 typy KOMÓREK ELEMENTARNYCH, rozdzielone pomiędzy 7
UKŁADÓW KRYSTALOGRAFICZNYCH, różniących się relacjami
pomiędzy a, b, c i a, b, g
Szczegółowa analiza wykazała, że strukturę geometryczną
wszystkich kryształów, można odtworzyć przyjmując, że istnieją
4 typy KOMÓREK ELEMENTARNYCH, rozdzielone pomiędzy
7
UKŁADÓW KRYSTALOGRAFICZNYCH
, różniących się relacjami
pomiędzy a, b, c i a, b, g
Siedem układów
krystalograficznych:
1. • trójskośny T
2. • jednoskośny M
3. • rombowy lub ortogonalny O
4. • romboedryczny lub
trygonalny R
5. • tetragonalny lub kwadratowy
Q
6. • heksagonalny H
7. • kubiczny lub regularny K
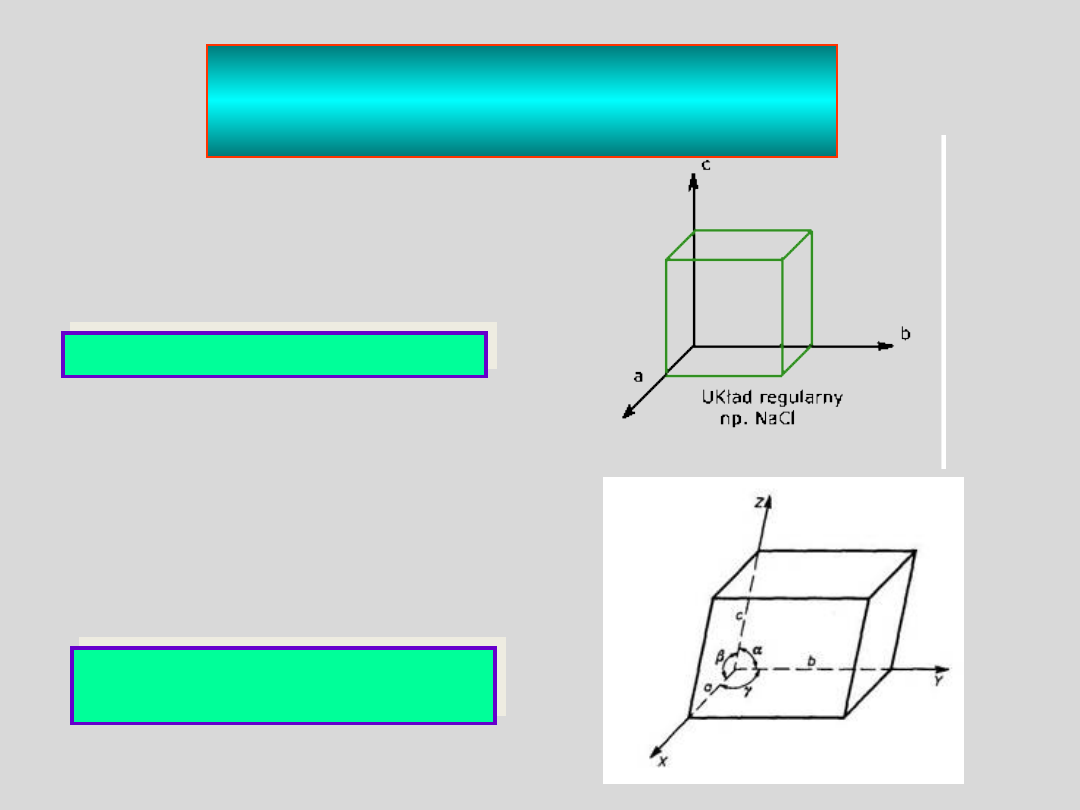
a = b = c a = b = g = 90°
a = b = c a = b = g = 90°
UKŁAD REGULARNY
a <> b <> c a = b = g =
90°
a <> b <> c a = b = g =
90°
UKŁAD ROMBOWY
...przykładowo:
UKŁADY
KRYSTALOGRAFICZNE
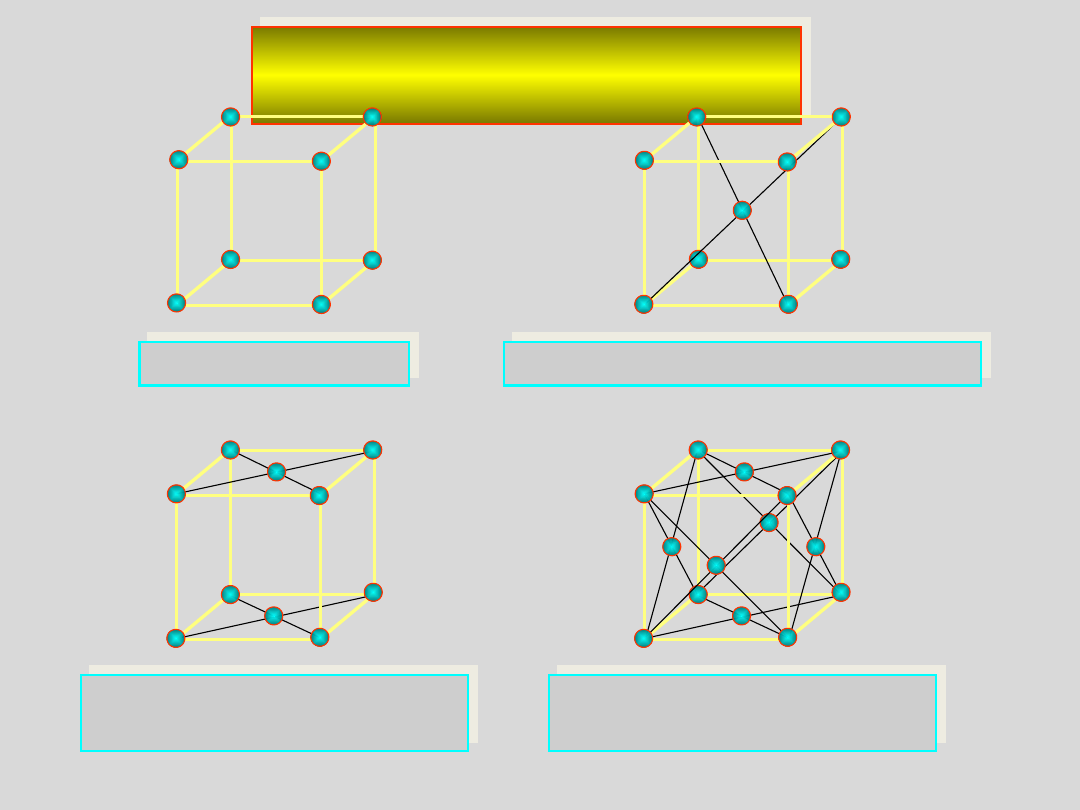
Typy komórek
elementarnych
Typy komórek
elementarnych
prymitywna P
prymitywna
P
przestrzennie centrowana I
przestrzennie centrowana
I
płasko centrowana na
dwóch ścianach C
płasko centrowana na
dwóch ścianach
C
płasko centrowana na
wszystkich ścianach F
płasko centrowana na
wszystkich ścianach
F
Wiązania w sieci
krystalicznej
W zależności od typu wiązań pomiędzy elementami
tworzącymi kryształ wyróżniamy:
atomy połączone wiązaniem
metalicznym
metaliczny
jony połączone wiązaniem
jonowym
jonowy
atomy połączone wiązaniami s
lub p
kowalencyjny
cząsteczki lub atomy
oddziaływujące siłami Van der
Waalsa
molekularny
elementy struktury i
wiązanie
typ kryształu
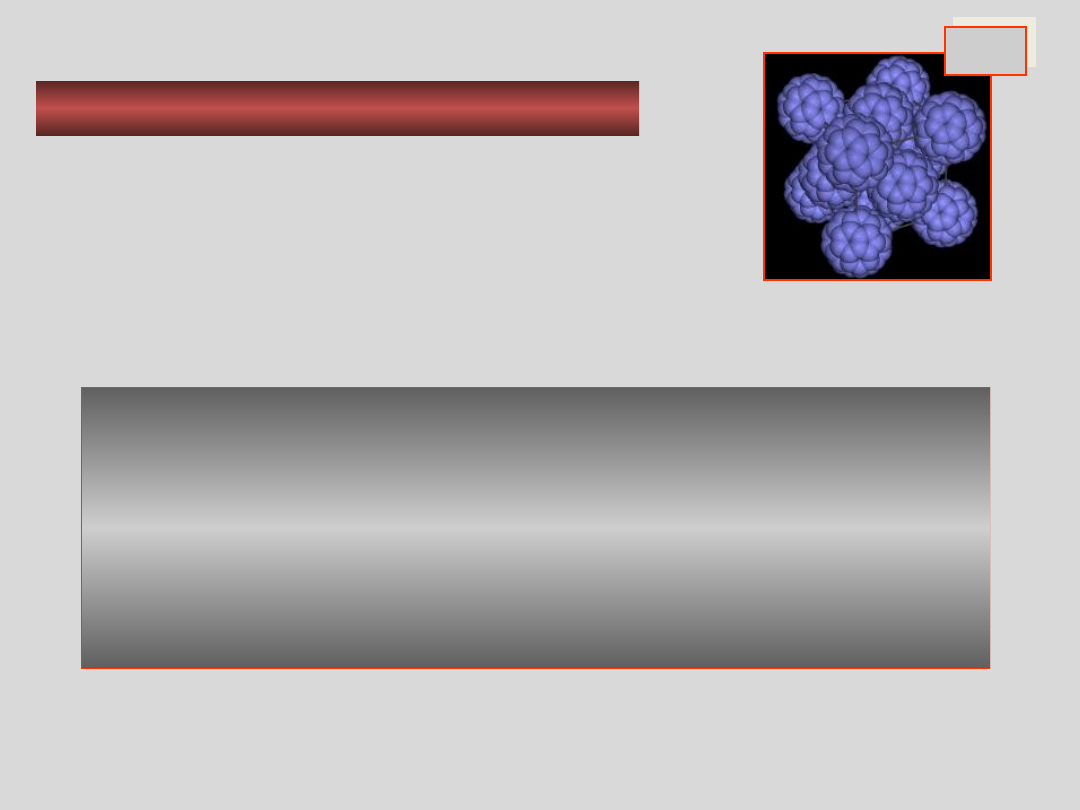
KRYSZTAŁY MOLEKULARNE
C
60
C
60
właściwości:
•mała wytrzymałość mechaniczna i mała
twardość
•niska temperatura topnienia
•duży współczynnik rozszerzalności cieplnej
•izolatory
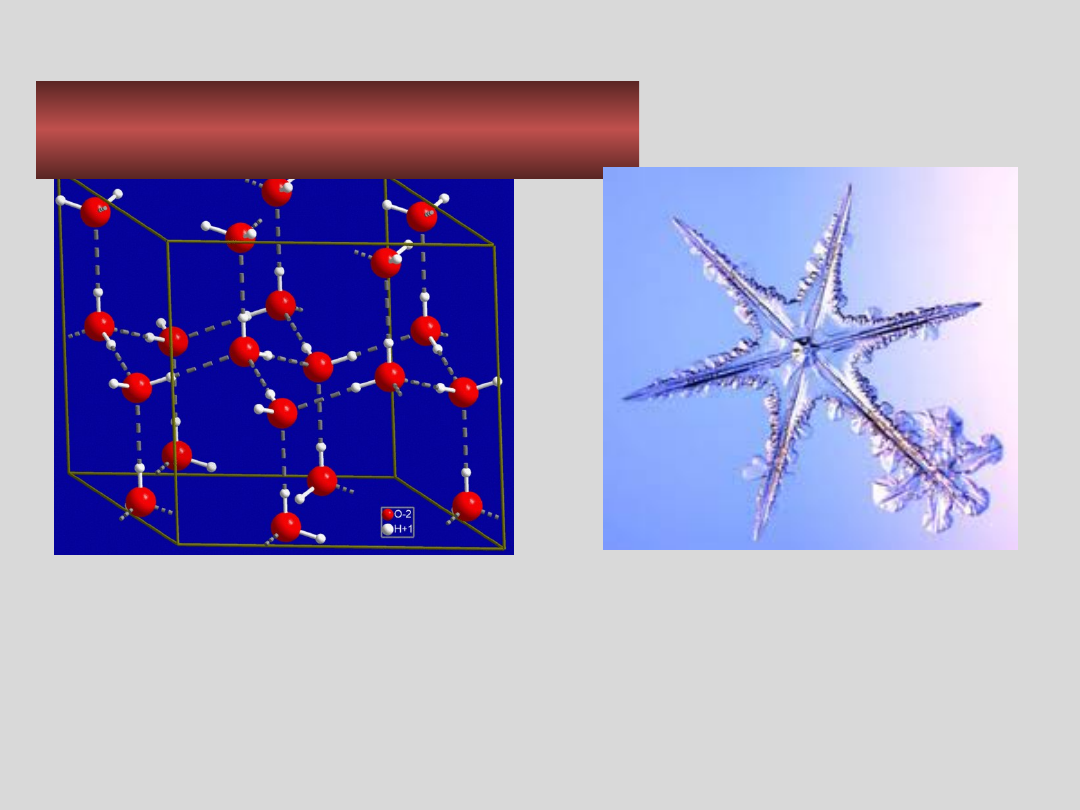
KRYSZTAŁY MOLEKULARNE –
przykłady
Heksagonalna sieć krystaliczna lodu
Kryształ lodu
T
top
= 0 °C
KRYSZTAŁY MOLEKULARNE –
przykłady
Regularna sieć krystaliczna stałego CO
2
Kostki suchego lodu
T
sub
KRYSZTAŁY MOLEKULARNE –
przykłady
Sieć krystaliczna stałego jodu
(struktura ortorombowa)
T
sub
= 113,7 °C
Kryształy jodu
KRYSZTAŁY
KOWALENCYJNE
właściwości
:
•duża wytrzymałość mechaniczna i duża twardość
•wysoka temperatura topnienia
•mały współczynnik rozszerzalności cieplnej
•izolatory, po stopieniu nie przewodzą prądu
elektrycznego
diament
diament
KRYSZTAŁY JONOWE
NaCl
NaCl
właściwości:
•duża wytrzymałość mechaniczna i duża
twardość
•wysoka temperatura topnienia
•mały współczynnik rozszerzalności cieplnej
•izolatory,
po stopieniu przewodzą prąd
elektryczny
KRYSZTAŁY
METALICZNE
właściwości:
•różna wytrzymałość mechaniczna i
twardość, zwykle dobra ciągliwość
• raczej wysokie temperatury topnienia
•mały współczynnik rozszerzalności
cieplnej
•przewodniki prądu elektrycznego
•nieprzezroczyste o charakterystycznym
połysku metalicznym
bizmut
bizmut
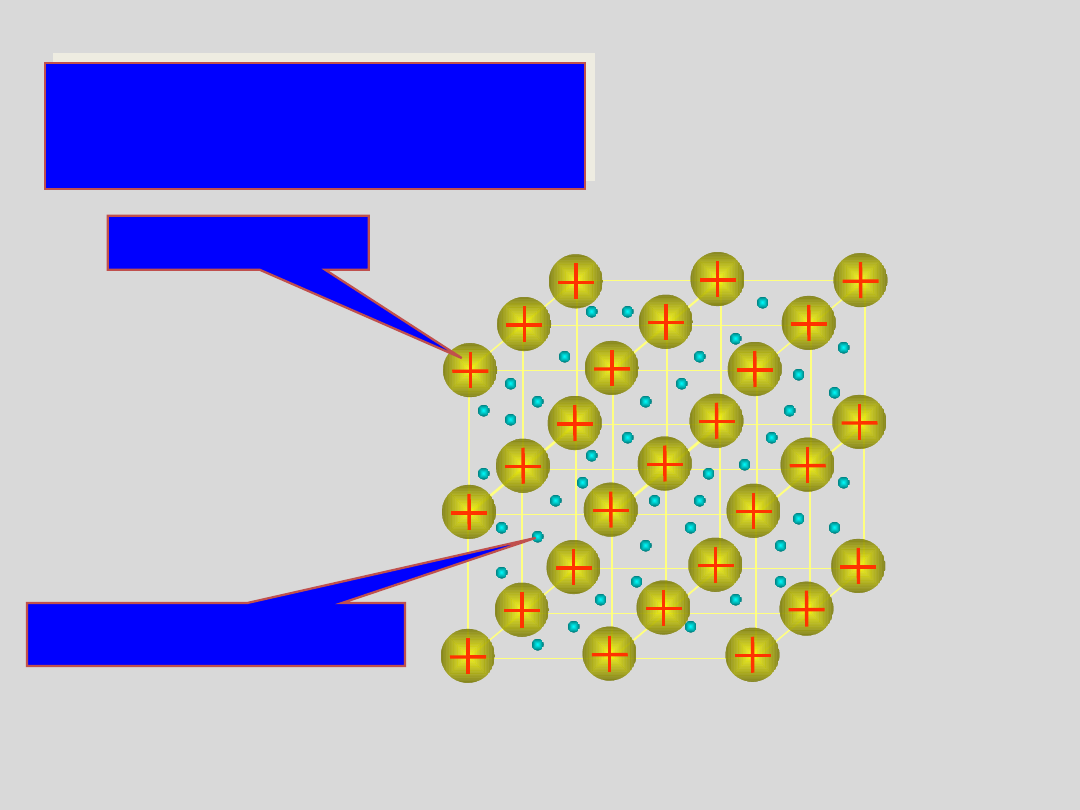
WIĄZANIE
METALICZNE
WIĄZANIE
METALICZNE
jony dodatnie
gaz elektronowy
DEFEKTY W KRYSZTAŁACH
Żaden kryształ w temperaturze T > 0 K
NIE MOŻE
mieć idealnej struktury dlatego w sieci krystalicznej
ZAWSZE
istnieją
DEFEKTY
Defekty w sieci krystalicznej możemy
podzielić na:
punktowe
(zerowymiarowe)
liniowe
(jednowymiarowe)
płaskie (dwuwymiarowe)
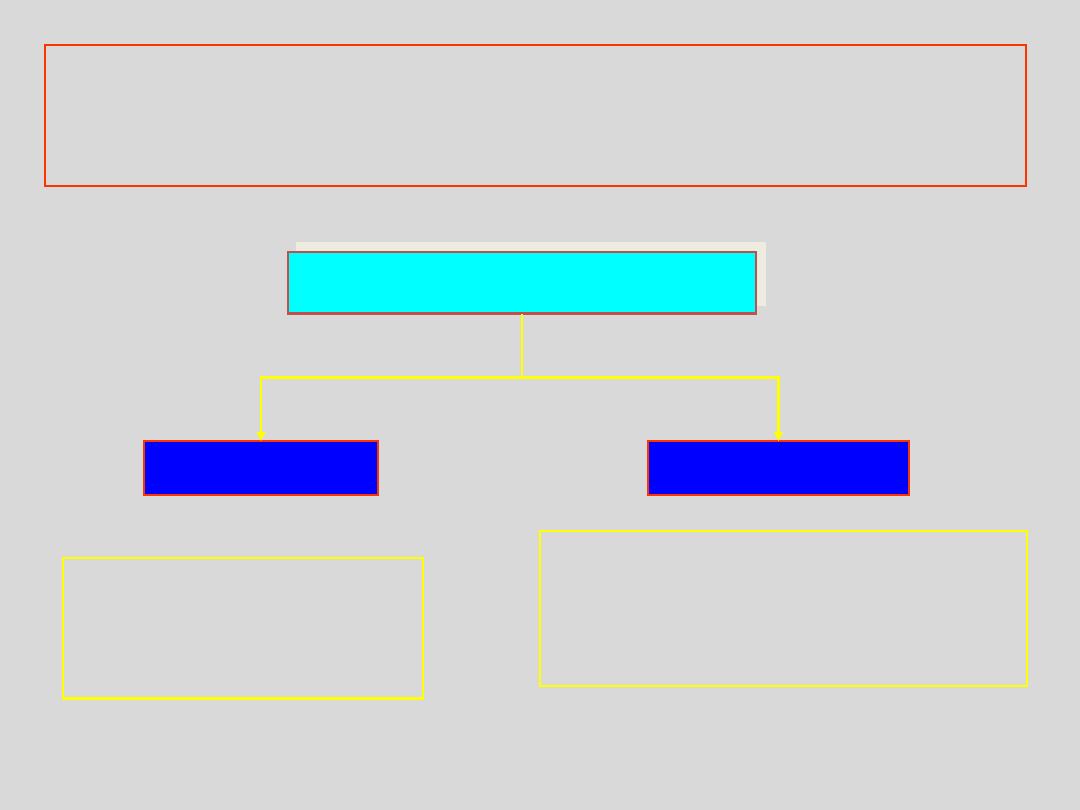
DEFEKTY PUNKTOWE
DEFEKTY PUNKTOWE
Zaburzenia regularności sieci krystalicznej o
rozmiarach rzędu rozmiarów elementów tworzących
kryształ (jonów, atomów lub cząsteczek) to....
atomowe
elektronowe
dotyczą
całego
atomu, jonu lub
cząsteczki
dotyczą wyłącznie sytuacji
związanych z zachowaniem
się
elektronu
w
sieci
krystalicznej
ATOMOWE DEFEKTY PUNKTOWE
defekt Schottky’ego
ATOMOWE DEFEKTY PUNKTOWE
defekt Schottky’ego
wakancja
kationowa
wakancja
anionowa
sieć idealna
kation
anion
ATOMOWE DEFEKTY PUNKTOWE
defekt Frenkla
ATOMOWE DEFEKTY PUNKTOWE
defekt Frenkla
sieć idealna
kation
anion
kation
międzywęzłowy
wakancja
kationowa
O
Defekty punktowe i stechiometria związków
chemicznych
Defekty punktowe i stechiometria związków
chemicznych
O
2-
Ni
2+
Ni
2+
Ni
2+
O
2-
Ni
2+
O
2-
O
2-
O
2-
Ni
2+
O
2-
Ni
2+
Ni
2+
Ni
2+
O
2-
Ni
2+
O
2-
O
2-
O
2-
Ni
2+
O
2-
Ni
2+
Ni
2+
Ni
2+
O
2-
Ni
2+
O
2-
O
2-
O
2-
Ni
2+
O
2-
Ni
2+
Ni
2+
Ni
2+
O
2-
Ni
2+
O
2-
O
2-
O
2-
Ni
2+
O
O
2-
Ni
3+
Ni
3+
NiO
NiO
Ni
3+
O
2-
Ni
2+
Ni
2+
O
2-
O
2-
O
2-
O
2-
Ni
2+
O
2-
Ni
2+
Ni
2+
Ni
2+
O
2-
Ni
2+
O
2-
O
2-
O
2-
Ni
2+
O
2-
Ni
3+
Ni
3+
O
2-
Ni
2+
Ni
2+
O
2-
O
2-
O
2-
O
2-
Ni
2+
O
2-
Ni
2+
Ni
2+
Ni
2+
O
2-
Ni
2+
O
2-
O
2-
O
2-
Ni
2+
O
2-
Ni
3+
Gdy w jakiejkolwiek reakcji powstają kryształy tlenku
niklu NiO liczba jonów tlenkowych O
2-
jest zawsze
większa od liczby jonów niklu. Zatem praktycznie
wzór tlenku niklu ma postać:
2
1
1
x
)
III
(
x
)
II
(
x
O
Ni
Ni
wartość x (lub y) zależy od sposobu otrzymywania
tlenku niklu (rodzaju reagentów, temperatury,
atmosfery
otaczająca
reagenty
i
produkty,
szybkości prowadzenia reakcji)
y
NiO
1
ZWIĄZKI NIESTECHIOMETRYCZNE - BERTOLIDY
ZWIĄZKI NIESTECHIOMETRYCZNE -
BERTOLIDY
Związki chemiczne, których skład zależy od
sposobu i warunków otrzymywania noszą nazwę
związków niestechiometrycznych lub bertolidów.
Związki chemiczne, których skład zależy od
sposobu i warunków otrzymywania noszą nazwę
związków niestechiometrycznych
lub
bertolidów
.
Istnienie
bertolidów
uwarunkowane
jest
obecnością defektów w sieci krystalicznej, dlatego
związki niestechiometryczne występują wyłącznie
w grupie ciał stałych.
Istnienie
bertolidów
uwarunkowane
jest
obecnością defektów w sieci krystalicznej, dlatego
związki niestechiometryczne występują wyłącznie
w grupie ciał stałych.
powszechnie występującymi bertolidami są tlenki
i siarczki pierwiastków bloków d i f
powszechnie występującymi bertolidami są tlenki
i siarczki pierwiastków bloków d i f