Układy wieloskładnikowe jedno i
wielofazowe

Roztwory gazowe (gaz w gazie):

ciśnienie cząstkowe,

wyrażanie składu,

prawo Daltona

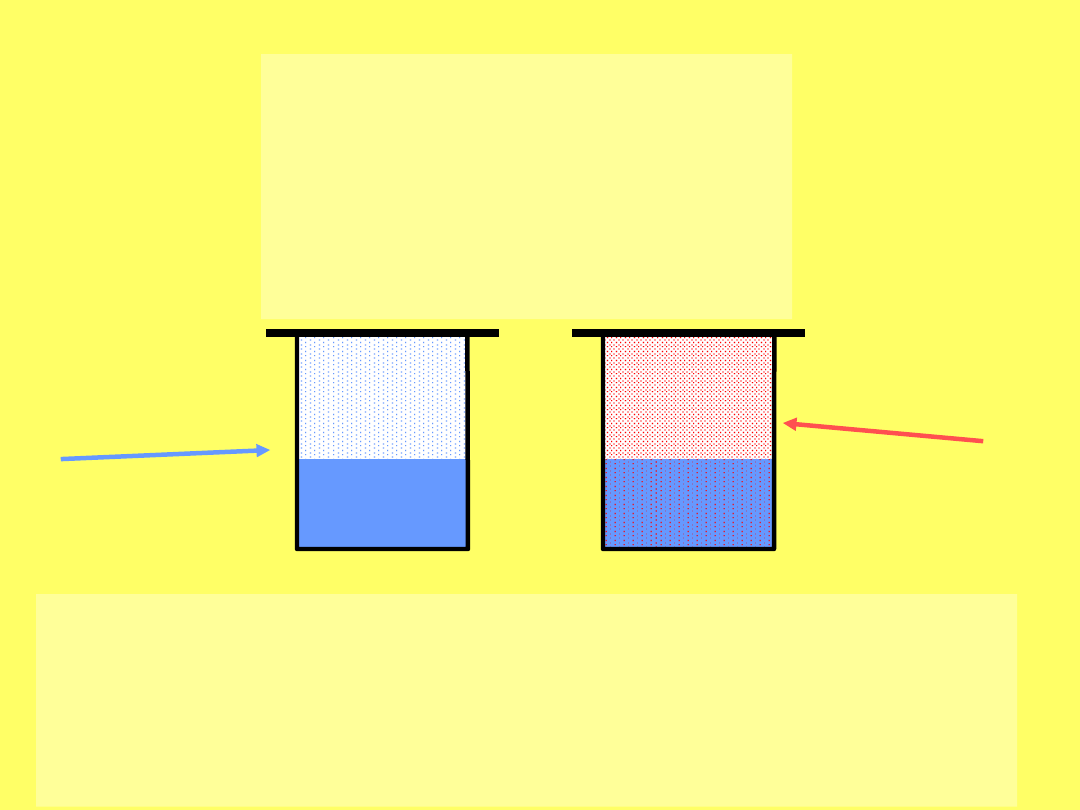
Roztwory gazów w
cieczach

Prawo Henry’ego:

m = k * p

W stałej temperaturze masa (m) gazu
rozpuszczonego w danej objętości cieczy jest
wprost proporcjonalna do jego ciśnienia p
nad roztworem.

Układ
jednoskła
d-nikowy

Układ
dwuskład
ni-kowy

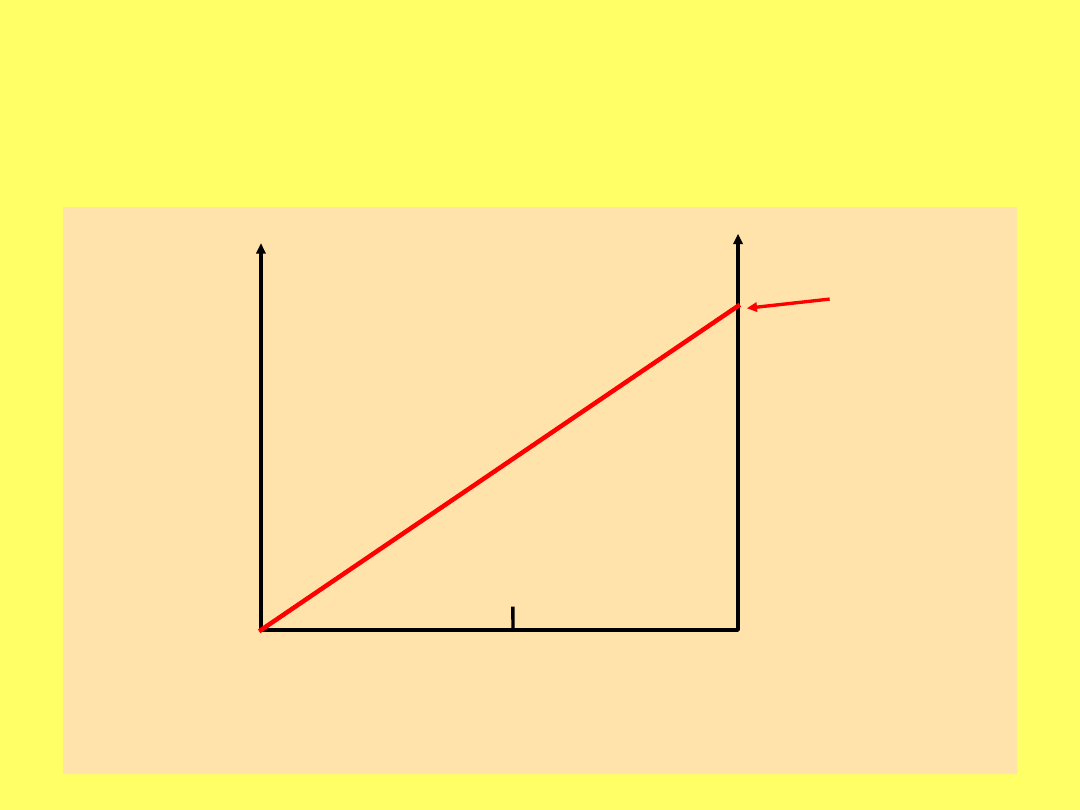
Dla roztworów rozcieńczonych:

X = k’ * p

H – stała Henry’ego

H

p

X

i



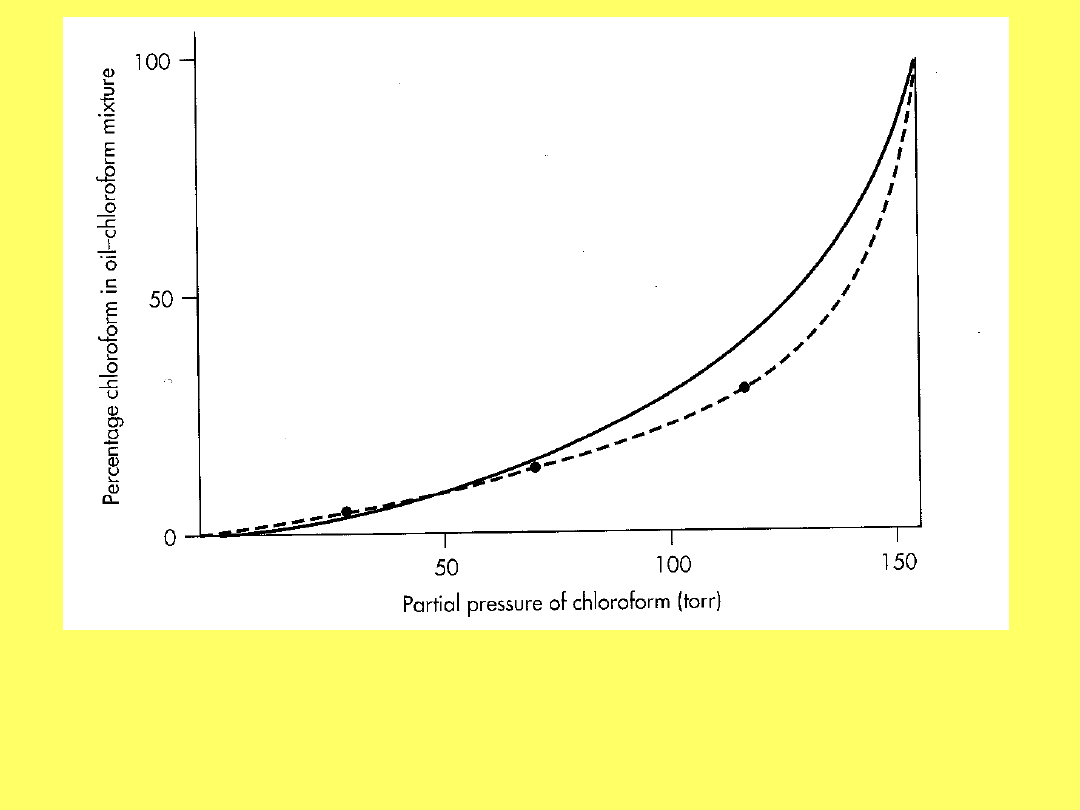
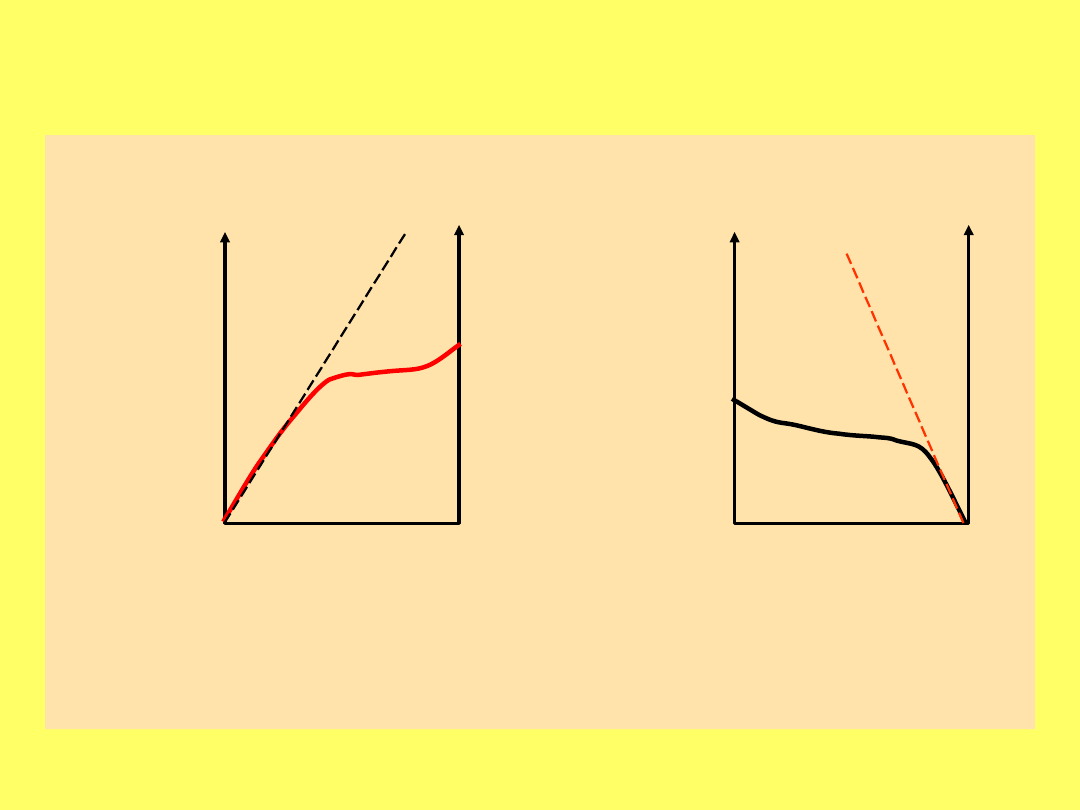
Krzywa kreskowana prezentuje doświadczalnie

wyznaczoną zależność stężenia procentowego

chloroformu w oleju

w zależności od ciśnienia cząstkowego

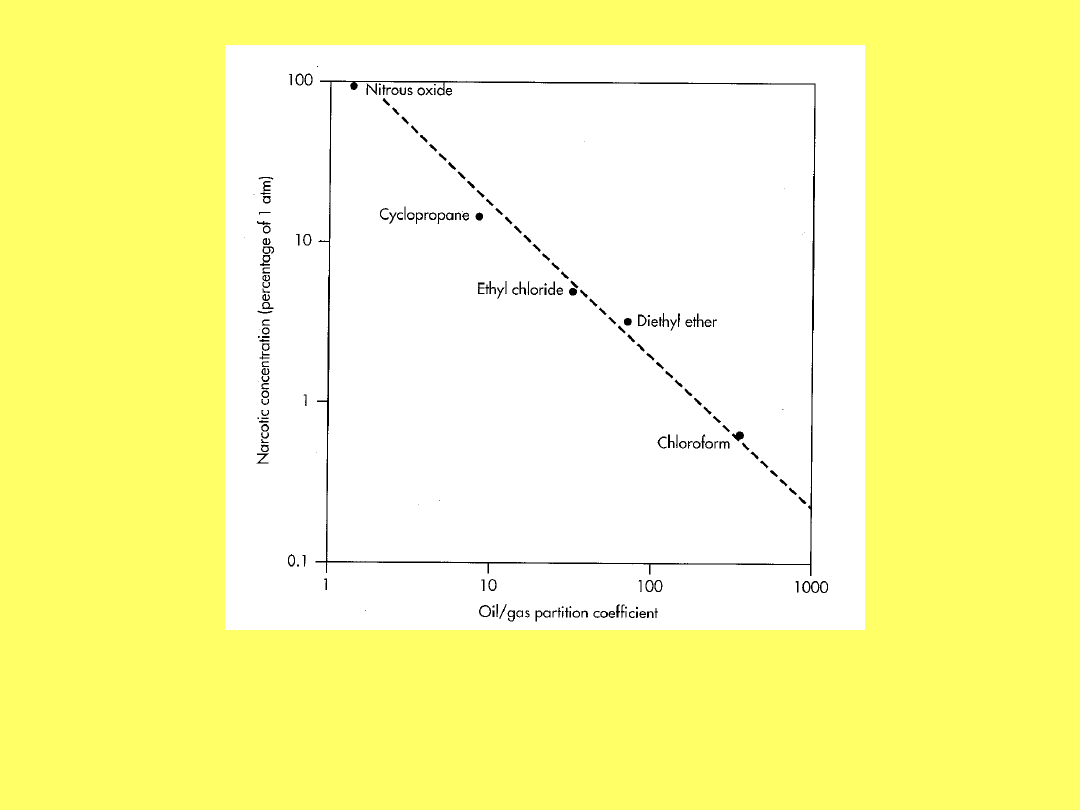
Zależność wartości narkotycznego stężenia

anestetyku od jego rozpuszczalności w alkoholu

olejowym (wyrażonej jako współczynnik podziału

olej/gaz)

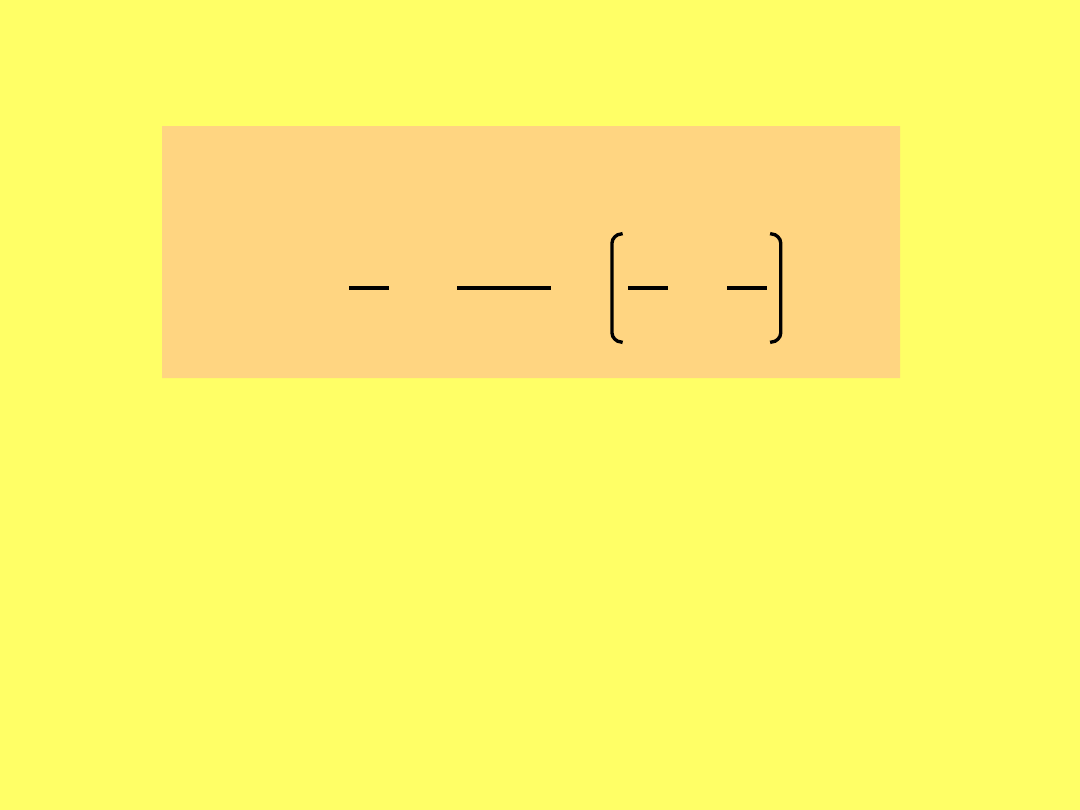
ln =
-

X

1

- H

o

rozp

1

1

X

2

R

T

1

T

2

Wpływ
temperatury:

X

CS2

0

1,0 X

ACETON

1

0

p

X

CS2

0

1,0 X

Aceton

1

0

T =
const

Roztwory idealne rozcieńczone

p

T =
const

Roztwory cieczy w cieczach

Roztwory cieczy mieszających się
nieograniczenie

Układ złożony z roztworu dwóch cieczy i pary
znajdującej się w równowadze nad tym
roztworem ma dwa stopnie swobody:

s = 2 – 2 + 2
= 2

Prężność pary nad układem dwóch cieczy
mieszających się nieograniczenie:

p

= p

A

+ p

B

Układ
dwuskład
ni-kowy

A

+B

A

p

o

A

p

o

B

B

Układ
jednoskła
dni-kowy

(A)

Układ
jednoskła
dni-kowy

(B)

Układ
dwuskład
ni-kowy

A

+ B

p

A

= p

o

A

*

X

A

p

B

= p

o

B

*

X

B

Prawo
Raoulta:

RAOULT Francois-Marie

Ur. 10.05.1830.

Zmarł 01.04.1901

X

BENZEN

0 0,5

1,0

X

TOLUEN

1 0,5

0

p T = const
p

o

BENZEN

Prężność pary nad roztworem
dwuskładnikowym (benzen + toluen)

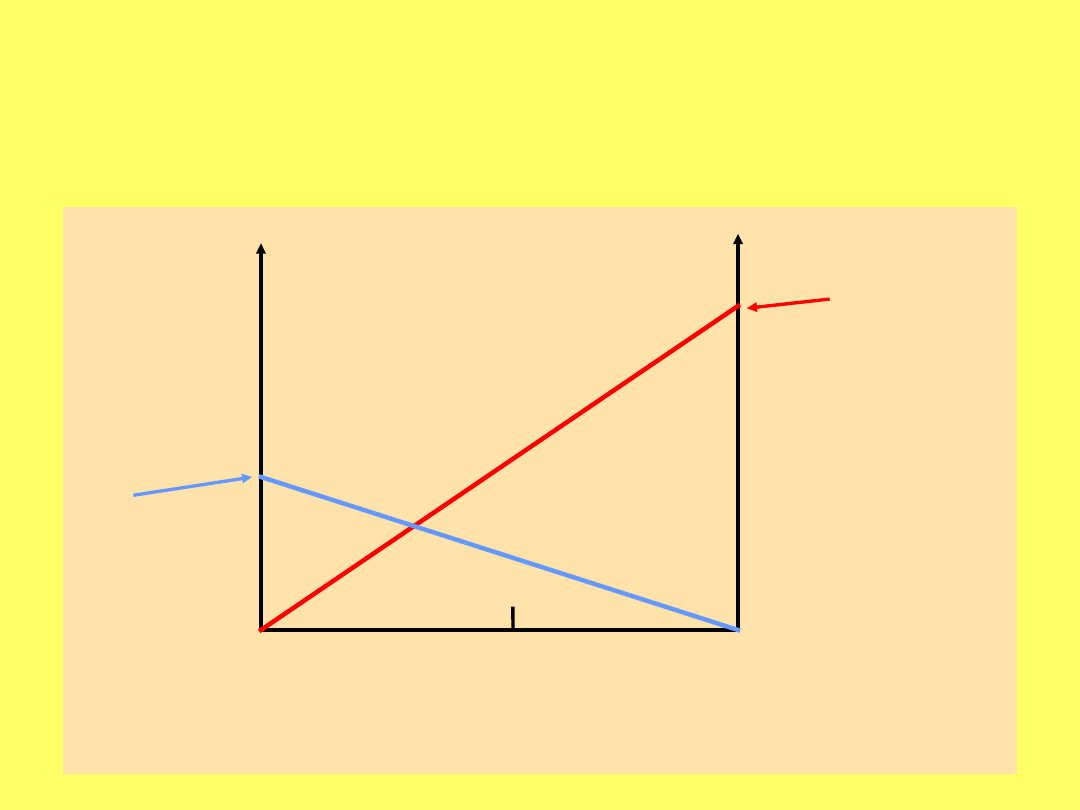
X

BENZEN

0 0,5

1,0

X

TOLUEN

1 0,5

0

p T = const
p

o

BENZEN

Prężność pary nad roztworem
dwuskładnikowym (benzen + toluen)

p

o

TOLUEN

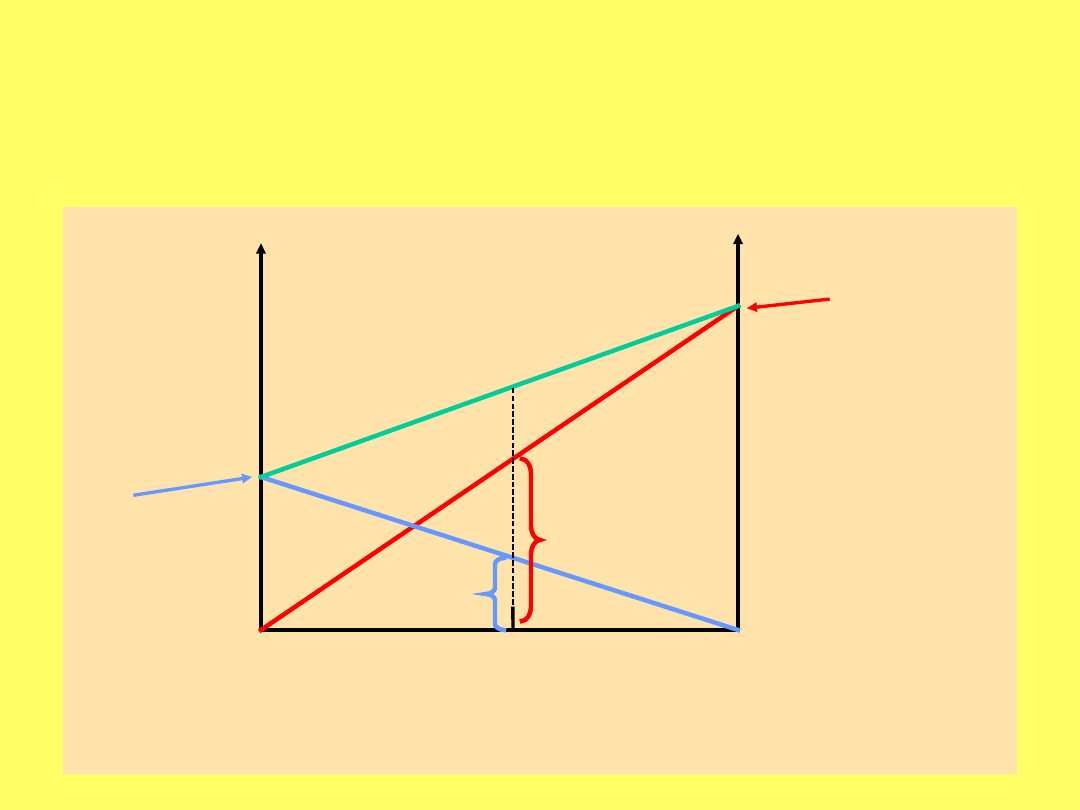
X

BENZEN

0 0,5

1,0

X

TOLUEN

1 0,5

0

p T = const
p

o

BENZEN

Prężność pary nad roztworem
dwuskładnikowym (benzen + toluen)

p

o

TOLUEN

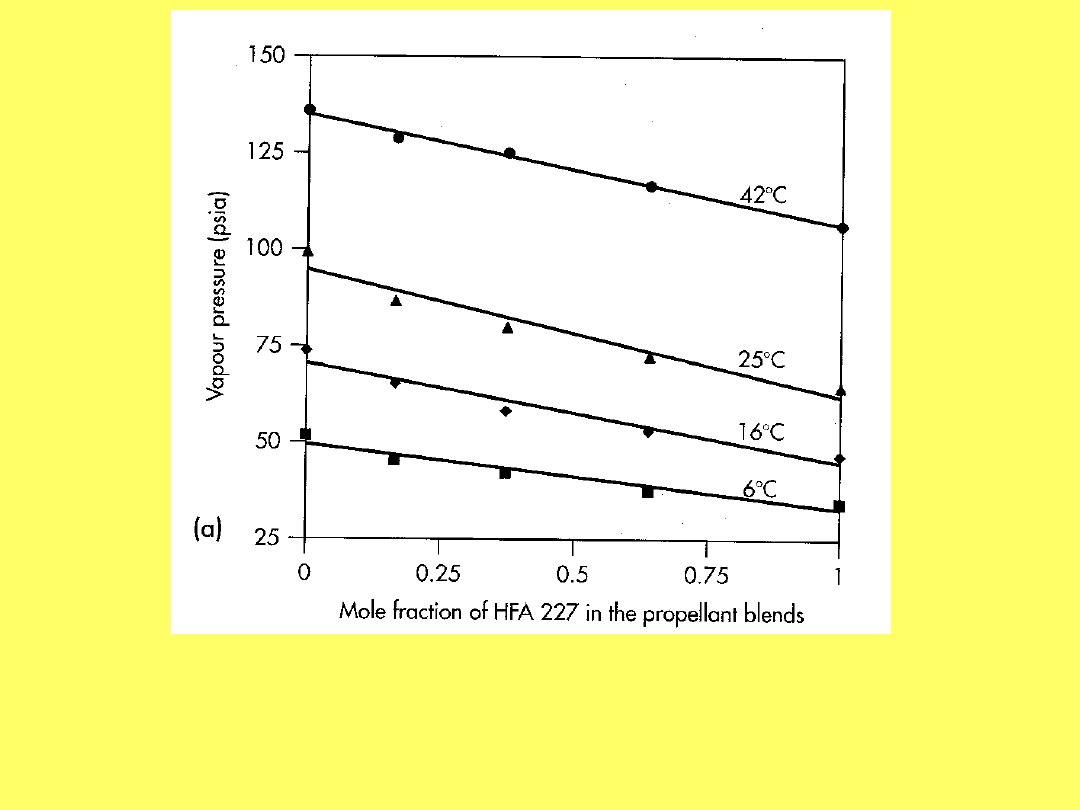
Zależność ciśnienia mieszaniny HFA 134a i HFA 227

od ułamka molowego jednego ze składników w

roztworze w różnych temperaturach

X

A

0

1,0 X

B

1

0

p T =
const

X

A

0

1,0 X

B

1

0

p T =
const

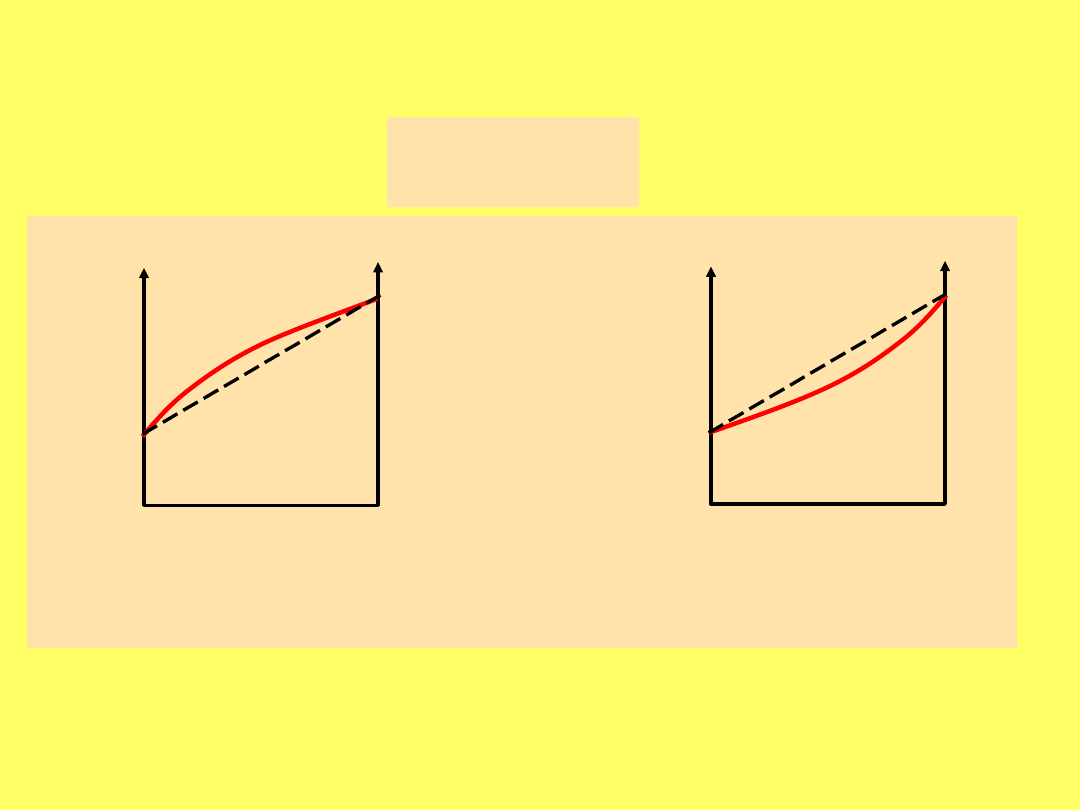
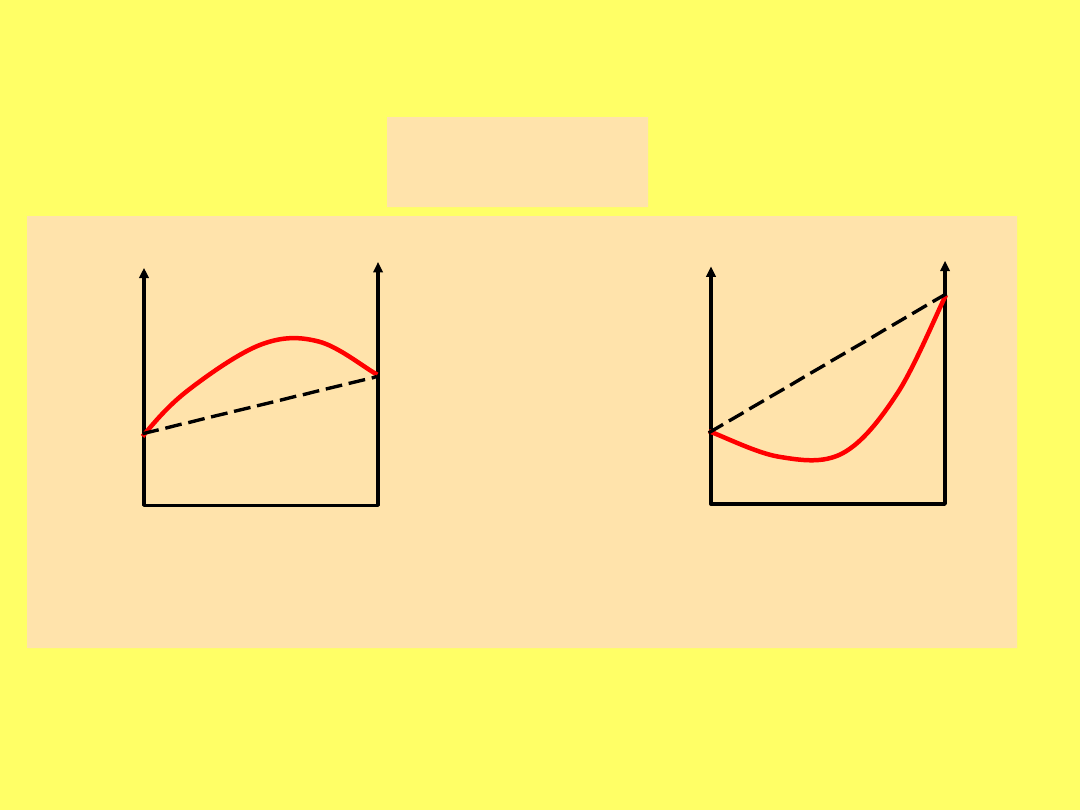
Roztwory wykazujące odchylenia od
prawa Raoulta:

ZEOTROP
Y

X

A

0

1,0 X

B

1

0

p T =
const

X

A

0

1,0 X

B

1

0

p T =
const

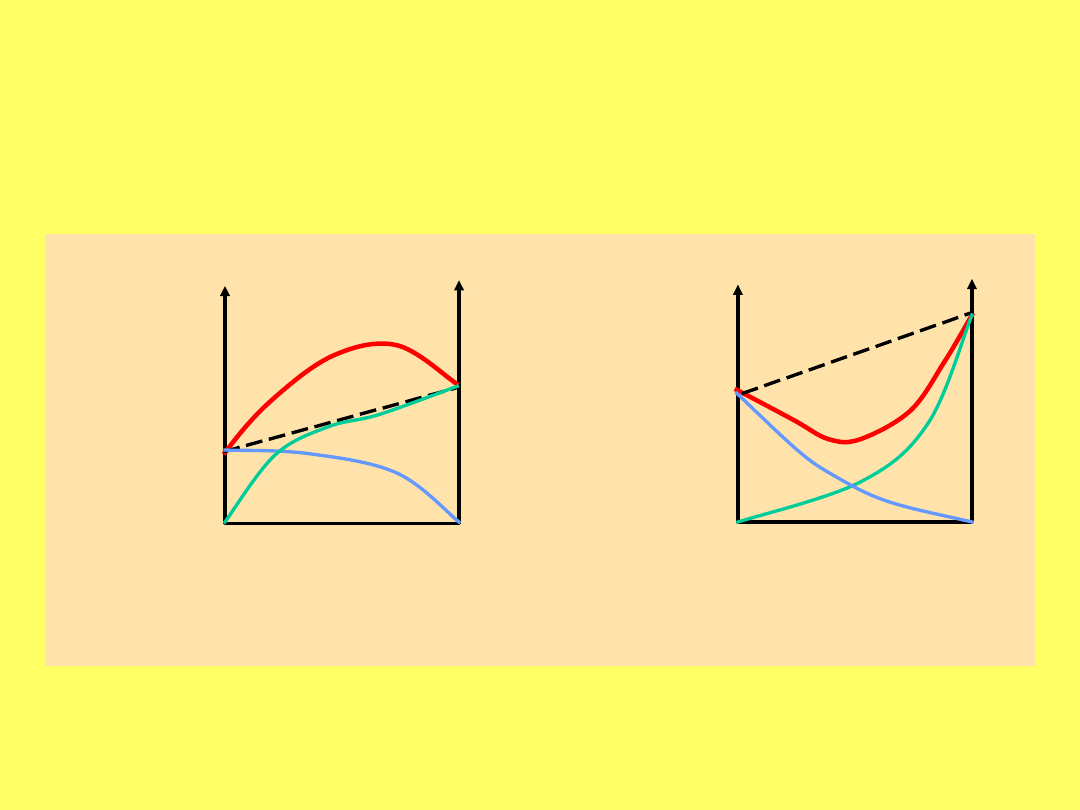
Roztwory wykazujące odchylenia od
prawa Raoulta:

AZEOTROPY

X

CS2

0

1,0 X

ACETON

1

0

p T =
const

X

ACETON

0

1,0 X

CHLOROFORM

1

0

p T =
const

Przykłady układów wykazujących
odchylenia od prawa Raoulta:

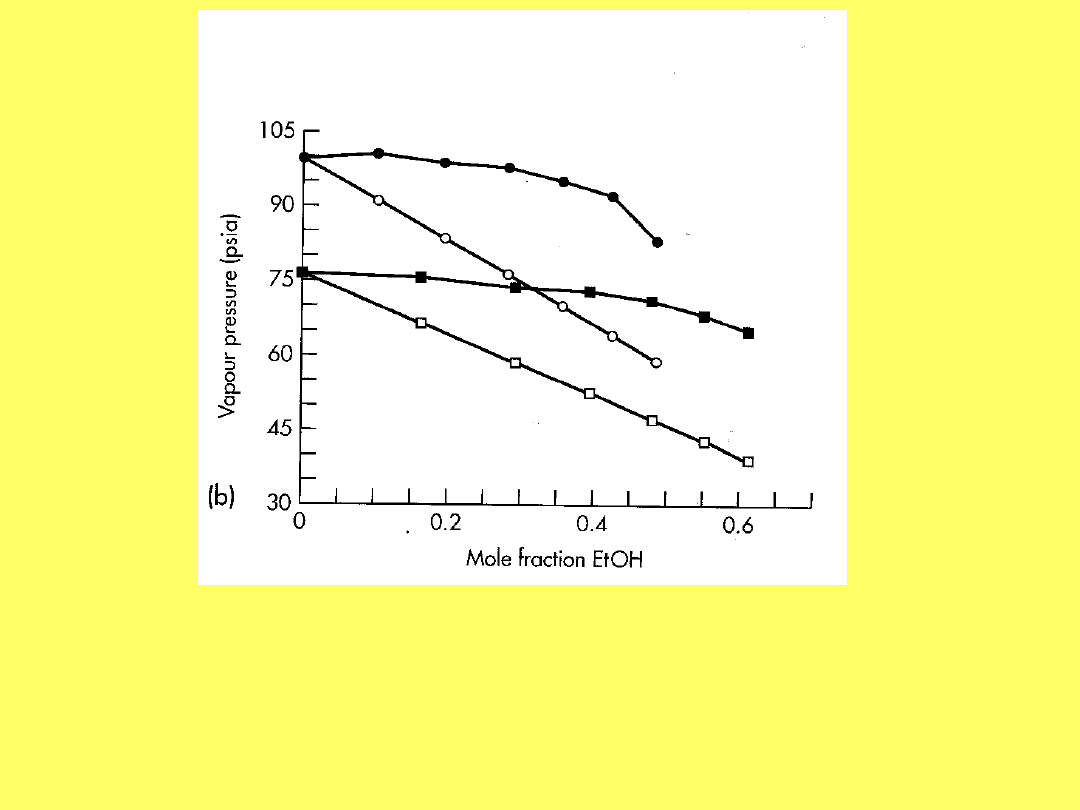
Zależność ciśnienia pary HFA 134a (koła) i HFA 227

(kwadraty) w funkcji ułamka molowego etanolu, temp.

21,5

o

C. Nie wypełnione punkty reprezentują układy

idealne

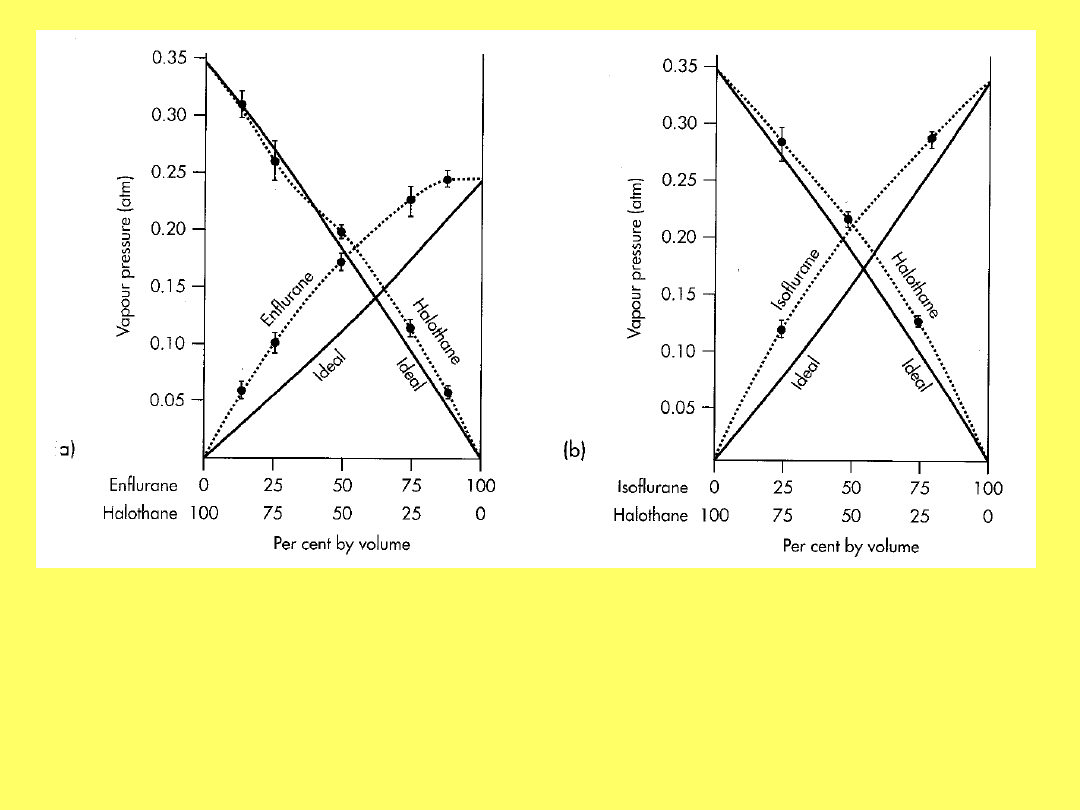
Eksperymentalne (linia kropkowana) i obliczone na

podst. pr. Raoulta (linia ciągła) zależności prężności

pary wybranych anestetyków od ich stężenia

procentowego (v/v).

Skład pary nad roztworem dwóch cieczy

mieszających się nieograniczenie

p

A

= X’

A

* p, X’

A

-

ułamek molowy składnika A w

fazie pary

p

B

= X’

B

* p, X’

B

-

ułamek molowy składnika B w

fazie pary

X’

A

* p = X

A

* p

o

A

X’

B

* p = X

B

* p

o

B

Po podzieleniu stronami:

X’

A

/ X’

B

= X

A

* p

o

A

/ X

B

*

p

o

B

lub (

X’

A

* X

B

)

/ (X’

B

*

X

A

) = * p

o

A

/

* p

o

B

To oznacza, że zawartość składnika bardziej
lotnego jest większa w fazie pary niż w fazie
cieczy

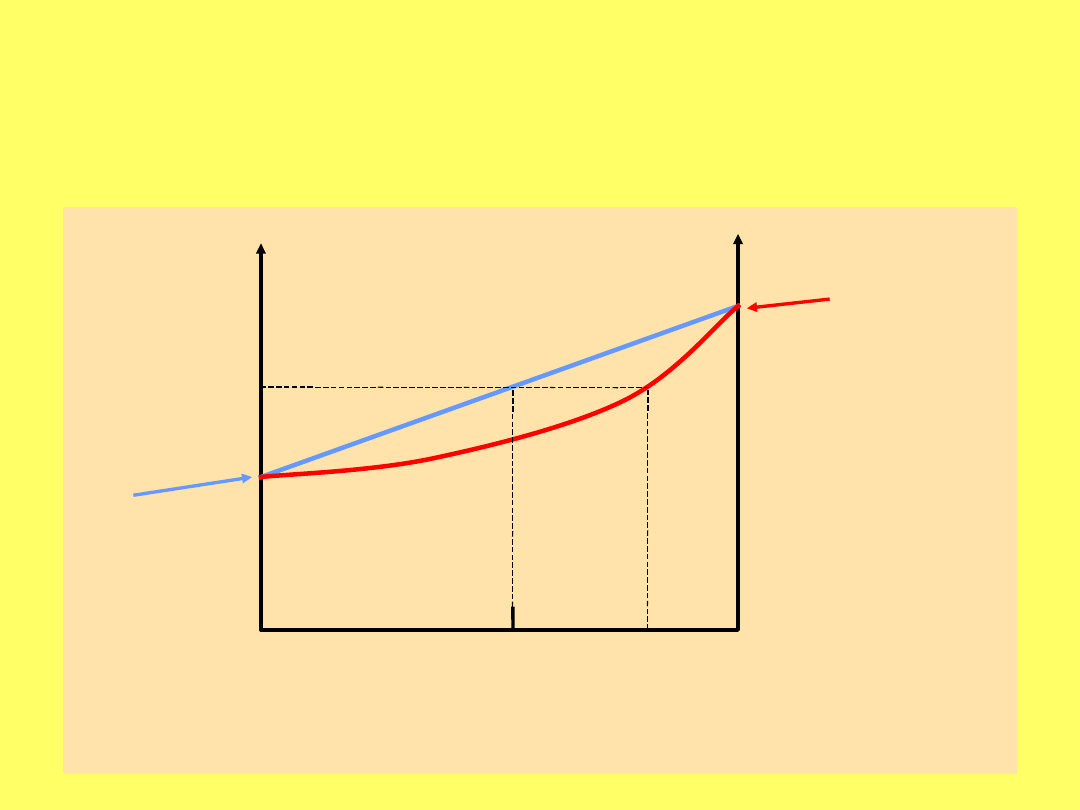
X

BENZEN

0 0,5

1,0

X

TOLUEN

1 0,5

0

p T = const
p

o

BENZEN

Zależność prężności pary od składu cieczy
(

ciecz

) i od składu pary (

para

)

p

o

TOLUEN

par

a

ciec

z

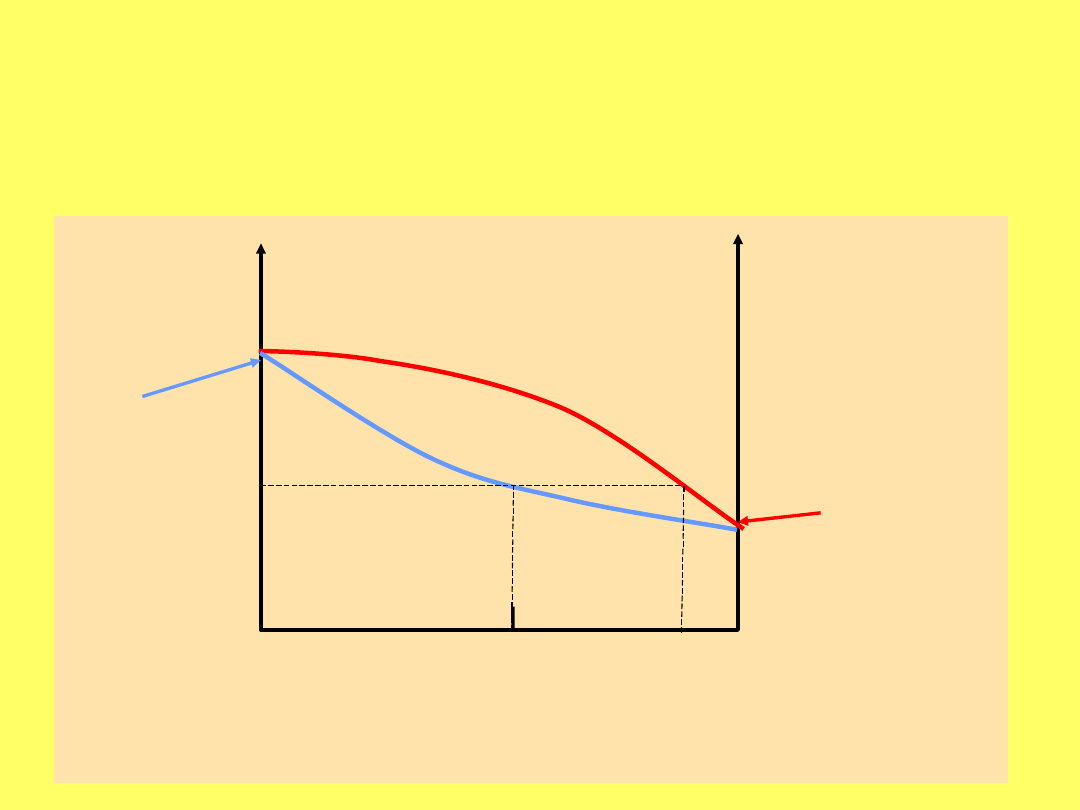
X

BENZEN

0 0,5

1,0

X

TOLUEN

1 0,5

0

T p =
const

Zależność temperatury wrzenia od składu
cieczy (

ciecz

) i od składu pary (

para

)

T

TOLUEN

para

ciecz

T

BENZE

N

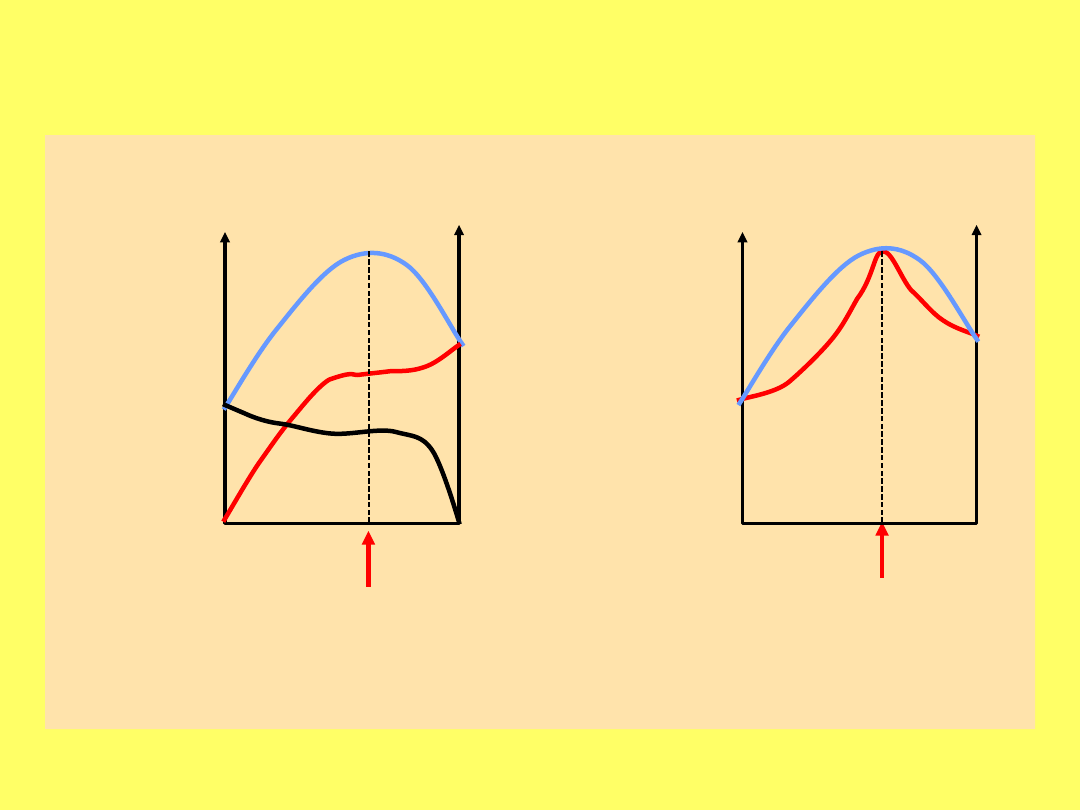
X

CS2

0

1,0 X

ACETON

1

AZ

0

p

X

CS2

0

1,0 X

Aceton

1

AZ

0

T =
const

p

T =
const

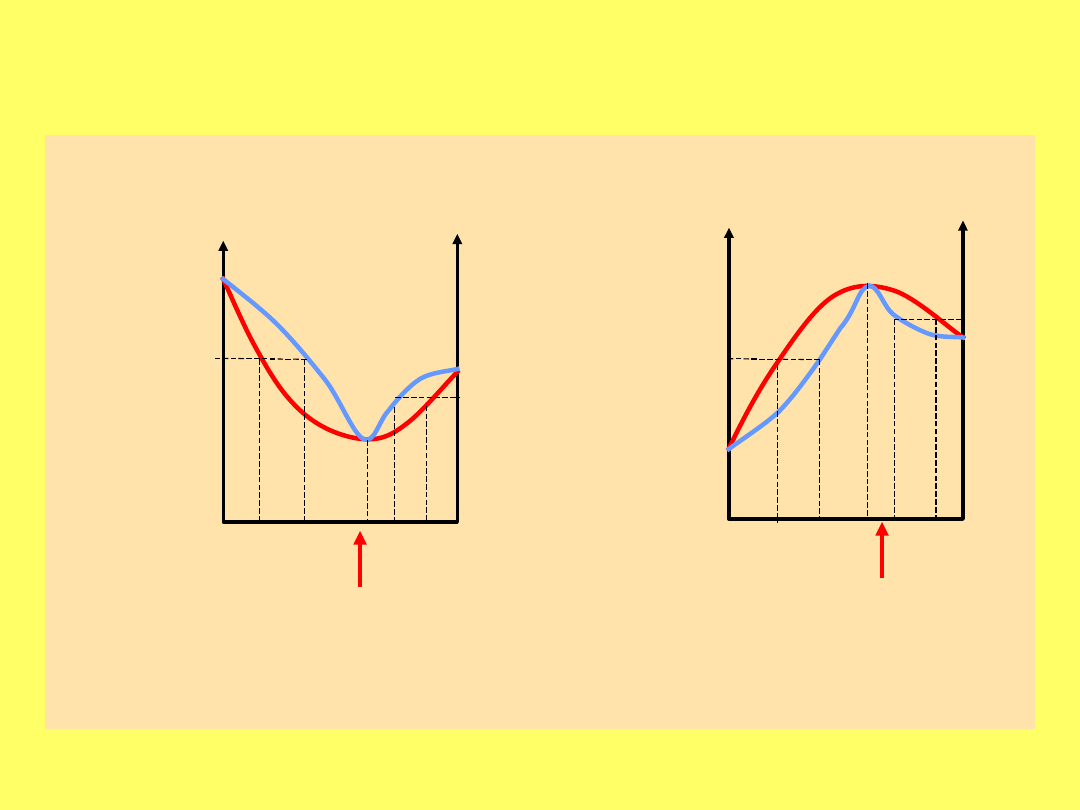
Krzywe równowagi ciecz – para dla układów
azeotropowych

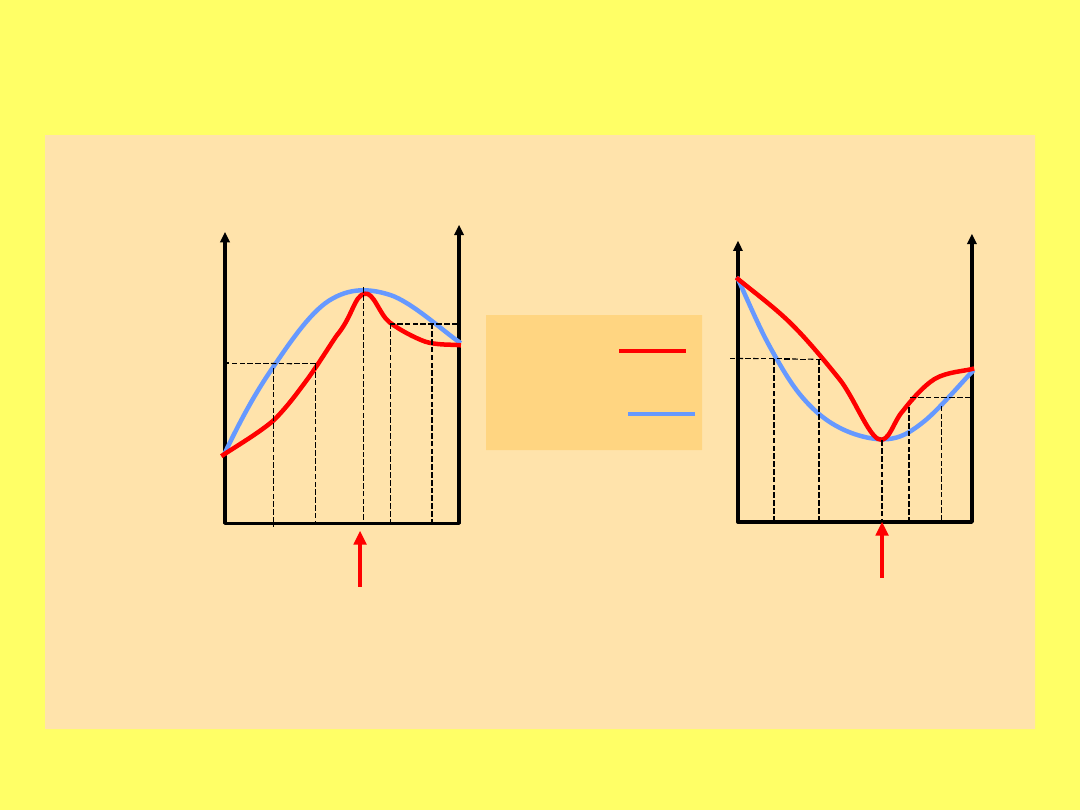
X

CS2

0

1,0 X

ACETON

1

AZ

0

p

X

CS2

0

1,0 X

Aceton

1

AZ

0

T

Krzywe równowagi ciecz – para dla układów
azeotropowych

T =
const

p =
const

Para =

Ciecz=

X

CHCl3

0

1,0 X

ACETON

1

AZ

0

p

X

CHCl3

0

1,0 X

ACETON

1

AZ

0

T

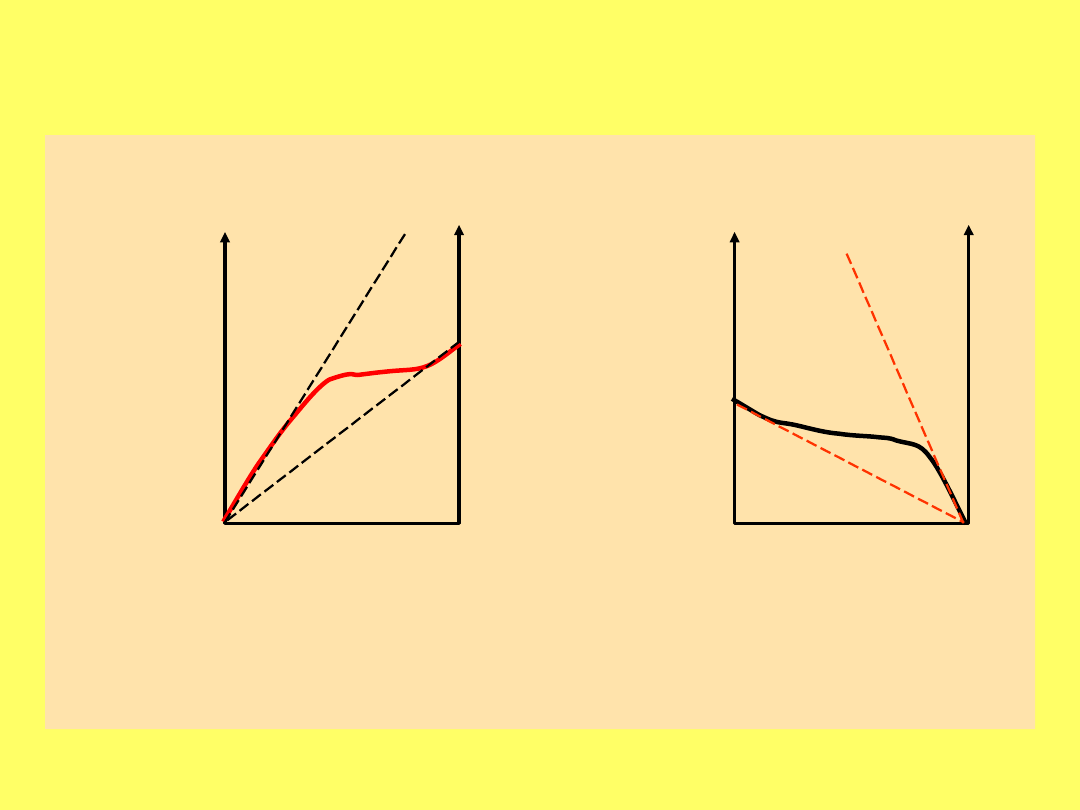
T =
const

p =
const

Krzywe równowagi ciecz – para dla układów
azeotropowych

X

CS2

0

1,0 X

ACETON

1

0

p

X

CS2

0

1,0 X

Aceton

1

0

T =
const

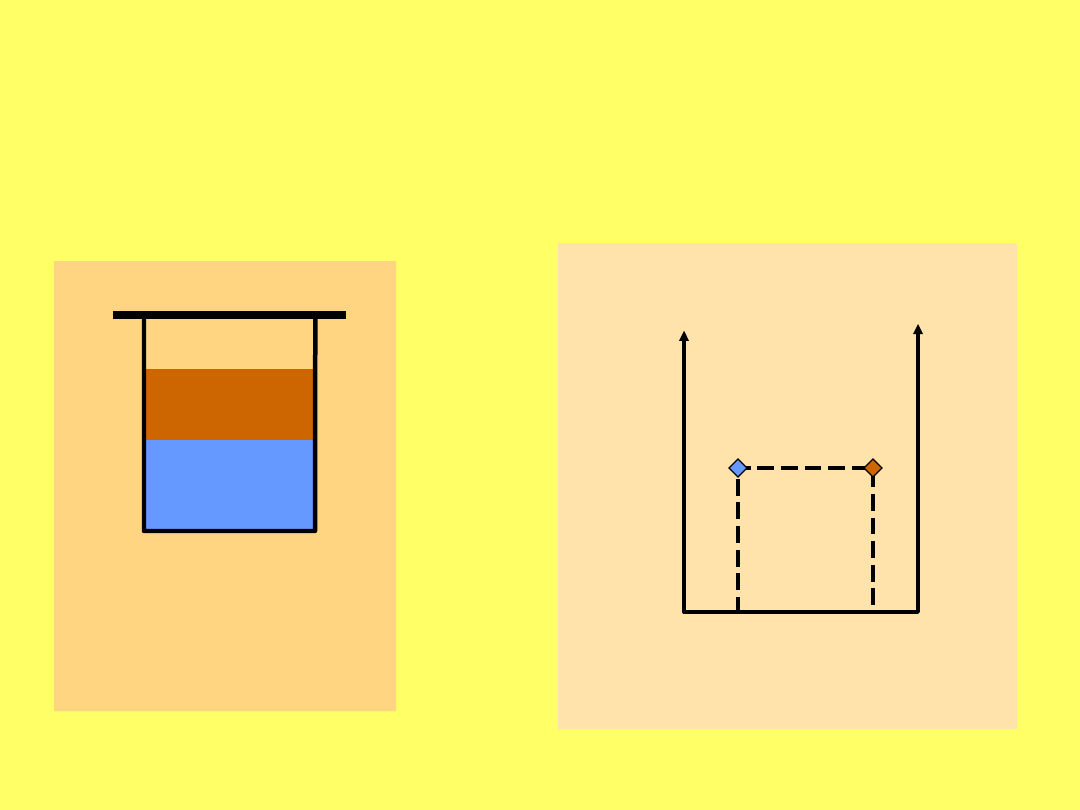
Stosowalność roztworów do praw: Raoulta i
Henry’ego:

p

T =
const

A

B

Układ
dwuskład-
nikowy

(A +

B)

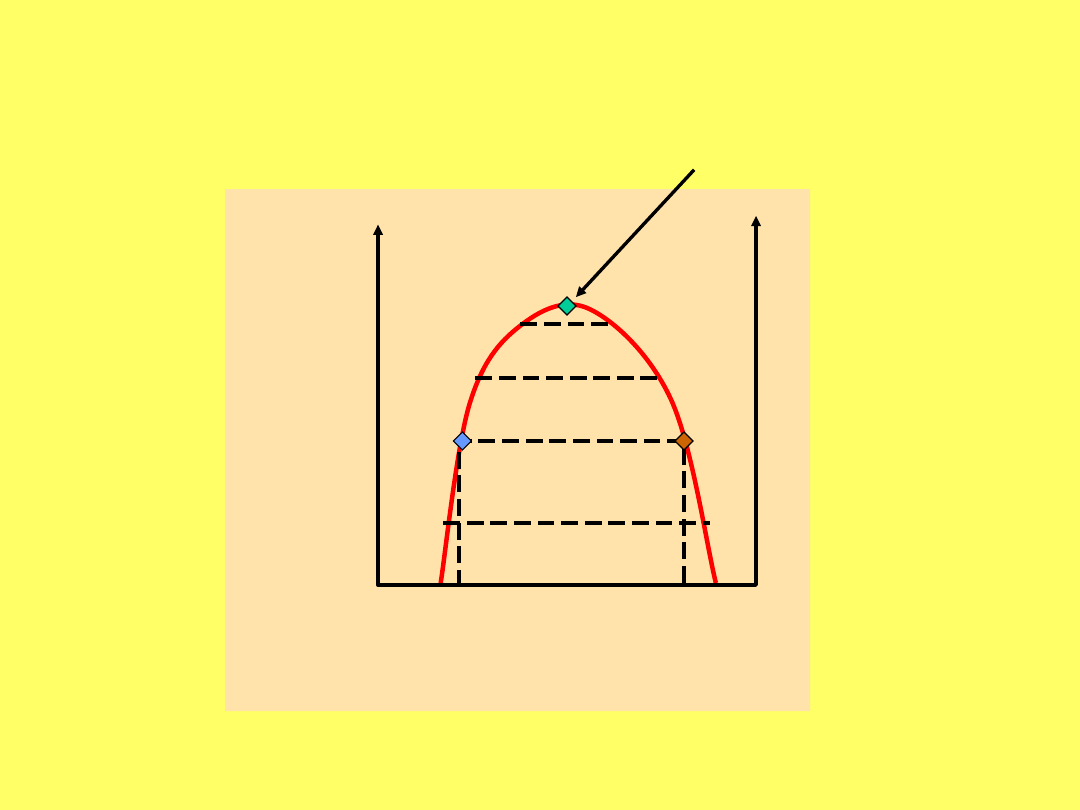
Ograniczona rozpuszczalność wzajemna
dwóch cieczy

T

A

0

100% B

100% 0

T

A

0

100% B

100%
0

Układ dwóch cieczy o ograniczonej wzajemnej
rozpuszczalności

punkt
krytyczny

Krzywa równowagi faz ciekłych w układzie
fenol - woda

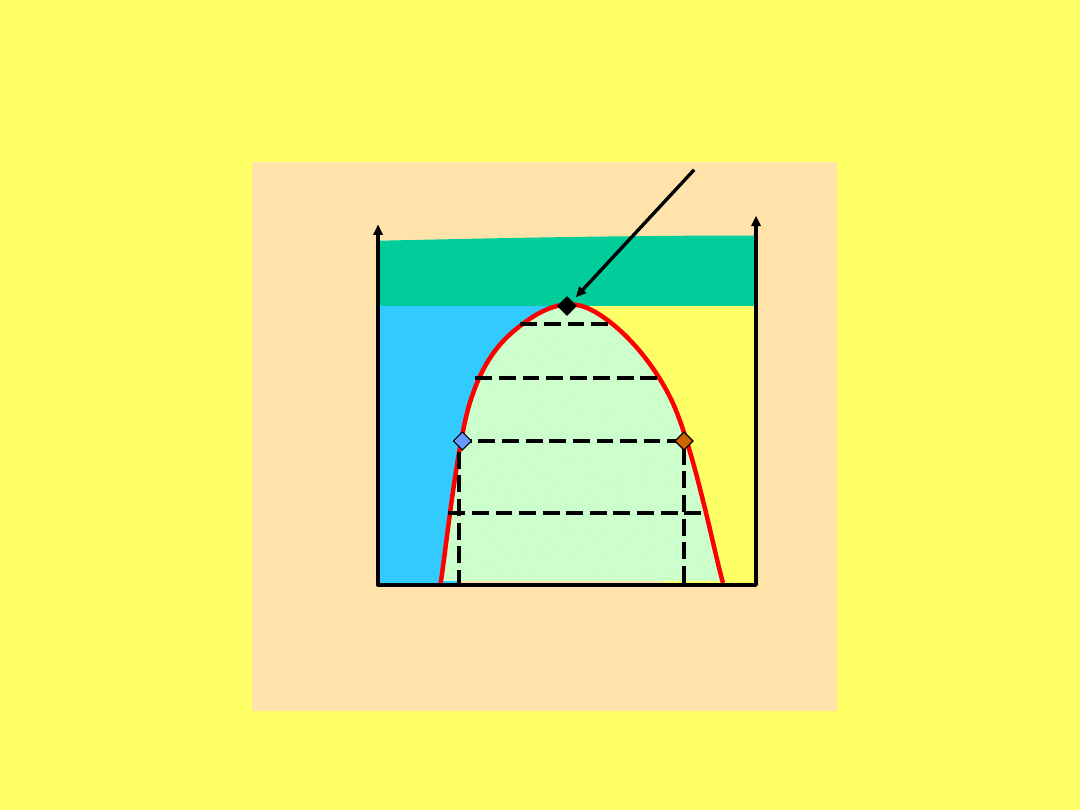
T

A

0

100% B

100%
0

Układ dwóch cieczy o ograniczonej wzajemnej
rozpuszczalności

punkt
krytyczny

Krzywa równowagi faz ciekłych w układzie
fenol - woda

I

II

III

IV

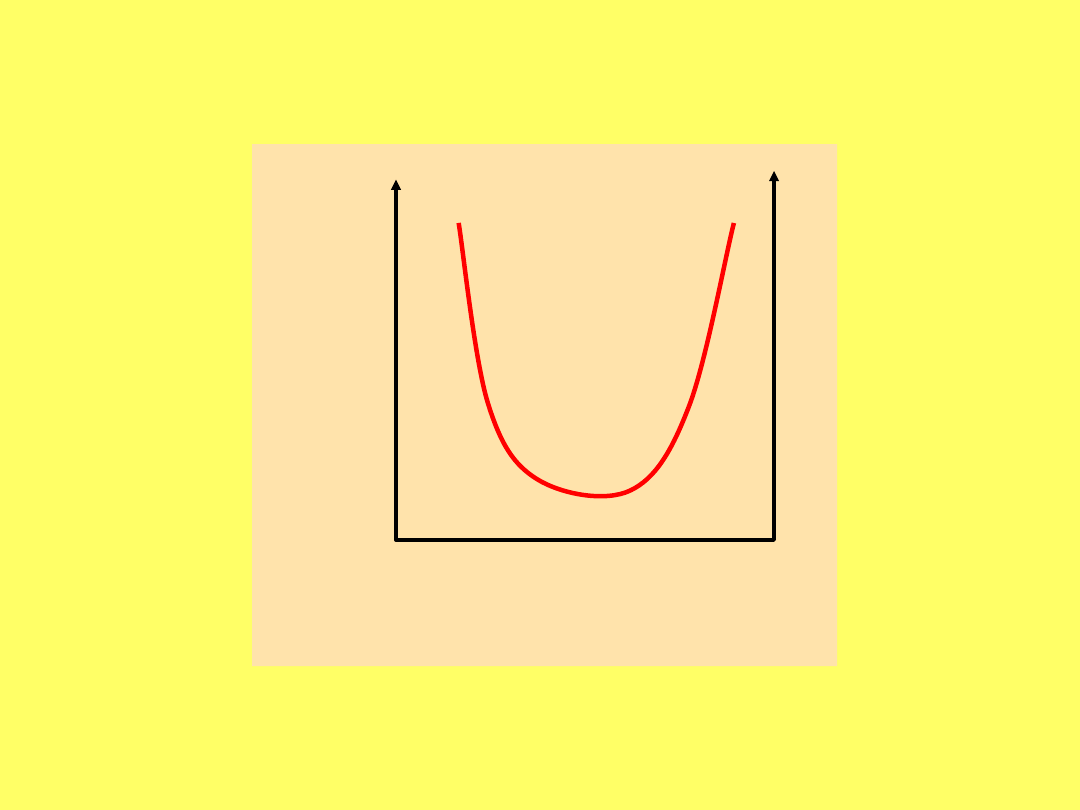
T

A

0

100% B

100 %
0

Krzywa wzajemnej rozpuszczalności
trójetyloaminy i wody

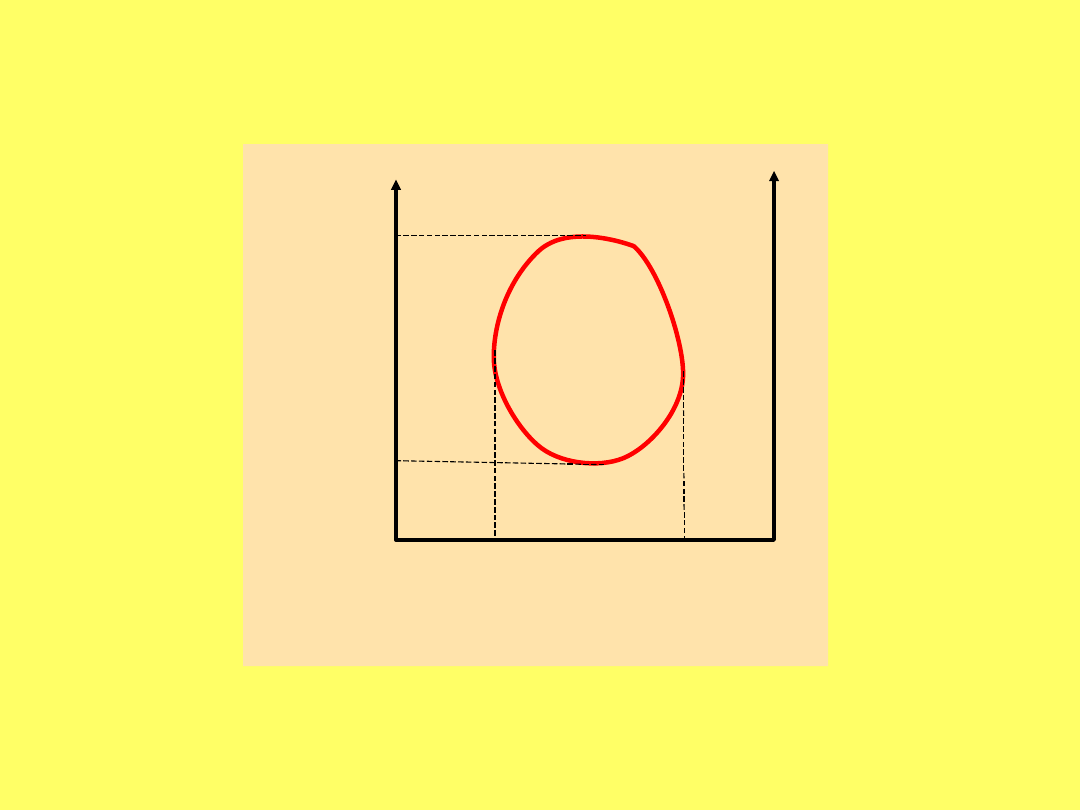
T

A

0

100% B

100%
0

Krzywa równowagi faz ciekłych w układzie nikotyna
- woda

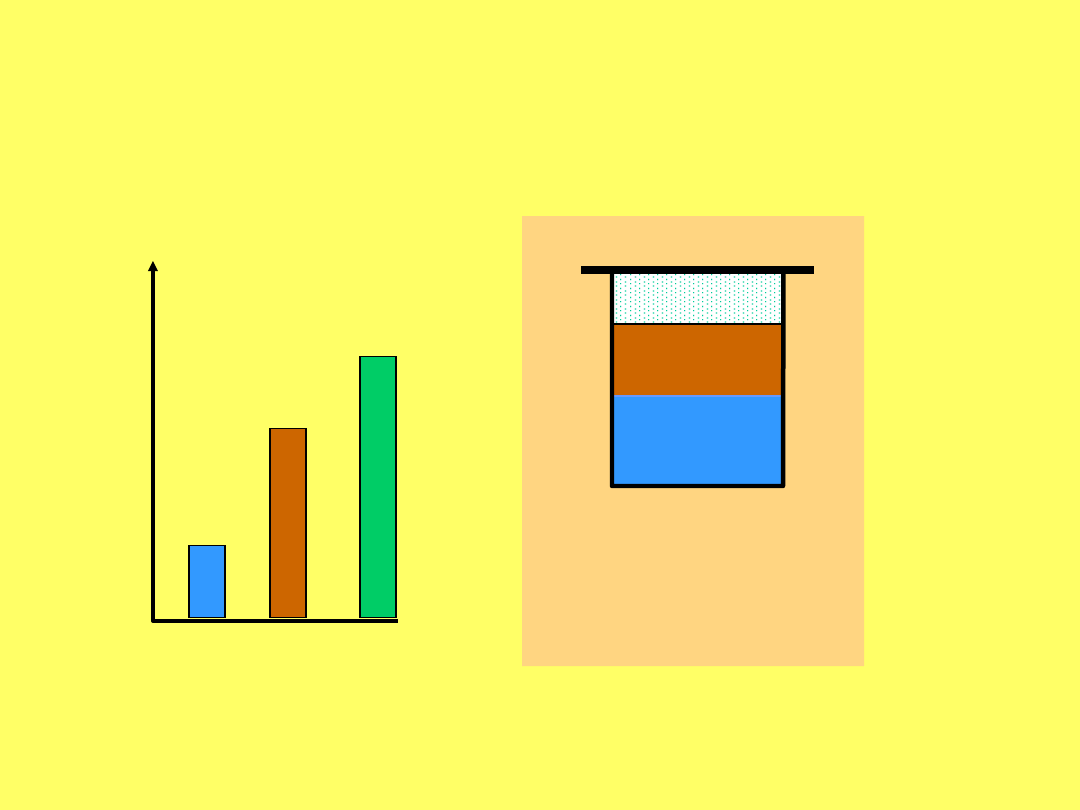
Prężność pary nad układem cieczy nie
mieszających się

W

B

Układ
dwuskład-
nikowy

(A + B)

np.: benzen +
woda

p

p = p

o

B

+

p

o

W

p

W

p

B

p

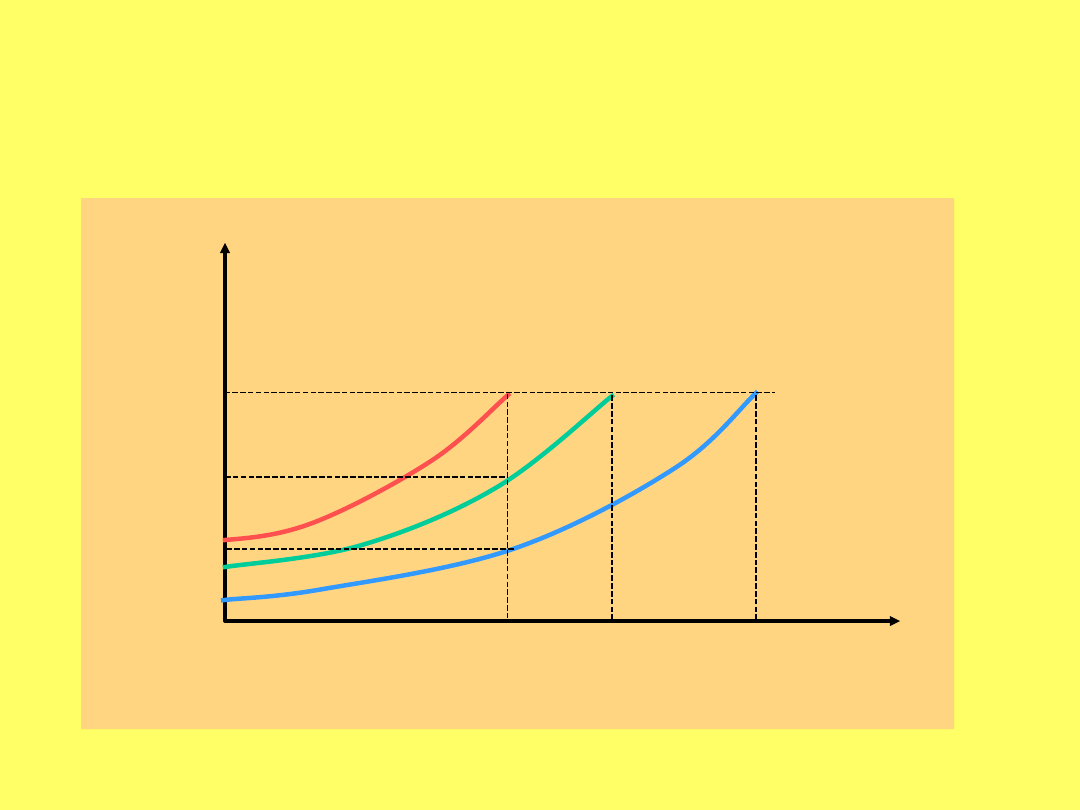
Destylacja z parą
wodną

p

Z

p

B

p

W

p

T

1

T

2

T

3

T

Przykład:

Prężności pary benzenu i wody w temperaturze
wrzenia ich mieszaniny wynoszą kolejno 71,31 * 10

3

i

29,99 * 10

3

N/m

2

. Obliczyć liczbę moli benzenu i wody

w parze.

p

o

B

: p

o

W

= n

B

: n

W

n

B

: n

W

= (71,31 * 10

3

) : (29,99 * 10

3

) = 2,37 : 1

Przykład:

Naftalen destylowano z parą wodną w temperaturze
327 K pod ciśnieniem 1 * 10

5

N/m

2

. Prężność pary

wodnej w tej temperaturze wynosi 0,98 * 10

5

N/m

2

.

Obliczyć ile kilogramów wody należy zużyć do
przedestylowania dwóch kilogramów naftalenu.

n

W

: n

N

=

p

o

W

: p

o

N

n = m / M

n

W

= n

N

*

p

o

W

/ p

o

N

m

W

= (M

W

* m

N

* p

o

W

) / (M

N

* p

o

N

)

m

W

= (18 * 2 * 0,96 * 10

5

) / (128 * 0,02 * 10

5

) =

13,76 kg

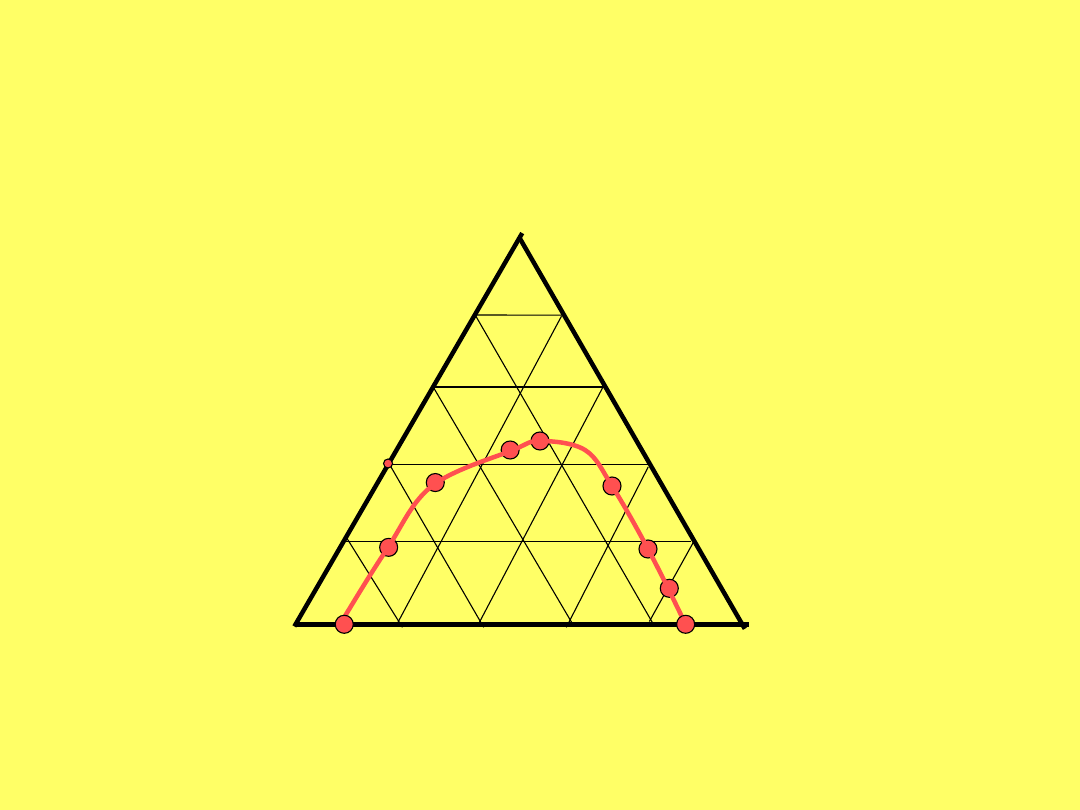
Równowagi fazowe w układach
trójskładnikowych

Jak przedstawić graficznie skład roztworu
trójskładnikowego?

A 0 20 40 60
80 100 B 100
80 60 40 20 0

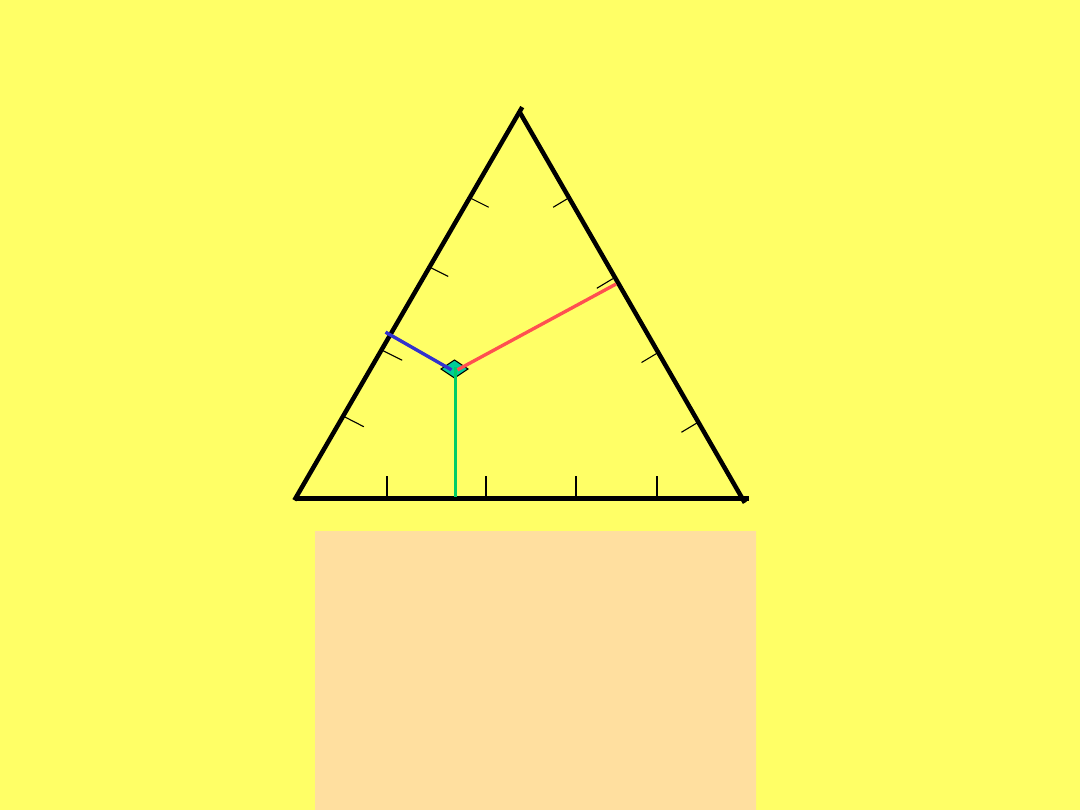
A

C

B

c

b

a

a + b + c = AB = AC
+ BC

%A = 100* a / AB

%B = 100 * b / AB

%C = 100 * c / AB

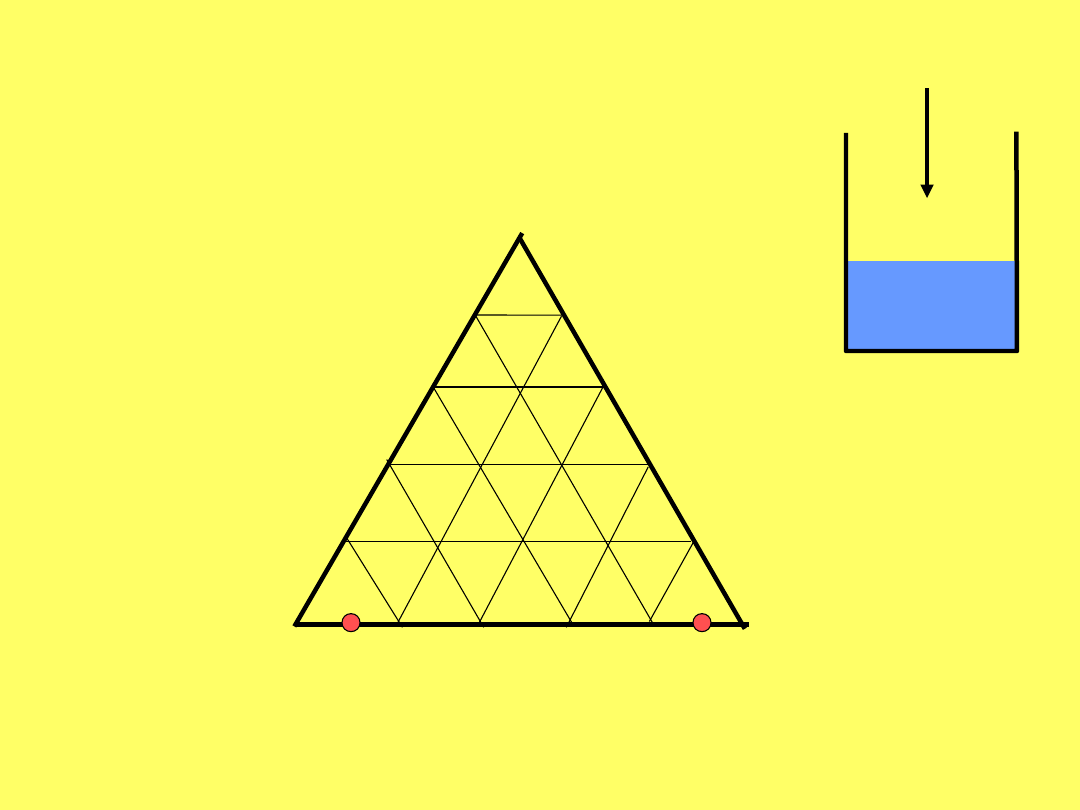
A

C

B

B

C

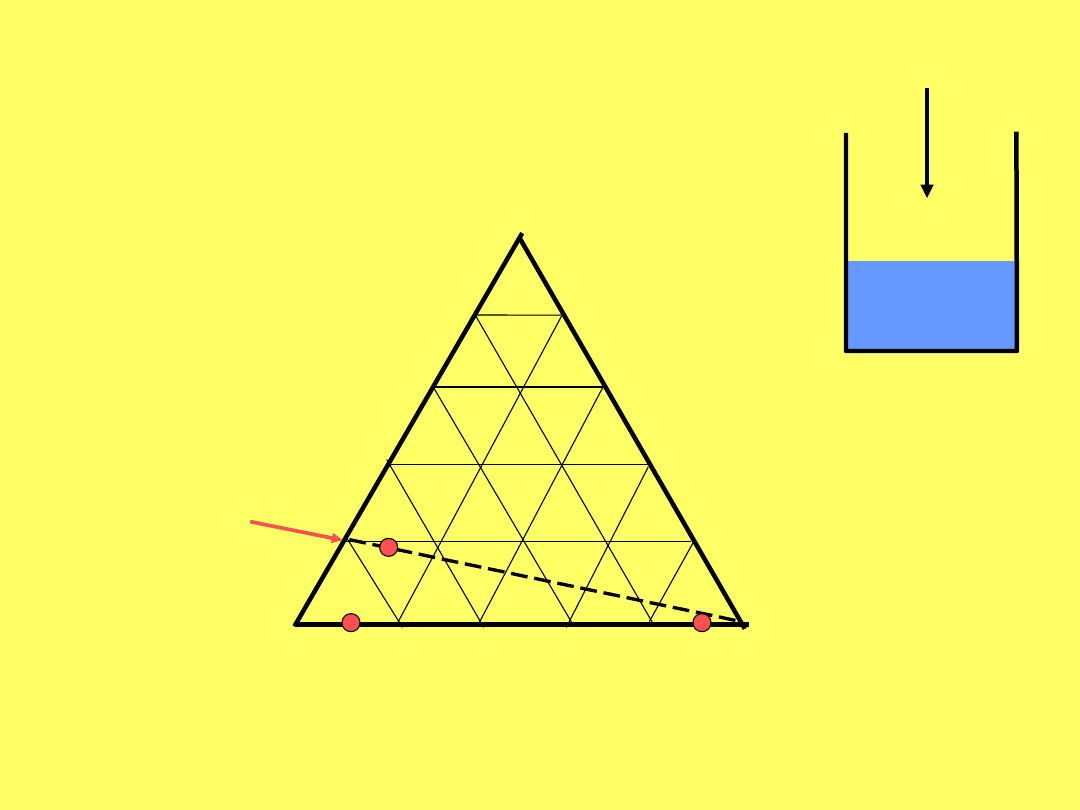
A

C

B

20% A w
B

A +
B

C

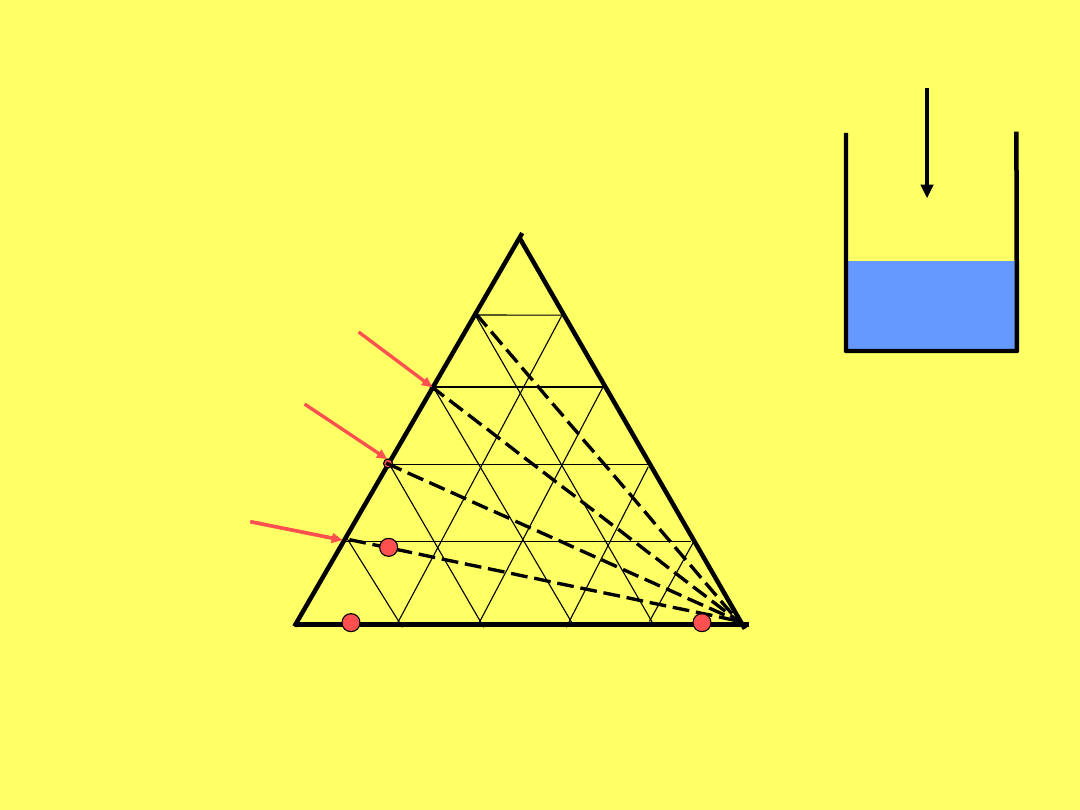
A

C

B

20% A w
B

40% A w
B

60% A w
B

A +
B

C

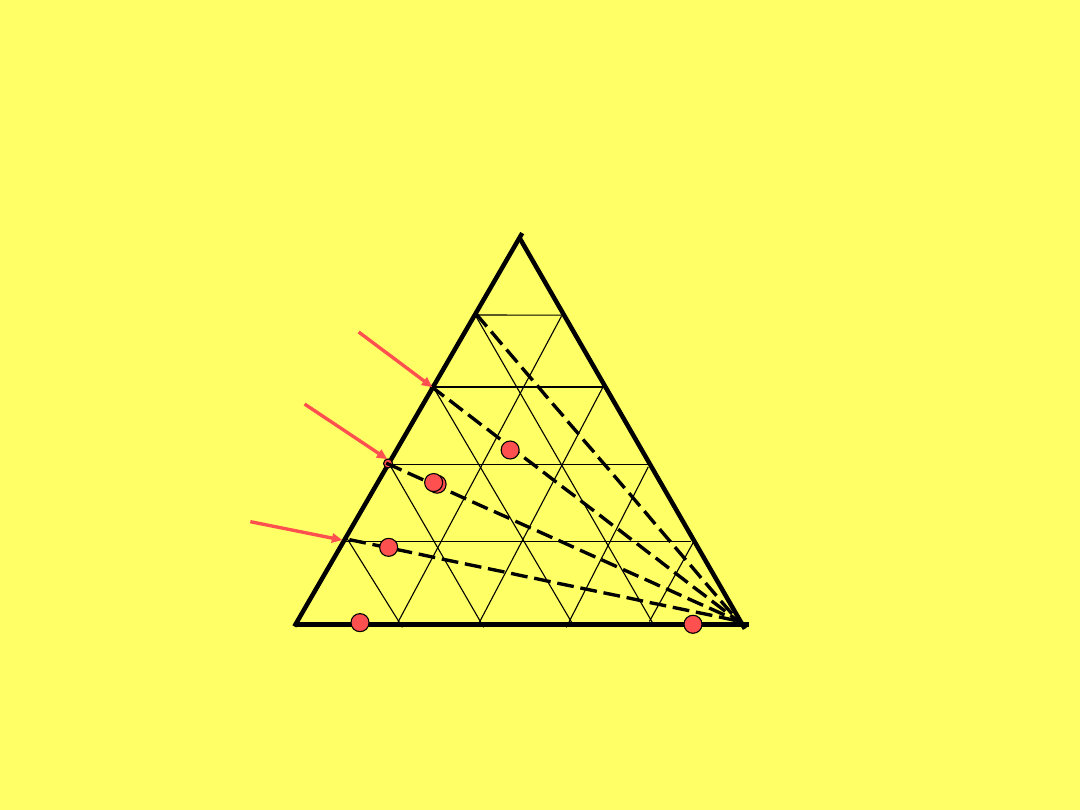
A

C

B

20% A w
B

40% A w
B

60% A w
B

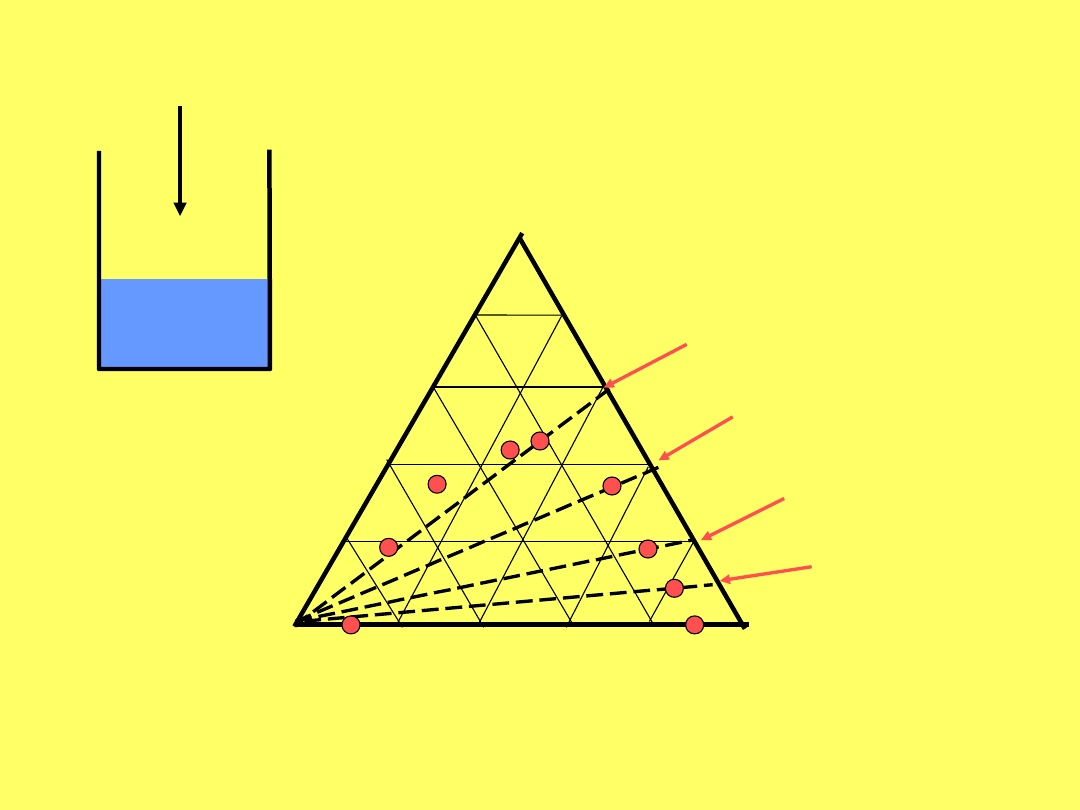
A

C

B

20% A w
C

40% A w
C

60% A w
C

10% A w
C

A +
C

B

A

C

B

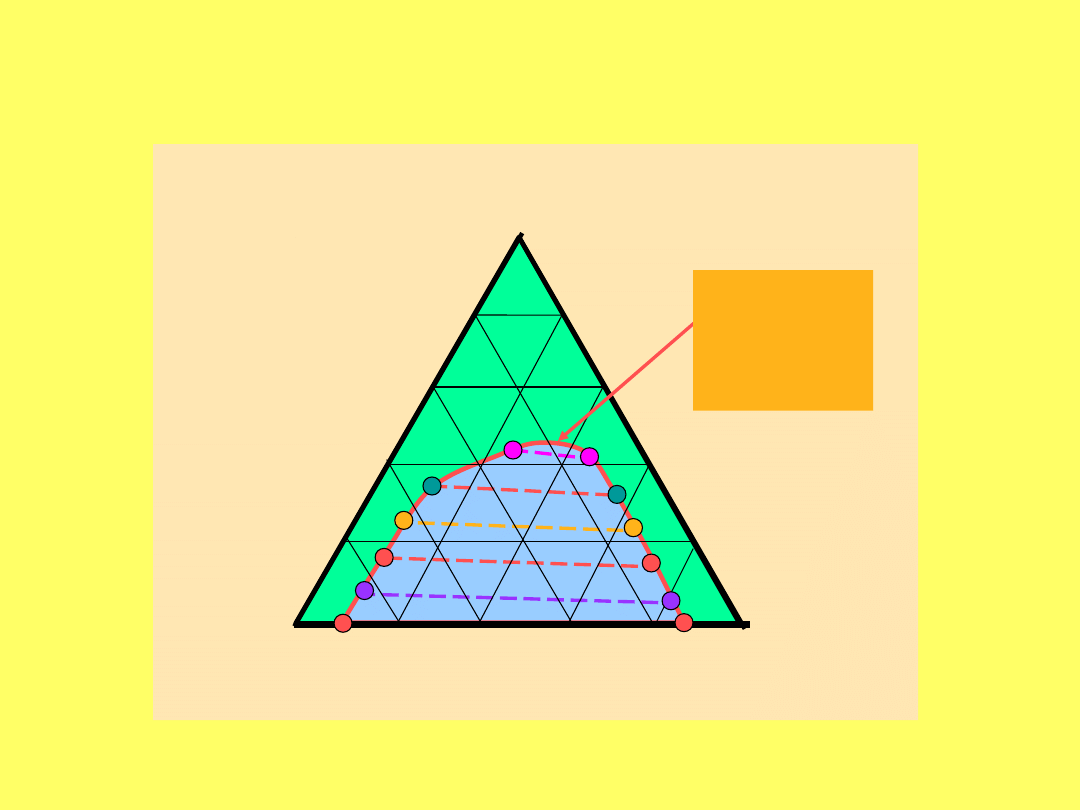
A

C

B

Punkt
krytyczn
y

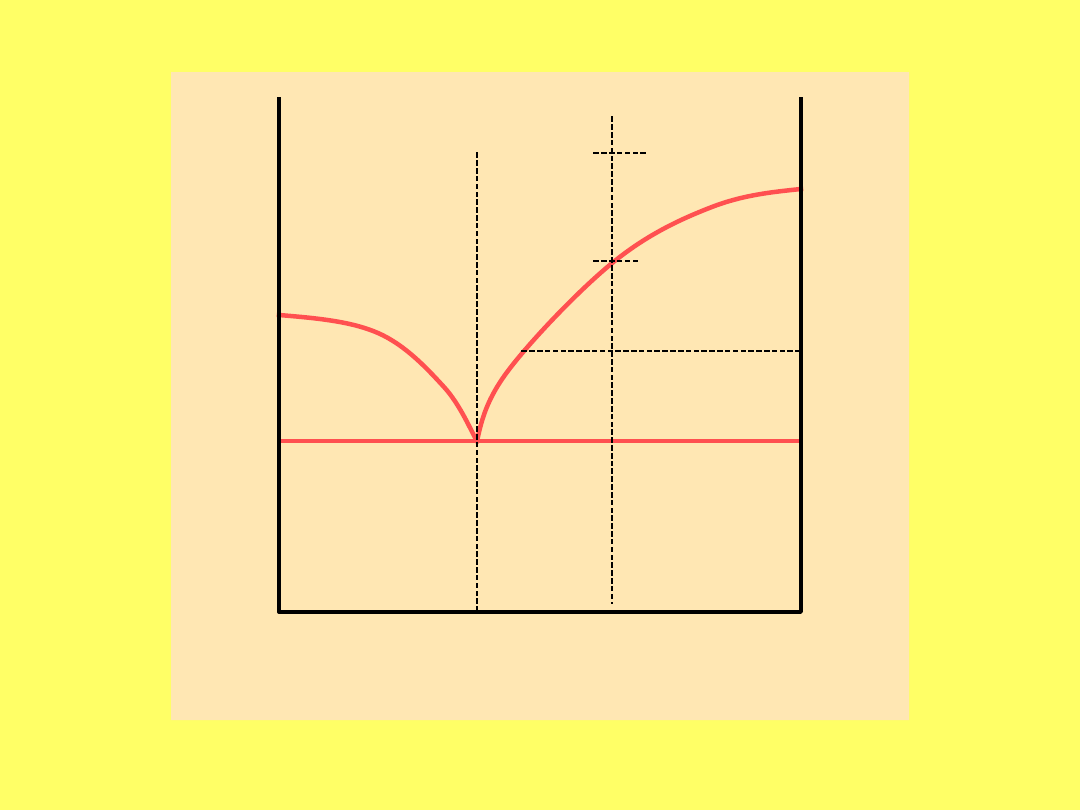
Ciecz

Ciecz
+
stały A

Ciało stałe A + B

Ciecz
+
stały
B

0% skład
100% A 100%
0% B

a

b

c

c1

d

e

Eutekty
ki

Przykład wykresu fazowego dwóch metali (np.
antymon + bizmut)

T

Ciecz

Ciecz
+
stały A

Ciało stałe A + B

Ciecz
+
stały
B

0% skład
100% A 100%
0% B

Eutekty
ki

T

Rozpuszczalność ciał stałych w
cieczach

Reguła Gibbsa dla układów ciecz – ciało stałe

f + s = n + 1

Rozpuszczalność ciał stałych jest procesem
samorzutny.

Można go podzielić na trzy etapy:

•niszczenie sieci krystalicznej,
•solwatacja oderwanych elementów sieci,
•dyfuzja rozpuszczonej substancji w głąb fazy
ciekłej, rozpuszczalnika w kierunku fazy stałej.

Rodzaje roztworów z uwagi na stopień rozpuszczenia
substancji stałej:

nienasycone, nasycone, przesycone.

Wpływ rozpuszczalnika na rozpuszczalność

„podobne rozpuszcza podobne”

Właściwości rozpuszczalników, które decydują o
rozpuszczalności:

stała dielektryczna

zdolność do solwatacji

charakter amfiprotyczny

zdolność do oddziaływań van der Waalsa

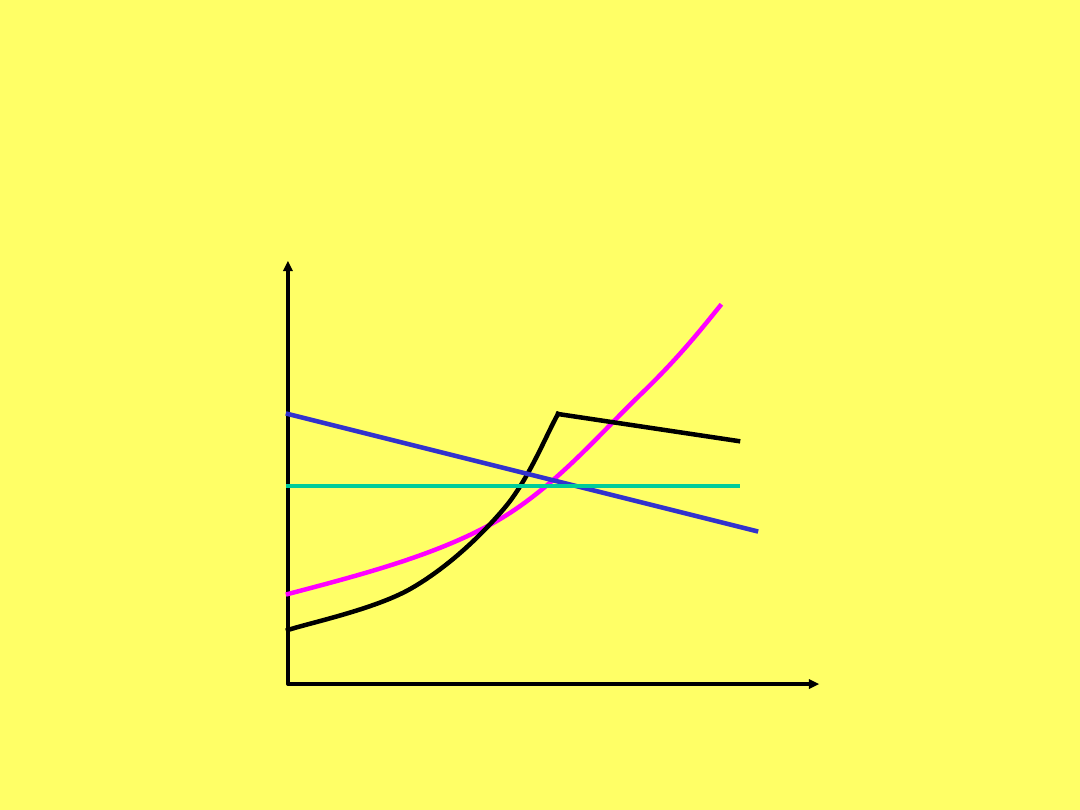
Wpływ temperatury na rozpuszczalność

nie ma prostych zasad opisujących wpływ

temperatury na rozpuszczalność ciał stałych

KCl

Na

2

SO

4

NaCl

Li

2

CO

3

Roz
pus
zcz
aln
ość

Temperatura

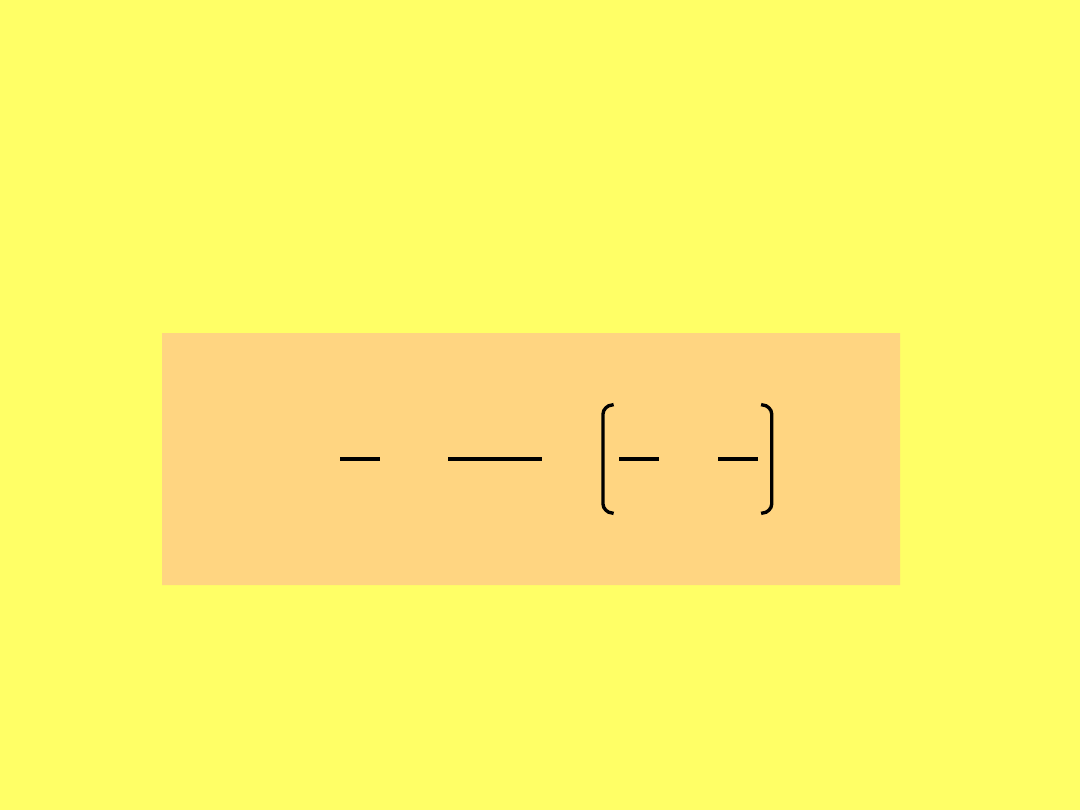
Zmiana rozpuszczalności w zależności od temperatury
jest związana z efektem cieplnym rozpuszczania (reguła
Le Chateliera)

Równanie Clausiusa – Clapeyrona można zastosować
do opisu rozpuszczalności w zależności od
temperatury:

ln =
-

S

1

- H

o

rozp

1

1

S

2

R

T

1

T

2

S

1

S

2

- rozpuszczalności substancji odpowiednio w

temperaturach T

1

i T

2

WŁAŚCIWOŚCI KOLIGATYWNE

(SPOKREWNIONE):

ciśnienie osmotyczne,

obniżenie temperatury

krzepnięcia,

podwyższenie temperatury

wrzenia.

Prężność par nad

roztworem

ciał

stałych:

Zgodnie z prawem Raoulta: p

A

=

p

o

A

* X

A

p

T

o

A

T

A

T

p

A

p

o

A

Obniżenie prężności pary jest równe:

p = p

o

A

- p

o

A

* X

A

p = p

o

A

* X

B

Obniżenie prężności pary jest wprost
proporcjonalne do ułamka molowego
substancji rozpuszczonej

Przykład:

Prężność pary nad czystą wodą w temp. 293 K
wynosi 2320 Pa. Jaka będzie prężność pary nad
roztworem, jeżeli w 1000 g wody rozpuścimy 2 mole
nielotnej substancji?

p = p

o

* X

A

p = 2320 * (1000 / 18) : [(1000 / 18) + 2)]

p = 2239 Pa

a także: p : p

o

= n : (n + N)

p = 2320 * 2 : [(1000 / 18) + 2] = 80,60 Pa
P = 2320 – 80,60 = 2239,4 Pa

Jeżeli roztwór nie zachowuje się w sposób idealny,
wówczas X

B

należy pomnożyć przez pewien czynnik

i

, nazywany współczynnikiem izotonicznym van’t

Hoffa

i = 1 –



+



*



Gdzie



jest liczbą jonów, na jakie rozpada się

cząsteczka elektrolitu.

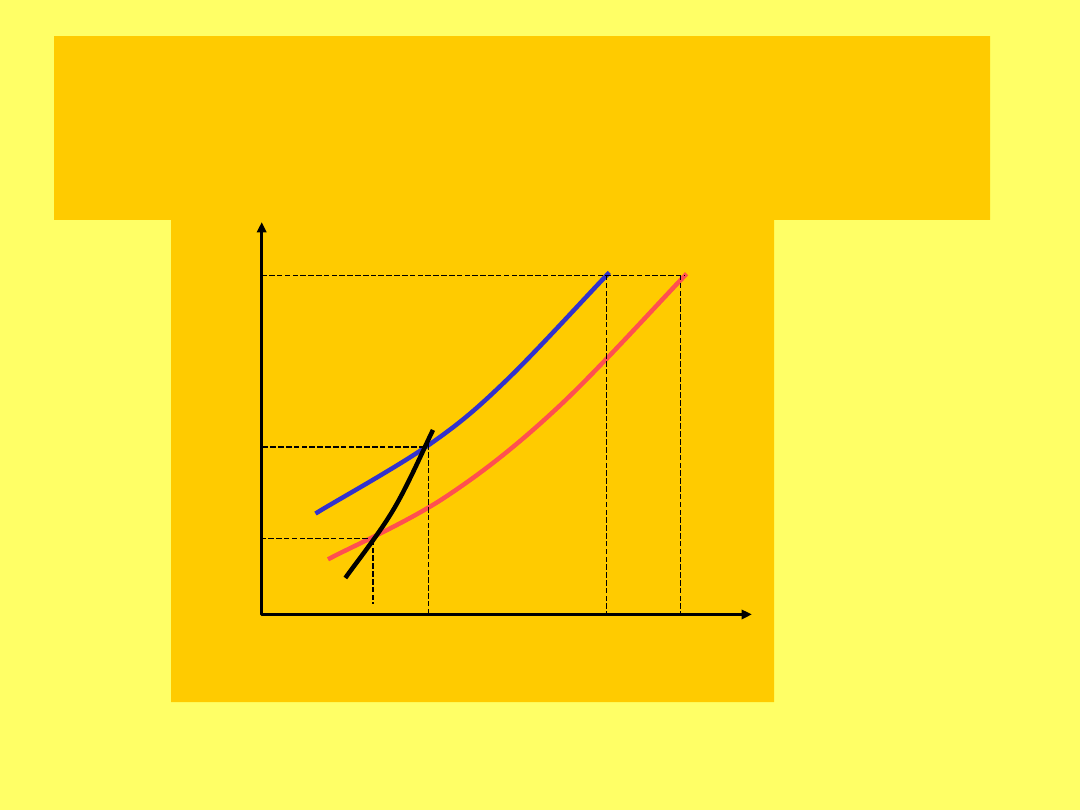
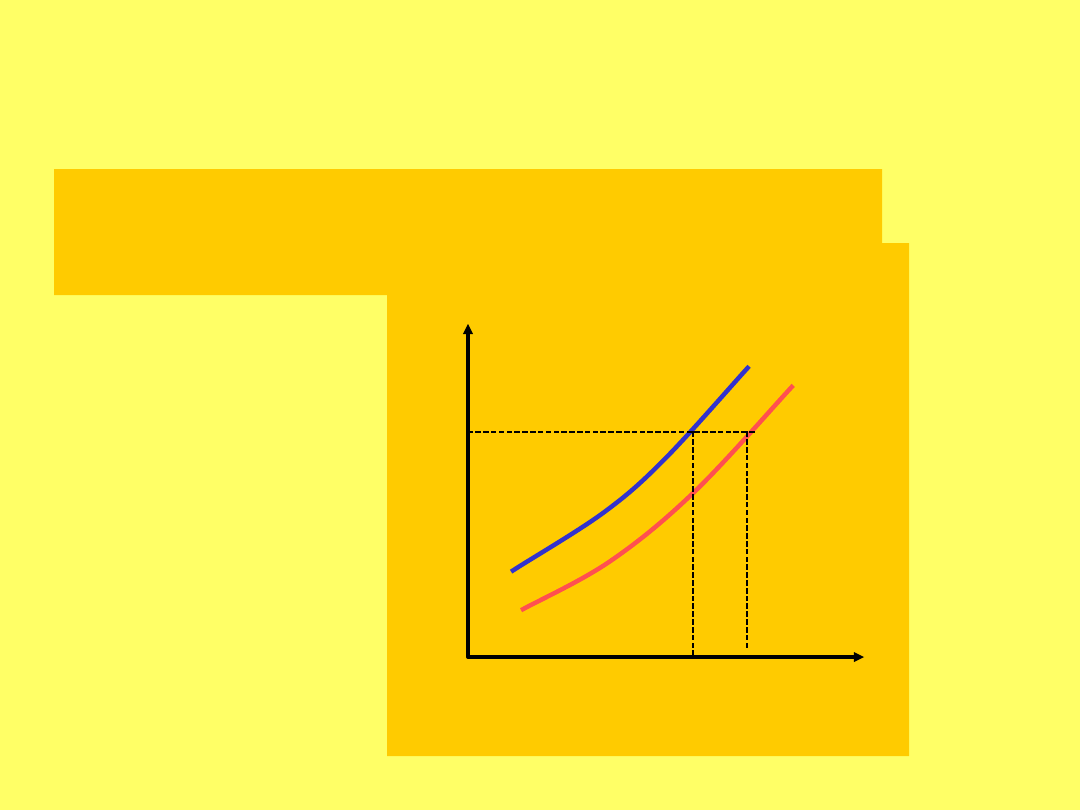
W ścisłym związku z obniżeniem prężności pary
nad roztworem pozostaje zjawisko podwyższenia
temperatury wrzenia cieczy i obniżenia jej
temperatury krzepnięcia

Krzywe prężności pary nad roztworem (

II

),

rozpuszczlnikiem (

I

) i nad fazą stałą (III)

p

T

TR

T

T

T

W

T

WR

T

II

I

III

T

TR

< T

T

T

WR

> T

W

p

Z

Podwyższenie temperatury wrzenia roztworu

jest

wprost proporcjonalne do stężenia molalnego
substancji rozpuszczonej

T

W

= E * C

T

W

- podwyższenie temperatury wrzenia roztworu,

C – stężenie molalne roztworu,

E – współczynnik proporcjonalności (stała
ebulioskopowa)

m * 1000

T

W

= E

M * m

o

Obniżenie temperatury krzepnięcia roztworu

jest

wprost proporcjonalne do stężenia molalnego
substancji rozpuszczonej

T

K

= K * C

T

K

- obniżenie temperatury krzepnięcia roztworu,

C – stężenie molalne roztworu,

K – współczynnik proporcjonalności (stała
krioskopowa)

m * 1000

T

K

= K

M * m

o

Dla roztworów nieidealnych należy wprowadzić
współczynnik izotoniczny „i”:

T

W

= E * i * C

T

K

= K * i * C

Pomiary ebuliometryczne i kriometryczne
wykorzystuje się do wyznaczania masy molowej, do
oznaczania składu roztworu, do oznaczania stopnia
dysocjacji.

Przykład:

W 100g wody rozpuszczono 3,74888 g substancji.
Temperatura wrzenia tego roztworu była wyższa o
0,2107 K od temperatury wrzenia rozpuszczalnika.
Oblicz masę cząsteczkową substancji rozpuszczonej.
Wiedząc, że był to siarczan sodowy oblicz współczynnik
izotoniczny „i”. Stała ebulioskopowa dla wody wynosi 0,
512 kg * K / mol.

m * 1000

M = E

T

W

* m

o

M = 0,512 * 3,7488 : (0,2107 * 0,1) [(kg K / mol) * g /
(K * kg)

M = 91,1 g / mol

i = M

TEOR

/ M

DOSW

i = 142 / 91,9 = 1,545

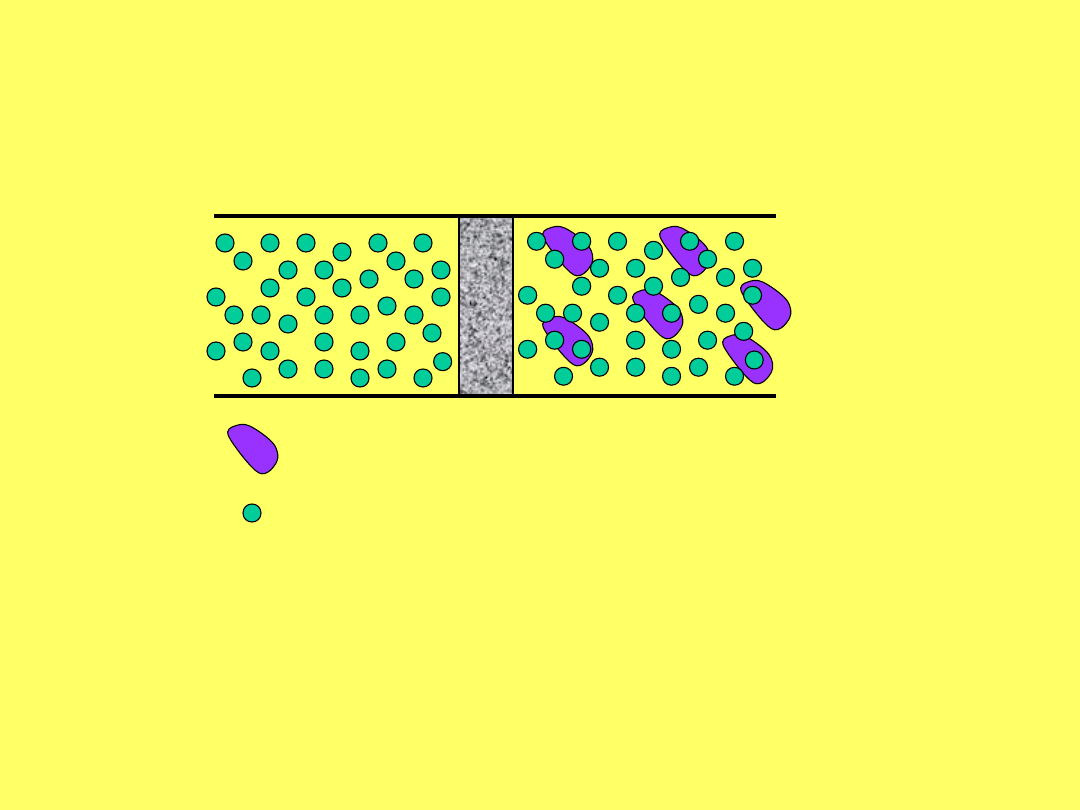
OSMOZA I CIŚNIENIE
OSMOTYCZNE

Cząsteczka substancji
rozpuszczonej

Cząsteczka wody

Jednostronną dyfuzję rozpuszczalnika przez błonę
półprzepuszczalną nazywamy osmozą

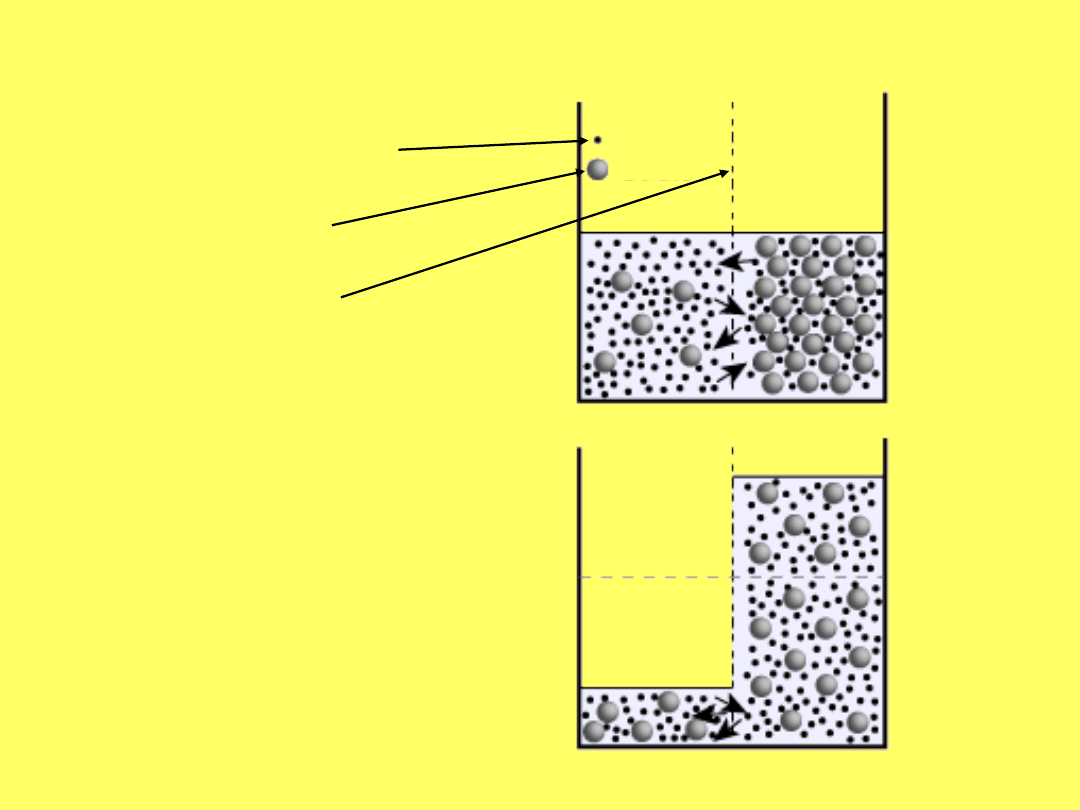
rozpuszczalnik

substancja

membrana
półprzepuszcza
lna

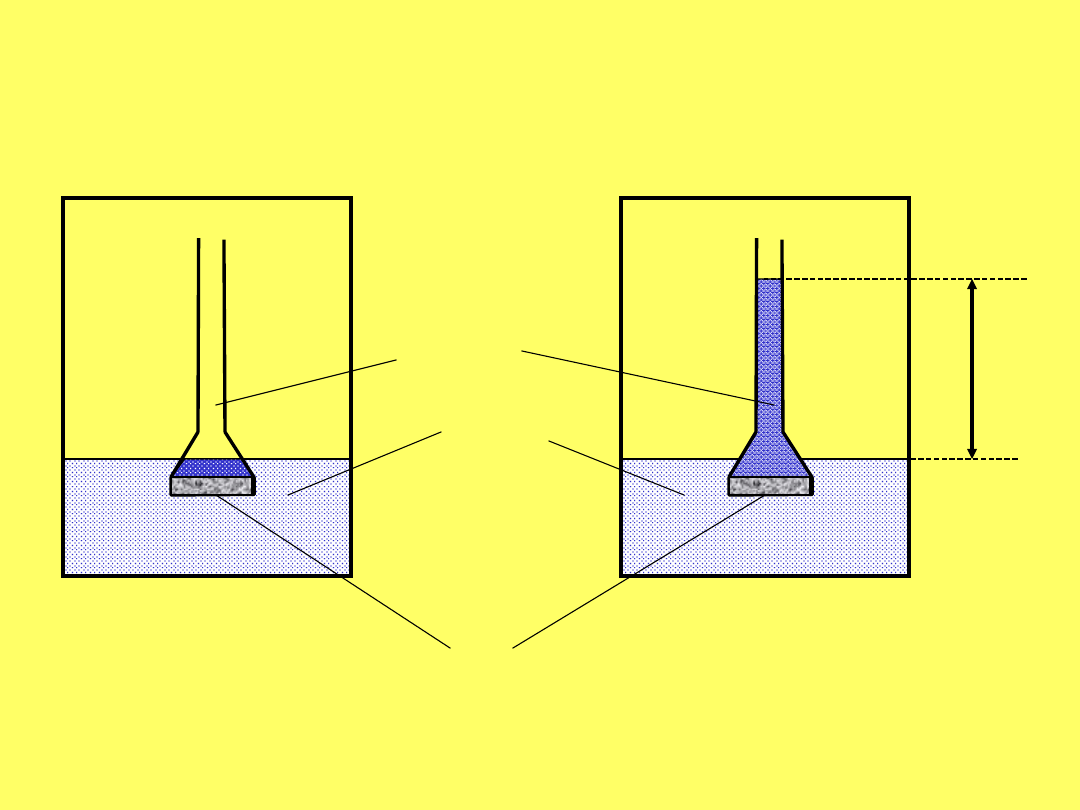
Ciśnienie osmotyczne

– ciśnienie wywierane przez

substancję rozpuszczoną na błonę
półprzepuszczalną

`

h

Roztwór

Rozpuszczalnik

Błona
półprzepuszczalna

`

Wzór empiryczny van’t Hoffa na ciśnienie
osmotyczne



:



* V = n

i

*R * T

V – objętość roztworu

n

i

– liczba moli substancji

Ciśnienie osmotyczne substancji rozpuszczonej w
danej objętości roztworu, w określonej
temperaturze, jest równe ciśnieniu, jakie
wykazywałaby ta substancja, gdyby tworzyła gaz,
który zajmowałby taką samą objętość i posiadał
taką samą temperaturę jak roztwór.

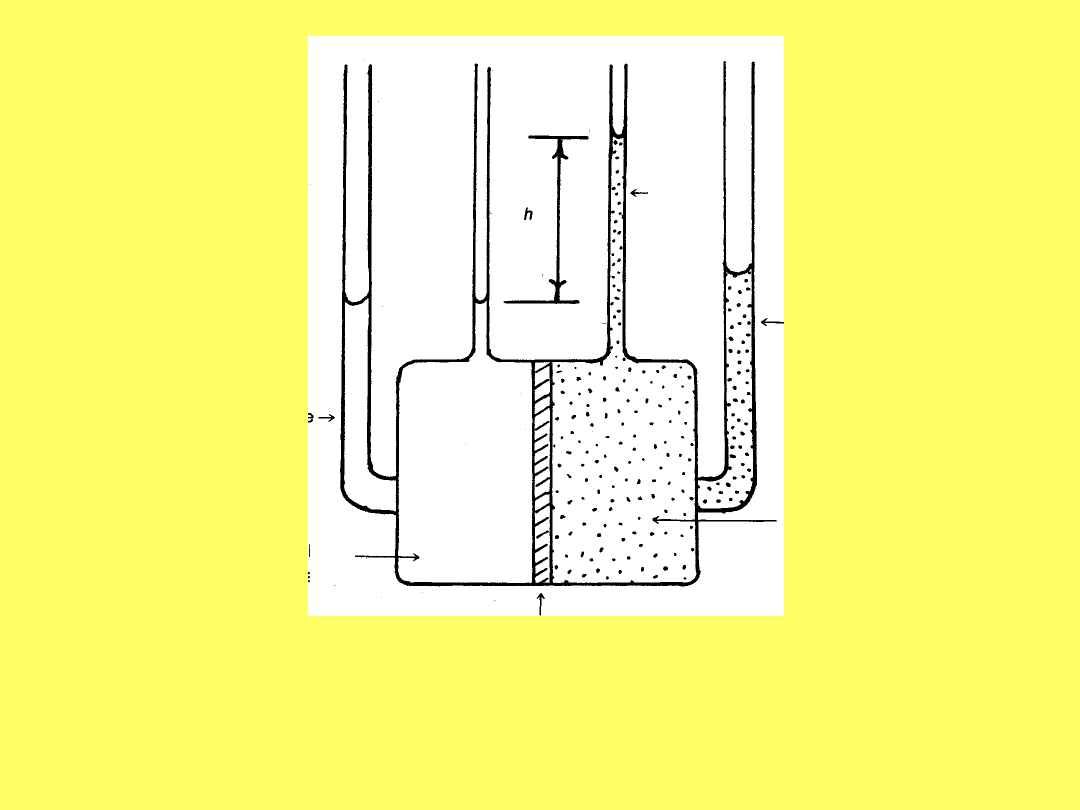
Schemat urządzenia do pomiaru ciśnienia

osmotycznego

π = wysokość, h * gęstość roztworu, ρ *

przyśpieszenie ziemskie, g

Rurka
napełniając
a

Wod
-ny
rozt-
wór

Rurka
napełniając
a

Roztwór:
substancja
+ woda

Woda



* V = n

i

*R * T

Ponieważ: c

i

= n

i

/ V

Można napisać:



= c

i

*R

* T

Wzory na ciśnienie osmotyczne są ważne dla
roztworów rozcieńczonych.

Jeżeli rozpuszczona substancja jest elektrolitem i
dysocjuje na jony, to wzory na ciśnienie
osmotyczne nie są spełnione. Należy wtedy
wprowadzić poprawkę „i” (współczynnik
izotoniczny).



= i * c

i

*R * T

Np. dla KCl i = 2, dla CaCl

2

i = 3.

W przypadku roztworów bardziej

stężonych należy uwzględnić

współczynnik aktywnosci



= i * f * c

i

* R * T



= i * c

* R * T

W praktyce zamiast stężenia molowego stosuje się
stężenie molalne:



= i * c

m

* R * T



= i * c

m

* R * T



' = ν * c

m

* R * T

g

i











,

i jest współczynnikiem izotonicznym
ν jest liczbą jonów na jakie dysocjuje
cząsteczka
g jest współczynnikiem osmotycznym
ξ

m

jest osmolalnością,



= ν * g * c

m

* R * T

ξ

m

= ν * c

m

* g

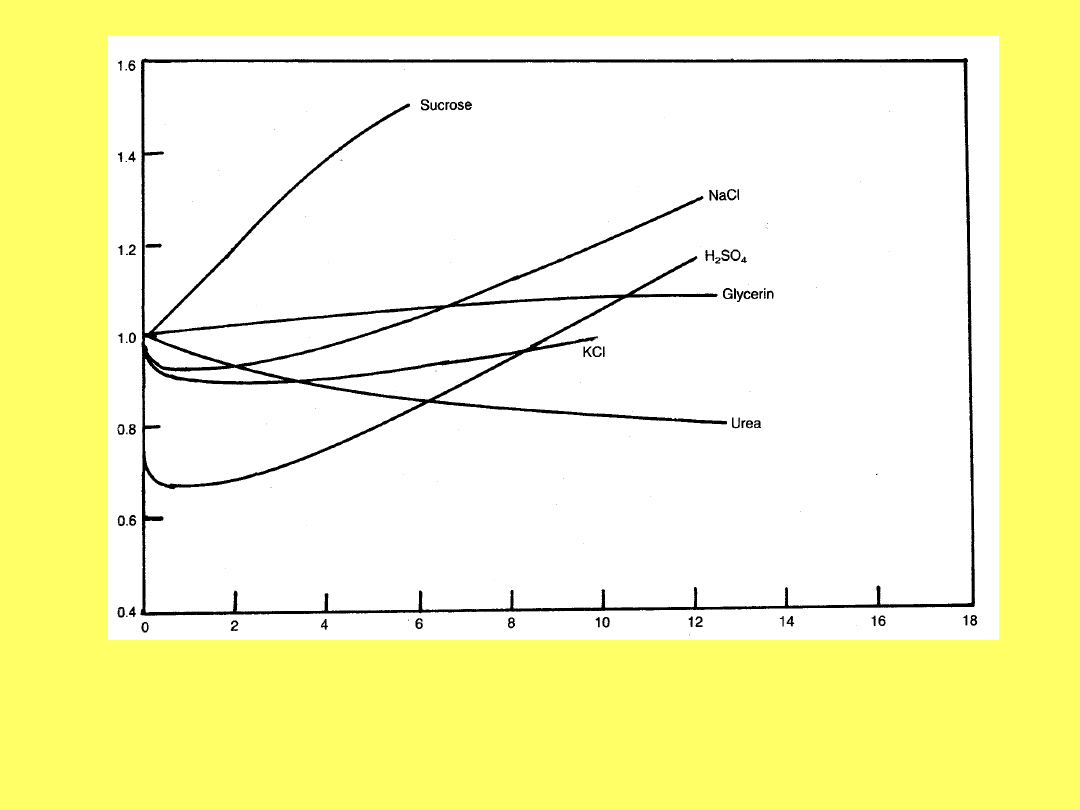
W

sp

ó

łc

zy

n

n

ik

o

sm

o

ty

cz

n

y,

g

Stężenie jonów, ν
* c

m

Zależność współczynnika osmotycznego, g, od stężenia

wybranych związków w roztworach wodnych.

Osmolalność i osmolarność

Praktyczną miarą aktywności osmotycznej jest
osmolalność, ξ

m

(ksi).

Jednostką osmolalności jest osmol * kg

-1

Roztwór zawierający 1 mol nie
dysocjującej substancji w 1 kg wody jest
roztworem o osmolalności równej
1 osmol * kg

-1

Jednostką osmolarności jest osmol * dm

-3

Roztwór zawierajacy 1 mol nie
dysocjującej substancji
w 1 litrze roztworu wodnego jest
roztworem o osmolarności równej 1
osmol * dm

-3

Przykład: obliczanie osmolalności

Roztwór chlorku sodu (M = 58,5 g/mol) o stężeniu
0,90% w/w wykazuje współczynnik osmotyczny g =
0,928. Oblicz osmolalność roztworu.

Osmolalność ξ

m

można obliczyć korzystając z

wyrażenia:

ξ

m

= ν * c

m

* g

1

-

1

-

kg

mosmol

286

kg

osmol

286

,

0

928

,

0

5

,

58

0

,

9

2















m



Ciśnienie osmotyczne odgrywa bardzo
ważną rolę w procesach biologicznych.

Tkanki i błony organizmów żywych są
przegrodami półprzepuszczalnymi.

Roztwory izotoniczne, hipotoniczne i
hipertoniczne.

Osmoza i równowaga osmotyczna -

znaczenie i zastosowanie

...

•Transport wody przez błony komórkowe roślin
i zwierząt, sztywność liści roślin oraz
elastyczność tkanek zwierząt.

•Ciśnienie osmotyczne osocza krwi ludzkiej
wynosi ok. 0,6 MPa (ok. 0.9 % wag. NaCl);
wprowadzenie do krwi wody destylowanej
powoduje hemolizę tzn. pękanie czerwonych
ciałek krwi, które "pęcznieją" wskutek migracji
do ich wnętrza wody - płyny iniekcyjne muszą
być izotoniczne z osoczem krwi

Osmoza i równowaga osmotyczna -

znaczenie i zastosowanie

...

•”Mięknięcie" liści sałaty, kapusty lub
pokrojonych ogórków po ich posoleniu, wynika
z utraty przez ich komórki wody wskutek
osmozy.

• Pomiar ciśnienia osmotycznego
rozcieńczonego roztworu nieelektrolitu
umożliwia wyznaczenie jego stężenia molowego
(masy molowej) - jest to jedna z metod
wyznaczania średnich mas molowych
polimerów.

• Jeżeli roztworowi zamkniętemu przegrodą
półprzepu- szczalną narzuci się ciśnienie
większe od jego ciśnienia osmotycznego, to
zawarty w nim rozpuszczalnik będzie migrował
z roztworu do czystego rozpuszczalnika - jest to
jedna z metod odsalania wody morskiej.

Przykład:

Obliczyć ciśnienie osmotyczne roztworu glukozy w
wodzie o stężeniu równym 0,1 mol / dm

3

w temp. 295

K.



= 0,1 * 8,314 * 295 [mol dm

3

J mol

-1

K

-1

]



= 245,26 [J dm

-3

]



= 245260 Pa

Przykład:

Obliczyć ciśnienie osmotyczne w temp. 273 i 293 K
roztworu, który w objętości 50cm

3

zawiera 2 g

sacharozy.

M

C12H22O11

= 342 g mol

-1

N = 2 / 342 = 0,0058

50 cm

3

= 5* 10

-5

m

3

5* 10

-5

m

3

- 0,0058 mol

1 m

3

- x

x = 1 * 0,0058 : 5 * 10

-5

= 116 mol m

-3



273

= c * R * T = 116 * 8,313 * 273 = 263256 Pa



273

= c * R * T = 116 * 8,313 * 293 = 282542 Pa

Zadanie:

Obliczyć ciśnienie osmotyczne roztworu
NaCl o stężeniu 0,03 mol/l w temp 25

o

C.

Zadanie:

Osocze krwi w temp. 36,6

o

C wywołuje

ciśnienie osmotyczne względem wody
równe 7,6 atm. Jakie jest stężenie
procentowe roztworu NaCl, który
zrównoważy ciśnienie osmotyczne osocza
krwi? Przyjąć współczynnik aktywności f =
0,9 i gęstość d = 1 g/cm

3

.

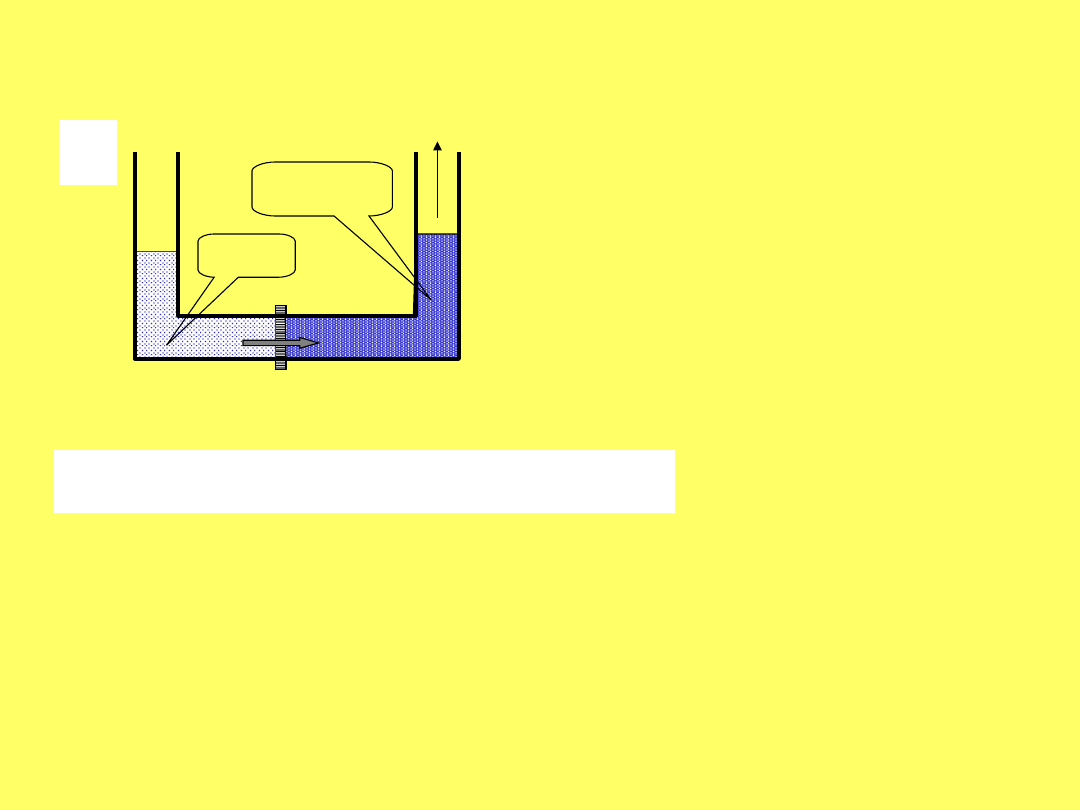
OSMOZA ODWRÓCONA

ROZTWÓ
R

a)

p <



WOD
A

a) osmoza, p – ciśnienie
hydrostatyczne

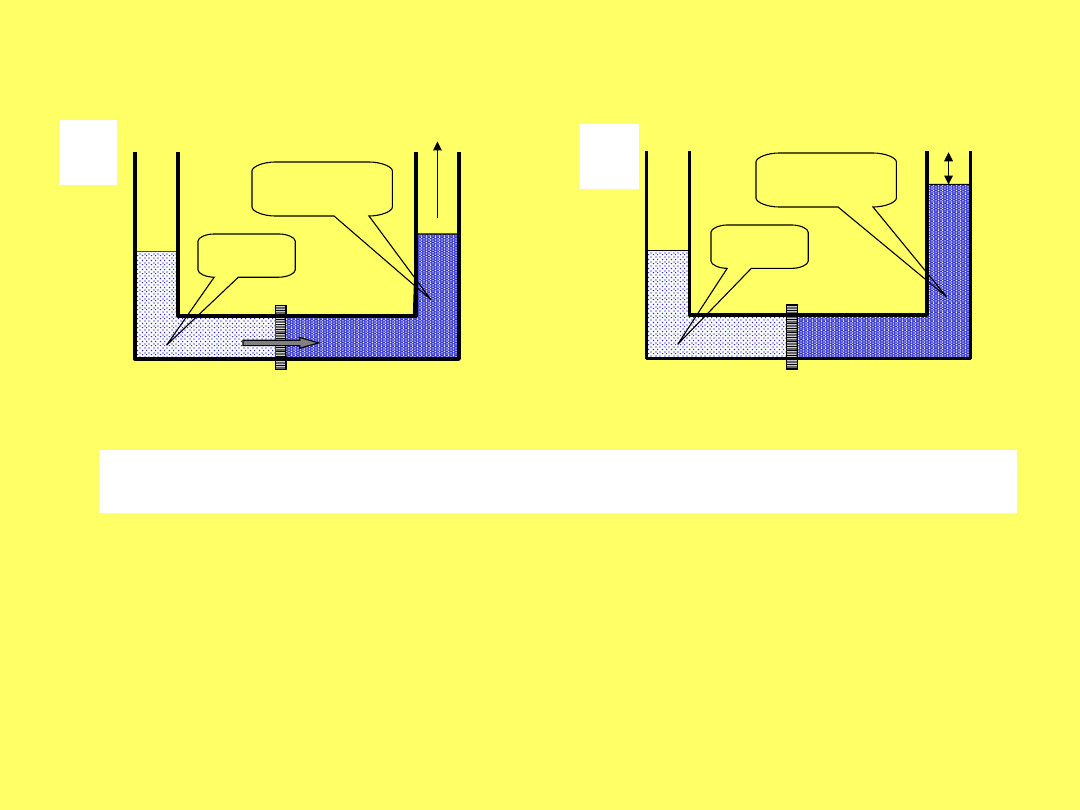
OSMOZA ODWRÓCONA

ROZTWÓ
R

a)

p <



WOD
A

ROZTWÓ
R

p =



b)

WOD
A

a) osmoza, b) równowaga

osmotyczna,

p – ciśnienie

hydrostatyczne

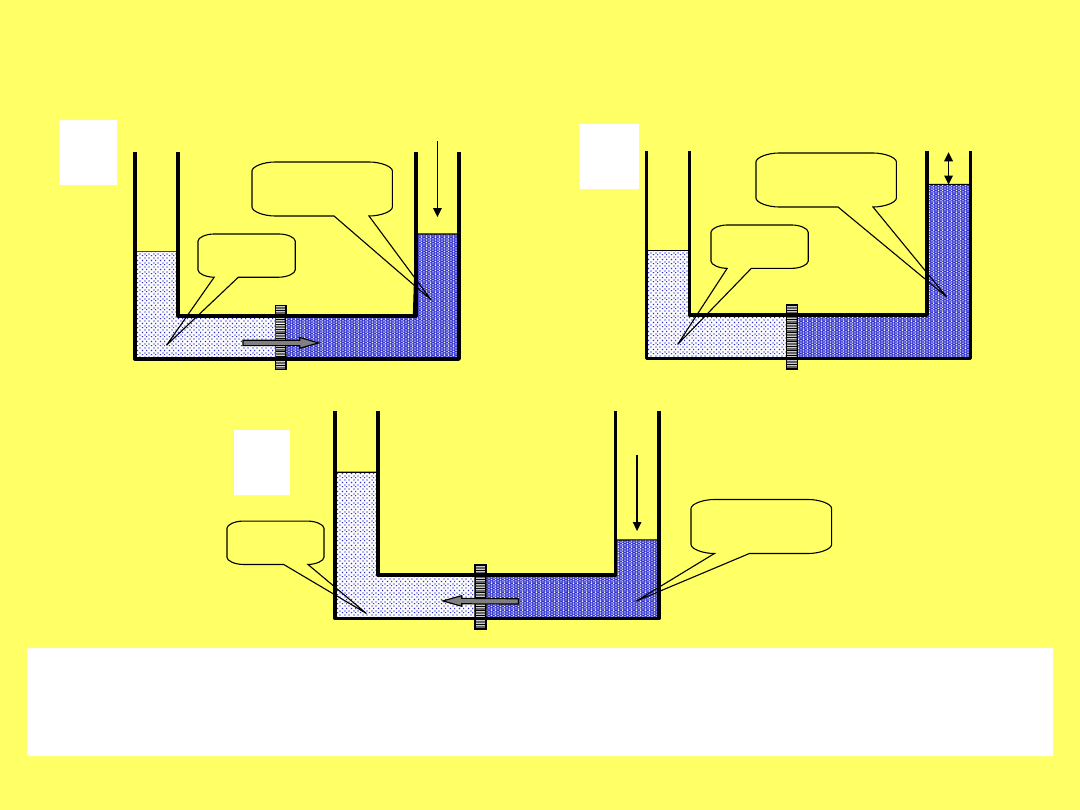
OSMOZA ODWRÓCONA

ROZTWÓ
R

a)

p <



WOD
A

ROZTWÓ
R

p =



b)

WOD
A

c)

WOD
A

ROZTWÓ
R

p >



a) osmoza, b) równowaga osmotyczna, c) odwrócona
osmoza;



- ciśnienie osmotyczne, p – ciśnienie

hydrostatyczne

Wyrównywanie się stężeń w fazach ciekłych

1. Roztwór jest oddzielony od czystego

rozpuszczalnika porowatą przegrodą
przepuszczalną – wyrównywanie się stężeń w
obu fazach ciekłych będzie zachodzić w wyniku
dyfuzji substancji rozpuszczonej do
rozpuszczalnika.

2. Gdy roztwór i rozpuszczalnik są oddzielone

przegrodą półprzepuszczalną - zachodzi
zjawisko osmozy.

3. Gdy między roztworem i rozpuszczalnikiem

znajduje się przegroda nie przepuszczająca
składników układu – zachodzi zjawisko
destylacji, która przenosi rozpuszczalnik do
roztworu.