Zadania z analizy matematycznej - całki nieoznaczone

1. Wyznaczyć całki wykorzystując podstawowe wzory całkowe:

a)
, b)
, c)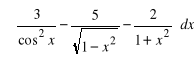

d)
, e)
, f)
, g)
.

2. Wyznaczyć całki za pomocą metody podstawiania:

a)
, b)
, c)
, d)
,

e)
, f)
, g)
, h)
,

i)
, j)
, k)
, l)
.

3. Wyznaczyć całki za pomocą metody całkowania przez części:

a)
, b)
, c)
, d)
,

e)
, f)
, g)
, h)
,

i)
.

4. Wyznaczyć całki z funkcji wymiernych:

a)
, b)
, c)
, d)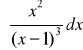
,

e)
, f)
.

5. Wyznaczyć całki:

a)
, b)
, c)
, d)
.

6. Korzystając z tablic wyznaczyć całki funkcji niewymiernych:

a)
, b)
, c)
, d)
.

Uwaga. Wykorzystując dostępne podręczniki wyznaczyć także całki nieoznaczone innych funkcji niż proponowane w tych zadaniach.

Poprawność obliczeń sprawdzić wykorzystując np. matematyczny program komputerowy DERIVE.

J. Szymczak

Zadania z analizy matematycznej - całki oznaczone i ich zastosowania

1. Obliczyć całki oznaczone: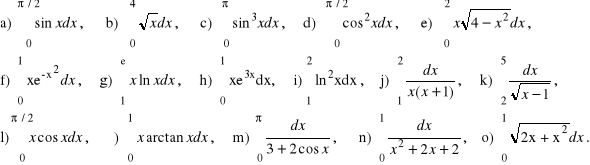

2. Obliczyć pole obszaru płaskiego ograniczonego krzywymi:

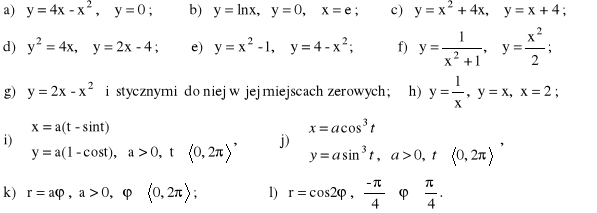
3. Obliczyć długość łuków podanych krzywych:

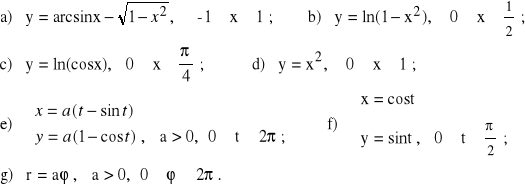
4. Obliczyć objętość bryły powstałej przez obrót wokół osi Ox figury ograniczonej liniami:

a) y = 0, x = 0, x = 1, y = x² ,

b) y = sinx, y = 0 (dla x ∈<0, π〉 ),

c)
, y = 0, x = 4,

d) y = xe^-2x, y = 0, x = 2,

e) y = 1/x, y = 0, x = 1, x = 3.

W przypadku (b) i (c) obliczyć też pole powierzchni bocznej otrzymanej bryły.

5. Obliczyć całki niewłaściwe:

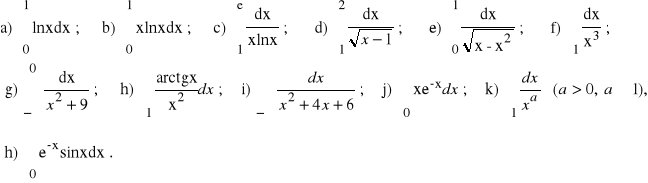
6. Jaka jest objętość bryły obrotowej powstałej przez obrót dookoła osi Ox krzywej y = e^-2x w przedziale nieograniczonym od 0 do ∞ ?

J. Szymczak

Zadania z analizy matematycznej: Funkcje wielu zmiennych

1. Wyznaczyć dziedzinę danej funkcji 2 zmiennych i naszkicować ją:

2. Naszkicować wykresy funkcji 2 zmiennych:

3. Podać przykłady ciągów zbieżnych w przestrzeni metrycznej R² i R³.

4. Podać definicję Heinego granicy funkcji n zmiennych w punkcie p₀.

5. Wyznaczyć granice:

6. Zbadać istnienie granicy funkcji
w punkcie (0,0).

Wyznaczyć granice iterowane tych funkcji w punkcie (0,0).

7. Czy funkcja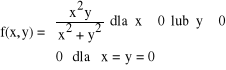
jest ciągła ?

8. Pochodne cząstkowe funkcji wielu zmiennych. Wyznaczyć m.in. pochodne cząstkowe funkcji:

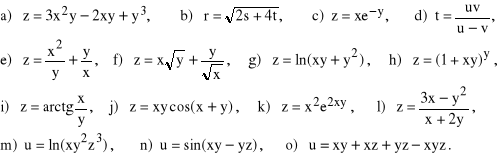
9. Wyznaczyć gradienty podanych funkcji:

10. a) Wyznaczyć gradient funkcji w punkcie M = (1, 2, 2).
b) Obliczyć kąt między gradientami funkcji w punktach .

11. Wyznaczyć pochodne cząstkowe funkcji złożonych:

12. Pochodna kierunkowa.
a) Znaleźć pochodną kierunkową funkcji w punkcie M = (1, 1) w kierunku
wektora
b) Wyznaczyć pochodną kierunkową funkcji w punkcie M = (1, 0, 0)
w kierunku: (1) osi Ox; (2) osi Oy; (3) wektora .
c) Wyznaczyć pochodną kierunkową funkcji u = xy² w punkcie M = (2, 1) w kierunku:
(1) wektora (2) gradientu tej funkcji w danym punkcie.

13. Sprawdzić, że funkcja u(x,y) spełnia dane równanie różniczkowe:

14. Wyznaczyć różniczkę zupełną następujących funkcji:

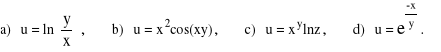
15. Stosując różniczkę zupełną wyznaczyć przybliżoną wartość wyrażeń:

16. Wyznaczyć pochodne cząstkowe rzędu drugiego podanych funkcji:

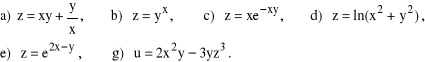
17. Sposób wyznaczania ekstremum funkcji wielu zmiennych. Jak znaleźć wartość najmniejszą i
wartość największą funkcji n zmiennych w pewnym zbiorze ?
Wyznaczyć ekstrema lokalne funkcji:

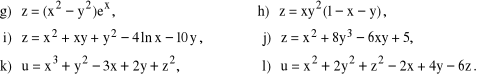
18. Wyznaczyć największą i najmniejszą wartość funkcji
w trójkącie
o wierzchołkach (0, 0), (6, 0), (0, 6).

19. Wyznaczyć największą i najmniejszą wartość funkcji z = x² + 2y² w obszarze

{(x,y): x² + y² ≤ 25, y ≥ 3}

20. Wyznaczyć globalne ekstrema warunkowe funkcji, stosując pomocniczą funkcję Lagarange'a:

a) f(x,y) = xy przy warunku x² + y² = 8

b) f(x,y) = 4y² - x² przy warunku y = x² + 1.

21. Prostopadłościenny kontener ma mieć objętość 8 m³. Podać wymiary kontenera, przy których mamy zminimalizowany koszt materiału potrzebnego do jego wykonania, jeżeli materiał na spód i wierzch jest dwa razy droższy niż materiał na boki tego kontenera.

22. Omówić zasady metody najmniejszych kwadratów w przypadku wyznaczania linii regresji dla następujących danych:

xi	2	3	4	5	6
yi	4	4	3	2	2

J. Szymczak

2

---