Wydział: Mechaniczno-Technologiczny Dzień: Czwartek
Kierunek: MiBM (dzienne) Godzina: 12.00
Grupa dziekańska: 5
Semestr: 2
Laboratorium Mechaniki Ogólnej
Ćwiczenie: C.
MACIERZOWA ANALIZA SIŁ W PRĘTACH KRATOWNICY PŁASKIEJ
Sekcja nr. 5:
Zawisz Roman
Śliwiak Paweł
Szymiczek Krzysztof
Słomka Jan
Wieczorek Michał
1. CEL ĆWICZENIA
Celem ćwiczenia jest zapoznanie się z zastosowaniem rachunku macierzowego do określania sił w prętach płaskiej kratownicy statycznie wyznaczalnej.
2. OBOWIĄZUJĄCY ZAKRES WIEDZY
Student przed przystąpieniem do ćwiczenia powinien znać następujące zagadnienia:
• Założenia technicznej teorii kratownic.
• Metody rozwiązywania kratownic.
• Podstawy rachunku macierzowego.
3. WSTĘP TEORETYCZNY
Kratownicą statycznie wyznaczalną będziemy nazywali kratownicę, w której liczba niewiadomych sił w prętach oraz reakcji podporowych jest równa liczbie równań równowagi. Rozważania ograniczymy do kratownic płaskich, spełniających założenia technicznej teorii kratownic, tzn. odpowiednio podpartych (statycznie zewnętrznie wyznaczalnych), geometrycznie niezmiennych zbudowanych z prętów przegubowych i obciążonych w węzłach. W takim przypadku siły w prętach tworzą w każdym z węzłów kratownicy zbieżny układ sił. Dla kratownicy posiadającej m węzłów oraz n prętów możemy napisać 2m równań równowagi odpowiadających rzutom sił na osie układu współrzędnych:
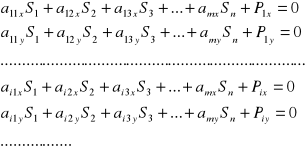
i=1...,m, j=1...,n (14.1)
gdzie: S, - siła wewnętrzna w pręcie o numerze j=1.., n,
aijx, aijy - współczynniki w równaniu równowagi dla węzła i=1..., m zrzutowanym odpowiednio na osie x i y układu współrzędnych stojące przy sile wewnętrznej o numerze j,
Pix, Piy - rzuty sił zewnętrznych (uwzględniając reakcje węzłów) na osie x i y układu współrzędnych, przyłożonych w węźle i.
Współczynniki aijx aijy mogą być równe zero lub być różne od zera w zależności od tego, czy dany pręt występuje w rozpatrywanym węźle. czy też nie występuje. Układ równań równowagi (14.1) możemy zapisać zatem w postaci macierzowej:
P=-A*S (14 .2)
gdzie: P - macierz kolumnowa składowych sił zewnętrznych przyłożonych w węzłach
zawierająca niewiadome podporowe,
A - macierz współczynników równań równowagi węzłów,
S - macierz kolumnowa sił wewnętrznych.
Istota macierzowej metody wyznaczania sił w prętach kratownicy polega więc
a automatycznym generowaniu równań równowagi wszystkich węzłów kratownicy zapisaniu ich w postaci macierzowej. Równania te umożliwiają wyznaczenie sił we wszystkich n prętach oraz wyznaczenie 3 niewiadomych reakcji podporowych. Kluczem do tej metody jest macierz A, której struktura zależy od postaci konstrukcyjnej analizowanej kratownicy. W dalszej części pokażemy sposób budowy tej macierzy. Dla lepszego rozumienia prezentowanego algorytmu w rozdziale 4 zamieszczono przykład obliczeniowy.
3.1. Budowa macierzy połączeń
Macierz połączeń zawiera konfigurację kratownicy, tzn. zapisana jest w niej informacja o połączeniach prętów w poszczególnych węzłach. Obliczenia rozpoczynamy od ponumerowania w dowolnej kolejności węzłów i prętów kratownicy [9] (rys. 14.2). Przyjmujemy, że początkiem pręta jest węzeł o niższym numerze. Następnie budujemy macierz włączeń węzłów
![]()
i=1,2,...,m; j=1,2,...,n. (14.3)
gdzie: m - liczba węzłów,
n - liczba prętów,
i - numer węzła,
j - numer pręta.
Wiersze macierzy A odpowiadają węzłom, a kolumny prętom (patrz (14.12)). W każdej kolumnie znajdują się tylko dwa niezerowe elementy:
„1" - w wierszu o numerze równym numerowi węzła, który jest początkiem pręta,
„-l" - w wierszu odpowiadającym końcowi pręta.
3.2. Budowa macierzy współrzędnych węzłów.
Obieramy dowolny prostokątny układ współrzędnych. Dla uproszczenia zapisu osie układu oznaczymy jako 7 i 2 w miejsce x i y (rys. 14.1). Macierz współrzędnych węzłów ma następującą postać:
![]()
i=1,2,...,m; j=1,2. (14.4)
Wiersze macierzy odpowiadają poszczególnym węzłom kratownicy, natomiast kolumny współrzędnym węzłów względem osi 1 i 2 (patrz (14.13)).
3.3. Budowa macierzy cosinusów kierunkowych.
W macierzy tej zapisane są cosinusy kierunkowe poszczególnych prętów kratownicy, a co za
tym idzie, poszczególnych sił wewnętrznych. Zbudowanie tej macierzy wymaga określenia składowych długości prętów w przyjętym układzie współrzędnych oraz wyznaczenie ich całkowitej długości. Na tej podstawie możemy dopiero określić cosinusy nachylenia poszczególnych prętów kratownicy do osi układu współrzędnych. Macierz składowych długości prętów:
(14.5)
![]()
i=1,2,...,n; j=1,2.
obliczymy z równania (patrz (14.14)).
![]()
(14.6)
Długości prętów są równe (patrz (14.15))
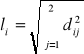
(14.7)
a ich cosinusy kierunkowe
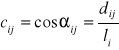
i=1,...,n; j=1,2.
Macierz cosinusów kierunkowych C ma następującą postać:
![]()
Wiersze macierzy odpowiadają poszczególnym prętom kratownicy, natomiast cosinusom kątów nachylenia prętów do osi 1 i 2 układu współrzędnych (patrz (14.16)). Pomiędzy siłami zachodzi następująca zależność (rys. 14.1.)
Sij= -cij Si. (14.10)
Rys. 14.1
Zakładamy, że w węzłach kratownicy przyłożone są siły zewnętrzne, których składowe są elementami macierzy P (patrz (14.16)). Między macierzami sił zewnętrznych P i wewnętrznych S zachodzi związek (14.2) wynikający z równowagi węzłów:
P = -A S
3.4. Budowa macierzy współczynników równań równowagi węzłów
Macierz A (patrz (14.17)) powstaje z macierzy K przez podstawienie w miejsce elementów:
„l" - odpowiednich wierszy macierzy cosinusów kierunkowych z macierzy C, odpowiadających poszczególnym prętom kratownicy,
„-l" - jw., ale ze znakiem przeciwnym,
„O" - dwuelementowego wektora zerowego.
Wyznaczenie sił wewnętrznych wymaga wyeliminowania z macierzy A wierszy, a z macierzy kolumnowej P elementów odpowiadających warunkom podparcia. Po rozwiązaniu takiego uproszczonego układu równań (14.18) wyznaczymy siły wewnętrzne w prętach kratownicy. Wartość dodatnia siły oznacza, że pręt jest rozciągany, a ujemna, że ściskany.
Znając wartości tych sił i korzystając z odrzuconych równań zawierających składowe reakcji możemy wyznaczyć reakcje w podporach (14.19).
4. OPIS PROGRAMU
Na podstawie przedstawionego algorytmu obliczeń opracowano program komputerowy. Program bezpośrednio buduje macierz współczynników równań równowagi węzłów. Jeżeli reakcja w podporze przesuwnej nie jest równoległa do którejś z osi układu współrzędnych, program przeprowadza transformację tego układu tak, aby jedna z osi była do niej równoległa. Po wyeliminowaniu wierszy odpowiadających warunkom podparcia rozwiązywany jest układ równań metodą Gaussa z wyborem elementu podstawowego. Następnie korzystając z wyznaczonych wartości sił wewnętrznych oraz odrzuconych wierszy odpowiadających równaniom, w których występują składowe reakcji podporowych, wyznaczamy reakcje w punktach podparcia. Program umożliwia wprowadzanie danych z klawiatury lub ze zbioru zapisanego na dysku. Po uruchomieniu programu, wprowadzając dane z klawiatury, należy podać:
• liczbę węzłów,
• liczbę prętów,
dla każdego węzła:
• numery prętów o początkach w tym węźle,
• numery prętów o końcach w tym węźle,
• współrzędne x, y,
dla węzłów podporowych:
• numer węzła z podporą stałą RAy,
• numer węzła z podporą przesuwną RB,
• kąt zawarty pomiędzy reakcją RB i osią (Oy, dla każdego węzła, w którym przyłożono siłę zewnętrzną:
• numer węzła,
• wartość składowej siły równoległej do osi Ox,
• wartość składowej siły równoległej do osi Oy.
Ponadto program umożliwia zapis wyników obliczeń do zbioru wyników na dysku, wydruk wyników obliczeń lub ich podgląd na ekranie monitora.
5. PRZEBIEG ĆWICZENIA
Określić wymiary kratownicy oraz charakter obciążenia.
Narysować kratownicę i przyjmując układ współrzędnych ponumerować pręty i węzły.
Przygotować dane do programu zgodnie z punktem 14.4.
Przeprowadzić obliczenia numeryczne.
Wyznaczyć wartości sił wewnętrznych w prętach kratownicy oraz reakcje w podporach.
Zmienić stan obciążenia kratownicy i ponownie przeprowadzić obliczenia.
Obliczenia powtórzyć dla różnych wariantów konstrukcji kratownicy.
Przeprowadzić analizę otrzymanych wyników.
Sporządzić sprawozdanie z przebiegu ćwiczenia
5
Wyszukiwarka
Podobne podstrony:
Doswiadczalne wyznaczanie sil w pretach kratownicy plaskiej , Księgozbiór, Studia, Mechnika Doświadc
Prety kratownicy plaskiej, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Analiza ruchu prostolinioweg1, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Proto analiza ruchu, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Sprawozdanie ilustracji zasady zachowania pedu, Księgozbiór, Studia, Mechnika Doświadczalna
Pomiar bezwladnosci ciala sztywnego za pomoca wahadla skretn, Księgozbiór, Studia, Mechnika Doświadc
Metoda Rungego-Kutty, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Plan laboratoriow, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Protokol pomiarowy, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
tarcie w naszym wykonaniu, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Ilustracja zasady zachowania pedu, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Protokol pomiarowy 1, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Sprawozdanie A-do wydruku, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Wyznaczanie polozenia srodka masy i masowego momentu bezwlad, Księgozbiór, Studia, Mechnika Doświadc
Protokol pomiarowy do cwiczenia, Księgozbiór, Studia, Mechnika Doświadczalna
więcej podobnych podstron