Okrąg opisany na czworokącie

przez

matematix

» 09 Mar 2015, 21:40

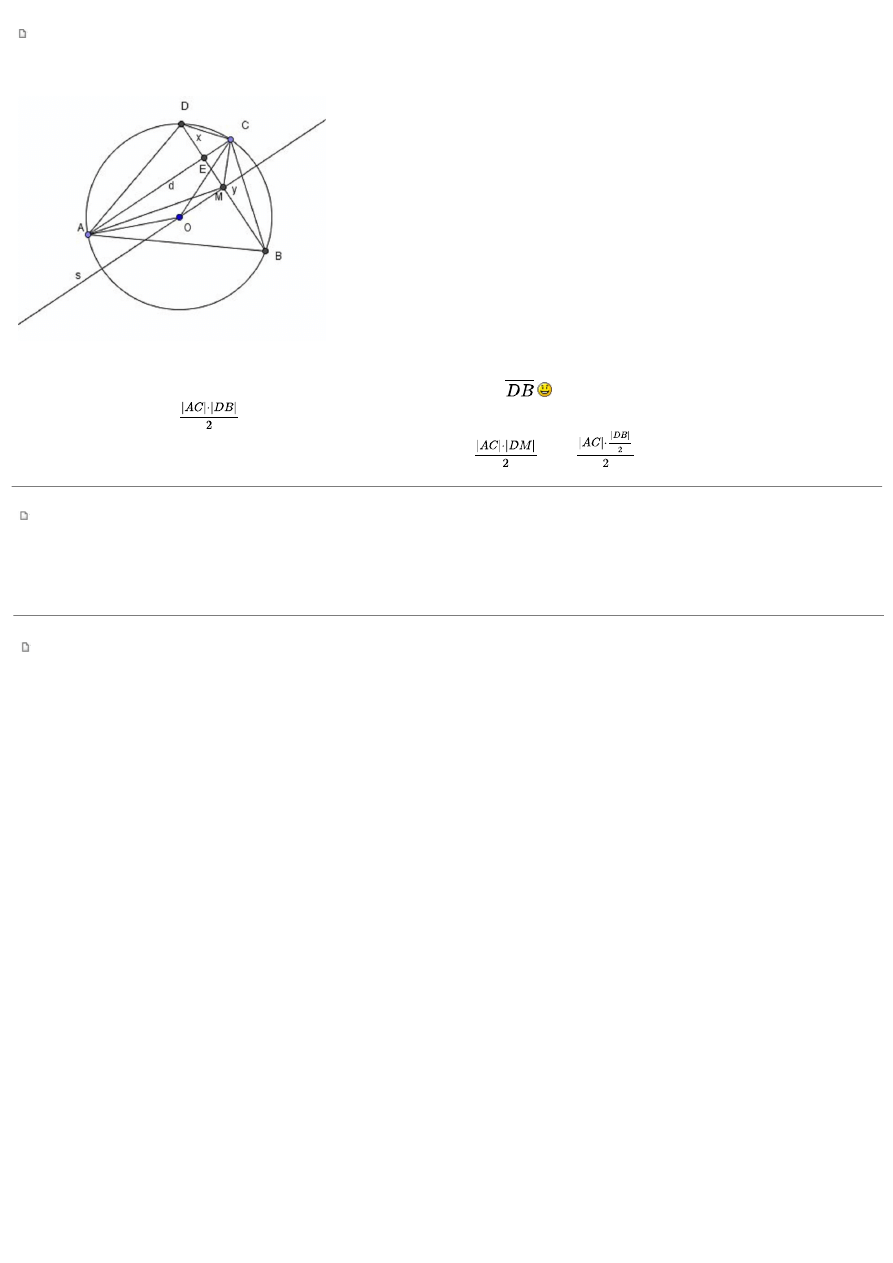
W czworokącie ABCD przekątne są prostopadłe oraz na tym czworokącie można opisać okrąg o środku w punkcie O. Udowodnij, że łamana AOC
dzieli czworokąt ABCD na dwie figury o równych polach.

przez

Crazy Driver

» 10 Mar 2015, 03:18

Rozwiązanie jest mało eleganckie i pewnie można znaleźć lepsze.

Najlepiej zacząć rysunek od okręgu i wybrania dwóch cięciw prostopadłych

i

. Niech

będzie promieniem okręgu,

,

.

Teraz, wykorzystując kąty wpisane oparte na tych samych łukach i prostopadłość przekątnych czworokąta, można wyznaczyć:

Kąt

jest kątem środkowym opartym na tym samym łuku co

, więc

.

Teza mówi, że

Okrąg opisany na czworokącie

jest też okręgiem opisanym na trójkątach

i

. Skorzystamy ze wzoru na pole trójkąta w

zależności od promienia okręgu opisanego i kątów wewnętrznych.

przez

radagast

» 10 Mar 2015, 08:14

Bardzo fajne zadanie gimnazjalne:

Wystarczy zauważyć, że pola trójkątów ACO oraz ACM są równe (s to symetralna

Pole czworokąta ABCD to

Pole czworokąta AOCD jest takie jak pole czworokąta AMCD, a ono wynosi

czyli

przez

matematix

» 10 Mar 2015, 16:41

Czemu symetralna odcinka DB ma przechodzić przez środek okręgu?

I czy pole każdego czworokąta to iloczyn jego przekątnych podzielony przez 2?

przez

radagast

» 10 Mar 2015, 16:44

matematix napisał(a):Czemu symetralna odcinka DB ma przechodzić przez środek okręgu?

Bo symetralna odcinka to zbiór wszystkich punktów równo odległych od jego końców.

matematix napisał(a):I czy pole każdego czworokąta to iloczyn jego przekątnych podzielony przez 2?

Tylko wówczas gdy przekątne są prostopadłe.