VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

MATEMATYKA

1

alfabetgrecki

2

cyfryrzymskie

2

jednostkimiar

3

wzoryskróconegomnożenia

4

podzielnośćliczb

4

przedrostki

5

skala

5

zbiory

6

funkcje

7

trójkąty

8

podziałkątów

10

wielokąty

11

kołoiokrąg

12

bryły

13

działanianaprocentach

13

pojęciamatematycznewpigułce

SpiS treści

ALFABet GrecKi

Duża litera

Mała litera

Nazwa litery

Α

α

alfa

Β

β

beta

Γ

γ

gamma

Δ

δ

delta

Ε

ε

epsilon

Ζ

ζ

dzeta

Η

η

eta

Θ

θ

teta

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

cYFrY rZYMSKie

cyfra rzymska

cyfra arabska

I

1

IV

4

V

5

VI

6

IX

9

X

10

XI

11

L

50

C

100

D

500

M

1000

JeDNOStKi MiAr

JEDNOSTKI DŁUGOŚCI

kilometr

hektometr

metr

decymetr

centymetr

milimetr

mikrometr

km

hm

m

dm

cm

mm

µm

1 km

0,1 km

0,001 km

0,0001 km

0,00001 km

0,000001 km

0,000000001 km

10 hm

1 hm

0,01 hm

0,001 hm

0,0001 hm

0,00001 hm

0,00000001 hm

1 000 m

100 m

1 m

0,1 m

0,01 m

0,001 m

0,000001 m

10 000 dm

1 000 dm

10 dm

1 dm

0,1 dm

0,01 dm

0,00001 dm

100 000 cm

10 000 cm

100 cm

10 cm

1 cm

0,1 cm

0,0001 cm

1 000 000 mm

100 000 mm

1 000 mm

100 mm

10 mm

1 mm

0,001 mm

1 000 000 000 µm

100 000 000 µm

1 000 000 µm

100 000 µm

10 000 µm

1 000 µm

1 µm

JEDNOSTKI MASY

tona

kwintal

kilogram

dekagram

gram

miligram

t

q

kg

dag

g

mg

1 t

0,1 t

0,001 t

0,00001 t

0,000001 t

0,000000001 t

10 q

1 q

0,01 q

0,0001 q

0,00001 q

0,00000001 q

1 000 kg

100 kg

1 kg

0,01 kg

0,001 kg

0,000001 kg

100 000 dag

10 000 dag

100 dag

1 dag

0,1 dag

0,0001 dag

1 000 000 g

100 000 g

1 000 g

10 g

1 g

0,001 g

1 000 000 000 mg

100 000 000 mg

1 000 000 mg

10 000 mg

1 000 mg

1 mg

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

JEDNOSTKI OBJĘTOŚCI

kilometr

sześcienny

metr

sześcienny

hektolitr

decymetr

sześcienny

/litr/

centymetr

sześcienny

/mililitr/

milimetr

sześcienny

km

3

m

3

hl

dm

3

/l/

cm

3

/ml/

mm

3

1 km

3

0,000000001 km

3

0,0000000001 km

3

1 000 000 000 m

3

1 m

3

0,1 m

3

0,001 m

3

0,000001 m

3

0,000000001 m

3

10

10

hl

10 hl

1 hl

0,01 hl

0,00001 hl

0,00000001 hl

10

12

dm

3

/l/

1 000 dm

3

/l/

100 dm

3

/l/

1dm

3

/l/

0,001 dm

3

/l/

0,000001 dm

3

/l/

10

15

cm

3

/ml/

1 000 000 cm

3

/ml/

100 000 cm

3

/ml/

1 000 cm

3

/ml/

1 cm

3

/ml/

0,001 cm

3

/ml/

10

18

mm

3

1 000 000 000 mm

3

100 000 000 mm

3

1 000 000 mm

3

1 000 mm

3

1 mm

3

JEDNOSTKI POLA POWIERZCHNI

kilometr

kwadratowy

hektar

ar

metr

kwadratowy

decymetr

kwadratowy

centymetr

kwadratowy

milimetr

kwadratowy

km

2

ha

a

m

2

dm

2

cm

2

mm

2

1 km

2

0,01 km

2

0,0001 km

2

0,000001 km

2

0,00000001 km

2

0,0000000001

km

2

0,000000000001

km

2

100 ha

1 ha

0,01 ha

0,0001 ha

0,000001 ha

0,00000001 ha

0,0000000001 ha

10 000 a

100 a

1 a

0,01 a

0,0001 a

0,000001 a

0,00000001 a

1 000 000 m

2

10 000 m

2

100 m

2

1 m

2

0,01 m

2

0,0001 m

2

0,000001 m

2

100 000 000 dm

2

1 000 000 dm

2

10 000 dm

2

100 dm

2

1 dm

2

0,01 dm

2

0,0001 dm

2

10

10

cm

2

10

8

cm

2

1 000 000 cm

2

10 000 cm

2

100 cm

2

1 cm

2

0,01 cm

2

10

12

mm

2

10

10

mm

2

10

8

mm

2

1 000 000 mm

2

10 000 mm

2

100 mm

2

1 mm

2

WZOrY SKrÓcONeGO MNOŻeNiA

(a–b)

2

=a

2

–2ab+b

2

kwadratróżnicy

(a+b)

2

=a

2

+2ab+b

2

kwadratsumy

a

2

–b

2

=(a–b)(a+b)

różnicakwadratów

a

3

–b

3

=(a–b)(a

2

+ab+b

2

)

różnicasześcianów

a

3

+b

3

=(a+b)(a

2

–ab+b

2

)

sumasześcianów

(a–b)

3

=a

3

–3a

2

b+3ab

2

–b

3

sześcianróżnicy

(a+b)

3

=a

3

+3a

2

b+3ab

2

+b

3

sześciansumy

(a+b+c)

2

=a

2

+b

2

+c

2

+2ab+2ac+2bc

kwadratsumytrzechskładników

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

pODZieLNOśĆ LicZB

Dowolna liczba naturalna jest podzielna przez:

2

gdyjejostatniącyfrąjest0,2,4,6lub8

3

gdysumajejcyfrdzielisięprzez3

4

gdyliczba,wyrażonadwiemaostatnimijejcyframi,dzielisięprzez4

5

gdyjejostatniącyfrąjest0albo5

6

gdydzielisięprzez2i3

7

gdyróżnicamiędzyliczbąwyrażonąkolejnymitrzemaostatnimicyframidanejliczby

aliczbąwyrażonąpozostałymicyframitejliczby(lubodwrotnie)dzielisięprzez7

8

gdyliczbawyrażonatrzemaostatnimijejcyframidzielisięprzez8

9

gdysumajejcyfrdzielisięprzez9

10

gdyostatniąjejcyfrąjest0

11

gdyróżnicasumyjejcyfrstojącychnamiejscachparzystychisumycyfrstojącychnamiejscach

nieparzystychdzielisięprzez11

prZeDrOStKi

powiększają

przedrostek

skrót

ilerazyzwiększajednostkę

tera

T

10

12

bilion

giga

G

10

9

miliard

mega

M

10

6

milion

kilo

k

10

3

tysiąc

hekto

h

10

2

sto

deka

da

10

dziesięć

pomniejszają

przedrostek

skrót

jakatoczęśćjednostki

decy

d

dziesiątaczęść

centy

c

setnaczęść

mili

m

tysięcznaczęść

mikro

k

milionowaczęść

nano

n

miliardowaczęść

piko

p

bilionowaczęść

femto

f

biliardowaczęść

atto

a

trylionowaczęść

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

SKALA

Skala

1 : 1

1 : k

k : 1

wymiary

rzeczywiste

każdywymiarzmniejszony

krazy

każdywymiarzwiększony

krazy

obwód

O

krazymniejszy[O:k]

krazywiększy[O·k]

polepowierzchni

P

k

2

razymniejsze[P:k

2

]

k

2

razywiększe[P·k

2

]

objętość

V

k

3

razymniejsza[V:k

3

]

k

3

razywiększa[V·k

3

]

ZBiOrY

podstawowe symbole i oznaczenia

Symbol

Znaczenie

Symbol

Znaczenie

i(koniunkcja)

zbiór,któregoelementamisąa,b,c

lub(alternatywa)

iloczynkartezjańskizbiorówAiB

nieprawdaże(zaprzeczenie)

zbiórpusty

wtedyitylkowtedy(równoważność)

przedziałotwartyokońcachaib

jeżeli...,to...(implikacja)

przedziałdomkniętyokońcachaib

zawierasięw

jestrówny

należydo

jesttożsamościoworówny(jestprzystający)

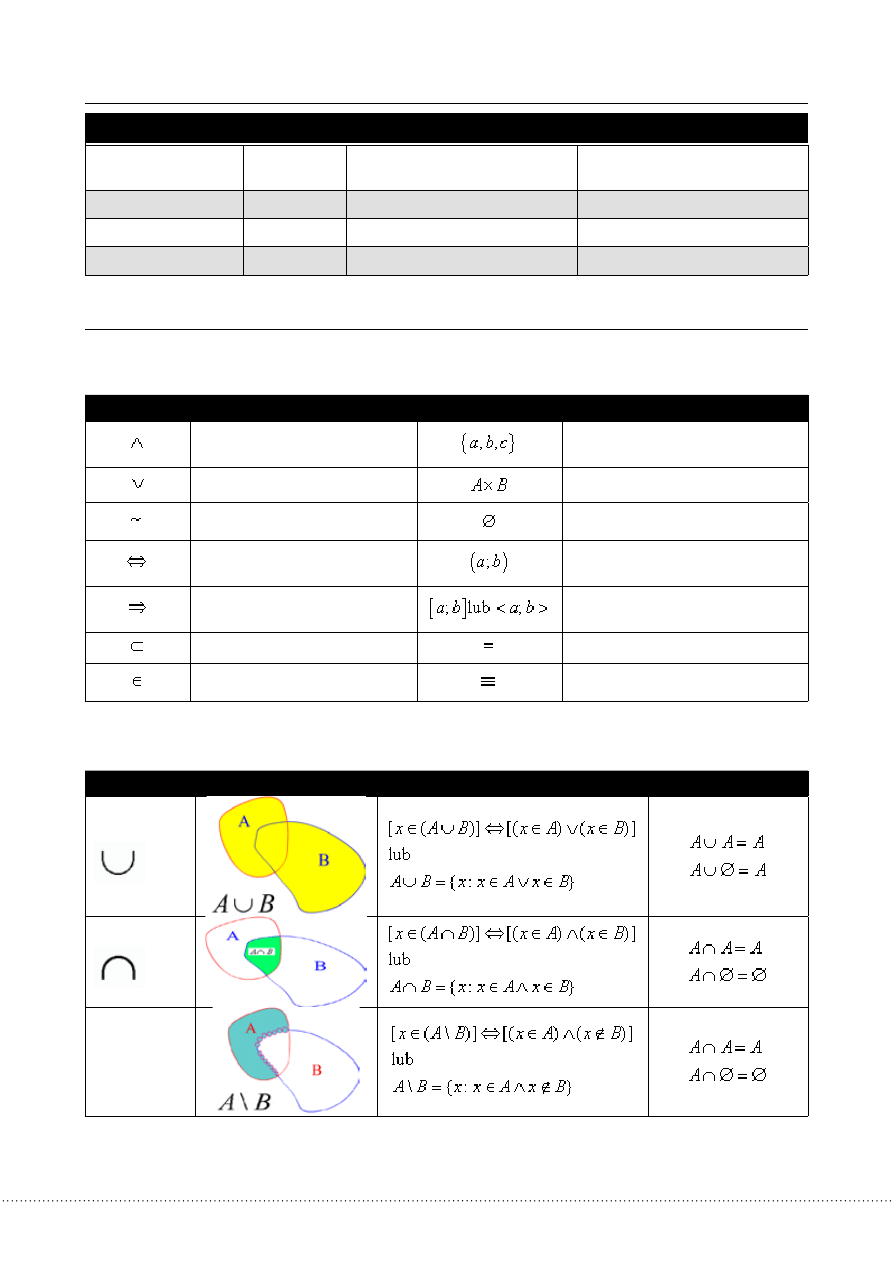
Działania na zbiorach

Działanie

ilustracja graficzna

Zapis symboliczny definicji

Niektóre własności

Sumazbiorów

Iloczynzbiorów

Różnicazbiorów\

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

relacje między zbiorami

Równośćzbiorów

ZbioryAiBnazywamyrównymiwtedyitylkowtedy,gdykażdyelementzbioruAjestelementemzbioruB

inaodwrót.

Zawieraniesię

zbiorów(inkluzja)

ZbiórAzawierasięwzbiorzeB

wtedyitylkowtedy,

gdykażdyelementzbioruAjest

elementemzbioruB(Anazywamy

podzbioremB,Bzaśnadzbiorem

zbioruA).

Jeżeli

i

to

Zbioryrozłączne

Zbiory,którychiloczynjestzbiorem

pustym,nazywamyrozłącznymi.

FUNKcJe

JeżelimamydwaniepustezbioryA,BikażdemuelementowizezbioruAprzyporządkujemydokładniejedenelement

zezbioruB,totakieprzyporządkowanienazywamyFUNKCJĄokreślonąnazbiorzeAowartościachwzbiorzeB.

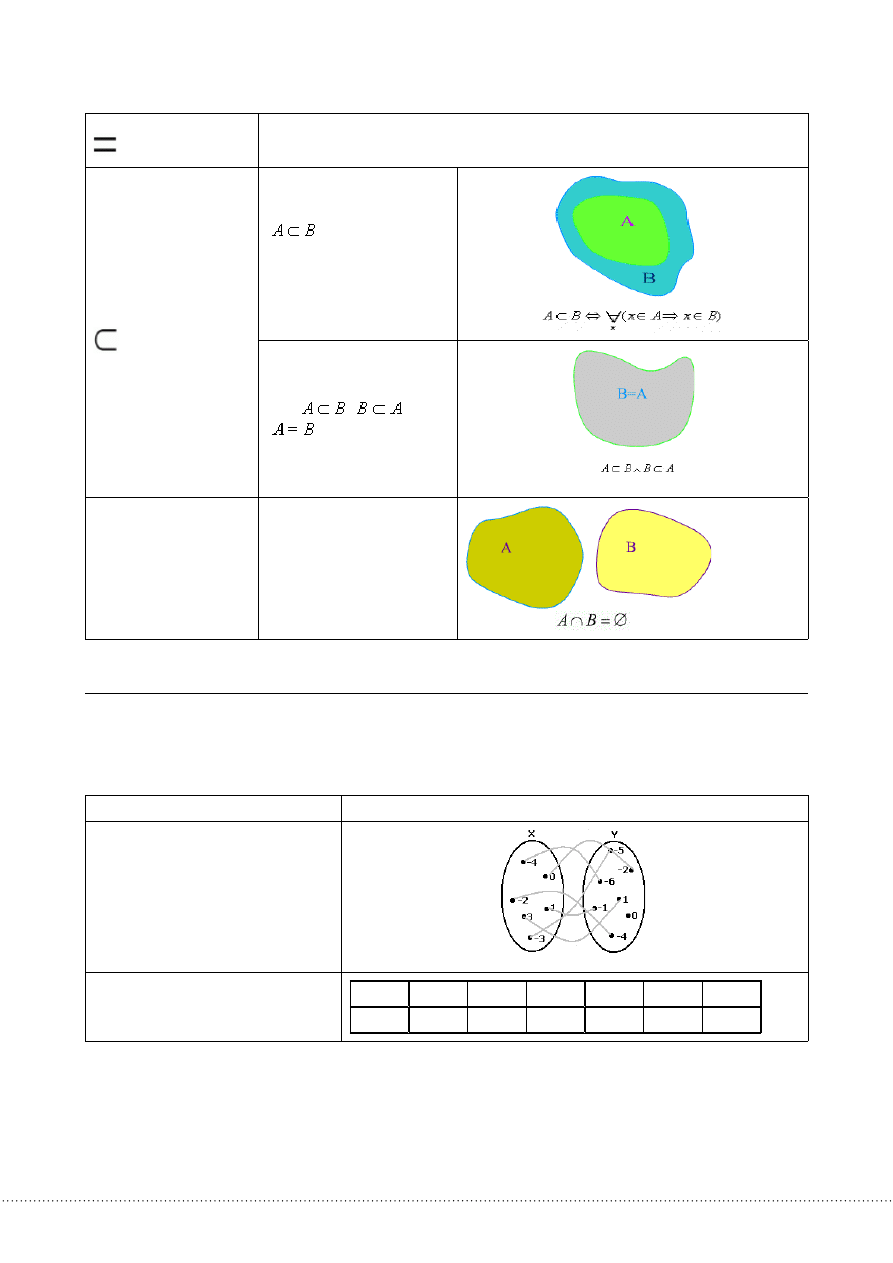
Sposoby opisywania funkcji

opissłowny

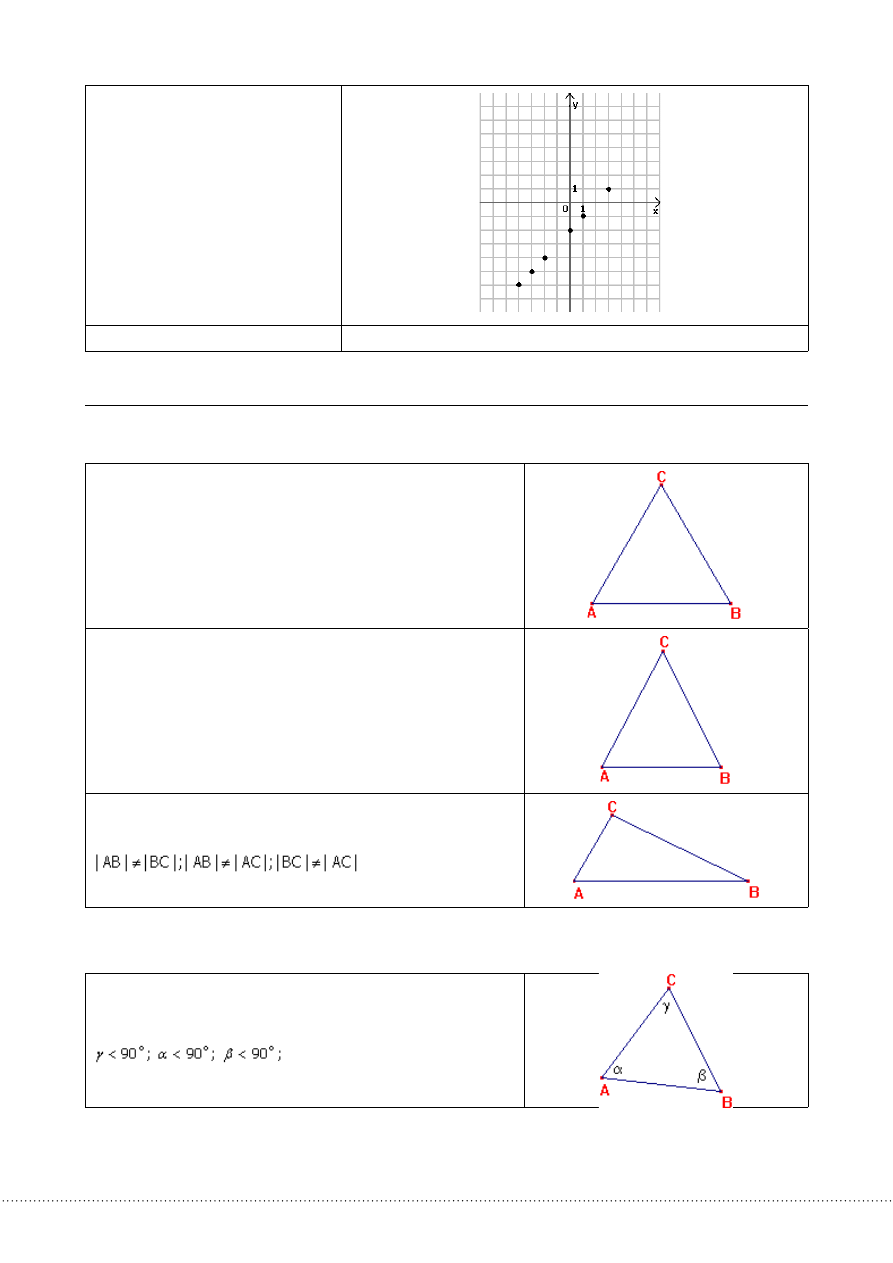
Każdejliczbiezezbioru{-4,-3,-2,0,1,3}przypisujemyliczbęodwaodniejmniejszą

graficzny

tabelka

x

-4

-3

-2

0

1

3

y

-6

-5

-4

-2

-1

1

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona 7 z 7

wykres

wzór

y=x-2;xnależy{-4,-3,-2,0,1,3}lub(-4,-6);(-3,-5);(-2,-4);(0,-2);(1,-1);(3,1)

trÓJKĄtY

Klasyfikacja ze względu na boki

Trójkątemrównobocznymnazywamytrójkąt,któregowszystkiebokimajątęsamą

długość.

|AB|=|BC|=|AC|

Trójkątemrównoramiennymnazywamytrójkąt,którego(conajmniej)dwabokimają

tęsamądługość.

|AC|=|BC|

Trójkątemróżnobocznymnazywamytrójkąt,któregobokimająróżnedługości.

Klasyfikacja ze względu na kąty

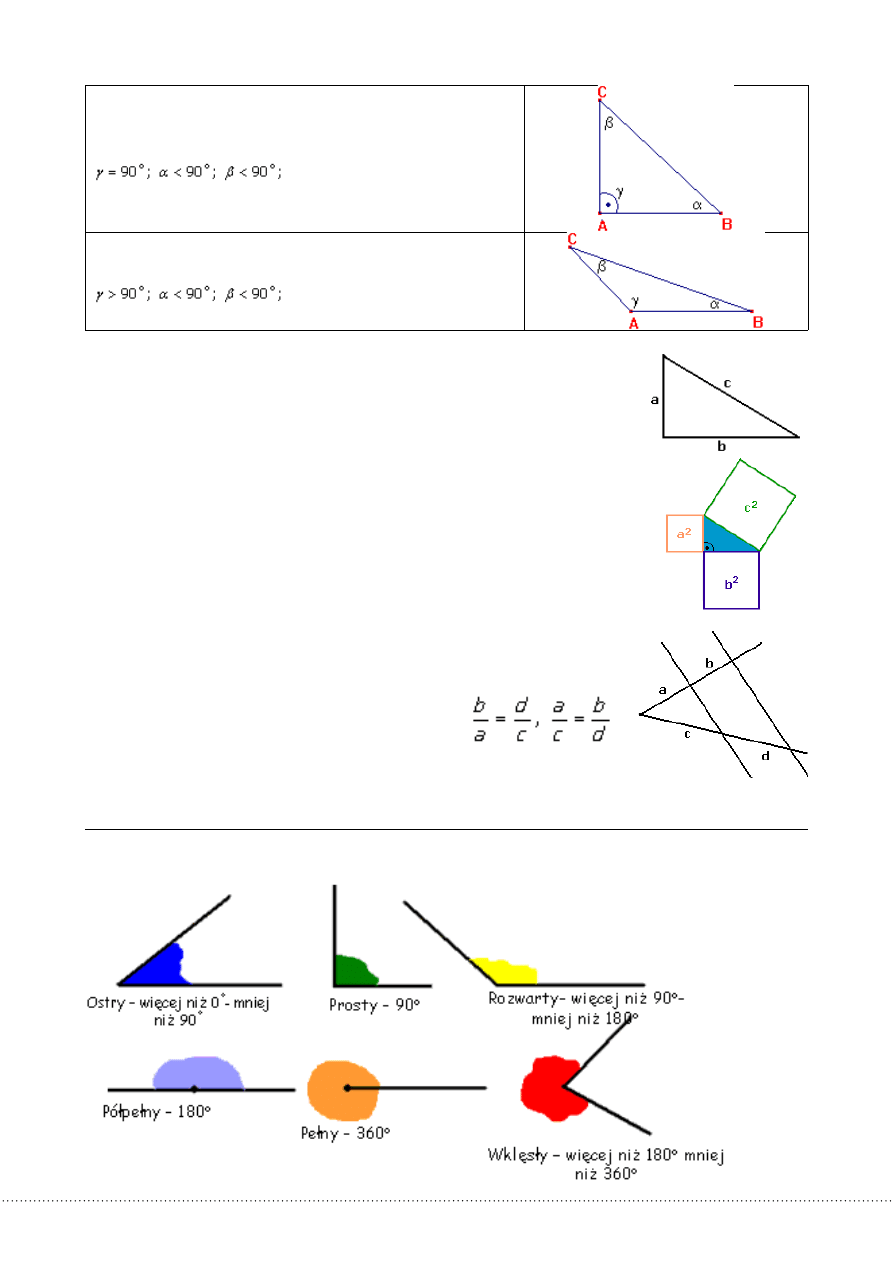
Trójkątemostrokątnymnazywamytrójkąt,któregowszystkiekątysąostre.

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

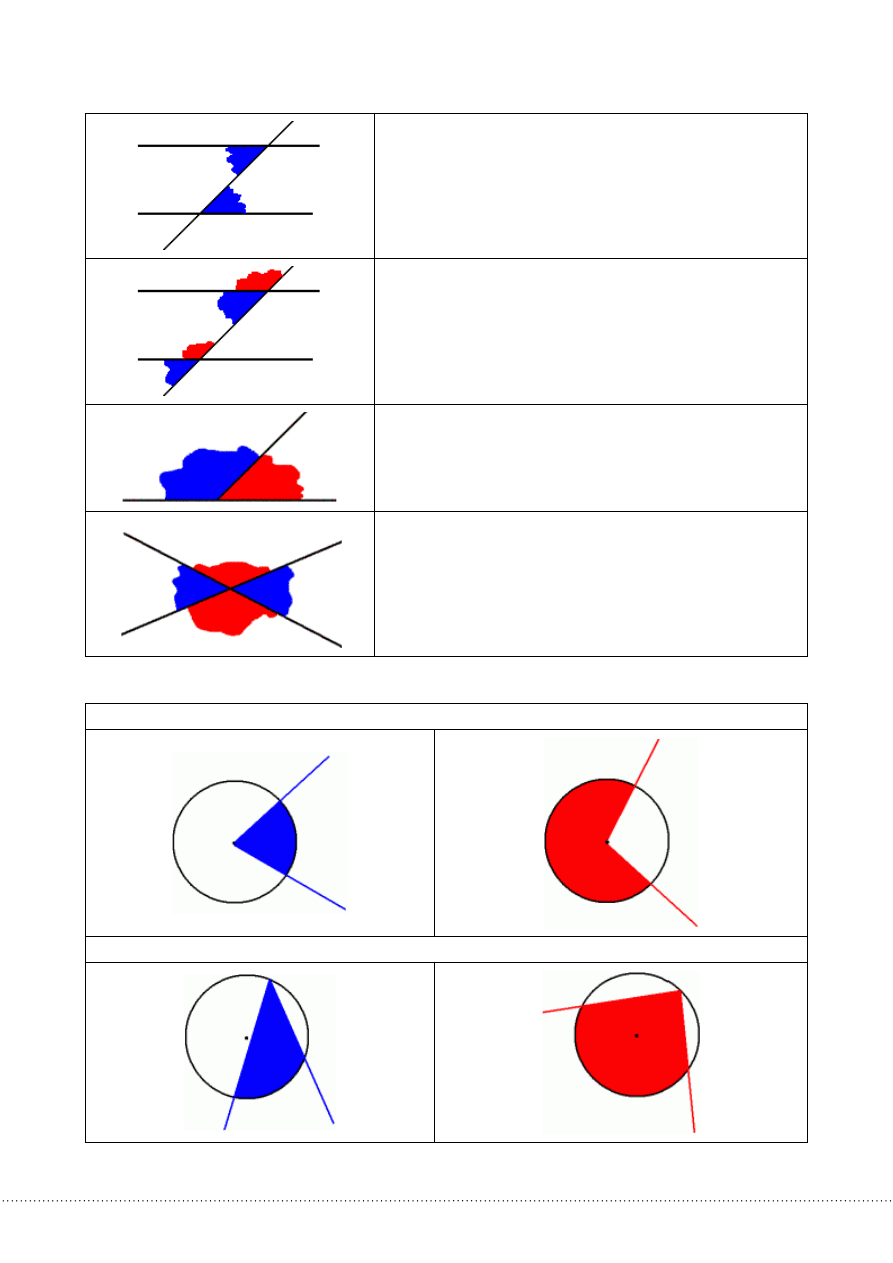
Trójkątemprostokątnymnazywamytrójkąt,któregojedenzkątówjestprosty.

Trójkątemrozwartokątnymnazywamytrójkąt,któregojedenzkatówjestrozwarty.

twierdzenie pitagorasa

W trójkącie prostokątnym kwadrat długości przeciwprostokątnej jest równy sumie

kwadratówdługościobuprzyprostokątnych.
c

2

= a

2

+ b

2

Wtrójkącieprostokątnymkwadratdługościprzeciwprostokątnejjestrównysumie

kwadratówdługościobuprzyprostokątnych.

twierdzenie talesa

Jeżeliramionakątaprzetniemyprostymirównoległymi,toodcinkiwyznaczonenajed-

nymramieniukątasąproporcjonalnedoodpowiednichodcinkównadrugimramieniu

kąta.Np.

pODZiAŁ KĄtÓW

podział ze względu na miary

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

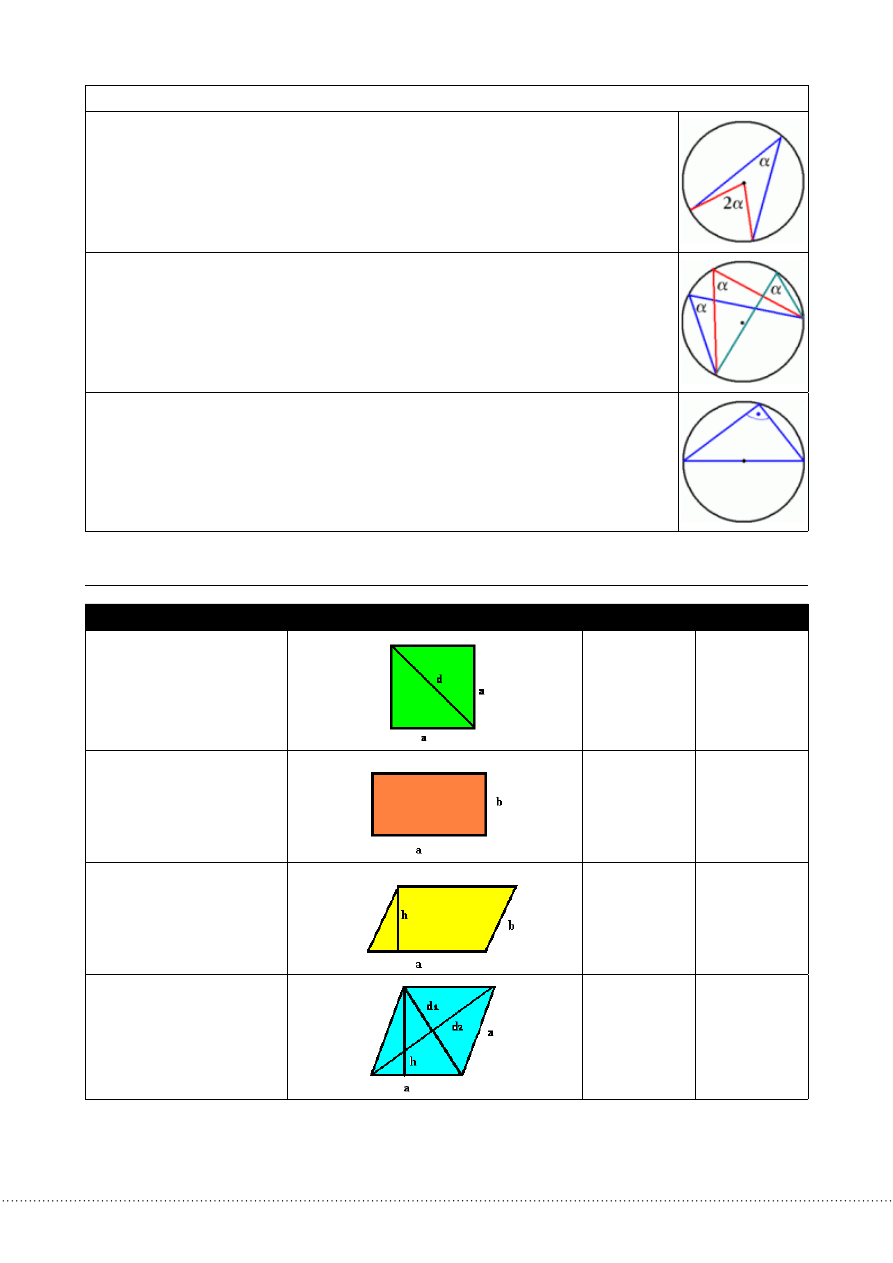
Kąty naprzemianległe, odpowiadające, przyległe i wierzchołkowe

Kątypołożonetakjaknarysunkuobok,nazywamykątaminaprzemianległymi.

Kątypołożonetakjaknarysunkuobok,nazywamykątamiodpowiadającymi.

Kątamiprzyległyminazywamytakiedwakąty,któremająjednoramęwspólne,

apozostałeramionasąpółprostymidopełniającymisię.

Sumamiarkątówprzyległychrównasię180stopni

Kątywypukłe,którychramionawzajemniesięprzedłużają,nazywamykątami

wierzchołkowymi.

Kątywierzchołkowemająrównemiary.

Kąty w kole

Wierzchołekkażdegoztychkątówjestśrodkiemkoła.Są to kąty środkowe.

Wierzchołekkażdegozkątów(mniejszyniż180stopni)leżynaokręgu,aramionaprzecinająokrąg.Są to kąty wpisane.

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona 0 z 7

Kąty w kole - własności

Kątwpisanyjestdwarazymniejszyodkątaśrodkowegoopartegonatymsamymłuku

Kątywpisaneopartenatymsamymłukumająrównemiary

Kątwpisanyopartynaśrednicyjestkątemprostym

WieLOKĄtY

Figura

Obwód

pole pow.

KWADRAT

O=4a

P=a

2

P=½d

2

PROSTOKĄT

O=2a+2b

P=ab

RÓWNOLEGŁOBOK

O=2a+2b

P=ah

ROMB

O=4a

P=ah

P=½d

1

d

2

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

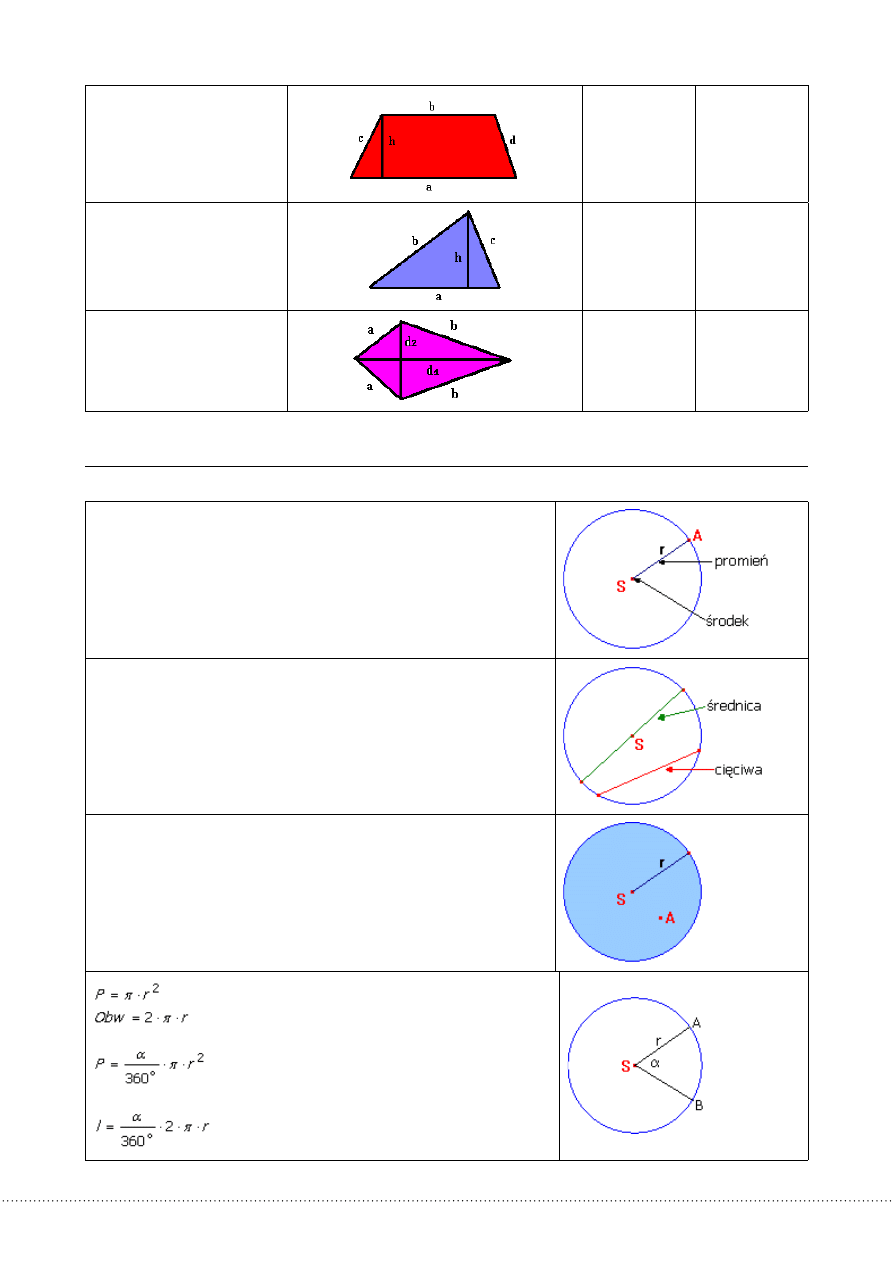
TRAPEZ

O=a+b+c+d

P=½(a+b)h

TRÓJKĄT

O=a+b+c

P=½a

DELTOID

LATAWIEC

O=2a+2b

P=½d

1

d

2

KOŁO i WieLOKrĄG

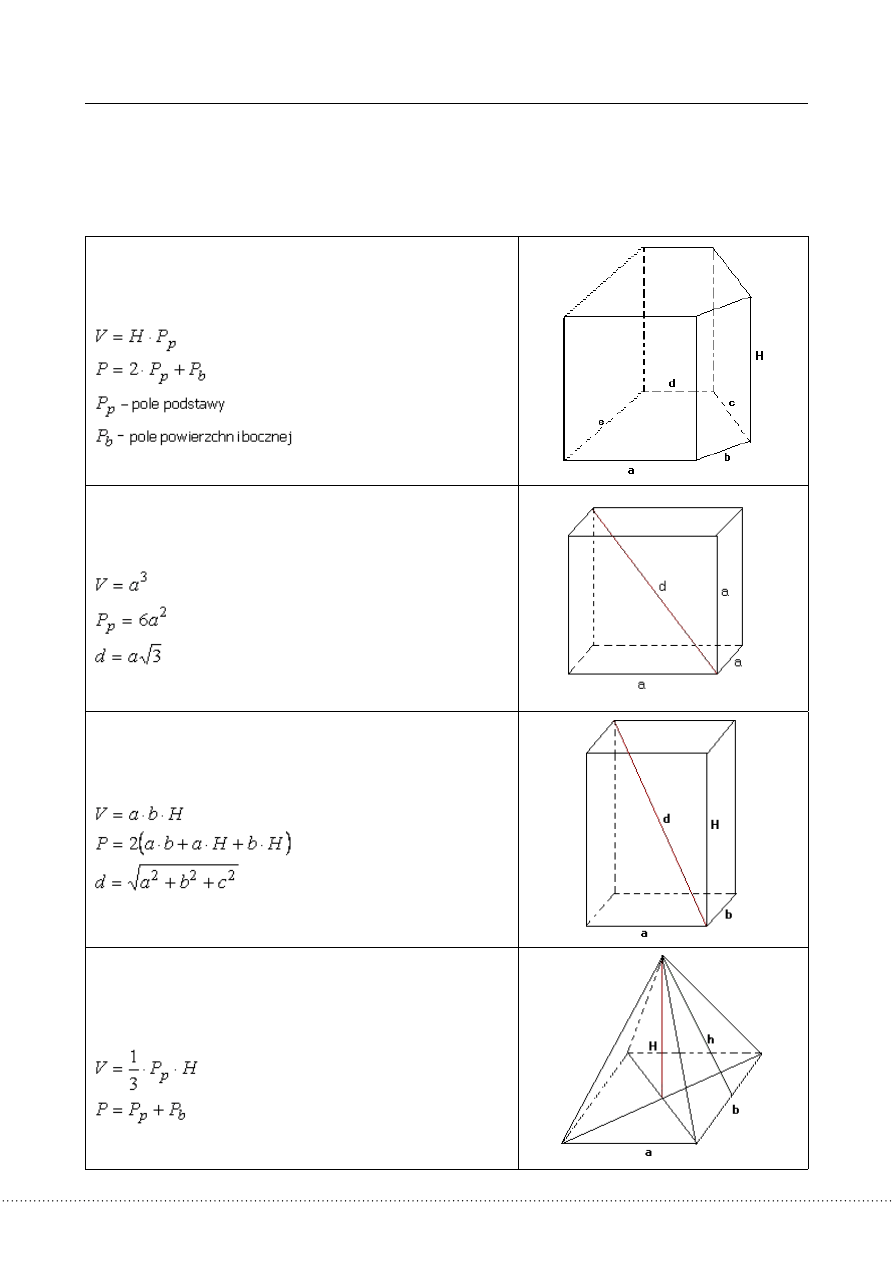
OkręgiemośrodkuSipromieniur>0nazywamyfiguręzłożonązwszystkichpunktów

płaszczyzny,którychodległośćodpunktuSjestrównar.

Cięciwąokręgunazywamyodcinek,któregokońcamisądwaróżnepunktyokręgu.

Średnicąokręgunazywamycięciwę,któraprzechodziprzezśrodekokręgu.

Cięciwaokręgudzieliokrągnadwieczęści.Każdąznichnazywamyłukiem,tegookręgu.

Łukokręguwyznaczonyprzezśrednicęnazywamypółokręgiem.

KołemośrodkuSipromieniur>0nazywamyfiguręzłożonązwszystkichpunktów

płaszczyzny,którychodległośćodśrodkajestniewiększaniżr.

PolewycinkaAOB

DługośćłukuAB

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

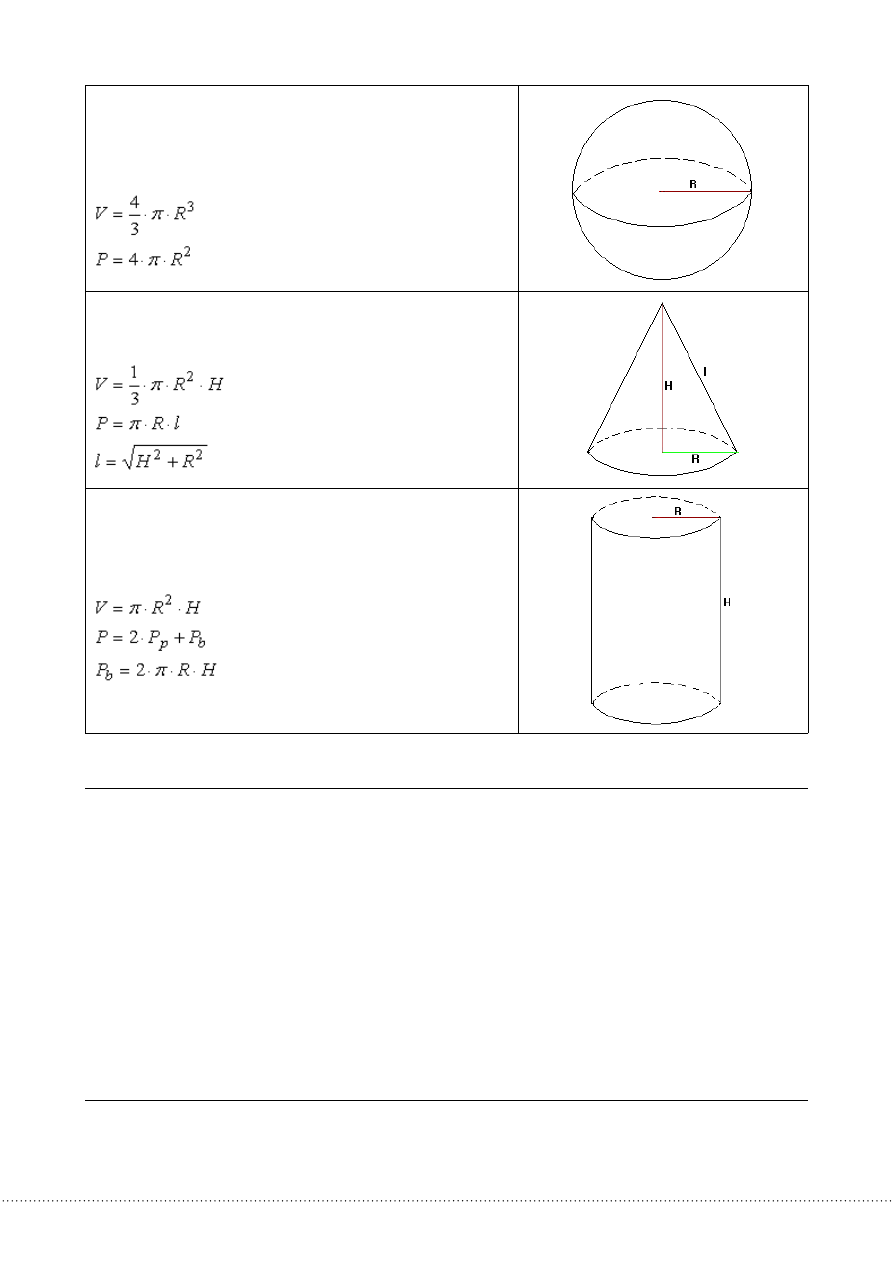
BrYŁY

V–objętość
Pp–polepodstawy
Pb–polepowierzchnibocznej
P–polecałkowite

Graniastosłuptowielościan,któregowierzchołkinależądodwóchrównoległych

płaszczyzn,krawędziezaś,któreniesązawartewtychpłaszczyznach,są

równoległe.

Sześciantograniastosłup,któregościanysąprzystającymikwadratami,awkażdym

wierzchołkuspotykająsiętrzyściany.

Prostopadłościantograniastosłupprosty,wktórymwszystkieścianybocznesą

prostopadłedopodstawy.

Ostrosłupjestwielościanemtakim,żejednajegościana,zwanapodstawą,jest

wielokątem,zaśpozostałeścianysątrójkątamiwyznaczonymiprzezwierzchołek

tegoostrosłupaiwierzchołkiwielokątapodstawy.

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

KuląośrodkuOipromieniurnazywamyzbiórwszystkichpunktówprzestrzeni,

którychodległośćodpunktuOjestmniejszalubrównadługościpromienia.

Powierzchniąkuli(sferą)ośrodkuOipromieniudługościrnazywamyzbiór

wszystkichpunktówprzestrzeni,którychodległośćodpunktuOjestrówna

długościpromienia.

Stożekobrotowytofigurapowstałazobrotutrójkątaprostokątnegowokółprostej

zawierającejjednązprzyprostokątnych(lubogólnie:figurępowstałąprzezobrót

danejprostejwokółprostejmającejzdanąjedenpunktwspólny).

Walectofigurapowstałaprzezobrótprostokątawokółprostejzawierającejjedenz

jegoboków(lubogólnie:figurępowstałąprzezobrótprostejwokółprostejdoniej

równoległej).

DZiAŁANiA NA prOceNtAcH

Abyzamienić%naułamekwystarczyliczbę%podzielićprzez100:np.35%=35:100=0,35
Abyzamienićułamekna%wystarczytenułamekpomnożyćprzez100%:np.0,12=0,12*100%=12%
Abyobliczyć%zliczbywystarczyprocentzamienićnaułamekipomnożyćgoprzeztęliczbę:np.45%zliczby20=

0,45*20=9
Abyznaleźćliczbęnapodstawiedanegojej%,wystarczypodanąwartośćpodzielićprzezliczbę%ipomnożyćprzez

100:np.znajdźliczbęwiedząc,żejej20%wynosi16.
Szukanaliczba=16:20%=16:0,2=80
Abyobliczyćjakim%liczbyAjestliczbaB,wystarczypodzielićliczbęBprzezliczbęAiwynikpomnożyćprzez100%:
np.jakim%liczby60jestliczba9?
9:60*100%=0,15*100%=15%,więcliczba9to15%liczby60.

pOJĘciA MAteMtYcZNe W piGUŁce

Liczby nieujemne toliczbydodatnieizero.
Liczby niewymiernetoliczby,którychniemożnaprzedstawićwpostaciułamka.

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

Liczby odwrotnetodwieliczby,którychiloczynjestrównyjeden.
Liczby pierwszetotakieliczbynaturalnewiększeod1,któremajątylkodwaróżnedzielniki.
Liczby przeciwnetoliczby,którychsumajestrównazero.
Liczby złożone toliczbynaturalne,któremająwięcejniżdwadzielniki.Rozwinięciedziesiętneliczbytoprzedstawie-

nieliczbywpostacidziesiętnej.
rozwinięcie dziesiętnenieskończenie okresowetorozwinięciedziesiętnepewnychliczbniewymiernych.
rozwinięcie dziesiętne skończonetodziesiętnepostaćpewnychliczbwymiernych
Wartość bezwzględna liczbyrzeczywistejtoodległośćodzerapunktuodpowiadającegotejliczbienaosiliczbo-

wej.
Wartością bezwzględnąliczbynieujemnejjesttasamaliczba,wartościąbezwzględnąliczbyujemnejjestprzeciwna

doniejliczbadodatnia.
Jednomiantoliczbazmiennalubiloczynzmiennychipewnegowspółczynnikaliczbowego
Suma algebraiczna jesttosumajednomianów.
Odejmowanielubdodawaniejednomianówpodobnychnazywamyredukcją wyrazów podobnych.
Sumę algebraicznąmożnarozłożyćnaczynnikiprzez:wyłączaniewspólnegoczynnikaprzednawias,stosowanie

wzorówskróconegomnożenia,grupowaniewyrazów.
równaniejesttorównośćdwóchwyrażeńalgebraicznych,wktórychwystępujejednalubkilkaniewiadomych.
Wyrażenie algebraiczne tosymbolicznezapisyliczbidziałań.
Wartość liczbowa wyrażenia jesttowartośćotrzymanapopodstawieniuliczbwmiejsceliterwwyrażeniuiwyko-

naniuwskazanychdziałań.
Zmiennesątoliteryzastępująceliczbywwyrażeniachalgebraicznych.
Współczynnik liczbowytoliczbawystępującanapoczątkuuporządkowanegojednomianu.
Jeżeliwrównaniuwystępujetylkojednaniewiadoma,tootakichrównaniachmówimy,żesątorównaniapierwszego

stopnia z jedną niewiadomą.
Jeżelirównaniejesttożsamością,toznaczy,żekażdaliczbaspełniatorównanie.
Jeżelirównaniejestsprzeczne, toznaczy,żeniematakiejliczbyrzeczywistej,któraspełniatorównanie.
Nierówności równoważnetonierównościmającetensamzbiórrozwiązań.
równania równoważnesątorównaniamającedokładnietensamzbiórrozwiązań.
proporcja torównośćdwóchstosunków,któramatęsamąwłasność,żeiloczynwyrazówskrajnychrównyjestiloczy-

nowiwyrazówśrodkowych.
DanesądwazbioryAiB.Funkcję określoną na zbiorze A o wartościach w zbiorze Bnazywamytakieprzyporząd-

kowanie,wktórymkażdemuelementowizbioruAjestprzyporządkowanydokładniejedenelementzbioruB.
ZbiórAnazywamy dziedziną funkcji,ajegoelementyargumentami funkcji.
ElementzbioruB,któryzostałprzyporządkowanyelementowixzbioruA,nazywamywartością funkcji.
Funkcja malejąca totaka,wktórejzewzrostemwartościargumentówxmalejąwartościfunkcjiy.
Funkcja rosnącatotaka,wktórejzewzrostemwartościargumentówxrosnąwartościfunkcjiy.
Funkcja stała totaka,wktórejkażdejwartościargumentuxprzyporządkowanajesttasamawartośćfunkcjiy.
Wykres funkcji jesttograficzneprzedstawieniefunkcjiwukładziewspółrzędnych.
Miejsce zerowefunkcjitokażdyargument,dlaktóregowartośćfunkcjirównajestzeru.
Układ współrzędnych prostokątnych na płaszczyźnie to układ dwóch prostych prostopadłych zwanych osiami

współrzędnych;ośpionoway–oś rzędnych, ośpoziomax–oś odciętych.
Układrównańpierwszegostopnia,któregorozwiązaniemjestjednaparaliczb,nazywamyukładem oznaczonym.
Układrównańpierwszegostopnia,któregoniespełniażadnaparaliczb,nazywamy układem sprzecznym.
Układrównańpierwszegostopnia,któryspełnianieskończeniewieleparliczb,nazywamyukładem nieoznaczo-

nym.

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

Wykresem równania pierwszego stopnia zdwiemaniewiadomymijestprosta.
ilustracją graficzną oznaczonego układu równań sądwieprosteprzecinającesię.Współrzędnepunktuprzecięcia

siętychprostychsąrozwiązaniemtegoukładurównań.
ilustracja graficzną nieoznaczonego układu równań jestprosta.Układtenmanieskończeniewielerozwiązań.
ilustracja graficzną układu równań sprzecznych sądwieróżneprosterównoległe.Rozwiązaniemukładurównań

sprzecznegojestzbiórpusty.
Współrzędne punktu na płaszczyźnietouporządkowanaparaliczbokreślającapołożeniepunktuwzględemosi

współrzędnych.
rozkład liczby na czynniki pierwsze toprzedstawienieliczbywpostaciiloczynuliczbpierwszych.
rozstęp danych toróżnicamiędzynajwiększąanajmniejsząliczbąwdanejpróbie.
Sondaż tobadanieopiniipublicznejnapodstawieprzeprowadzonegowywiadu.
próbatowybranagrupaelementów,którebadamywceluwyciągnięciawnioskówocałejpopulacji.
Medianatoliczbaznajdującasiępośrodkudanychzpróby,uporządkowanychwkolejnościodnajmniejszejdonaj-

większej.
Moda tocecha,którawpróbiewystępujenierzadziejniżinne.
Histogramjesttodiagramsłupkowyprzedstawiającedanepochodzącezobserwacji.
Ankietatozbiórpytańnaokreślonytemat.
Każdyczworokątmadwieprzekątne
trapezytowszystkieczworokątywypukłe,wktórychjestprzynajmniejjednaparabokówrównoległych.
trapezoidytoczworokątywypukłe,któreniemająbokówrównoległych.
trapez równoramienny:ramionasąrównejdługości,przekątnesąrównejdługości,kątyprzypodstawachsąrów-

nejmiary,mająjednąośsymetrii.
trapez prostokątny:jednoramięjestjednocześniewysokościątrapezu.
równoległoboki sątotrapezy,któremajądwieparybokówrównoległych.
równoległobok:bokirównoległesąrównejdługości,przeciwległekątysąrównejmiary,przekątnedzieląsięna

połowy.
romb jesttorównoległobok,wktórymdługościwszystkichbokówsąrówne.
romb: wysokościsąrówne,madwieosiesymetrii;przekątne:sąprostopadłe,zawierająsięwdwusiecznychkątów

wewnętrznych,zawierająsięwosiachsymetriirombu,przecinająsięwśrodkuokręguwpisanegowromb.
prostokąt torównoległobok,wktórymwszystkiekątywewnętrznesąproste.
prostokąt:przekątnesąrównejdługości,symetralnebokówrównoległychsąosiamisymetriiprostokąta,punktprze-

cięciaprzekątnychjestśrodkiemokręguopisanegonaprostokącie.
Kwadrattoprostokąt,którymawszystkiebokirównejdługości.
Kwadrat: maczteryosiesymetrii;przekątne:sąprostopadłeirównejdługości,zawierająsięwosiachsymetrii,zawie-

rająsięwdwusiecznychkątówwewnętrznych,przecinająsięwewspólnympunkcie,wśrodkuokręgówopisanegona

kwadracieiwpisanegowkwadrat.
Każdyczworokątmożnapodzielićnadwatrójkąty,azatemsumamiarkątówwewnętrznychczworokątajestrówna

360

0

.

W czworokąt można wpisać okrągtylkowtedy,gdysumydługościprzeciwległychbokówsąrówne.
Na czworokącie można opisać okrągtylkowtedy,gdysumymiarkątówprzyległychsąrówne180

0

.

Jeżeliliczbabokówwielokątajestrównan,tosumakątówwewnętrznychjestrówna:
(n–2)x180.
Wielokątwypukły,któregowszystkiebokisąjednakowejdługości,akątywewnętrznejednakowejmiary,towielokąt

foremny.
Nakażdymwielokącieforemnymmożnaopisaćokrągiwkażdywielokątforemnymożnawpisaćokrąg.

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona z 7

twierdzenie pitagorasa: Wtrójkącieprostokątnymkwadratdługościprzeciwprostokątnejjestrównysumiekwadra-

tówdługościprzyprostokątnychtegotrójkąta.
twierdzenie odwrotne do twierdzenia pitagorasa: Jeżeliwtrójkąciekwadratdługościnajdłuższegobokujestrów-

nysumiekwadratówdługościpozostałychbokówtrójkąta,totentrójkątjestprostokątny.
trójkąt pitagorejski totrójkątprostokątny,któregodługościbokówwyrażonesąliczbaminaturalnymi
twierdzenie talesa: Jeżeliramionakątaprzeciętesąprostymirównoległymi,tostosunekdługościktórychkolwiek

dwóchodcinkówutworzonychnajednymramieniujestrównystosunkowidługościodpowiednichodcinkówutwo-

rzonychnadrugimramieniu.
twierdzenie odwrotne do twierdzenia talesa: Jeżeliprosteprzecinająceramionakątawyznaczająnajednymra-

mieniuodcinkiproporcjonalnedoodpowiednichodcinkówutworzonychnadrugimramieniu,toteprostesąrówno-

ległe.
Graniastosłupy: podstawysąprzystającymiwielokątami,podstawyleżąwpłaszczyznachrównoległych,krawędzie

bocznesąrównoległe,ścianybocznesąrównoległobokami.
Graniastosłupprosty,któregowszystkieścianysąkwadratami, to sześcian.
Graniastosłupprosty,któregopodstawąjestwielokątforemny,nazywamy graniastosłupem prawidłowym.
przekątne graniastosłupatokażdyodcinekłączącywierzchołkiobupodstawnienależącedotejsamejściany.
przekrój graniastosłupa toczęśćpłaszczyzny,któradzieligraniastosłupnadwieczęści.
Ostrosłupy:podstawajestwielokątem,majednąpodstawę,ścianybocznesątrójkątamiowspólnymwierzchołku,

którynazywamywierzchołkiempodstawy;krawędziewychodzącezwierzchołkaostrosłupanapłaszczyznępodsta-

wytospodekwysokościtegoostrosłupa;odcinekłączącywierzchołekostrosłupazjegospodkiemwysokościtowy-

sokośćostrosłupa.
Ostrosłuptrójkątnynazywamyczworościanem.
Czworościan,któregowszystkieścianysątrójkątamirównobocznymi,nazywamy czworościanem foremnym.
Ostrosłup,któregopodstawąjestwielokątforemny,aścianybocznesąprzystającymitrójkątamirównoramiennymi,

nazywamyostrosłupem prawidłowym.
Kątem nachylenia ściany bocznej ostrosłupa do płaszczyzny podstawynazywamyliniowykąt,któregowierz-

chołekleżynawspólnejkrawędzi,aramionasądoniejprostopadłeijednoramięleżynaścianiebocznej,adrugiena

podstawie.
Walecjesttobryłą,którąotrzymujemyprzezobrótprostokątao360

0

dookołaprostejzawierającejjedenzjegobo-

ków.
podstawy walcatodwieścianywyznaczoneprzezobrótprostopadłychdoosiobrotubokówprostokąta,któresą

przystającymikołamiileżąwzględemsiebierównolegle.
przekrojem osiowym walca jestprostokąt.
przekrojem poprzecznym walcanazywamyczęśćwspólnąwalcaipłaszczyznyprzecinającejwalecrównolegledo

podstawy.
przekrojem poprzecznym walcajestkoło.
Stożekjesttobryła,którąotrzymujemy,obracająctrójkątprostokątnydokołaprostejzawierającejjednązprzypro-

stokątnychokąt360

0

.

Przekrojemosiowymstożkajesttrójkątrównoramienny.
przekrojem poprzecznym stożkajestkołolubpunkt.
Kulajestbryłą,którąotrzymujemy,obracającpółkoleokąt360

0

dokołaprostejzawierającejśrednicę.

Powierzchniękulinazywamysferą.
Przekrójosiowykulinazywamykołem wielkim.
cięciwatoodcinek,któregokońcamisąpunktyleżącenaokręgu.
Dwusieczna kątatopółprostaopoczątkuwwierzchołkikąta,dzielącatenkątnapołowy.
Figury przystające totakie,któreponałożeniunasiebiesiępokrywają.
Kąt dwuściennytojednazdwóchczęściprzestrzeniwyznaczonaprzezdwiepółpłaszczyznyowspólnejkrawędzi.

VADEMECUM GIMNAZJALISTY |

MATEMATYKA

strona 7 z 7

Kąt środkowyjesttokąt,któregowierzchołekjestśrodkiemkoła.
Kąt wpisanytokątwypukły,któregowierzchołekjestpunktemokręgukoła,aramionazawierającięciwytegokoła.
Odcinek kołatojednazdwóchczęścikoławyznaczonaprzezcięciwętegokoła.
Okrąg opisany na wielokącie jesttookrąg,naktórymleżąwszystkiewierzchołkiwielokąta.
Okrąg wpisany w wielokąt jesttookrągstycznydowszystkichbokówwielokąta.
Oś symetrii figurytoprosta,względemktórejkażdypunktfiguryipunktdoniegosymetrycznywzględemtejprostej

należydofigury.
podstawy graniastosłupatodwierównoległeścianytegograniastosłupa,naktórychleżąwszystkiewierzchołkigra-

niastosłupa.
promień okręgu toodcinek,któregojednymkońcemjestśrodekokręgu,adrugimkońcempunktleżącynaokręgu.
przekątna wielokątatoodcinekłączącydowolnedwaniekolejnewierzchołkiwielokąta.
Symetralna odcinkatoprostaprostopadładoodcinkaprzechodzącegoprzezjegośrodek.
średnia arytmetycznaliczbjesttoilorazsumytychliczbprzezichliczebność.
średnica tocięciwaprzechodzącaprzezśrodekokręgu.
środek symetrii figuryjesttopunkt,względemktóregokażdypunktfiguryipunktdoniegosymetrycznywzględem

tegopunktunależądofigury.
środkowa trójkąta toodcinekłączącywierzchołektrójkątaześrodkiembokurównoległego.
Wielościany tobryły,którychścianamisąwielokąty.
Wysokość graniastosłupatokażdyodcinekokońcachleżącychnapodstawachgraniastosłupaiprostopadłydotych

podstaw.
Wysokość trójkątatoodcinekprostejprzeprowadzonejprzezwierzchołektrójkąta,prostopadłejdoprzeciwległego

boku,liczonyodwierzchołkadoprzecięciasięprostejzprzeciwległymbokiemlubjegoprzedłużeniem