FUNKCJE I ICH WŁASNOŚCI
|
Matematyka z plusem Pojawia się w II klasie Wprowadzone jako drugi dział „Funkcje” po dziale: Liczby i wyrażenia algebraiczne” Przypomnienie i rozszeżenie w III klasie Pierwszym tematem w tym dziale jest Odczytywanie wykresów. Uczniowie zapoznają się z wykresami i uczą się odczytywać z nich dane. W następnym temacie Pojęcie funkcji. Zależności funkcyjne Wprowadzone za pomocą tabelki wyników biegu. x-nr zawodnika, y-uzyskany czas. Opisana jest na tym przykładzie definicja funkcji: mamy zbiór X (zawodnicy) i Y (czas), Każdemu elementowi x przyporządkujemy dokładnie jeden element ze zbioru Y (każdemu zawodnikowi przypisany jest dokładnie jeden czas). Następnie dla funkcji y=1/2x2-1 i dla X={-3, -2, -1, 0, 1, 2, 3} przedstawiono tabelkę graf i wykres. Funkcje można przedstawić słownie, tabelką, wzorem, grafem, wykresem. W temacie O czym mówią współczynniki funkcji liniowej? Wprowadzone jest rozróżnianie funkcji ze względu na współczynnik a. Malejąca, rosnąca, stała
|
W którym miejscu wprowadzone |
|
Sposób wprowadzenia |
|
Problemy i trudności podczas realizacji |
Określanie monotoniczności funkcji (znalezienie we wzorze funkcji liniowej współczynnika a)Rysowanie wykresu- mylenie osi x z osią y
|
Późniejsze wykorzystanie |
Przy funkcjach liniowych, i innych, np. trygonometrycznych. Rozwiązywanie równań i nierówności metodą graficzną |
Cele operacyjne |
- uczeń zna pojęcie funkcji - uczeń zna pojęcia dziedziny, zbioru wartości, argumentu i wartości - uczeń umie sporządzić tabelkę funkcji - uczeń umie narysować graf przedstawiający funkcję - uczeń umie narysować wykres funkcji - uczeń umie określić funkcję słownie, tabelką, wzorem, grafem, wykresem, jako pary uporządkowane - uczeń zna pojęcie miejsc zerowego - uczeń wie jak rozpoznać funkcję malejącą, rosnącą, stałą |
Podstawowe zadania |
|
Zadania ciekawe |
|
FUNKCJE I ICH WŁASNOŚCI
Patrycja Piwońśka
Wykorzystanie w innych przedmiotach
Geografia- rysowanie wykresów temperatur, opadów, ciśnienia, wzrostu liczby ludności
Fizyka- wykresy np. prędkości (czas do drogi)
Ścieżki edukacyjne
Edukacja czytelnicza i medialna
Cena biletu kolejowego zależy od odległości, jaka jest między stacją początkową, a docelową. Znajdź aktualą tabelę taryf kolejowych. Sporządź wykres zależności ceny od odległości przejazdu pociągiem osobowym drugieij klasy w zakresie od 0 km do 200km.
Edukacja prozdrowotna
Przez tydzień mierz temperaturę swojego ciała, rano i wieczorem. Zaznacz wyniki tych pomiarów na wykresie. Co zauważasz? Jaka była w tym okresie średnia temperatura Tojego ciała?
Edukacja regionalna
Na rysunku przedstawiono wykres ruchu dwóch piechurów wyruszających z punktów A i B. Na podstawie wykresu określ:
a) o której godzinie wyszedł każdy z nich,
b) ile czasu był w drodze,
ile czasu każdy znich przeznaczył na odpoczynek (rys 2)
Egzaminy zewnętrzne
Standard: wyszukiwanie i sortowanie informacji- uczeń odczytuje informacje przedstawiane w formie wykresu
Zadnie jest bardziej biologiczne (fizyczne), ale uczeń musi umieć przeanalizować pytanie, żeby odpowiedzieć na zadane pytanie.
Zadanie
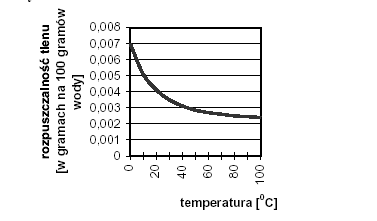
Jednym z warunków istnienia życia w środowisku wodnym jest obecność
rozpuszczonego w wodzie tlenu. Przeanalizuj poniższy wykres i wyjaśnij jednym
zdaniem, dlaczego wzrost temperatury wody w akwarium może przyczynić się do uśnięcia ryb.
Zadanie
Na wykresie przedstawiono zależność natężenia I od napięcia U dla czterech
odbiorników prądu.
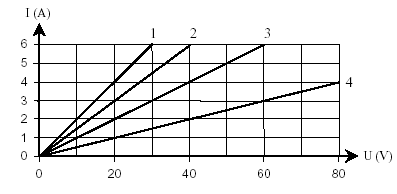
Który odbiornik ma największy opór?
A. 1 B. 2 C. 3 D. 4
Standard: Wskazywanie i opisywanie faktów, związków zależności- uczeń posługiwane się funkcjami: analizuje funkcje przedstawione w różnej postaci i wyciąga wnioski.
Obserwując zużycie benzyny w swoim samochodzie, pan Nowak stwierdził, że jeśli
wystartuje z pełnym bakiem i będzie jechał po autostradzie ze stałą prędkością, to zależność
liczby litrów benzyny w baku (y) od liczby przejechanych kilometrów (x) wyrazi się wzorem:
y= -0,50x+45
Zadanie
Ile benzyny zostanie w baku po przejechaniu 200 km? Zapisz obliczenia.
Zadanie
Jaką pojemność ma bak tego samochodu?
Zadanie
Na przejechanie ilu kilometrów wystarczy pełny bak? Zapisz obliczenia.
Zadanie
Przekształcając wzór pana Nowaka, wyznacz x w zależności od y.
Standard: Wskazywanie i opisywanie faktów, związków i zależności, w szczególności funkcyjnych- uczeń posługuje się funkcjami: wskazuje zależności funkcyjne, opisuje funkcje za pomocą wzorów.
Most zbudowany jest z przęseł o długości 10 m każde. Przęsło pod wpływem wzrostu
temperatury wydłuża się. Przyrost tego wydłużenia jest wprost proporcjonalny do przyrostu
temperatury. Wartość przyrostu długości przęsła dla wybranych wartości przyrostu
temperatury przedstawia poniższa tabela.

Zadanie
Wpisz do tabeli brakującą wartość przyrostu długości przęsła.
Zadanie
Zapisz zależność przyrostu długości przęsła (Δl) od przyrostu temperatury (Δt) za
pomocą wzoru. Podaj współczynnik proporcjonalności Δl do Δt z odpowiednią jednostką.
KONSPEKT LEKCJI
Patrycja Piwońska
Klasa III gimnazjum
Temat: Pojęcie funkcji. Zależności funkcyjne.
Cele operacyjne:
uczeń wie co to jest funkcja;
uczeń zna pojęcia dziedziny, argumentu, zbioru wartości funkcji i wartości funkcji;
uczeń zna sposoby określania funkcji: opis słowny, tabelka, wzór, graf i wykres;
uczeń umie sporządzić wykres funkcji;
uczeń zna pojęcie miejsca zerowego i wie jak je znaleść na wykresie;
Środki dydaktyczne:
podręcznik;
tablica;
kreda;
Metoda lekcji:
podająca- wyjaśnienie;
praktyczna- ćwiczenia przedmiotowe;
Forma pracy:
zbiorowa;
Przebieg lekcji:
Podanie definicji funkcji:
Dane są dwa zbiory A i B. Funkcją określaną na zbiorze A o wartościach w zbiorze B nazywamy takie podporządkowanie, w którym każdemu elementowi zbioru A został przyporządkowany dokładnie jeden element zbioru B.
Wyjaśnienie definicji na grafach.
Każdemu elementowi ze zbioru A (dziedzina) jest przyporządkowany dokładnie jeden element ze zbioru B (zbiór wartości).
Przedstawienie sposobów określania funkcji
Opis słowny:
Każdej liczbie ze zbioru A={-2, -1, 0, 1, 2} przyporządkowano iloczyn tej liczby i 2.
Graf:
Pary uporządkowane:
(-2, -4), (-1,-2), (0, 0), (1,2), (2,4)
Tabelka
x |
-2 |
-1 |
0 |
1 |
2 |
y |
-4 |
-2 |
0 |
2 |
1 |
Wzór:
y=2x, x {-2, -1, 0, 1, 2}
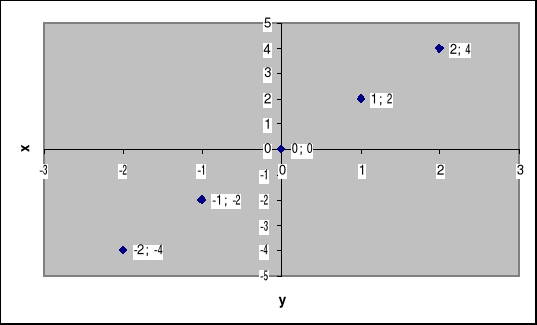
Wykres funkcji:
Zadanie 1
Funkcja określona jest tabelką;
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
y |
2 |
1 |
0 |
1 |
0 |
-1 |
3 |
2 |
a) Wymień wszystkie ujemne argumenty tej funkcji
b) Odczytaj wartość funkcji dla argumentu x=-3 oraz dla argumentu x=-2
Dla jakich argumentów funkcja przykuje wartość 1?
Czy punkt (-2,1) należy do wykresu tej funkcji?
e) Narysuj wykres tej funkcji
f) Podaj jej miejsce zerowe.
Odp.
a) -3, -2, -1
b) f(-3)= 2, f(-2)= 1
Funkcja przyjmuje wartość 1 dla x=-2, x=0
tak,
e)
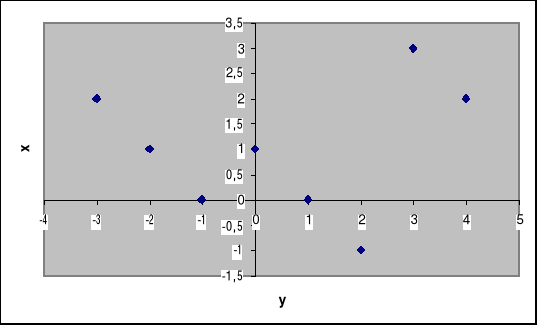
f) x=-1, x=1
Zadanie 2
Sporządź wykres funkcji y=2x-1 określonej na zbiorze:
a) {-2, -1, 0, 1, 2}
b) liczb naturalnych jednocyfrowych
liczb całkowitych ujemnych większych od -7
Odp.
a)
x |
-2 |
-1 |
0 |
1 |
2 |
y |
-5 |
-3 |
-1 |
1 |
3 |
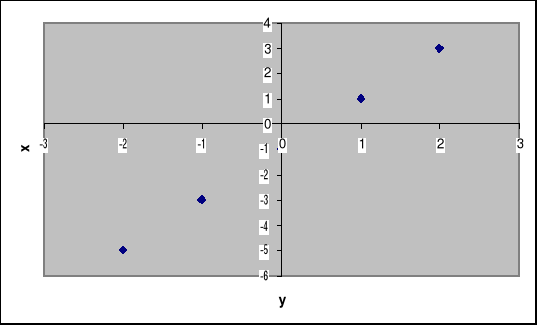
b)
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
y |
-1 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
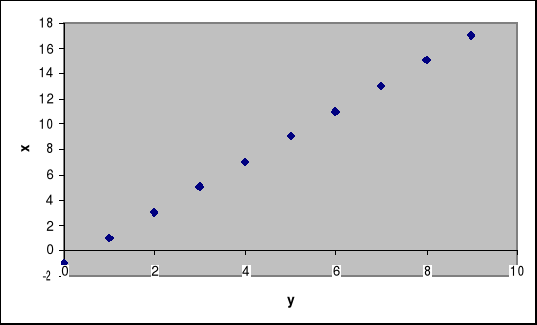
c)
x |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
y |
-15 |
-13 |
-11 |
-9 |
-7 |
-5 |
-3 |
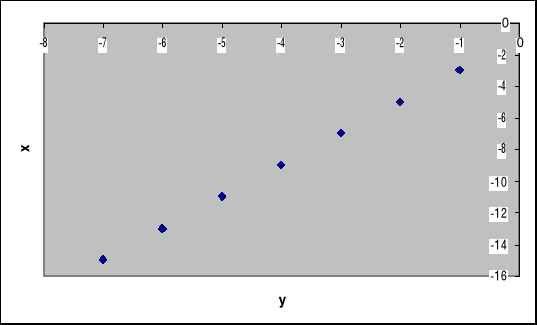
Zadanie 3
Określ wszystkimi znanymi sposobami funkcję: każdej liczbie naturalnej dodatniej mniejszej niż 10 przyporządkowana jest jej odwrotność.
Odp.
Wzór: y= -x, x {1, 2, 3, 4, 5, 6, 7, 8, 9}
Tabelka:
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
y |
-1 |
-2 |
-3 |
-4 |
-5 |
-6 |
-7 |
-8 |
-9 |
Graf:
Zbiór par uporządkowanych:
-1), (2, -2), (3, -3), (4, -4), (5,-5), (6, -6), (7, -7), (8, -8), (9, -9)
Wykres funkcji:
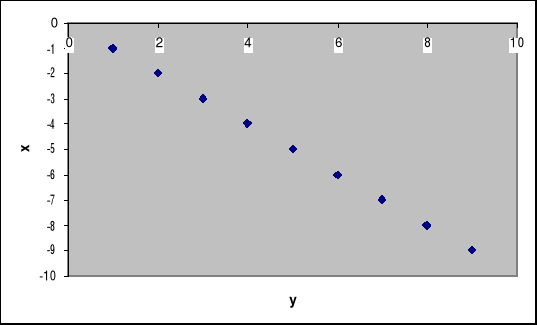
Uwagi własne:
Zadania, których nie zdążymy zrobić na lekcji będą zadane do domu.
Wyszukiwarka
Podobne podstrony:
matematyka z plusem gimnazjum 2
Funkcja liniowa - gimnazjum, Matematyka
Funkcje - zadania powtórzeniowe, edukacja, GIMNAZJUM, matematyka
funkcje liniowe, Matematyka gimnazjum, sprawdziany-Matematyka gimnzjum, klasa3
gim Wykresy funkcji - gimnazjum, gimnazjum i podstawówka, gimnazjum, polak, matma
Wzór funkcji y, SZKOŁA, Matematyka, Matematyka
1 PLAN WYNIKOWY DLA KLASY III GIMNAZJUM, Matematyka, Gimnazjum kl 3, Plany Rozkłady PSO
Funkcja kwadratowa, matematyka
Figury przystające - gimnazjum, Matematyka
Funkcja liniowa, Matematyka
nowy egzamin gimnazjalny z matematyki 2012 przykładowy zestaw zadań
egzamin gimnazjalny matematyka 2012 karta odpowiedzi
Prawo i jego funkcje gimnazjum
FUNKCJA KWADRATOWA, Matematyka
Wybrane zastosowania pochodnej funkcji, Analiza matematyczna
Funkcja Liniowa, Matematyka- zadania
Funkcja, SZKOŁA, Matematyka, Matematyka
Arkusz3, Katedra Analizy Funkcjonalnej Wydziału Matematyki Uniwersytetu Łódzkiego
więcej podobnych podstron