Funkcja kwadratowa
Znajdź największą i najmniejszą wartość funkcji (a) f(x) = -x2 + 4x + 1 dla x ∈<0;3> (b) f(x)= x2 - 4x + 1 dla x ∈ <0;3> (c) f(x) =
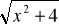
dla x∈<-1; 3> (d) f(x) =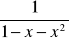
dla x ∈ <0;2>.Dla jakiej wartości α równanie
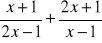
=cosα ma tylko jeden pierwiastek?Oblicz b jeżeli pierwiastki równania 5x2 + bx + 15 = 0 są liczbami całkowitymi.
Wyznaczyć p i q tak, by suma kwadratów pierwiastków równania x2 + px + q = 0 była równa 10, natomiast suma ich odwrotności 4/3.
Rozwiąż równanie: (a)x2 - 5|x| + 4 = 0 ; (b)x2 - 4x + |x-3| + 3 = 0 (c)
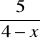
=|x| (d)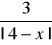
=x (e)2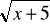
=x+2 (f)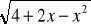
=x-2 (g)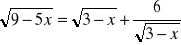
(h)4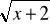
=|x+1| +4 (i)2x2 + 3x - 5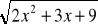
+ 3 = 0 (j)(9-x2)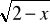
=0 (k)x2+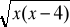
=2(1+2x) (l)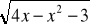
(|x-1|-4)=0Rozwiąż równanie, w którym a jest parametrem: (a)
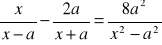
(b)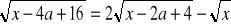
Znajdź liczbę pierwiastków w zależności od parametru a
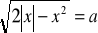
Wiadomo, że x+y=2 i x+z = 1. Oblicz najmniejszą wartość wyrażenia 2x3 + y3 + z3 .
Dla jakich wartości parametru m równanie ma jedno rozwiązanie? (a) mx2 - 3x +m=0 (b)(4m+1)x2 - (4m-11)x + m-1 = 0 (c)(m-1)x2 - 2(m+3)x + m - 3 = 0
Oblicz c, jeśli jeden z pierwiastków równania ax2 + bx + c = 0 jest równy
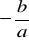
Dla jakich wartości parametru a jeden z pierwiastków równania 4x2 - 15x + 4a = 0 jest kwadratem drugiego?
Dla jakich wartości parametru m równania mają wspólny pierwiastek? (a) x2 + x - m = 0 i x2 + 2x + m = 0 (b)2x2 - (3m+2)x + 12 = 0 i 4x2 - (9m-2)x + 36 = 0; (c)x2 + mx + 1 = 0 i x2 + x + m = 0
Liczby a i b są pierwiastkami równania x2 + 2x - 5 = 0. Napisz równanie, którego pierwiastkami są liczby: (a)a+b i ab (b)
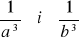
Dla jakich wartości m liczba 1 zawiera się między różnymi pierwiastkami równania (m-4)x2 - 4x + m - 3 = 0 ?
Dla jakich wartości m równanie x2 - (2m-1)x + m2 - 4 = 9 ma dwa różne pierwiastki mniejsze od 4?
Dla jakich wartości m pierwiastki równania x2 + (3m-2)x + m + 2 = 0 spełniają warunek x12 + x22 > 1?
Dla jakich wartości m pierwiastki równania x2 + (m+1)x + 1 = 0 spełniają warunek x12 + x22 < 3x1x2 ?
Dla jakich wartości m pierwiastki równania (2m-3)x2 + 4mx + m - 1 = 0 spełniają warunek -mx1x2 < x1 + x2 ?
Dla jakich wartości m pierwiastki równania x2 - (m+1)x +
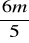
=0 są równe sinusowi i cosinusowi tego samego kąta ostrego?Dla jakich wartości m oba pierwiastki równania x2 + (2m+6)x + 4m + 12 = 0 s a większe od -1?
Dla jakich wartości m dwa różne pierwiastki rzeczywiste równania x2 - 2mx + m2 - 1 = 0 należą do (-2; 4)?
Dla jakich wartości m∈ <0 ; π/2> równanie x2∙sinm + x + cosm = 0 ma dwa różne pierwiastki rzeczywiste?
Dla jakich wartości m równanie |x-1| = m2 - 4m - 1 ma dwa pierwiastki dodatnie?
Dla jakich wartości m najmniejsza wartość funkcji f(x) = x2 - x - 2m + ¼ należy do przedziału <1;4>?
Dla jakich wartości m funkcja y = x2 + mx + m2 + 6m ma wartość ujemną dla dowolnego x∈(2;3)?
Dla jakich wartości m równanie 2x2 - (m-1)x +m+1=0 ma pierwiastki spełniające warunek |x2 - x1| = 1?
Dla jakich wartości m pierwiastki równania
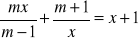
spełniają nierówność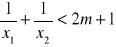
?Dla jakich wartości m suma kwadratów pierwiastków równania x2 + (m-3)x + m - 5 = 0 jest najmniejsza?
Dla jakich wartości m nierówność jest spełniona dla każdego x? (a) (m2-1)x2 + 2(m-1)x + 2 > 0 (b) (m-2)x2 - |m-2|x + 2 > 0
Dla jakich wartości m nierówność |x-m| < 2 - m2 jest spełniona przez co najmniej jedną liczbę ujemną?
Udowodnić, że jeśli x2 + y2 = 1 to -
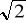
≤x+y≤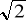
Udowodnić, że jeśli m>0 to m +
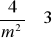
Niech x+y =2. Wykazać, że (a) x2 + y2 ≥ 2 (b)x4 + y4 ≥ 2 (c)x8 + y8 ≥ 2.
Rozwiąż graficznie i algebraicznie układ : (a)
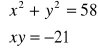
(b)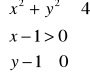
(c)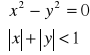
(d)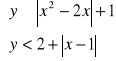
(e)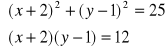
Dla jakich wartości parametru m układ ma dokładnie jedno rozwiązanie? (a)
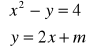
(b)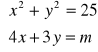
(c)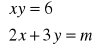
(d)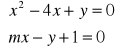
(e)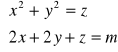
(f)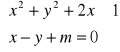
Zbadaj liczbę rozwiązań układu w zależności od m (a)
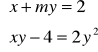
(b)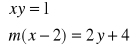
(c)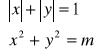
(d)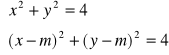
Wyszukiwarka
Podobne podstrony:
FUNKCJA KWADRATOWA, Matematyka
funkcja kwadratowa (2), Matematyka, Liceum
Funkcja kwadratowa, Matematyka - zadania liceum
Zastosowania funkcji kwadratowej, Matematyka. Zadania i rozwiązania
miejsca zerowe funkcji kwadratowej, Matematyka, Liceum
funkcja kwadratowa, Matematyka, Liceum
funkcja kwadratowa 2, Matematyka, Liceum
Zadania z funkcji kwadratowej z matemaks pl docx
funkcja kwadratowa, Technikum, Matematyka
Matematyka Funkcja kwadratowa
Funkcja kwadratowa - zestawienia wzorów, MATEMATYKA
Wykres funkcji kwadratowej, POLITECHNIKA LUBELSKA, ROK 1, SEMESTR 1, Ćwiczenia, Matematyka
Matematya Funkcja Kwadratowa, Do Matury, Matematyka
Matematyka Funkcja Kwadratowa, Do Matury, Matematyka
Funkcja kwadratowa, Sprawdziany, Liceum, Matematyka
Funkcja kwadratowa i jej wlasnosci, Matematyka. Zadania i rozwiązania
Matematyka Wzory z funkcji kwadratowej odt
więcej podobnych podstron