1 3 . 1 . U k ∏ a d w s p ó ∏ r z ´ d n y c h k a r t e z j a ƒ s k i c h

13. FUNKCJE

75

13.

Funkcje

13.1.

UK¸AD WSPÓ¸RZ¢DNYCH KARTEZJA¡SKICH

2

– 2

– 4

– 6

4

6

8

2

– 2

– 4

– 6

– 8

4

6

8

0

X

Y

P=(5, 3)

oÊ rz´dnych

oÊ odci´tych

I çwiartka

IV çwiartka

II çwiartka

III çwiartka

2

– 2

– 4

4

6

2

– 2

– 4

– 6

– 8

4

6

8

0

X

Y

K=(– 5, 3)

P=(5, 3)

M=(– 7, – 4)

N=(7, – 4)

2

– 2

– 6

4

6

2

– 2

– 4

– 6

– 8

4

6

8

0

X

Y

L = (– 3, –4)

H = (– 3, 4)

S = (7, 5)

D = (7, – 5)

– 4

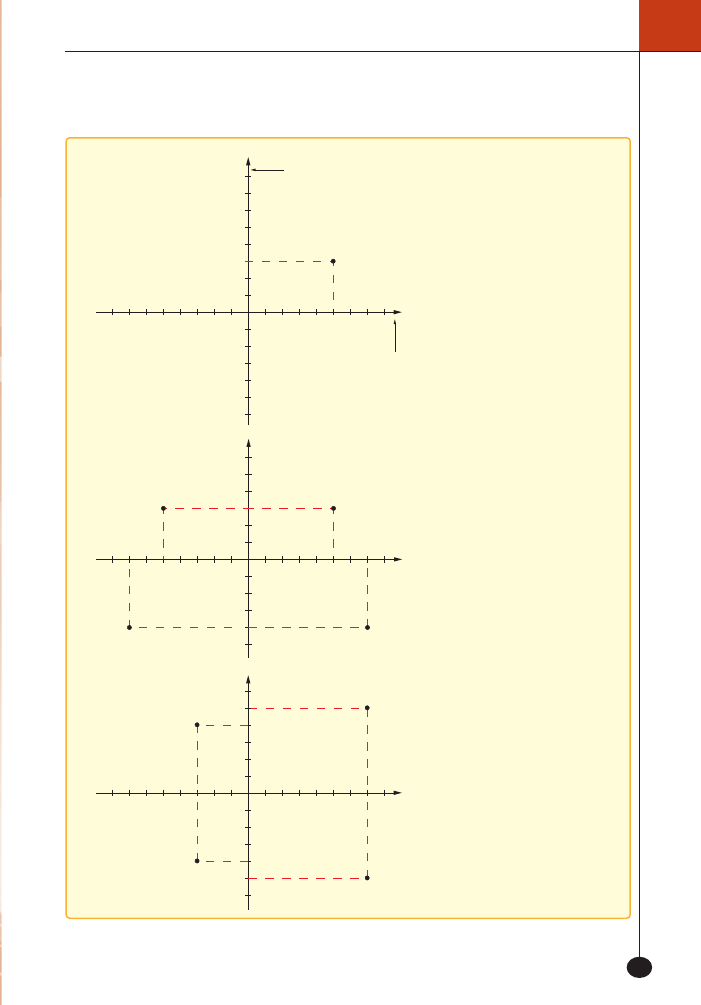
Prostokàtny uk∏ad wspó∏rz´d-

nych to dwie wzajemnie pros-
topad∏e osie liczbowe o wspólnym
punkcie

,

0 0

_

i, zwanym poczàt-

kiem uk∏adu wspó∏rz´dnych.

OÊ poziomà (oÊ

OX) nazywamy

osià odci´tych, a oÊ pionowà (oÊ

OY) nazywamy osià rz´dnych.

Osie te dzielà p∏aszczyzn´ na

cztery çwiartki.

W uk∏adzie wspó∏rz´dnych

mo˝na opisaç po∏o˝enie ka˝-
dego punktu za pomocà jego
wspó∏rz´dnych (np.:

,

P

5 3

=

_

i).

Zawsze jako pierwszà wspó∏-
rz´dnà wymieniamy t´, którà
odczytujemy na osi

X, a jako

drugà t´, którà odczytujemy na
osi

Y.

Punkty, których pierwsze

wspó∏rz´dne sà liczbami przeci-
wnymi, a drugie sà takie same,
sà po∏o˝one po przeciwnych
stronach osi OY i w tej samej
odleg∏oÊci od tej osi, na przy-
k∏ad:
punkt

,

K

5 3

= -

_

i i punkt

,

P

5 3

=

_

i

oraz punkt

,

M

7

4

= - -

_

i

i punkt

,

N

7

4

=

-

_

i.

Punkty, których drugie wspó∏-

rz´dne sà liczbami przeciwnymi,
a pierwsze sà takie same, sà po-
∏o˝one po przeciwnych stronach
osi

OX i w tej samej odleg∏oÊci

od tej osi, na przyk∏ad:
punkt

,

H

3 4

= -

_

i i punkt

,

L

3

4

= - -

_

i

oraz punkt

,

S

7 5

=

_

i i punkt

,

D

7

5

=

-

_

i.

1 3 . F u n k c j e

13. FUNKCJE

76

Funkcjà okreÊlonà na zbiorze

X o wartoÊciach

w zbiorze

Y nazywamy takie przyporzàdkowanie,

które ka˝demu elementowi x

X

!

przyporzàdko-

wuje jeden element

y

Y

! .

X – zbiór argumentów lub dziedzina funkcji

Y – zbiór, do którego nale˝à wartoÊci funkcji
x – argument funkcji
y – wartoÊç funkcji

13.2.

DEFINICJA FUNKCJI I SPOSOBY JEJ OPISYWANIA

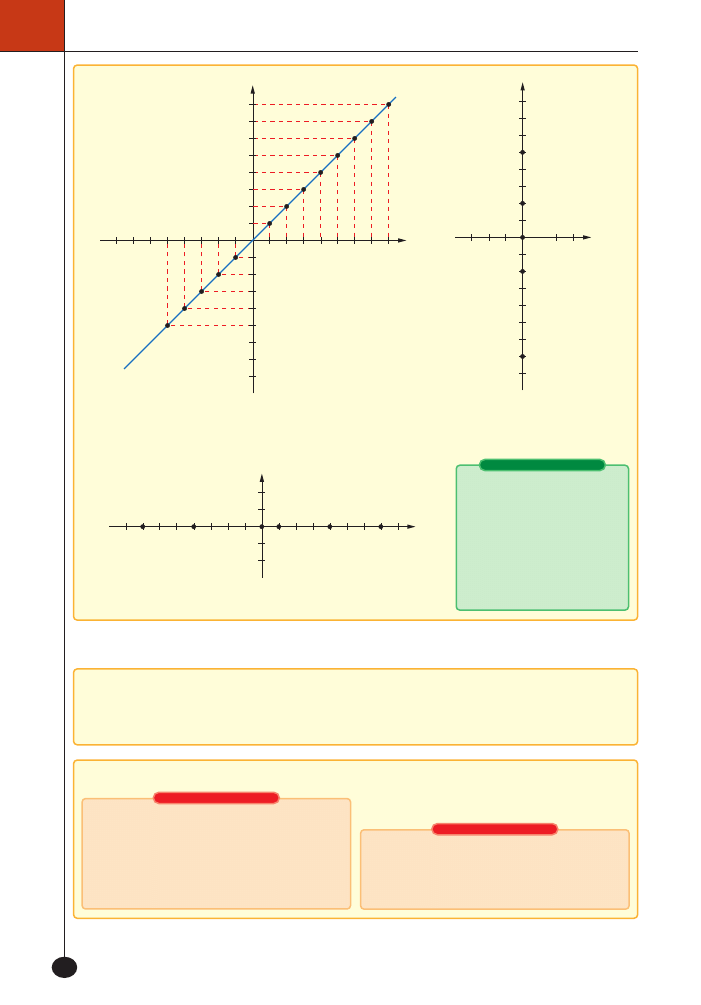
Punkty, których druga wspó∏rz´dna jest równa zero, le˝à na osi

OX.

Punkty, których pierwsza

wspó∏rz´dna jest równa zero,
le˝à na osi

OY.

Punkty, których obie wspó∏rz´dne majà jednakowà wartoÊç, na

przyk∏ad

,

A

1 1

=

_

i,

,

B

3

3

= - -

_

i,

,

O

0 0

=

_

i, le˝à na prostej o rów-

naniu

y x

= .

2

– 2

– 6

– 8

4

6

8

2

– 2

– 4

– 6

– 8

4

6

8

0

X

Y

– 4

(8, 8)

(7, 7)

(6, 6)

(5, 5)

(4, 4)

(3, 3)

(2, 2)

(1, 1)

(

– 1, – 1)

(

– 2, – 2)

(

– 3, – 3)

(

– 4, – 4)

(

– 5, – 5)

2

– 2

2

– 2

(0, 0)

(0, 2)

(0, 5)

(0,

– 2)

(0,

– 7)

0

X

Y

4

6

8

– 4

– 6

– 8

2

– 2

2

– 2

– 4

– 6

– 8

(

– 7, 0) (– 4, 0)

(0, 0)

(1, 0)

(4, 0)

(7, 0)

4

6

8

0

X

Y

Inna nazwa prostokàtne-

go uk∏adu wspó∏rz´dnych to
uk∏ad wspó∏rz´dnych karte-
zjaƒskich. Nazwa ta pocho-
dzi od nazwiska jego twórcy
– Kartezjusza (1596-1650),
autora s∏ynnego powiedze-
nia „MyÊl´, wi´c jestem”.

CHCESZ WIEDZIEå WI¢CEJ?

Uwaga!
Nie ka˝de przyporzàdkowanie jest funkcjà!

„Ka˝demu miastu Polski przyporzàdkowuje-

my rzek´, która przez to miasto przep∏ywa”.

To przyporzàdkowanie nie jest funkcjà, bo

sà miasta w Polsce, które nie le˝à nad rzekà.

PRZYK¸AD

„Ka˝demu uczniowi klasy III a przyporzàd-

kowujemy jego numer w dzienniku”.

„Ka˝dej liczbie ze zbioru

{ , , }

A

2 4 6

=

przy-

porzàdkowujemy liczb´ do niej przeciwnà”.

„Ka˝demu kwadratowi przyporzàdkowuje-

my jego pole”.

PRZYK¸ADY

13.2.1.

Opis s∏owny

1 3 . 2 . D e f i n i c j a f u n k c j i i s p o s o b y j e j o p i s y w a n i a

13. FUNKCJE

77

Tabela opisuje funkcj´, której dziedzinà sà wszystkie elementy w pierwszym wierszu, a zbiorem

wartoÊci sà wszystkie elementy z drugiego wiersza. Elementowi z pierwszego wiersza przyporzàd-
kowany jest element z drugiego wiersza, który le˝y bezpoÊrednio pod nim.

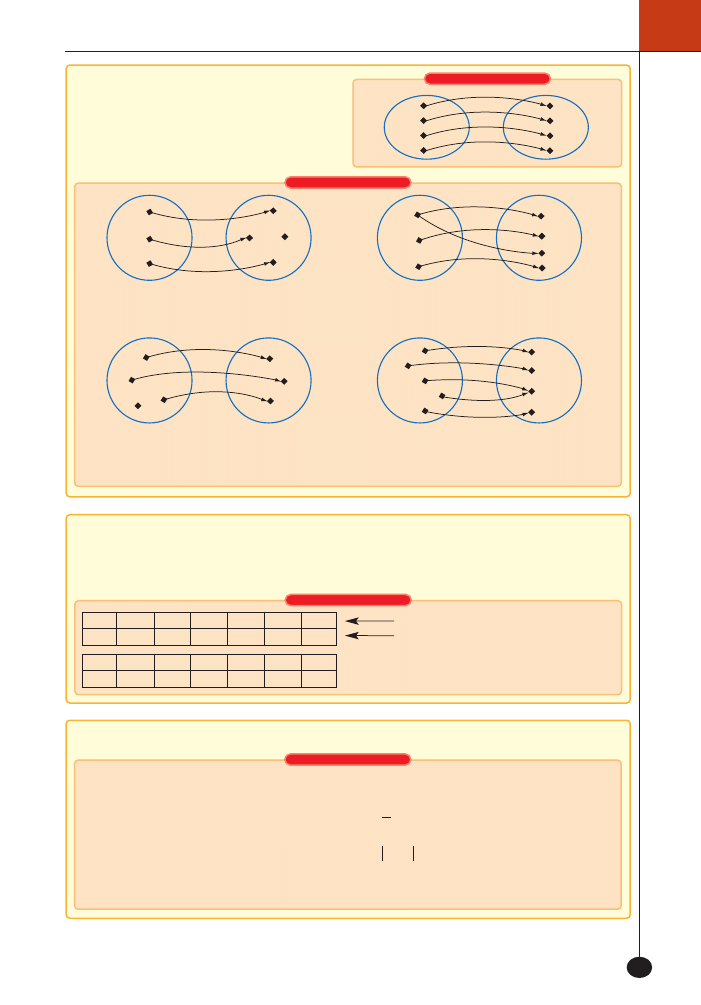
Graf opisuje funkcj´, której dziedzinà jest pier-

wszy zbiór (z którego strza∏ki wychodzà),
zbiorem wartoÊci – drugi zbiór, a przyporzàd-
kowanie jest zapisane za pomocà strza∏ek.

13.2.2.

Graf

13.2.3.

Tabela

13.2.4.

Wzór

y

x

2

3

=

+ , x

R

!

Wzór opisuje funkcj´, której zarówno dzie-

dzina, jak i zbiór wartoÊci nale˝à do liczb rze-
czywistych.

Uwaga!
Powy˝szà funkcj´ mo˝na te˝ zapisaç za pomocà

wzoru f x

x

2

3

=

+

_ i

. f x

_ i jest to wartoÊç funkcji f

okreÊlonej danym wzorem dla argumentu

x.

Inne przyk∏ady wzorów funkcji:
y

x

4

=- + dla x

R

!

y

x

5

=

dla

x

0

!

y x

x

4

3

2

=

+

- dla x

R

!

y

x

1

=

+

dla

x

R

!

,

y

x 1

NWD

=

_

i dla x N

!

+

y

x

2

$

= r

dla

,

x

0

3

!

_

i

PRZYK¸ADY

PRZYK¸AD

– ta tabela nie opisuje funkcji, gdy˝ argumentowi

5 przyporzàdkowane sà dwie liczby

x
y

1

3

3
5

5
7

7
9

9

11

11

13

dziedzina funkcji
zbiór wartoÊci funkcji

x
y

2
4

5
7

7
8

5
9

6

10

8

12

PRZYK¸AD

1
2
3
4

4
3
2
1

– ten graf przedstawia funkcj´ (z ka˝dego ele-
mentu pierwszego zbioru wychodzi jedna
strza∏ka)

– ten graf nie przedstawia funkcji (istnieje ele-
ment w pierwszym zbiorze, z którego nie
wychodzi ˝adna strza∏ka)

– ten graf nie przedstawia funkcji (z jednego
z elementów pierwszego zbioru wychodzà
dwie strza∏ki)

– ten graf przedstawia funkcj´ (z ka˝dego ele-
mentu pierwszego zbioru wychodzi jedna
strza∏ka).

A

1

B

2

C

5

D

E

7

2

c

b

1

a

3

d

1

2

a

b

3

c

4

K

L

0

1

M

3

1

PRZYK¸ADY

1 3 . F u n k c j e

13. FUNKCJE

78

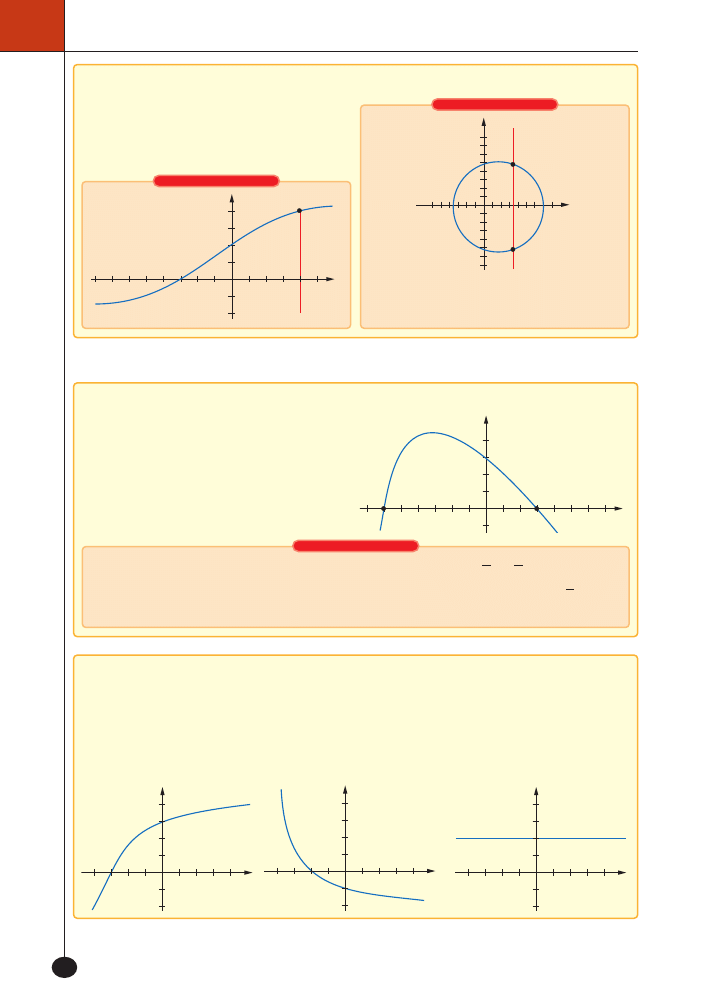
W funkcji przedstawionej za pomocà wykresu

argument

x to pierwsza wspó∏rz´dna, tzw. „od-

ci´ta” (odczytywana na poziomej osi

OX),

a wartoÊç

y to druga wspó∏rz´dna, tzw. „rz´dna”

(odczytywana na pionowej osi

OY).

Ta krzywa nie przedstawia funkcji, bo jednej

liczbie

x przyporzàdkowane sà dwie liczby y

1

i

y

2

.

X

Y

(x, y

2

)

(x, y

1

)

PRZYK¸AD

PRZYK¸AD

X

Y

(x, y)

Miejsce zerowe funkcji jest to ten argument

x

X

! , dla którego wartoÊç funkcji f jest równa

zero (

f x

0

=

_ i

). Na wykresie miejscem zerowym

jest odci´ta punktu przeci´cia si´ wykresu
funkcji z osià

OX.

Miejsce zerowe funkcji mo˝emy tak˝e obliczyç,

rozwiàzujàc równanie

f x

0

=

_ i

.

13.3.

W¸ASNOÂCI FUNKCJI

13.3.1.

Miejsce zerowe funkcji

X

Y

x

1

x

2

Znajdê miejsce zerowe

funkcji

y

x

4

2

=

+ , x

R

! .

f x

x

4

2

=

+

_ i

Wiemy, ˝e dla miejsca zerowe-
go

f x

0

=

_ i

, to znaczy

x

4

2

0

+ =

x

4

2

=-

x

4

2

2

1

=-

=-

Miejsce zerowe to

2

1

- .

PRZYK¸AD

Funkcja

f jest rosnàca, gdy

wraz ze wzrostem argumentów
rosnà wartoÊci funkcji, to zna-
czy dla ka˝dego

x

X

1

!

i

x

X

2

!

takich, ˝e <

x

x

1

2

, zachodzi:

<

f x

f x

1

2

`

`

j

j

.

Funkcja

f jest malejàca, gdy

wraz ze wzrostem argumentów
malejà wartoÊci funkcji, to zna-
czy dla ka˝dego

x

X

1

!

i

x

X

2

!

takich, ˝e <

x

x

1

2

, zachodzi:

>

f x

f x

1

2

`

`

j

j

.

Funkcja

f jest sta∏a, gdy wraz

ze wzrostem argumentów war-
toÊç funkcji nie ulega zmianie
(jest sta∏a), to znaczy dla ka˝-
dego

x

X

1

!

i

x

X

2

!

zachodzi:

f x

f x

1

2

=

`

`

j

j

.

13.3.2.

MonotonicznoÊç funkcji

X

Y

X

Y

X

Y

13.2.5.

Wykres

1 3 . 3 . W ∏ a s n o Ê c i f u n k c j i

13. FUNKCJE

79

13.3.3.

Najmniejsza i najwi´ksza wartoÊç funkcji

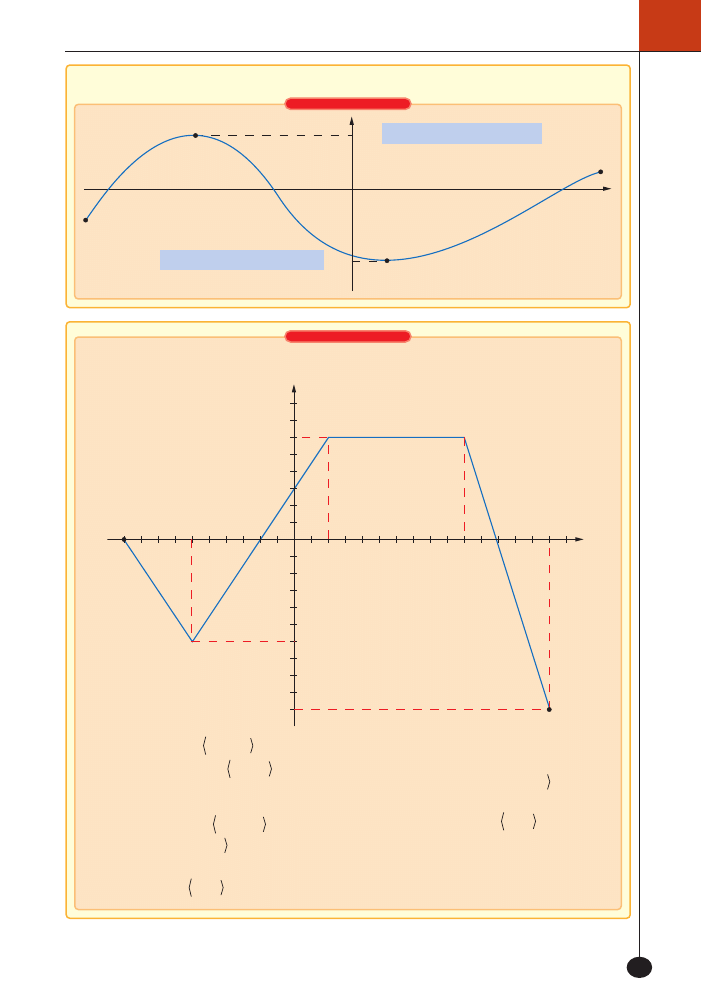
1. Dziedzina funkcji:

,

10 15

-

.

2. Zbiór wartoÊci funkcji:

,

10 6

-

.

3. Miejsca zerowe funkcji: 10

- , 2

- , 12.

4. Funkcja jest:

malejàca w przedziale

,

10

6

-

-

oraz w przedziale

,

10 15

`

,

rosnàca w przedziale

,

6 2

-

`

i,

sta∏a w przedziale ,

2 10 .

5. Funkcja przyjmuje wartoÊci dodatnie

dla

,

x

2 12

! -

`

i, a wartoÊci ujemne

dla

,

x

10

2

! -

-

`

i i dla

,

x

12 15

!

`

.

6. Najwi´kszà wartoÊç równà 6 (

f

6

max

= )

funkcja przyjmuje dla

,

x

2 10

!

.

7. Najmniejszà wartoÊç równà 10

-

(f

10

min

=-

) funkcja przyjmuje dla x 15

=

.

PRZYK¸AD

2

– 2

– 6

– 8

4

6

8

2

– 2

– 4

– 6

– 8

4

6

8

0

X

Y

– 10

– 10

10

12

14

16

– 4

Na podstawie wykresu odczytaj w∏asnoÊci funkcji.

PRZYK¸AD

X

Y

najwi´ksza wartoÊç funkcji

najmniejsza wartoÊç funkcji

f

max

f

min

0

1 3 . F u n k c j e

13. FUNKCJE

80

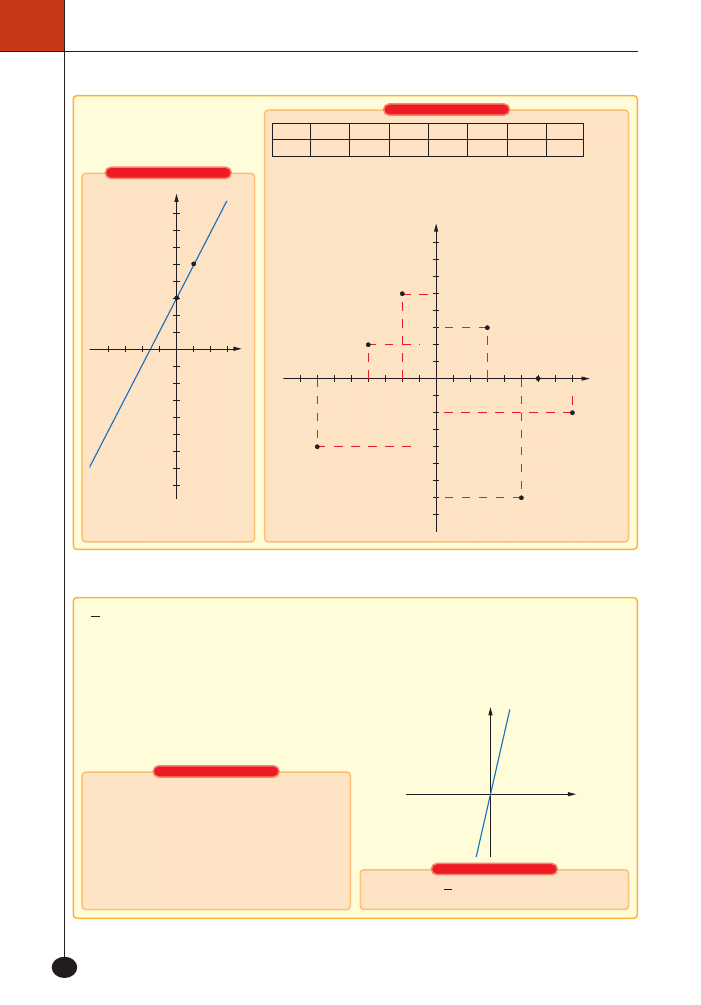
Funkcja jest funkcjà liczbo-

wà, jeÊli zarówno dziedzina, jak
i zbiór wartoÊci sà zbiorami
liczbowymi.

PRZYK¸AD

f x

x

2

3

=

+

_ i

,

gdzie

X

R

1 i Y R

1

PRZYK¸AD

2

– 2

– 6

– 8

4

6

8

2

– 2

– 4

– 6

– 8

4

6

8

0

X

Y

– 4

x
y

7

-

4

-

4

-

2

2

-

5

3
3

5

7

-

6
0

8

2

-

{

,

,

, , , , }

X

7

4

2 3 5 6 8

= -

-

-

{

,

,

, , , , }

Y

7

4

2 0 2 3 5

= -

-

-

2

– 2

– 6

– 8

4

6

8

2

– 2

0

X

Y

– 4

x

y

a

=

Zale˝noÊç mi´dzy dwiema wielkoÊciami, któ-

rych iloraz jest sta∏y, nazywamy proporcjonal-
noÊcià prostà.

Liczb´

a nazywamy sta∏à proporcjonalnoÊci,

a o wielkoÊciach

x i y mówimy, ˝e sà wprost pro-

porcjonalne. Mo˝emy tak˝e powiedzieç (przy za-
∏o˝eniu, ˝e >

a

0), ˝e wielkoÊci sà wprost propor-

cjonalne, jeÊli wraz ze wzrostem jednej wielkoÊci,
druga wielkoÊç tak˝e proporcjonalnie roÊnie.

ProporcjonalnoÊç prosta jest funkcjà, którà mo˝-

na zapisaç wzorem:

f x

ax

=

_ i

,

a

0

! . Jej dziedzinà

jest zbiór liczb rzeczywistych. Liczb´

a nazywamy

wspó∏czynnikiem proporcjonalnoÊci. Wykresem
proporcjonalnoÊci prostej jest prosta przechodzà-
ca przez poczàtek uk∏adu wspó∏rz´dnych.

13.5.

PROPORCJONALNOÂå PROSTA I JEJ WYKRES

13.4.

FUNKCJA LICZBOWA I JEJ WYKRES

0

X

Y

WielkoÊciami wprost proporcjonalnymi sà

na przyk∏ad:
– liczba kilogramów cukru zakupiona w skle-
pie i kwota, którà za niego nale˝y zap∏aciç,
– pr´dkoÊç, z jakà jedzie rowerzysta, i droga,
jakà przejedzie w danym czasie (im szybciej
jedzie, dalej zajedzie),
– d∏ugoÊç boku kwadratu i jego obwód.

PRZYK¸AD

f x

x

3

1

=

_ i

,

f x

x

3

=

_ i

,

f x

x

2

=-

_ i

PRZYK¸ADY

1 3 . 6 . F u n k c j a l i n i o w a

13. FUNKCJE

81

Funkcja liniowa to funkcja ok-

reÊlona wzorem

f x

a x

b

$

=

+

_ i

,

gdzie

a i b sà liczbami rzeczy-

wistymi. Liczb´

a nazywamy

wspó∏czynnikiem kierunkowym,
a liczb´

b – wyrazem wolnym.

Dziedzinà funkcji liniowej jest
zbiór liczb rzeczywistych.

W przypadku, gdy wyraz wolny

b jest równy 0 i a

0

! , to funkcja

liniowa przedstawia proporcjon-
alnoÊç prostà.

Wykresem funkcji liniowej jest

prosta. Aby narysowaç wykres
takiej funkcji, wystarczy znaleêç
wspó∏rz´dne dwóch punktów
nale˝àcych do wykresu i popro-
wadziç przez nie prostà.

13.6.

FUNKCJA LINIOWA

PUNKTY PRZECI¢CIA WYKRESU FUNKCJI

LINIOWEJ Z OSIAMI UK¸ADU

WSPÓ¸RZ¢DNYCH

Wykres funkcji liniowej przecina oÊ

OX w pun-

kcie

,

a

b 0

-

d

n

, jeÊli a

0

! . Odci´ta tego punktu to

miejsce zerowe funkcji.

Wykres funkcji liniowej przecina oÊ

OY w pun-

kcie

, b

0

_

i.

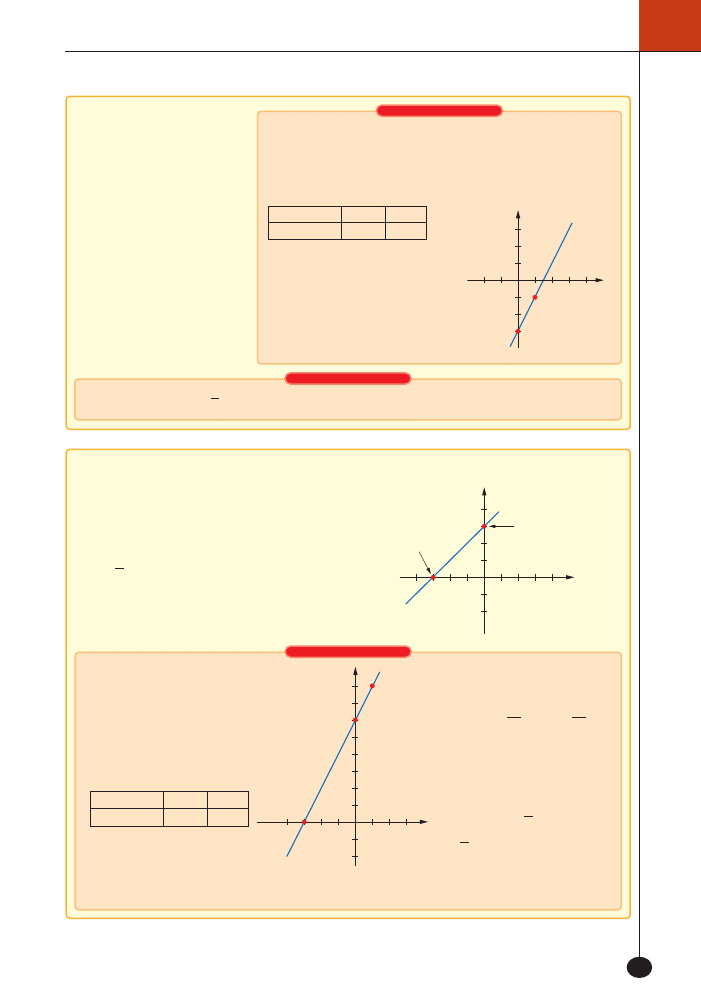
Narysuj wykres funkcji okreÊlonej wzorem f x

x

2

3

=

-

_ i

.

Poniewa˝ dziedzinà funkcji sà liczby rzeczywiste, wi´c bierze-

my dowolne dwie liczby (np.

x

0

1

= , x

1

2

= ) i obliczamy wartoÊci

funkcji dla tych argumentów:

f x

f 0

2 0

3

3

1

$

=

=

- =-

`

_

j

i

,

f x

f 1

2 1

3

1

2

$

=

=

- =-

`

_

j

i

.

W uk∏adzie wspó∏rz´dnych na-

nosimy punkty

,

0

3

-

_

i i ,

1

1

-

_

i,

a nast´pnie prowadzimy prostà
przechodzàcà przez te dwa punk-
ty. W ten sposób otrzymujemy wy-
kres zadanej funkcji.

PRZYK¸AD

f x

x

6

1

5

=

-

_ i

,

f x

x

4

7

=-

+

_ i

,

f x

x

3

=

_ i

(

b 0

= ), f x

2

=

_ i

(

a 0

= )

PRZYK¸ADY

(1,

– 1)

(0,

– 3)

X

Y

0

3

-

1

1

-

x

y

x

2

3

=

-

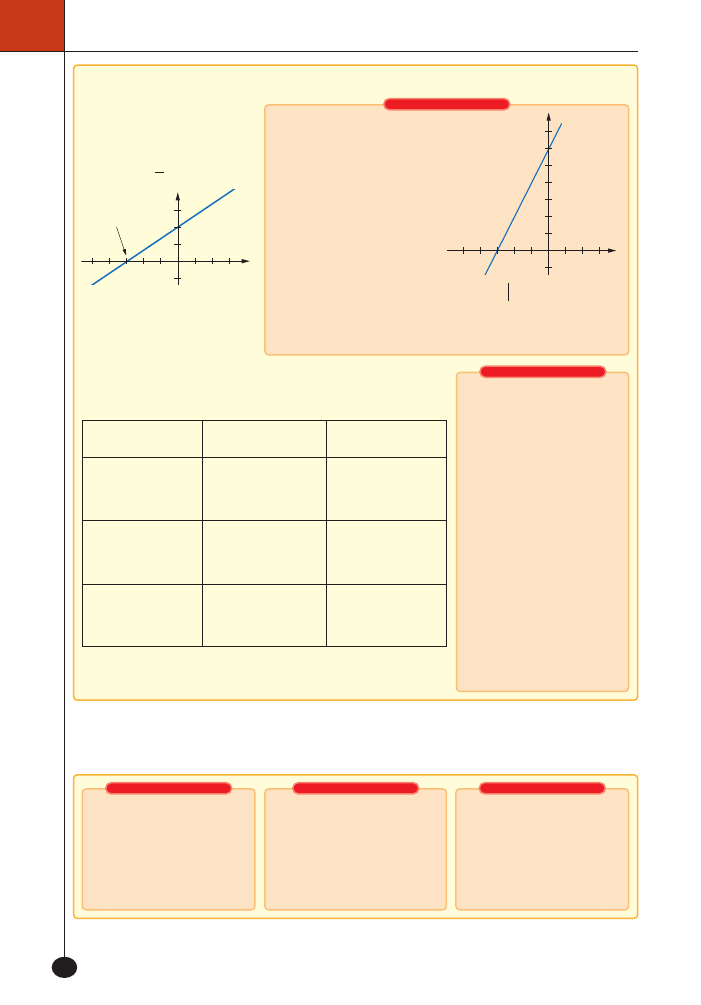
Wyznacz punkty przeci´cia

wykresu funkcji okreÊlonej
wzorem

f x

x

2

6

=

+

_ i

z osiami

uk∏adu wspó∏rz´dnych.

I sposób:
Rysujemy wykres i szukane

punkty odczytujemy z wykresu.

Z wykresu odczytujemy, ˝e

punkty przeci´cia wykresu
funkcji z osiami uk∏adu majà
wspó∏rz´dne:

,

3 0

-

_

i i ,

0 6

_

i.

Sposób ten jest ma∏o precyzyj-

ny, gdy˝ zale˝y od dok∏adnoÊci

rysunku i mo˝liwoÊci odczytania
liczby na osiach (trudno powie-
dzieç, czy wykres przecià∏ oÊ

w punkcie

,

15

13 0

d

n

, czy

,

15

12 0

d

n

).

II sposób:
Obliczamy wspó∏rz´dne

punktów:
– punkt przeci´cia wykresu

z osià

OX:

,

a

b 0

-

d

n

, to znaczy

,

2

6 0

-

d

n

, czyli

,

3 0

-

_

i,

– punkt przeci´cia wykresu z osià

OY: , b

0

_

i, to znaczy ,

0 6

_

i.

PRZYK¸AD

0
6

1

8

x

f x

_ i

(1, 8)

(0, 6)

(

– 3, 0)

X

Y

(0, b)

X

Y

(

– b

a

– , 0)

13.6.1.

W∏asnoÊci funkcji liniowej (I)

1 3 . F u n k c j e

13. FUNKCJE

82

13.6.1.

W∏asnoÊci funkcji liniowej (II)

MIEJSCA ZEROWE FUNKCJI

Miejscem zerowym funkcji

jest argument, dla którego
wartoÊç funkcji jest równa 0, to

znaczy

x

a

b

0

=- , dla a 0

! .

JeÊli

a 0

= i b 0

= , to funkcja ma

nieskoƒczenie wiele miejsc zero-
wych. JeÊli

a 0

= i b 0

! , to funk-

cja nie ma miejsc zerowych.

MONOTONICZNOÂå FUNKCJI

Rodzaj monotonicznoÊci funkcji liniowej okreÊlonej wzorem

f x

ax

b

=

+

_ i

zale˝y od wspó∏czynnika kierunkowego

a.

Uwaga!
Je˝eli

a

0

! , to funkcja liniowa nie ma najmniejszej i najwi´kszej

wartoÊci.

X

Y

x

0

=

– –b

a

Wyznacz miejsce zerowe fun-

kcji

f x

x

2

6

=

+

_ i

.

I sposób:
Rysujemy wykres funkcji (w spo-
sób opisany wy˝ej) i miejsce ze-
rowe odczytujemy z wykresu.
Miejsce zerowe:

x

3

=- .

II sposób:
Miejsce zerowe mo˝na obli-
czyç, wiedzàc, ˝e w miejscu
zerowym wartoÊç funkcji jest
równa zero.
f x

0

=

_ i

x

0

2

6

=

+

:

x

2

6

2

-

=

-

_

i

x

3

=-

Miejscem zerowym funkcji jest

3

- .

PRZYK¸AD

X

Y

– 3

0

1

1

Zbadaj monotonicznoÊç

funkcji okreÊlonej wzorem:

f x

x

4

2

=

+

_ i

.

Korzystamy z definicji mono-
tonicznoÊci funkcji. Bierzemy
dwa dowolne punkty

x

1

i

x

2

takie, ˝e <

x

x

1

2

, nast´pnie

obliczamy

f x

f x

2

1

-

`

`

j

j

:

f x

f x

2

1

-

=

`

`

j

j

x

x

4

2

4

2

2

1

=

+ -

+

=

`

j

x

x

4

2

1

=

-

`

j

.

x

x

4

2

1

-

`

j

jest liczbà dodat-

nià, bo <

x

x

1

2

.

Stàd >

f x

f x

0

2

1

-

`

`

j

j

, czyli

>

f x

f x

2

1

`

`

j

j

, wi´c funkcja

jest rosnàca.

PRZYK¸AD

Wspó∏czynnik

kierunkowy

Rodzaj monoto-

nicznoÊci funkcji

Przyk∏ady funkcji

>

a

0

funkcja rosnàca

f x

x

5

4

=

+

_ i

f x

x

7

= -

_ i

f x

x

=

_ i

<

a

0

funkcja malejàca

f x

x

5

4

=-

+

_ i

f x

x

1

=- +

_ i

f x

x

=-

_ i

a 0

=

funkcja sta∏a

f x

4

=

_ i

f x

0

=

_ i

f x

6

=-

_ i

13.7.

PRZYK¸ADY ZALE˚NOÂCI FUNKCYJNYCH WYST¢PUJÑCYCH

W PRZYRODZIE, GOSPODARCE I ˚YCIU CODZIENNYM

w przyrodzie:

– wraz ze wzrostem tempe-
ratury powietrza obni˝a si´
w stawie poziom wody;
– im wi´cej wytniemy lasów,
tym bardziej zmniejszy si´
iloÊç tlenu w otoczeniu.

PRZYK¸ADY

w gospodarce:

– im wi´cej zu˝yjemy pràdu,
tym wi´kszy zap∏acimy rachu-
nek;
– im wi´kszy zaciàgniemy
kredyt w banku, tym wi´cej
b´dziemy sp∏acaç odsetek.

PRZYK¸ADY

w ˝yciu codziennym:

– im szybciej jedziemy, tym
czas potrzebny na prze-
jechanie danego odcinka
trasy jest krótszy.

PRZYK¸ADY

1 3 . 8 . O d c z y t y w a n i e i n f o r m a c j i z w y k r e s u f u n k c j i o p i s u j à c e j s y t u a c j ´ p r a k t y c z n à

13. FUNKCJE

83

13.8.

ODCZYTYWANIE INFORMACJI Z WYKRESU FUNKCJI

OPISUJÑCEJ SYTUACJ¢ PRAKTYCZNÑ

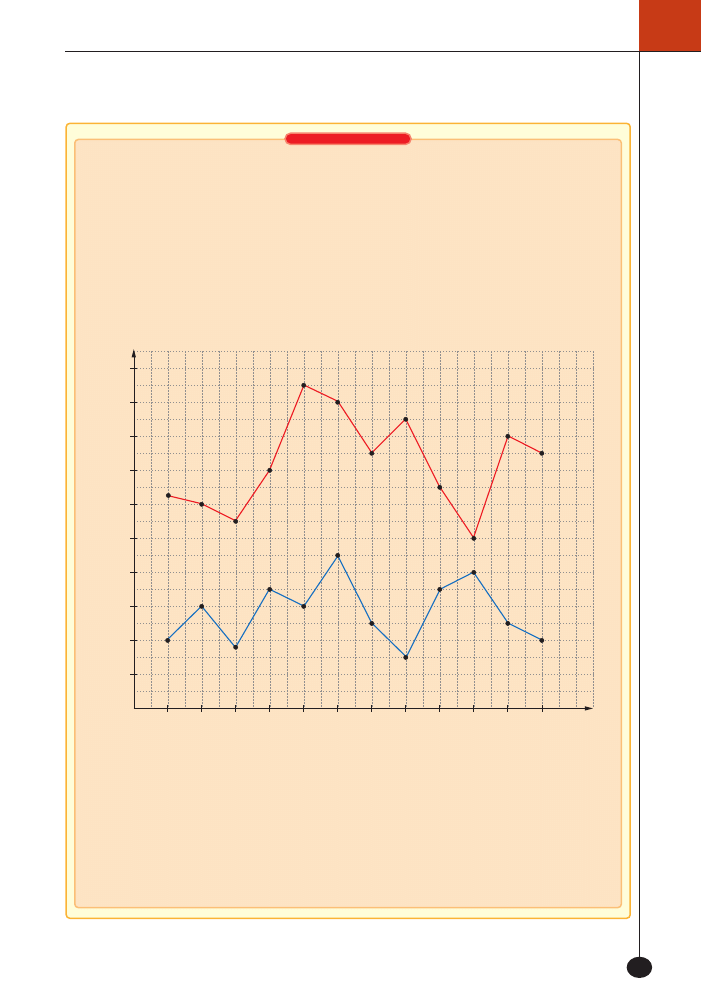
Na poni˝szym wykresie przedstawiono obroty w handlu zagranicznym w Polsce w ciàgu jednego

roku.

Po przeanalizowaniu wykresu odpowiedz na pytania:

W jakim miesiàcu Polska uzyska∏a najwi´kszy dochód, a w jakim najmniejszy?

W jakim miesiàcu Polska wyda∏a najwi´cej, a w jakim najmniej?

W jakim miesiàcu deficyt (ró˝nica mi´dzy dochodem a kosztami) by∏ najwi´kszy?

W jakim miesiàcu deficyt by∏ najmniejszy?

Przez ile miesi´cy odnotowano sta∏y lub rosnàcy dochód?

Przez ile miesi´cy odnotowano sta∏e lub malejàce koszty?

O ile wi´kszy od dochodu w styczniu by∏ dochód w listopadzie?

Odpowiedzi:

Najwi´kszy dochód Polska uzyska∏a w maju, a najmniejszy w paêdzierniku.

Najwi´cej wydano w czerwcu, a najmniej w sierpniu.

Najwi´kszy deficyt zanotowano w sierpniu.

Najmniejszy deficyt zanotowano w paêdzierniku.

Sta∏y lub rosnàcy dochód zanotowano w 4 miesiàcach.

Sta∏e lub malejàce koszty zanotowano w 6 miesiàcach.

Dochód w listopadzie by∏ o 350 mln dolarów wi´kszy od dochodu w styczniu.

2000

I

II

III

IV

2200

2400

2600

2800

3000

3200

3400

3600

3800

4000

V

VI

VII

VIII

IX

X

XI

XII

dochód

koszty

miesiàc

mln USD

PRZYK¸AD

1 4 . 1 . Z b i e r a n i e , p o r z à d k o w a n i e , p r z e d s t a w i a n i e i i n t e r p r e t o w a n i e d a n y c h

14. STATYSTYKA

OPISOWA

IWST¢P

DO

PRAWDOPODOBIE¡STWA

87

14.

Statystyka opisowa i wst´p

do prawdopodobieƒstwa

Statystyka to nauka zajmujàca si´ metodà pozyskiwania, porzàdkowania, przedstawiania i inter-

pretowania zjawisk (procesów) masowych. Jej celem jest poznanie wyst´pujàcych prawid∏owoÊci
i ich iloÊciowe przedstawienie.

Statystyk´ dzielimy na:

– statystyk´ opisowà, zajmujàcà si´ metodami zbierania i prezentowania informacji statystycznych
i ich iloÊciowym opisem,
– statystyk´ matematycznà, opierajàcà si´ na rachunku prawdopodobieƒstwa.

Do najbardziej znanych sposobów zbierania

informacji nale˝à ankiety. Nale˝y przy tym pa-
mi´taç, ˝e jeÊli chcemy, by nasze badania mia∏y
(przynajmniej w przybli˝eniu) przedstawiaç
pewnà rzeczywistoÊç i by by∏y reprezentatywne,
liczba ankietowanych ludzi powinna byç mo˝li-
wie najwi´ksza i wybrana losowo.

14.1.1.

Zbieranie danych

14.1.

ZBIERANIE, PORZÑDKOWANIE, PRZEDSTAWIANIE

I INTERPRETOWANIE DANYCH

Porzàdkowanie danych polega na przyporzàd-

kowaniu danemu przypadkowi (mo˝liwoÊci)
okreÊlonej wielkoÊci liczbowej.

14.1.2.

Porzàdkowanie danych

ZapytaliÊmy 200 uczniów naszej szko∏y

(szko∏a liczy 450 uczniów), jaki jest ich ulu-
biony kolor. Ka˝dy móg∏ zaznaczyç jednà
z podanych odpowiedzi: czerwony, zielony,
niebieski, ˝ó∏ty, bia∏y, czarny, inny.

PRZYK¸AD

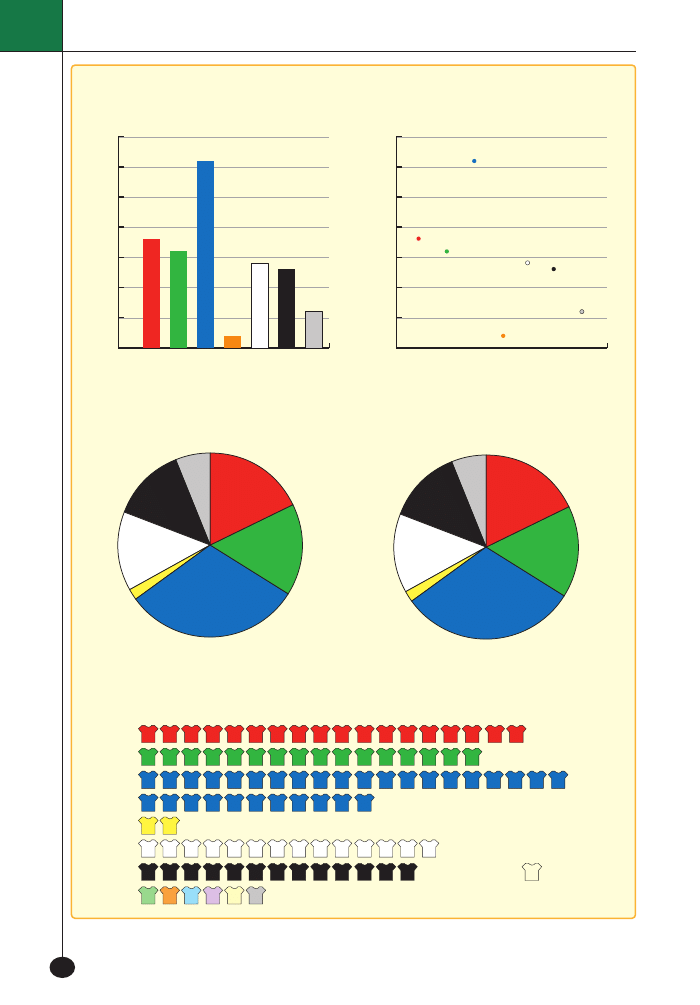
Na podstawie ankiety dowiedzieliÊmy si´,

˝e niebieski wybra∏o 62 uczniów, czerwony
– 36, zielony – 32, bia∏y – 28, czarny – 26,
˝ó∏ty – 4, inny – 12.

PRZYK¸AD

Dane mo˝na prezentowaç graficznie na wiele

sposobów. To, jaki sposób wybierzemy, zale˝y
od tego, jakie dane b´dziemy przedstawiaç, na
przyk∏ad:
– wykres s∏upkowy – gdy chcemy porównaç da-
ne (liczba uzyskanych przez ucznia na egzami-
nie punktów na tle klasy);
– wykres liniowy – gdy wraz ze zmianà jednej
wartoÊci zmienia si´ druga (zmiana temperatury
podczas dnia);
– diagram ko∏owy – gdy przedstawiamy coÊ ja-
ko cz´Êç ca∏oÊci (liczba dziewczàt/ch∏opców
w klasie);
– diagram rysunkowy – na przyk∏ad gdy dane
dotyczà du˝ych liczb (jeden rysunek przedstawia
pewnà liczb´).

Poni˝ej przedstawimy tylko te najcz´Êciej u˝ywa-

ne sposoby przedstawiania danych. Diagramy te
odnoszà si´ do omawianego przyk∏adu „ulubiony
kolor”.

14.1.3.

Przedstawianie danych (I)

Tabela

Kolor

Liczba osób

czerwony

36

zielony

32

niebieski

62

˝ó∏ty

4

bia∏y

28

czarny

26

inny

12

Razem

200

1 4 . S t a t y s t y k a o p i s o w a i w s t ´ p d o p r a w d o p o d o b i e ƒ s t w a

14. STATYSTYKA

OPISOWA

IWST¢P

DO

PRAWDOPODOBIE¡STWA

88

14.1.3.

Przedstawianie danych (II)

Diagram s∏upkowy

Wykres

Diagram ko∏owy

Diagram ko∏owy procentowy

Diagram rysunkowy

0

10

20

30

40

50

60

70

36

32

62

4

28

26

12

Liczba osób

˝ó∏ty

2%

czerwony

18%

niebieski

31%

zielony

16%

bia∏y

14%

inny

6%

czarny

13%

Ulubiony kolor

0

10

20

30

40

50

60

70

36

32

62

4

28

26

12

Liczba osób

˝ó∏ty

4

czerwony

36

niebieski

62

zielony

32

bia∏y

28

inny

12

czarny

26

Ulubiony kolor

= 2

1 4 . 2 . W i e l k o Ê c i s t a t y s t y c z n e

14. STATYSTYKA

OPISOWA

IWST¢P

DO

PRAWDOPODOBIE¡STWA

89

Dominanta (wartoÊç modalna, moda) to naj-
cz´Êciej wyst´pujàca wartoÊç.
Ârednià arytmetycznà n liczb a

1

, a

2

,..., a

n

obli-

czamy ze wzoru:

...

S

n

a

a

a

n

n

1

2

=

+

+ +

.

Aby obliczyç median´ z n liczb, najpierw usta-
wiamy je w kolejnoÊci rosnàcej: a

1

, a

2

,..., a

n

.

JeÊli n jest nieparzyste, to mediana jest liczbà
stojàcà na Êrodkowej pozycji –

a

n

2

1

+

. JeÊli n jest

parzyste, to mediana jest Êrednià arytmetycznà
dwóch liczb znajdujàcych si´ na Êrodkowych

pozycjach –

a

a

2

n

n

2

2

1

+

+

.

14.2.

WIELKOÂCI STATYSTYCZNE

DoÊwiadczenie losowe to proces, który w jed-

nakowych lub zbli˝onych warunkach mo˝na
przeprowadzaç wielokrotnie, ale którego wyniku
nie mo˝emy przewidzieç.

Zdarzenie elementarne (wynik doÊwiadczenia

losowego) – poj´cie pierwotne, czyli takie, któ-
rego nie definiujemy ale intuicyjnie rozumiemy,
np.: w rzucie monetà: wypad∏a reszka, w rzucie
kostkà do gry: wypad∏a „5”.

Zbiór zdarzeƒ elementarnych (przestrzeƒ

zdarzeƒ elementarnych) – zbiór wszystkich
mo˝liwych wyników doÊwiadczenia losowego
(np.: w rzucie monetà –

,

O R

#

-, w rzucie kostkà

do gry –

, , , , ,

1 2 3 4 5 6

#

-)

Zdarzenie losowe – podzbiór zbioru zdarzeƒ

elementarnych (np.: w rzucie kostkà – „wypad-
nie nieparzysta liczba oczek”

, ,

1 3 5

#

-).

Je˝eli w wyniku doÊwiadczenia losowego otrzy-

mano wynik, który wchodzi w sk∏ad pewnego

zdarzenia losowego, to mówimy, ˝e sprzyja temu
zdarzeniu (np.: zdarzenie losowe brzmi: „wypad∏a
parzysta liczba oczek w rzucie szeÊciennà kostkà
do gry”, a w wyniku doÊwiadczenia losowego,
jakim jest rzut kostkà, wypad∏a „6”, która jest
liczbà parzystà. Mówimy, ˝e wypadni´cie „szóstki”
sprzyja naszemu zdarzeniu losowemu).

Zdarzenie niemo˝liwe – zdarzenie, któremu nie

sprzyja ˝adne zdarzenie elementarne (np. z urny,
w której sà tylko bia∏e pi∏ki, wyciàgni´cie czarnej
pi∏ki jest zdarzeniem niemo˝liwym).

Zdarzenie pewne – zdarzenie, któremu ka˝de

zdarzenie elementarne jest sprzyjajàce (np.: z urny,
w której sà tylko bia∏e pi∏ki, wyciàgni´cie bia∏ej pi∏ki
jest zdarzeniem pewnym).

Cz´stoÊç zdarzenia losowego

n

k

d n

– iloraz

liczby zajÊç zdarzeƒ sprzyjajàcych

k do liczby prze-

prowadzonych doÊwiadczeƒ losowych

n (np.: jeÊli

rzucono 20 razy kostkà do gry i 7 razy wypad∏a
parzysta liczba oczek, to cz´stoÊç takiego zdarze-

nia losowego wynosi

20

7 ).

14.3.

PRZYK¸ADY PROSTYCH DOÂWIADCZE¡ LOSOWYCH (I)

Interpretujàc powy˝szy przyk∏ad, mo˝emy dowiedzieç si´, ˝e najprawdopodobniej (nie wszyscy

zostali przebadani) najbardziej lubianym przez uczniów kolorem jest niebieski. To badanie mo˝emy
wykorzystaç przy projektowaniu mundurków, a dok∏adniej – kolorystyki.

14.1.4.

Interpretowanie danych

Uczniowie na egzaminie matematyczno-przyrodniczym uzyskali nast´pujàce wyniki punktowe:

11, 24, 35, 21, 24, 22, 26, 22, 32, 40, 39, 21, 22, 22, 27, 21, 22, 26, 22, 42.

Wyznacz mod´, median´ i wartoÊç Êrednià.
Porzàdkujemy dane od najni˝szej do najwy˝szej liczby uzyskanych punktów:

11, 21, 21, 21, 22, 22, 22, 22, 22, 22, 24, 24, 26, 26, 27, 32, 35, 39, 40, 42

Moda to 22, bo uzyska∏o t´ liczb´ punktów szeÊciu uczniów.
Mediana to 23 (jest to Êrednia arytmetyczna liczb stojàcych na dziesiàtej i jedenastej pozycji).
WartoÊç Êrednia to

,

26 05, bo

20

11 21 21 21 22

22

22

22

22

22

24

24

26

26

27

32

35

39

40

42

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

=

,

26 05

=

.

PRZYK¸AD

DoÊwiadczeniami losowymi sà: rzut kostkà

do gry, rzut monetà, gry losowe typu totolotek.

PRZYK¸AD

1 4 . S t a t y s t y k a o p i s o w a i w s t ´ p d o p r a w d o p o d o b i e ƒ s t w a

14. STATYSTYKA

OPISOWA

IWST¢P

DO

PRAWDOPODOBIE¡STWA

90

DoÊwiadczenie losowe mo˝na przedstawiç za pomocà opisu s∏ownego, diagramów lub tabel.

14.3.

PRZYK¸ADY PROSTYCH DOÂWIADCZE¡ LOSOWYCH (II)

1. Rzucono trzykrotnie monetà. Wypisz przestrzeƒ zdarzeƒ elementarnych.
Do rozwiàzania tego zadania mo˝e nam si´ przydaç drzewko opisujàce to doÊwiadczenie:

Przestrzeƒ zdarzeƒ elementarnych:

,

,

,

,

,

,

,

OOO OOR ORO ORR ROO ROR RRO RRR

#

-.

2. Rzucono 150 razy kostkà szeÊciennà do gry, przy czym „czwórka” wypad∏a 24 razy. Oblicz

cz´stoÊç zdarzenia

A – „wypada liczba 4 w rzucie kostkà do gry”.

n – liczba wykonanych doÊwiadczeƒ (rzutów): 150
k – liczba zdarzeƒ sprzyjajàcych zdarzeniu A: 24

Cz´stoÊç zdarzenia

A: n

k

150

24

25

4

=

=

.

3. Z urny zawierajàcej 5 ˝ó∏tych kul i 2 bia∏e wylosowano 1 kul´. Które z poni˝szych zdarzeƒ

losowych sà zdarzeniami pewnymi, a które z nich sà zdarzeniami niemo˝liwymi?

a) „Wylosowano kul´ niebieskà”.
b) „Wylosowano kul´ ˝ó∏tà”.
c) „Wylosowano kul´ bia∏à”.
d) „Wylosowano kul´ ˝ó∏tà lub bia∏à”.
Odpowiedê:
a) zdarzenie niemo˝liwe, b) zdarzenie mo˝liwe, c) zdarzenie mo˝liwe, d) zdarzenie pewne.

STA R T

R

RO

ROO

ROR

RR

RRO

RRR

R

OO

OOO OOR

OR

ORO

ORR

I rzut

II rzut

III rzut

PRZYK¸ADY ZADA¡

a) Na zaj´ciach wychowania fizycznego uczniowie 24-osobowej klasy rzucali pi∏k´ do kosza.
Ka˝dy rzuca∏ tylko raz. By∏o 15 trafieƒ celnych.

b) Przyk∏ad z rzutami do kosza mo˝na przedstawiç w tabeli:

c) Ten sam przyk∏ad mo˝na przedstawiç na diagramie ko∏owym:

trafiony

15

nietrafiony

9

Rzut pi∏kà do kosza

PRZYK¸ADY

trafiony

nietrafiony

15

9