Ewelina Dąbrowska

PODOBIEŃSTWO - GIMNAZJUM

Omówienie podręcznika „matematyka krok po kroku”, „matematyka nowej ery”, „matematyka z plusem”.

1. Wprowadzenie:

• W którym miejscu zostało wprowadzone oraz co jest potrzebne, aby je wprowadzić?

Aby wprowadzić podobieństwo należy znać własności figur płaskich, proporcjonalność oraz umieć obliczać pola figur.

1. „matematyka krok po kroku”

Wprowadzone jest na początku pierwszego semestru 3 klasy

Aby wprowadzić podobieństwo potrzebna jest znajomość pojęcia izometrii, jednokładności, skali jednokładności oraz symetrii względem prostej.

2. „matematyka nowej ery”

Wprowadzone jest na początku drugiego semestru 2 klasy.

Aby wprowadzić potrzebna jest znajomość jednokładności i skali jednokładności.

3. „matematyka z plusem”

Wprowadzone jest na początku drugiego semestru 3 klasy.

4. „matematyka wokół nas”

Podobieństwo wprowadzone jest pod koniec drugiego semestru w 3 klasie

• Sposoby wprowadzenia:

1. „matematyka krok po kroku”

Na początku są przytoczone przykłady podobieństwa w życiu codziennym. Następnie podobieństwo zostało przedstawione z matematycznego punktu widzenia, na przykładzie figury przekształconej przez jednokładność a następnie przez symetrię względem prostej. Później została wprowadzona definicja podobieństwa w oparciu o jednokładność, a następnie na przykładach zostały omówione zależności występujące w podobieństwie (stosunki długości boków, równość miar odpowiednich kątów, skala podobieństwa okręgów, stosunek obwodu i pola figur podobnych i jego równość skali podobieństwa). Następnie pokazany jest sposób rozwiązania zadania i przejście do zadań.

2. „matematyka nowej ery”

Na początku są przytoczone przykłady podobieństwa w życiu codziennym. Następnie podobieństwo zostało przedstawione z matematycznego punktu widzenia. Później została wprowadzona definicja figur podobnych, skali podobieństwa i oznaczenie podobieństwa. Wyjaśnienie pojęcia „odpowiednie odcinki”, na przykładzie dwóch figur składających się z dwóch odcinków. Na przykładzie został pokazany związek jednokładności z podobieństwem, a następnie przejście do zadań. Kolejno zostało zostały wprowadzone cechy podobieństwa trójkątów i twierdzenie o figurach podobnych (o równości miar kątów), co było poparte zadaniami. Następnie przejście do zadań.

3. „matematyka z plusem”

Przedstawienie trzech par figur. W każdej parze jedna z figur powstała przez pomniejszenie lub powiększenie drugiej figury (lub jej lustrzanego odbicia w pewnej skali).

Wprowadzenie definicji podobieństwa i skali podobieństwa oraz własność, że stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa. Następnie zostały wprowadzone prostokąty podobne, trójkąty prostokątne podobne oraz jednokładność

Następnie są zadania.

2. Trudności dotyczące „podobieństwa”

Uczniowie mogą nie zauważać podobieństwa figur, mogą mieć problemy z policzeniem skali podobieństwa oraz z narysowaniem figur podobnych.

Uczniom myli się podobieństwo figur z przystawaniem figur.

3. Późniejsze wykorzystanie podobieństwa

Wykorzystanie przy jednokładności (w matematyce wokół nas, z plusem, /ponieważ w niektórych programach jednokładność została wprowadzona przed podobieństwem/), podobieństwie trójkątów, prostokątów, brył,

4. Występowanie na egzaminach zadań związanych z podobieństwem;

Na egzaminach nie występują zadania związane z podobieństwem figur.

ZADANIA DO STANDARDÓW:

1. Standard I.2 /wykonywanie obliczeń w sytuacjach praktycznych/

Średnica koła roweru Marka jest równa 1 cali, natomiast średnica koła roweru Piotra stanowi
średnicy koła roweru Marka. Podaj skalę podobieństwa tych kół.

2. Standard I.3 /posługiwanie się własnościami figur/

Działka Tadeusza ma powierzchnię 3 a i jest w kształcie prostokąta, którego jeden bok ma długość równą 20 m. Tadeusz narysował plan swojej działki w skali 1: 50. Oblicz obwód prostokąta przedstawiającego plan działki.

Jak zmieni się pole trójkąta prostokątnego, gdy:

1. powiększymy go w skali 1,2?

2. Zmniejszymy go w skali 3?

3. Standard IV.2 /analizowanie sytuacji problemowej/

Dwa trójkąty są podobne i mają jednakowe pola. Suma obwodów tych trójkątów jest równa 2. Czy na podstawie tych danych możesz wyznaczyć obwód któregoś z tych trójkątów?

4. Standard IV.4 / tworzenie i realizowanie planu rozwiązania/

Skonstruuj trójkąt A₁B₁C₁ podobny do dowolnego trójkąta równobocznego ABC w skali k = 0,8

5. Ścieżki międzyptrzedmiotowe oraz realizacja tematu na innych przedmiotach:

Podobieństwo można wykorzystać podczas realizacji programu z innych przedmiotów np.

• na technice- zadanie typu: mamy daną bryłę i rzutujemy ją na kartkę.

• na przyrodzie- zadanie typu: Na mapie w skali 1:25000 las zajmuje obszar o polu 20 cm²., Jakie jest pole obszaru, który zajmuje ten las w rzeczywistości? (ścieżka regionalna)

Zadania wykorzystujące podobieństwo w realizacji ścieżek międzyprzedmiotowych

1. ścieżka europejska -treść znajduje się w punkcie 7 „zadania ciekawe” zadanie nr 1

2. ścieżka regionalna - zadanie wyżej wykorzystywane na przyrodzie.

3. Ścieżka filozoficzna - pole powierzchni podłogi w klasie wynosi 54 m2., Jaką powierzchnię kartki papieru zajmie plan tej podłogi narysowany w skali 1:200?

6. Cele operacyjne

• znajomość pojęcia podobieństwa figur i skali podobieństwa

• znajomość cech podobieństw figur

• rozpoznawanie figur podobnych

• określenie skali podobieństw

• rysowanie figur podobnych

• obliczanie długości boków, obwodów i pól figur podobnych, korzystając z cech podobieństwa

• rozwiązywanie prostych zadań rachunkowych i konstrukcyjnych z zastosowaniem własno­ści trójkątów podobnych

7. Zadania

ZADANIA TYPOWE:

1. W trójkącie ostrokątnym ABC narysowano trzy wysokości tak, że podzieliły one trójkąt ABC na 6 trójkątów prostokątnych. Wskaż pary trójkątów podobnych

2. W prostokącie ABCD odcinki EF i GH łączące środki przeciwległych boków przecinają się w punkcie J. Oblicz skalę podobieństwa prostokątów DEJG i ABCD.

3. Pole prostokąta wynosi 36 cm2. Dłuższy bok prostokąta podobnego w skali k = 3 wynosi 27 cm. Oblicz obwody obu prostok¹tów.

4. Skala podobieństwa dwóch odcinków jest równa 1/3, a długość jednego z nich jest równa 6 cm. Znajdź długość drugiego odcinka.

5. Oblicz sumę pól rombów R₁ i R₂, wiedząc, że R₁ jest obrazem R₂ w podobieństwie o skali 3 i przekątne rombu R₁ mają długość 12 i 8.

ZADANIA CIEKAWE:

1. W USA boisko do koszykówki ma wymiary 16 2/3 jarda x 31 1/3 jarda. W Europie koszykarze grają na boisku o wymiarach 15m x 26m Czy boiska te są prostokątami podobnymi?
   1 Yard angielski = 0,91440186 m

2. Ania chce powiększyć fotografię, która ma kształt prostokąta o wymiarach 6 cm x 8 cm. Powiększona fotografia ma mieć krótszy bok długości 16 cm. Jaka będzie skala podobieństwa tych fotografii? Jakie będzie pole powierzchni powiększonej fotografii?

ZADANIA DLA UCZNIÓW BARDZO DOBRYCH:

1. Zbuduj trójkąt ABC, w którym
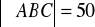
   , bok BC ma długość 6cm, zaś wysokości poprowadzone z wierzchołków A, C są do siebie w stosunku 7:10

2. Obwód równoległoboku jest równy 24 cm, a stosunek jego wysokości wynosi 5:7. Oblicz boki równoległoboku.

3. Dwa zewnętrzne styczne okręgi są styczne do ramion kąta. Odległość ich środków od wierzchołka kąta wynoszą 7 cm i 12 cm. Oblicz promienie tych okręgów.

4. Oblicz długość odcinków, na które podzieli dwusieczna kąta prostego przeciwprostokątną w trójkącie prostokątnym o przyprostokątnych 18 cm i 24 cm.

5. W trapezie równoramiennym połączono środki jego wszystkich boków i otrzymano czworokąt. Udowodnij, że powstały w ten sposób czworokąt jest rombem.

8. Metody, środki

Środkami dydaktycznymi, jakie można wykorzystać na zajęciach mogą być plansze, karty do gry z figurami podobnymi, prezentacje multimedialne, narysowanie obrazków za pomocą figur podobnych, np.:

9. Konspekt lekcji

Temat: Podobieństwo figur

Czas: 45 min

Metody pracy: pogadanka, ćwiczeniowa, gra-zabawa

Środki pracy: kartki z figurami, kreda, tablica, podręcznik

Cele lekcji:

Uczeń:

• Zna pojęcie figur podobnych, skali podobieństwa

• Umie rozpoznawać figury podobne

• Określić skalę podobieństwa

• Umie podawać wymiary figury podobnej do innej figury w danej skali,

• Umie rozwiązywać zadania tekstowe związane z figurami podobnymi.

Przebieg lekcji:

1. Wprowadzenie pojęcia podobieństwa oraz skali podobieństwa:

Przyczepienie na tablicy.

Te figury są podobne, ponieważ mają ten sam kształt, a różnią się tylko wielkością.

Zapisanie do zeszytu definicji figur podobnych.

O figurach, które mają taki sam kształt, a różnią się najwyżej wielkością, mówimy, że są podobne.

Mamy dwie figury, są one podobne.

Kąty wielokąta F' mają takie same miary jak odpowiednie

kąty wielokąta F. Długości boków wielokąta F' są proporcjonalne

do długości odpowiednich boków wielokąta F, tzn

Liczbę k równą stosunkowi długości któregokolwiek boku wielokąta F'

do długości odpowiedniego boku wielokąta F nazywamy skalą

podobieństwa wielokąta F' do wielokąta F.

i
itd.

Obliczenie skali podobieństwa figury F' do figury F, jeśli wiadomo, że wszystkie boki wielokąta F są równe i mają długość 10 cm, a boki figury F' są również tej samej długości równe 5 cm.

Zatem skala podobieństwa jest równa ½ 

2. Przejście do rozwiązywania zadań z podręcznika.

1. zadanie 1

Prostokąt ABCD ma wymiary 1 cm x 2,5 cm.

1. Jakie wymiary ma prostokąt podobny do prostokąta ABCD w skali 3?

2. Jaki obwód ma prostokąt podobny do prostokąta ABCD w skali 6/5?

2. zadanie 2

W jakiej skali kwadrat o boku długości 3,5 cm jest podobny do kwadratu o boku długości 4,5 cm?

3. zadanie 5

Prostokąty ABCD i A'B'C'D' są podobne. Prostokąt ABCD ma boki długości 7 cm i 8 cm, a dłuższy bok prostokąta A'B'C'D' ma długość 12 cm. Oblicz obwód prostokąta A'B'C'D'.

3. Praca domowa:

Zadanie 3:

Narysowanie poniżej czworokąty są podobne.

1. w jakiej skali większy czworokąt jest podobny do mniejszego?

2. W jakiej skali mniejszy czworokąt jest podobny do większego?

3. Oblicz obwody obu czworokątów.

8

6

9

3

16

F

F'

---