Wzór Maxwella-Mohra

Przykłady rachunkowe

Mechanika budowli

Przemieszczenia w układach statycznie wyznaczalnych

Semestr letni 2010/2011

dr inż. Bartosz Miller

Katedra Mechaniki Konstrukcji

Politechnika Rzeszowska

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

1

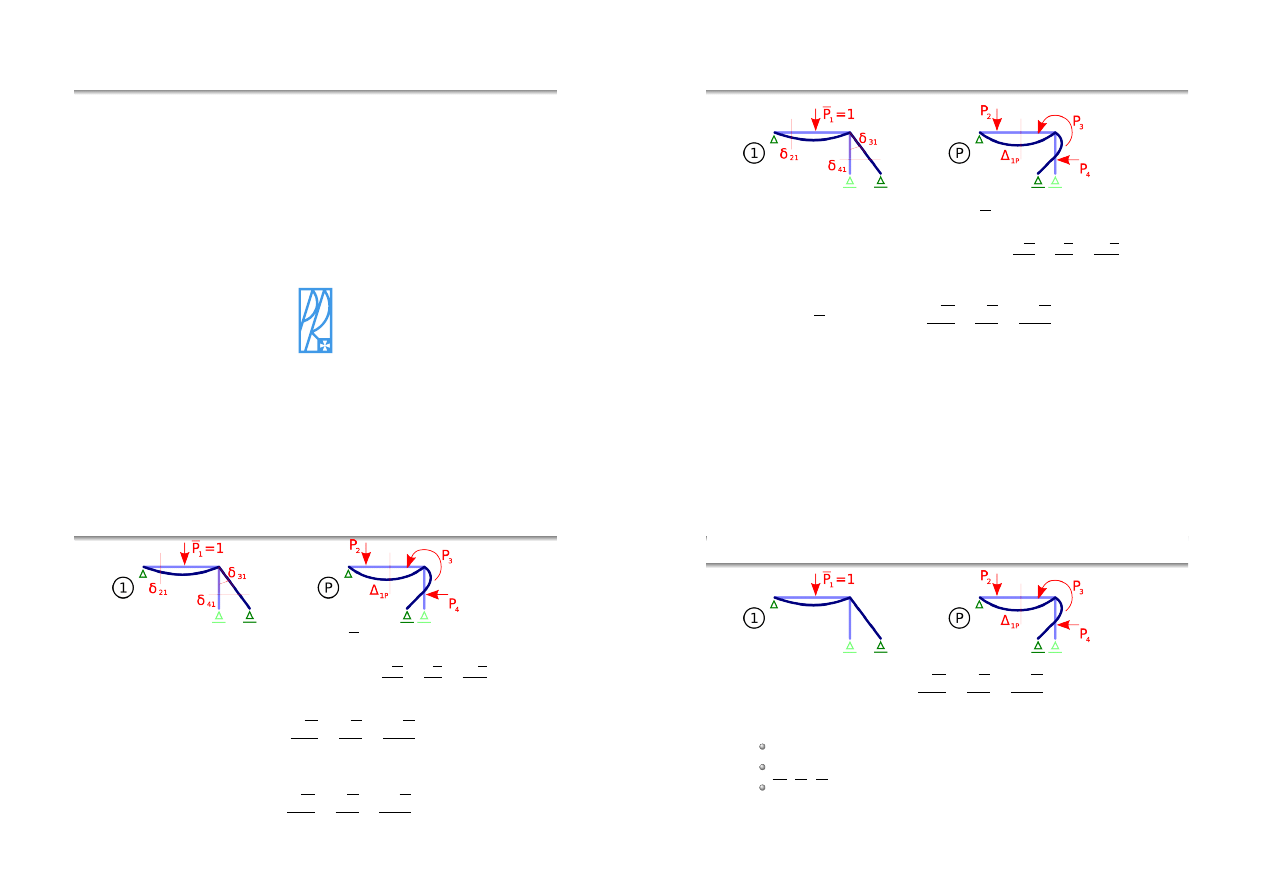
Wzór Maxwella-Mohra

Przykłady rachunkowe

Wyprowadzenie

Stany jednostkowe
Dyskusja wzoru

Zasada wzajemności prac wirtualnych: P

1

∆

1P

=

4

P

i =2

P

i

δ

i 1

Zasada prac wirtualnych:

4

P

i =2

P

i

δ

i 1

=

P

(u)

R

(s)

MM

EI

+

NN

EA

+

κQQ

GA

ds

Ostatecznie:

P

1

∆

1P

=

X

(u)

Z

(s)

MM

EI

+

NN

EA

+

κQQ

GA

!

ds

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

2

Wzór Maxwella-Mohra

Przykłady rachunkowe

Wyprowadzenie

Stany jednostkowe
Dyskusja wzoru

Zasada wzajemności prac wirtualnych: P

1

∆

1P

=

4

P

i =2

P

i

δ

i 1

Zasada prac wirtualnych:

4

P

i =2

P

i

δ

i 1

=

P

(u)

R

(s)

MM

EI

+

NN

EA

+

κQQ

GA

ds

Ostatecznie:

1∆

1P

=

X

(u)

Z

(s)

MM

EI

+

NN

EA

+

κQQ

GA

!

ds

Ostatecznie:

∆

1P

=

X

(u)

Z

(s)

MM

EI

+

NN

EA

+

κQQ

GA

!

ds

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

3

Wzór Maxwella-Mohra

Przykłady rachunkowe

Wyprowadzenie

Stany jednostkowe
Dyskusja wzoru

Wzór Maxwella-Mohra

∆

1P

=

X

(u)

Z

(s)

MM

EI

+

NN

EA

+

κQQ

GA

!

ds

∆

1P

— szukane przemieszczenie

M, Q, N — siły wewnętrzne wywołane obc. rzeczywistym

M, Q, N — siły wewn. wywołane działaniem obc.
jednostkowego przyłożonego na kierunku szukanego
przemieszczenia

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

4

Wzór Maxwella-Mohra

Przykłady rachunkowe

Wyprowadzenie

Stany jednostkowe

Dyskusja wzoru

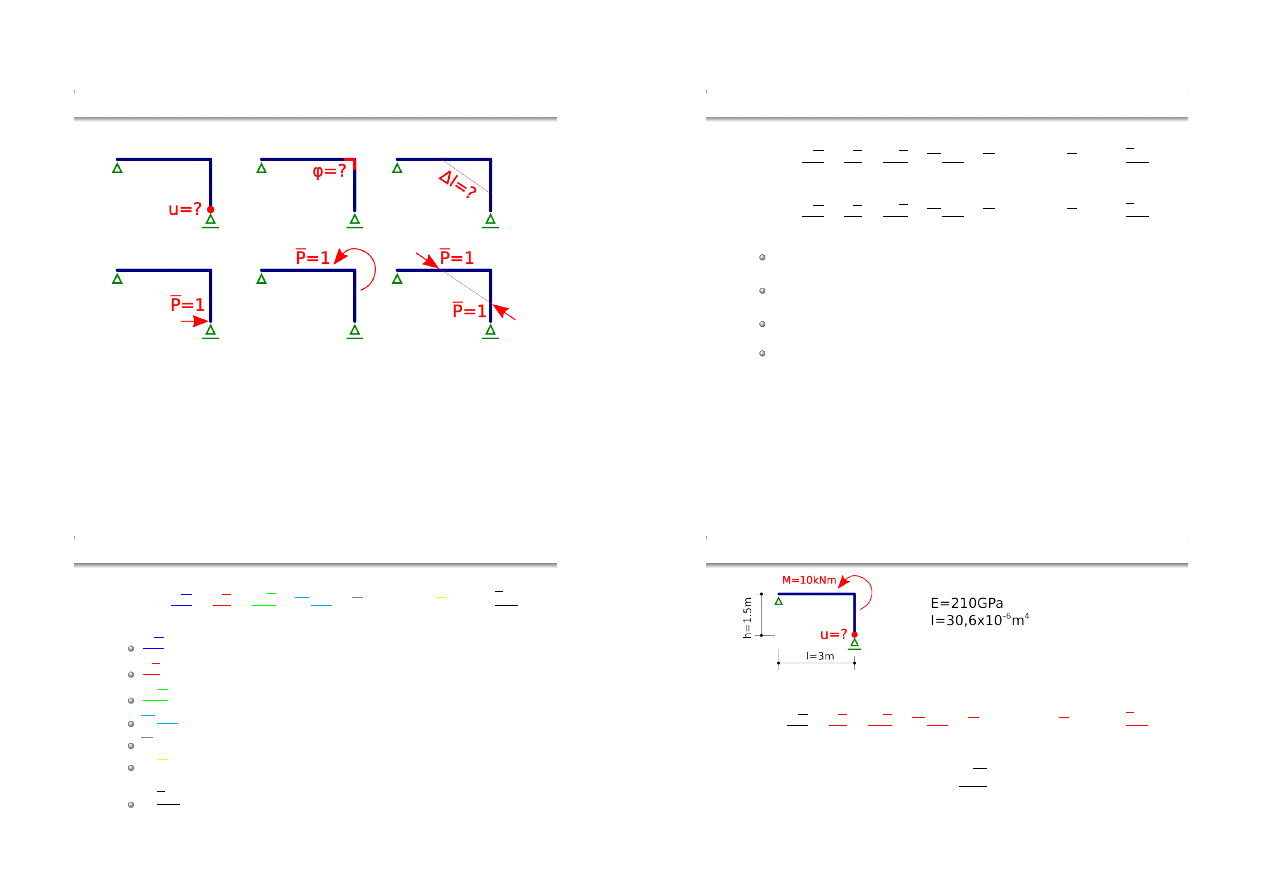
Wzór Maxwella-Mohra — siły jednostkowe

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

5

Wzór Maxwella-Mohra

Przykłady rachunkowe

Wyprowadzenie
Stany jednostkowe

Dyskusja wzoru

Wzór Maxwella-Mohra — dyskusja

∆

1P

=

=

P

(u)

R

(s)

MM

EI

+

NN

EA

+

κQQ

GA

+ M

α∆t

h

+ Nαt

0

ds −

P

i

R

i

∆

i

+

P

j

R

j

R

j

k

j

∆

1P

=

=

P

(u)

R

(s)

MM

EI

+

NN

EA

+

κQQ

GA

+ M

α∆t

h

+ Nαt

0

ds

−

P

i

R

i

∆

i

+

P

j

R

j

R

j

k

j

P

(u)

— sumowanie po wszystkich prętach układu

R

(s)

(·)ds

— całkowanie po długości pręta

P

i

— sumowanie po wszystkich osiadających podporach

P

j

— sumowanie po wszystkich podporach sprężystych

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

6

Wzór Maxwella-Mohra

Przykłady rachunkowe

Wyprowadzenie
Stany jednostkowe

Dyskusja wzoru

Wzór Maxwella-Mohra — dyskusja

∆

1P

=

=

P

(u)

R

(s)

MM

EI

+

NN

EA

+

κQQ

GA

+

M

α∆t

h

+

Nαt

0

ds−

P

i

R

i

∆

i

+

P

j

R

j

R

j

k

j

MM

EI

— wpływ momentu zginającego (belki, ramy, łuki)

NN

EA

— wpływ siły osiowej (kratownice)

κQQ

GA

— wpływ siły poprzecznej (tylko pręty krępe)

M

α∆t

h

— wpływ różnicy temperatur

Nαt

0

— wpływ stałej temperatury

P

i

R

i

∆

i

— wypływ osiadania podpór

P

j

R

j

R

j

k

j

— wpływ podpór sprężystych

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

7

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie

Całkowanie graficzne
Wzór Simpsona
Belka obciążona różnicą temperatur
Rama obciążona osiadaniem podpór

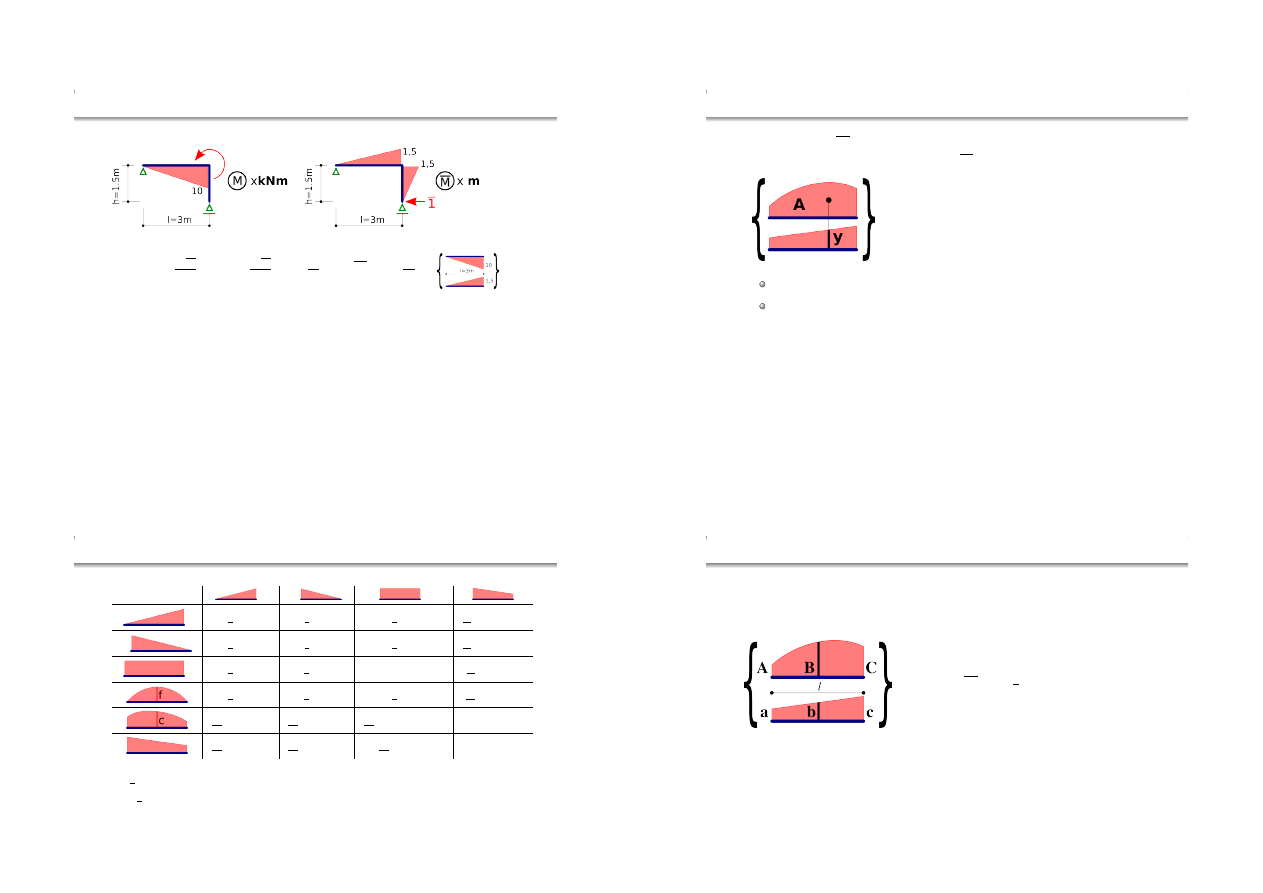
Przykład rachunkowy — przemieszczenie poziome u

Wzór Maxwella-Mohra
u =

P

(u)

R

(s)

MM

EI

+

NN

EA

+

κQQ

GA

+

M

α∆t

h

+

Nαt

0

ds −

P

i

R

i

∆

i

+

P

j

R

j

R

j

k

j

uprości się do

u =

X

(u)

Z

(s)

MM

EI

ds

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

8

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie

Całkowanie graficzne
Wzór Simpsona
Belka obciążona różnicą temperatur
Rama obciążona osiadaniem podpór

Przykład rachunkowy

u =

P

(u)

R

(s)

MM

EI

ds =

R

(s)

MM

EI

ds =

1

EI

R

(s)

MMds =

1

EI

R

(s)

ds

Przemieszczenie u zostanie obliczone z zastosowaniem
uproszczonej (ale dokładnej!) metody całkowania graficznego.

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

9

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie

Całkowanie graficzne

Wzór Simpsona
Belka obciążona różnicą temperatur
Rama obciążona osiadaniem podpór

Całkowanie graficzne

Całki typu

R

MMds można bardzo szybko rozwiązywać, jeżeli

przynajmniej jedna z funkcji M lub M jest liniowa.

R

ds =A · y

A — pole powierzchni pod wykresem

y — wartość odczytana z drugiego wykresu pod środkiem
ciężkości pierwszego wykresu

Wykres, z którego odczytywane jest y , musi być wykresem
liniowym! Drugi wykres może być dowolny.

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

10

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie

Całkowanie graficzne

Wzór Simpsona
Belka obciążona różnicą temperatur
Rama obciążona osiadaniem podpór

Całkowanie graficzne — podstawowe wzory

A

A

A

A

B

a

1
3

aAl

1
6

aAl

1
2

aAl

al

6

(A + 2B)

a

1
6

aAl

1
3

aAl

1
2

aAl

al

6

(2A + B)

a

1
2

aAl

1
2

aAl

aAl

al

2

(A + B)

1
3

Af l

1
3

Af l

2
3

Af l

f l

3

(A + B)

a

b

Al

6

(b + 2c)

Al

6

(a + 2c)

Al

6

(a + b + 4c)

*)

a

b

Al

6

(a + 2b)

Al

6

(2a + b)

Al

2

(a + b)

**)

*)

l

6

[Aa + Bb + 2c(A + B)]

**)

l

6

[Aa + Bb + (a + b)(A + B)]

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

11

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne

Wzór Simpsona

Belka obciążona różnicą temperatur
Rama obciążona osiadaniem podpór

Wzór Simpsona

R

=

R

MMds =

l

6

(aA + 4bB + cC )

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

12

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne

Wzór Simpsona

Belka obciążona różnicą temperatur
Rama obciążona osiadaniem podpór

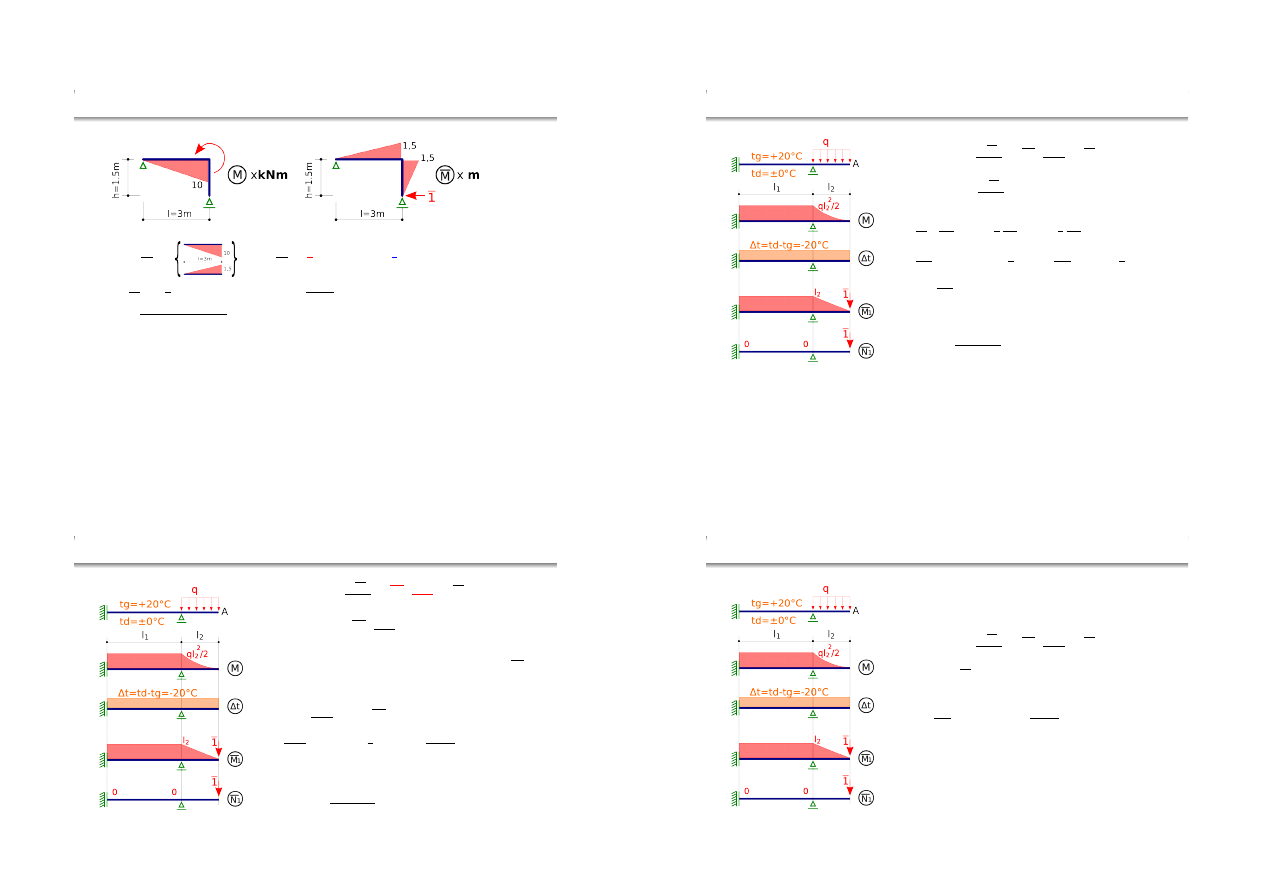
Przykład liczbowy, ciąg dalszy

u =

1

EI

R

(s)

ds =

1

EI

h

1
2

· 3 · 10e3

·

2
3

· (−1.5)

i

=

=

1

EI

−

1
3

· 10000 · 1.5 · 3

= −

15000

EI

=

= −

15000

210·10

9

·30.6·10

−6

= −2.334 · 10

−3

m = −2.334mm ∼

= −2.3mm

Przemieszczenie jest w kierunku przeciwnym do założonego.

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

13

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne
Wzór Simpsona

Belka obciążona różnicą temperatur

Rama obciążona osiadaniem podpór

Przykład rachunkowy — ugięcie w punkcie A

v

A

=

P

(u)

R

(s)

MM

1

EI

+ M

1

α∆t

h

+ N

1

αt

0

ds

v

P

A

=

P

(u)

R

(s)

MM

1

EI

ds =

=

1

EI

ql

2

2

2

l

2

l

1

+

1
3

ql

2

2

2

l

2

l

2

−

1
3

ql

2

2

8

l

2

l

2

=

=

ql

3

2

6EI

3l

1

+ l

2

−

1
4

l

2

=

ql

3

2

6EI

3l

1

+

3
4

l

2

v

P

A

=

ql

3

2

8EI

(4l

1

+ l

2

)

Obliczenia na jednostkach:

h

v

P

A

i

=

h

N/m·m

3

N/m

2

·m

4

m

i

= [m]

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

14

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne
Wzór Simpsona

Belka obciążona różnicą temperatur

Rama obciążona osiadaniem podpór

Przykład rachunkowy — ugięcie w punkcie A

v

A

=

P

(u)

R

(s)

MM

1

EI

+

M

1

α∆t

h

+ N

1

αt

0

ds

v

∆t

A

=

P

(u)

R

(s)

M

1

α∆t

h

ds

α: wsp. rozszerzaln. term., α

stal

≈ 10

−5 1

0

C

h: wysokość przekroju poprzecznego
∆t = t

d

− t

g

: różnica temperatur

v

∆t

A

=

α∆t

h

P R

M

1

ds =

=

α∆t

h

−l

2

l

1

−

1
2

l

2

2

= −

l

2

α∆t

2h

(2l

1

+ l

2

)

Dla ∆t < 0 otrzymamy v

∆t

A

> 0

Obliczenia na jednostkach:

h

v

∆t

A

i

=

h

m

0

C /

0

C

m

m

i

= [m]

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

15

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne
Wzór Simpsona

Belka obciążona różnicą temperatur

Rama obciążona osiadaniem podpór

Przykład rachunkowy — ugięcie w punkcie A

v

A

=

P

(u)

R

(s)

MM

1

EI

+ M

1

α∆t

h

+ N

1

αt

0

ds

Ponieważ N

1

≡ 0 ostatecznie

v

A

= v

P

A

+ v

∆t

A

v

A

=

ql

3

2

8EI

(4l

1

+ l

2

) −

l

2

α∆t

2h

(2l

1

+ l

2

)

co dla ∆t < 0 da ostatecznie wartość
dodatnią

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

16

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne
Wzór Simpsona

Belka obciążona różnicą temperatur

Rama obciążona osiadaniem podpór

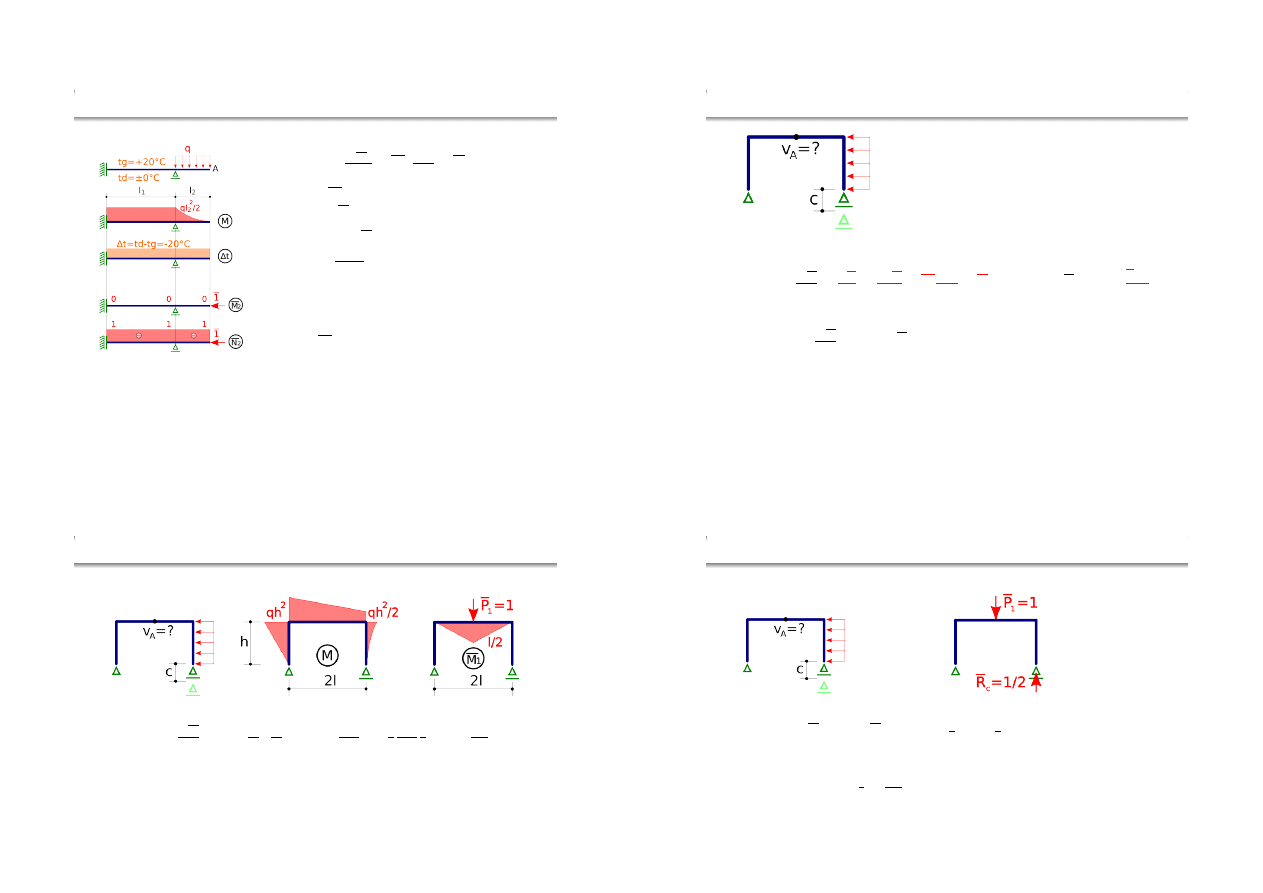
Przykład rachunkowy — przemieszczenie poziome A

u

A

=

P

(u)

R

(s)

MM

2

EI

+ M

2

α∆t

h

+ N

2

αt

0

ds

Ponieważ M

2

≡ 0 ostatecznie

u

A

=

P R

N

2

αt

0

ds

u

A

= αt

0

P R

N

2

ds = αt

0

(−(l

1

+ l

2

))

gdzie t

0

=

t

g

+t

d

2

to temperatura średnia.

Ostatecznie
u

A

= −αt

0

(l

1

+ l

2

)

Obliczenia na jednostkach:

[u

A

] =

h

1

0

C

0

C m

i

= [m]

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

17

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne
Wzór Simpsona
Belka obciążona różnicą temperatur

Rama obciążona osiadaniem podpór

Przykład liczbowy — przemieszczenie pionowe A

Wzór Maxwella-Mohra:
v

A

=

=

P R

MM

EI

+

NN

EA

+

κQQ

GA

+

M

α∆t

h

+

Nαt

0

ds −

P

i

R

i

∆

i

+

P

j

R

j

R

j

k

j

Uprości się do:

v

A

=

P R

MM

EI

ds −

P

i

R

i

∆

i

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

18

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne
Wzór Simpsona
Belka obciążona różnicą temperatur

Rama obciążona osiadaniem podpór

Przykład liczbowy — przemieszczenie pionowe A

v

P

A

=

P R

MM

EI

ds = −

1

EI

h

l

2

12

ql

2

+ 2

3ql

2

4

+

1
3

3ql

2

4

l

2

l

i

= −

ql

4

3EI

Jednostki: [m]

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

19

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne
Wzór Simpsona
Belka obciążona różnicą temperatur

Rama obciążona osiadaniem podpór

Przykład liczbowy — przemieszczenie pionowe A

v

c

A

= −

P

i

R

i

∆

i

= −R

c

c = −

−

1
2

c =

c
2

Jednostki: [m]

Ostatecznie: v

A

=

c
2

−

ql

4

3EI

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

20

Wzór Maxwella-Mohra

Przykłady rachunkowe

Przemieszczenie poziome w ramie
Całkowanie graficzne
Wzór Simpsona
Belka obciążona różnicą temperatur

Rama obciążona osiadaniem podpór

Zakres wykładu

1

Podstawowe zasady mechaniki budowli

2

Linie wpływu

3

Obliczanie przemieszczeń

4

Układy statycznie niewyznaczalne

Metoda sił
Metoda przemieszczeń

5

Dynamika

6

Stateczność

Politechnika Rzeszowska

Bartosz Miller

Mechanika budowli — obliczanie przemieszczeń

21