P O M O C E   N A U K O W E   I   D Y D A K T Y C Z N E

 

P

O R T A L U  

B

U D O W N I C T W O P O L S K I E

.

P L

 

 

 

1 | 

S t r o n a

 

 

 

 

 
 
 
 
 
 

 
 

METODA 

 

CLEBSCHA

 
 
 

 

 

P

RZYKŁAD

 

 
 

 

 

 

P O M O C E   N A U K O W E   I   D Y D A K T Y C Z N E

 

P

O R T A L U  

B

U D O W N I C T W O P O L S K I E

.

P L

 

 

 

2 | 

S t r o n a

 

 

Obliczyć kąt obrotu przekroju w punkcie D - 

 oraz pionowe przemieszczenie 

punktu B - 

. Obliczenia wykonać przy pomocy metody Clebscha. 

 

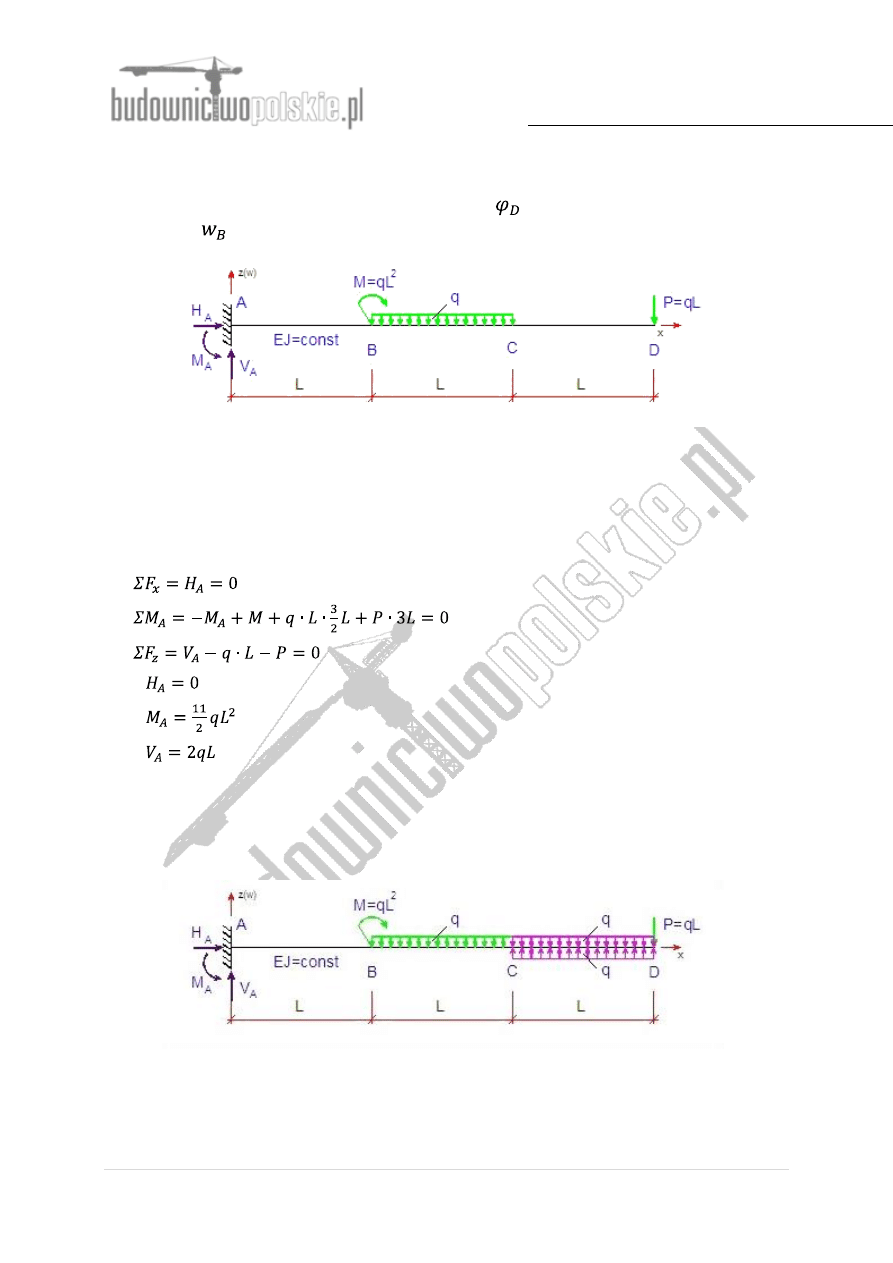
Rys.1 Schemat belki

 

W  pierwszej  kolejności  z  równań  równowagi  obliczymy  reakcje  w  punktach  podparcia. 
Reakcja  pozioma  H

A

  w  utwierdzeniu  ze  względu  na  brak  poziomego  obciążenia  jest  równa 

zero.  Belka  jest  układem  statycznie  wyznaczalnym  zatem  do  obliczenia  pozostałych  reakcji 
wystarczą równania równowagi: 

1.   

 

2.   

 

3.   

 

z 1.   

 

z 2.   

 

z 3.   

 

Początek układu współrzędnych przyjmujemy w punkcie A. Aby poprawnie zapisać równanie 
różniczkowe  należy  w  zadanym  schemacie  przedłużyć  do  końca  belki  (czyli  do  punktu  D) 
obciążenie  ciągłe  i  zrównoważyć  go  obciążeniem  o  takiej  samej  wartości  ale  przeciwnie 
skierowanym (zgodnie z rys.2 w kolorze różowym) 

 

Rys.2 Schemat belki z przedłużonym obciążeniem ciągłym 

 

Belkę można podzielić na trzy przedziały oznaczone w równaniu linią pionową z indeksem 
oznaczającym koniec danego przedziału, mamy zatem: 

 

 

 

P O M O C E   N A U K O W E   I   D Y D A K T Y C Z N E

 

P

O R T A L U  

B

U D O W N I C T W O P O L S K I E

.

P L

 

 

 

3 | 

S t r o n a

 

 

1. 

 

Całkując powyższe równanie otrzymujemy: 

2. 

 

Kolejne całkowanie prowadzi do uzyskania równania linii ugięcia: 

3. 

  

Stałe całkowania wyznaczymy z warunków brzegowych:        

dla  

 ; 

        

 

 

 

dla  

 ; 

      

 

 

 

Przemieszczenie pionowe punktu B obliczymy podstawiając do równania 5. wyznaczone stałe 
całkowania oraz odległość punktu B od początku układu współrzędnych czyli 

 (punkt B 

leży  na  końcu  przedziału  1  zatem  podstawiamy  wartości  tylko  do  pierwszego  przedziału 
równania) 

  

Kąt obrotu przekroju w punkcie D obliczymy podstawiając do równania 4. wyznaczone stałe 
całkowania oraz odległość punktu D od początku układu współrzędnych czyli 

 (punkt 

D leży na końcu belki zatem korzystamy z całego równania 4.)