
UNIWERSYTET ZIELONOGÓRSKI
WYDZIAŁ INŻYNIERII LĄDOWEJ I ŚRODOWISKA
INSTYTUT BUDOWNICTWA
Ć
WICZENIE PROJEKTOWE nr 2 Z MECHANIKI BUDOWLI
Wykonał Piotr Kramski
Rok akademicki 2006 / 2007
Imię .................................................................... Grupa ................................................................
Nazwisko ........................................................... Nr indeksu .........................................................
PROJEKT NR 2 Z MECHANIKI BUDOWLI I
OBLICZANIE PRZEMIESZCZEŃ – ZASADA PRAC WIRTUALNYCH
Korzystając z zasady prac wirtualnych obliczyć zadane przemieszczenia. W zadaniach (oprócz
nr3) zaprojektować pręty układu na maksymalny moment gnący lub siłę normalną (kratownica,
CE w zadaniu nr4) przyjmując R=100MPa. W zadaniu nr2 osobno zaprojektować odcinek BC.
W zadaniu nr3 przyjąć dwuteownik na podstawie ostatniej cyfry numeru indeksu (0=I80,
1=I100 itd.)
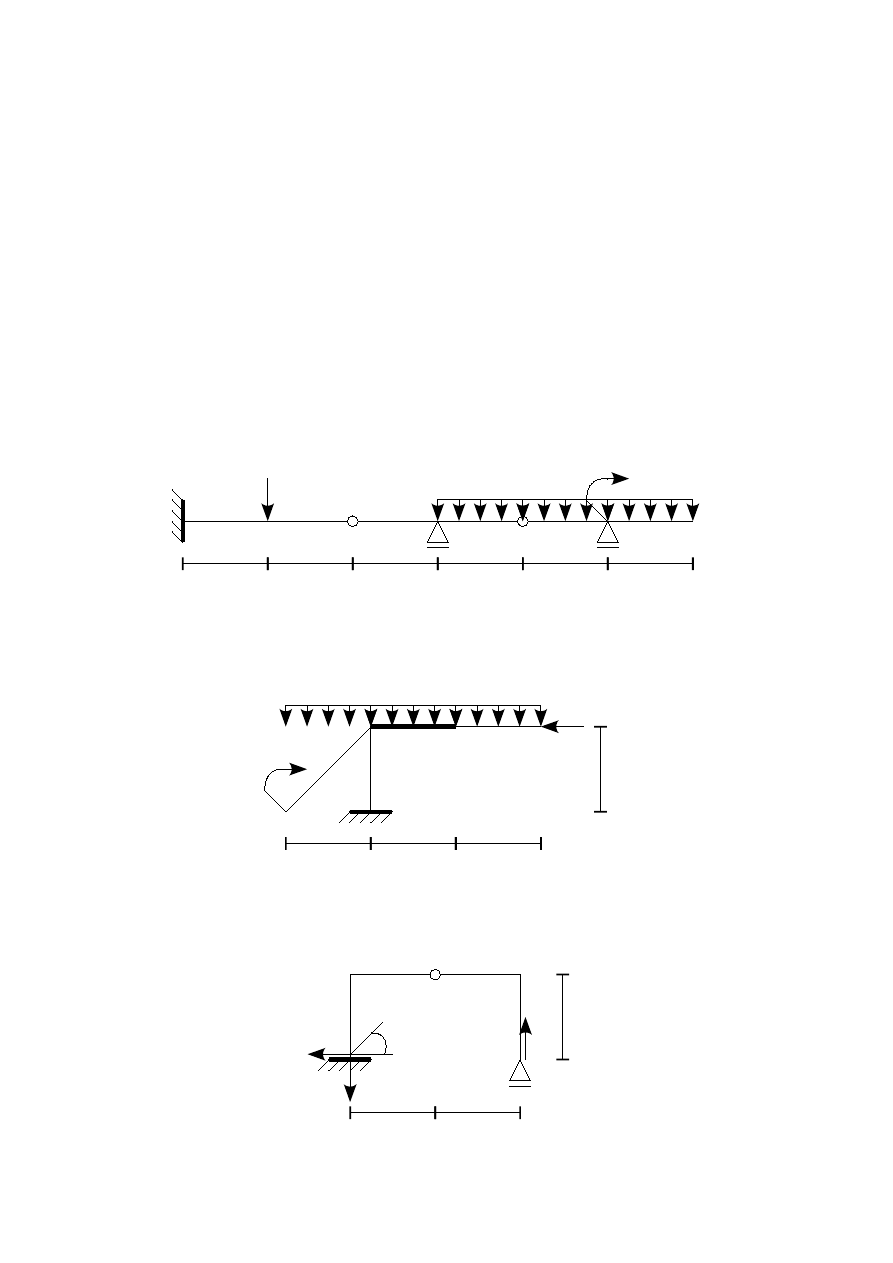
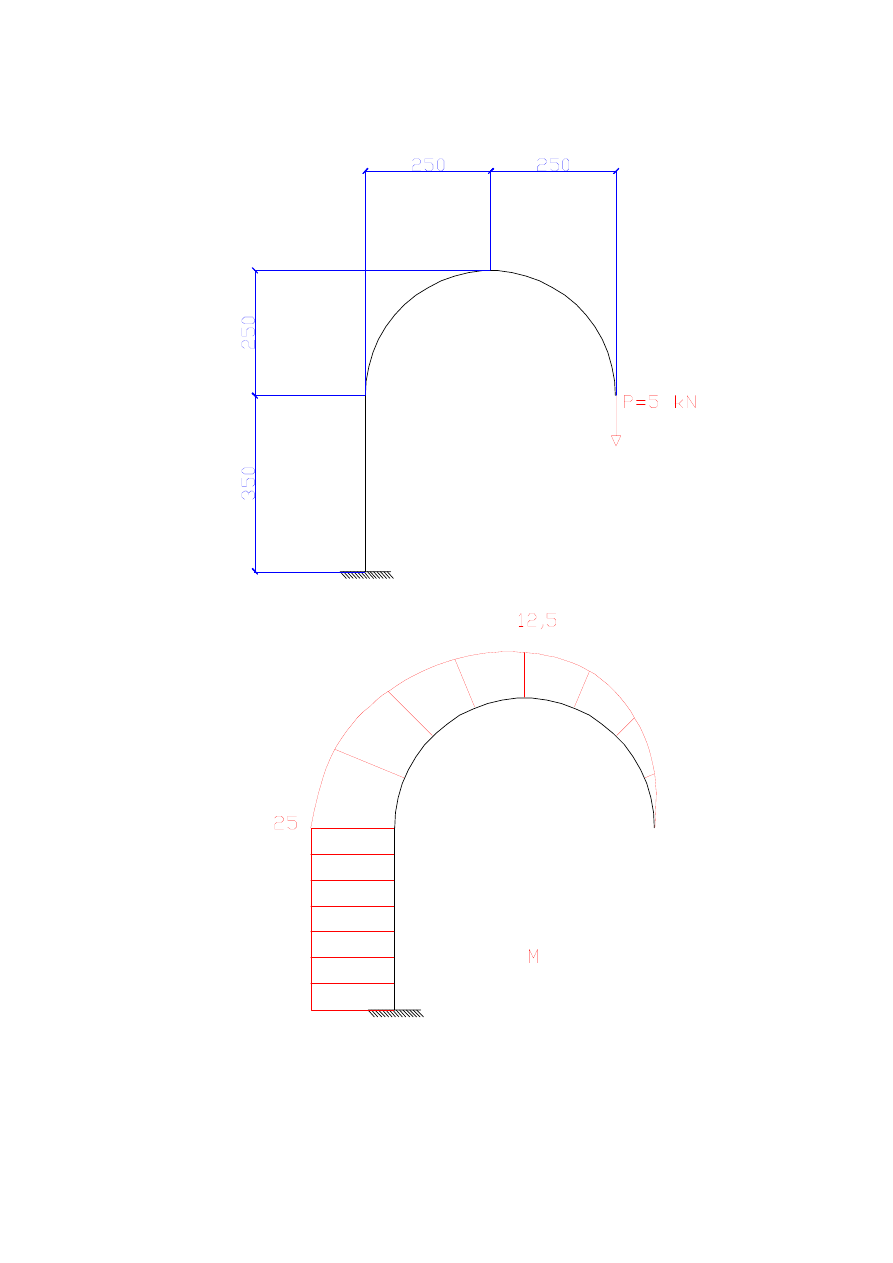
Zadanie 1
pionowe B – wpływ M
wzajemny obrót prętów w E – wpływ M
pionowe G – wpływ M, T (porównać wpływ M i T)
a
b
c
a
b
P
M
q
A
C
D
E
F
G
a
B
Zadanie 2
poziome A – wpływ M, T, N (porównać wpływ M, T i N)
obrót B – wpływ M
wzajemne zbliżenie A i D – wpływ M
obrót cięciwy AD – wpływ M
q
P
M
a
b
c
A
C
B
D
E
c
Zadanie 3
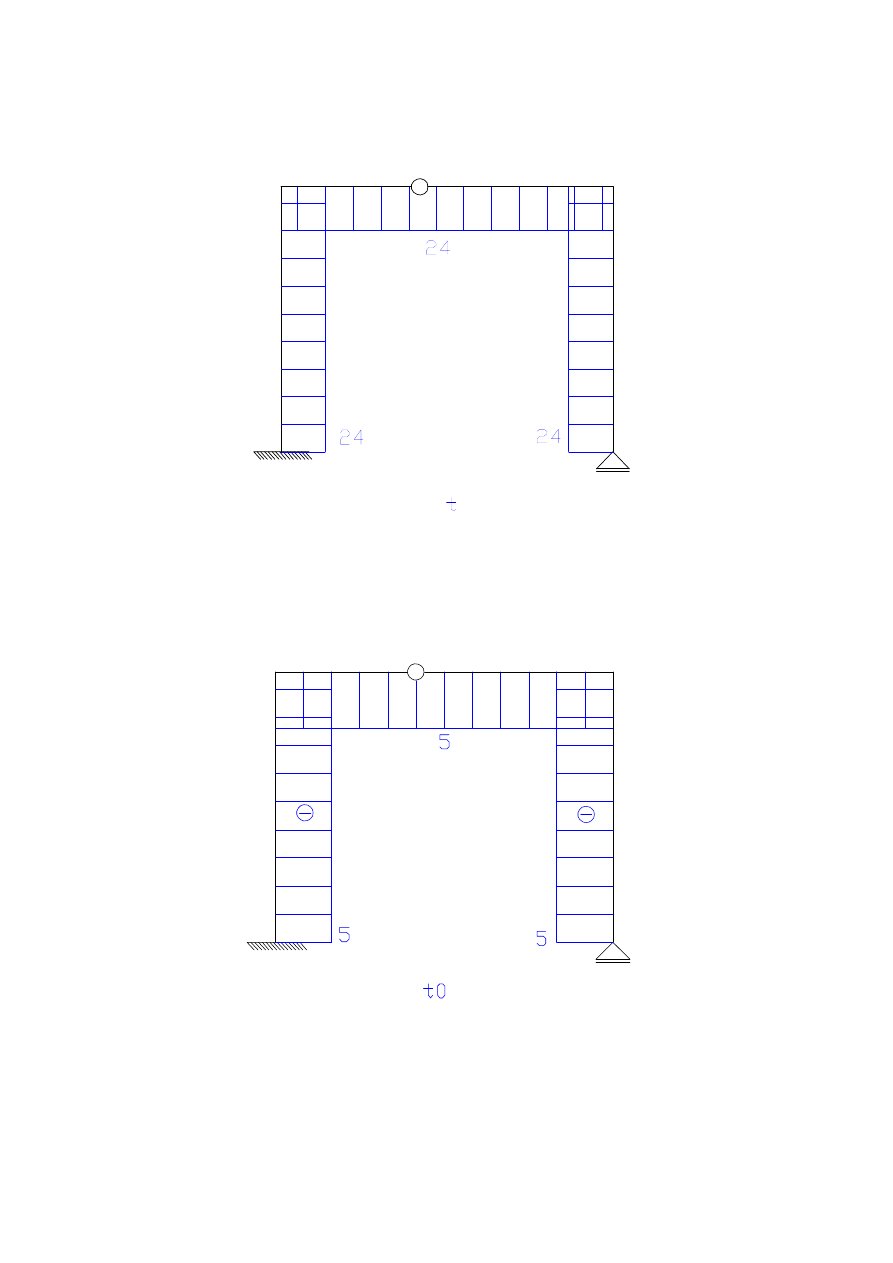
pionowe C, obrót D – wpływ temperatury i osiadania podpór
poziome D – wpływ osiadania podpór
obrót B – wpływ temperatury
t
1
A
B
C
D
E
2Δ
Δ
Δ
α
t
2
a
b
c
Zadanie 4
pionowe i obrót D – wpływ M, N
23 A
Piotr
Kramski
47616
For Evaluation Only.
Copyright (c) by Foxit Software Company, 2004
Edited by Foxit PDF Editor
a
b
c
a
q
P
A
B
C
D
E
M
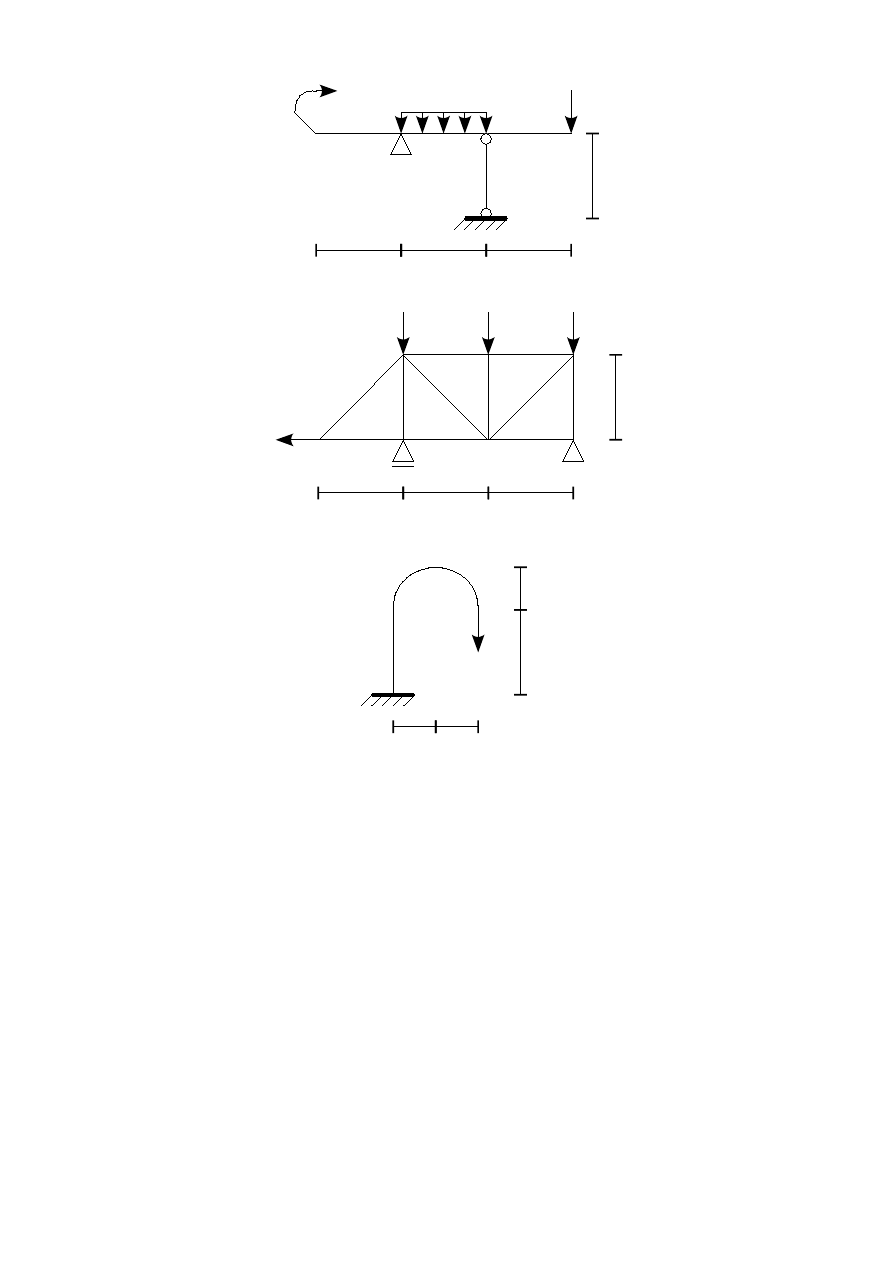
Zadanie 5
pionowe C, poziome A, kąt obrotu EC, wzajemny kąt obrotu EC i GC – wpływ N
a
b
b
c
P
P
P
P
A
B
C
D
E
F
G
Zadanie 6
pionowe i poziome D, obrót C – wpływ M
Dane do wszystkich zadań:
a=............... [m] (liczba liter w imieniu/2)
b=............... [m] (liczba liter w nazwisku/2)
c=............... [m] (średnia cyfr numeru indeksu)
P=............... [kN] (liczba liter w imieniu)
M=............... [kNm] (przedostatnia cyfra numeru indeksu, jeśli 0 to przyjąć 10)
q=............... [kN/m] (ostatnia cyfra numeru indeksu, jeśli 0 to przyjąć 10)
t
1
=............... [°C] (-liczba liter w imieniu
∗
2)
t
2
=............... [°C] (+liczba liter w nazwisku
∗
2)
t
m
=............... [°C] (+liczba liter w imieniu/2)
α=............... [rad] (średnia cyfr numeru indeksu/100)
Δ=............... [m] (liczba liter w imieniu/200)
Termin oddania: ..............................
P
a
b
a
a
A
B
C
D
2,5
3,5
4,8
5
1
6
-10
+14
+2,5
0,048
0,025
04.02.2007
For Evaluation Only.
Copyright (c) by Foxit Software Company, 2004
Edited by Foxit PDF Editor
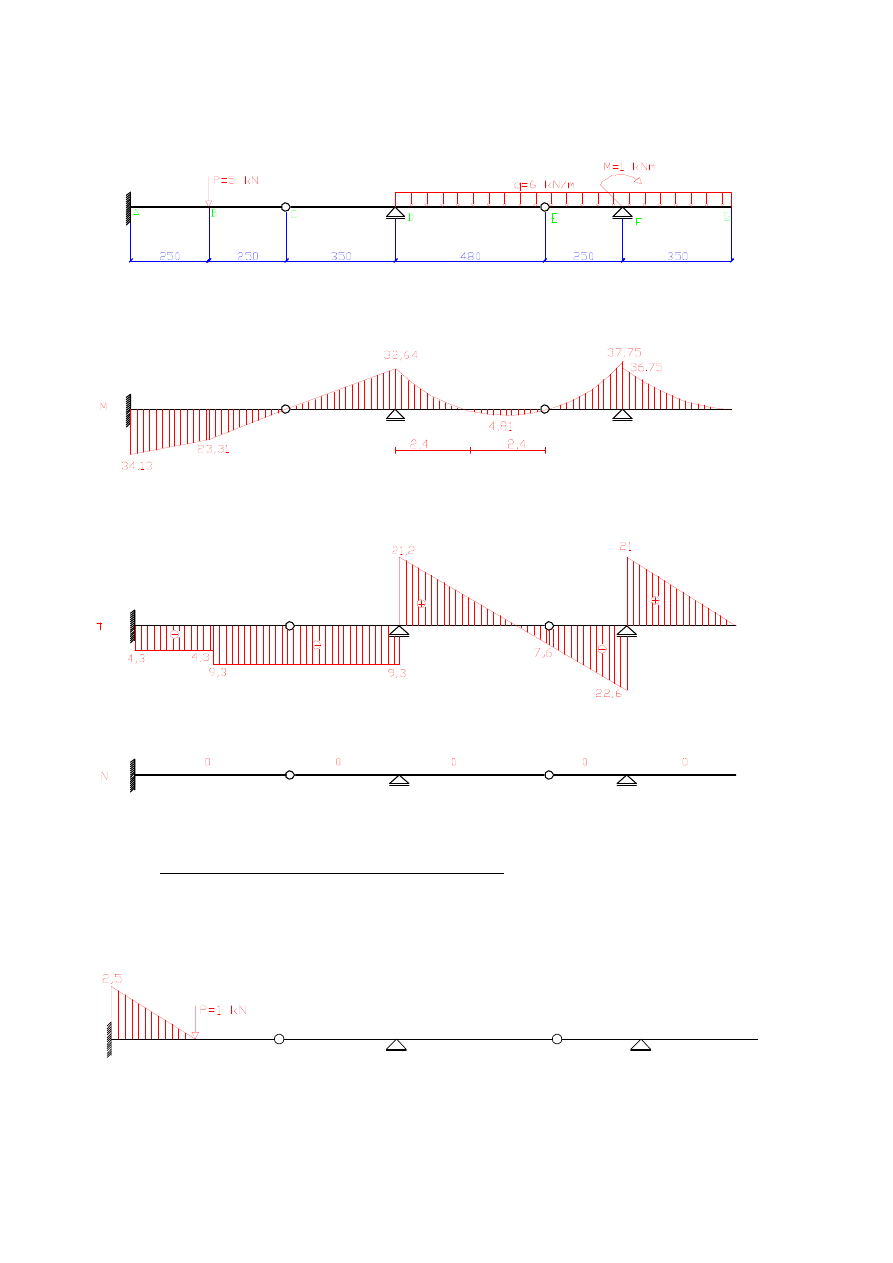
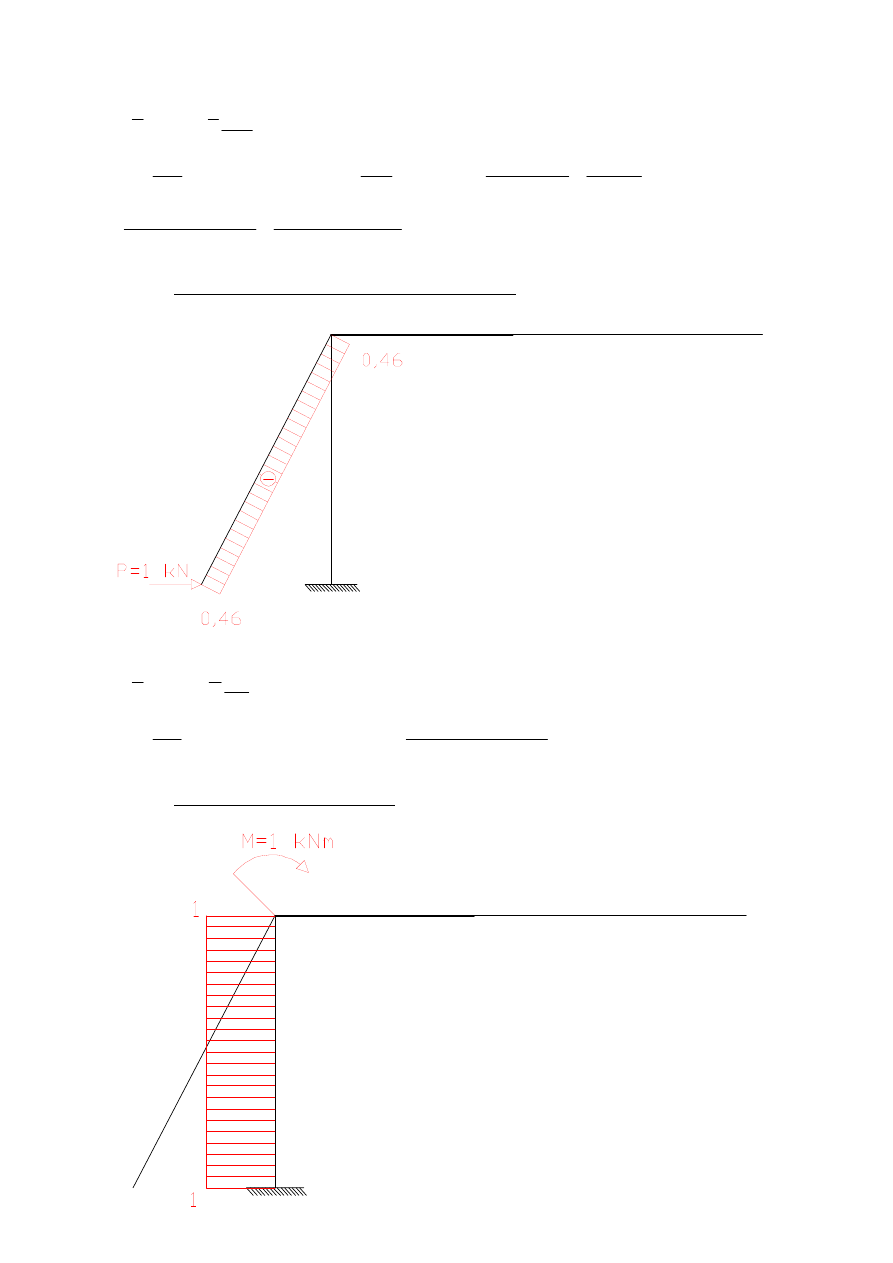
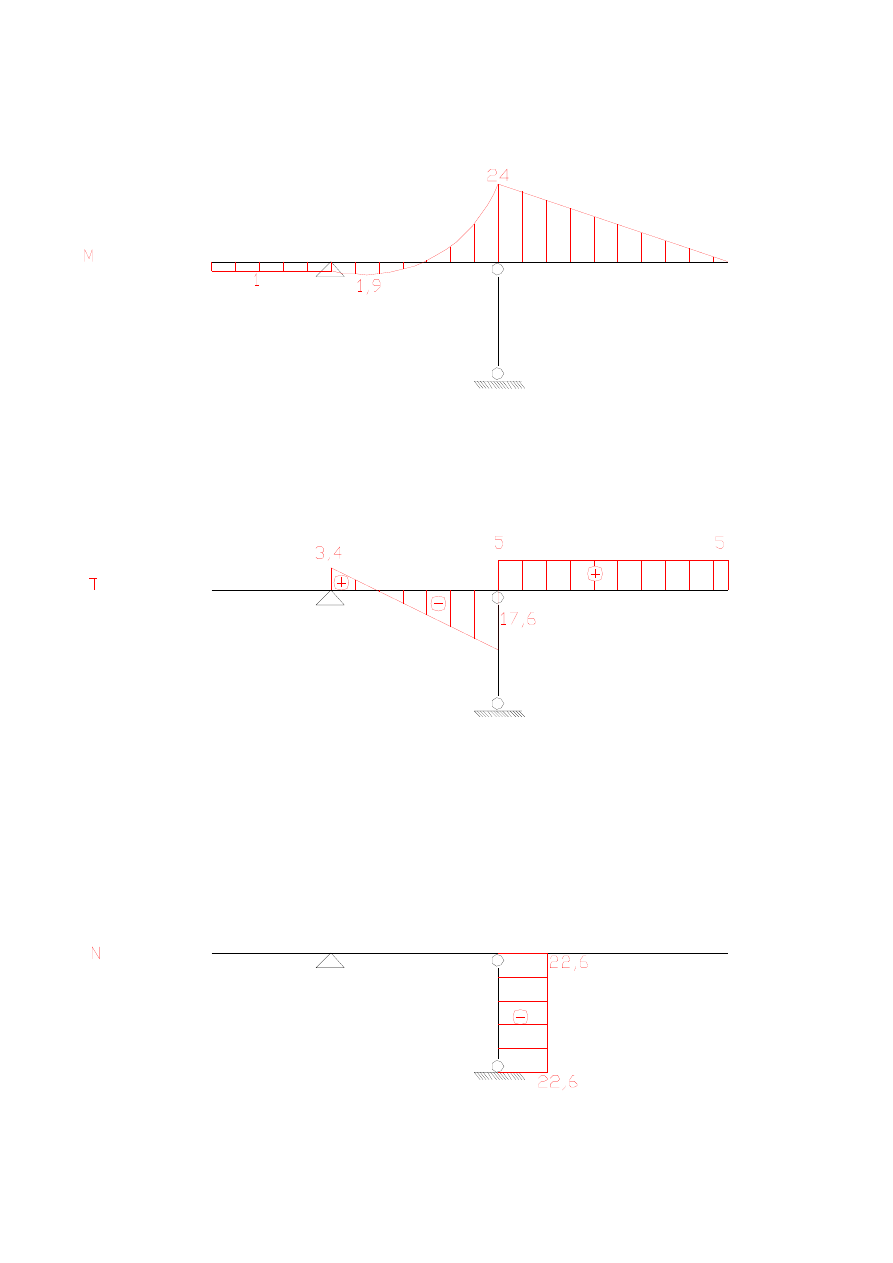
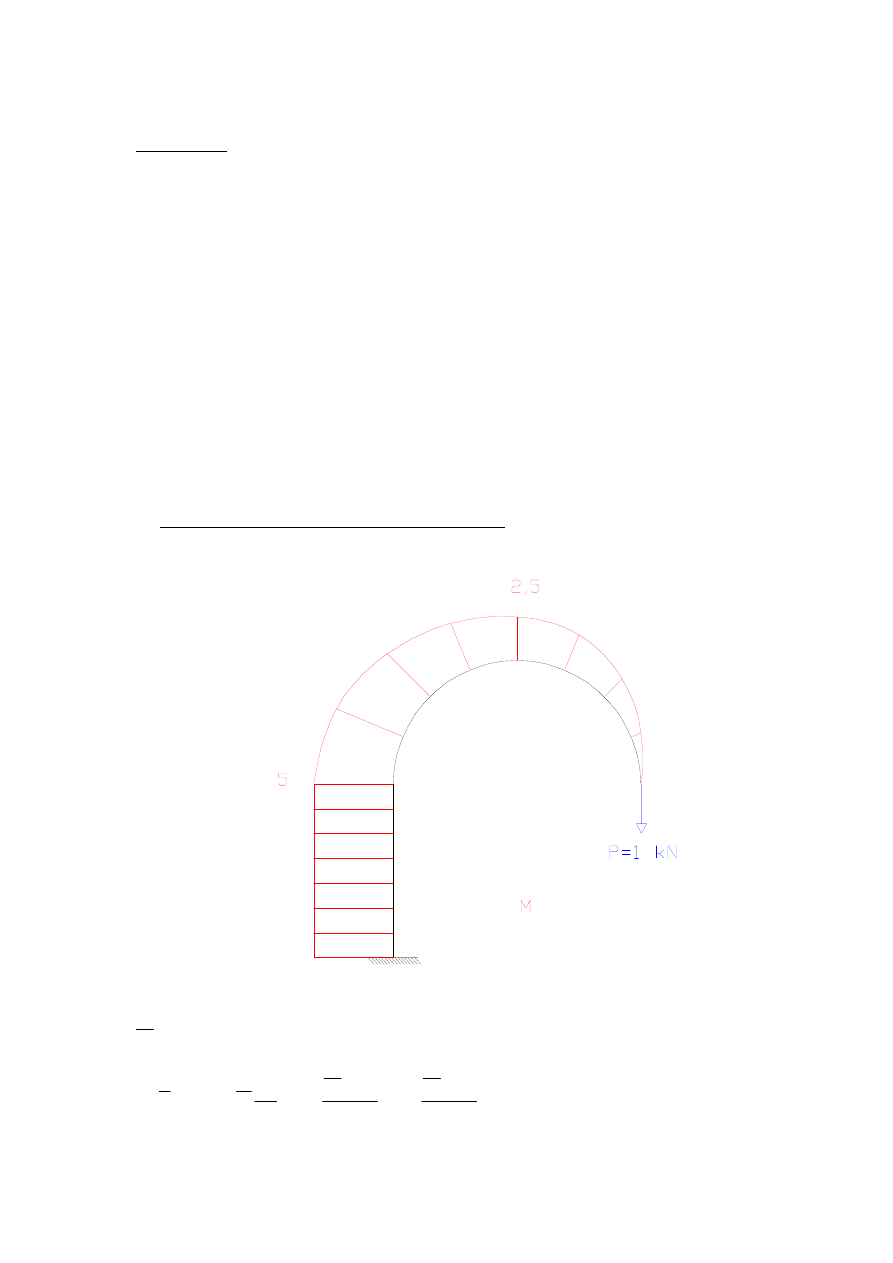
ZADANIE 1
a)
przemieszczenie pionowe punktu B – wpływ M
ds
EI
M
M
P
∑
∑∫
=
δ
cm
m
EI
EI
B
1
01
,
0
10
5740
10
205
67
,
119
67
,
119
5
,
2
3
1
31
,
23
5
,
2
2
1
5
,
2
3
2
13
,
34
5
,
2
2
1
1
1
8
6
−
=
−
=
=
⋅
⋅
⋅
−
=
−
=
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
=
−
δ
b)
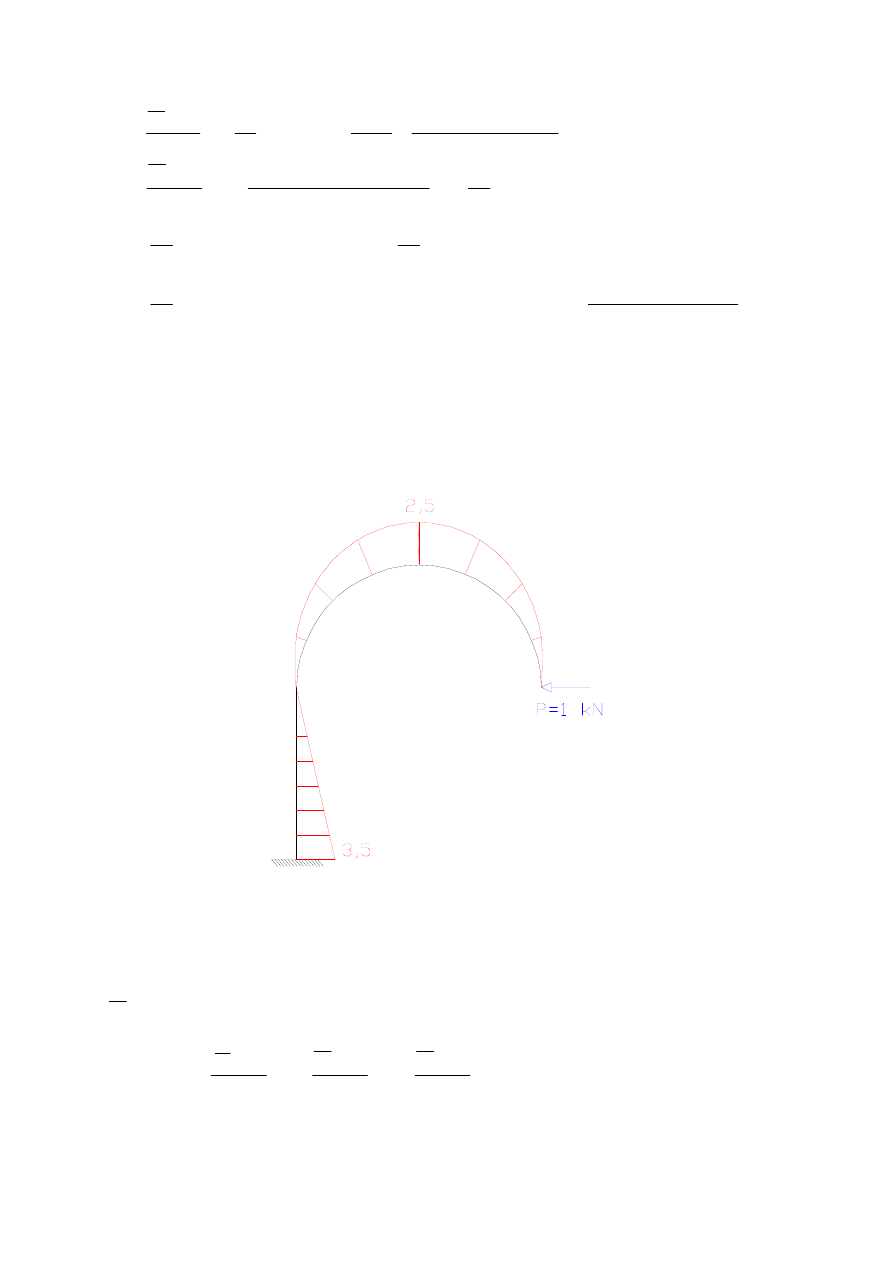
obrót w punkcie E – wpływ M
ds
EI
M
M
P
∑
∑∫
=
δ
(
)
cm
m
EI
EI
E
4
04
,
0
10
5740
10
205
38
,
475
38
,
475
1
5
,
0
5
,
2
8
5
,
2
6
3
2
1
3
1
5
,
0
5
,
2
75
,
37
1
5
,
0
92
,
2
5
,
0
8
,
4
8
8
,
4
6
3
2
92
,
2
3
2
92
,
2
5
,
0
3
1
5
,
0
8
,
4
64
,
32
93
,
2
3
2
5
,
0
64
,
32
5
,
3
17
,
4
5
,
0
3
2
5
,
2
5
,
0
31
,
23
17
,
4
5
,
0
3
2
17
,
4
3
1
5
,
0
31
,
23
5
,
2
17
,
4
3
2
17
,
4
5
,
0
3
1
5
,
0
5
,
2
13
,
34
1
1
8
6
2
2
−
=
−
=
⋅
⋅
⋅
−
=
−
=
=
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
−
−
⋅
+
⋅
⋅
⋅
⋅
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
−
−
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
⋅
−
−
⋅
⋅
+
⋅
⋅
⋅
⋅
−
⋅
+
⋅
⋅
⋅
⋅
⋅
−
=
=
−
δ
c)
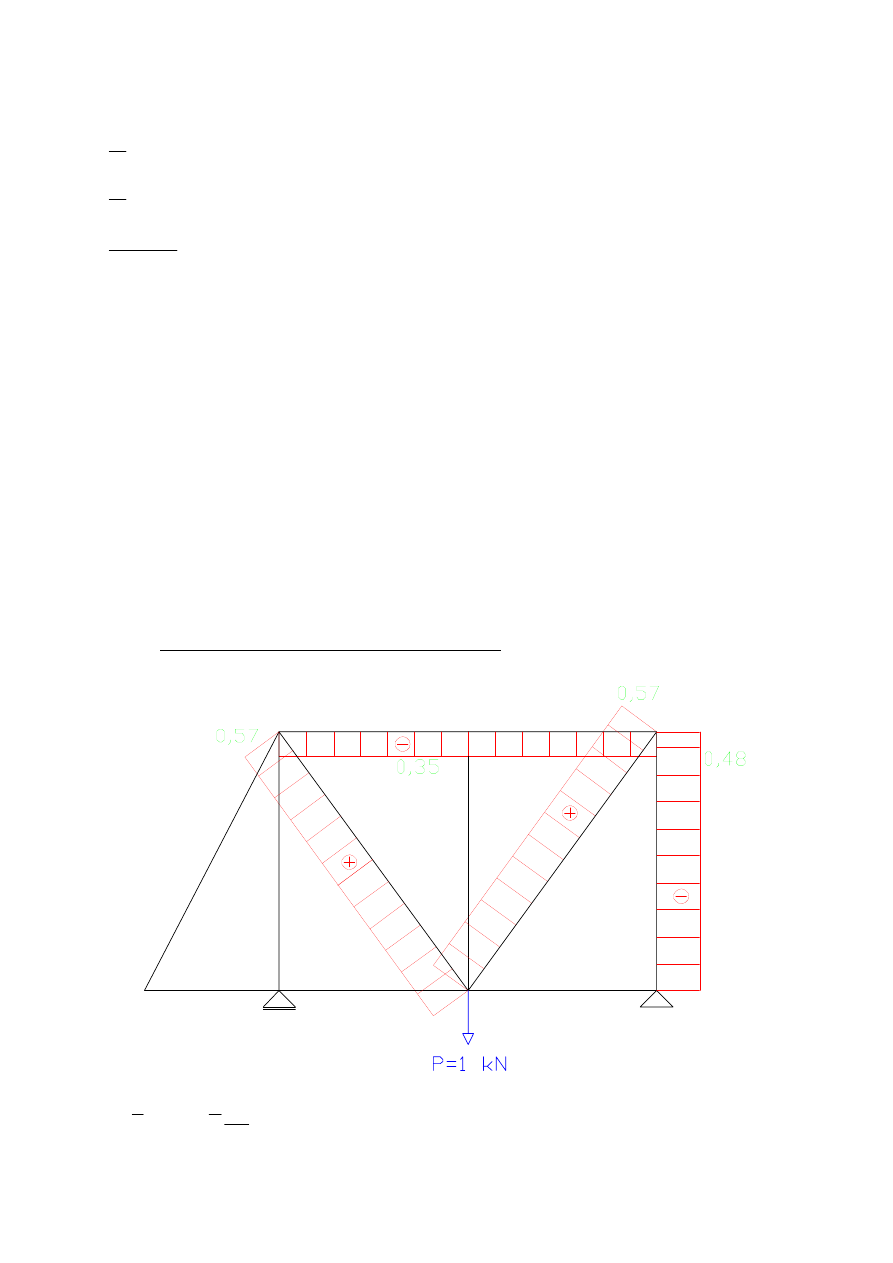
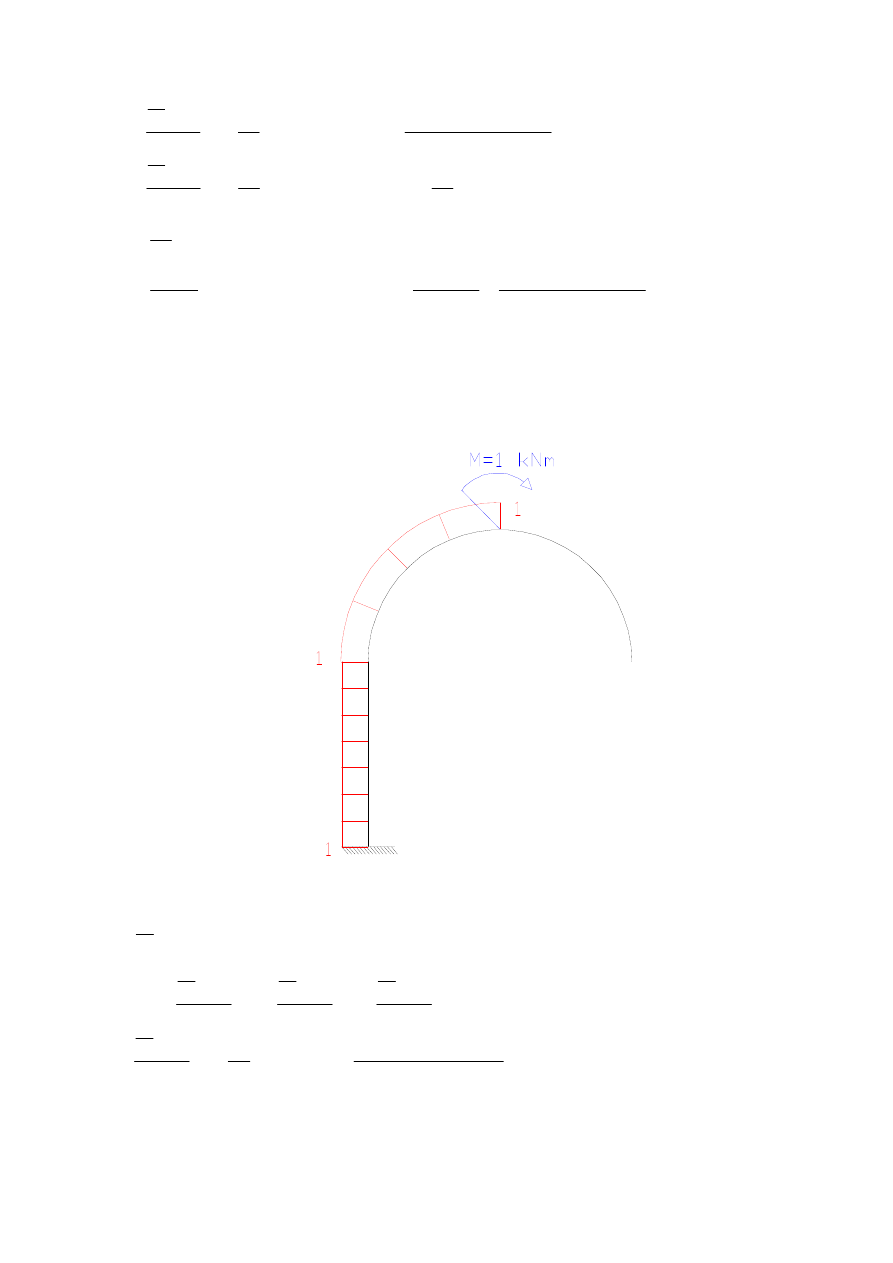
przemieszczenie pionowe punktu G – wpływ M
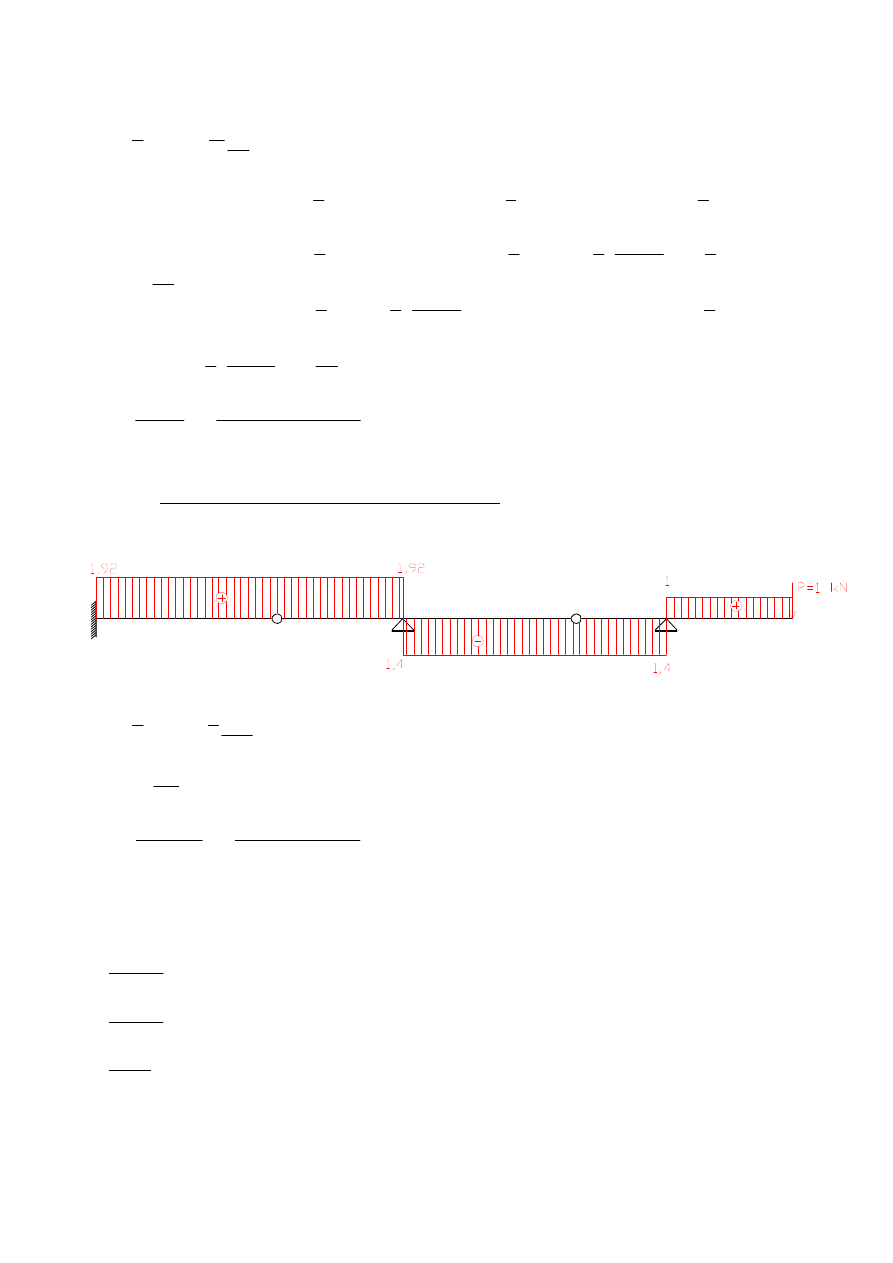
ds
EI
M
M
P
∑
∑∫
=
δ
cm
m
EI
EI
G
7
,
5
057
,
0
10
5740
10
205
38
,
675
38
,
675
2
5
,
3
5
,
3
8
5
,
3
6
3
2
5
,
3
3
2
5
,
0
575
,
36
5
,
3
5
,
3
5
,
0
5
,
2
8
5
,
2
6
3
2
5
,
3
3
2
5
,
0
75
,
37
5
,
2
75
2
1
8
,
4
8
8
,
4
6
3
2
75
,
6
3
2
5
,
0
64
,
32
8
,
4
75
,
6
3
2
5
,
0
64
,
32
5
,
3
82
,
4
3
2
5
,
0
31
,
23
5
,
2
64
,
9
3
1
5
,
0
31
,
23
5
,
2
64
,
9
3
2
5
,
0
13
,
34
5
,
2
1
1
8
6
2
2
2
−
=
−
=
⋅
⋅
⋅
−
=
−
=
=
⋅
⋅
⋅
⋅
−
−
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
−
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
=
−
δ
d)
przemieszczenie pionowe punktu G – wpływ T
ds
GA
T
T
P
∑
∑∫
∂
=
l
δ
(
) (
) (
) (
)
(
) (
) (
)
cm
GA
GA
G
046
,
0
410
,
53
10
80
33
,
2
872
,
83
872
,
83
1
5
,
0
5
,
3
21
4
,
1
5
,
0
5
,
2
6
,
7
4
,
1
5
,
0
5
,
2
6
,
22
4
,
1
5
,
0
8
,
4
6
,
7
4
,
1
5
,
0
8
,
4
2
,
21
92
,
1
3
,
9
6
92
,
1
5
,
2
3
,
4
1
6
6
−
=
⋅
⋅
⋅
−
=
∂
−
=
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
⋅
+
+
⋅
⋅
⋅
+
⋅
⋅
⋅
−
⋅
⋅
−
⋅
⋅
−
∂
=
−
l
l
δ
3
5
,
377
3775
,
0
100
75
,
37
max
max
cm
W
W
W
W
R
M
R
W
M
=
≥
≤
≤
≤

Przyjmuję dwuteownik 260
h=260mm
s=113mm
g=9,3mm
t=14,1mm
Ix=5740cm
4
A=53,4cm
2
,
G=80GPa,
E=205GPa
(
)
33
,
2
41
,
1
26
93
,
0
4
,
53
)
(
=
−
⋅
=
−
⋅
=
=
∂
t
h
g
A
Asr
A
l
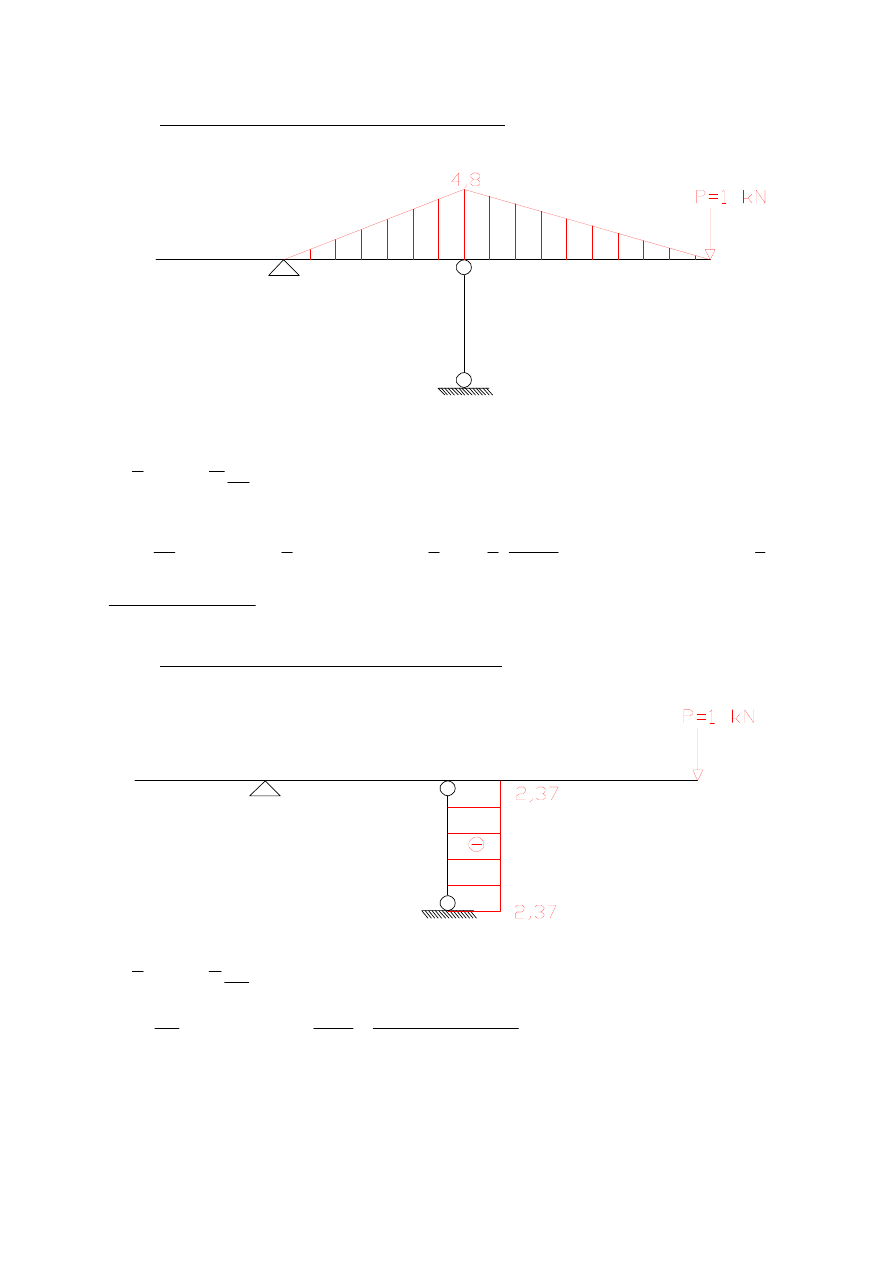
ZADANIE 2

Projektuję pręt układu na maksymalny moment gnący
MPa
R
W
R
M
R
W
M
100
max
max
=
≤
≤
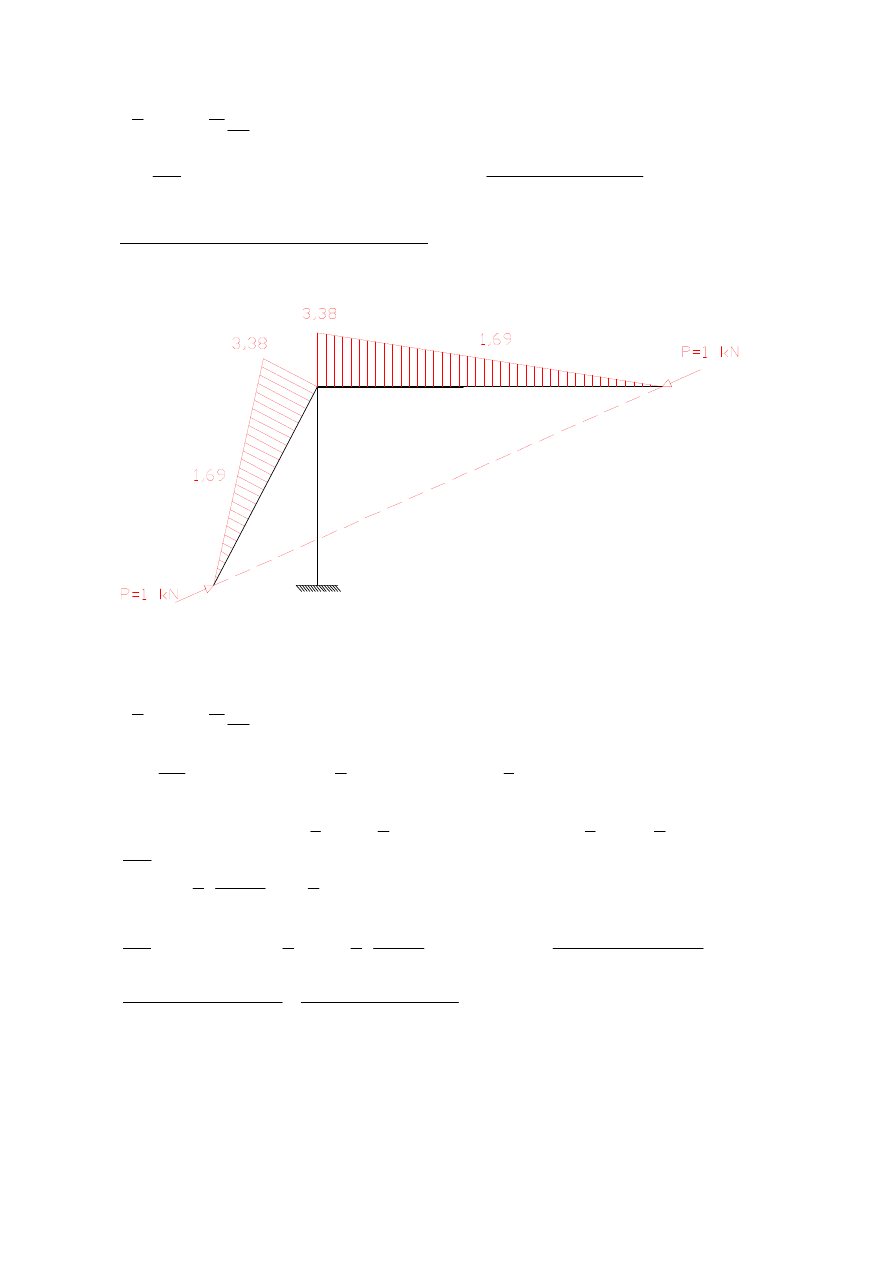
a) dla pręta A – B (EI
1
)
3
3
214
5
,
177
1000
100
1000000
75
,
17
75
,
17
max
cm
W
W
cm
kNm
M
=
≤
=
⋅
⋅
=
Przyjmuję dwuteownik 200
h=200mm
s=90mm
g=7,5mm
t=11,3mm
A=33,5cm
2
I=2140cm
4
G=80*10
6
Pa
E=205*10
6
Pa
(
)
367
,
2
13
,
1
20
75
,
0
5
,
33
=
−
⋅
=
=
∂
Asr
A
l
b) dla pręta B – C (EI
2
)
3
3
2380
7
,
2066
1000
100
1000000
67
,
206
67
,
206
max
cm
W
W
cm
kNm
M
=
≤
=
⋅
⋅
=
Przyjmuję dwuteownik 475
h=475mm
s=178mm
g=17,1mm
t=25,6mm
A=163cm
2
I=56480cm
4
G=80*10
6
Pa
E=205*10
6
Pa
(
)
121
,
2
56
,
2
5
,
47
71
,
1
163
=
−
⋅
=
=
∂
Asr
A
l

c) dla pręta C – D (EI
3
)
3
3
782
2
,
691
1000
100
1000000
12
,
69
12
,
69
max
cm
W
W
cm
kNm
M
=
≤
=
⋅
⋅
=
Przyjmuję dwuteownik 320
h=320mm
s=131mm
g=11,5mm
t=17,3mm
A=77,8cm
2
I=12510cm
4
G=80*10
6
Pa
E=205*10
6
Pa
(
)
234
,
2
73
,
1
32
15
,
1
8
,
77
=
−
⋅
=
=
∂
Asr
A
l
d) dla pręta B – E (EI
4
)
3
3
2040
2
,
1889
1000
100
1000000
92
,
188
92
,
188
max
cm
W
W
cm
kNm
M
=
≤
=
⋅
⋅
=
Przyjmuję dwuteownik 450
h=450mm
s=170mm
g=16,2mm
t=24,3mm
A=147cm
2
I=45850cm
4
G=80*10
6
Pa
E=205*10
6
Pa
(
)
131
,
2
43
,
2
45
62
,
1
147
=
−
⋅
=
=
∂
Asr
A
l
a)
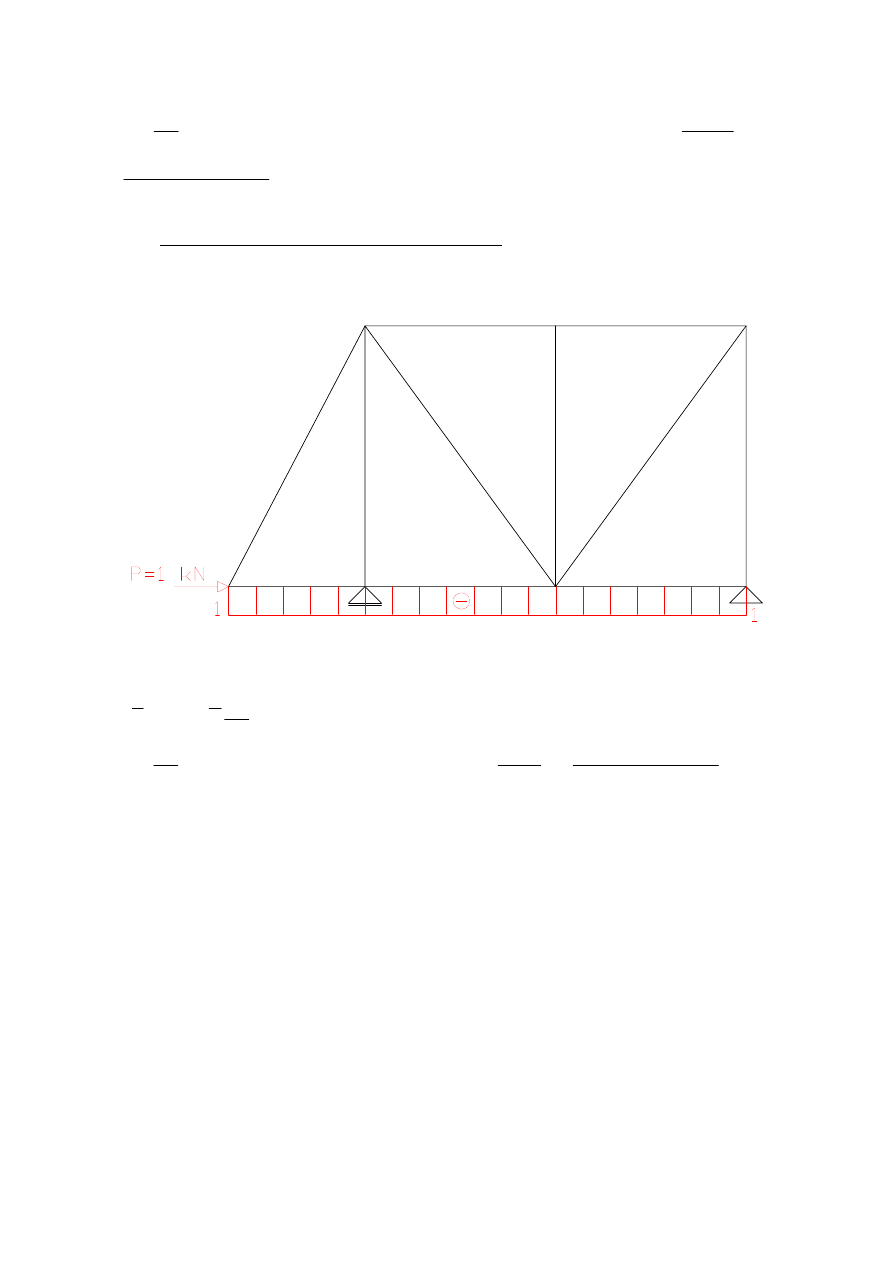
przemieszczenie pionowe punktu A – wpływ M
ds
EI
M
M
P
∑
∑∫
=
δ
cm
m
EI
EI
EI
EI
A
9
,
1
019
,
0
10
45850
10
205
84
,
1582
10
2140
10
205
03
,
158
84
,
1582
03
,
158
8
,
4
3
1
8
,
4
92
,
164
5
,
0
8
,
4
3
2
8
,
4
92
,
188
5
,
0
1
8
,
4
3
1
412
,
5
1
5
,
0
8
,
4
3
2
412
,
5
75
,
17
5
,
0
1
1
8
6
8
6
4
1
4
1
=
=
⋅
⋅
⋅
−
⋅
⋅
⋅
=
=
−
=
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
⋅
+
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
=
−
−
δ
b)
przemieszczenie pionowe punktu A – wpływ T
ds
GA
T
T
P
∑
∑∫
∂
=
l
δ
[
]
[
]
cm
m
GA
GA
GA
GA
A
1
01
,
0
10
147
10
80
24
131
,
2
10
5
,
33
10
80
617
,
16
361
,
2
24
617
,
16
1
8
,
4
5
89
,
0
412
,
5
5
,
0
9
,
6
1
6
6
6
6
4
4
1
1
4
4
1
1
=
=
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
=
=
⋅
∂
−
⋅
∂
=
⋅
⋅
⋅
∂
−
⋅
⋅
⋅
⋅
∂
=
−
−
l
l
l
l
δ
c)
przemieszczenie pionowe punktu A – wpływ N
ds
EA
N
N
P
∑
∑∫
=
δ
(
)
[
]
cm
m
EA
A
241
,
0
00241
,
0
10
5
,
33
10
205
56
,
16
46
,
0
412
,
5
5
,
0
3
,
13
1
1
6
6
1
=
=
⋅
⋅
⋅
−
=
⋅
⋅
⋅
−
⋅
=
−
δ
d)
obrót w punkcie B – wpływ M
ds
EI
M
M
P
∑
∑∫
=
δ
[
]
cm
m
EI
B
9
,
0
009
,
0
10
45850
10
205
216
,
849
1
8
,
4
92
,
164
5
,
0
1
8
,
4
92
,
188
5
,
0
1
1
8
6
4
=
=
⋅
⋅
⋅
=
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
=
−
δ
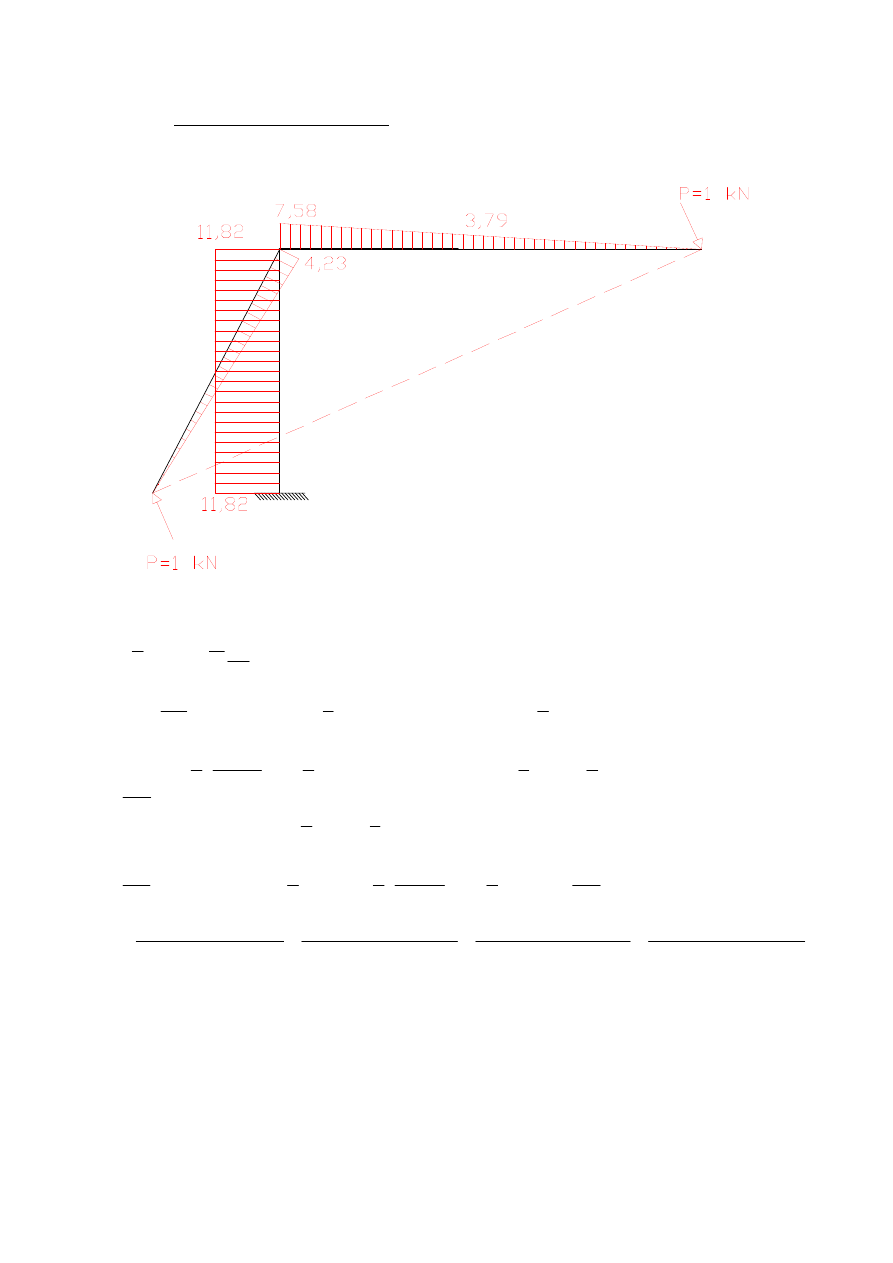
e) wzajemne zbliżanie się A i D – wpływ M
ds
EI
M
M
P
∑
∑∫
=
δ
cm
m
EI
EI
EI
AD
19
,
4
0419
,
0
10
12510
10
205
175
,
140
10
56480
10
205
274
,
1291
10
2140
10
205
279
,
111
69
,
1
5
,
0
8
,
4
8
8
,
4
6
3
2
69
,
1
3
2
8
,
4
12
,
69
5
,
0
1
38
,
3
4
3
5
,
3
8
5
,
3
6
3
2
69
,
1
3
2
38
,
3
3
1
5
,
3
12
,
69
5
,
0
38
,
3
3
2
69
,
1
3
1
5
,
3
67
,
206
5
,
0
1
38
,
3
3
1
412
,
5
5
,
0
1
38
,
3
3
2
412
,
5
5
,
0
75
,
17
1
1
8
6
8
6
8
6
2
3
2
2
1
=
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
+
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
⋅
⋅
−
−
⋅
+
⋅
⋅
⋅
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
=
−
−
−
δ
f)
obrót cięciwy AD – wpływ M
ds
EI
M
M
P
∑
∑∫
=
δ
cm
m
EI
EI
EI
EI
AD
5
,
17
175
,
0
107
,
0
0123
,
0
0239
,
0
0317
,
0
10
45850
10
205
733
,
10037
10
12510
10
205
357
,
314
10
56480
10
205
94
,
2773
10
2140
10
205
26
,
139
82
,
11
8
,
4
5
,
0
92
,
164
82
,
11
8
,
4
5
,
0
92
,
188
1
58
,
7
4
1
8
,
4
8
8
,
4
6
3
2
79
,
3
3
2
8
,
4
12
,
69
5
,
0
1
58
,
7
3
1
79
,
3
3
2
5
,
3
12
,
69
5
,
0
58
,
7
3
2
79
,
3
3
1
5
,
3
67
,
206
5
,
0
58
,
7
4
3
5
,
3
8
5
,
3
6
3
2
1
23
,
4
3
2
412
,
5
5
,
0
75
,
17
23
,
4
3
1
412
,
5
5
,
0
1
1
1
8
6
8
6
8
6
8
6
4
2
3
2
2
1
=
=
+
+
+
=
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
⋅
−
=
=
⋅
⋅
⋅
+
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
⋅
+
+
⋅
+
⋅
⋅
⋅
⋅
+
+
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
−
⋅
+
+
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
⋅
=
−
−
−
−
δ
ZADANIE 3
Przyjmuję dwuteownik 200
367
,
2
3
,
0
10
205
10
85
,
78
85
,
78
)
1
(
2
2140
5
,
33
13
,
1
75
,
0
9
20
6
6
4
2
=
=
∂
=
⋅
=
⋅
=
=
+
⋅
=
=
=
=
=
=
=
sr
A
A
Pa
E
Pa
GPa
E
G
cm
I
cm
A
cm
t
cm
g
cm
s
cm
h
l
υ
υ
C
t
t
t
t
m
°
=
⋅
−
=
5
2
2
1
0
α
2∆
∆
∆
∆
a)
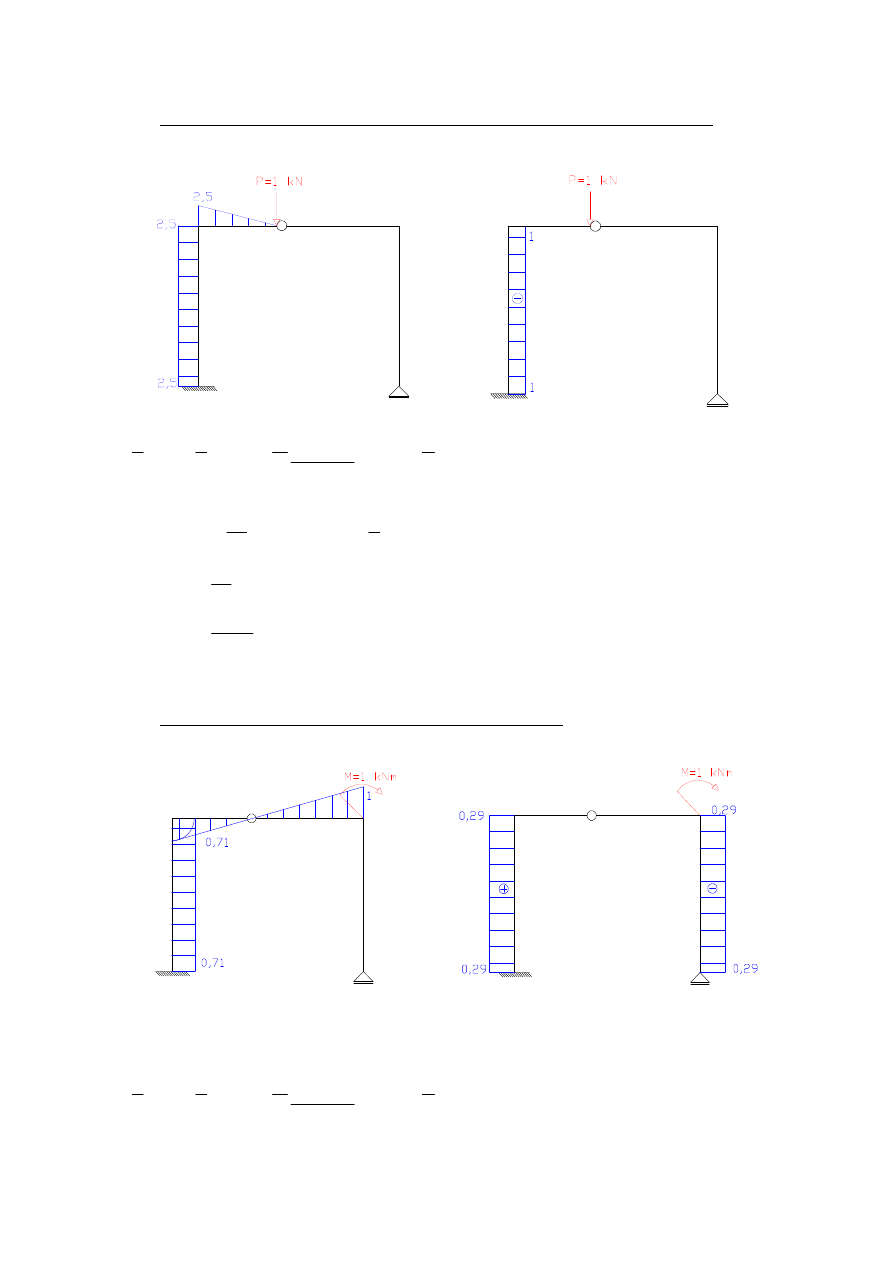
przemieszczenie pionowe punktu C – wpływ temperatury i osiadania podpór
∑∫
∑
∑∫
∑
⋅
+
∆
⋅
=
∆
+
ds
t
N
ds
h
t
M
M
R
P
t
t
0
α
α
δ
[
]
(
)
(
)
453
,
2
048
,
0
24
363
8
,
4
048
,
0
025
,
0
1
24
363
025
,
0
1
5
8
,
4
1
24
5
,
2
5
,
2
2
1
24
8
,
4
5
,
2
1
025
,
0
1
−
=
⋅
+
−
⋅
=
−
+
−
⋅
=
−
⋅
⋅
+
⋅
⋅
⋅
−
⋅
⋅
−
=
⋅
−
D
D
t
t
D
t
t
D
h
h
δ
δ
α
α
δ
α
α
δ
b)
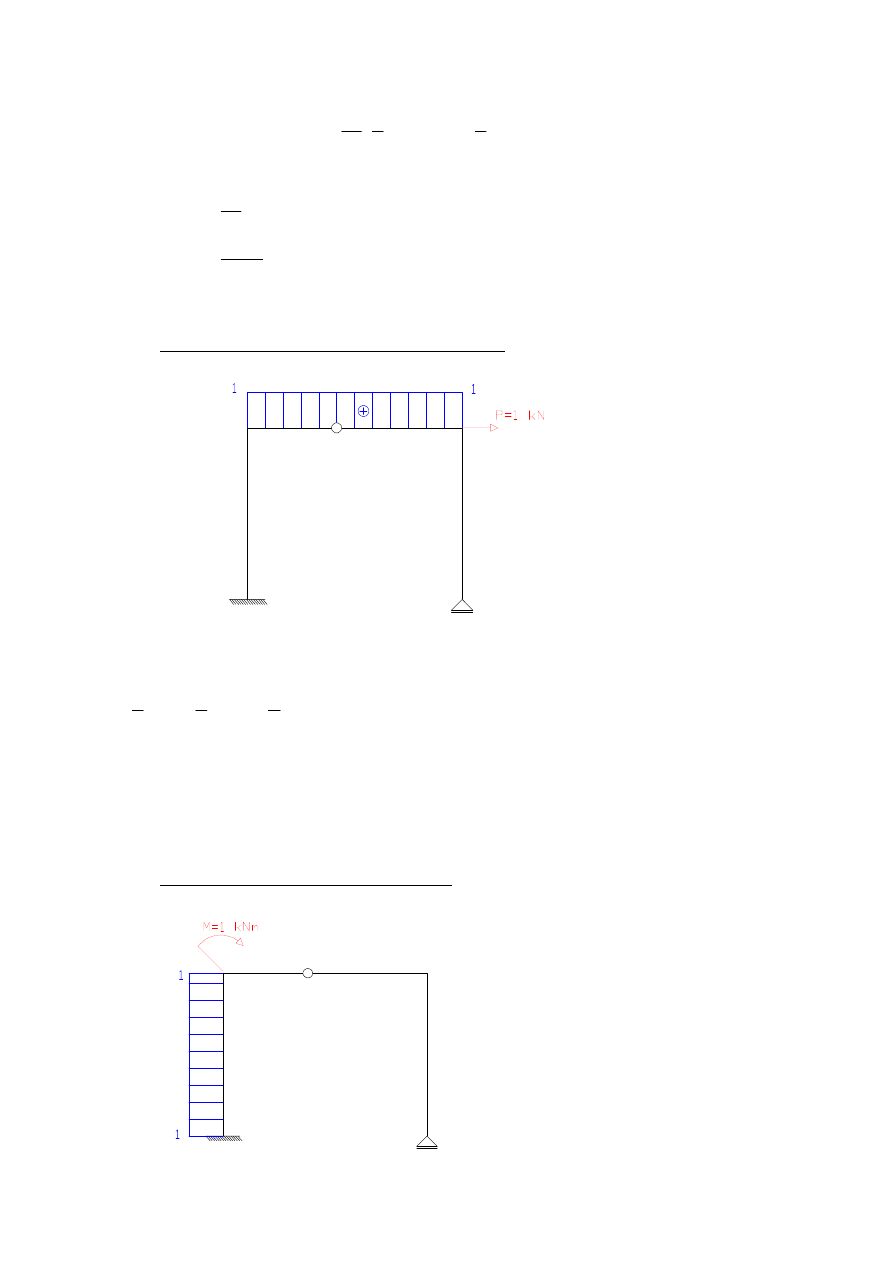
obrót punktu D - wpływ temperatury i osiadania podpór
∑∫
∑
∑∫
∑
⋅
+
∆
⋅
=
∆
+
ds
t
N
ds
h
t
M
M
R
P
t
t
0
α
α
δ
[
]
429
,
1
09
,
145
8
,
4
048
,
0
0217
,
0
1
09
,
145
0217
,
0
1
2
8
,
4
29
,
0
2
8
,
4
29
,
0
24
71
,
0
8
,
4
24
71
,
0
5
,
2
2
1
24
1
5
,
3
2
1
29
,
0
05
,
0
025
,
0
29
,
0
1
=
⋅
=
+
⋅
=
+
⋅
⋅
−
⋅
⋅
+
+
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
⋅
=
⋅
+
⋅
+
D
D
t
D
t
t
D
h
h
δ
δ
α
δ
α
α
δ
c)
przemieszczenie poziome D – osiadanie podpór
∑∫
∑
∑
⋅
=
∆
+
ds
t
N
R
P
t
0
α
δ
[
]
( )
( )
576
,
0
12
048
,
0
1
12
1
2
6
1
1
−
=
−
⋅
=
−
⋅
=
⋅
⋅
−
=
D
D
t
D
t
D
δ
δ
α
δ
α
δ
d)
obrót w punkcie B – wpływ temperatury

ds
h
t
M
M
R
P
t
∑
∑∫
∑
∆
⋅
=
∆
+
α
δ
[
]
(
)
(
)
177
,
1
2
,
115
8
,
4
048
,
0
025
,
0
1
2
,
115
025
,
0
1
24
8
,
4
1
3
1
025
,
0
05
,
0
3
1
1
−
=
−
⋅
=
+
−
⋅
=
+
⋅
⋅
−
=
−
⋅
−
⋅
+
B
B
t
B
t
B
h
h
δ
δ
α
δ
α
δ
ZADANIE 4
Projektuję pręty układu na maksymalny moment gnący i siłę normalną
A
R
N
R
A
N
W
R
M
R
W
M
MPa
R
≤
≤
≤
≤
=
max
max
max
max
100

1. Pręty A- B, B – C, C – D na Momot gnący
3
278
240
1000
100
1000000
24
cm
W
W
=
≤
=
⋅
⋅
Przyjmuję dwuteownik 220
35
,
2
10
205
10
80
3060
6
,
39
22
,
1
81
,
0
8
,
9
22
6
6
4
2
=
∂
⋅
=
⋅
=
=
=
=
=
=
=
l
Pa
E
Pa
G
cm
I
cm
A
cm
t
cm
g
cm
s
cm
h
2. Pręt C – E na maksymalną siłę normalną
2
3
4
58
,
7
26
,
2
10
100
10
6
,
22
cm
A
A
=
≤
=
⋅
⋅
Przyjmuję dwuteownik 80
623
,
2
10
205
10
80
8
,
77
58
,
7
59
,
0
39
,
0
2
,
4
8
6
6
4
2
=
∂
⋅
=
⋅
=
=
=
=
=
=
=
l
Pa
E
Pa
G
cm
I
cm
A
cm
t
cm
g
cm
s
cm
h
a)
przemieszczenie pionowe punktu D – wpływ M
ds
EI
M
M
P
∑
∑∫
=
δ
cm
m
EI
D
99
,
4
0499
,
0
10
3060
10
205
4
,
313
8
,
4
3
1
5
,
3
5
,
0
9
,
1
8
,
4
5
,
0
5
,
3
8
5
,
3
6
3
2
8
,
4
3
2
5
,
3
24
5
,
0
8
,
4
3
2
8
,
4
24
5
,
0
1
1
8
6
2
=
=
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
=
−
δ
b)
przemieszczenie pionowe punktu D – wpływ N
ds
EA
N
N
P
∑
∑∫
=
δ
[
]
cm
m
EA
EA
D
6
,
8
086
,
0
10
58
,
7
10
205
9
,
133
9
,
133
37
,
2
5
,
2
6
,
22
1
1
6
6
=
=
⋅
⋅
⋅
=
=
⋅
⋅
=
−
δ
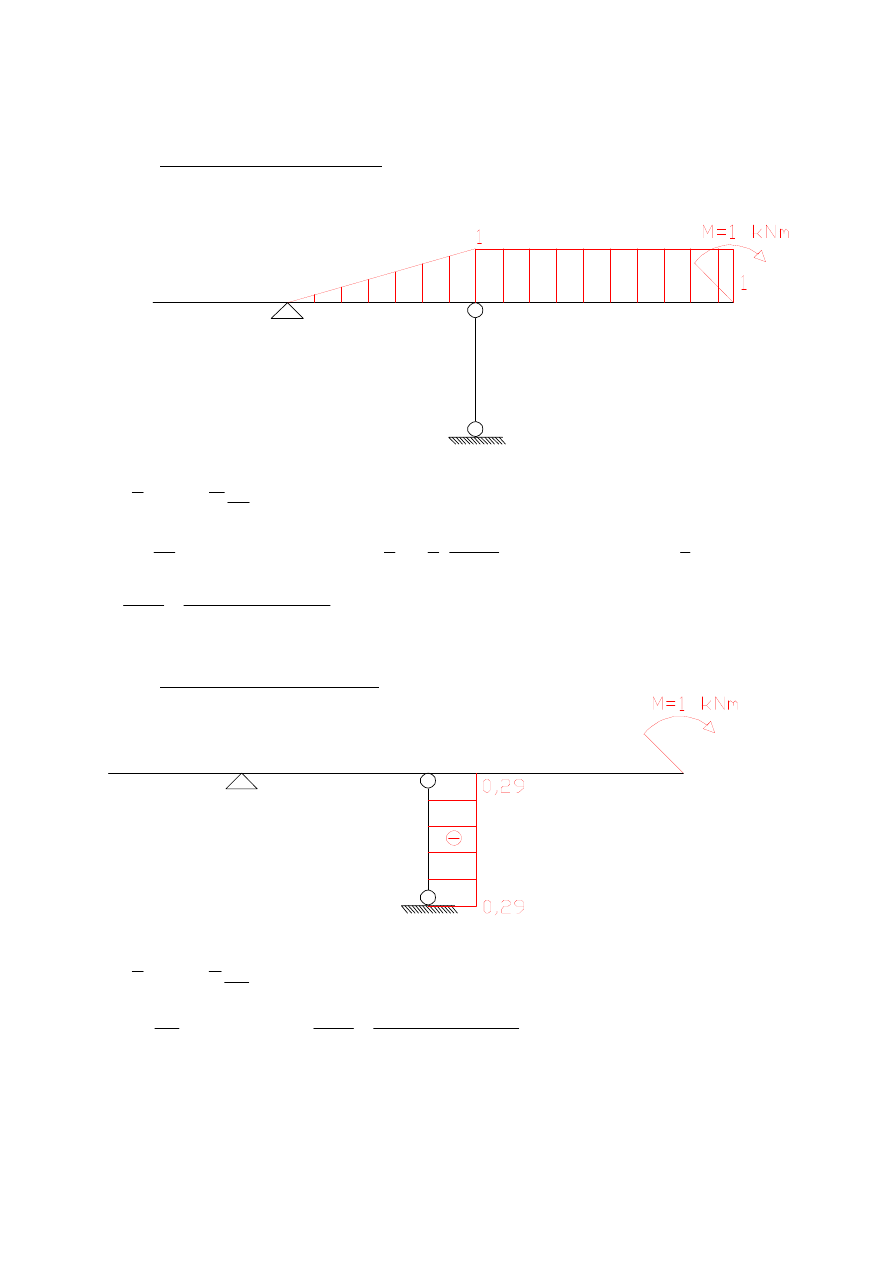
c)
obrót w punkcie D – wpływ M
ds
EI
M
M
P
∑
∑∫
=
δ
cm
m
EI
EI
D
17
,
1
0117
,
0
10
3060
10
205
77
,
73
77
,
73
1
3
1
5
,
3
5
,
0
9
,
1
1
5
,
0
5
,
3
8
5
,
3
6
3
2
1
3
2
5
,
3
24
5
,
0
1
8
,
4
24
5
,
0
1
1
8
6
2
=
=
⋅
⋅
⋅
=
=
=
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
=
−
δ
d)
obrót w punkcie D – wpływ N
ds
EA
N
N
P
∑
∑∫
=
δ
[
]
cm
m
EA
EA
D
05
,
1
0105
,
0
10
58
,
7
10
205
38
,
16
38
,
16
29
,
0
5
,
2
6
,
22
1
1
6
6
=
=
⋅
⋅
⋅
=
=
⋅
⋅
=
−
δ
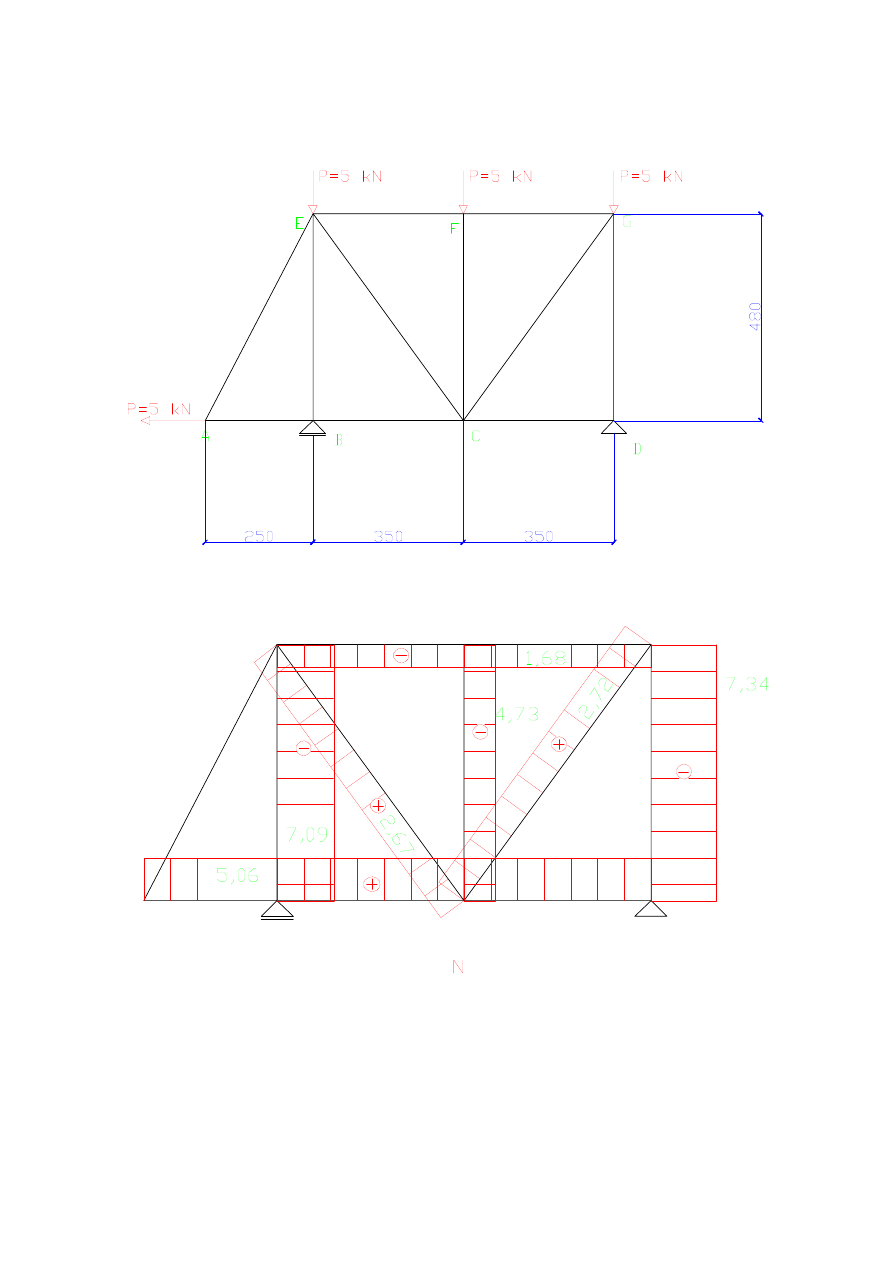
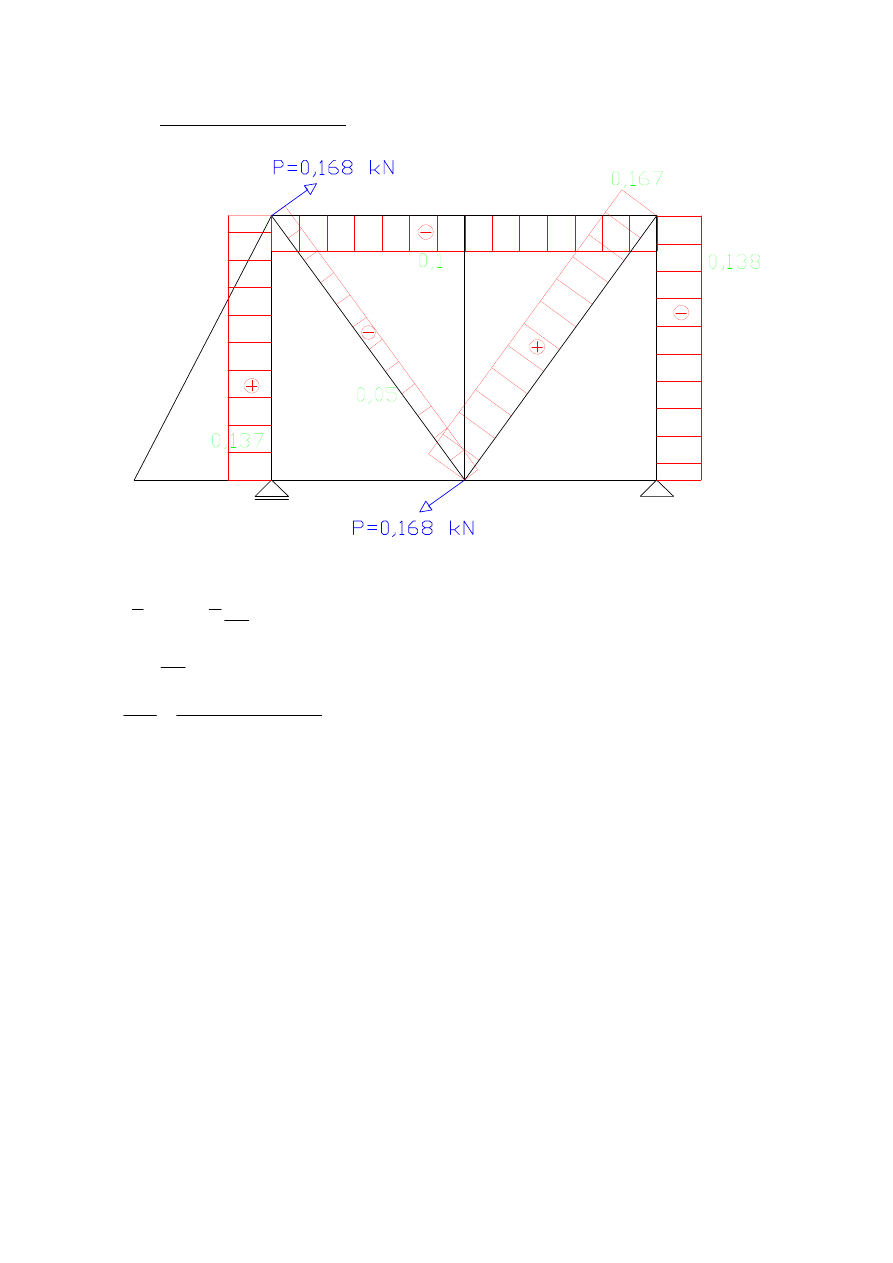
ZADANIE 5
Projektuję pręt układu na maksymalną siłę normalną
2
3
4
58
,
7
734
,
0
10
100
10
34
,
7
cm
A
A
A
R
N
R
A
N
=
≤
=
⋅
⋅
≤
≤
Przyjmuję dwuteownik 80
623
,
2
10
205
10
80
8
,
77
58
,
7
59
,
0
39
,
0
2
,
4
8
6
6
4
2
=
∂
⋅
=
⋅
=
=
=
=
=
=
=
l
Pa
E
Pa
G
cm
I
cm
A
cm
t
cm
g
cm
s
cm
h
a)
przemieszczenie pionowe punktu C – wpływ N
ds
EA
N
N
P
∑
∑∫
=
δ
[
]
cm
m
EA
EA
C
53
,
2
0253
,
0
10
58
,
7
10
205
277
,
39
277
,
39
48
,
0
8
,
4
34
,
7
57
,
0
94
,
5
72
,
2
57
,
0
94
,
5
67
,
2
35
,
0
7
68
,
1
1
1
6
6
=
=
⋅
⋅
⋅
=
=
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
⋅
=
−
δ
b)
przemieszczenie poziome punktu A – wpływ N
ds
EA
N
N
P
∑
∑∫
=
δ
[
]
cm
m
EA
EA
A
08
,
3
0308
,
0
10
58
,
7
10
205
97
,
47
97
,
47
1
5
,
3
06
,
5
1
5
,
3
06
,
5
1
5
,
2
06
,
5
1
1
6
6
=
=
⋅
⋅
⋅
−
=
−
=
⋅
⋅
−
⋅
⋅
−
⋅
⋅
−
=
−
δ
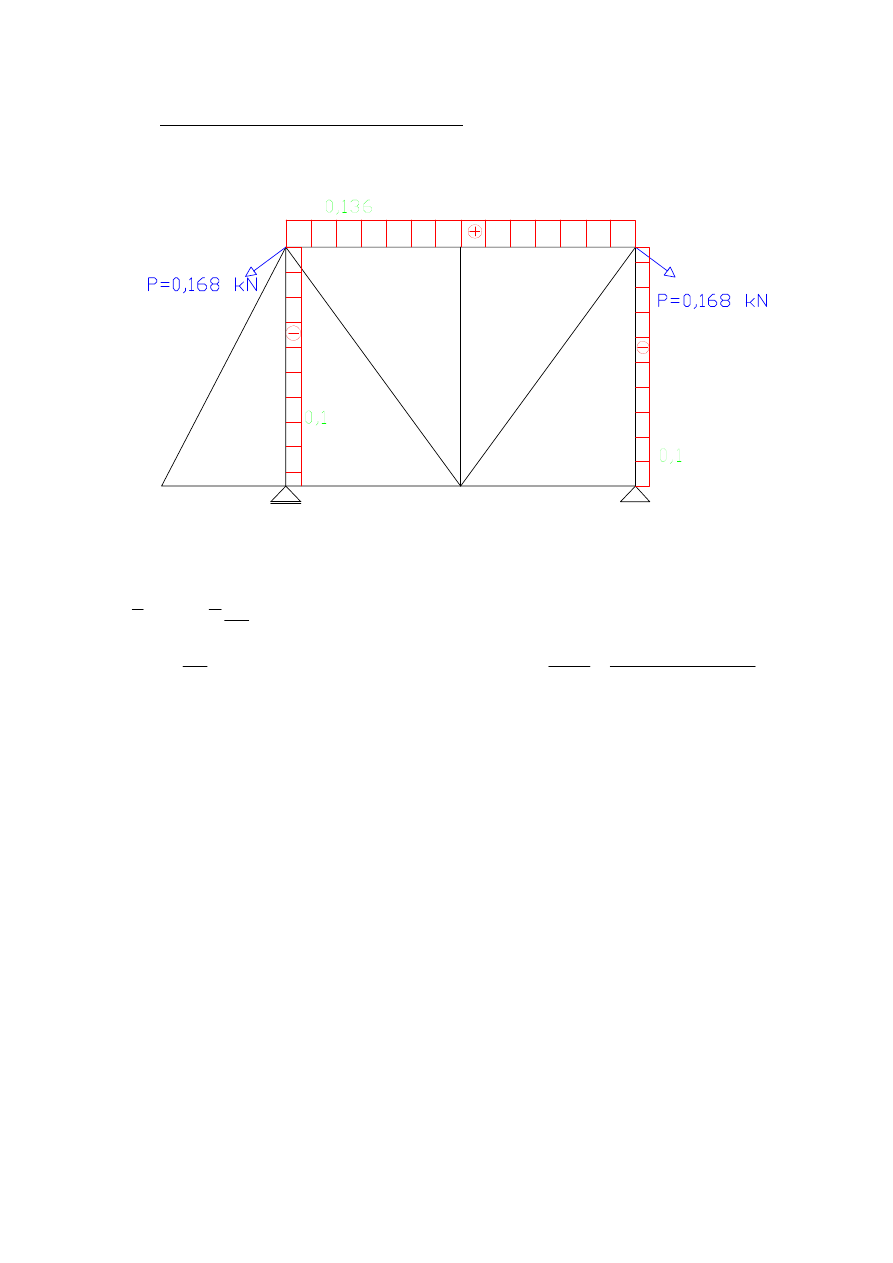
c)
kąt obrotu EC – wpływ N
ds
EA
N
N
P
∑
∑∫
=
δ
[
]
cm
m
EA
EA
EC
022
,
0
10
2
,
2
10
58
,
7
10
205
34
,
0
34
,
0
138
,
0
8
,
4
34
,
7
167
,
0
93
,
5
72
,
2
05
,
0
93
,
5
67
,
2
1
,
0
7
68
,
1
137
,
0
8
,
4
98
,
7
1
1
4
6
6
=
⋅
=
⋅
⋅
⋅
=
=
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
−
⋅
⋅
−
⋅
⋅
−
=
−
−
δ
d)
wzajemny kąt obrotu EC i GC – wpływ N
ds
EA
N
N
P
∑
∑∫
=
δ
[
]
cm
m
EA
EA
GC
EC
343
,
0
00343
,
0
10
58
,
7
10
205
327
,
5
327
,
5
136
,
0
7
68
,
1
1
,
0
8
,
4
34
,
7
1
,
0
8
,
4
09
,
7
1
1
6
6
=
=
=
⋅
⋅
⋅
=
=
⋅
⋅
−
⋅
⋅
+
⋅
⋅
=
−
−
δ
ZADANIE 6
Projektuję pręty układu na maksymalny moment gnący
3
278
240
1000
100
1000000
25
cm
W
W
=
≤
=
⋅
⋅
Przyjmuję dwuteownik 220
35
,
2
10
205
10
80
3060
6
,
39
22
,
1
81
,
0
8
,
9
22
6
6
4
2
=
∂
⋅
=
⋅
=
=
=
=
=
=
=
l
Pa
E
Pa
G
cm
I
cm
A
cm
t
cm
g
cm
s
cm
h
a)
przemieszczenie pionowe punktu D – wpływ M
(
)
(
)
x
a
M
x
a
P
Mp
−
⋅
−
=
−
⋅
−
=
1
ds
EI
Mp
M
ds
EI
Mp
M
ds
EI
M
M
P
D
B
B
A
∫
∫
∑
∑∫
⋅
+
⋅
=
=
δ
[
]
cm
m
EI
EI
ds
EI
Mp
M
B
A
97
,
6
0697
,
0
10
3060
10
205
5
,
437
5
,
437
5
5
,
3
25
1
8
6
=
=
⋅
⋅
⋅
=
=
⋅
⋅
=
⋅
−
∫
(
) ( )
( ) (
)
(
)
cm
cm
m
d
d
d
EI
ds
x
x
EI
ds
x
x
EI
ds
x
x
EI
ds
EI
x
a
x
a
P
ds
EI
Mp
M
V
D
D
B
D
B
D
B
D
B
92
,
8
97
,
6
95
,
1
95
,
1
0195
,
0
10
3060
10
205
125
,
78
5
,
0
cos
125
,
78
cos
25
,
156
125
,
78
1
5
25
25
,
31
1
)
5
,
2
(
)
5
5
,
12
(
1
5
,
2
1
)
5
,
2
(
)
5
(
1
)
(
1
8
6
0
0
0
2
2
=
+
=
=
=
=
⋅
⋅
⋅
⋅
⋅
=
⋅
+
⋅
−
⋅
=
=
+
−
⋅
=
+
−
⋅
+
−
⋅
=
=
−
⋅
−
⋅
−
⋅
−
⋅
=
−
⋅
−
⋅
−
⋅
−
=
⋅
−
∫
∫
∫
∫
∫
∫
∫
δ
π
ϕ
ϕ
ϕ
ϕ
ϕ
π
π
π
b)
przemieszczenie poziome punktu D – wpływ M
y
M
x
x
a
P
Mp
a
y
a
x
−
=
−
⋅
−
=
−
⋅
−
=
⋅
=
⋅
=
)
5
,
2
(
5
)
(
sin
cos
ϕ
ϕ
∫
∫
∑∫
⋅
+
⋅
=
⋅
=
D
B
B
A
H
D
ds
EI
Mp
M
ds
EI
Mp
M
ds
EI
Mp
M
δ
[
]
(
)
cm
cm
m
EI
d
EI
d
EI
ds
y
xy
EI
ds
y
x
EI
ds
EI
Mp
M
cm
m
EI
ds
EI
Mp
M
H
D
D
B
D
B
D
B
B
A
93
,
4
49
,
2
44
,
2
49
,
2
0249
,
0
10
3060
10
205
25
,
156
2
125
,
78
)
sin
sin
cos
(
125
,
78
5
,
2
sin
5
,
2
5
,
12
sin
5
,
2
cos
5
,
2
5
1
)
5
,
12
5
(
1
)
(
)
5
,
12
5
(
1
44
,
2
0244
,
0
10
3060
10
205
125
,
153
5
,
3
5
,
0
5
,
3
25
1
0
8
6
8
6
=
+
=
=
=
⋅
⋅
⋅
=
⋅
=
+
⋅
−
⋅
=
=
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
−
⋅
=
=
+
−
⋅
=
−
⋅
−
⋅
=
⋅
=
=
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
⋅
∫
∫
∫
∫
∫
−
−
δ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
π
c)
obrót punktu C – wpływ M
1
5
,
12
5
)
(
=
−
=
−
⋅
−
=
M
x
Mp
x
a
P
M
(
)
cm
m
EI
ds
EI
Mp
M
ds
EI
Mp
M
ds
EI
Mp
M
ds
EI
Mp
M
c
B
A
C
B
B
A
99
,
0
00996
,
0
10
3060
10
205
5
,
62
1
5
,
3
25
1
8
6
=
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
⋅
=
⋅
+
⋅
=
⋅
=
−
∫
∫
∫
∑∫
δ

(
)
cm
c
cm
m
EI
d
EI
d
EI
ds
x
EI
ds
EI
Mp
M
C
B
C
B
29
,
0
28
,
1
99
,
0
28
,
1
0128
,
0
10
3060
10
205
57
,
2
25
,
31
2
1
25
,
31
)
1
(cos
25
,
31
5
,
2
)
25
,
31
cos
25
,
31
(
1
1
)
5
,
12
5
(
1
2
8
6
2
−
=
−
=
−
=
−
=
⋅
⋅
⋅
−
⋅
=
−
−
⋅
=
−
⋅
=
=
⋅
−
⋅
⋅
=
⋅
−
⋅
=
⋅
∫
∫
∫
∫
−
ϕ
π
ϕ
ϕ
ϕ
ϕ
π
π
π
π
Wyszukiwarka
Podobne podstrony:
cwicz mechanika budowli przemieszczen metoda pracy wirtualnej
cwicz mechanika budowli przemieszczen metoda pracy wirtualnej
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil krata
cwicz mechanika budowli metoda przemieszczen rama ugiecie
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil luk
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil rama
cwicz mechanika budowli metoda przemieszczen rama
cwicz mechanika budowli metoda przemieszczen rama temperatura
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil luk
cwicz mechanika budowli metoda przemieszczen rama osiadanie
Mechanika budowli Obliczanie pr Nieznany
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil krata
Mechanika Budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil (rama przestrzenna)
więcej podobnych podstron