
X L V I I I K O N F E R E N C J A N AU K O W A
KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN
I KOMITETU NAUKI PZITB
Opole – Krynica
2002
Joanna JANKOWSKA-SANDBERG
1
Szymon PAŁ KOWSKI
2
PARAMETRYCZNA ANALIZA
ZWICHRZENIA SPRĘ Ż YSTEGO KRATOWNIC
1. Wprowadzenie
Praktyczne wskazó wki dotyczące długości wyboczeniowej prętó w kratownic podano np.
w [1]. W przypadku rozpatrywania wyboczenia z płaszczyzny kratownicy moż na wg tych
wytycznych długość wyboczeniową pasa przyjmować ró wną odległości między bocznymi
stęż eniami kratownicy. To zalecenie normowe prowadzi na ogó ł do bezpiecznego, ale też
często do nieekonomicznego projektowania kratownic. Opiera się ono bowiem na uprosz-
czonym traktowaniu pasa kratownicy jako pręta przegubowo podpartego, ściskanego stałą
siłą na całej długości i nie powiązanego z pozostałymi elementami kratownicy.
Istnieje bardzo duż a analogia między zjawiskiem zwichrzenia kratownicy a dobrze
znanym zjawiskiem zwichrzenia belki zginanej. To drugie zagadnienie ma, jak wiadomo,
bardzo obszerną literaturę (por. np. [2,3]), gdy tymczasem zjawisku zwichrzenia kratownic
jest poświęcona bardzo mała liczba prac. Na podstawie tych prac, np. [4,5,6], moż na
stwierdzić , ż e rzeczywista długość wyboczeniowa ściskanego pasa kratownicy (lub jego siła
krytyczna) zależ y nie tylko od rozstawu bocznych stęż eń kratownicy, ale takż e od takich
czynnikó w, jak np.:
-
rozkład siły normalnej na długości pasa (w kratownicach swobodnie podpartych jest on
w przybliż eniu paraboliczny),
-
rodzaj skratowania oraz jego sztywność w stosunku do sztywności ściskanego pasa,
-
sposó b połączenia skratowania z pasem (sztywny lub przegubowy),
-
rodzaj obciąż enia kratownicy (obciąż enie pasa dolnego lub gó rnego).
W artykule przedstawiono wybrane wyniki dość obszernej analizy numerycznej
uwzględniającej wpływ wymienionych parametró w na wartość obciąż enia krytycznego
kratownicy (na długość wyboczeniową ściskanego pasa kratownicy). Wyniki te mają pewną
wartość zaró wno poznawczą, jak i praktyczną i mogą być wykorzystane przy racjonalnym
wymiarowaniu kratownic.
1
Dr inż ., Katedra Konstrukcji Metalowych Politechniki Koszalińskiej
2
Prof. dr hab. inż ., Katedra Konstrukcji Metalowych Politechniki Koszalińskiej
192
2. Opis metody rozwiązania
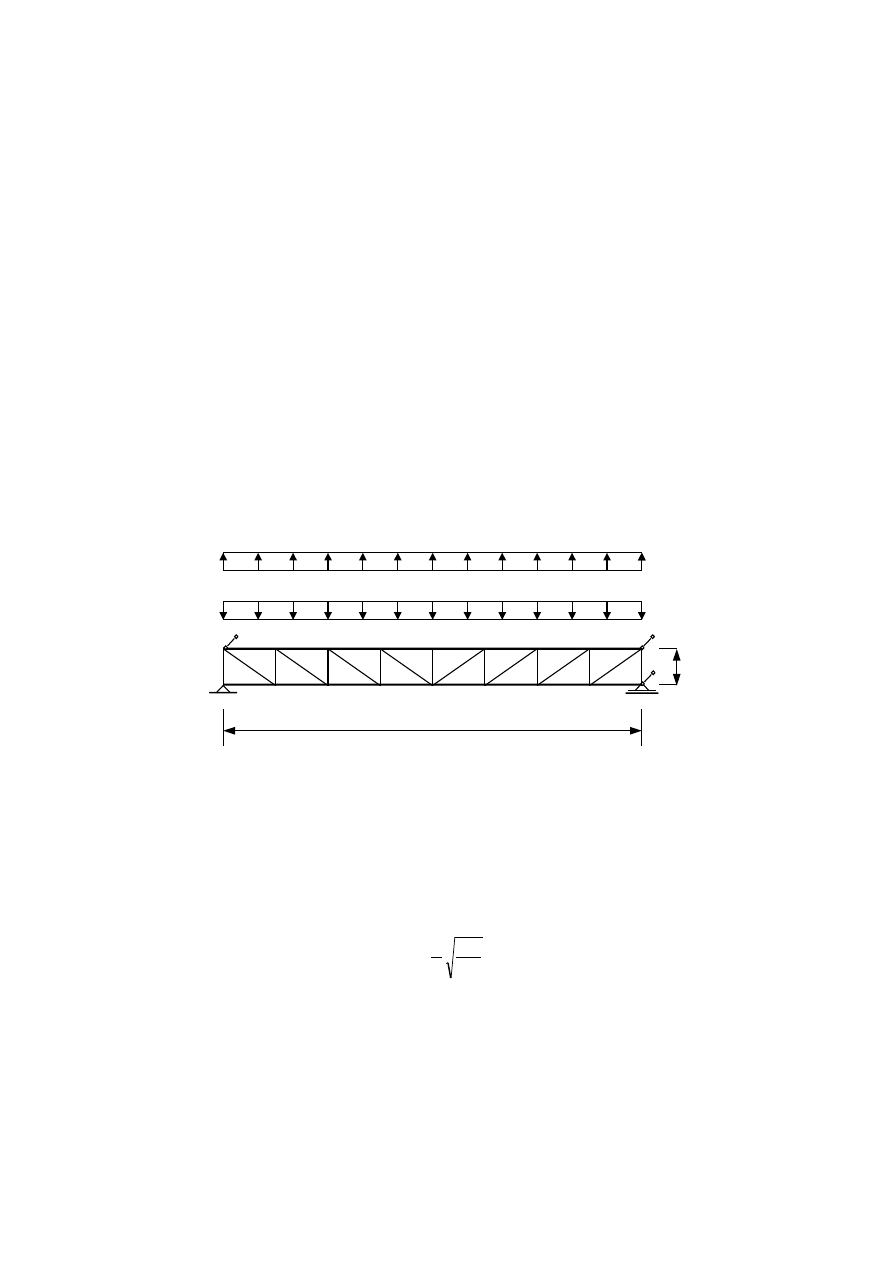
Do analizy numerycznej przyjęto kratownicę przedstawioną na rys. 1. Założ ono, ż e pasy
kratownicy oraz jej skratowanie są wykonane z kwadratowych przekrojó w rurowych.
Szczegó łowe obliczenia wykonano dla następujących danych liczbowych:
·
rozpiętość kratownicy l = 6m,
·
wysokość h = 0,6 m,
·
pasy kratownicy: rura 25
´
25
´
2 (A = 1,44 cm
2
, I
x
= 1,6345 cm
4
),
·
słupki i krzyż ulce: 20
´
20
´
2 (A = 1,84 cm
2
, I
x
= 0,7872 cm
4
).
Do obliczeń przyjęto dwa rodzaje obciąż enia kratownicy przedstawione na rys. 1a oraz
1b. Pierwszy rodzaj jest typowy np. dla przypadku obciąż enia śniegiem, a drugi – dla
przypadku obciąż enia wiatrem. W celu wykazania wpływu stęż enia pasa gó rnego (np. za
pomocą niepodatnych płatwi) na wartości obciąż enia krytycznego kratownicy uwzględniano
w obliczeniach zmienny rozstaw stęż eń tego pasa od wartości ró wnej rozpiętości kratownicy
do wartości ró wnej rozpiętości między sąsiednimi węzłami kratownicy. Ponadto w
obliczeniach uwzględniono dwa rodzaje połączenia skratowania z pasami kratownicy:
połączenie idealnie przegubowe oraz sztywne połączenie prętó w w węzłach.
Rys. 1. Schemat kratownicy przyjętej do analizy
Wartość bifurkacyjnego obciąż enia krytycznego rozważ anej kratownicy, i odpo-
wiadającą temu obciąż eniu wartość maksymalnej siły ściskającej w pasie kratownicy,
określano na podstawie tzw. kryterium wyznacznikowego, polegającego na poszukiwaniu
takiego obciąż enia (obciąż enia krytycznego), któ remu odpowiada zerowa wartość globalnej
macierzy sztywności ustroju. Znajomość siły ściskającej w pasie kratownicy w chwili
wyboczenia ustroju pozwala na łatwe wyznaczenie wspó łczynnika długości wyboczeniowej
m
pasa kratownicy zgodnie ze wzorem
cr
N
EI
l
p
m
=
, (1)
w któ rym:
– EI – sztywność pasa na zginanie,
– N
cr
– siła krytyczna w pasie kratownicy.
h
l
a)
b)
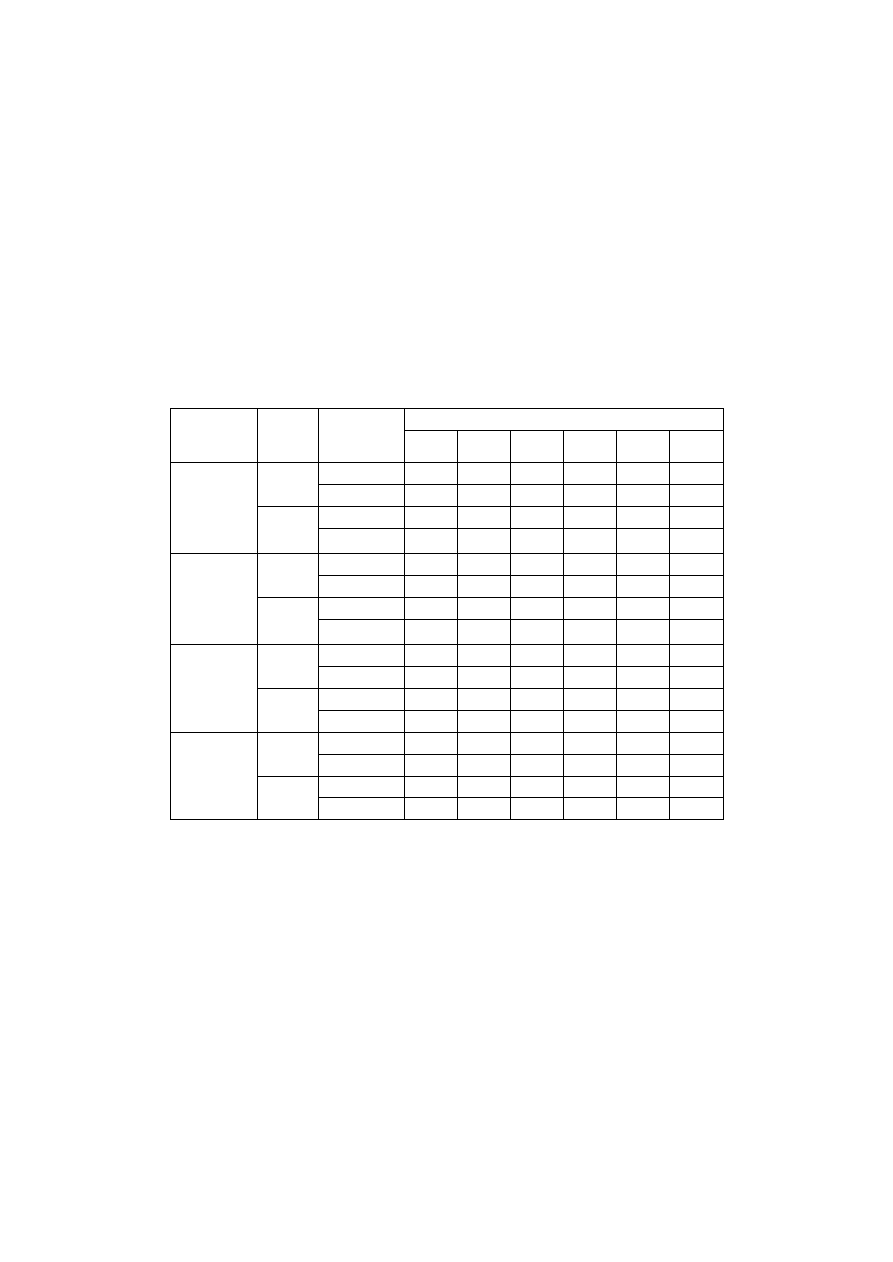
193
3. Wyniki obliczeń numerycznych
Obliczone wg wzoru (1) wartości wspó łczynnika długości wyboczeniowej
m
(l
e
=
m×
l),
z uwzględnieniem zmiennych parametró w omó wionych w p. 2, zestawiono w tablicach 1
i 2, przy czym tab. 1 obejmuje przypadek obciąż enia przedstawiony na rys. 1a (wartości
m
dotyczą pasa gó rnego), a tab. 2 – przypadek obciąż enia 1b (wartości
m
dotyczą pasa
dolnego). Założ ono przy tym, ż e wymienione rodzaje obciąż eń mogą działać zaró wno na pas
dolny, jak i na pas gó rny. W tablicach tych uwzględniono dodatkowo stosunek sztywności na
zginanie pasa gó rnego do dolnego (EI
g
/EI
d
).
Tablica 1. Wartości wspó łczynnika wyboczeniowego μ (obc. wg rys. 1a)
EI
g
/EI
d
Rodzaj
stęż eń
kratownicy
Rodzaj
obciąż e-
nia
Połączenie
skratowania
z pasami
0.1
0.33
1
3
6.5
15
przegubowe 0.617 0.637 0.660 0.856 1.003 1.163
gó rą
sztywne
0.197 0.308 0.376 0.493 0.578 0.680
przegubowe 0.454 0.512 0.555 0.680 0.746 0.793
stęż one
skrajne
węzły
kratownicy
wg rys. 1
dołem
sztywne
0.179 0.282 0.346 0.448 0.517 0.588
przegubowe 0.365 0.366 0.370 0.434 0.464 0.483
gó rą
sztywne
0.163 0.192 0.223 0.288 0.338 0.388
przegubowe 0.326 0.328 0.332 0.388 0.413 0.428
dodatkowe
stęż enie
pasa
gó rnego w
środku rozp.
dołem
sztywne
0.156 0.179 0.205 0.260 0.303 0.345
przegubowe 0.215 0.215 0.216 0.227 0.232 0.235
gó rą
sztywne
0.158 0.166 0.175 0.198 0.211 0.222
przegubowe 0.208 0.209 0.210 0.220 0.224 0.226
stęż ony co
drugi węzeł
pasa
gó rnego
dołem
sztywne
0.154 0.163 0.171 0.193 0.205 0.214
przegubowe 0.113 0.113 0.113 0.116 0.116 0.117
gó rą
sztywne
0.108 0.108 0.108 0.113 0.115 0.116
przegubowe 0.113 0.113 0.113 0.116 0.116 0.117
stęż ony
każ dy węzeł
pasa
gó rnego
dołem
sztywne
0.108 0.108 0.108 0.113 0.115 0.116
Na podstawie przedstawionych wynikó w moż na wyciągnąć kilka wnioskó w praktycznych.
1. Wartość obciąż enia krytycznego powodującego zwichrzenie kratownicy, podobnie jak
w przypadku zwichrzenia belek, w duż ym stopniu zależ y od miejsca działania obciąż enia. Na
podstawie wynikó w przedstawionych w tab. 1 moż na zauważ yć , ż e obciąż eniu gó rnego pasa
kratownicy towarzyszą większe wartości wspó łczynnika
m
(mniejsze wartości obciąż enia
krytycznego) niż w wypadku obciąż enia pasa dolnego. W przypadku np. ssania wiatru
(tab. 2) zachodzi odwrotne zjawisko; obciąż enie pasa gó rnego jest wtedy bardziej korzystne
niż obciąż enie pasa dolnego. Moż na przy tym zauważ yć dość oczywiste zjawisko, ż e –
generalnie – w wypadku przegubowego połączenie skratowania z pasami otrzymuje się
mniejszą wartość obciąż enia krytycznego kratownicy niż w wypadku sztywnego połączenia
prętó w w węzłach.
194
Tablica 2. Wartości wspó łczynnika wyboczeniowego μ (obc. wg rys. 1b)
EI
g
/EI
d
Rodzaj
stęż eń
Rodzaj
obciąż e-
nia
Połączenie
skratowania
z pasami
0.1
0.33
1
3
6.5
15
przegubowe 0.722 0.640 0.531 0.479 0.437 0.400
gó rą
sztywne
0.542 0.461 0.375 0.301 0.244 0.194
przegubowe 0.994 0.797 0.631 0.599 0.580 0.566
stęż one
skrajne
węzły
kratownicy
wg rys. 1
dołem
sztywne
0.605 0.504 0.407 0.330 0.272 0.222
przegubowe 0.680 0.444 0.343 0.339 0.337 0.337
gó rą
sztywne
0.386 0.285 0.234 0.204 0.179 0.158
przegubowe 0.993 0.768 0.560 0.553 0.551 0.551
dodatkowe
stęż enie
pasa
gó rnego w
środku rozp.
dołem
sztywne
0.485 0.358 0.268 0.223 0.191 0.167
przegubowe 0.680 0.440 0.343 0.339 0.337 0.337
gó rą
sztywne
0.386 0.253 0.195 0.170 0.157 0.147
przegubowe 0.990 0.767 0.559 0.553 0.551 0.551
stęż ony co
drugi węzeł
pasa
gó rnego
dołem
sztywne
0.484 0.358 0.268 0.223 0.191 0.166
przegubowe 0.680 0.436 0.340 0.337 0.337 0.336
gó rą
sztywne
0.381 0.244 0.189 0.166 0.152 0.145
przegubowe 0.989 0.767 0.559 0.553 0.551 0.551
stęż ony
każ dy węzeł
pasa
gó rnego
dołem
sztywne
0.479 0.355 0.265 0.221 0.189 0.165
2. Wartość obciąż enia krytycznego kratownicy w duż ym stopniu zależ y od odległości między
stęż eniami bocznymi ściskanego pasa kratownicy, przy czym długość wyboczeniowa tego
pasa jest na ogó ł znacznie mniejsza od odległości między stęż eniami. Okoliczność ta jest
wynikiem tego, ż e skratowanie wspó łpracujące z rozciąganym pasem kratownicy stanowi
pewnego rodzaju podparcie spręż yste ściskanego pasa, co w znacznym stopniu przyczynia się
do wzrostu jego siły krytycznej. Wynika stąd, ż e zalecenie normowe polegające na
utoż samianiu długości wyboczeniowej z odległością między bocznymi stęż eniami ściskanego
pasa kratownicy prowadzi na ogó ł do bezpiecznego, ale jednocześnie do mało ekono-
micznego projektowania kratownic.
3. Na wartość obciąż enia krytycznego kratownicy mają dość istotny wpływ takż e inne
parametry, takie jak np. stosunek sztywności pasó w kratownicy oraz stosunek sztywności
skratowania (w tym sztywności na skręcanie) do sztywności pasó w.
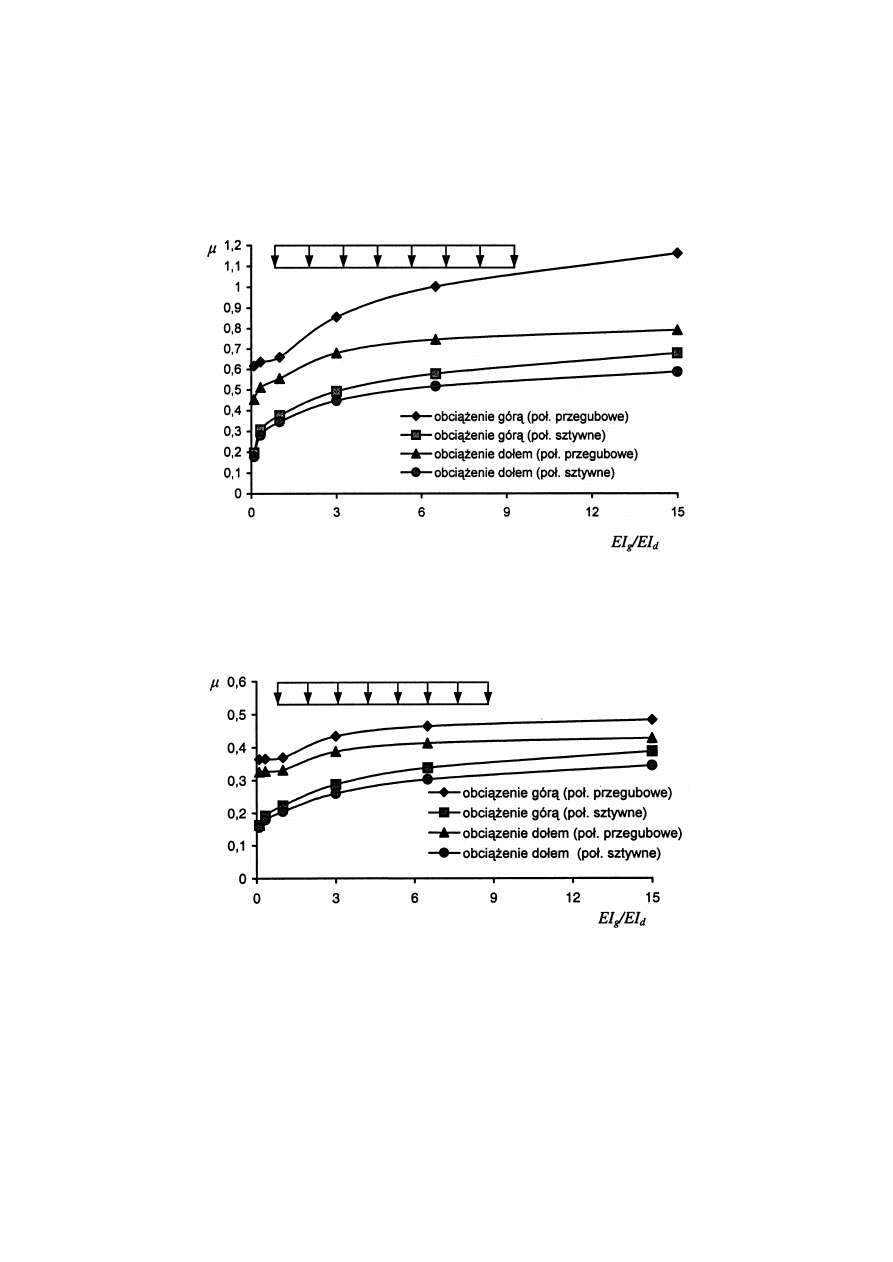
Niektó re wybrane wyniki liczbowe podane w tablicach 1 i 2 przedstawiono dodatkowo
w poglądowy sposó b na rysunkach 2
¸
5. Rysunki te przedstawiają zależ ność wspó łczynnika
wyboczeniowego
m
ściskanego (dolnego lub gó rnego) pasa kratownicy od rodzaju
obciąż enia, rodzaju połączenia skratowania z pasami, odległości między stęż eniami oraz od
stosunku sztywności na zginanie pasó w kratownicy.
195
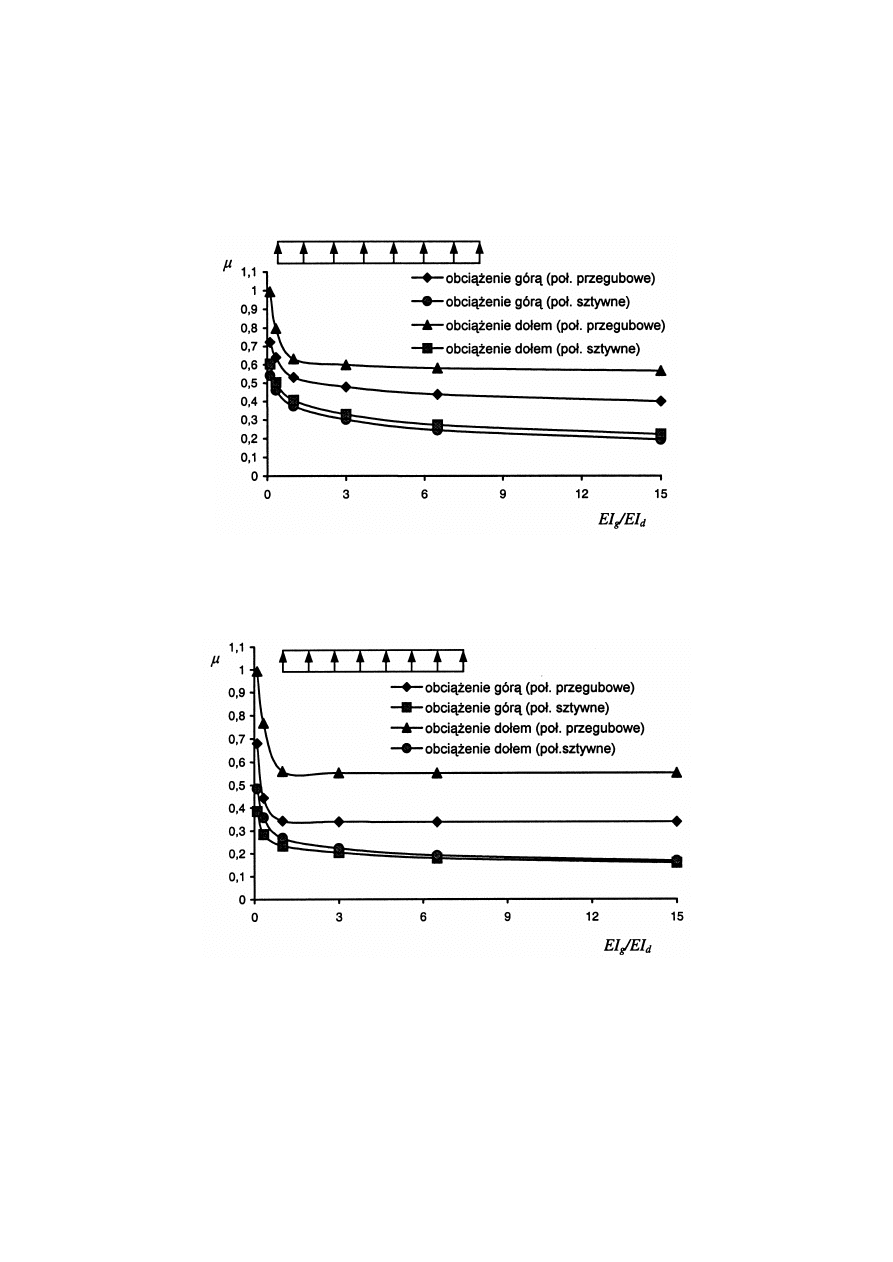
Rys. 2. Zależ ność wsp. wyboczeniowego μ gó rnego pasa kratownicy
od wybranych parametró w (stęż one są tylko skrajne węzły kratownicy)
Rys.3. Zależ ność wsp. wyboczeniowego μ gó rnego pasa kratownicy od wybranych
parametró w (stęż one są skrajne węzły kratownicy oraz środkowy węzeł pasa gó rnego)
196
Rys. 4. Zależ ność wsp. wyboczeniowego μ dolnego pasa kratownicy
od wybranych parametró w (stęż one są tylko skrajne węzły kratownicy)
Rys. 5. Zależ ność wsp. wyboczeniowego μ dolnego pasa kratownicy od wybranych
parametró w (stęż one są skrajne węzły kratownicy oraz środkowy węzeł pasa gó rnego)

197
4. Wnioski i uwagi koń cowe
W pracy przedstawiono wyniki analizy parametrycznej zwichrzenia spręż ystego pewnej
kratownicy, na podstawie któ rych moż na w racjonalny sposó b określić długość
wyboczeniową ściskanego pasa kratownicy. Wykazano, ż e uwzględnienie wspó łpracy
ściskanego pasa z pozostałymi prętami kratownicy moż e się przyczynić do bardziej
ekonomicznego projektowania dźwigaró w kratowych.
Prezentowana analiza parametryczna zwichrzenia kratownicy z konieczności uwzglę-
dnia tylko kilka wybranych, zdaniem autoró w, istotnych parametró w. Obszerniejsza analiza
obejmująca dodatkowo takie czynniki jak np. ró ż ne rodzaje kratownic i skratowań oraz
zró ż nicowanie przekrojó w elementó w byłaby bardzo uciąż liwa. Postępowanie takie przy
powszechnym obecnie dostępie do programó w komputerowych byłoby też chyba mało
celowe. Wydaje się, ż e bardziej racjonalne w praktyce projektowej jest korzystanie z od-
powiedniego programu, umoż liwiającego rozwiązanie konkretnego zadania z uwzględnie-
niem wszystkich istotnych czynnikó w mających wpływ na wartość obciąż enia krytycznego
kratownic.
Literatura
[1] PN-90/B-03200., Konstrukcje stalowe. Obliczenia statyczne i projektowanie.
[2] GOSOWSKI B., Stateczność przestrzenna stężonych podłużnie i poprzecznie
pełnościennych elementó w konstrukcji metalowych. Prace Naukowe Instytutu
Budownictwa Politechniki Wrocławskiej, Seria Monografie nr 29, Wrocław 1992.
[3] WEISS S., GIŻEJOWSKI M., Stateczność konstrukcji metalowych. Arkady, Warszawa
1991.
[4] KLÖ PPEL K., FRIEMANN H., REUSCHLING D., Beitrag zur Berechnung der
Stabilitä t beliebig gelagerter zweigurtiger Fachwerkträ ger oder Vollwandträ ger mit
Querschnittverformung gegen Ausweichen aus der Tragwerksebene. Institut fü r Statik
und Stahlbau. Technische Hochschule Darmstadt, Heft 8 (1969).
[5] MISIAK J., Obliczenia konstrukcji prętowych. PWN, Warszawa 1993.
[6] PAŁ KOWSKI Sz., KOŁ ODZIEJ J., Parametryczna analiza zwichrzenia spreż ystego
słupó w złoż onych ściskanych mimośrodowo. Inż. i Bud., nr 11/1988, 401-403.
PARAMETRIC ANALYSIS OF ELASTIC LATERAL BUCKLING
OF TRUSSES
Summary
According to Polish Standard [1] the effective length of the compression chord of a truss
is equal to the distance between bracings of this chord. This recommendation is very
approximative because it neglects an influence of the another trussmember (verticals and
diagonas) on the critical load of the truss. This paper presents the chosen results of
comprehensive numerical analysis that takes into acccount the influence of all essential
parameters on the critical load (effective length) of trusses. The presented results have
theoretical as well as practical aspects and can be applied in designing practice.
Wyszukiwarka
Podobne podstrony:
Parametryczna analiza zwichrzenia sprężystego kratownic
Macierzowa analiza sil w pretach (kratownicy plaskiej), Księgozbiór, Studia, Mechnika Doświadczalna
Komputerowa analiza parametrów jakości energii elektrycznej z wykorzystaniem programu?syLab
analiza parametryczna
1 Szczegółowa analiza parametrów sieci
Analiza parametryczna
1 ćwiczenie (Analiza jakościowa wody) PARAMETRY FIZYCZNE WODY
Analiza kinematyczna kratownic płaskich
ANALIZA PARAMERTYCZNA
Analiza wplywu parametrow proce Nieznany (2)
Analiza kinetyczna belki, ramy i kratownice płaskie
Analiza parametrów i dobieranie zasilaczy do zadanych konfiguracji sprzętowych
Analiza parametryczna!
Analiza kinematyczna kratownic płaskich
ANALIZA WYBRANYCH PARAMETRÓW POŻAROWYCH WEŁNY MINERALNEJ I UKŁADÓW WEŁNA MINERALNA TYNKI CIENKOWARST
Analiza parametryczna i optymal Nieznany (2)
Analiza wybranych biochemicznych i morfologicznych parametrów krwi u krów i cieląt noworodków
42Główne parametry ośrodka przenoszącego fale sprężyste
więcej podobnych podstron