
6.05.2008
T
WORZENIE
ORAZ
OPERACJE
NA
MACIERZACH
O
ELEMENTACH
BĘDĄCYMI
LICZBAMI
ZESPOLONYMI
W
PROGRAMIE
M
ATH
C
AD
®
Autor:
Radosław Krowiak
Spis treści
1.Macierze liczb zespolonych w programie MathCad........................................................................2
1.1.Tworzenie macierzy liczb zespolonych krok po kroku [1,2]....................................................2
1.2.Zapis moduł-faza liczb zespolonych w programie MathCad...................................................3
2.Operacje na macierzach....................................................................................................................4
3.Przykłady zastosowań oraz interakcji z systemem operacyjnym [1]...............................................5
Bibliografia:................................................................................................................................7
1
1. Macierze liczb zespolonych w programie MathCad.
1.1. Tworzenie macierzy liczb zespolonych krok po kroku [1,2].
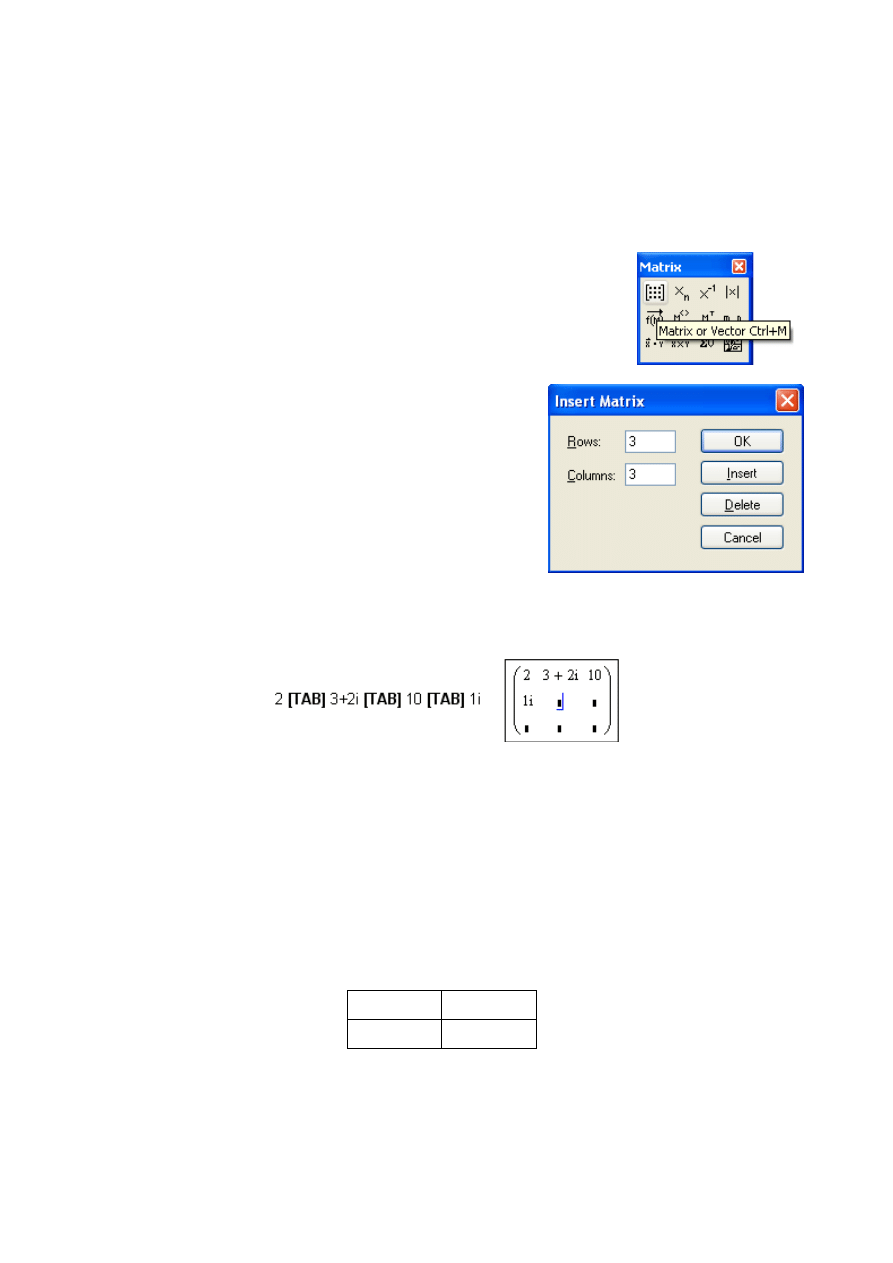
1. Wcisnąć kombinację klawiszy [CTR M] lub kliknąć lewym
klawiszem myszki na ikonkę Matrix or Vector na pasku
Macierzy, jak pokazuje zrzut ekranu obok:
2. Wpisać pożądane wymiary macierzy w okienku,
które ukaże się po przejściu kroku pierwszego, jak
na zrzucie obok:
3. Wypełnić macierz pożądanymi elementami macierz używając klawisza [TAB] do
przesuwania się między pozycjami, jak na załączonym zrzucie:
Uwaga!
Należy pamiętać o symbolicznym zapisie liczb zespolonych w programie MathCad, otóż
jednostkę urojoną i zapisujemy:
DOBRZE
BŁĄD
1i
1*i
Jest tak ponieważ w drugim przypadku MathCad odczyta i jako zupełnie nową zmienną.
2

1.2. Zapis moduł-faza liczb zespolonych w programie MathCad.
Dla przypomnienia podaję równanie Euler'a opisujące przejście między dwoma zapisami:
{
z =aib
z=r⋅e
i
=
r⋅cosisin
⇒
{
r=
a
2
b
2
=
arctg
b
a
W MathCadzie nie istnieje domyślny operator zapisu liczb zespolonych moduł-faza, jednak
bardzo łatwo takowy utworzyć:
1. Zgodnie z przyjętymi powyżej oznaczeniami tworzymy nową funkcję operującą
znakiem (sam znak kopiujemy z Extra Math Symbols w dziale quicksheets):
∢
r , :=r⋅cos i⋅sin
2. Wywołanie funkcji odbywać będzie się poprzez pasek Evaluation:
Na przykład:
3
∠
π
3
1.5
2.598i
+
=
,
lub:
1
∠
π
4
0.707
0.707i
+
=
Adnotacja:
Niekoniecznie musimy używać operatora - równie dobrze możemy jawnie nazwać
definiowaną funkcję, np. „phasor” czy też inną pasująca nam nazwę a funkcjonalność jej
się nie zmieni, co ukazuje poniższy przykład:
1
( ) phasor
π
3
0.5
0.866i
+
=
3
Kliknięcie na zaznaczony na czerwono przycisk spowoduje
pojawienie się wypełniacza, który należy wypełnić zgodnie z przyjętą
notacją funkcji:

2. Operacje na macierzach [1].
W niniejszym rozdziale przedstawię sposoby operacji na macierzach w programie
MathCad 13. Operacje przedstawiam w przejrzystej formie tabelki:
# Wywołanie Wygląd
Komentarz odnośnie wyniku lub działania
1
|
|M|
Zwraca wartość wyznacznika macierzy (dla wektora
zwraca normę, wartość bezwzględną dla skalara)
2
^−1
M^−1
Zwraca macierz będącą odwrotnością M, jeśli macierz
taka nie istnieje wysłany zostaje odpowiedni komunikat o
błędzie
3
[Ctrl 1]
M^T
Zwraca macierz transponowaną do M
NxM
(zamienia
kolumny z wierszami) o wymiarze MxN
4
+
x + y
Wynik jest:
– skalarem – sumą x oraz y, jeśli x i y to skalary
– macierzą – jeśli X to macierz a y – skalar, każdy element
wynikowej macierzy jest sumą y oraz odpowiedniego el.
X
– macierzą – sumą X oraz Y, jeśli x i y to macierze o tych
samych wymiarach
5
–
x – y
Patrz komentarz wyżej
6
[Ctrl 8]
x × y
Wynikiem jest iloczyn wektorowy macierzy X oraz Y
7
*
x * y
Wynikiem jest iloczyn skalarny macierzy X oraz Y
8
[Ctrl /]
x / y
Wynikiem jest iloczyn skalarny macierzy: x * y^-1
9
^
y ^ x
Dla macierzy wynik zależy od x:
– x = 0, zwraca macierz jednostkowa o wymiarach takich
samych co Y
– x = –1, zwraca odwrotność macierzy Y
– x>0, wynikiem jest macierz Y pomnożona przez siebie x
razy
– x<0 (bez –1), wynikiem jest odwrotność macierzy Y
pomnożona przez siebie x razy
10
eigenvals
eigenvals(M)
Zwraca wektor, którego elementami są posortowane
wartości własne macierzy M
11
eigenvec
eigenvec(M,
z)
Zwraca pojedynczy, znormalizowany wektor, skojarzony z
wartością własną z macierzy M
12
[
M[m,n
Zwraca element macierzy będący przecięciem m-tego
wiersza oraz n-tej kolumny
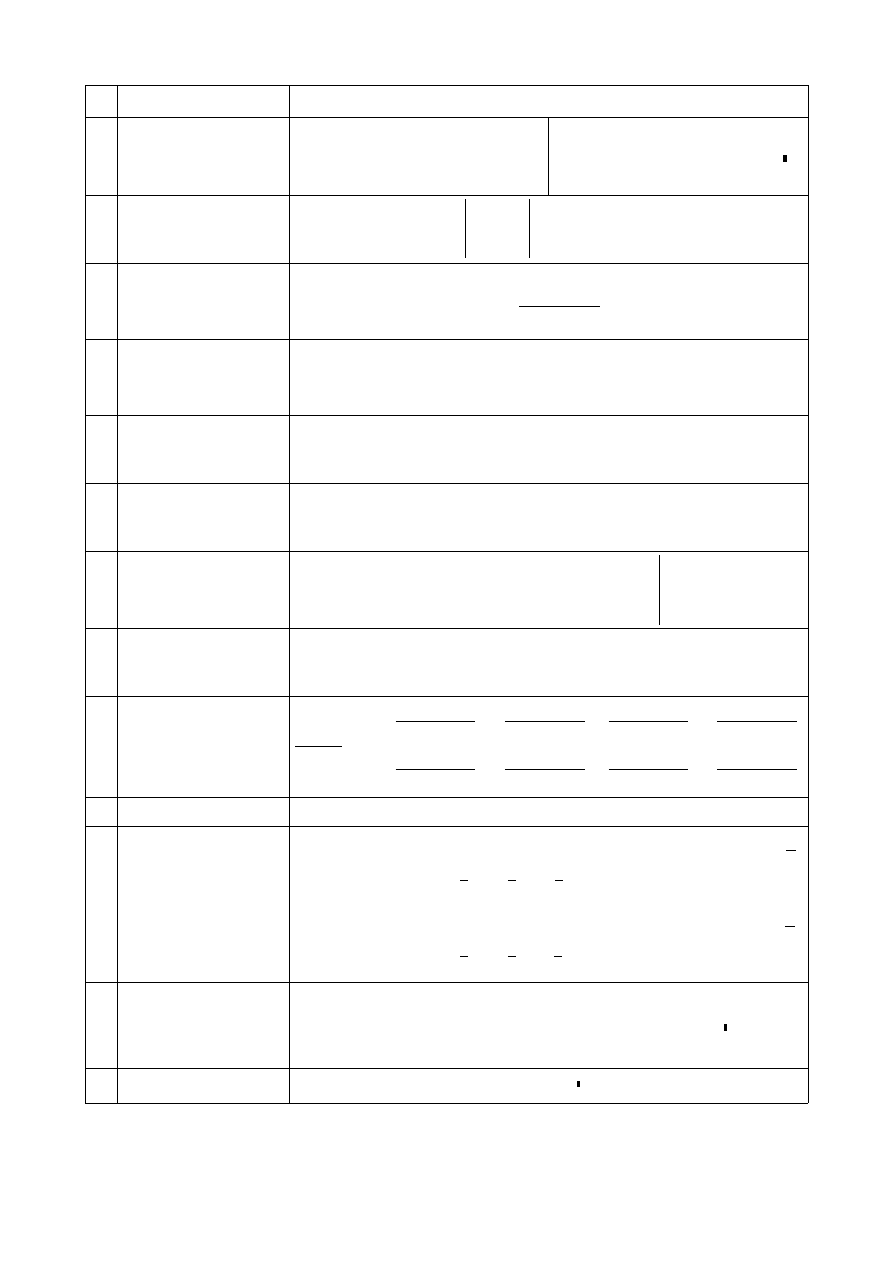
Na następnej stronie zamieszczam przykłady operowania na macierzach o
współczynnikach symbolicznych. Dla uproszczenia ilustracji zakładam iż wymiary
macierzy wynoszą 2x2. Operacje nie obsługiwane przez MathCada symbolicznie są
zilustrowane przykładami numerycznymi.
4
#
Wygląd
Przykład operacji:
0
Założenia:
M
2
1i
+
100
54
1i
2
7
2
3
1
:=
eigenvals M
( )
16.732
3.589i
+
8.038
−
7.458i
−
3.694
−
4.869i
+
=
1
|M|
a
1
a
3
a
2
a
4
a
1
a
4
⋅
a
2
a
3
⋅
−
→
2
M^−1
a
1
a
3
a
2
a
4
1
−
1
a
1
a
4
⋅
a
2
a
3
⋅
−
a
4
a
3
−
a
2
−
a
1
⋅
→
3
M^T
a
1
a
3
a
2
a
4
T
a
1
a
2
a
3
a
4
→
4
x + y
a
1
a
3
a
2
a
4
b
1
b
3
b
2
b
4
+
a
1
b
1
+
a
3
b
3
+
a
2
b
2
+
a
4
b
4
+
→
5
x – y
a
1
a
3
a
2
a
4
b
1
b
3
b
2
b
4
−
a
1
b
1
−
a
3
b
3
−
a
2
b
2
−
a
4
b
4
−
→
6
x × y
13
3
−
50
33
6
−
2i
+
82
×
54
100 1i
⋅
−
584
21
26 1i
⋅
+
→
7
x * y
a
1
a
3
a
2
a
4
b
1
b
3
b
2
b
4
⋅
a
1
b
1
⋅
a
2
b
3
⋅
+
a
3
b
1
⋅
a
4
b
3
⋅
+
a
1
b
2
⋅
a
2
b
4
⋅
+
a
3
b
2
⋅
a
4
b
4
⋅
+
→
8
x / y
a
1
a
3
a
2
a
4
b
1
b
3
b
2
b
4
a
1
−
( )
b
4
b
1
−
( )
b
4
⋅
b
2
b
3
⋅
+
⋅
a
2
b
3
b
1
−
( )
b
4
⋅
b
2
b
3
⋅
+
⋅
+
a
3
−
( )
b
4
b
1
−
( )
b
4
⋅
b
2
b
3
⋅
+
⋅
a
4
b
3
b
1
−
( )
b
4
⋅
b
2
b
3
⋅
+
⋅
+
a
1
b
2
b
1
−
( )
b
4
⋅
b
2
b
3
⋅
+
⋅
a
2
b
1
b
1
−
( )
b
4
⋅
b
2
b
3
⋅
+
⋅
−
a
3
b
2
b
1
−
( )
b
4
⋅
b
2
b
3
⋅
+
⋅
a
4
b
1
b
1
−
( )
b
4
⋅
b
2
b
3
⋅
+
⋅
−
→
9
y ^ x
10
eigenvals(M)
eigenvals
b
1
b
3
b
2
b
4
1
2
b
1
⋅
1
2
b
4
⋅
+
1
2
b
1
( )
2
2 b
1
b
4
⋅
⋅
−
b
4
( )
2
+
4 b
2
b
3
⋅
⋅
+
1
2
⋅
+
1
2
b
1
⋅
1
2
b
4
⋅
1
2
b
1
( )
2
2 b
1
b
4
⋅
⋅
−
b
4
( )
2
+
4 b
2
b
3
⋅
⋅
+
1
2
⋅
−
+
→
11
eigenvec(M, z)
eigenvec M 3.694
−
4.869i
+
,
(
)
0.044
0.056i
−
0.771
−
4.794i
10
4
−
×
−
0.018
−
0.632i
+
=
12
M[m,n
M
1 2
,
3
=
5
3. Przykłady zastosowań oraz interakcji z systemem
operacyjnym [1].
Na przykładzie interakcji z programem MC Excel ukazać można ogrom użyteczności
programu MathCad w pracy z macierzami i seriami danych:
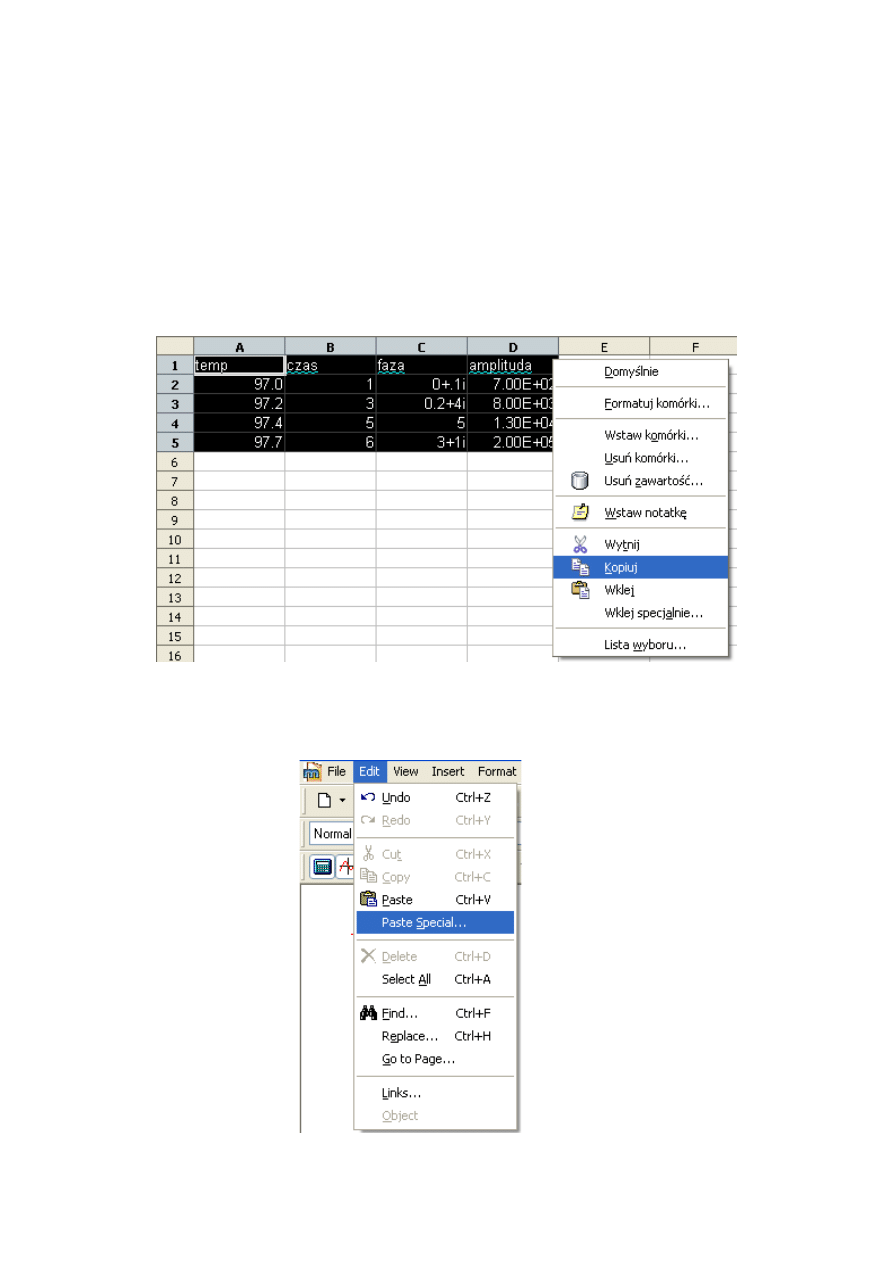
1. Otworzyć pożądany plik *.xls i skopiować interesujące nas kolumny danych, jak
pokazuje zrzut ekranu:
2. W programie MathCad wybrać opcję Paste Special z menu Edit:
6
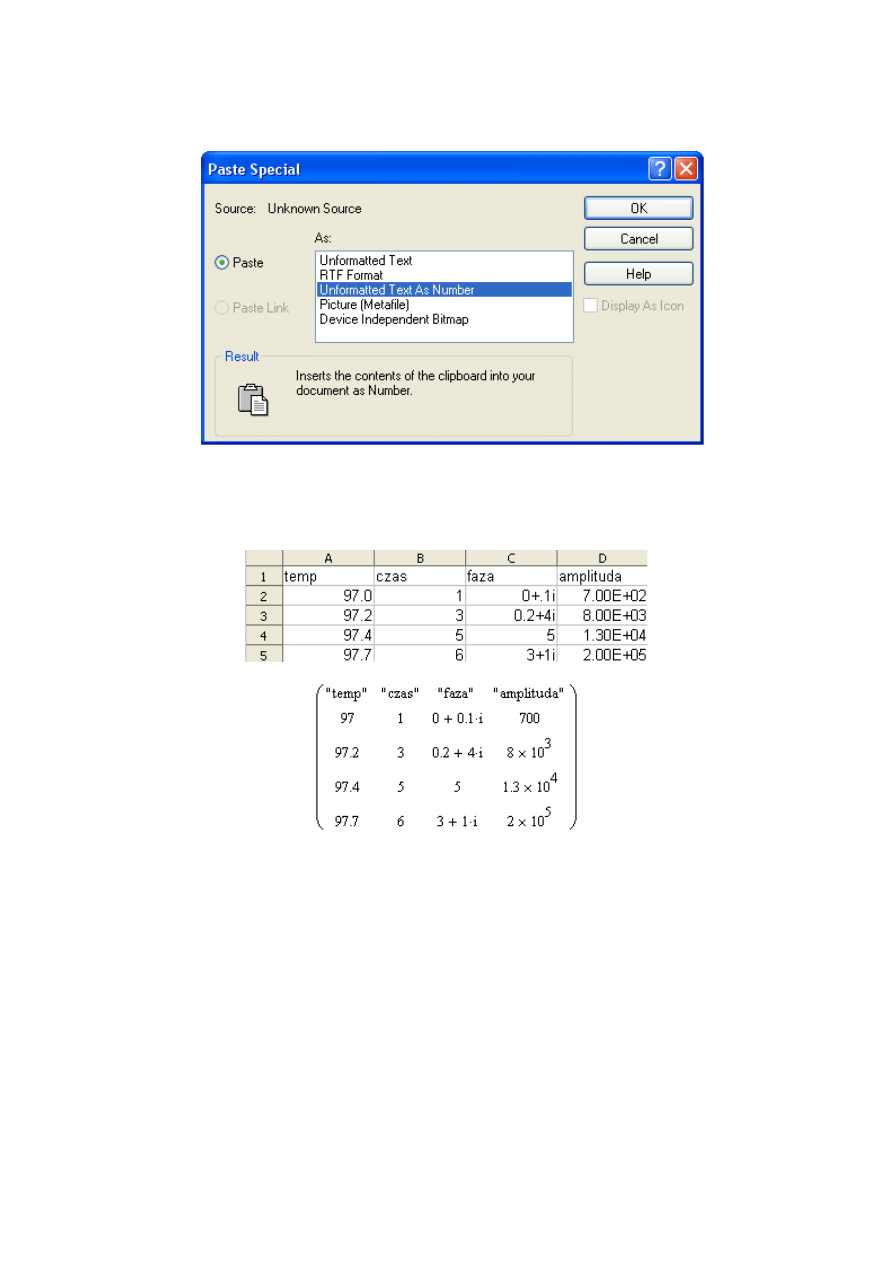
3. Wybrać Unformatted Text As Number i nacisnąć OK
4. Z wybranego pliku przykładowego otrzymać można macierz:
Komentarz:
Jest to bardzo przydatne rozwiązanie jeśli zauważymy iż kolumn i wierszy może być
bardzo wiele – tutaj w jednym kroku otrzymujemy interesujące dane, na których już można
operować dzięki adnotacji zawartej w przekopiowanej treści.
7

Bibliografia:
[1] MathCad 12 quicksheets -> Vectors and Matrices
[2] MathCad 12 quicksheets -> Extra Math Symbols
8
Document Outline
- 1.Macierze liczb zespolonych w programie MathCad.
- 2.Operacje na macierzach [1].
- 3.Przykłady zastosowań oraz interakcji z systemem operacyjnym [1].
Wyszukiwarka
Podobne podstrony:
COMO APRENDER INGLES TUTORIAL COMPLETO (1)
Joomla and Mambo template tutorial The Complete Guide to Joomla Templates a
MathCAD Tutorial PL
lecture3 complexity introduction
L 3 Complex functions and Polynomials
Mathcad przepona kotwiczna projekt 2
Mathcadtymczasowy
Mathcad fundamenty ramowe
bugzilla tutorial[1]
freeRadius AD tutorial
Mathcad Projekt metal
Alignmaster tutorial by PAV1007 Nieznany
free sap tutorial on goods reciept
Mathcad TW kolos 2
Mathcad Sprzeglo id 287200
ms excel tutorial 2013
Mathcad filarek wewnetrzny 1 kondygnacj
Joomla Template Tutorial
więcej podobnych podstron