P. De Visschere

1

Patrick De Visschere

University of Gent

Department of Electronics and Information Systems,

St. Pietersnieuwstraat 41, B-9000 Gent, Belgium.

[e-mail]

Abstract

A model is developed for the electrostatic loudspeaker, which incorporates

simultaneously the mechanical, the acoustical and the electrical behaviour

of the diaphragm. The non-linear model can be solved fairly accurate in

steady-state and is used for calculating the frequency- and level-dependent

sensitivity and distortion for an infinite strip push-pull electrostatic

loudspeaker. The results are compared with previously published and new

improved small-signal approximations.

1 Introduction.

The push-pull electrostatic loudspeaker (pp-ESLS) is known as a high-

quality loudspeaker. The basic characteristics of this transducer have been

studied by Hunt[1]. In this monograph, which was first published in 1954, a

one-dimensional model for the pp-ESLS (as well as for the single-sided

ESLS) is worked out. To handle the inherent non-linear behaviour of the

ESLS Hunt performed a harmonic analysis and by neglecting higher order

harmonics was able to calculate these harmonics consecutively. The radia-

tion loading was incorporated by means of a mechanical impedance.

Although probably all relevant properties could be addressed in this way a

more accurate and more general model for the ESLS should at least be two-

dimensional in order to describe the vibration of the diaphragm properly.

Such an analysis must cope with two complications. Since the vibration of

the diaphragm is to a large extent determined by the air-reaction, the me-

chanical problem of the vibrating diaphragm must be solved together with

the radiation equation. This was done by Streng[2,3] for a circular mem-

brane. In a subsequent paper the same author addressed the second compli-

cation[4], namely the dependence of the diaphragm-charge distribution on

the diaphragm-vibration. This effect is due to the finite diaphragm

resistivity and is responsible for a level-dependent sensitivity and for the

harmonic distortion. The analysis given was restricted to small-signals

however and focused mainly on the sensitivity question.

Accurate model for the push-pull electrostatic loudspeaker.

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

2

In the present paper we develop a global two-dimensional model for a

pp-ESLS, in which the three coupled sub-models (mechanical, acoustical

and electrical) are solved together. Our current analysis is restricted to an

idealised pp-ESLS, which is described in section 2, together with the basic

equations for the three sub-models. In section 3 the perfect pp-ESLS is

considered. In this perfect pp-ESLS the diaphragm charge is supposed to be

fixed and consequently the transducer is linear. Solving the coupled

mechanical/acoustical models enables us to calculate the response

characteristic. The solution of this (mathematical) problem will be published

elsewhere[6]. In section 4 a small signal analysis is given for a more

realistic device, with a finite diaphragm resistivity, and in section 5 the

harmonic analysis applied originally by Hunt in his one-dimensional model,

is given for our two-dimensional model. Some concluding remarks are

given in the last section. Although most of the material presented is equally

valid for a circular diaphragm, numerical results will be shown for an

infinite strip only.

2 Basic equations.

2.1 Physical model.

The idealised physical model for the pp-ESLS is shown in Fig. 1. A

stretched diaphragm, with tension T [kg/s

2

] and surface density

ρ

[kg/m

2

],

is placed exactly in the middle between two static electrodes. The wave ve-
locity in the diaphragm is denoted by

c =

T

ρ

T

ρ

. The static electrodes, which

are assumed to be electrically uniform but acoustically transparent, are a

distance 2

η

r

apart and are connected to signal voltages v

a

and -v

a

. The

diaphragm is fixed around its perimeter, has a surface conductivity

σ

[

Ω

-1

]

and carries a local surface charge density q [C/m

2

] whereas its local poten-

tial is denoted by v. By convention we denote the side where the signal volt-

age v

a

is applied as the frontside.

2.2 Electrical model.

Since the maximum deflection of the diaphragm

±

η

r

is much smaller than

the lateral dimensions of the diaphragm a quasi one-dimensional approach is

justified for calculating the electric field distribution. It follows that the

electric field is directed everywhere approximately normal to the static

electrodes and its strength in the front and at the back of the diaphragm are

simply given by :

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

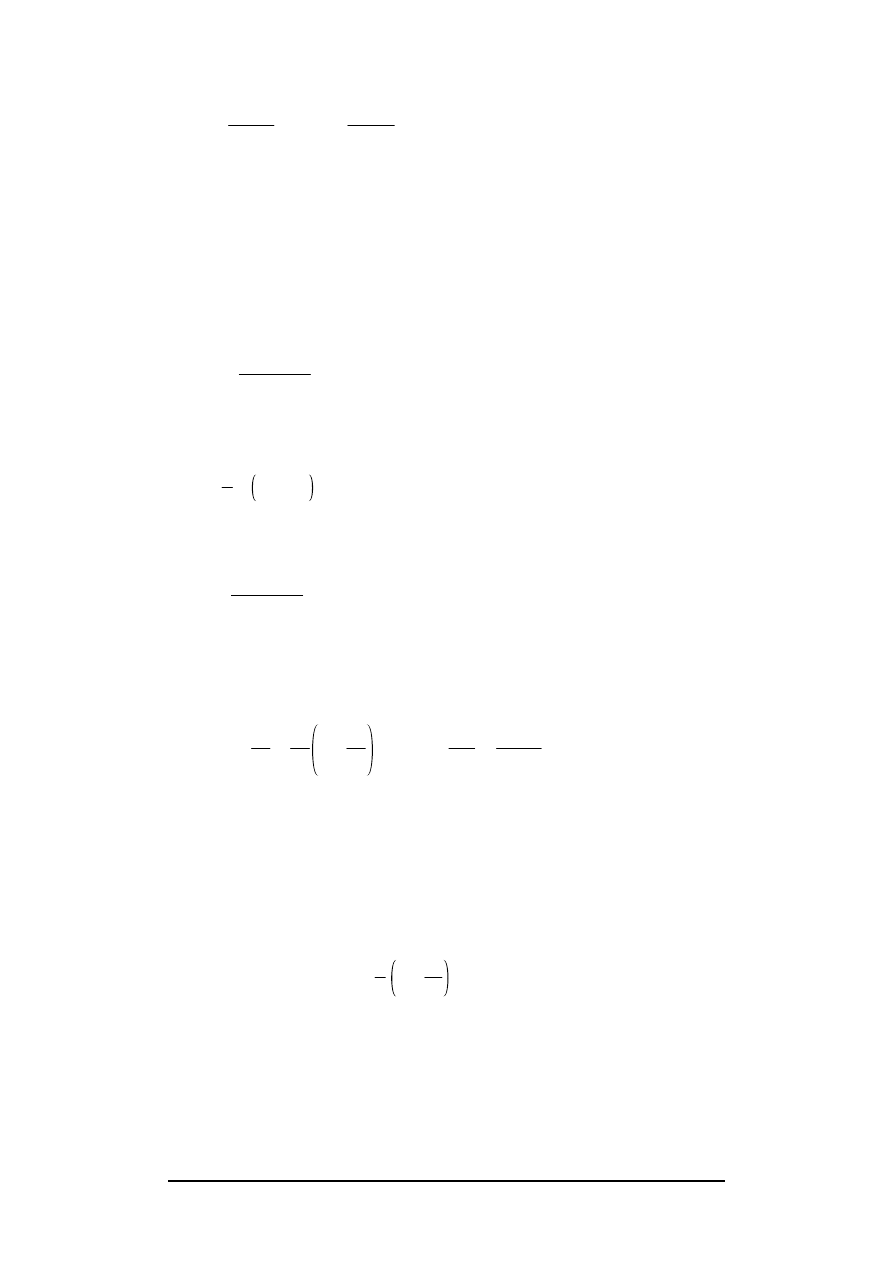
P. De Visschere

3

E

f

=

v – v

a

η

r

–

η

;

E

b

= –

v + v

a

η

r

+

η

,

(1)

where

η

is the local deflection of the diaphragm. The discontinuity of the

electric field at the diaphragm is due to the surface charge q :

q =

ε

(E

f

– E

b

) ,

(2)

where

ε

= 8.85 10

-12

F/m is the dielectric permittivity of air. Using (1) we

find q in terms of the local deflection and the local potential :

q = 2

ε

v

η

r

– v

a

η

η

r

2

–

η

2

.

(3)

The electric force (towards the frontside) on the diaphragm is given by :

f

e

= 1

2

q. E

f

+ E

b

.

(4)

Again using (1) we find :

f

e

= q

v

η

– v

a

η

r

η

r

2

–

η

2

(5).

A more useful expression is found by eliminating the potential in (1) and (4)

using (3) :

E

f,b

= –

v

a

η

r

±

q

2

ε

1

±

η

η

r

,

f

e

= –

qv

a

η

r

+

q

2

η

2

ε η

r

,

(6)

where the +signs holds for the frontside and the -signs for the backside.

These expressions have a straightforward interpretation. The first contribu-

tion to the fields and the force are due to the homogeneous field set up be-

tween the static electrodes by the signal voltages v

a

and -v

a

. The remaining

contributions are due to the image-charges induced by q in the static elec-

trodes. These induced charges are easily found using Ramo’s theorem [5]

and are given by :

q

f ,b

= –

q
2

1

± η

η

r

. With this the contributions to the

electric fields and to the electric force are easily found. The image force in

(6) corresponds with a negative stiffness for the diaphragm.

Due to the surface conductivity

σ

of the diaphragm, potential differences

will cause surface charge density variations according to :

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

4

σ ∇

2

v =

∂

q

∂

t

.

(7)

This equation must be completed with a suitable boundary condition, which,

in its simplest form, becomes v = -V

o

along the perimeter of the diaphragm,

this being the bias voltage A more complicated boundary condition is

needed when the bias voltage -V

o

is applied through a series resistor R

o

.

2.3 Mechanical model.

The deflection of the diaphragm

η

satisfies the classical equation for a

stretched diaphragm :

ρ

∂

2

η

∂

t

2

= T

∇

2

η

– R

∂η

∂

t

+ f

e

– 2 p ,

(8)

where p is the acoustical pressure at the frontside and where the term
involving R [kg/m

2

/s = Rayl] is an optional damping term. Around the

perimeter of the diaphragm the boundary condition

η

= 0 applies.

2.4 Acoustical model.

The pressure, which is anti-symmetrical with respect to the plane of the di-

aphragm, satisfies the wave equation :

∇

2

p – 1

c

o

2

∂

2

p

∂

t

2

= 0 ,

(9)

with boundary condition on the diaphragm :

ρ

0

∂

2

η

∂

t

2

= –

∂

p

∂

z

,

(10)

where z is the direction normal to the diaphragm (see Fig.1). In these equa-
tions

ρ

o

is the density of air (1.18 kg/m

3

) and c

0

is the wave velocity in air

(343 m/s).

3 The perfect pp-ESLS.

Ideally the conductivity

σ

of the diaphragm should be zero and the charge

density should be fixed (and usually uniform)

q = Q

0

= –

2

ε

V

0

η

r

. In that

case, the electric force (see eq. (6)) becomes linear in the deflection and the

applied voltage :

f

e

= –

Q

0

η

r

v

a

+

Q

0

2

2

εη

r

η

.

(11)

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

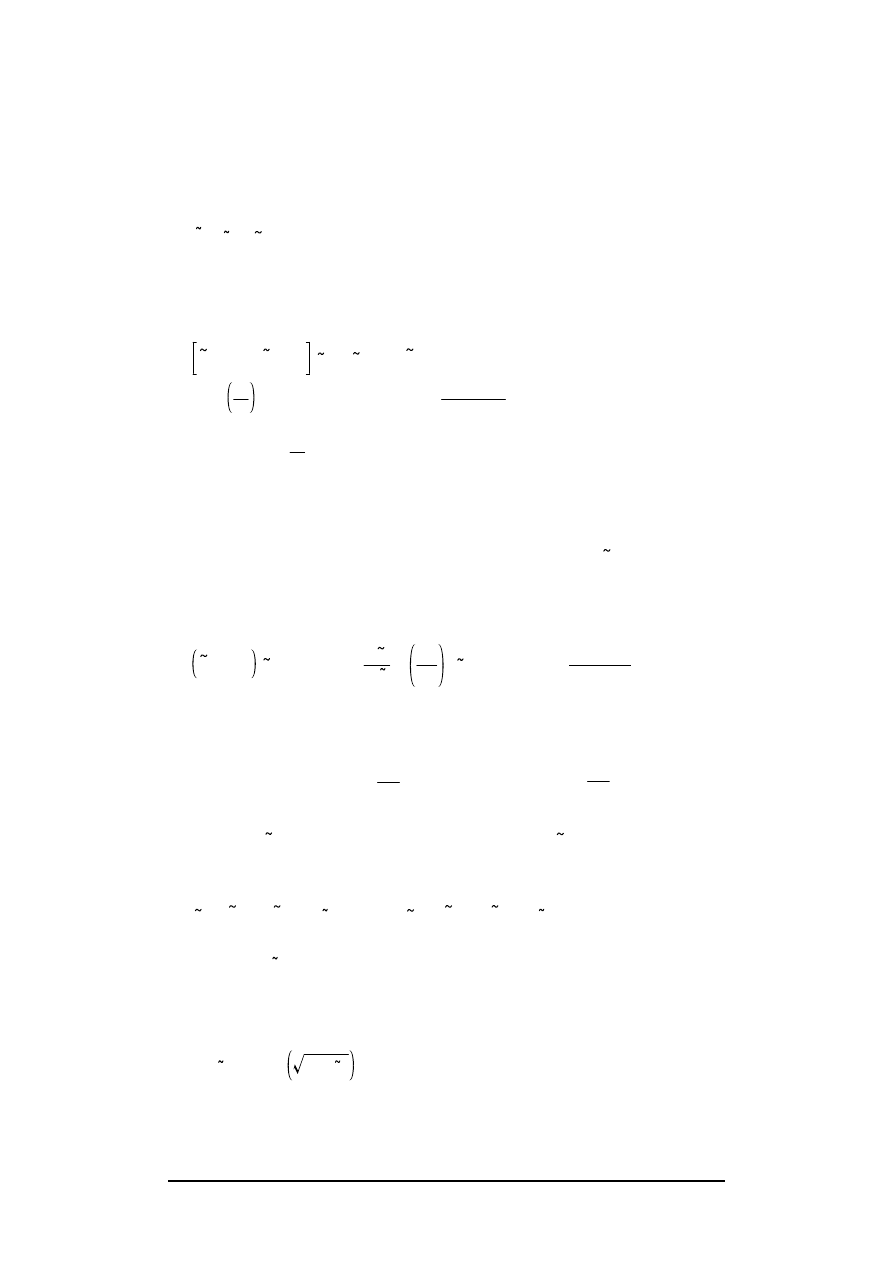
P. De Visschere

5

In the remainder of the paper we will use normalised quantities. To avoid

any ambiguity however normalised quantities will be indicated with a tilde

(~). The reference quantities used for normalising are shown in Table 1. In

normalised form eq. (11) then reads as :

f

e

= v

a

+

η

.

(12)

For a sinusoidal signal

v

a

= V

a

cos (

ω

t) , the mechanical equation can now

be written as :

∇

2

– j

β

R +

β

i

2

η

1

= p

1

–

β

e

2

V

a

β

i

2

=

c

0

c

2

β

2

+

β

e

2

,

β

e

2

=

2

ε

V

0

2

a

2

η

r

3

T

,

(13)

where

β

= k a =

ω

c

0

a

and a represents a typical dimension, the radius for a

circular diaphragm and half the width for an infinite strip. Except for the

signal voltage the complex representations are denoted by an index 1.

This equation must be solved with the boundary condition

η

1

= 0

along the

perimeter of the diaphragm, and together with the wave equation (9) and its

boundary condition (10), which become :

∇

2

+

β

2

p

1

= 0,

∂

p

1

∂

z

=

β

β

m

2

η

1

,

β

m

2

=

T

2 a

ρ

0

c

0

2

.

(14)

A method for solving this problem, is published elsewhere [6]. We just want

to mention that we do not assume, as was done in [2], that the tangential

derivative of the pressure (

∂

p

∂

x

for an infinite strip or

∂

p

∂

r

for a circular

diaphragm) vanishes along the perimeter. Furthermore the pressure on the
diaphragm

p

1

and the diaphragm deflection

η

1

are obtained as

developments into suitable base-functions or modes :

p

1

= V

a

P

1,k

ψ

k

(x)

Σ

k = 0

∞

η

1

= V

a

H

1,k

φ

k

(x)

Σ

k = 0

∞

,

(15)

where the

φ

k

(x) are the eigenfunctions of the diaphragm. In what follows

numerical results will only be presented for the

∞

strip and the base-func-

tions are then given by :

ψ

k

(x) = T

2 k + 1

1 – x

2

,

(16)

where T

n

(x) are the Chebychev polynomials, and by :

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

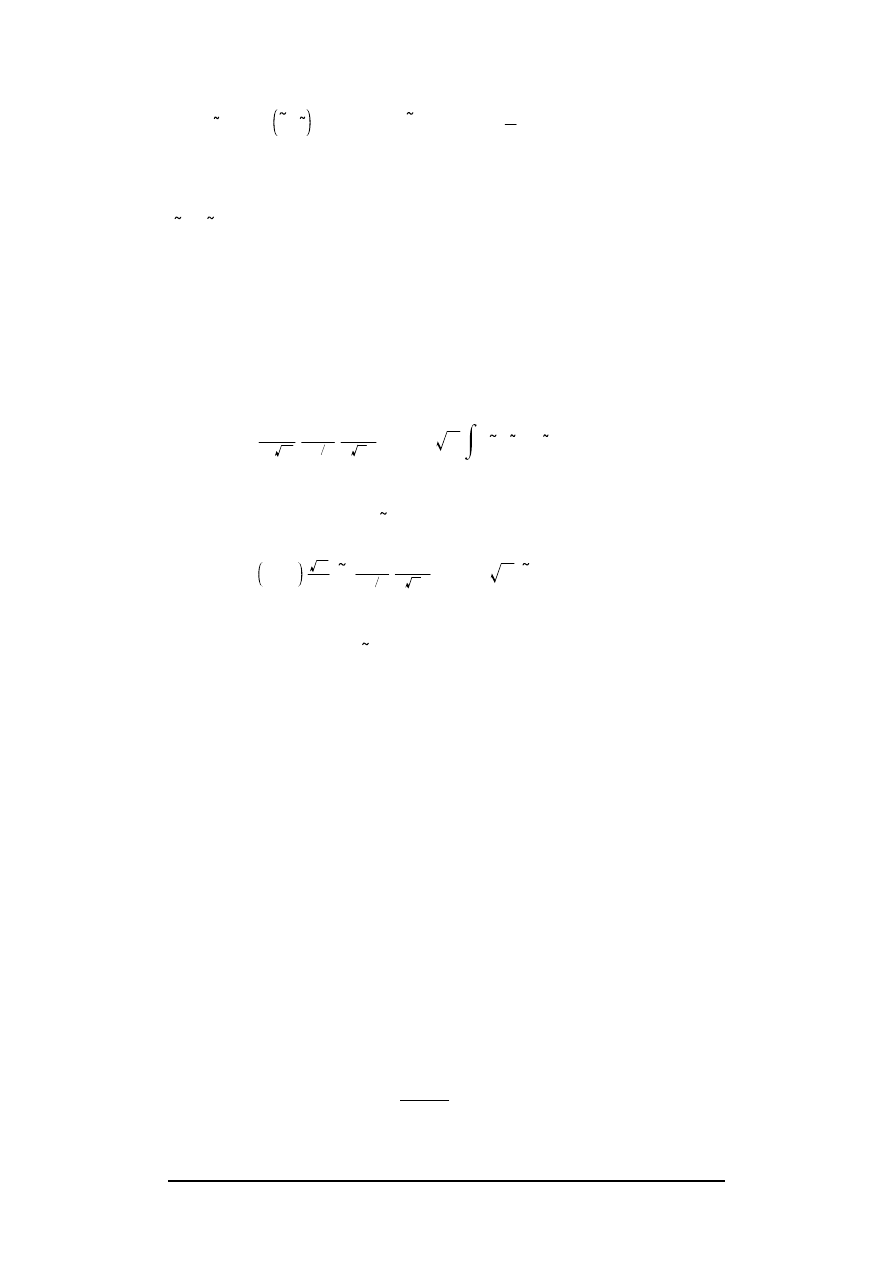
P. De Visschere

6

φ

k

(x) = cos

λ

k

x

λ

k

= (2 k + 1)

π

2

.

(17)

In addition the numerical calculations are restricted to the parameter values

shown in Table 2. The absolute values of the first three coefficients

P

1,k

, H

1,k

, occurring in (15), are shown in fig.2 as a function of the

normalised frequency

β

. The damping factor R has been chosen somewhat

arbitrarily and does not correspond with critical damping of the lowest

resonance. It can be shown that the far-field pressure p

1

(r,

θ

) is determined

by the mean pressure on the diaphragm (

θ

being the angle with the vertical

on the diaphragm and r the distance from the central axis of the

diaphragm) :

p

1

(r,

θ

) =

1 + j

2

π

η

r

T

a

3

2

3

2

e

– j k r

r

cos (

θ

)

β

p

1

(x) d x

0

1

.

(18)

Using (15) and (16) it can then be shown that the mean pressure depends on
the first pressure coefficient

P

1,0

only, namely :

p

1

(r,

θ

) = 1 + j

π

8

V

a

η

r

T

a

3

2

3

2

e

– j k r

r

cos (

θ

)

β

P

1,0

.

(19)

Apart from the

β

1/2

factor in (19) the frequency response of the perfect

pp-ESLS is thus given by

P

1,0

.

In a more realistic pp-ESLS the diaphragm will possess some conductivity

σ

≠

0, and then q will not longer be remain fixed but will instead adapt to

the vibration of the diaphragm. Mathematically this means that, in addition

to the previous equations, eq.(7) and its boundary condition, and relation (3)

must now be taken into account to. The main difficulty arises from the non-

linearity of relation (3) and (6) and a general solution seems unattainable.

However there are two possible simplifications we can make. In section 5

we again consider a sinusoidal regime and perform a harmonic development

of the quantities involved, as has been done by Hunt[1] for a simple one-

dimensional model. Since this is a steady-state model all information

regarding the temporal behaviour of the system is lost however. Therefore

we consider in section 4 a small-signal analysis, where that information is

retained.

First we consider the static stability of the diaphragm assuming a fixed di-

aphragm charge density

Q

0

= –

2

ε

0

V

0

η

r

. It is easily verified with eq. (8) and

(11) that the equilibrium position (v

a

= 0, p = 0,

η

= 0) is stable only if :

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

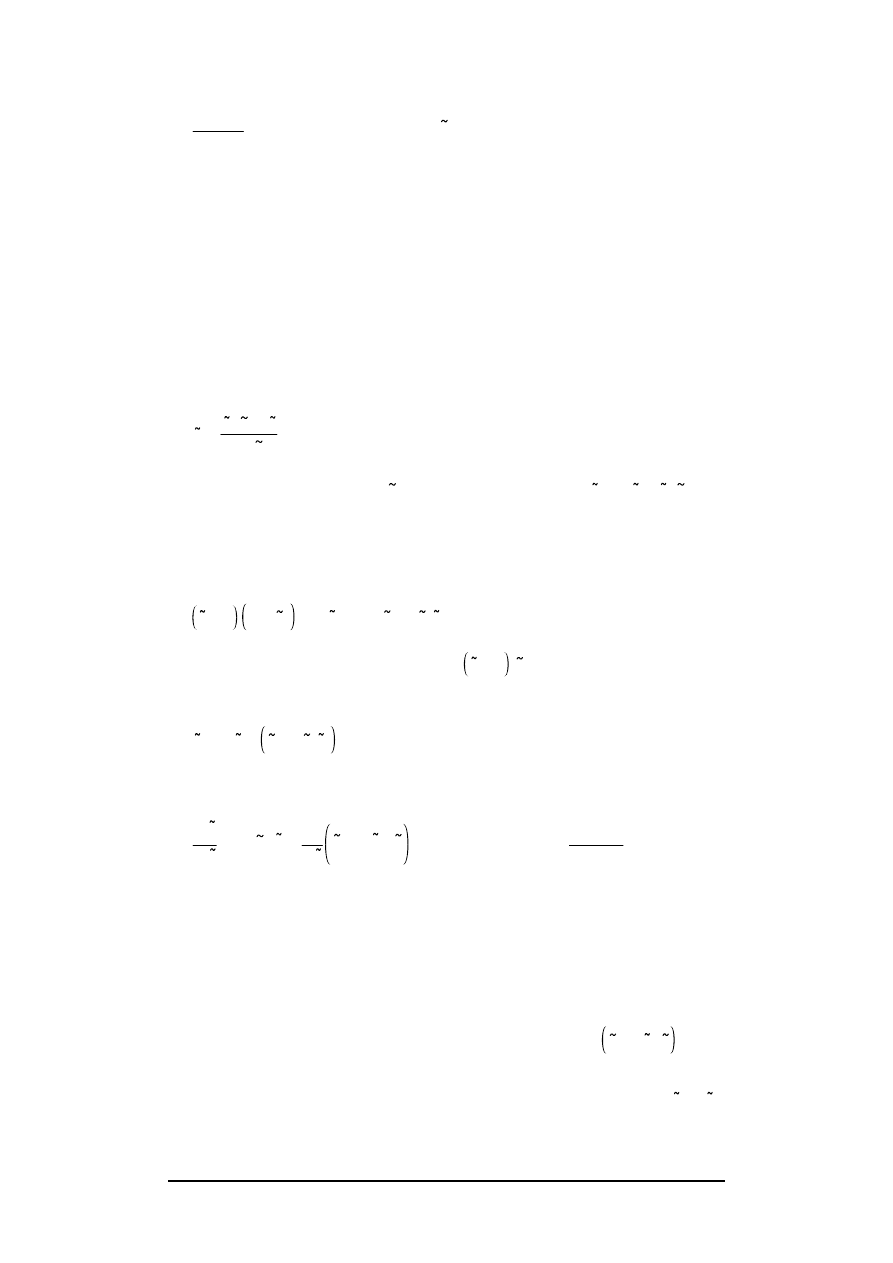
P. De Visschere

7

2

ε

0

V

0

2

η

r

3

< T

λ

min

2

, or

β

e

<

λ

min

,

(20)

where

λ

min

is the smallest diaphragm-eigenvalue. This condition ensures

that for all eigenmodes the net stiffness is positive. For the infinite strip this

means

β

e

<

π

/2.

4 Small-Signal analysis.

The problems associated with the non-linearity of eq.(3) can be avoided by

considering only small excursions of the diaphragm[4]. Using normalised

quantities eq.(3) is rewritten as :

q =

v

a

η

– v

1 –

η

2

.

(21)

It is tempting to neglect the

η

2

term and then we find

v = – q + v

a

η

[4].

Note however that the last term in this expression is also of the 2nd order

and therefore this is not a consistent approximation. If we introduce the

charge variation, then eq.(21) can be written as :

q – 1 1 –

η

2

= – v – 1 +

η

2

+

η

v

a

,

(22)

and now the third order term on the left

q – 1

η

2

can be neglected with re-

spect to all other terms, leading to :

q = – v +

η

2

+

η

v

a

.

(23)

Substituting this in eq. (7) leads to :

∂

v

∂

t

–

β

σ

∇

2

v =

∂

∂

t

η

2

+ va

η

β

σ

=

σ η

r

4

ε

a c

0

.

(24)

This equation enables us to calculate the modified charge distribution if the

deflection is known. Neglecting second order terms in (6) leads to the ideal

eq. (12) and therefore, in eq. (24), we can use the ideal deflection, calculated

in the previous section. Equation (24) can be solved for an arbitrary signal.

However in order to compare with the results of the following section we

consider a sinusoidal excitation. The driving term in (24),

η

2

+ v

a

η

, then

contains a DC-term and a 2nd harmonic term and gives rise to correspond-
ing terms for the potential and the charge density. The DC-parts

∆

v

0

,

∆

q

0

are found from :

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

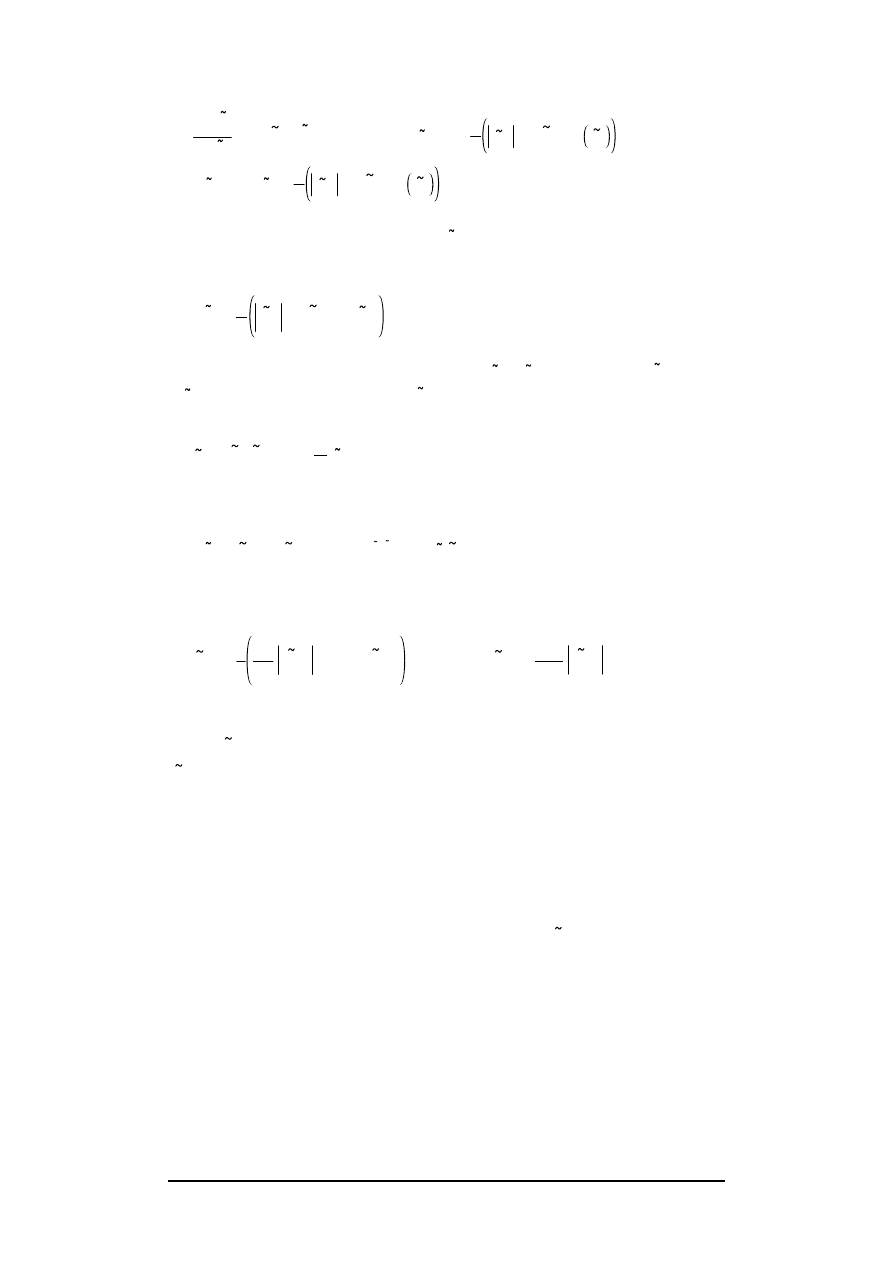
P. De Visschere

8

∂ ∆

v

0

∂

t

–

β

σ

∇

2

∆

v

0

= 0,

∆

v

0

(0) = 1

2

η

1

2

+ V

a

Re

η

1

∆

q

0

= –

∆

v

0

+ 1

2

η

1

2

+ V

a

Re

η

1

.

(25)

Eventually the potential variation

∆

v

0

will become zero again and the

charge density variation will become equal to :

∆

q

0

=

1
2

η

1

2

+ V

a

Re (

η

1

) .

(26)

In order to find the time dependence of

∆

v

0

,

∆

q

0

, we expand

∆

v

0

(0)

(and

∆

v

0

) with the eigenfunctions

φ

k

(x) . For low frequencies the deflection is

dominated by the lowest eigen-function :

η

1

= V

a

H

1,0

cos (

π

2

x)

(27)

and we then find the following solution :

∆

q

0

= V

a

2

Q

0,k

(1 – e

–

β

σ

λ

k

2

t

) cos (

λ

k

x)

Σ

k = 0

∞

,

(28)

where the first two coefficients are given by :

Q

0,0

=

1
2

8

3

π

H

1,0

2

+ Re (H

1,0

)

Q

0,1

=

8

30

π

H

1,0

2

,

(29)

These are shown in Fig.3 in full lines (for comparison the dashed curve
shows

Q

0,0

when the quadratic term in the deflection is neglected). Note that

Q

0,0

vanishes for

β ≈

0.1 . For this particular frequency the 2nd mode domi-

nates the charge variation. The charge density variations build up with a

typical time constant for each mode. For the infinite strip the eigenvalues

are given by (17), and with

σ

-1

= 1000 M

Ω

, the lowest time-constant equals

31.1 ms, corresponding with a cut-off frequency of 5.1 Hz. The cut-off fre-

quencies for the higher modes are then 46 Hz, 128 Hz, 250 Hz, …. For a

circular diaphragm (radius a) they are given by

λ

n

= j

0 n

(n = 1, 2, …),

where j

0 n

are the zeros of the Bessel function J

o

(z) (j

01

= 2.40, j

02

= 5.52,

j

03

= 8.65, j

04

= 11.8,…). For a circular diaphragm with diameter

2a = 50 cm (which has nearly the same area as the previous strip with a

height of 1 meter) the frequencies are 1.9 Hz, 10 Hz, 25 Hz, 46 Hz, …. On

the strip with its poor aspect ratio charge does not have to travel so far in

order to reach equilibrium, which explains the faster response. This is also

the reason why the higher modes build-up much faster.

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

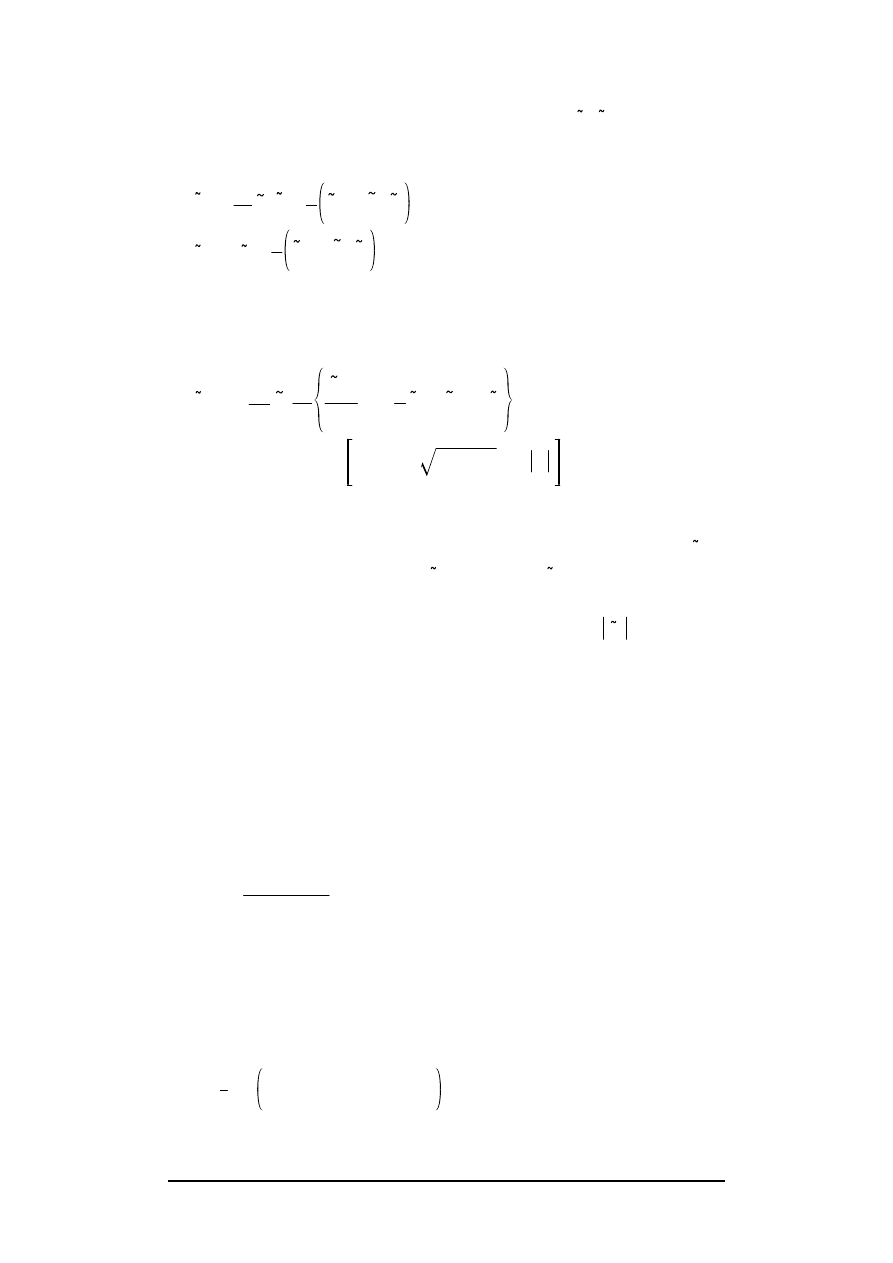
P. De Visschere

9

The (complex representation of the) 2nd harmonics

v

2

, q

2

can be found

from :

v

2

+ j

β

σ

β ∇

2

v

2

=

1
2

η

1

2

+ Va

η

1

q

2

= – v

2

+

1
2

η

1

2

+ Va

η

1

.

(30)

With the low-frequency expression for the deflection (27) the solution is
easily found. For

β

σ

< <

β

, this solution is given by :

q

2

= – j

β

σ

β

V

a

2

π

2

4

H

1,0

2

cos (

π

2

x) + H

1,0

2

h(x)

h(x) = cos (

π

x) + exp – (1 + j)

β

/

2

β

σ

(1 – x )

.

(31)

The second contribution, which is due to the quadratic terms in (30), can
again not be neglected and has a somewhat peculiar behaviour (

h(x) is

almost everywhere equal to

cos (

π

x) except near

x = 1 , where it drops to

zero; this transition occurs more abrupt if

β

σ

becomes smaller). Note also

that with

σ

-1

= 1000 M

Ω

(

β

σ

= 1.9 10

-3

), and for

β

= 0.05,

q

2

is of the or-

der of 4 % at the maximum drive level. We can expect third harmonic dis-

tortion components for the deflection and the pressure being of the same or-

der.

5 Steady-state analysis.

5.1 General theory

We consider a sinusoidal signal voltage :

v

a

= V

a

e

j

ω

t

+ e

–j

ω

t

2

.

(32a)

Due to the non-linear terms in eq.(3) and (6) all relevant quantities (q, v,

η

,

f

e

, p) will contain higher order harmonic components. However the di-

aphragm charge density (q) and the diaphragm voltage (v) will only show

even harmonics :

u =

1
2

Σ

n = 0

∞

u

2n

e

j2n

ω

t

+ u

2n

†

e

– j2n

ω

t

,

(32b)

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

10

where u stands for q or v and were † denotes the complex conjugate; for the

DC-component we have

u

0

†

= u

0

; the electric force (f

e

), the deflection of the

diaphragm (

η

), and consequently the pressure (p) will only show odd har-

monics :

u =

1
2

Σ

n = 0

∞

u

2n + 1

e

j[2n + 1]

ω

t

+ u

2n + 1

†

e

– j[2n + 1]

ω

t

,

(32c)

where u now stands for f

e

,

η

or p (the coefficients of f

e

will be denoted as

f

2n+1

however). Substituting these developments into the basic equations

and equating the harmonic components of like order leads to a set of equa-

tions for the coefficients. The details of this calculation can be found in the

Appendix A. A considerable simplification occurs if, as was done by

Hunt[1], higher order harmonics are neglected with respect to lower order

ones. We then find the following (simplified) expression for the fundamen-

tal force term :

f

1

= q

0

V

a

+q

0

2

η

1

,

(33)

and for its third harmonic :

f

3

= q

2

V

a

+q

0

2

η

3

+ q

0

q

2

η

1

.

(34)

For the DC-component of the charge density we find :

q

0

= – v

0

+

V

a

4

(

η

1

+

η

1

†

) +

1
2

η

1

2

q

0

,

(35)

and for its 2nd harmonic :

q

2

= – v

2

+

1
2

V

a

η

1

+

1
2

η

1

2

q

2

+

1
2

η

1

2

q

0

.

(36)

5.2 Fundamental frequency

With these approximate expressions the harmonics can now be calculated

consecutively. Starting point is eq. (A1) for n = 0, with the obvious solution

v

0

= – 1 . From eq.(35) we then find the DC charge distribution in terms of

the fundamental of the deflection and the applied voltage :

q

0

=

1 + 1

2

V

a

Re (

η

1

)

1 – 1

2

η

1

2

.

(37a)

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

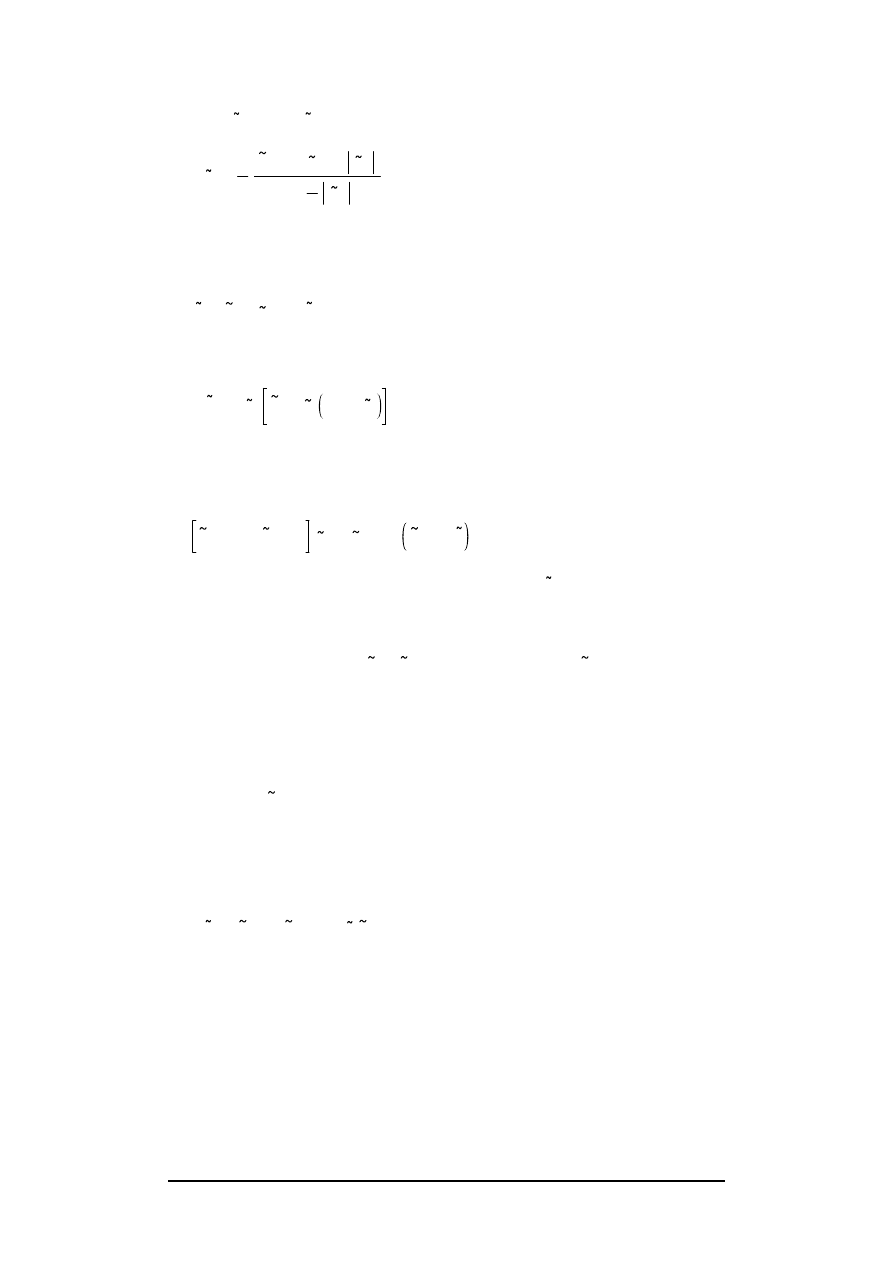
P. De Visschere

11

Writing

q

0

= 1 +

∆

q

0

, we find :

∆

q

0

= 1

2

V

a

Re (

η

1

) +

η

1

2

1 – 1

2

η

1

2

.

(37b)

This should be compared with the small-signal result (26). The fundamental

of the electric force (33) can then be written as :

f

1

= V

a

+

η

1

+

∆

f

1

,

(38a)

with :

∆

f

1

=

∆

q

0

V

a

+

η

1

2 +

∆

q

0

.

(38b)

The first two contributions in (38a) correspond with the perfect case

considered in section 3. Finally the first order equation (A2) reduces to :

∇

2

– j

β

R +

β

i

2

η

1

= p

1

–

β

e

2

V

a

+

∆

f

1

,

(39)

which, apart from the non-linear force correction

∆

f

1

, is equivalent with the

ideal equation (13) (eq. (14) remains unchanged). These equations can be

solved by iteration. We can still use developments (15), but should keep in
mind that the coefficients

P

1,k

, H

1,k

do now depend on

V

a

, due to the non-

linearity. Fig.4 shows this dependence for the absolute value of the first

pressure coefficient for a number of frequencies. Below the first resonance

the response increases with the driving level, above the first resonance it de-

creases slightly. Note also that for

β

= 0.05 run away occurs for an excita-

tion beyond

V

a

≈

0.75

. The coresponding DC charge variations are shown

in Fig.3 with the dash-dotted lines for two drive levels. As for the small-

signal approximations shown in the same figure, the DC charge variation is

expanded into the diaphragm modes :

∆

q

0

= V

a

2

Q

0,k

cos (

λ

k

x)

Σ

k = 0

∞

.

(40)

The discrepancy manifested in the upper frequency region in Fig.3b, be-

tween the accurate curves and the small-signal approximations is due to the

higher order deflection modes becoming important (see Fig.2b). These have

not been taken into account by the small-signal analysis.

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

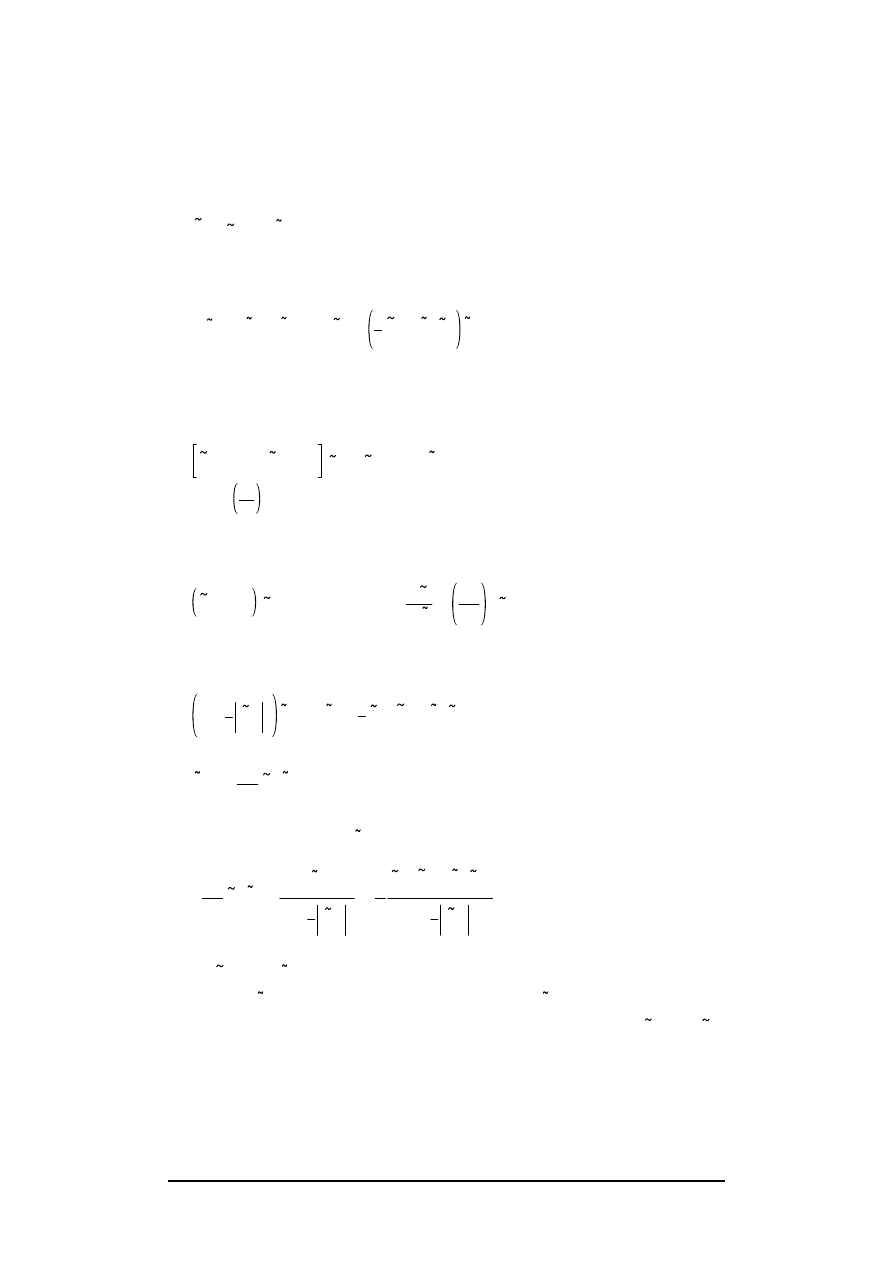
P. De Visschere

12

5.3 Harmonic distortion

The third harmonic can be treated in a similar way. The force component

(34) is written as :

f

3

=

η

3

+

∆

f

3

,

(41a)

with :

∆

f

3

=

∆

q

0

(

∆

q

0

+ 2)

η

3

+

1
2

V

a

+ q

0

η

1

q

2

.

(41b)

Substituting this in (A2) with n = 1, gives the equation for the third order

deflection :

∇

2

– j

β

3

R +

β

i,3

2

η

3

= p

3

–

β

e

2

∆

f

3

β

i,3

2

=

c

0

c

2

β

3

2

+

β

e

2

,

β

3

= 3

β

,

(42a)

and the wave equation (A3) becomes :

∇

2

+

β

3

2

p

3

= 0,

∂

p

3

∂

z

=

β

3

β

m

2

η

3

.

(42b)

The 2nd order charge density in (41b) is found from (36) and (A1, n = 1) :

1 –

1
2

η

1

2

q

2

= – v

2

+

1
2

η

1

(V

a

+ q

0

η

1

) ,

(43a)

q

2

= j

β

σ

β

∇

2

v

2

,

(43b)

with boundary condition

v

2

= 0 . The potential then satisfies the equation :

j

β

σ

β

∇

2

v

2

+

v

2

1 –

1
2

η

1

2

=

1
2

η

1

(V

a

+ q

0

η

1

)

1 –

1
2

η

1

2

.

(43c)

With

η

1

and

q

0

known from the fundamental analysis, eq.(43c) can be

solved for

v

2

. The second order charge density

q

2

, given by (43a) then

serves as the driving factor for the third harmonic components

p

3

and

η

3

according to (41b) and (42). The parameter determining the third harmonic

distortion is the resistivity of the diaphragm through the parameter

β

σ

in

(43c). The third harmonic distortion of the pressure in the radiation field is

shown in Fig.5 for a resistivity of 1000 M

Ω

. Shown is the amplitude of the

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

13

first mode of the third harmonic of the pressure relative to the same value

for the fundamental of the pressure. Modes (i = 0, 2, 4) are shown in Fig.6
as a function of frequency for

V

a

= 0.75 . For higher frequencies the higher

modes become dominant. These modes are not radiated but will be present

in the near-field. It is also apparent from these results that the R = 50 Rayl

damping is not sufficient for damping the higher resonances.

Whereas the DC charge density needs some time to adapt to an applied

driving voltage, as shown in section 4, the third harmonic distortion mani-

fests itself immediately. The results shown in Fig.5 and Fig.6 are steady-

state values, which are manifested if the charge density has equilibrated. In

Fig.7 this steady-state value is compared with the “immediate” value for the
distortion. The latter is found by using

q

0

= 1

(or

∆

q

0

= 0

) and the corre-

sponding (ideal) value for the deflection

η

1

in (43c, 43a, 41b).

6 Discussion

In a not perfect pp-ESLS the finite resistivity has two effects, a level de-

pendent sensitivity and non-linear distortion. In steady-state the sensitivity

changes become noticeable below the first resonance (see Fig.4) and in the

worst case even instability does occur. These sensitivity changes are inde-

pendent of the diaphragm resistivity. However the time required for their

manifestation does depend on the resistivity. With a resistivity

σ

-1

= 10

9

Ω

,

we have found a time-constant around 30 ms for the

∞

strip considered,

which is probably not acceptable. A resistivity 10

12

Ω

seems therefore more

appropriate, but note that driving this hypothetical loudspeaker at

β

= 0.05

(with the parameters shown in Table 2 this corresponds with a frequency of

27 Hz) and at a (normalised) level higher than 0.75 would still result in

instability after a multiple of 30 s.

Since the harmonic distortion is to a first approximation proportional with

the resistivity, increasing the resistivity from 10

9

Ω

to 10

12

Ω

, will reduce

the distortions, shown in Fig.5-7, with a factor 1000. Even for very low fre-

quencies the distortion then does not exceed 0.05 %. With

σ

-1

= 10

9

Ω

and

restricting the frequency range to

β

> 0.05

,

the worst case distortion equals

nearly 7 % however.

Well-known commercial designs like the famous Quad ESL 63 are reported

in the popular literature as having resistivities in the order of 10

12

Ω

[7].

Other commercial designs are mentioned with a much lower resistivity of

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

14

only 100 k

Ω

and these designs then rely on a series resistor. In Hunt’s one-

dimensional model [1] the resistivity of the diaphragm is irrelevant and the

role of the diaphragm resistivity is taken over by the series resistor through

which the diaphragm is biased. I wonder whether Hunt’s “model” may have

spurred the use of a fairly conductive diaphragm together with a series

resistor. Anyway it remains interesting to analyse to what extent the role of

the diaphragm resistivity can be taken over by a series resistor. To answer

this question we must replace the boundary condition for eq.(7) with a more

complicated one involving the series resistor and this is beyond the scope of

the present paper. However we can anticipate that as long as the charge

variations are dominated by the lowest mode, they can only be established

by a variation of the net charge on the diaphragm. In that case a series

resistor will be nearly as effective. However if higher order modes come

into play then some of the charge variations can be established by a mere

redistribution of the diaphragm charge and a series resistor will not be able

to suppress these variations. We believe therefore that a series resistor will

not be able to reduce the harmonic distortion at the high end of the

considered frequency range.

In this paper we have attempted to predict the distortion characteristics of an

ideal pp-ESLS. In addition to the mentioned incorporation of a series resis-

tor, another useful generalisation to be considered is the introduction of

asymmetry in the structure. In that case the neat distinction between quanti-

ties with even and odd harmonics will disappear. We hope to address these

topics in the future.

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

15

References

[1]

F. V. Hunt, “Electroacoustics : The Analysis of Transduction, and its

Historical Background,” 2nd edition, Acoustical Society of America,

1982, pp. 173-212. (Except for a list of errata this edition is identical

with the original edition from 1954.)

[2]

J.H. Streng, “Calculation of the surface pressure on a vibrating circu-

lar diaphragm in free space,” J. Acoust. Soc. Am. 82 (2), August

1987, pp. 679-686.

[3]

J. H. Streng, “Calculation of integrals which occur in the analysis of

circular stretched diaphragm sound radiation,” J. Acoust. Soc. Am. 83

(3), March 1988, pp. 1183-1185.

[4]

J. H. Streng, “Charge Movements on the Stretched Diaphragm in a

Circular Electrostatic Push-Pull Loudspeaker,” J. Audio Eng. Soc.,

Vol. 38, No. 5, May 1990, pp. 331-339.

[5]

P. De Visschere, “The validity of Ramo’s theorem,” Solid-State

Electronics, 33, pp.455-459, 1990.

[6]

P. De Visschere, “Calculation of the surface pressure on the

diaphragm of a perfect push-pull electrostatic loudspeaker,” to be

published.

[7]

E. Fikier, “Elektrostatische luidsprekers, zelf bouwen of zelf kopen,”

Elektuur BV, 1993, pp.77-92 and pp.122-132.

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

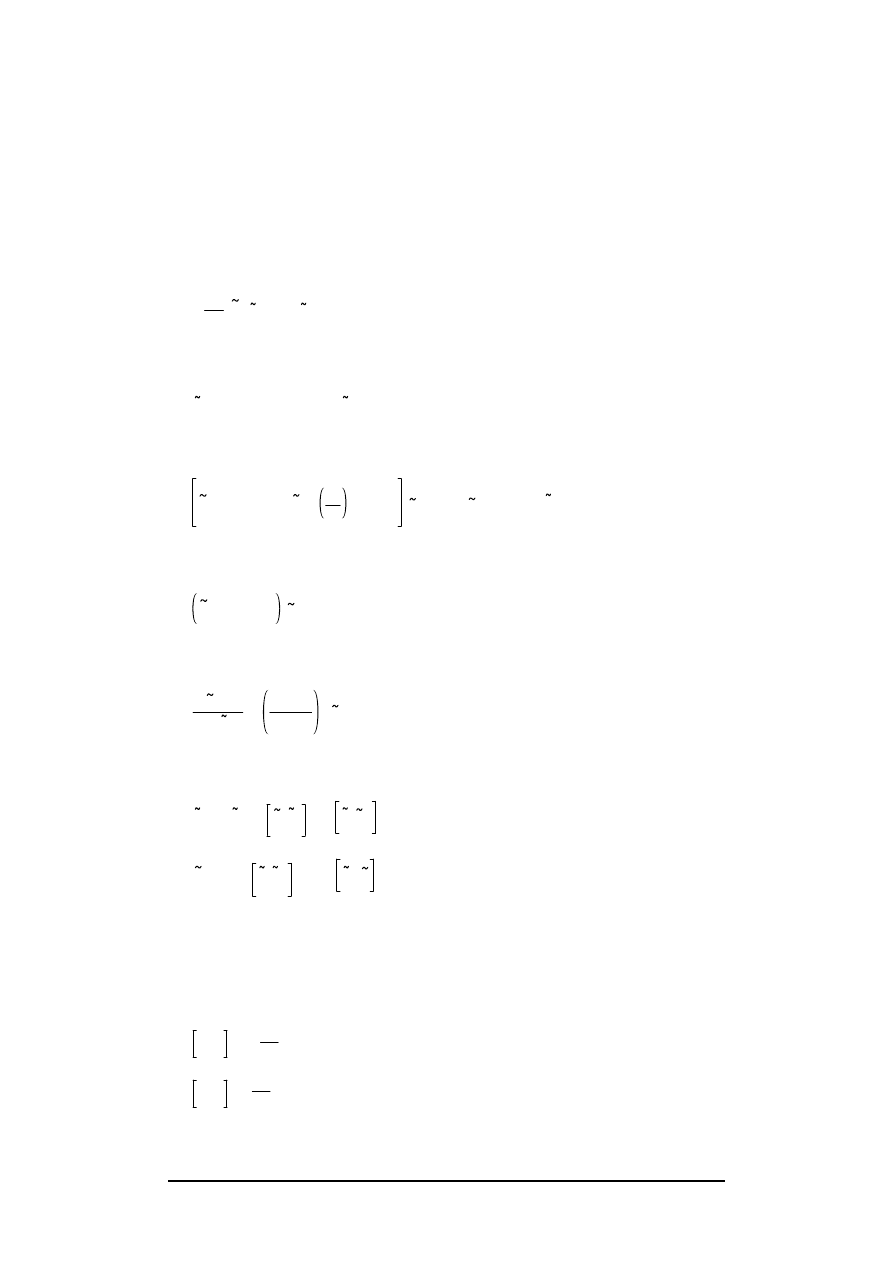
P. De Visschere

16

Appendix A

Substituting the developments (32) into the basic equations and equating the

harmonic components of like order leads to a set of equations for the

harmonic coefficients. The linear equations (7-10) lead to similar equations

for the corresponding coefficients :

j

β

σ

β ∇

2

v

2n

= n q

2n

,

(A1a)

with boundary conditions :

v

2n

= 0, (n

≠

0)

v

0

= – 1 .

(A1b)

The mechanical equation (8) and the acoustical equation (9) become :

∇

2

– j

β

2 n + 1

R +

c

0

c

2

β

2 n + 1

2

η

2 n + 1

= p

2 n + 1

–

β

e

2

f

2 n + 1

,

(A2)

and :

∇

2

+

β

2 n + 1

2

p

2 n + 1

= 0 ,

(A3a)

where

β

2 n + 1

= (2 n + 1)

β

and with boundary condition :

∂

p

2 n + 1

∂

z

=

β

2 n + 1

β

m

2

η

2 n + 1

.

(A3b)

From the non-linear equations (3) and (6) we find :

q

2n

+ v

2n

=

η

v

a

2n

+ q

η

2

2n

,

(A4a)

f

2n + 1

= q va

2 n + 1

+ q

2

η

2n + 1

.

(A4b)

The first contributions on the RHS are rather simple (in the remainder of

this appendix formulas are expressed with the original variables; it is easily

seen that normalised quantities obey the same relations) :

η

v

a

2n

=

V

a

2

(

η

2n – 1

+

η

2n + 1

)

(n

≠

0)

η

v

a

0

=

V

a

4

(

η

1

+

η

1

†

)

,

(A5a)

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

17

q v

a 2 n + 1

=

V

a

2

q

2 n

+ q

2 n + 2

(n

≠

0)

q v

a 1

=

V

a

2

2 q

0

+ q

2

.

(A5b)

The remaining contributions in(A4) however contain terms involving all the

harmonics of q and

η

. This makes the resulting system of equations difficult

to solve. Fortunately higher order harmonics are supposed to be small with

respect to lower ones (|

η

3|

<< |

η

1|

, |q

2|

<< |q

0|

and so on). Following Hunt[1]

we retain only the dominant terms and (A5) then simplify :

η

v

a 2n

=

V

a

2

η

2n – 1

(n

≠

0)

η

v

a 0

=

V

a

4

(

η

1

+

η

1

†

)

,

(A6a)

q v

a 2 n + 1

=

V

a

2

q

2 n

(n

≠

0)

q v

a 1

= V

a

q

0

.

(A6b)

The second contributions in the RHS of (A4) now become much simpler :

η

2q

2n

=

1
2

Σ

l = 0

n

η

2

2l

q

2[n – l]

+

1
2

η

2

2n

q

0

+

1
4

q

2n

η

1

2

,

(A7a)

with :

η

2

2n

=

1
2

Σ

l = 0

n – 1

η

2[n – l] – 1

η

2l + 1

(n

≠

0)

η

2

0

=

1
2

η

1

2

.

(A7b)

and :

q2

η

2n + 1

=

1
2

η

2n + 1

q0

2 +

1
2

Σ

l = 0

n

q2

2[n – l]

η

2l + 1

,

(A8a)

with :

q

2

2n

= q

2n

q

0

+

1
2

Σ

l = 0

n

q

2[n – l]

q

2l

(n

≠

0)

q

2

0

= q

0

2

,

(A8b)

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

18

Figure captions

Fig.1 Model for an idealised push-pull electrostatic loudspeaker.

Fig.2 The normalised response of an ideal

∞

strip pp-ESLS. Shown are the

absolute values of the first three modes for (a) the diaphragm

pressure, and for (b) the diaphragm deflection. Parameters values are

shown in Table 2.

Fig.3 The normalised (a) first and (b) second mode of the steady-state DC

charge density variation for sinusoidal excitation. Shown are two

small signal approximations (full lines and dashed lines) and “exact”

results for two drive voltage levels (dashed dotted lines).

Fig.4 The variation of the absolute value of the first mode of the

diaphragm pressure with the sinusoidal driving voltage level for

different frequencies.

Fig.5 Third harmonic distortion as a function of driving voltage level for

different frequencies and for a diaphragm resistivity of 1000 M

Ω

.

Fig.6 The absolute value of the first, third and fifth mode of the third

harmonic diaphragm pressure normalised with the first mode of the

fundamental pressure as a function of frequency. Diaphragm

resistivity equals 1000 M

Ω

.

Fig.7 Comparison between the steady-state (full line) and the “immediate”

(broken line) third harmonic distortion. The “immediate” value is

valid insofar as the DC charge density has not yet adapted to the

driving level. Diaphragm resistivity equals 1000 M

Ω

.

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

19

Quantity normalised

with

voltage : v, v

a

, V

a

V

0

charge density : q

Q

0

= –

2

ε

V

0

η

r

deflection :

η

η

r

coördinates : x, …

a

time : t

a

2 c

0

electric force : f

e

2

ε

V

0

2

η

r

2

electric field : E

V

0

η

r

pressure : p

η

r

T

2 a

2

mechanical damping : R

T

a c

0

Table 1 : quantities shown on the left are normalised

with the values shown on the right.

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net

P. De Visschere

20

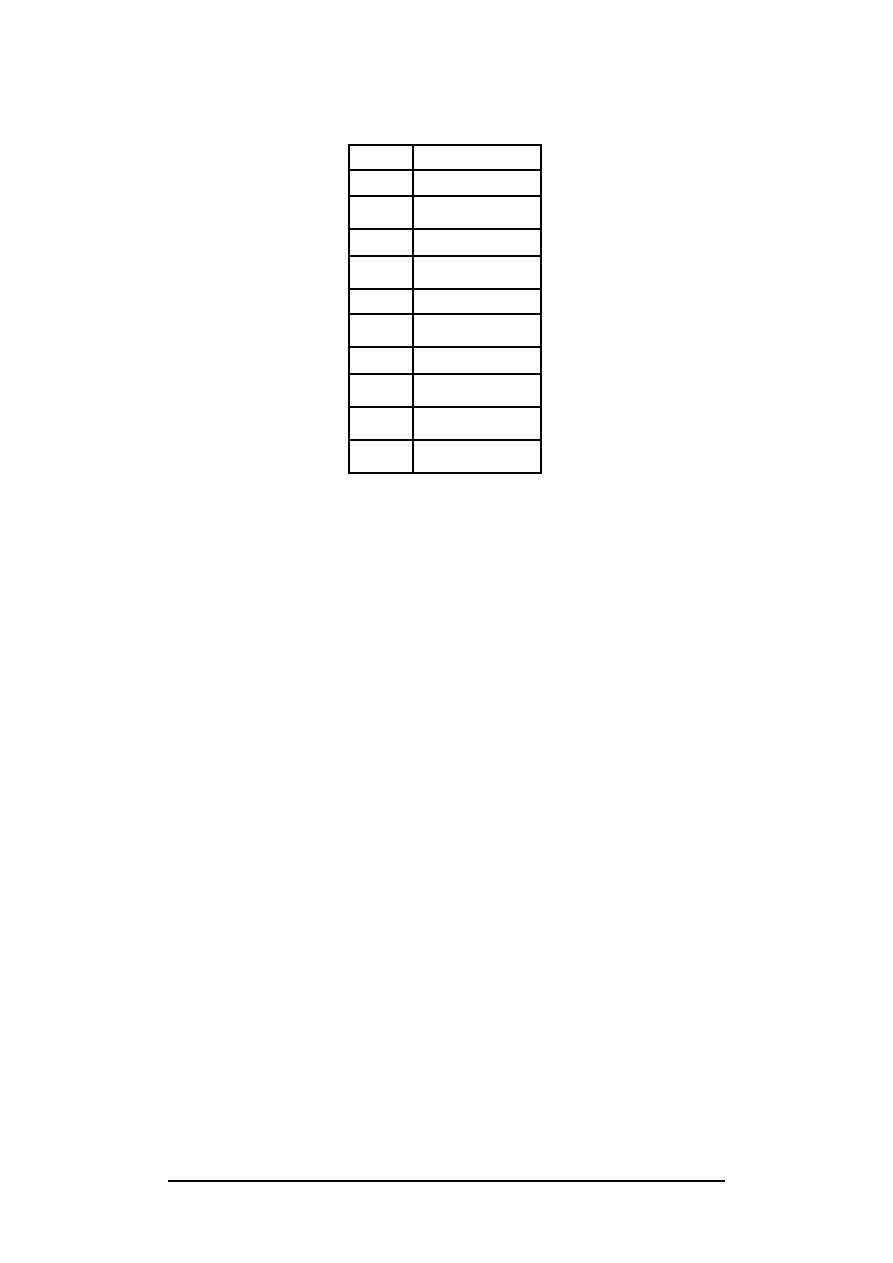
a

10 cm

T

100 N/m

ρ

0.02 kg/m

2

V

0

2000 V

η

r

2.3 mm

R

50 Rayl

σ

−1

10

9

Ω

c/c

0

0.206

β

e

0.763

β

m

0.06

β

s

1.89 10

-3

Table 2 : Parameter values used for the numerical

calculations. They reduce to 4 dimensionless pa-

rameters, which are also listed.

Example from "Loudspeaker Bibliography" www.shackman.reromanus.net

More know-how on http://www.shackman.reromanus.net