SYNTEZA METOD

Ą

MODELOWANIA

FIZYCZNEGO

Metoda matematyczna i falowodowa

Synteza dźwięku i obrazu

Wprowadzenie

Metody modelowania fizycznego należą do
najnowszych metod syntezy dźwięku.

Odmienne podejście do syntezy dźwięku:

bezpośrednia symulacja zjawisk fizycznych
zachodzących w rzeczywistych instrumentach.

Symulujemy instrument, a nie dźwięk przez
niego wytwarzany!

Główne metody modelowania fizycznego:

modelowanie matematyczne

metoda falowodowa

MODELOWANIE MATEMATYCZNE

Metoda modelowania matematycznego oparta
jest na bezpośrednim rozwiązywaniu równania
falowego opisującego powstawanie dźwięku
w instrumencie.

Funkcja będąca rozwiązaniem równania
falowego stanowi przebieg czasowy dźwięku
syntetycznego.

Rozwiązanie równania falowego wymaga
złożonego aparatu matematycznego
(układy równań różniczkowych).

Głównym problemem jest tu właściwy opis
matematyczny procesu powstawania dźwięku
w instrumencie.

Modelowanie matematyczne

Etapy modelowania matematycznego:

sformułowanie systemu, który odzwierciedla
proces wytwarzania dźwięku w rzeczywistym
instrumencie

wyznaczenie wartości parametrów
wykorzystywanych w równaniach

przeprowadzenie symulacji numerycznych

badanie wpływu zmian parametrów modelu
na jego charakterystyki

Model mat. piszczałki organowej

d x

dt

k

dx

dt

n x

F

i

i

i

i

i

i

2

2

2

+

+

=

λ

P t

P

P

P e

t

( )

(

)

(

/ )

=

+

−

−

0

1

0

τ

δ

τ

( )

( )

t

P

P t

fin a l

=

0

F

F

dx

dt

P t

nielin

=











.

, ( )

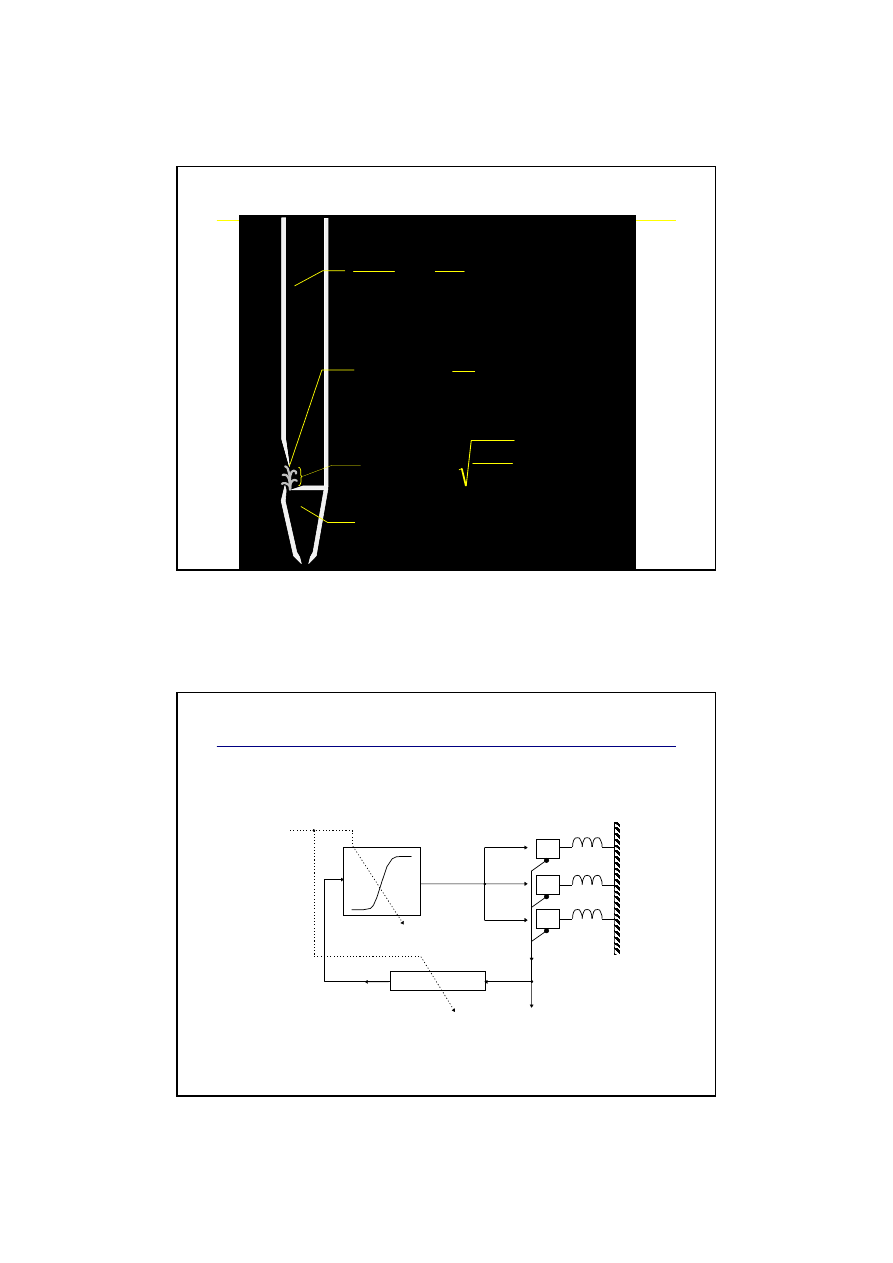
Model mat. piszczałki organowej

Model rezonatora

n

3

, k

3

n

2

, k

2

n

1

, k

1

v

3

v

2

v

1

v

m

Linia opó

ź

niaj

ą

ca

Wej

ś

cie

Wyj

ś

cie

M

1

M

2

M

1

v

Element

nieliniowy

F

3

F

2

P(t)

F

F

1

Sprz

ęż

enie zwrotne

Organowa piszczałka wargowa – model blokowy

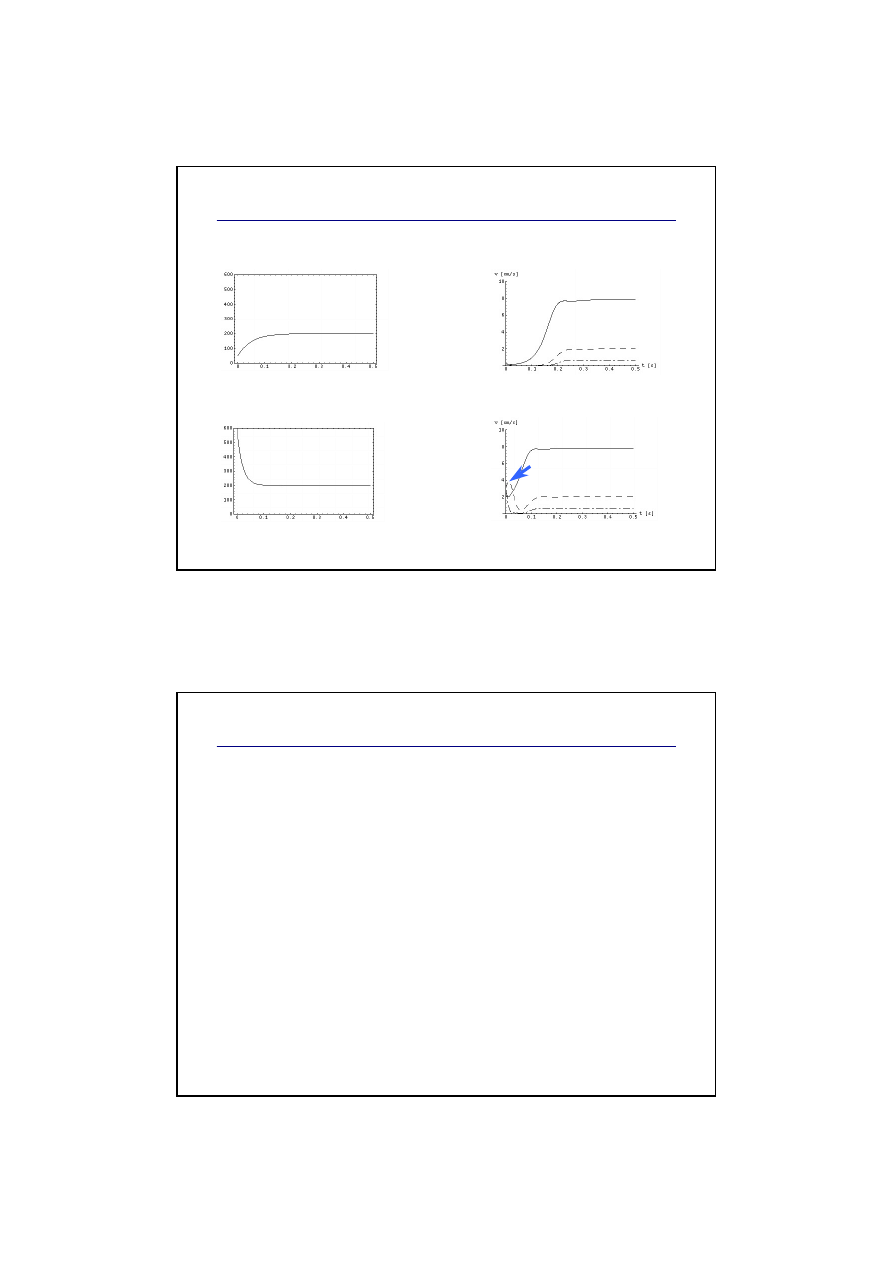
Model matematyczny piszczałki

Symulacja dla ataku wolnego

Symulacja dla ataku wybuchowego

przed

ę

cie

Metoda matematyczna

Zalety

metody matematycznej:

możliwość dokładnej symulacji rzeczywistych
instrumentów (wierność brzmienia)

możliwość uwzględnienia zjawisk
artykulacyjnych

Wady

metody:

duża złożoność obliczeniowa – konieczność
rozwiązywania układu nieliniowych równań
różniczkowych

trudność opisu matematycznego instrumentu

METODA FALOWODOWA

Metoda cyfrowego modelowania falowodowego
ang.

digital waveguide modeling

Opracowana na uniwersytecie w Stanford
(USA) na początku lat 90.

Polega na modelowaniu przy pomocy
cyfrowego falowodu fal bieżących
składających się na falę stojącą w danym
instrumencie.

Implementacja: algorytm cyfrowy,
np. program komputerowy.

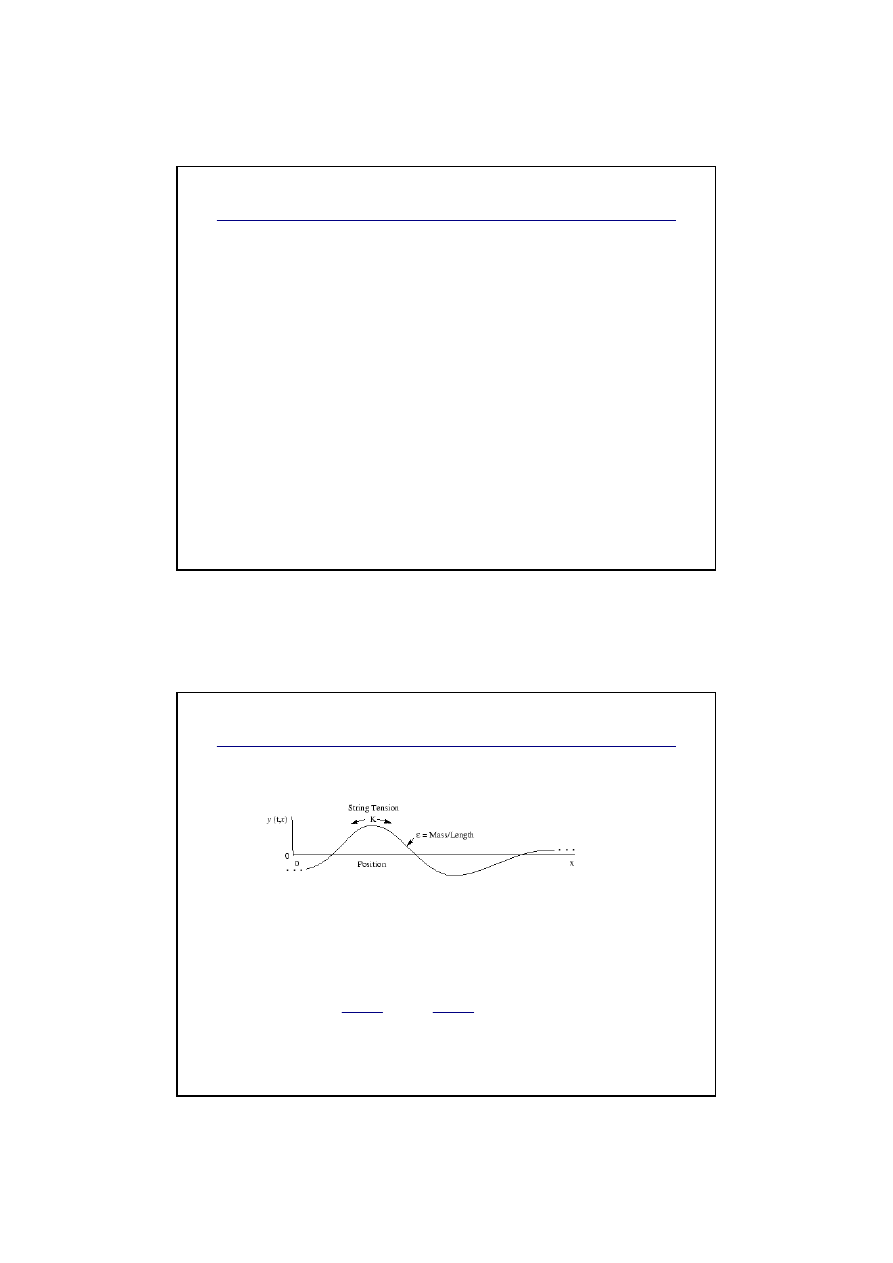
Model drgaj

ą

cej struny

Idealna (bezstratna) drgająca struna

Ciśnienie p jest funkcją czasu t oraz miejsca x:

p(x, t)

Równanie falowe (jednowymiarowe):

∂

∂

∂

∂

2

2

2

2

2

p

t

c

p

x

=

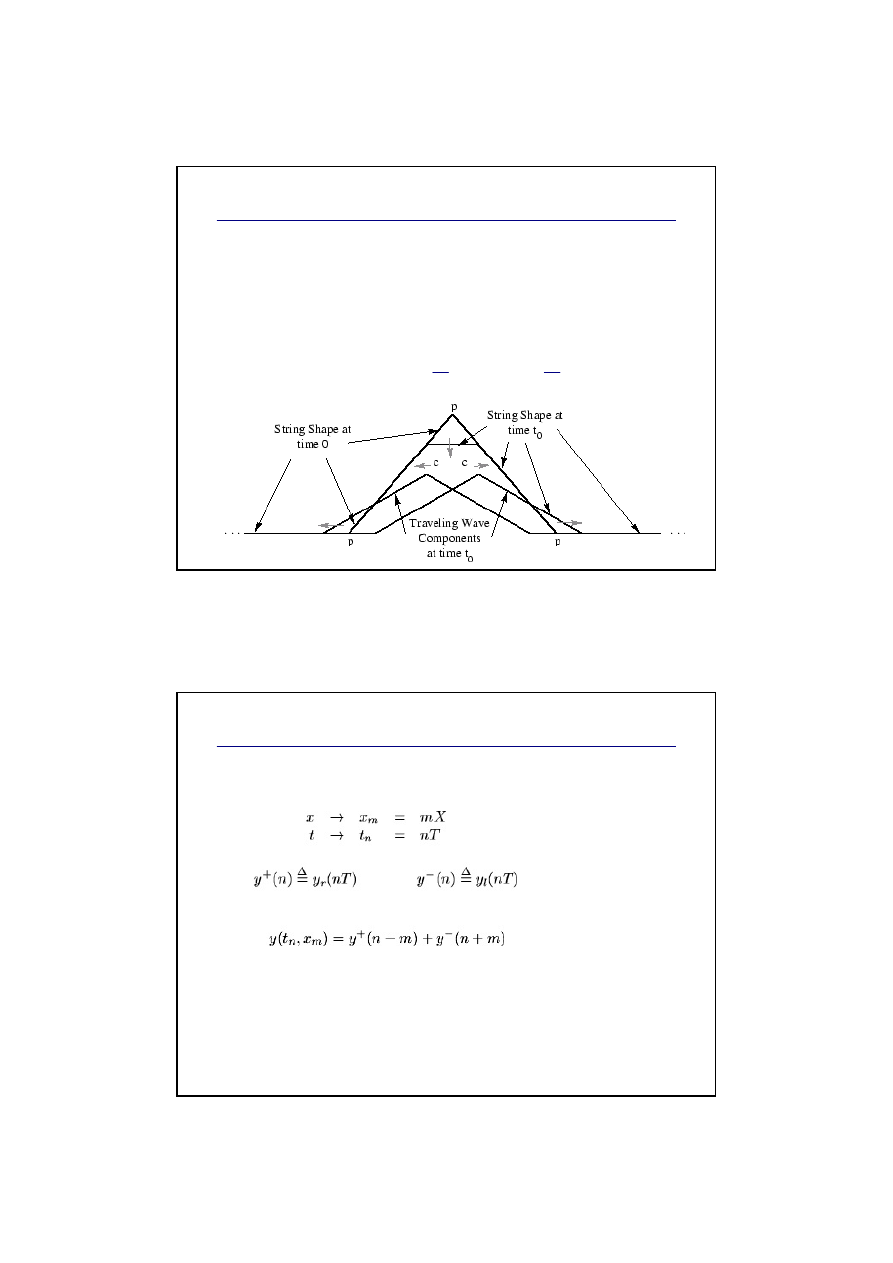
Model bezstratnej drgaj

ą

cej struny

Rozwiązanie ogólne równania falowego dla
idealnej (bezstratnej) drgającej struny:
suma dwóch

fal bieżącyc

h (travelling waves)

propagowanych w przeciwnych kierunkach

p x t

p t

x

c

p t

x

c

( , )

(

)

(

)

=

−

+

+

1

2

Próbkowanie modelu struny

Przejście do dziedziny cyfrowej:

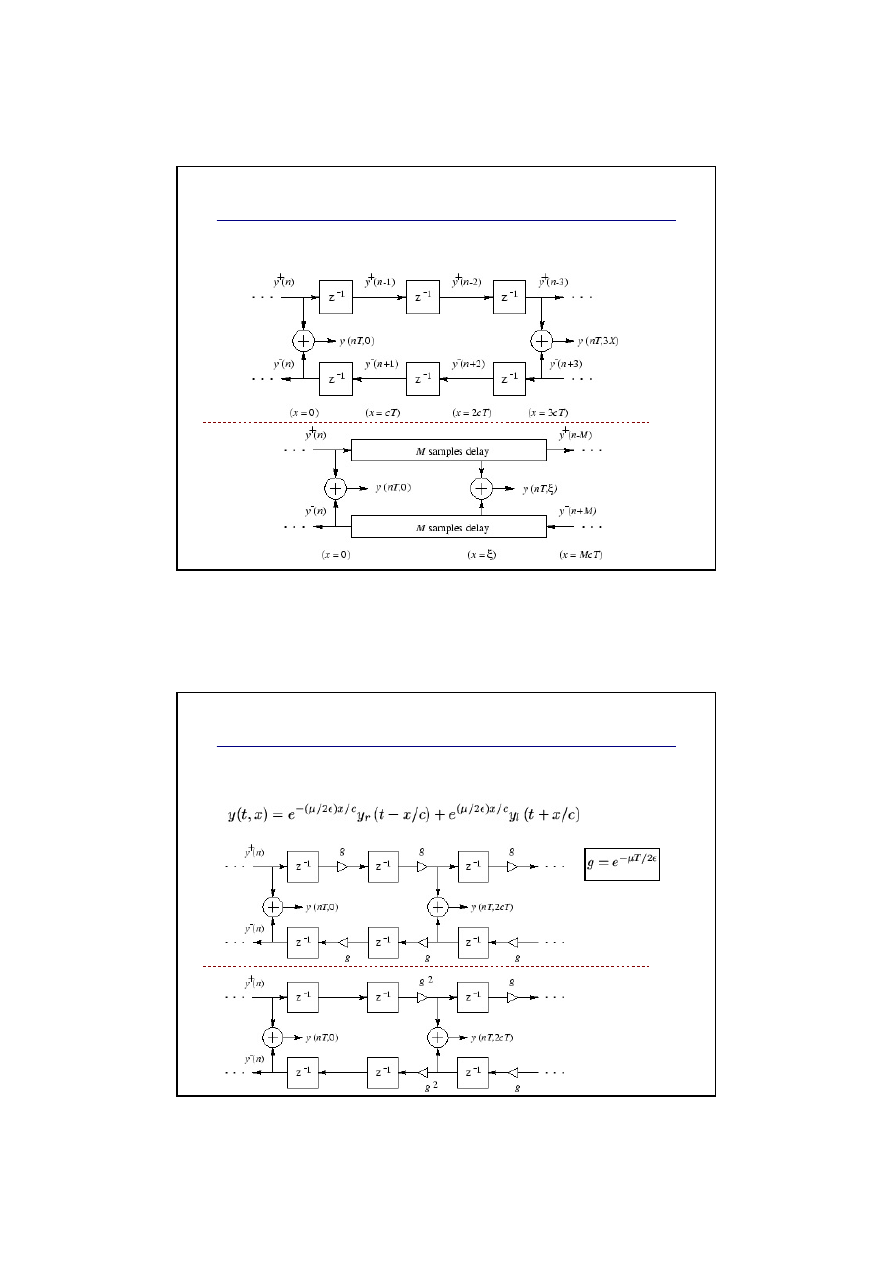
Cyfrowy model falowodowy

Model cyfrowy idealnego, bezstratnego falowodu

Model z uwzgl

ę

dnieniem strat energii

Uwzględnienie strat energii w modelu falowodowym

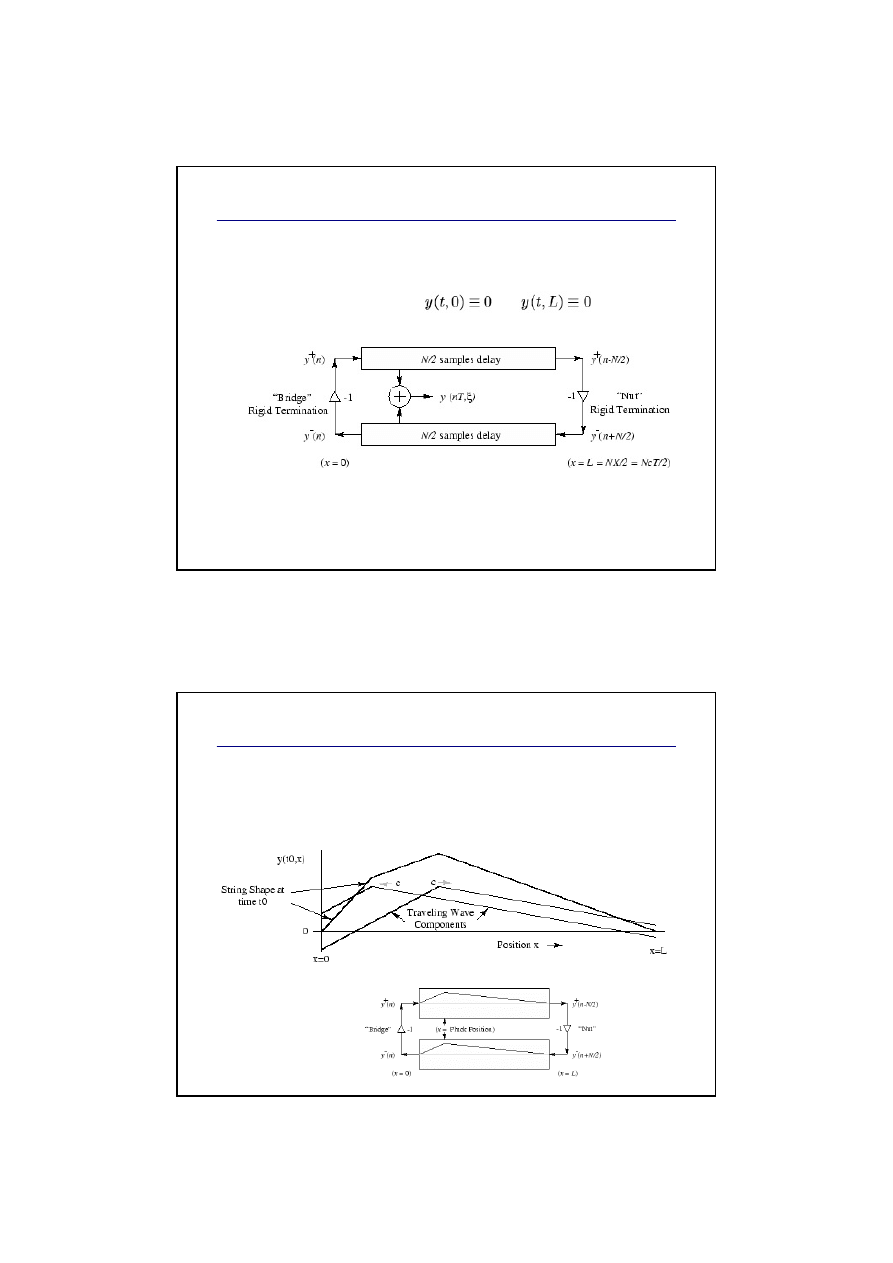
Modelowanie sztywnych zako

ń

cze

ń

Modelowanie drgającej struny ze sztywnymi
zakończeniami:
warunki początkowe

Model szarpni

ę

tej struny

Idealna struna ze sztywnymi zakończeniami,
pobudzona szarpnięciem (plucked string)
np. gitara

warunki
początkowe:

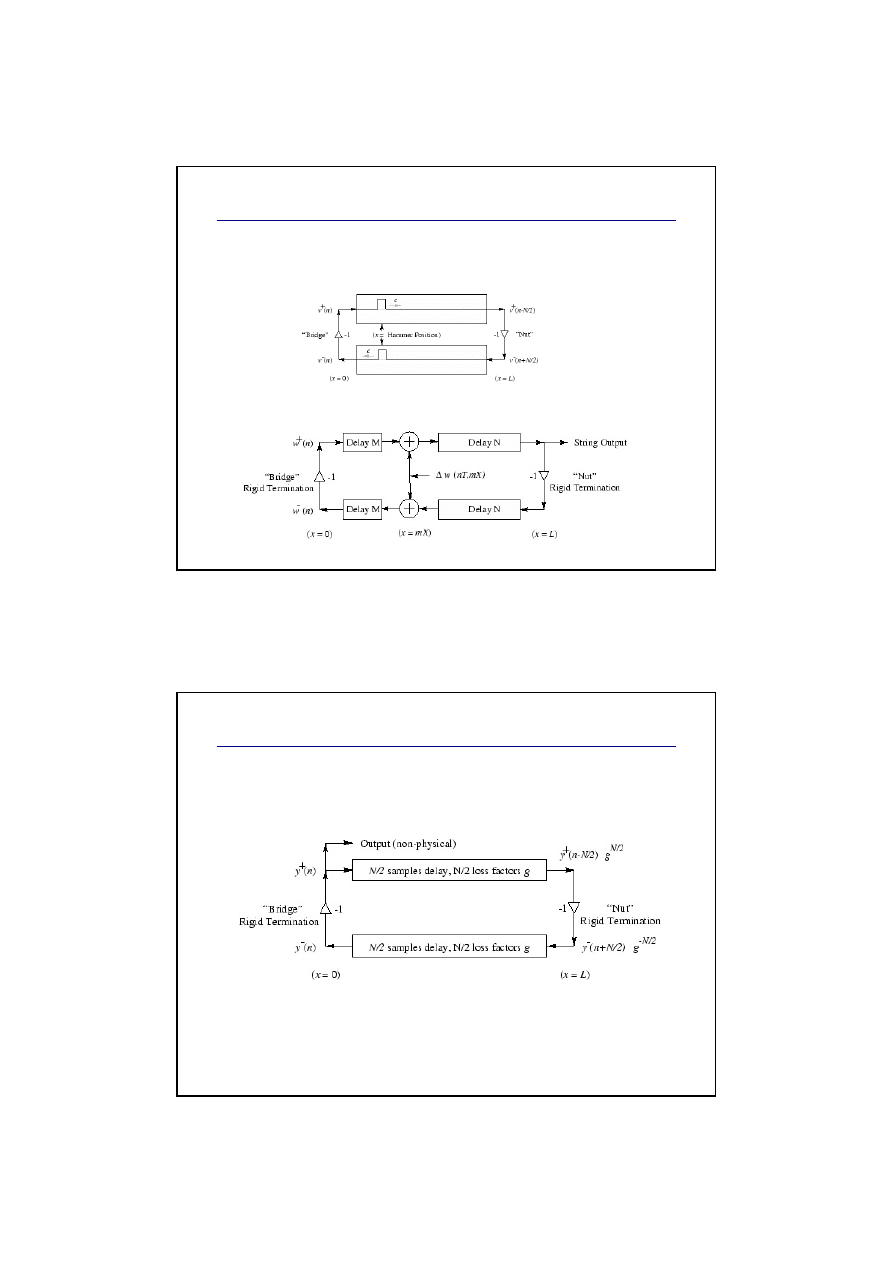
Inne modele struny

Model idealnej struny uderzonej (struck string),
np. fortepian

Model struny pobudzonej zewnętrznie:

Uwzgl

ę

dnienie strat energii

Model struny z uwzględnieniem strat energii
(tłumienia fali)

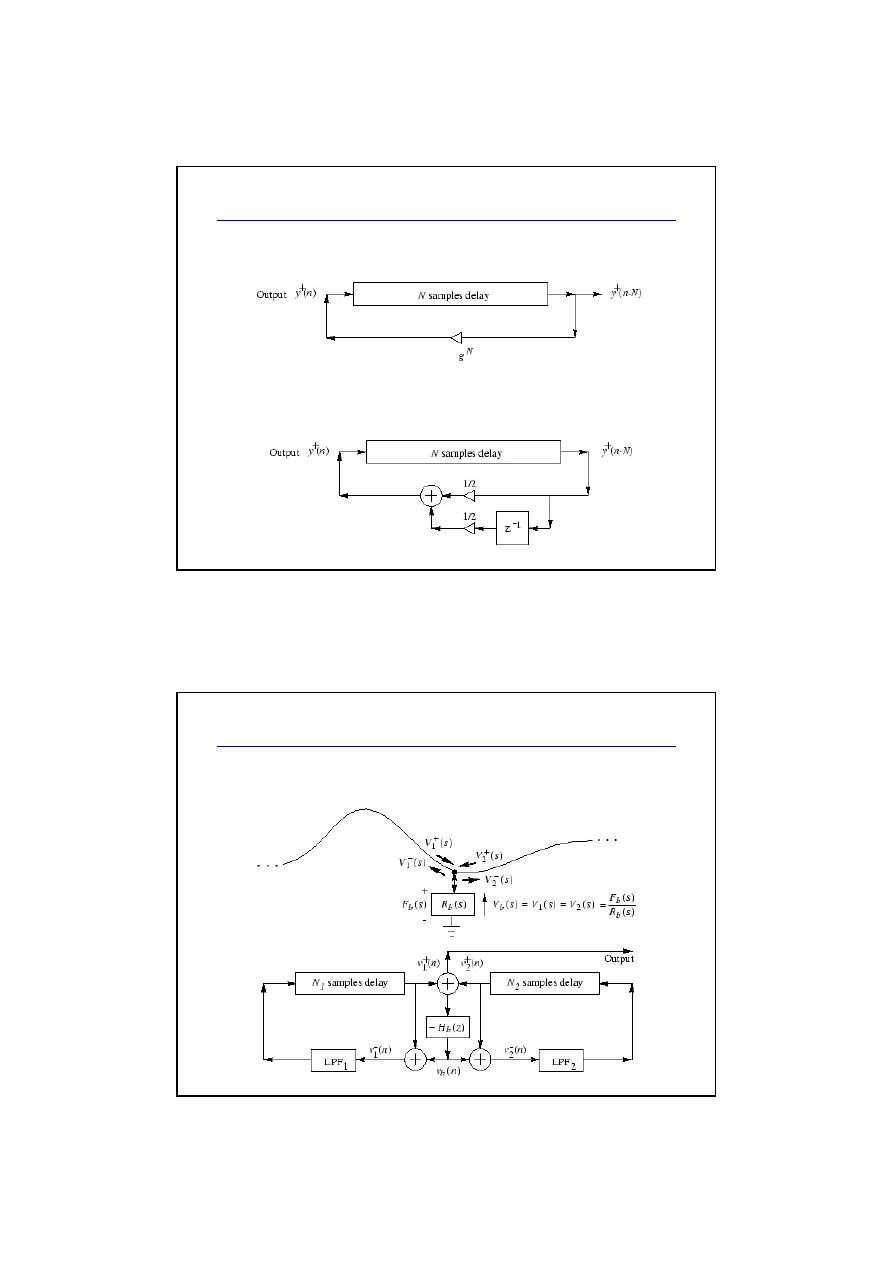
Uwzgl

ę

dnienie strat energii

Model struny z uwzględnieniem tłumienia stałego

Model struny

Karplusa-Stronga

z uwzględnieniem

tłumienia zależnego od częstotliwości

Sprz

ęż

enie dwóch strun

Model dwóch strun sprzężonych poprzez mostek

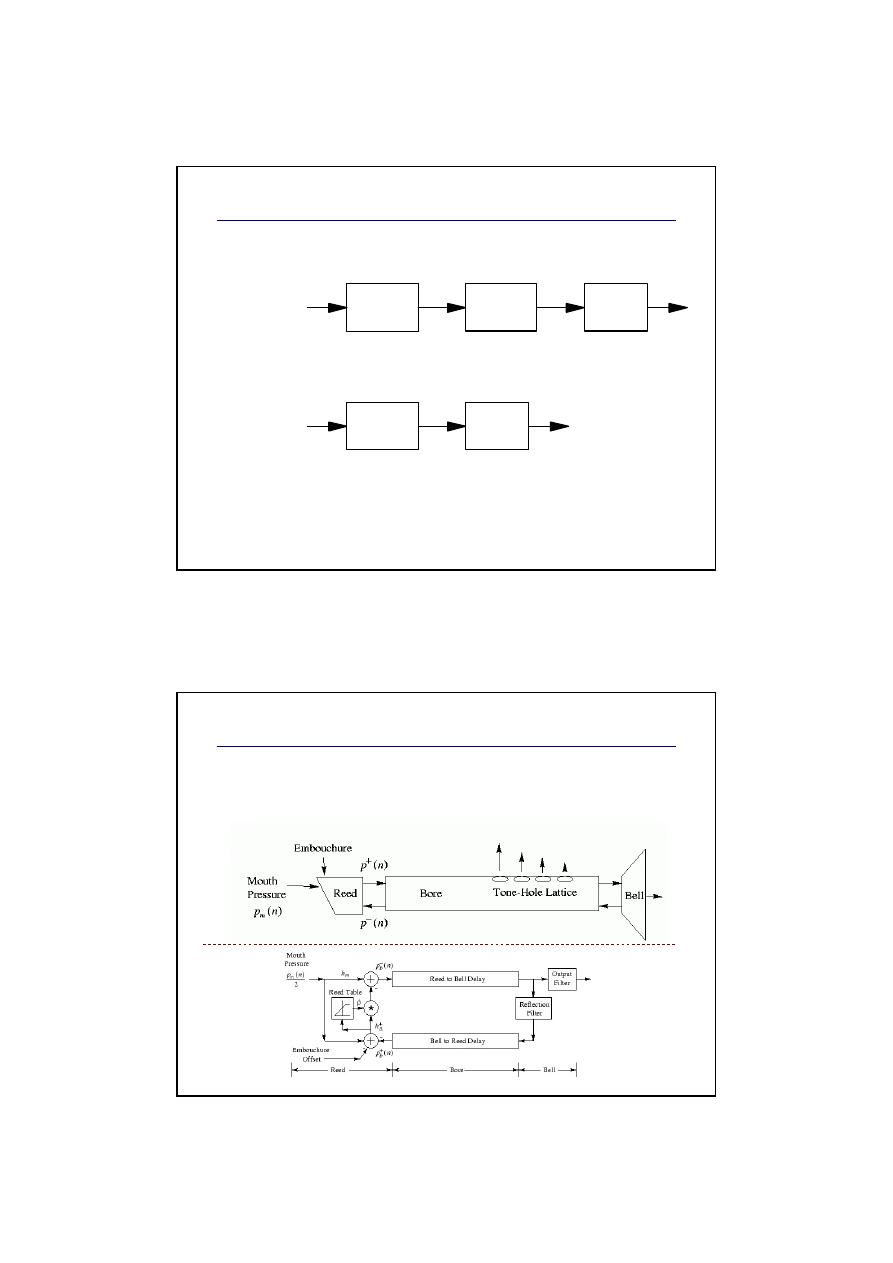
Model instrumentu strunowego

E(z)

S(z)

B(z)

δ

(n)

b(n)

Impuls

impulsowa

pudła rezon.

e(n)

y(n)

Wyj

.

Model

pojedynczej

struny

Model

pudła

rezonans.

Filtr

pobudzenia

y(n)

Wyjście

Model

pojedynczej

struny

E(z)

S(z)

Filtr

pobudzenia

(a)

(b)

Odpowiedź

)

(

*

)

(

)

(

)

(

)

(

)

(

)

(

n

s

n

e

n

b

n

b

n

s

n

e

n

y

∗

=

∗

∗

=

Model instrumentu d

ę

tego

Model instrumentu dętego z pojedynczym
stroikiem (single reed), np. klarnet

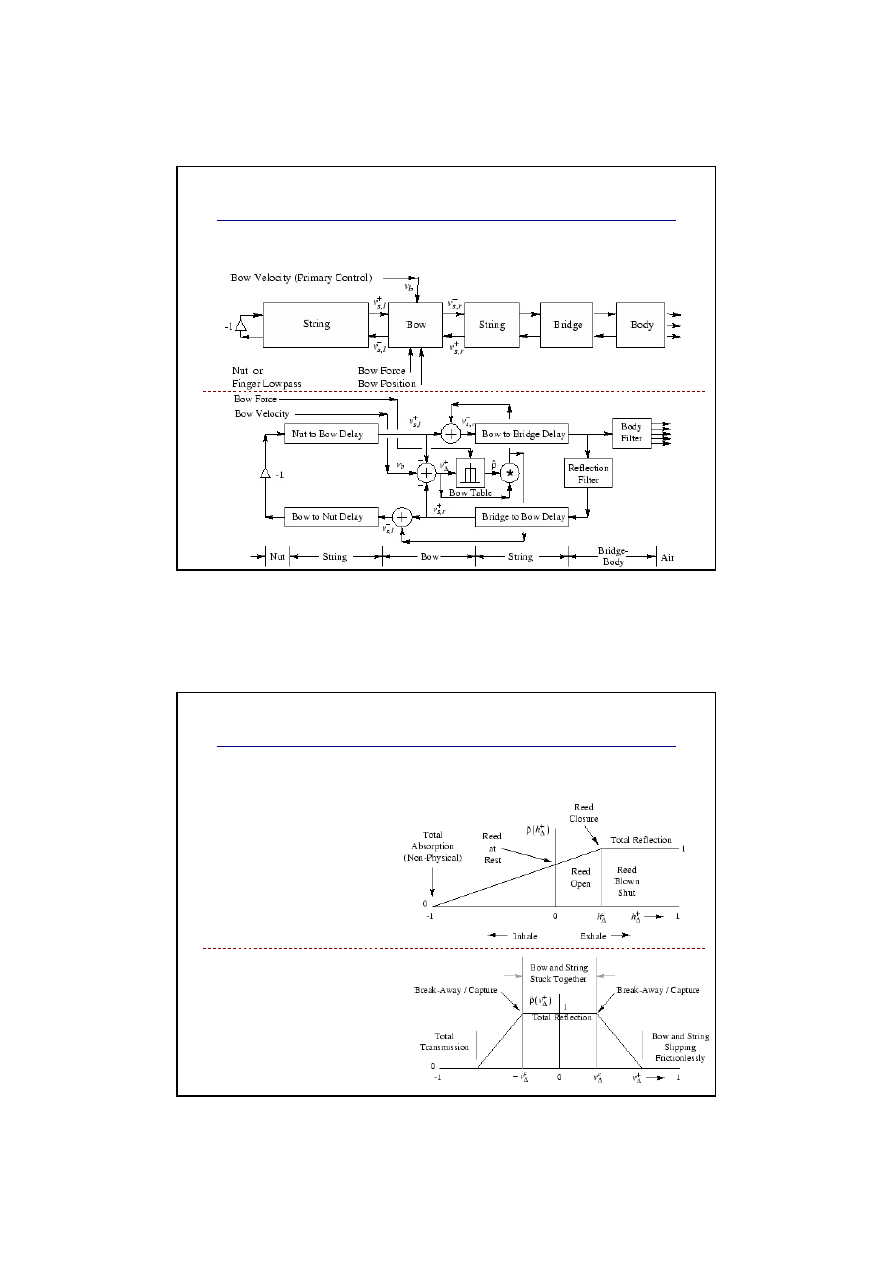
Model instrumentu smyczkowego

Model instr. smyczkowego (np. wiolonczela)

Modele pobudzenia

Modele pobudzenia zapisywane są w tablicy

Instr. stroikowy
reed table

Instr. smyczkowy
bow table

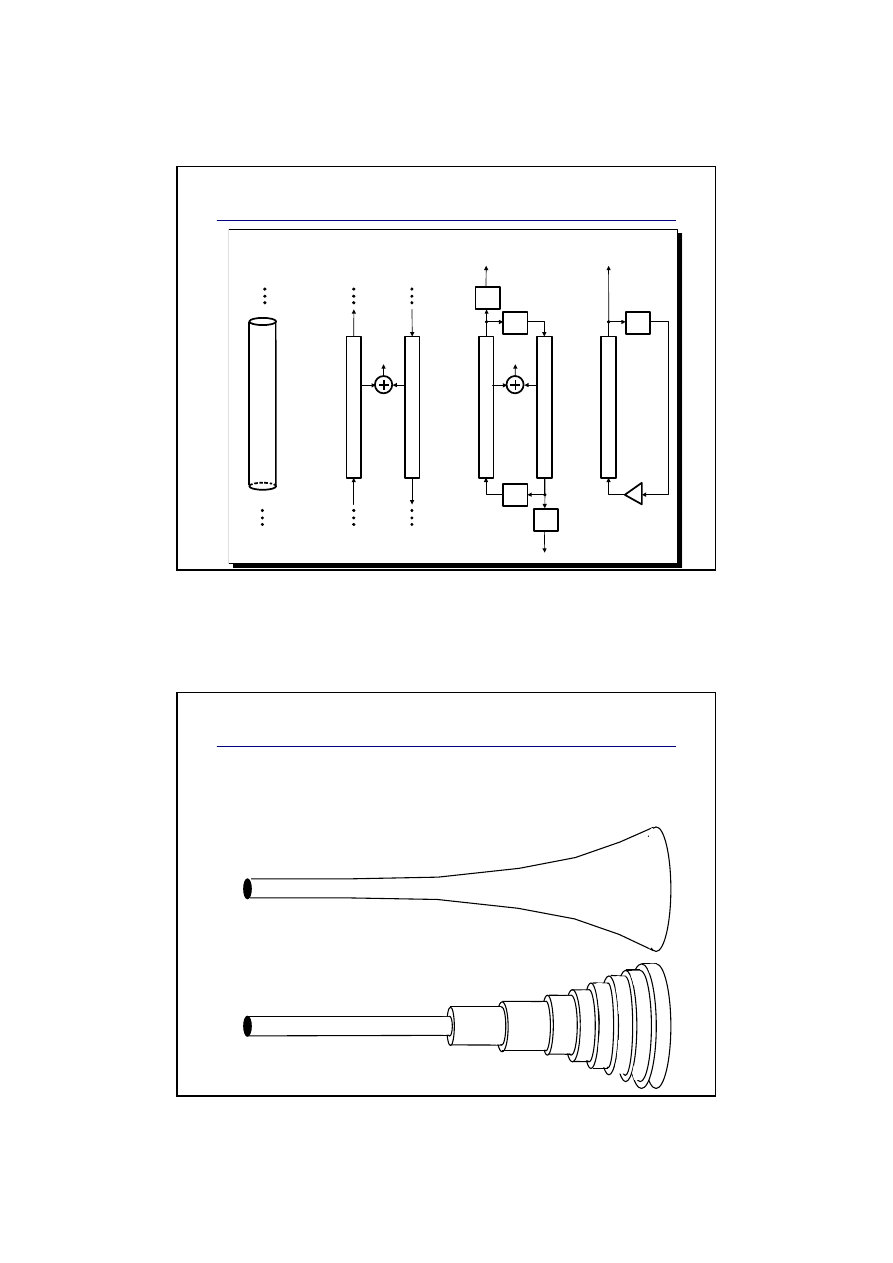
Modelowanie falowodu cylindrycznego

F

a

F

a

F

a

wy

g

1

∆

t

∆

t/2

∆

t/2

p(nT,x)

p

−

(n+M)

p

+

(n-M)

p(nT,x)

p

+

(n)

p

−

(n)

F

b

F

b

(d)

(c)

(a)

(b)

Modelowanie kształtu instrumentu

Kształt instrumentu jest aproksymowany za
pomocą układu falowodów cylindrycznych.

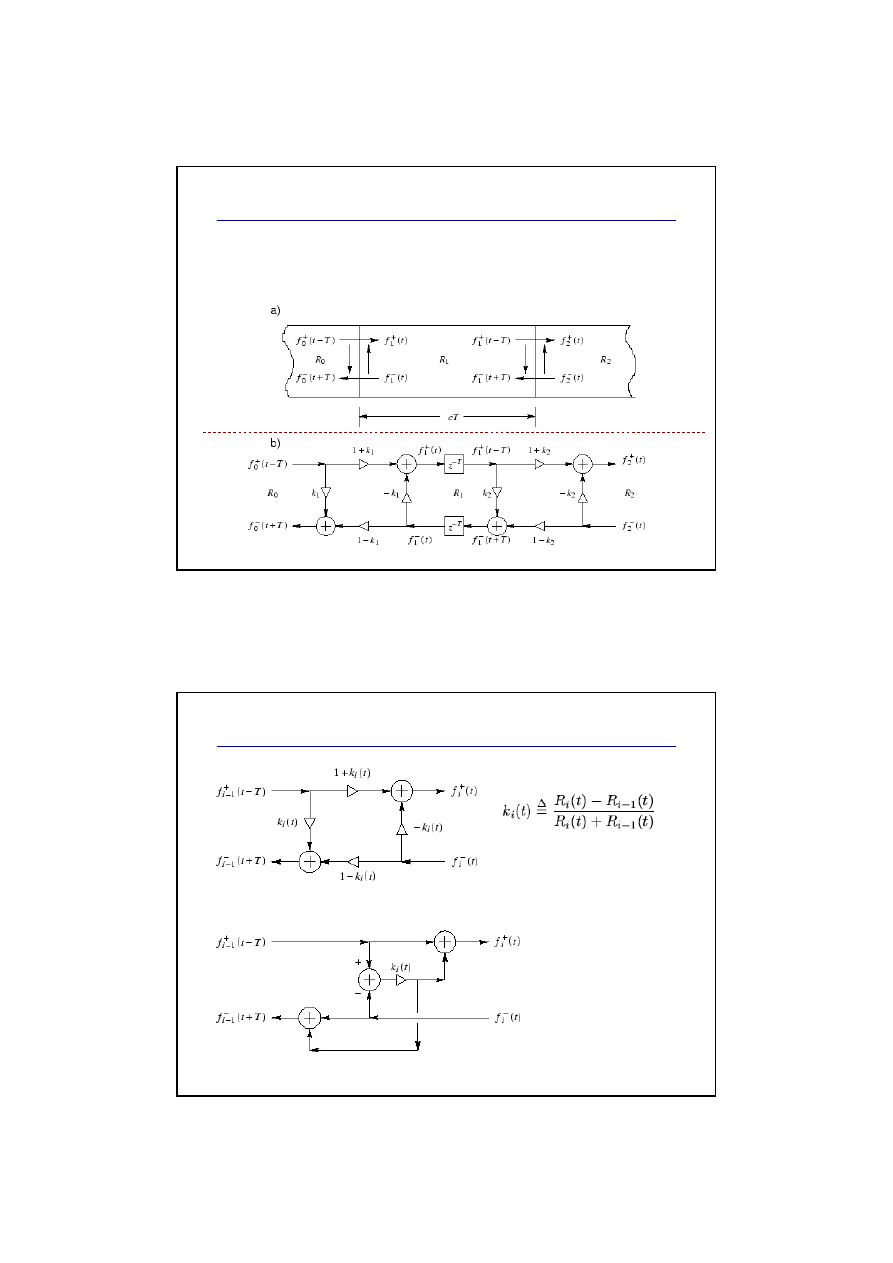
Modelowanie kształtu instrumentu

Różnica impedancji akustycznych jest
modelowana za pomocą połączeń rozpraszających

Poł

ą

czenie rozpraszaj

ą

ce

R – pole
powierzchni
przekroju
falowodu

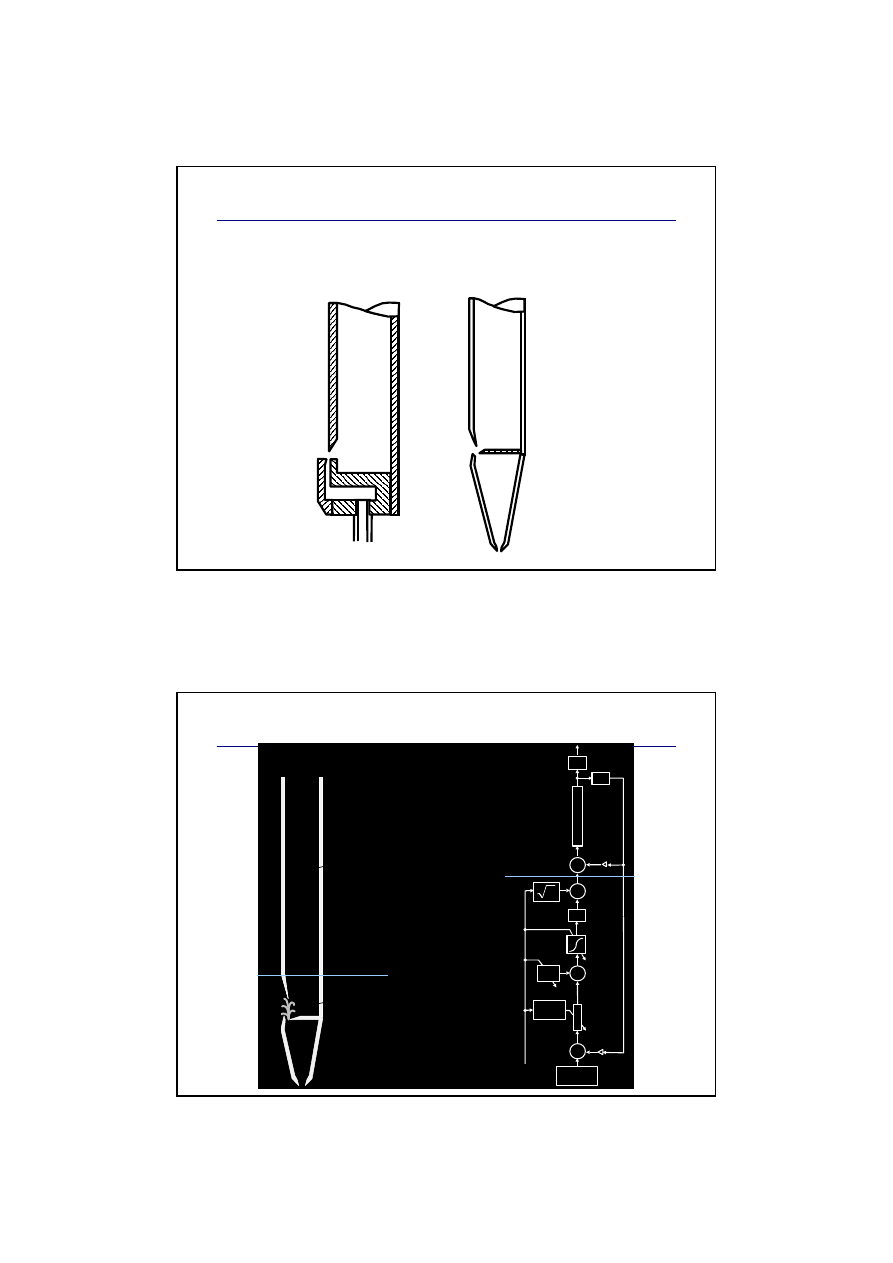
Model piszczałki organowej

Model organowej piszczałki wargowej sterowanej
trakturą mechaniczną

Model piszczałki wargowej

g.sz

.

P(t)

y

0

g

2

g

1

dl

2

dl

1

F

a

F

b

u.k.

DC

4

*

+

+

+

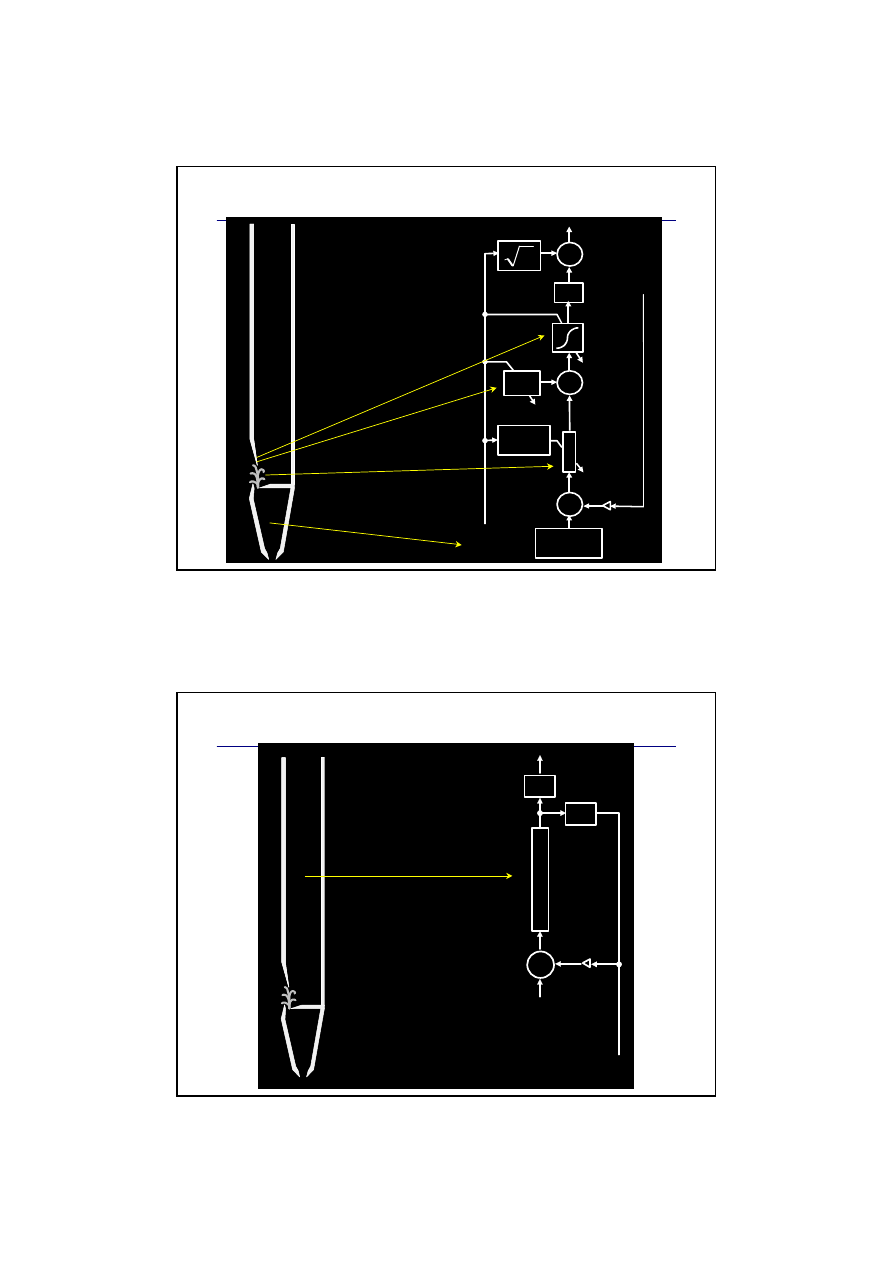
Model strumienia powietrza

P(t)

y

0

g

2

dl

2

g.sz.

u.k.

DC

4

*

+

+

Model korpusu piszczałki

g

1

dl

1

F

a

F

b

+

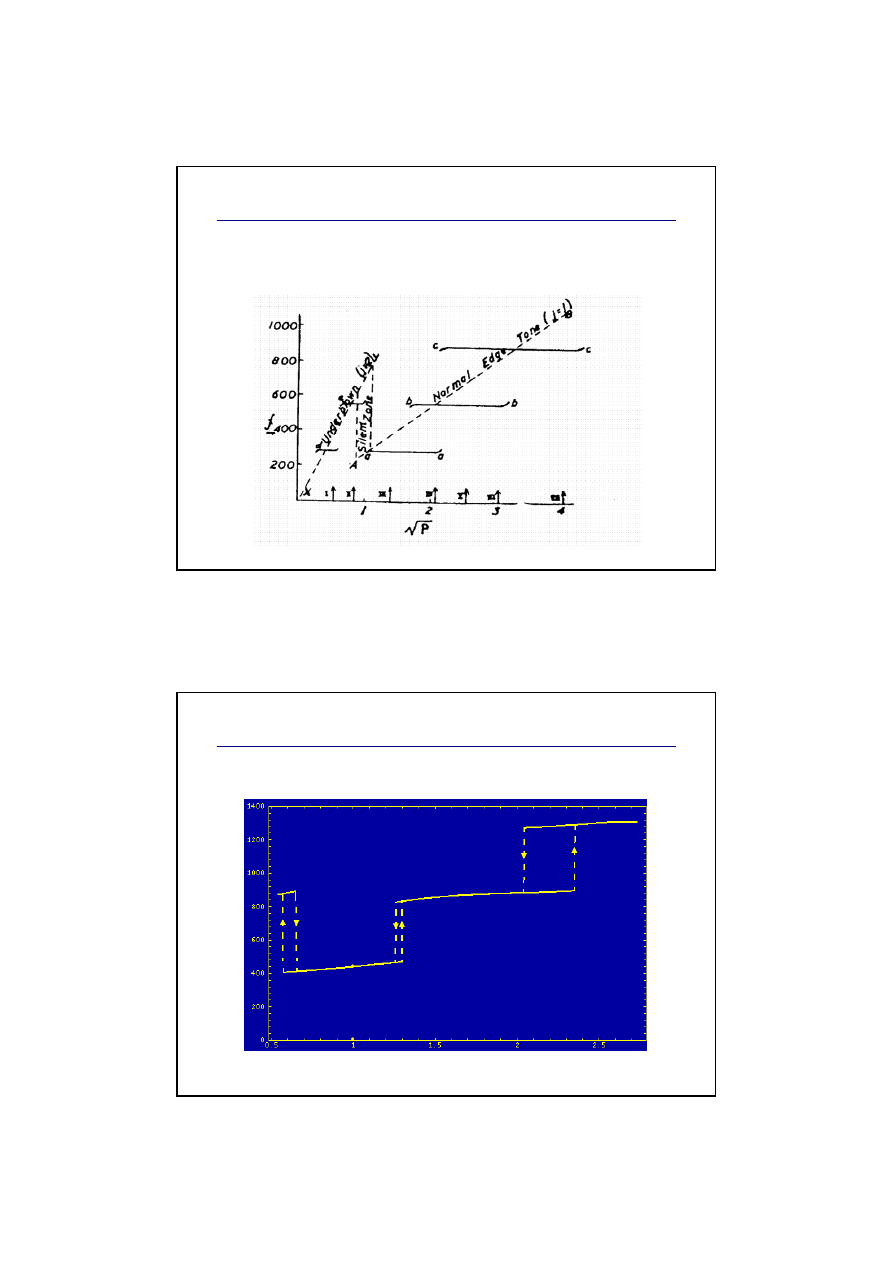
Modelowanie zmian ci

ś

nienia

Odpowiedź rzeczywistej piszczałki na zmiany
ciśnienia

Modelowanie zmian ci

ś

nienia

Odpowiedź modelu piszczałki na zmiany ciśnienia

P

nom

P

nom

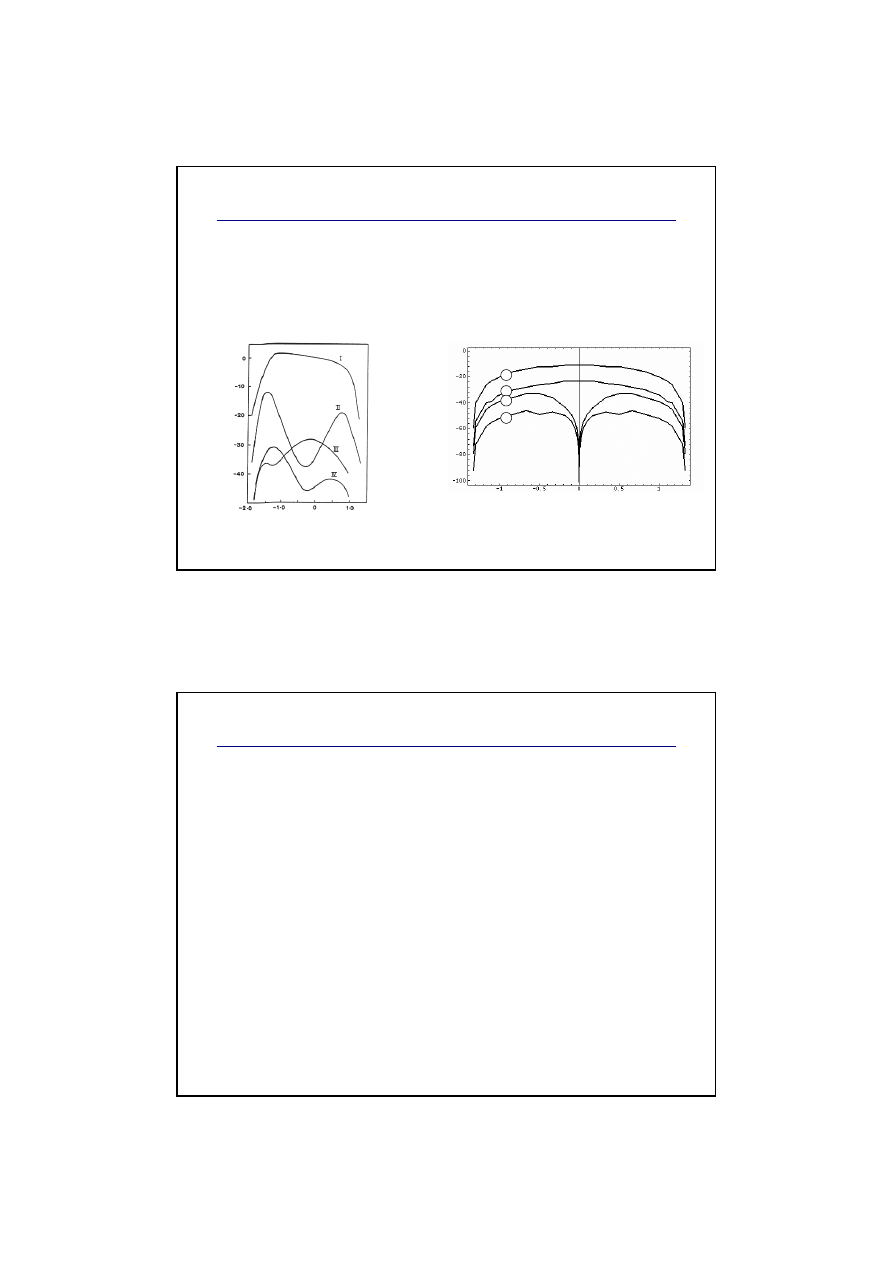
Symulacja przesuni

ę

cia górnej wargi

Symulacja zmiany kąta nachylenia strumienia
powietrza względem górnej wargi piszczałki

rzeczywista piszczałka

model falowodowy

y

0

[mm]

L

[dB]

1

3

2

4

Zalety i wady metody falowodowej

Zalety

metody falowodowej:

możliwość dokładnej symulacji rzeczywistych
instrumentów (wierność brzmienia)

możliwość uwzględnienia zjawisk
artykulacyjnych

działanie w czasie rzeczywistym

mniejsza złożoność obliczeniowa niż
w metodzie modelowania matematycznego

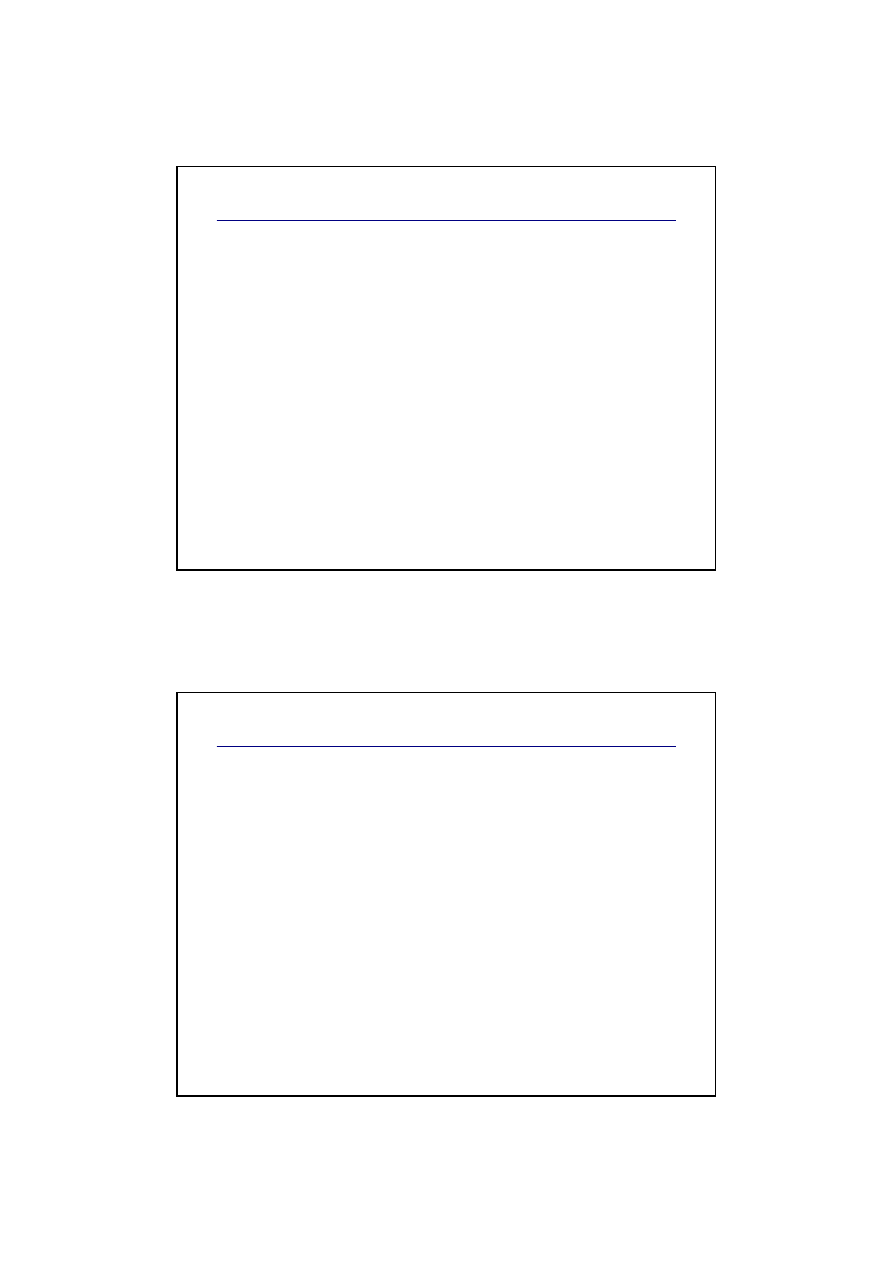
Zalety i wady metody falowodowej

Wady

metody falowodowej:

trudność w formułowaniu modelu fizycznego
instrumentu

duża złożoność obliczeniowa (w porównaniu
z „klasycznymi” metodami syntezy)

problem modelowania pewnych bardziej
skomplikowanych procesów

Wykorzystanie modeli fizycznych

Zastosowanie fizycznych modeli instrumentów
muzycznych w syntezie dźwięku:

badania naukowe – Stanford Univ. (Smith),
Helsinki Univ. of Tech.

instrumenty muzyczne firmy Yamaha

karta dźwiękowa Creative Labs AWE 64
– wybrany zestaw instrumentów (opcja)

syntetyzer programowy Yamaha Sondius XG

Przykład implementacji modeli falowodowych
(C++): Synthesis Toolkit – STK (Perry R. Cook).

Wykorzystanie modeli fizycznych

Lata 70. i 80. XX wieku: metody
matematycznego modelowania instrumentów,
zarzucone – zbyt mała moc obliczeniowa
komputerów, trudność dokonywania obliczeń.

Początek lat 90.: powstaje metoda
falowodowa, rozwijana w wielu ośrodkach
naukowych, duże nadzieje, zainteresowanie
firm komercyjnych.

Druga połowa lat 90.: pojawiają się istotne
ograniczenia metody falowodowej, częściowe
zarzucenie prac, utrata zainteresowania.

Wykorzystanie modeli fizycznych (cd.)

Obecnie: stopniowy powrót do metod
modelowania matematycznego (wzrost mocy
obliczeniowej komputerów, nowe narzędzia
matematyczne).

Przyszłość: połączenie obu metod?