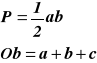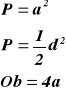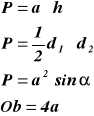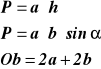IX. PLANIMETRIA

I. Figury płaskie 1. Trójkąt dowolny Wzór Herona:

2. Trójkąt równoboczny

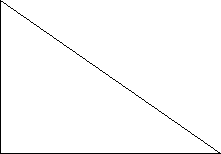
3. Trójkąt prostokątny

Kwadrat

Prostokąt

Romb

Równoległobok

Trapez

II. Twierdzenie sinusów W dowolnym trójkącie stosunek długości boku do sinusa przeciwległego kąta jest stały i równy średnicy okręgu opisanego na tym trójkącie.

III. Twierdzenie cosinusów

IV. Twierdzenie Pitagorasa Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.

V. Twierdzenie Talesa Jeżeli ramiona kąta przetniemy dwiema prostymi równoległymi, to długości odcinków wyznaczonych przez te proste na jednym ramieniu kąta są proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu.

VI. Okrąg wpisany w trójkąt i opisany na okręgu

VII. Odcinki występujące w trójkącie Środkowe trójkąta przecinają się w jednym punkcie, który dzieli każdą z nich w stosunku 2 : 1 (dłuższa część to ta mierzona od wierzchołka). Punkt przecięcia środkowych trójkąta nazywamy środkiem ciężkości trójkąta. Dwusieczna kąta wewnętrznego trójkąta dzieli bok przeciwległy kątowi na dwa odcinki, których stosunek długości jest równy odpowiedniemu stosunkowi długości pozostałych boków.

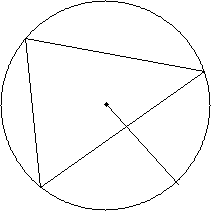
VIII. Czworokąt wpisany w okrąg i opisany na okręgu Czworokąt można wpisać w okrąg, gdy suma miar jego przeciwległych kątów jest równa 180^0. Czworokąt można opisać na okręgu, gdy sumy długości przeciwległych boków są równe.

52

a - długość boku rombu

h - wysokość rombu ⊥ do boku a

d₁ , d₂ - długości przekątnych rombu

α - miara kąta między dwoma bokami rombu

a - długość boku kwadratu

d - długość przekątnej

P - pole trójkąta

Ob = obwód trójkąta

a - długość boku

h - długość wysokości

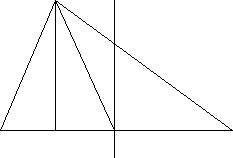
h - wysokość (odcinek poprowadzony z wierzchołka
prostopadle do przeciwległego boku)

d - symetralna boku (prosta prostopadła do boku trójkąta
przechodząca przez jego środek)

e - środkowa trójkąta (odcinek łączący wierzchołek
trójkąta ze środkiem przeciwległego boku)

d

e

h

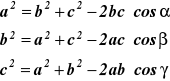
a

b

c

γ

α

β

a, b - długości podstaw trapezu
h - długość wysokości

R - długość promienia okręgu

opisanego na trójkącie

a

b

c

r

R

Środek okręgu wpisanego w trójkąt znajduje się w punkcie przecięcia dwusiecznych kątów wewnętrznych trójkąta.

P - pole trójkąta
r - długość promienia okręgu
wpisanego w trójkąt
a, b, c, - długości boków trójkąta

Środek okręgu opisanego na trójkącie znajduje się w
punkcie przecięcia symetralnych boków trójkąta.

a - podstawa trójkąta

h - wysokość opuszczona na podstawę

a, b - długości boków trójkąta

α - kąt zawarty między bokami a i b

a, b, c - długości boków trójkąta

R - promień okręgu opisanego na trójkącie

Ob - obwód trójkąta

r - promień okręgu wpisanego w trójkąt

a

b

a, b - długości boków równoległoboku

h - długość wysokości ⊥ do boku a

α - kąt między sąsiednimi bokami równoległoboku

a, b - długości boków prostokąta

a, b - długości przyprostokątnych

c - długość przeciwprostokątnej
w trójkącie prostokątnym

c

.

γ

a

b

c

R

α

β

---