- 1 -

PODSTAWY ELEKTROTECHNIKI I ELEKTRONIKI

dr inż. Marek KUCHTA

[e-mail]

p. 79 / S tel. 6 837 – 585

Warunkiem zaliczenia przedmiotu jest zaliczenie ćwiczeń

rachunkowych i ćwiczeń laboratoryjnych.



Warunkiem zaliczenia ćwiczeń rachunkowych jest zaliczenie pracy
kontrolnej na ostatnich zajęciach oraz uzyskanie oceny średniej z
odpowiedzi w czasie zajęć nie mniej niż 3,0. Nieobecności na więcej
niż 1 ćwiczeniach rachunkowych wymaga zaliczenia opuszczonych
zajęć w ramach konsultacji.



Warunkiem zaliczenia ćwiczeń laboratoryjnych jest uzyskanie
wymaganej liczby punktów. Student otrzymuje z każdego ćwiczenia
punkty za:



przygotowanie do ćwiczenia

(w skali 0

4);



praktyczne wykonanie ćwiczenia (w skali 0

2);



sprawozdanie z ćwiczenia

(w skali 0

4);

Ocena końcowa za ćwiczenia laboratoryjne wystawiana jest zgodnie z
poniższą tabelą.

Liczba punktów

0

10,5

11

12,5 1314,5 1516,5 1718,5 1920

Ocena końcowa

2 (ndst)

3 (dst)

3.5

(dst+)

4 (db)

4.5

(db+)

5 (bdb)



Zaliczenie przeprowadzane jest w formie pisemnej i ustnej.

UWAGA: do laboratorium ZOiSE p. 81/S należy dostarczyć wykaz

studentów grupy z podziałem na zespoły.

- 2 -

1. SYGNAŁY ELEKTRYCZNE

1.1. KLASYFIKACJA SYGNAŁÓW

W elektronice

PRZEBIEGI CZASOWE
napięcia lub prądu elektrycznego nazywamy
SYGNAŁAMI ELEKTRYCZNYMI

Sygnały elektryczne mogą być dowolnymi funkcjami rzeczywistymi
czasu, a więc zmiennej rzeczywistej t.

Badając zmienności tych funkcji:

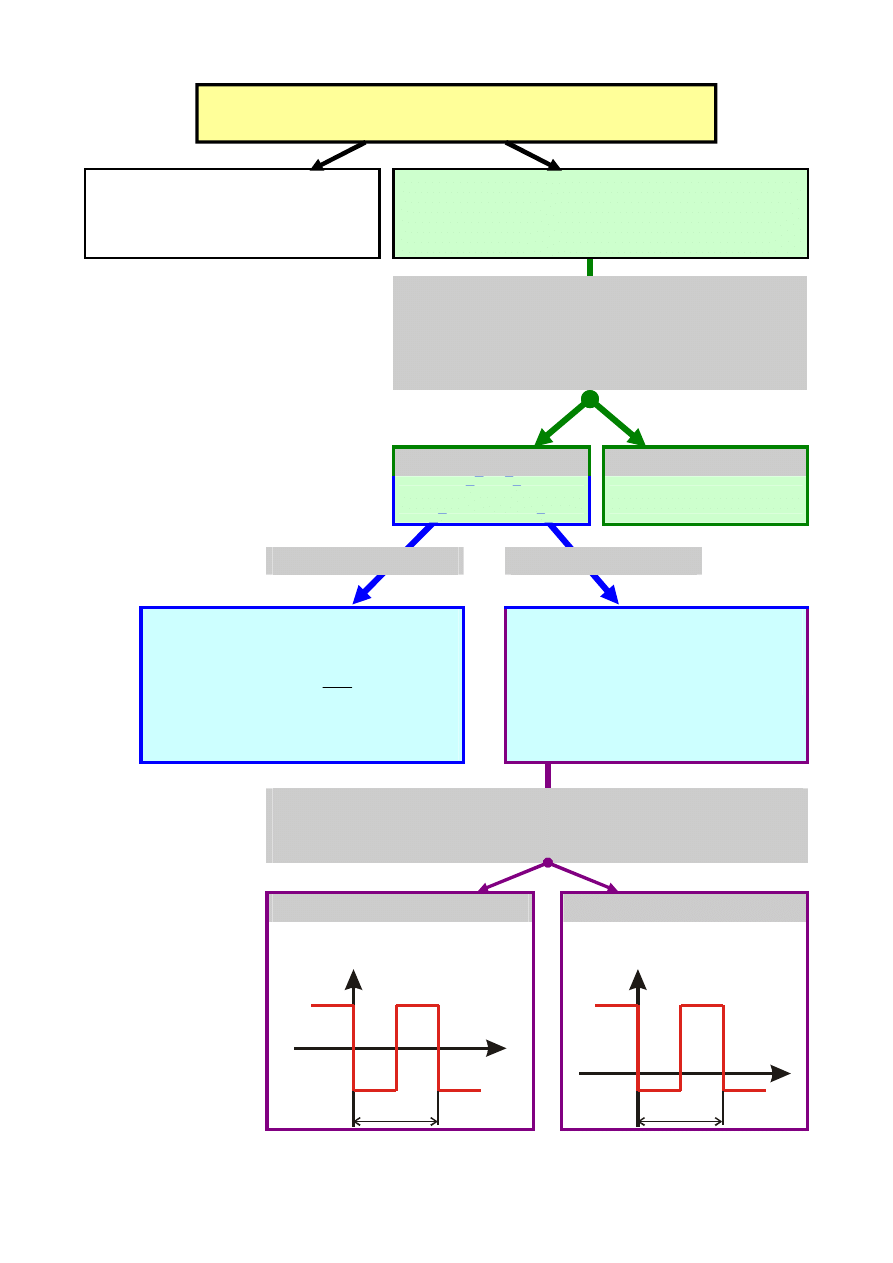
SYGNAŁY ELEKTRYCZNE

SYGNAŁY ZDETERMINOWANE

Sygnałem

zdeterminowanym

nazywamy

sygnał,

którego

wystąpienie można przewidzieć i
który daje się opisać analitycznie

SYGNAŁY STOCHASTYCZNE

Sygnałem losowym nazywamy
sygnał, którego wystąpienia ani
wartości

nie

możemy

przewidzieć.

- 3 -

STAŁE

f(t) = const. dla













,

t

,

oznaczane: U, I

ZMIENNE

f(t) ≠ const. dla













,

t

,

oznaczane: u(t), i(t),

Jeżeli warunek okresowości

 





kT

t

f

t

f

t

T









0

T- okres właściwy, k – liczba całkowita

jest spełniony

nie jest spełniony

OKRESOWE

NIEOKRESOWE

sinusoidalne

niesinusoidalne

HARMONICZNE

 





















t

T

F

t

f

m

2

sin

dla













,

t

,

ODKSZTAŁCONE

Jeżeli warunek:

 

0

0





dt

t

f

T

jest spełniony

nie jest spełniony

PRZEMIENNE

f t

( )

t

T

-

+

TĘTNIĄCE

f t

( )

t

T

-

+

SYGNAŁY ZDETERMINOWANE

- 4 -

1.2. PARAMETRY SYGNAŁÓW OKRESOWYCH

Dla sygnału okresowego x o wartościach x(t):

 Moc średnia

 

dt

t

x

T

P

T

x





0

2

1

(1.1)

 Wartość maksymalna – największa wartość chwilowa jaką

sygnał osiąga – oznaczamy ją jako X

m

 Wartość średnia całookresowa

(jest to średnia arytmetyczna tego
sygnału obliczona za jeden okres)

 

 

dt

t

x

T

t

x

X

T

C

śr







0

1

(1.2)

 Wartość średnia półokresowa

(jest to średnia arytmetyczna tego
sygnału obliczona za połowę okresu)

 

dt

t

x

T

X

T

śr





2

/

0

2

(1.3)

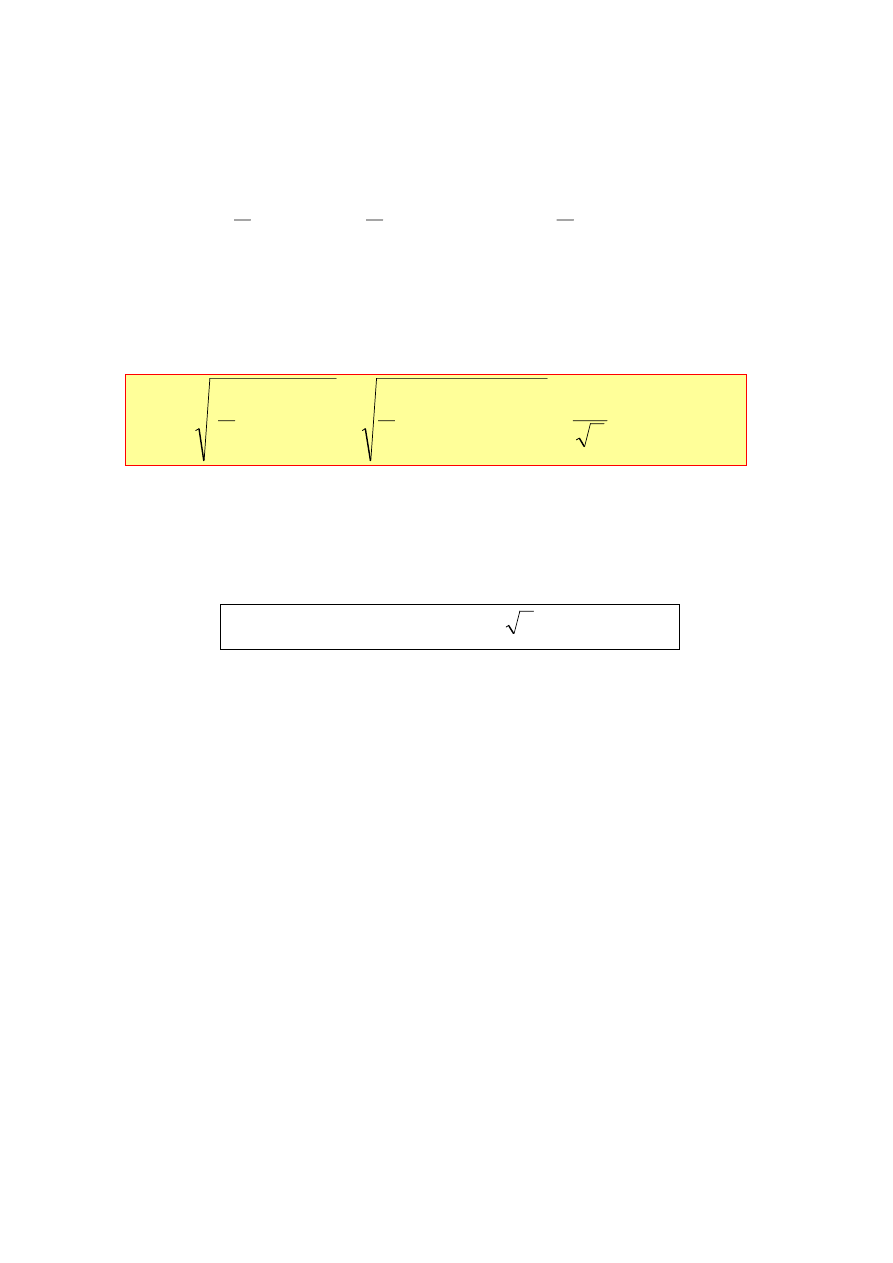
 WARTOŚĆ SKUTECZNA

(jest to pierwiastek kwadratowy z
wartości średniej kwadratu sygnału
obliczonej za jeden okres, inaczej -
pierwiastek kwadratowy ze średniej mocy
sygnału)

 

 

x

T

sk

P

t

x

dt

t

x

T

X

X











2

0

2

1

(1.4)

- 5 -

1.3. SYGNAŁY HARMONICZNE

W grupie przebiegów okresowych szczególne znaczenie mają sygnały

harmoniczne, tzn. cosinusoidalne i sinusoidalne. Ponieważ jednak





t

t







cos

2

sin





,

nazwiemy je ogólnie sinusoidalnymi (sinusoidalnie-zmiennymi).

Sygnałami harmonicznymi nazywamy sygnały, których przebieg

jest sinusoidalną funkcją czasu

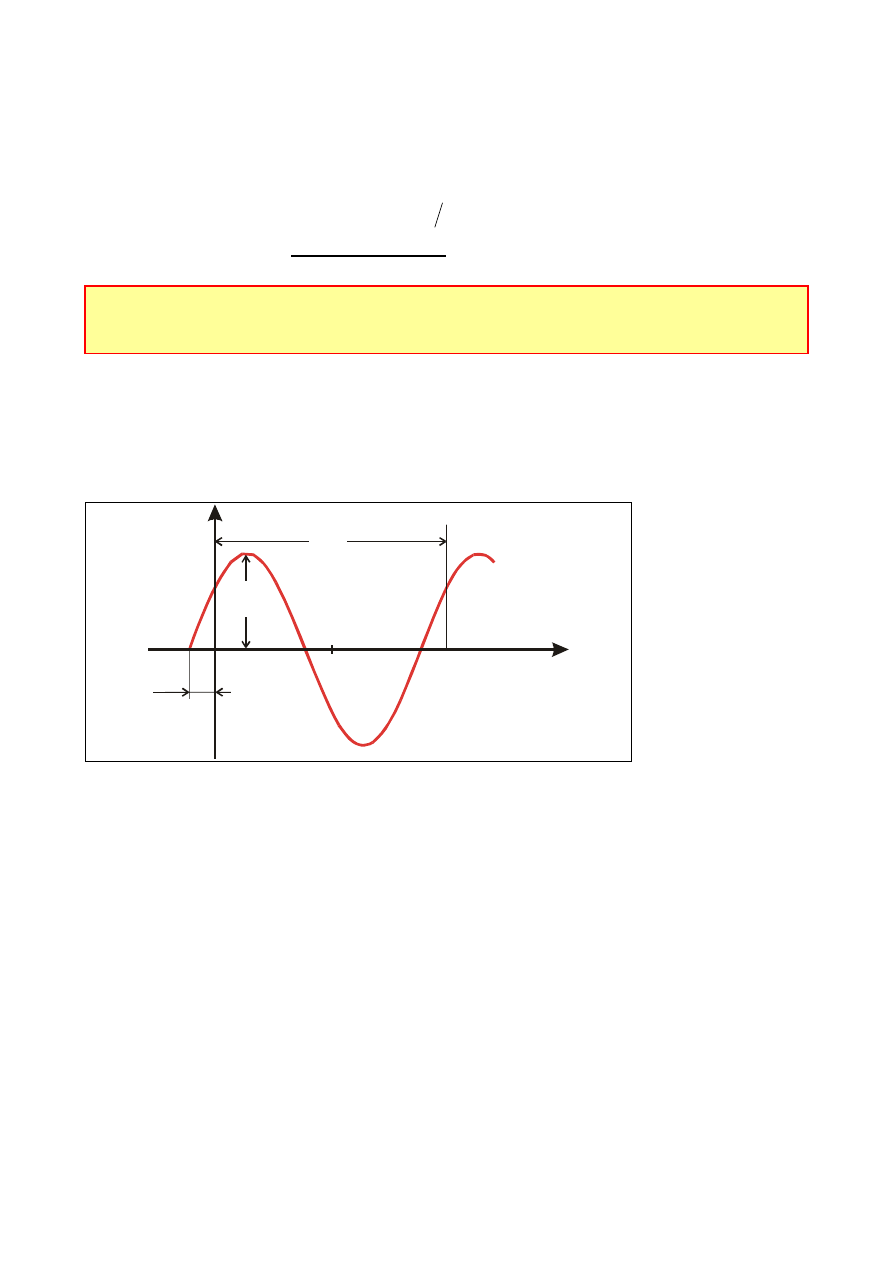
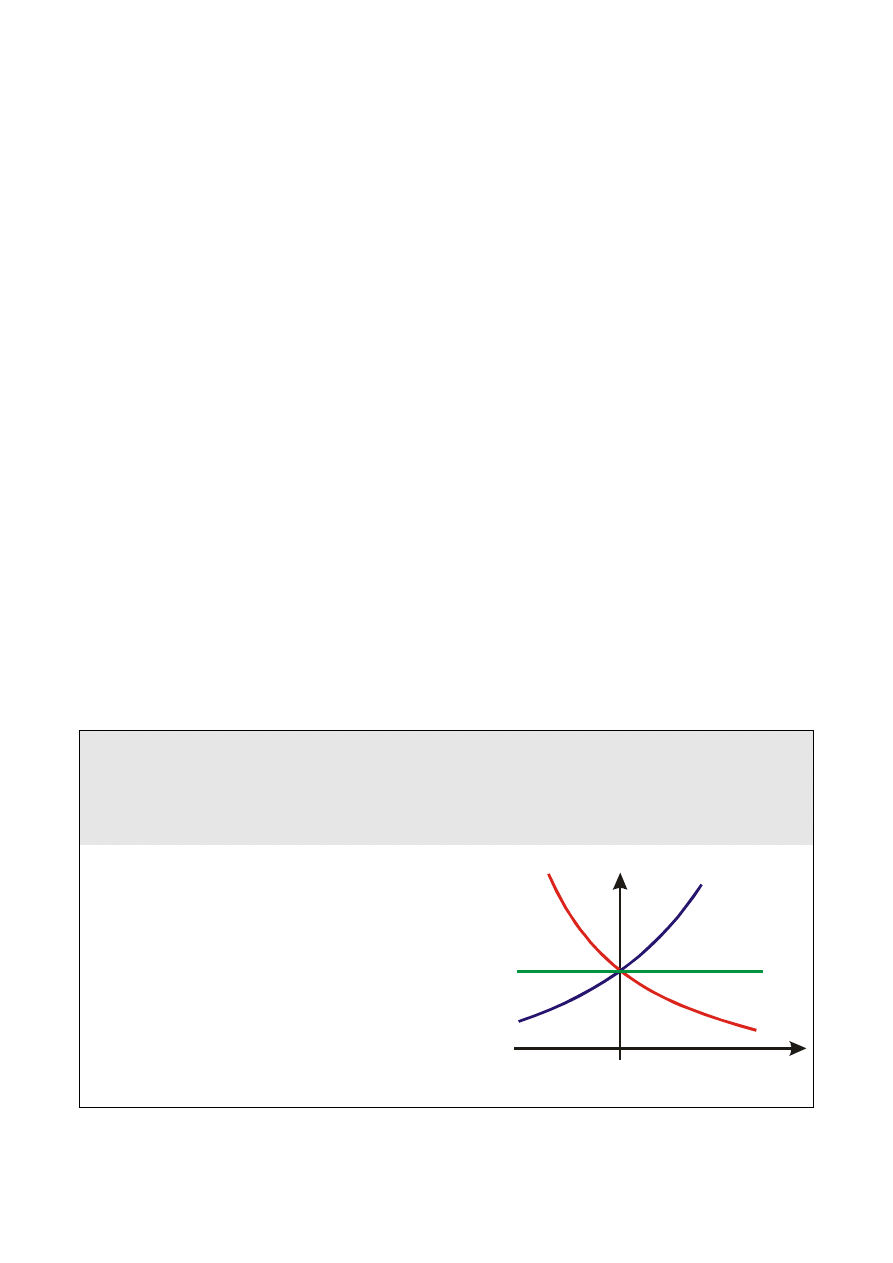
Załóżmy, że rozpatrujemy sygnał sinusoidalny w postaci napięcia:

 





u

m

t

U

t

u









sin

(1.5)

0

u



u t

( )

U

m

T/2

T





t

t

W czasie
odpowiadającym
jednemu okresowi
faza napięcia
zmienia się o 2



,

tzn.





2



T

. Na

rys. na osi
odciętych
oznaczono skalę
czasu i skalę
kątową.

gdzie: u(t)

- wartość chwilowa napięcia;

U

m

- wartość maksymalna napięcia (nazywana amplitudą);

u



- początkowy kąt fazowy, faza początkowa napięcia w

chwili t = 0;

u

t







- kąt fazowy, faza napięcia w chwili t;



=2



f - pulsacja (częstotliwość kątowa) mierzona w rad/s;

f =1/T

- częstotliwość mierzona w Hz, będąca odwrotnością

okresu.

- 6 -

Wartość średnia (półokresowa) napięcia sinusoidalnego wynosi wg

wzoru (1.3)

 

m

m

T

m

T

śr

U

U

dt

t

U

T

dt

t

u

T

U

637

,

0

2

sin

2

2

2

/

0

2

/

0

















(1.6)

Wartość skuteczna napięcia sinusoidalnego zgodnie ze wzorem (1.4)

wynosi

 

m

m

T

m

T

U

U

dt

t

U

T

dt

t

u

T

U

707

,

0

2

sin

1

1

0

2

2

0

2















(1.7)

Oznacza to, że równanie opisujące napięcie harmoniczne możemy
przedstawić jako

 









u

u

m

t

U

t

U

t

u

















sin

2

sin

(1.8)

- 7 -

1.4. SYGNAŁ WYKŁADNICZY

Funkcja wykładnicza jest traktowana niemal jako funkcja magiczna.

Wynika to stąd, że

 każdy sygnał występujący w praktyce może być zawsze wyrażony

w postaci sumy funkcji wykładniczych;

 w przypadku układów liniowych odpowiedź układu na wymuszenie

wykładnicze jest także wykładnicza.

Przyjmijmy, że sygnał wykładniczy ma postać:















,

)

(

t

e

A

t

x

t

s

dla

(1.9)

Współczynnik s występujący w wykładniku jest zespolony





j

s





(1.10)

a zatem





t

j

t

t

j

e

e

A

e

A

t

x















)

(

(1.12)

Rozpatrzmy szczególne przypadki w zależności od tego jakie wartości

przyjmuje s.

1.

Jeżeli s jest liczbą rzeczywistą (tzn.



= 0) wtedy

t

e

A

t

x





)

(

i ma charakter zależny od wartości



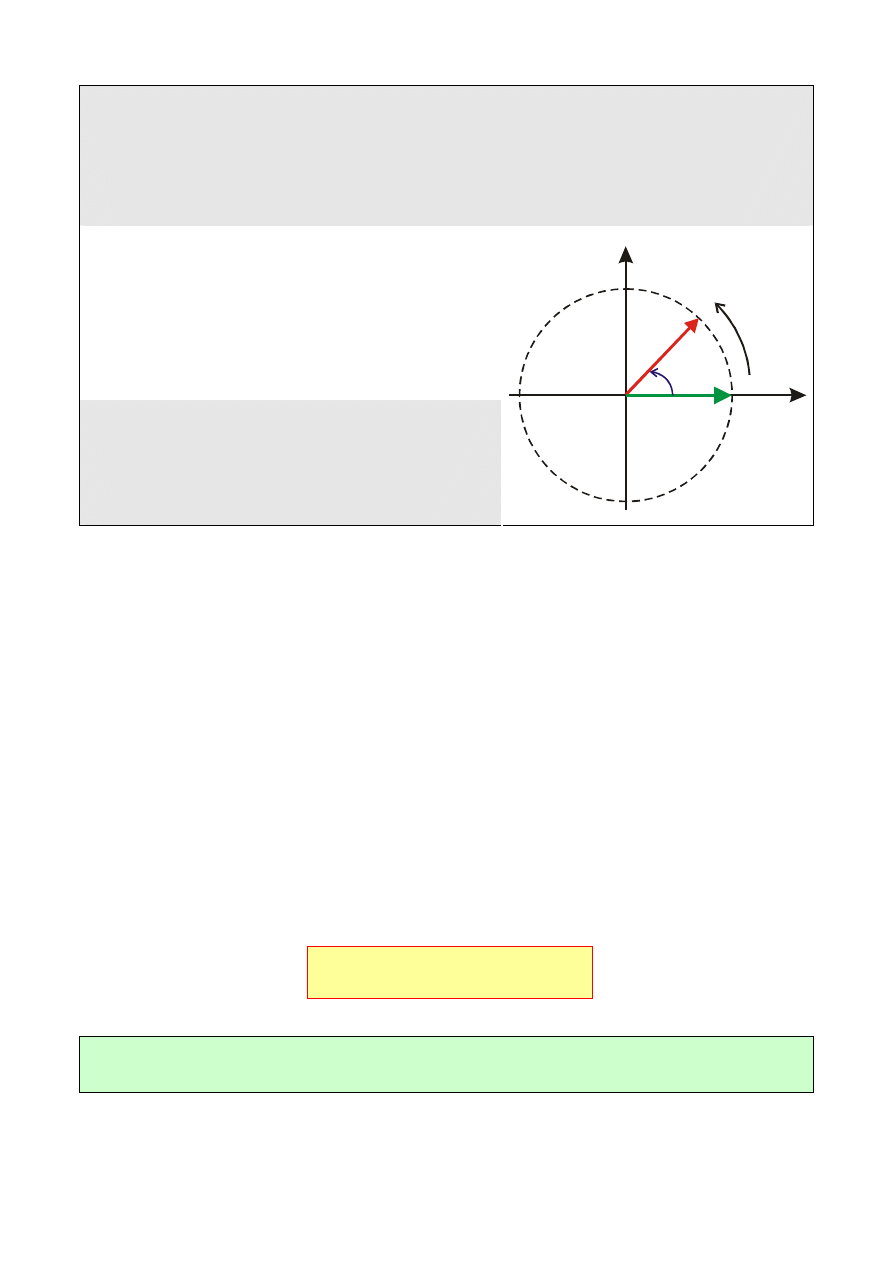
a) gdy



< 0

, sygnał x(t) ma charakter

monotonicznie malejącej funkcji
czasu;

b) gdy



= 0

, sygnał x(t) jest sygnałem

stałym o wartości A;

c) gdy



> 0

, sygnał x(t) ma charakter

monotonicznie rosnącej funkcji
czasu.

0

x t

( )

t

A

 0

>

 0

<

 = 0

- 8 -

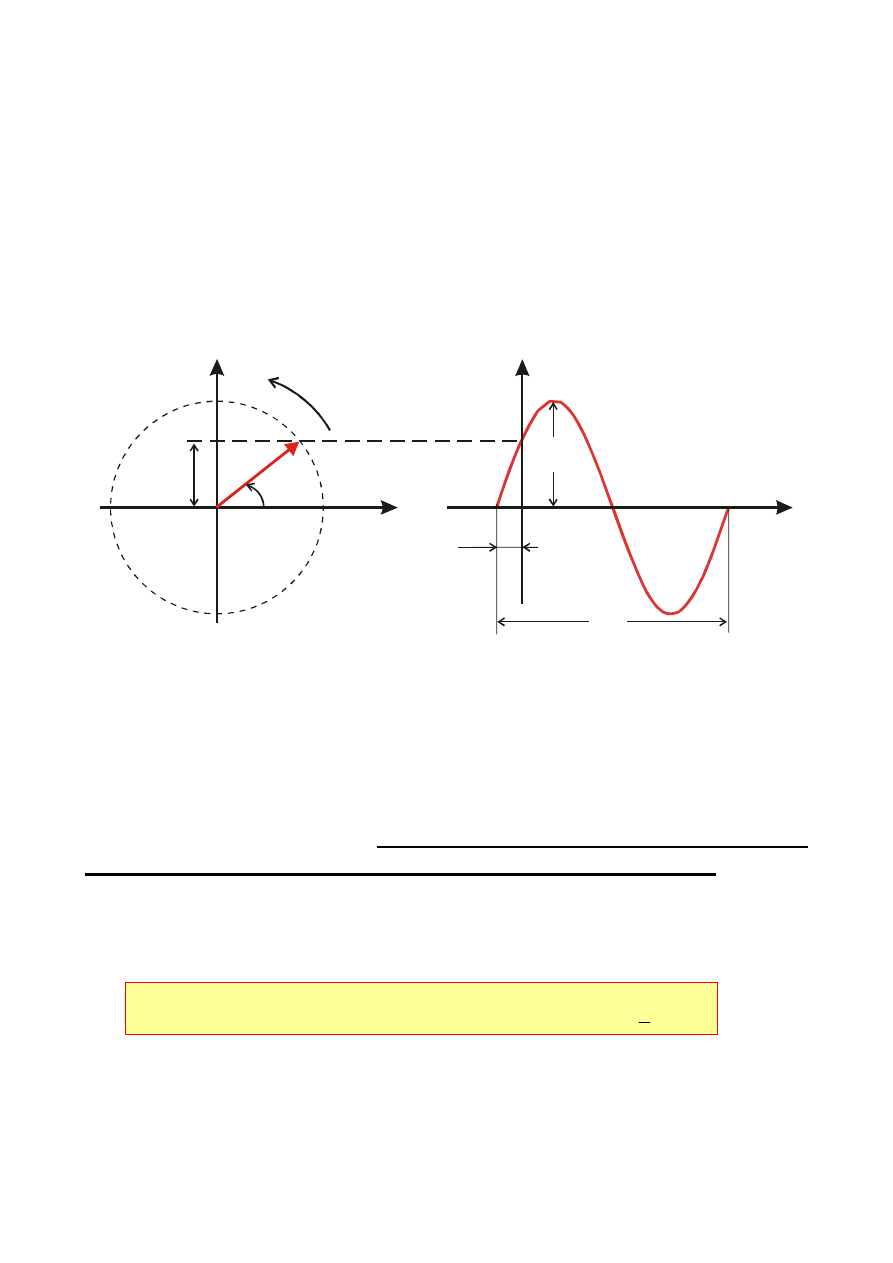
2. Jeżeli s jest liczbą urojoną (tzn.



=0) wtedy

t

j

e

A

t

x





)

(

sygnał x(t) może być interpretowany na płaszczyźnie zmiennej
zespolonej za pomocą tzw. wektora wirującego

obracającego się z prędkością kątową



w kierunku przeciwnym do ruchu
wskazówek zegara. Położenie tego
wektora na płaszczyźnie w danej chwili t
określone jest za pomocą kąta



t.

Czynnik

t

j

e



spełnia rolę operatora
obrotu,

natomiast

A

jest modułem wektora.

0

t = 0

A

t



Ae

j

t



Re

Im

Uwzględniając wzór Eulera

t

j

t

e

j







sin

cos





(1.13)

można wektor wirujący wyrazić za pomocą dwóch składowych

 

t

A

j

t

A

e

A

t

x

j







sin

cos







(1.14)

Część rzeczywista wektora wirującego przedstawia sygnał o charakterze
cosinusoidalnym





t

A

e

A

t

j





cos

Re



(1.15)

Część urojona wektora wirującego przedstawia sygnał o charakterze
sinusoidalnym





t

A

e

A

t

j





sin

Im



(1.16)

Wynika stąd, że najczęściej spotykane przebiegi wielkości elektrycznych
stanowią szczególne przypadki sygnału o charakterze wykładniczym.

- 9 -

1.5. OPIS SYMBOLICZNY SYGNAŁU HARMONICZNEGO

Rozpatrzmy ponownie sygnał sinusoidalny w postaci napięcia:

 





u

m

t

U

t

u









sin

(1.17)

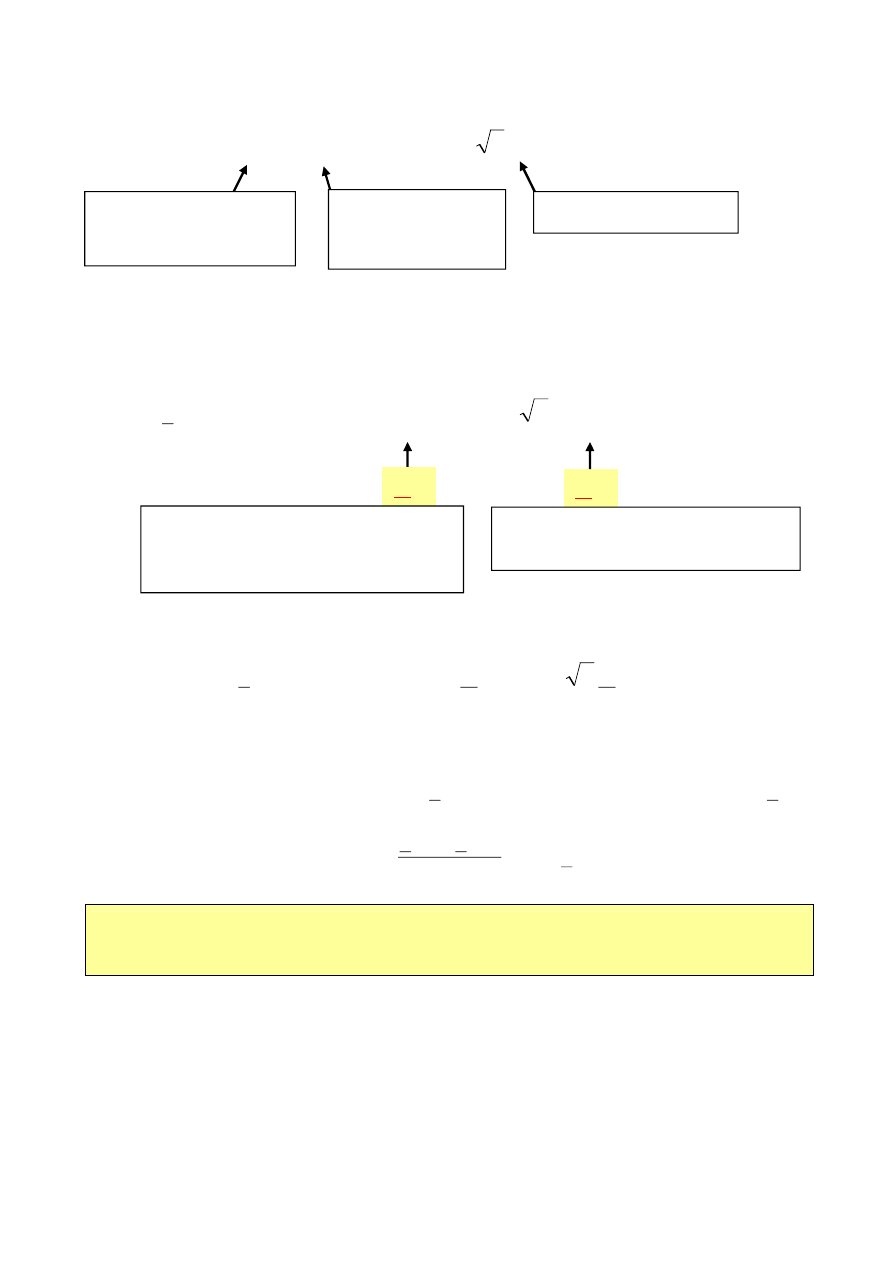
Związek pomiędzy wektorem wirującym na płaszczyźnie zmiennej

zespolonej a rozpatrywanym sygnałem sinusoidalnym przedstawia rys.

0



Re

Im

0

u



u t

( )

U

m

T

t

t

U

m

u



u(0)

u(0)

Wartość chwilowa napięcia w chwili t = 0 wynosi

 

u

m

U

u



sin

0



(1.18)

W chwili tej wektor wirujący o amplitudzie U

m

jest nachylony względem

osi liczb rzeczywistych pod kątem

u



. Rzut tego wektora na oś liczb

urojonych wynosi u(0), czyli wartość chwilowa sygnału sinusoidalnego
jest równa rzutowi wektora wirującego na oś liczb urojonych.

Analitycznie można to ująć, zgodnie z zależnością (1.16), następująco:

dla każdej chwili t

 













 

 

t

u

e

U

t

U

t

u

u

t

j

m

u

m

Im

Im

sin



















(1.19)

- 10 -

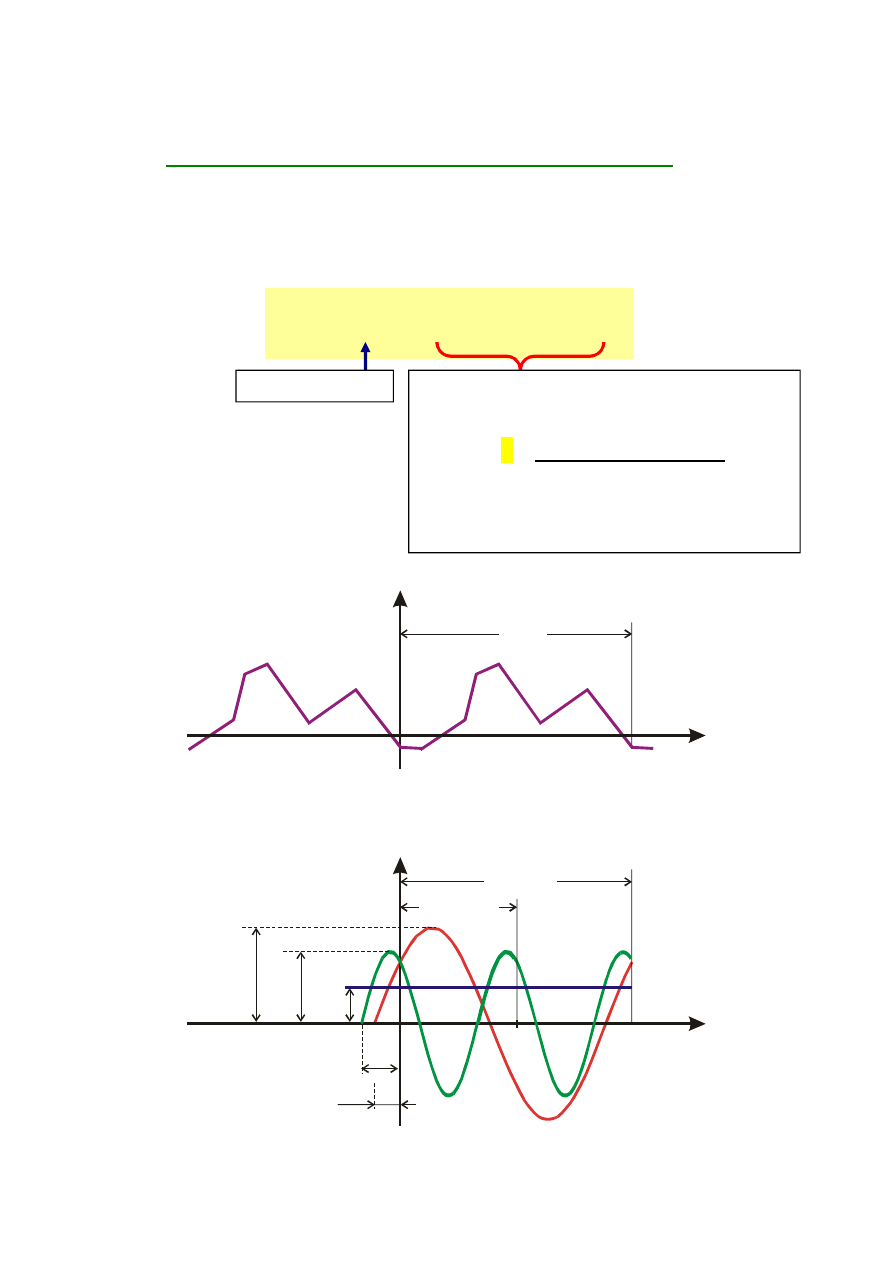
Sygnał sinusoidalny:

 









u

u

m

t

U

t

U

t

u

















sin

2

sin

posiada następującą

POSTAĆ SYMBOLICZNĄ (symboliczną wartość chwilową):





t

j

j

t

j

j

m

t

j

m

e

e

U

e

e

U

e

U

t

u

u

u

u



























2

)

(









(1.20)

Czyli:





t

j

t

j

m

t

j

m

e

U

e

U

e

U

t

u

u









2

)

(









(1.21)

UWAGI:



   

   

t

u

t

u

t

u

t

u





ˆ

ć

oś

odpowiedni

tylko

ć

równoś

zachodzi

nie

 natomiast:

   

 

 

 

t

u

j

t

u

t

u

t

u

Im

2

*







(1.22)

 Metoda symboliczna zapisu przebiegów sinusoidalnych pozwala

traktować je jako przebiegi wykładnicze.

(rzeczywista)

wartość chwilowa

amplituda

(wartość max.)

wartość skuteczna

U

m

U

symboliczna amplituda

/postać zespolona amplitudy/

/wskaz amplitudy/

symboliczna wartość skuteczna

/wskaz wartości skutecznej/

- 11 -

1.6. OPIS WIDMOWY SYGNAŁÓW ODKSZTAŁCONYCH

A) TRYGONOMETRYCZNY SZEREG FOURIERA

Dowolną funkcję okresową x(t) o okresie T, spełniającą warunki

Dirichleta, można przedstawić w postaci szeregu harmonicznego
nieskończonego zwanego szeregiem trygonometrycznym Fouriera:

 

















1

1

0

sin

k

k

k

m

t

k

F

F

t

x





(1.23)

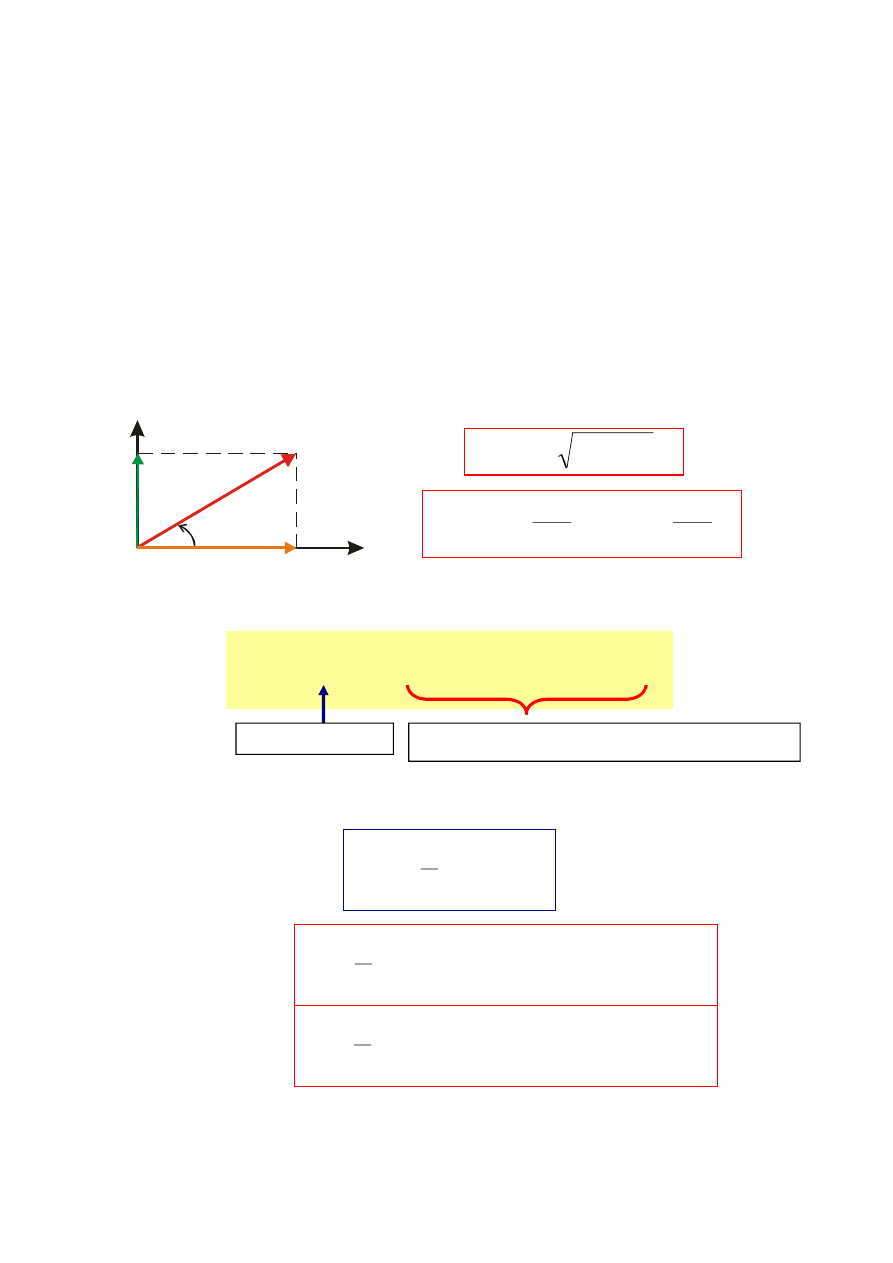
Interpretacja:

0

T

t

x t

( )

x(t)

=

F

0

+

F

m1

sin(



1

t+



1

)

+

F

m2

sin(2



1

t+



2

)

+ .........

0

F

m1

T

1

=T

t

t



1



2

F

m2

F

0

T

2

=T/2

k-ta harmoniczna rozwinięcia Fouriera

gdzie:



1

=2

/T – pulsacja podstawowa

k – rząd harmonicznej
F

mk

– amplituda k-tej harmonicznej



k

– faza początkowa k-tej harmonicznej

składowa stała

- 12 -

Wiadomo jednak, że









k

k

k

m

k

k

m

t

k

t

k

F

t

k

F













sin

cos

cos

sin

sin

1

1

1







(1.24)

Jeśli oznaczymy













k

k

k

m

k

k

k

m

B

F

A

F





cos

sin

(1.25)

to





t

k

B

t

k

A

t

k

F

k

k

k

k

m

1

1

1

sin

cos

sin















(1.26)

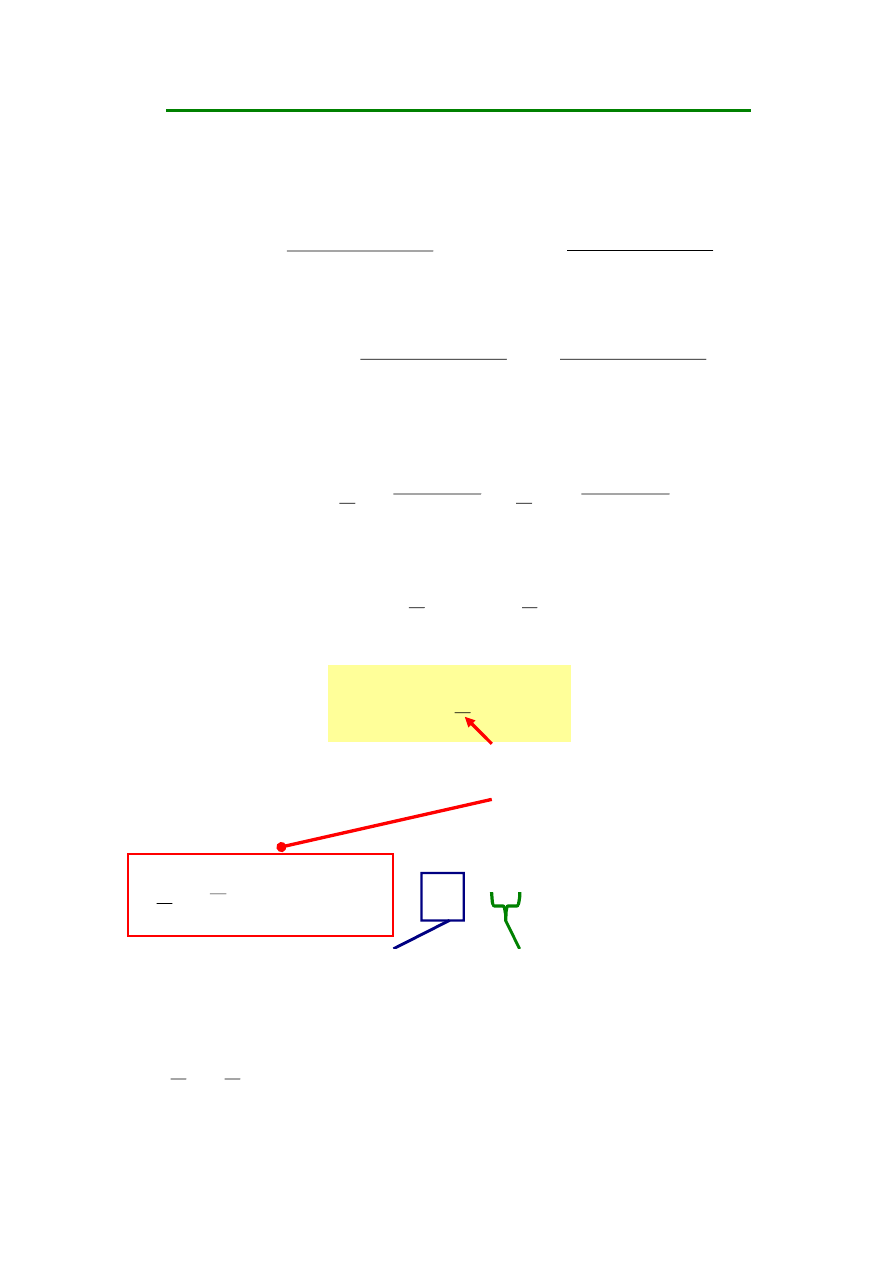
Gdy amplitudę k-tej harmonicznej przedstawimy jako wektor

wirujący, to z zależności trygonometrycznych wynikają wzory

Re

Im

F

mk



k

A

k

B

k

2

2

k

k

k

m

B

A

F





(1.27)

mk

k

k

mk

k

k

F

B

F

A









cos

,

sin

(1.28)

Uwzględniając powyższe zależności możemy szereg (1.23) przedstawić

 

















1

1

1

0

sin

cos

k

k

k

t

k

B

t

k

A

A

t

x





(1.29)

Współczynniki A

0

, A

k

, B

k

wyznacza się ze wzorów:

wartość średnia

 

dt

t

x

T

A

T

t

t







0

0

1

0

(1.30)

skład. kosinusoidalna

 



,

2

,

1

cos

2

1

0

0









k

dla

dt

t

k

t

x

T

A

T

t

t

k



(1.31)

skład. sinusoidalna

 



,

2

,

1

sin

2

1

0

0









k

dla

dt

t

k

t

x

T

B

T

t

t

k



(1.32)

k-ta harmoniczna rozwinięcia Fouriera

składowa stała

- 13 -

B) WYKŁADNICZY (ZESPOLONY) SZEREG FOURIERA

Jeśli w rozwinięciu w szereg Fouriera danym wyrażeniem (1.29)

zastosujemy podstawienie wynikające z wzorów Eulera

2

cos

1

1

1

t

jk

t

jk

e

e

t

k













,

j

e

e

t

k

t

jk

t

jk

2

sin

1

1

1













(1.33)

to otrzymamy

 





































1

0

2

2

1

1

1

1

k

t

jk

t

jk

k

t

jk

t

jk

k

j

e

e

B

e

e

A

A

t

x









(1.34)

Wprowadzając oznaczenia

2

,

2

,

0

0

k

k

k

k

k

k

jB

A

C

jB

A

C

A

C













(1.35)

stąd

 





















1

0

1

1

k

t

jk

k

t

jk

k

e

C

e

C

C

t

x





(1.36)

i ostatecznie

 











k

t

jk

k

e

C

t

x

1



(1.37)

którą to postać nazywamy postacią
zespoloną szeregu Fouriera.

 









T

t

t

t

k

j

k

dt

e

t

x

T

C

0

0

1

1





,

2

,

1

,

0









k

dla

e

C

k

j

k



(1.38)

Uwaga:

*

k

k

C

C





k

k

k

k

i

C

C















k-ty współczynnik wykładniczego
szeregu Fouriera

moduł k-tego współczynnika
wykładniczego szeregu Fouriera

argument k-tego współczynnika
wykładniczego szeregu Fouriera

- 14 -

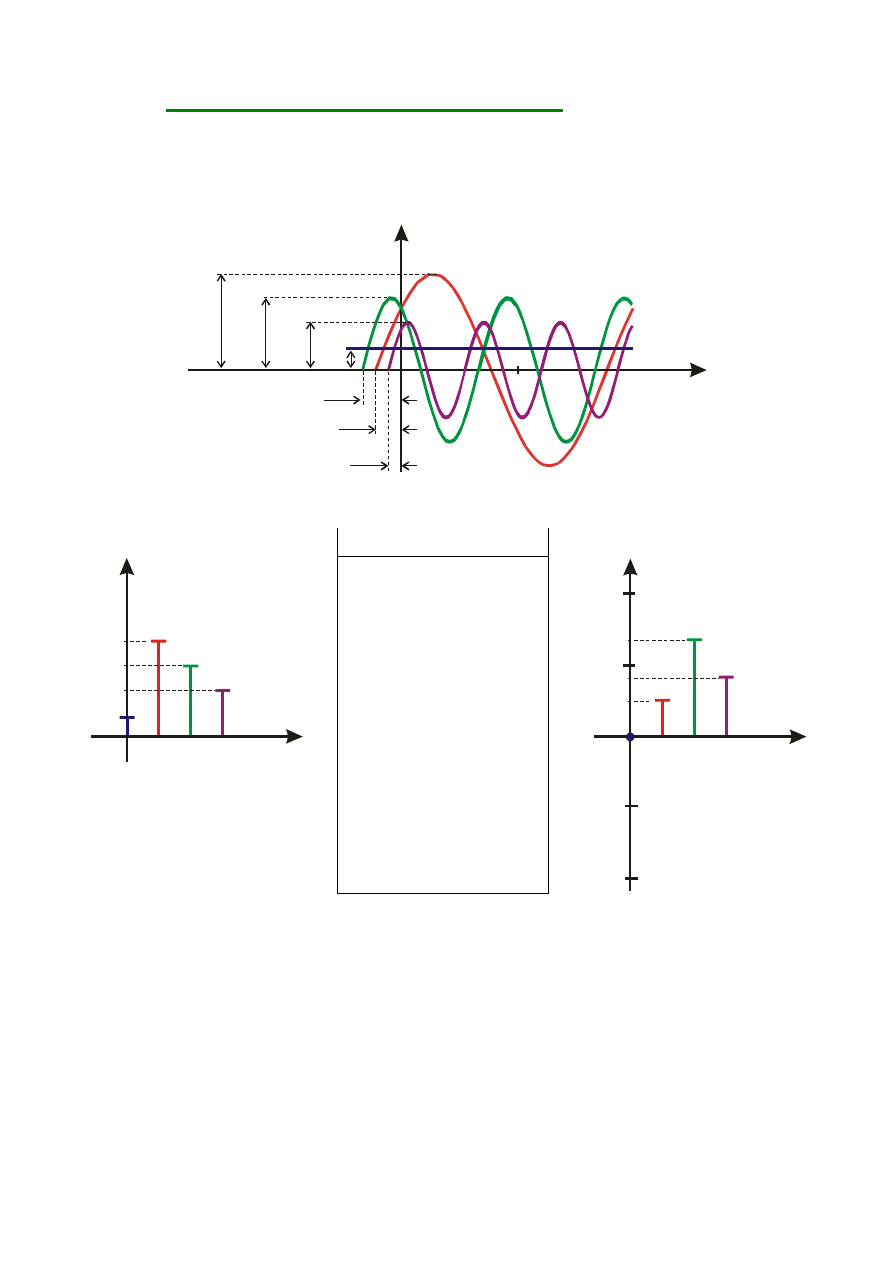
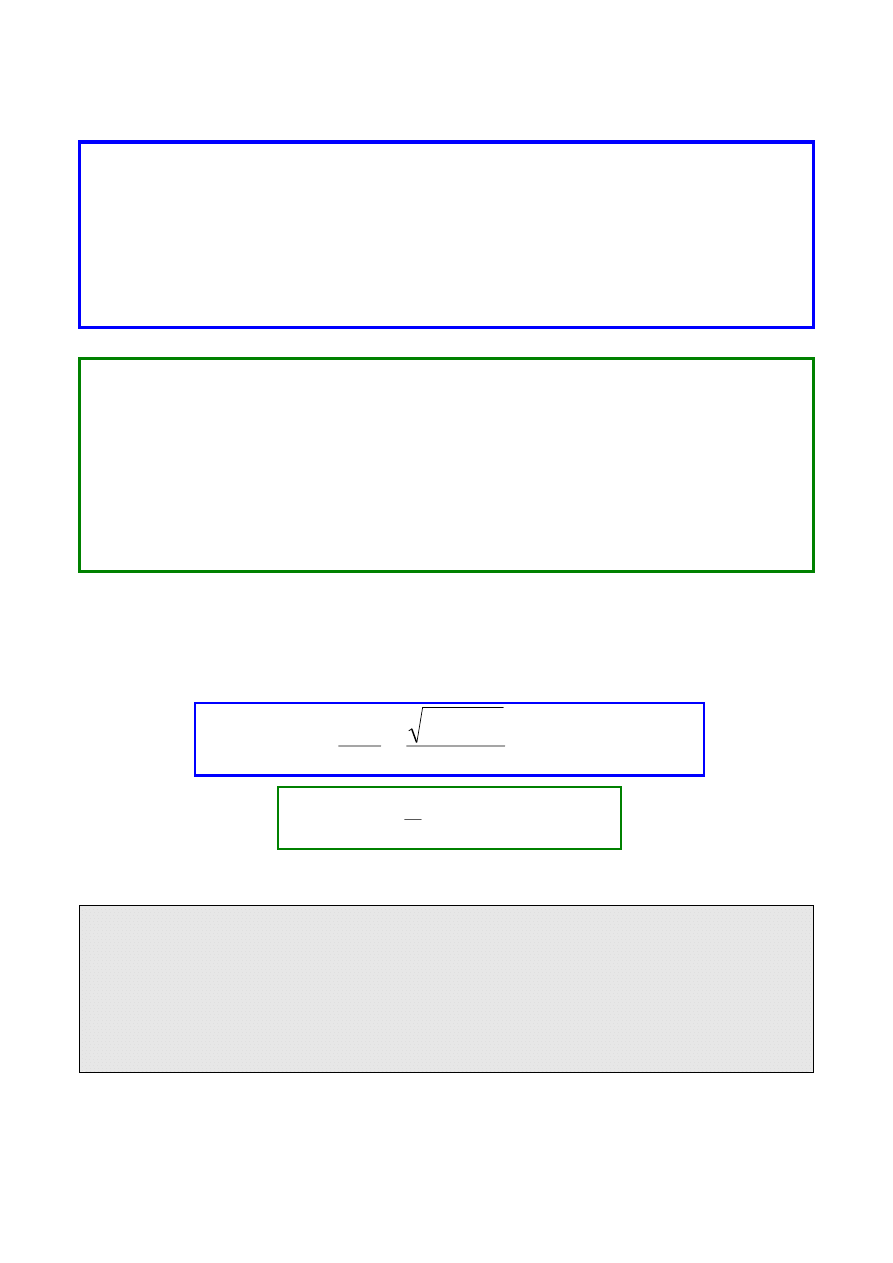
C) WIDMO AMPLITUDOWE I FAZOWE

Wprowadzenie:

0

F

m1

t

t



1



2



3

F

m2

F

m3

F

0

x(t) =

F

0

+

F

m1

sin(



1

t+



1

)

+

F

m2

sin(2



1

t+



2

)

+

F

m3

sin(3



1

t+



3

)

k





F

mk

F

m1

F

m2

F

m3

F

0

1 2 3

+ ....

k





1 2 3



1



2



3



k



/2



- 15 -

Wykres, w układzie współrzędnych prostokątnych, stanowiący

 zbiór

modułów C

k

współczynników zespolonego szeregu Fouriera

lub

 zbiór amplitud F

mk

poszczególnych harmonicznych

określony dla odpowiednich pulsacji



=k



1

(bądź częstotliwości f=kf

1

)

nazywamy dyskretnym

WIDMEM AMPLITUDOWYM

sygnału x(t).

ozbiór

argumentów



k

współczynników zespolonego szeregu

Fouriera

lub

ozbiór faz początkowych



k

poszczególnych harmonicznych

określony dla odpowiednich pulsacji



=k



1

(bądź częstotliwości f=kf

1

)

nazywamy dyskretnym

WIDMEM FAZOWYM

sygnału x(t).

Pomiędzy współczynnikami rozwinięcia w trygonometryczny i w

zespolony szereg Fouriera zachodzą następujące związki:



,

2

,

1

2

2

2

2













k

dla

B

A

F

C

C

k

k

k

m

k

k

(1.39)



,

2

,

1

2







k

dla

k

k







(1.40)

Znajomość obydwu widm, amplitudowego i fazowego
jednoznacznie określa sumę częściową szeregu Fouriera czyli
z założoną dokładnością opisuje analizowany sygnał x(t).
Widma (częstotliwościowe) są równoważnym opisem do
analitycznego zapisu w dziedzinie czasu tego sygnału - jest to
jego

reprezentacja widmowa

.

- 16 -

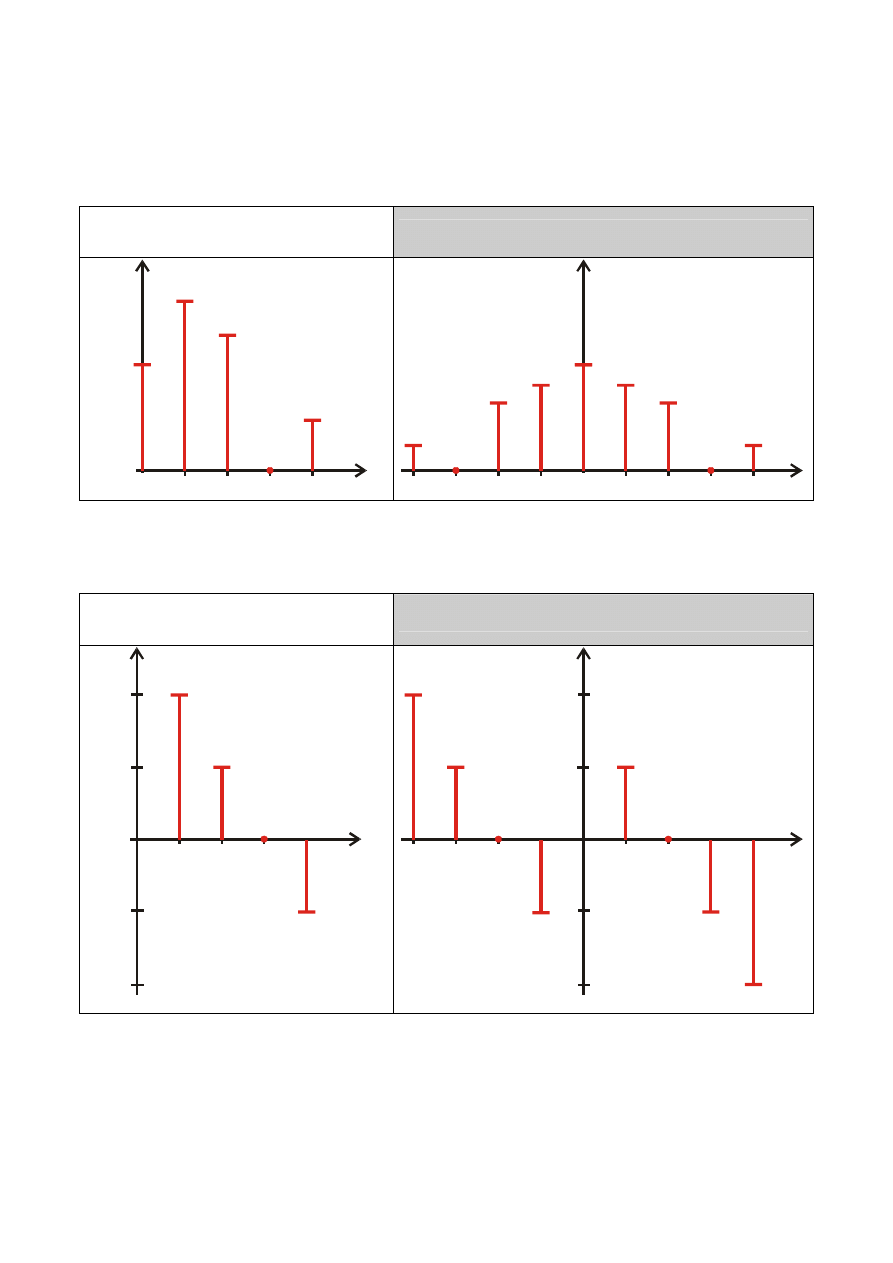
Wyjaśnienie:

WIDMO AMPLITUDOWE

SPORZĄDZONE W OPARCIU O POSTAĆ:

TRYGONOMETRYCZNĄ

ZESPOLONĄ

F

mk

k



1

0

1

2

3

4

C

k

k



1

0

1

2

3

4

-1

-2

-3

-4

WIDMO FAZOWE

SPORZĄDZONE W OPARCIU O POSTAĆ:

TRYGONOMETRYCZNĄ

ZESPOLONĄ



k

k



1

1

2

3

4



/2



/2



/2



k



1

1

2

3

4

-1

-2

-3

-4



k

/2

Widmo amplitudowe sygnału okresowego jest funkcją parzystą a widmo
fazowe funkcją nieparzystą. Prawostronne widma amplitudowe i fazowe
stanowią reprezentację sygnału okresowego w dziedzinie częstotliwości.

- 17 -

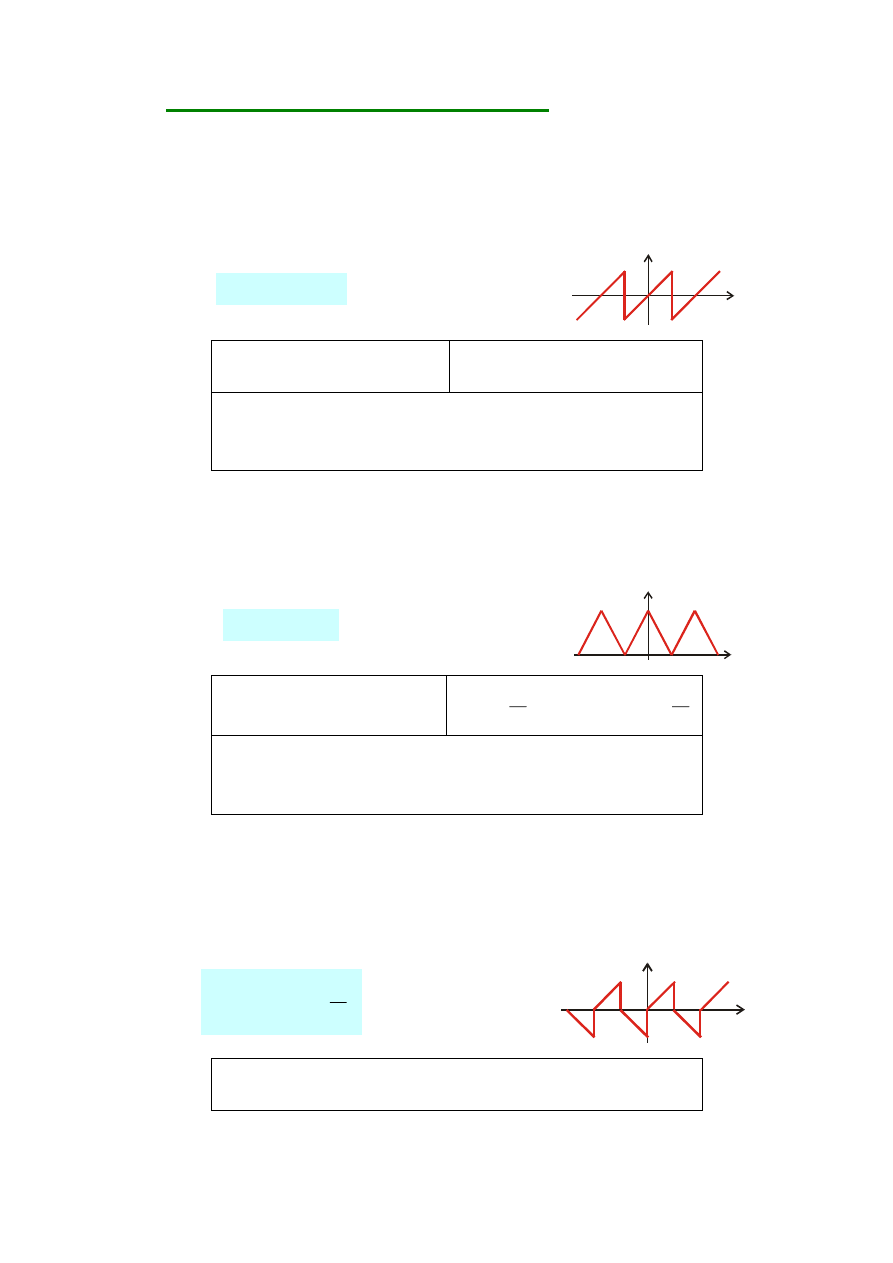
D) RODZAJE SYMETRII SYGNAŁÓW

1)

SYMETRIA WZGLĘDEM POCZĄTKU UKŁADU WSPÓŁRZĘDNYCH

Funkcję nazywamy symetryczną względem początku układu

współrzędnych lub

funkcją nieparzystą

jeśli spełnia ona zależność

 

 

t

x

t

x







(1.41)

x(t)

t

0

,

0

0





k

A

A

0

lub





k

k







 









1

1

sin

k

k

t

k

B

t

x



(1.42)

2)

SYMETRIA WZGLĘDEM OSI RZĘDNYCH

Funkcję nazywamy symetryczną względem osi rzędnych, lub

funkcją

parzystą

jeśli spełnia ona zależność

   

t

x

t

x





(1.43)

x(t)

t

0



k

B

2

lub

2















k

k

 











1

1

0

cos

k

k

t

k

A

A

t

x



(1.44)

3)

SYMETRIA WZGLĘDEM OSI ODCIĘTYCH

Funkcję nazywamy

antysymetryczną

(symetryczną względem osi

odciętych), jeśli rzędne funkcji okresowej powtarzają się co pół okresu ze
zmienionym znakiem, tzn.

 











 





2

T

t

x

t

x

(1.45)

x(t)

t

0

0



A

i



,

2

,

1

0

2

2







n

dla

B

A

n

n

- 18 -

1.7. OPIS WIDMOWY SYGNAŁÓW NIEOKRESOWYCH

A) PRZEKSZTAŁCENIE FOURIERA

Dla sygnałów nieokresowych f(t) można wyznaczyć transformatę

Fouriera (

F

- transformatę) określoną wzorem

 

 

 

 

t

f

dt

e

t

f

j

F

t

j

F





















,

(1.46)

będącą funkcją zespoloną zmiennej rzeczywistej



określoną w przedziale



(-,+).

Zależność (1.46) - nazywana

PROSTYM

PRZEKSZTAŁCENIEM

FOURIERA

- pozwala przyporządkować opisowi sygnału w dziedzinie

czasu, opis w dziedzinie częstotliwości.

B) WIDMA SYGNAŁU

Funkcja F(j



) nazywana jest funkcją gęstości widmowej sygnału

f(t). W ogólnym przypadku jest to funkcja zespolona, czyli:

 

 

 

 

 













X

R

j

F

j

F

e

F

j

F







(7.35)

gdzie:

 

 





j

F

F



 

 





2

2

X

R

F

F





 

 







j

F

arg



 

 

 

 

 

 













F

F

arc

F

F

arc

F

F

tg

arc

R

X

R

X

cos

sin







 

 

dt

t

t

f

F

R





cos













 

 

dt

t

t

f

F

X





sin















UWAGA:

Ww. widma są funkcjami CIĄGŁYMI zmiennej



.

 

 











j

F

j

F

F







-

funkcja parzysta

 

 















-

funkcja nieparzysta

gęstość widmowa

widmo gęstości fazy

widmo gęstości amplitud

- 19 -

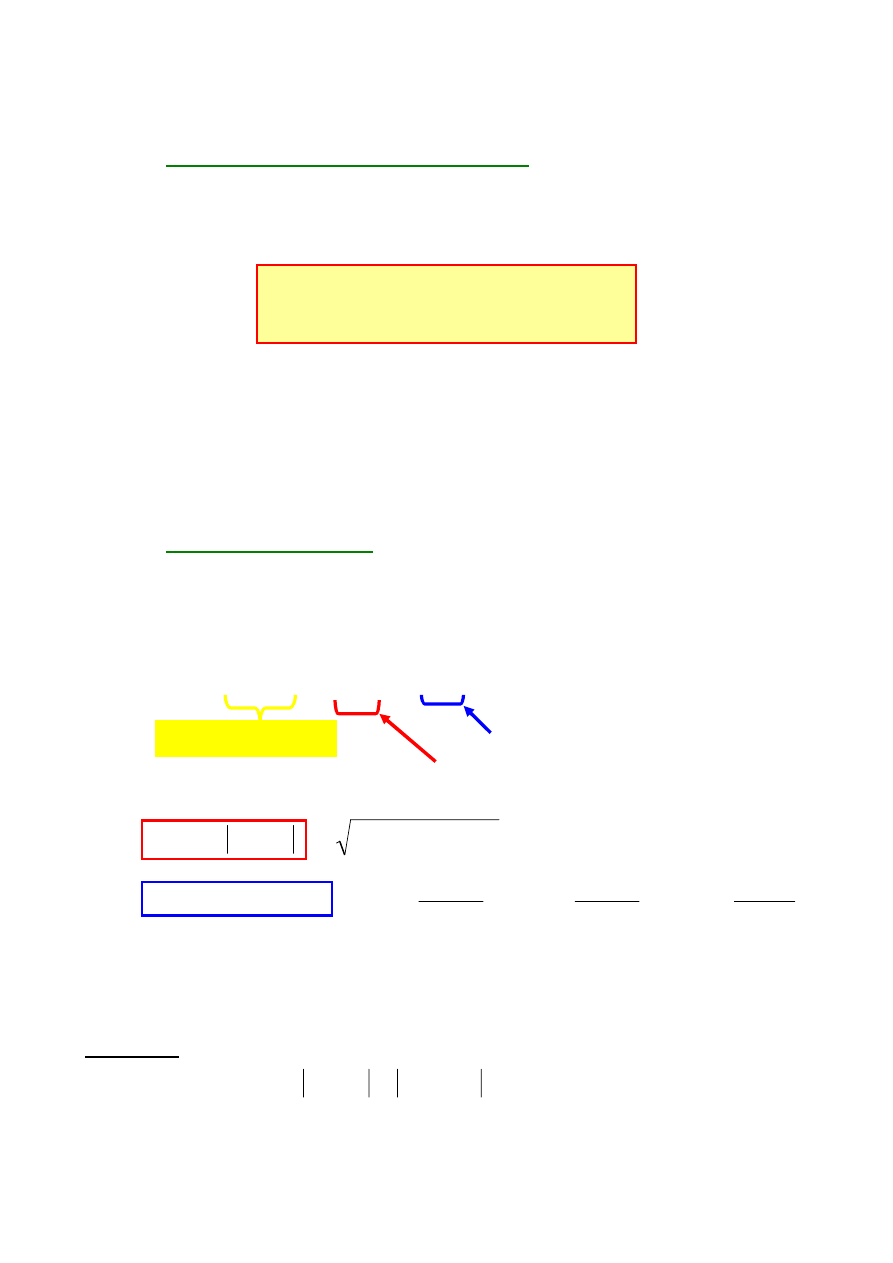
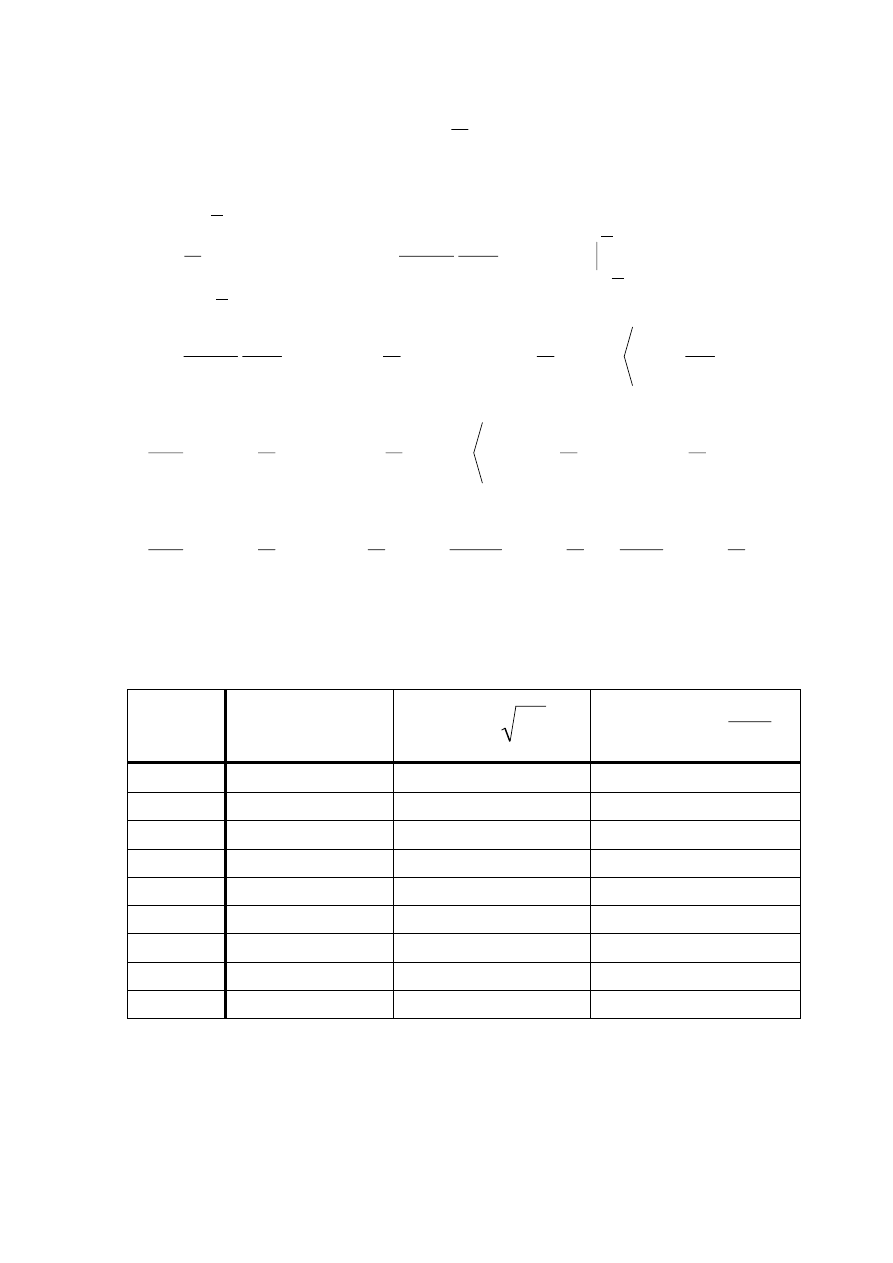
PRZYKŁAD 1:

Dany jest sygnał u(t) będący ciągiem impulsów
prostokątnych o okresie T=1ms, czasie trwania
t

i

=0,25ms oraz amplitudzie U

m

=10V. Wyznaczyć

widmo amplitudowe i fazowe sygnału.

1)

Opisujemy

sygnał

u(t)

analitycznie

w

przedziale

czasu

odpowiadającym okresowi:

 

























2

2

0

2

2

i

i

i

i

m

t

T

t

t

dla

t

t

t

dla

U

t

u

2)

Wybieramy postać szeregu Fouriera, dla której będziemy rozwijali
sygnał

 

















1

1

1

0

sin

cos

k

k

k

t

k

B

t

k

A

A

t

u





3)

Sprawdzamy rodzaj symetrii sygnał u(t)

Występuje symetria względem osi rzędnych (

 

 

t

f

t

f





). Ponieważ

jest to funkcja parzysta znikają wyrazy z sinusami (

0



k

B

).

Zatem:

 











1

1

0

cos

k

k

t

k

A

A

t

u



4)

Obliczamy składową stałą

 

dt

t

u

T

A

U

T

t

t









0

0

1

0

0

 

V

T

t

U

t

t

T

U

t

U

T

dt

U

T

U

i

m

i

i

m

t

t

m

t

t

m

i

i

i

i

5

,

2

4

1

10

2

2

1

1

1

2

2

2

2

0



















 













- 20 -

5)

Obliczamy współczynniki

 



,

2

,

1

cos

2

1

0

0









k

dt

t

k

t

u

T

A

T

t

t

k







2

2

1

1

1

2

2

sin

1

2

cos

2

i

i

i

i

t

t

m

t

t

m

k

t

k

k

T

U

dt

t

k

U

T

A

















T

t

k

t

k

k

T

U

A

i

i

m

k











2

2

sin

2

sin

1

2

1

1

1

1





































































 



















 

















4

sin

4

sin

4

sin

4

sin











k

k

k

k

k

U

m

































































4

sin

37

,

6

4

sin

2

4

sin

4

sin













k

k

k

k

U

k

k

k

U

m

m

6)

Obliczamy wartości amplitud i faz początkowych N-harmonicznych

k

k

A

2

k

k

m

A

F



k

m

k

k

F

A

arcsin





1.

4,502

4,502

90

o

2.

3,183

3,183

90

o

3.

1,501

1,501

90

o

4.

0

0

-

5.

-0,9

0,9

-90

o

6.

-1,061

1,061

-90

o

7.

-0,643

0,643

-90

o

8.

0

0

-

9.

0,5

0,5

90

o

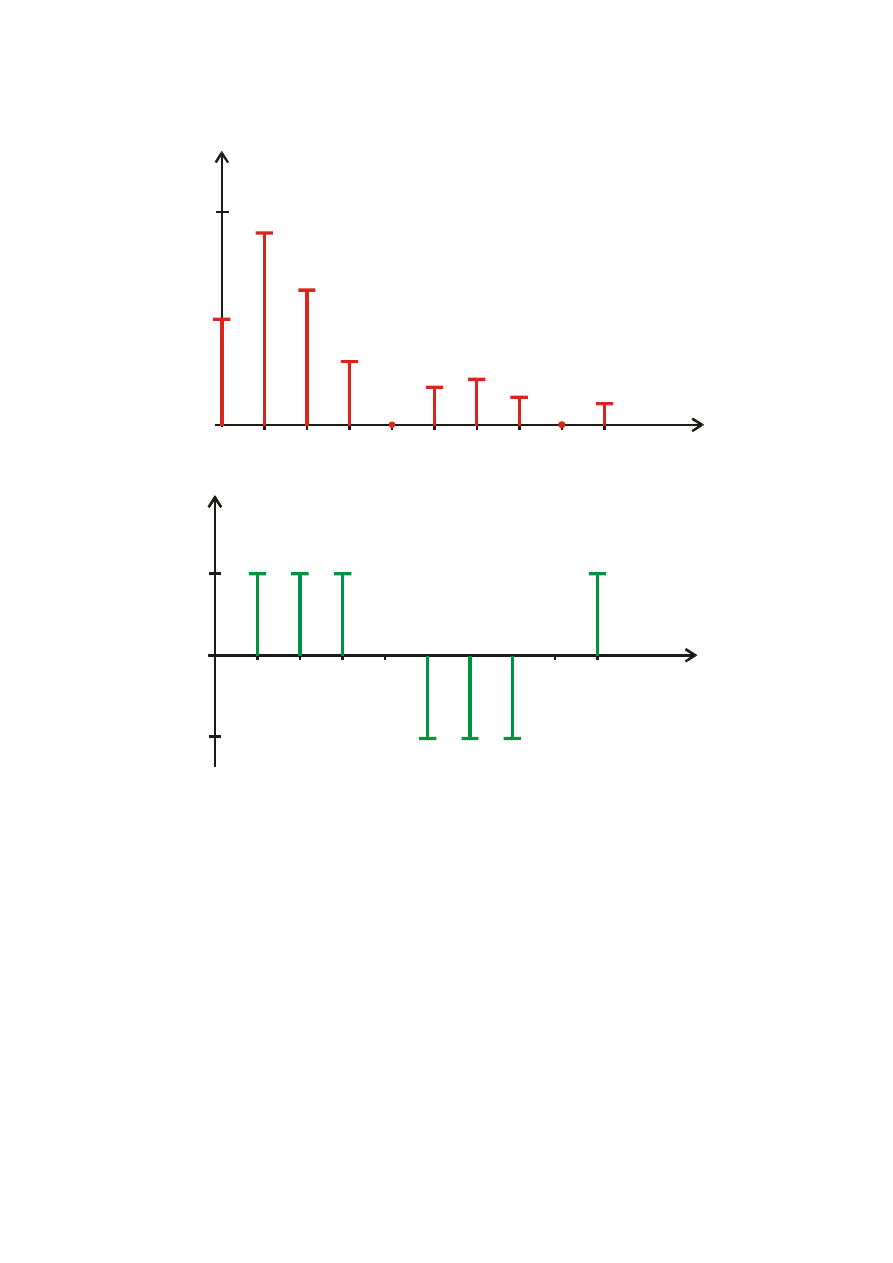
- 21 -

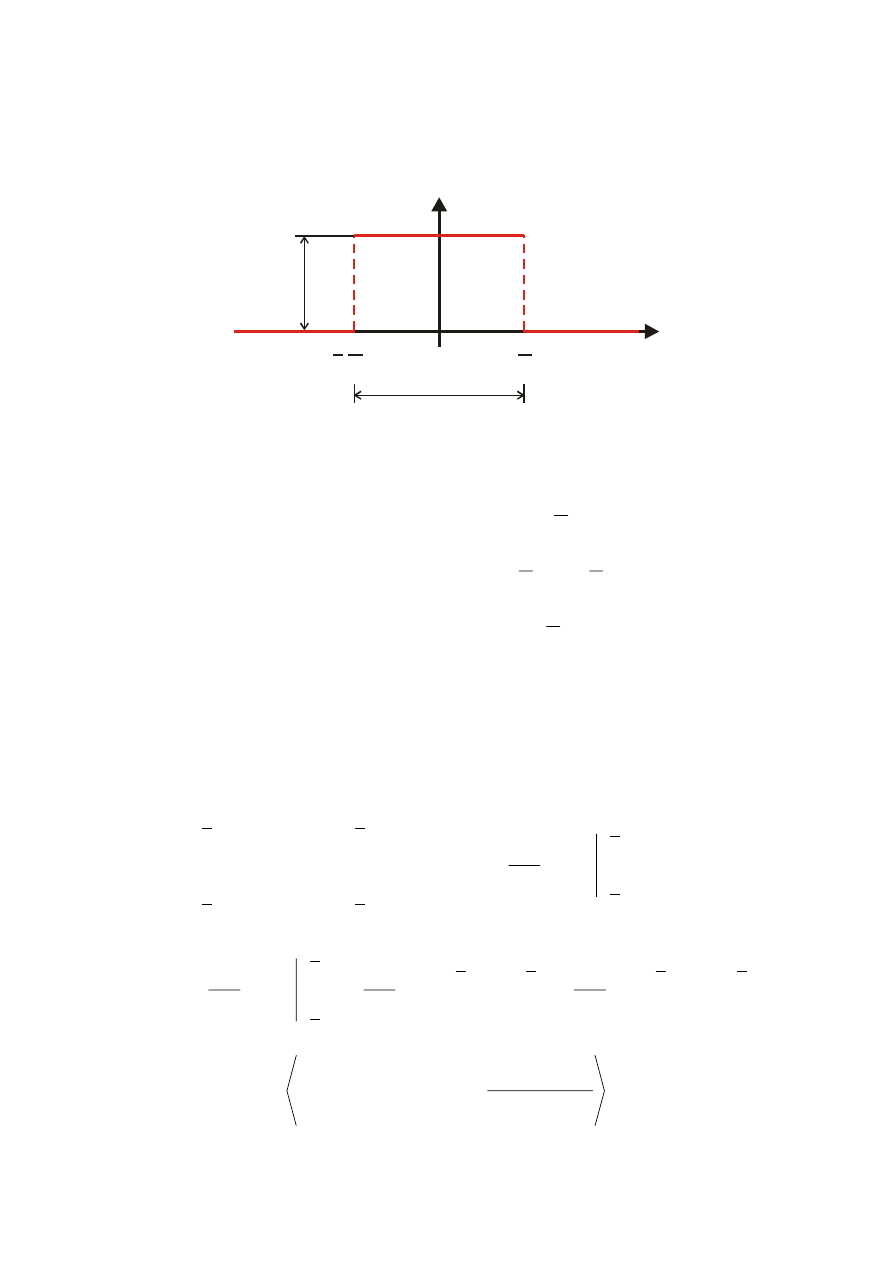
7)

Przedstawiamy widmo amplitudowe i fazowe sygnału

F

mk

0

1

2

3

4

5

6

7

8

9

5

2,5

f [kHz]



k

1

2

3

4

5

6

7

8

9

90

o

-90

o

f [kHz]

- 22 -

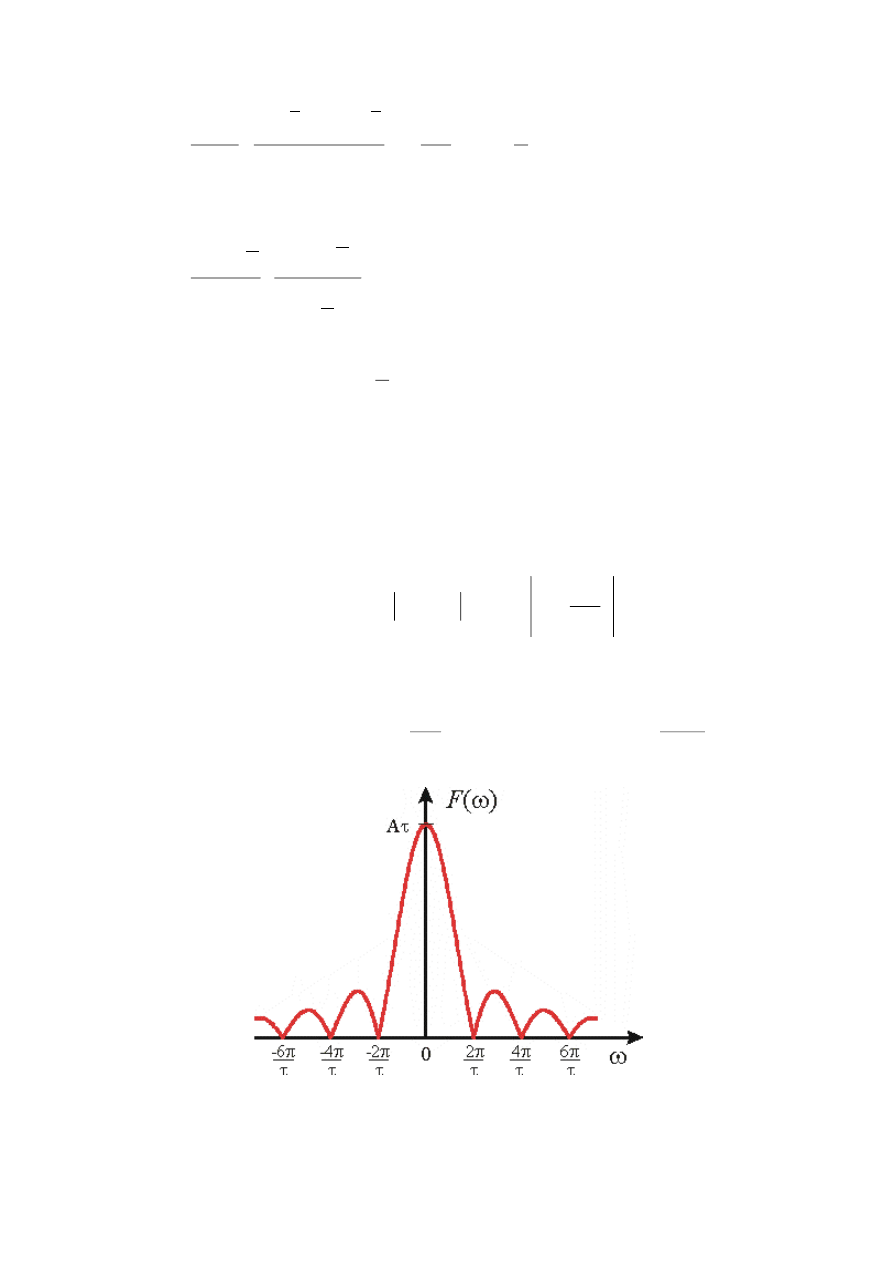
PRZYKŁAD 2:

Dany jest sygnał f(t) będący impulsem prostokątnym
(tzw. funkcja bramkowa) przedstawiony na rysunku.
Wyznaczyć widmo gęstości amplitud i fazy sygnału.

t

f(t)



A



2



2

1)

Opisujemy sygnał f(t) analitycznie

 































2

0

2

2

2

0









t

dla

t

dla

A

t

dla

t

f

2)

Wyznaczamy funkcję gęstości widmowej

(

F

- transformatę)

 

 

dt

e

t

f

j

F

t

j



















 



j

F





















































2

2

2

2

2

2

1





















t

j

t

j

t

j

e

j

A

dt

e

A

dt

Ae























































2

2

2

2

2

2





























j

j

j

j

t

j

e

e

j

A

e

e

j

A

e

j

A

j

e

e

że

wiemy

j

j

2

sin

,













- 23 -











































2

sin

2

2

2

2

2

















A

j

e

e

j

j

A

j

j

2

2

sin

2

2





























A

Zatem

 















2









Sa

A

j

F

Czyli funkcja gęstości widmowej F(j



) funkcji bramkowej jest funkcją

rzeczywistą a zatem F

X

(



) = 0.

3)

Wyznaczamy widmo gęstości amplitud

 

 



















2









Sa

A

j

F

F

Uwaga:

 



A

F



0

 

0





F

gdy

n







2

czyli dla







n

2



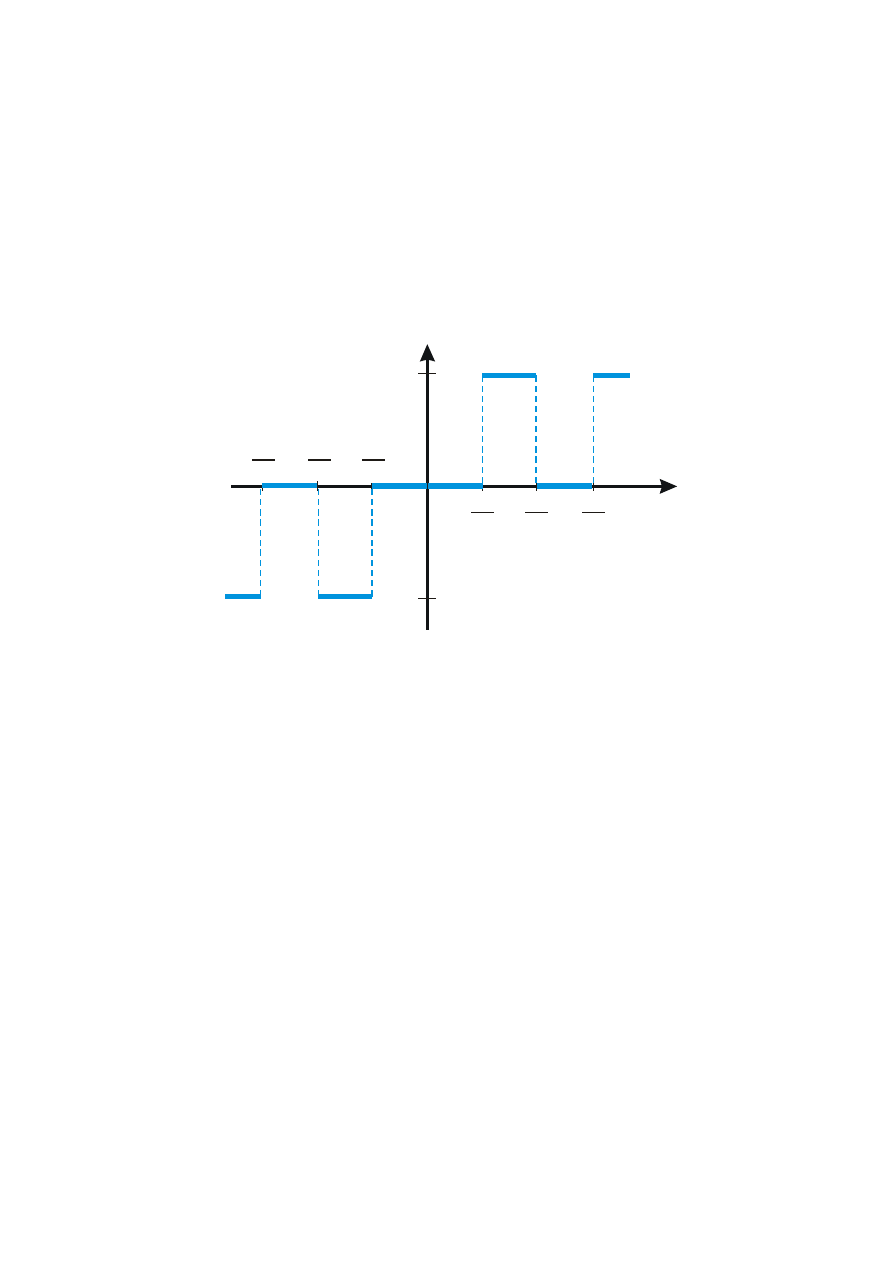
- 24 -

4)

Wyznaczamy widmo gęstości fazy

 

 







j

F

arg



Ponieważ funkcja gęstości widmowej rozpatrywanego sygnału jest
wielkością rzeczywistą, zatem widmo gęstości fazy jest przedziałami
stałe i przybiera wartości 0 lub





0

2













-2





-4





-6





 

( )

180

o

-180

o