Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych

Nr 58

Politechniki Wrocławskiej

Nr 58

Studia i Materiały Nr

25

2005

maszyny elektryczne, turbogeneratory, uzwojenia,

pręty elementarne, przeplot, straty

Dariusz GURAZDOWSKI

F

*

F

, Jan ZAWILAK

*

WPŁYW PRZEPLOTU PRZEWODÓW

ELEMENTARNYCH NA ROZKŁAD GĘSTOŚCI

PRĄDU W PRĘCIE TURBOGENERATORA

W pracy przedstawiono wpływ transpozycji Roebela przewodów elementarnych na rozkład gę-

stości prądu w pręcie warstwy dolnej i górnej uzwojenia stojana turbogeneratora Zaprezentowano
program komputerowy „Bar” umożliwiający wyznaczenie tego rozkładu dla różnych transpozycji
przewodów elementarnych w strefie żłobkowej i obu strefach czołowych. Obliczenia przeprowadzo-
no dla pręta warstwy dolnej i górnej wybranego typu turbogeneratora o mocy 450 MVA napięciu
21 kV i częstotliwości 60 Hz. W modelu obliczeniowym uwzględniono sprzężenia magnetyczne
między przewodami elementarnymi w strefie żłobkowej (środowisku ferromagnetycznym) i w strefie
czołowej (środowisku niemagnetycznym). Dla pręta warstwy dolnej i górnej leżących w żłobku nr 1 i
9 wykonano obliczenia rozkładu gęstości prądu wzdłuż wysokości pręta dla trzech typów transpozy-
cji Roebela: 0+180+0, 0+360+0, 0+540+0.

1. WSTĘP

Uzwojenia maszyn dużych mocy wykonuje się w postaci wiązki odizolowanych,

równoległych przewodów elementarnych połączonych skuwkami w strefie połączeń
czołowych. Dzięki takiemu podziałowi zmniejsza się straty energii wywoływane prą-
dami wirowymi występującymi w obrębie pojedynczego pręta. Jeśli przewody ele-
mentarne znajdują się w różnych warunkach magnetycznych to powstają prądy cyrku-
lacyjne o torach zamykających się przez sąsiednie, połączone na końcach, przewody
elementarne.

Prądy cyrkulacyjne powodują nierównomierny rozkład gęstości prądu wzdłuż wy-

sokości pręta, zmniejszają obciążalność prętów i moc przetwarzaną w maszynie. Prądy
te zmniejsza się konstrukcyjnie przez zastosowanie przeplotu Roebela o odpowiedniej
podziałce transpozycji [2, 3, 6, 9].

__________

*

Politechnika Wrocławska - Instytutu Maszyn, Napędów i Pomiarów Elektrycznych, 50-372 Wrocław,

ul. Smoluchowskiego 19, [e-mail], [e-mail]

Celem niniejszej pracy jest określenie wpływu przeplotu przewodów elementar-

nych i ich transpozycji w poszczególnych strefach na rozkład gęstości prądu wzdłuż
wysokości pręta uzwojenia stojana turbogeneratora.

2. MODEL OBLICZENIOWY

2.1. PROGRAM OBLICZENIOWY

Obliczenia określające rozkład gęstości prądu wzdłuż wysokości pręta dowolnej

(górnej i dolnej) warstwy i żłobka wykonano za pomocą programu komputerowego
„Bar”

F

1

F

.

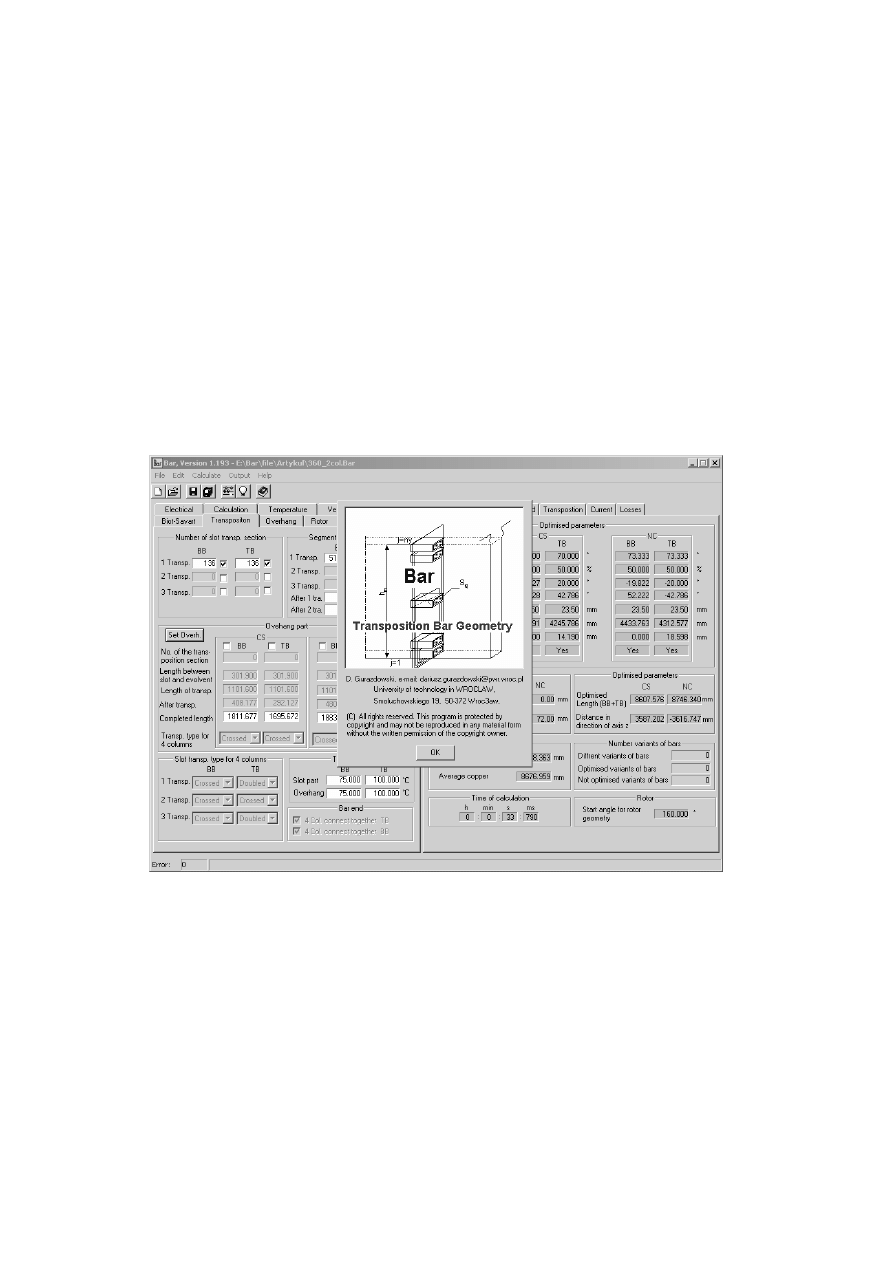
Rys. 1. Program „Bar” do obliczeń rozkładu gęstości prądu wzdłuż wysokości pręta.

Fig. 1. The Program “Bar” which makes it possible to calculate the current density distribution as a func-

tion of the bar height.

Aby wyznaczyć rozkład prądu w określonym pręcie uzwojenia, w programie wy-

konywane są następujące obliczenia:
− geometrii dwuwarstwowego uzwojenia stojana w strefie czołowej turbogeneratora,
__________

1 - Program „Bar” opracowano w ramach prac nad rozprawą doktorską jednego ze współautorów.

− pola magnetycznego w strefie czołowej od prądów uzwojenia stojana płynących w

tej strefie (metodą Biota-Savarta-Laplaca) [1, 5, 12, 13],

− pola magnetycznego w strefie czołowej uzwojenia stojana od prądów uzwojenia

wirnika płynących w tej strefie (metoda Biota-Savarta-Laplace’a) [1, 5, 12, 13],

− sprzężeń magnetycznych przewodów elementarnych w strefie żłobkowej (środowi-

sku ferromagnetycznym) [4, 7, 8, 12],

− sprzężeń magnetycznych przewodów elementarnych w strefie czołowej (środowi-

sku niemagnetycznym) [4, 7, 8, 12].

Za pomocą opracowanego programu można obliczyć rozkłady gęstości prądów

wzdłuż wysokości pręta dla różnych transpozycji przewodów elementarnych w strefie
żłobkowej i obu strefach czołowych. W strefie żłobkowej można zamodelować od 1
do 3 przeplotów o różnych całkowitych kątach transpozycji oraz od 1 do 2 odcinków
prostych nie zawierających przeplotu. Natomiast w każdej strefie czołowej modelo-
wany jest tylko jeden przeplot na odcinku ewolwentowym pręta. Umiejscowienie
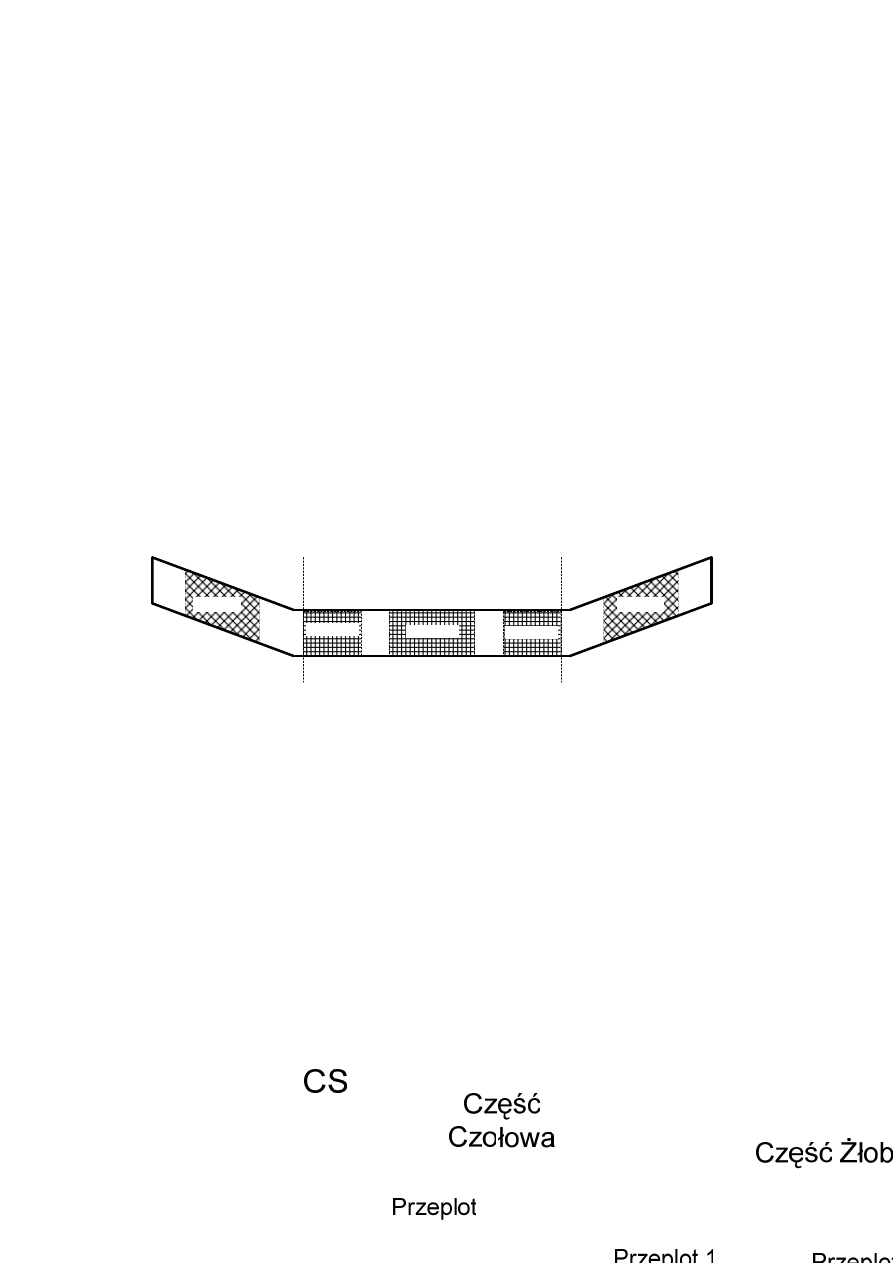
możliwych przelotów pręta przedstawiono na rysunku 2.

Rys. 2. Przeplot Roebela modelowany za pomocą programu „Bar”

Fig. 2. Roebel transposition simulated by the program „Bar”

W modelu obliczeniowym istotnym jest określenie sprzężeń magnetycznych między
przewodami elementarnymi w każdej części uzwojenia tzn. w strefie żłobkowej (śro-
dowisku ferromagnetycznym) i strefie czołowej (środowisku niemagnetycznym).

2.2. METODA OBLICZEŃ

Sprzężenia magnetyczne przewodów w pręcie uwzględniono w modelu matema-

tycznym wykorzystującym „metodę przewodów elementarnych”, która traktuje pręt w
żłobku jak sieć elektryczną o „n” gałęziach równoległych powiązanych wzajemnie
sprzężeniami magnetycznymi [4, 6, 7, 12]. Liczba gałęzi równoległych odpowiada
liczbie przewodów elementarnych pręta.
W programie „Bar” wykorzystano metodę odbić zwierciadlanych [1, 8, 10, 11, 13] i
Biota – Savarta – Laplace’a [5, 8, 11, 12] do określenia oddziaływania strefy czołowej
turbogeneratora. Wpływ strefy czołowej na rozkład gęstości prądu w pręcie zamode-
lowano w postaci dodatkowego napięcia indukowanego w każdym przewodzie ele-

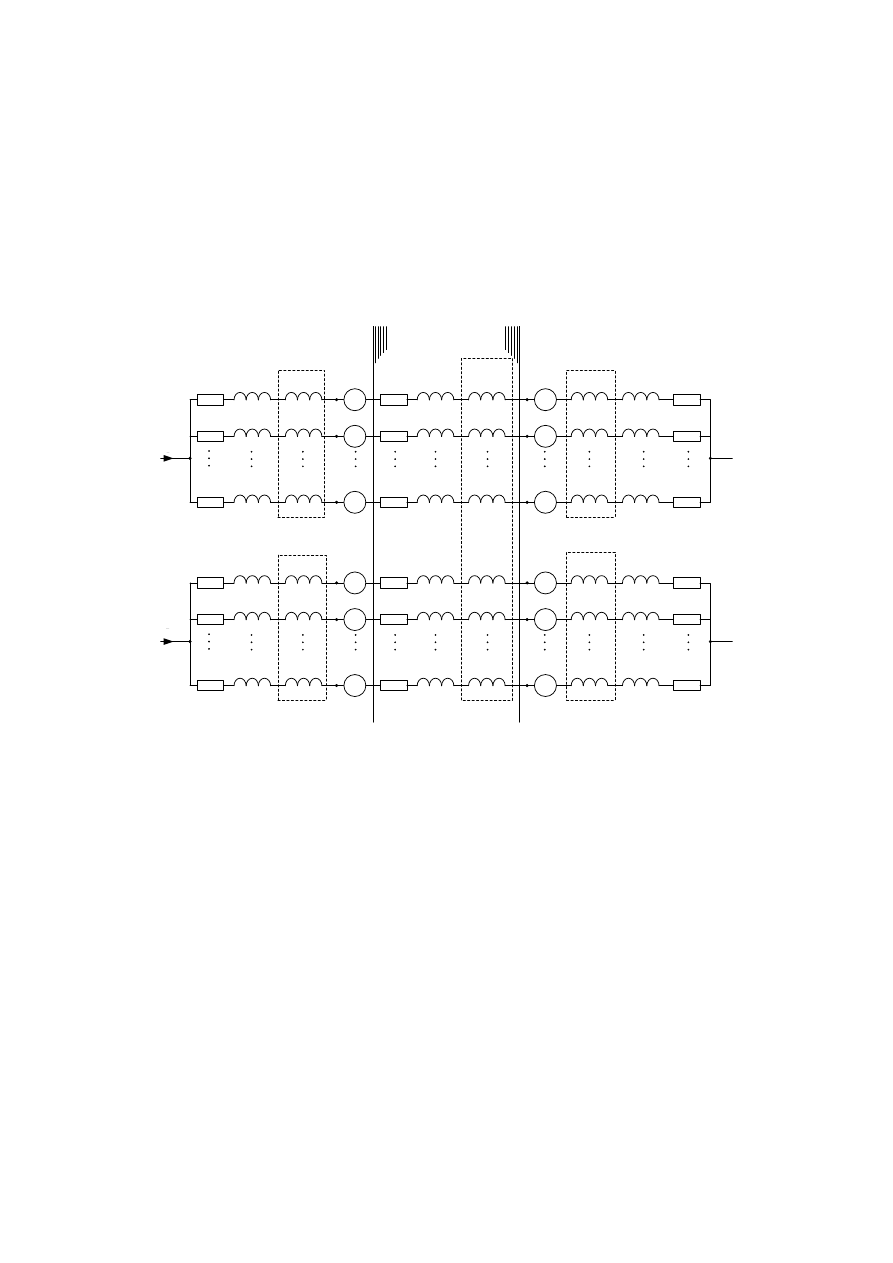
mentarnym danego pręta od strumienia magnetycznego pozostałych prętów uzwojenia
stojana i wirnika [5, 12].

Schemat zastępczy modelu matematycznego opisującego sprzężenia magnetyczne

przewodów elementarnych pręta warstwy dolnej i górnej uzwojenia stojana oraz od-
działywanie strefy czołowej turbogeneratora przedstawiono na rysunku 3.

I

TB

R

CS,TB,1

L

CS,TB,1

M

CS,TB,1j

U

EvCS,TB,1

Strefa czołowa pręta - CS

R

SP,TB,1

L

SP,TB,1

M

SP,TB,1j

U

EvNC,TB,1

M

SP,TBBB,1j

R

NC,TB,1

L

NC,TB,1

M

NC,TB,1j

Strefa czołowa pręta - NC

Strefa żłobkowa

R

CS,TB,N

L

CS,TB,N

M

CS,TB,Nj

U

EvCS,TB,N

R

SP,TB,N

L

SP,TB,N

M

SP,TB,Nj

U

EvNC,TB,N

M

SP,TBBB,Nj

R

NC,TB,N

L

NC,TB,N

M

NC,TB,Nj

TB - pręt warstwy górnej

R

CS,BB,1

L

CS,BB,1

M

CS,BB,1j

U

EvCS,BB,1

R

SP,BB,1

L

SP,BB,1

M

SP,BB,1j

U

EvNC,BB,1

M

SP,BBTB,1j

R

NC,BB,1

L

NC,BB,1

M

NC,BB,1j

R

CS,BB,N

L

CS,BB,N

M

CS,BB,Nj

U

EvCS,BB,N

R

SP,BB,N

L

SP,BB,N

M

SP,BB,Nj

U

EvNC,BB,N

M

SP,BBTB,Nj

R

NC,BB,N

L

NC,BB,N

M

NC,BB,Nj

BB - pręt warstwy dolnej

I

TB

Rys .3: Schemat zastępczy pręta warstwy górnej i dolnej uzwojenia stojana turbogeneratora.

Fig. 3 Equivalent circuit diagram of top and bottom bar of the turbogenerator stator winding

W schemacie tym przyjęto następujące oznaczenia:

TB – pręt warstwy górnej uzwojenia (top bar),
BB – pręt warstwy dolnej uzwojenia (bottom bar),
CS – strefa czołowa uzwojenia po stronie nienapędowej maszyny (connection si-

de),

NC – strefa czołowa uzwojenia po stronie napędowej maszyny (nonconnection si-

de),

SP – strefa żłobkowa maszyny (slot part),
Ev – napięcie dodatkowe strefy czołowej (external voltage).

Model uzwojenia podzielony jest na trzy strefy: strefę czołową po stronie nienapę-

dowej (CS), strefę żłobkową (SP) oraz strefę czołową uzwojenia po stronie napędowej
maszyny (NC). Dla k-tego przewodu elementarnego (k

∈ 1…N) pręta górnego i dolne-

go w poszczególnych strefach schematu zastępczego występują następujące elementy:

- wypadkowa rezystancja przewodu elementarnego

k

BB

CS

k

TB

CS

R

R

,

,

,

,

;

,

,

k

BB

SP

k

TB

SP

R

R

,

,

,

,

;

k

BB

NC

k

TB

NC

R

R

,

,

,

,

;

-wypadkowa indukcyjność własna przewodu elementarnego:

k

BB

CS

k

TB

CS

L

L

,

,

,

,

;

,

k

BB

SP

k

TB

SP

L

L

,

,

,

,

;

k

BB

NC

k

TB

NC

L

L

,

,

,

,

;

- wypadkowa indukcyjność wzajemna między przewodami k i l należącymi do tego

samego pręta uzwojenia:

kl

BB

CS

kl

TB

CS

M

M

,

,

,

,

;

,

kl

BB

SP

kl

TB

SP

M

M

,

,

,

,

;

kl

BB

NC

kl

TB

NC

M

M

,

,

,

,

;

- wypadkowa indukcyjność wzajemna między przewodami k i l należącymi do prę-

tów różnych warstw uzwojenia:

kl

BBTB

SP

kl

TBBB

SP

M

M

,

,

,

,

;

- napięcie indukowane w przewodzie elementarnym od pola magnetycznego wirni-

ka oraz pozostałych prętów uzwojenia stojana.

k

BB

NC

k

TB

NC

U

U

,

,

,

,

;

,

k

BB

CS

k

TB

CS

U

U

,

,

,

,

;

Na podstawie schematu zastępczego określono równania napięciowe i prądowe,

pozwalające wyznaczyć prądy w każdym przewodzie elementarnym pręta uzwojenia
stojana turbogeneratora. W zapisie macierzowym równania te przybierają postać
[4,6,12]:

[

]

[

]

[

]

[

]

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎣

⎡

−

−

−

−

−

−

=

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎣

⎡

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎣

⎡

−

−

−

−

−

−

−

−

BB

TB

N

BB

Ev

BB

Ev

N

TB

Ev

TB

Ev

BB

TB

N

BB

BB

N

TB

TB

BB

BB

TB

BB

BB

TB

TB

TB

I

I

U

U

U

U

U

U

I

I

I

I

Z

Z

Z

Z

,

,

1

,

,

,

,

1

,

,

,

1

,

,

1

,

*

0

0

1

1

0

0

0

0

0

0

1

1

1

0

1

0

0

1

0

1

M

M

L

L

L

L

M

M

M

M

(1)

3. ROZKŁAD PRĄDÓW DLA RÓŻNYCH TYPÓW PRZEPLOTU PRZEWODÓW

ELEMENTARNYCH

Wykorzystując opisany model obliczono rozkład gęstości prądu wzdłuż wysokości

pręta uzwojenia stojana turbogeneratora (program „Bar”). Obliczenia wykonano dla
pręta warstwy dolnej i górnej uzwojenia stojana wybranego typu turbogeneratora o
mocy znamionowej 450 MVA, napięciu 21 kV, częstotliwości 60 Hz i 54 żłobkach w
rdzeniu stojana.
Dla pręta warstwy dolnej i górnej leżących w żłobku nr 1 i 9 wykonano obliczenia
rozkładu gęstości prądu dla trzech typów transpozycji Roebela:

• przeplot tylko w części żłobkowej typu 0+180+0
• przeplot tylko w części żłobkowej typu 0+360+0
• przelot tylko w części żłobkowej typu 0+540+0

Każdy pręt turbogeneratora ma 136 przewodów elementarnych ułożonych w

dwóch kolumnach po 68 przewodów. Na rysunkach 4, 5, 6 pokazano rozkład gęstości
prądu wzdłuż wysokości żłobka. Rozkład ten przedstawiono w dwóch kolumnach,
które odzwierciedlają rzeczywiste ułożenie przewodów elementarnych w pręcie uzwo-
jenia stojana. Na prezentowanych wykresach przyjęto następujące oznaczenia gęstości
prądu:

ac

J

- gęstość prądu przy przepływie prądów cyrkulacyjnych,

dc

J

- gęstość prądu przy braku wpływu prądów cyrkulacyjnych (jednakowa war-

tość prądu w każdym przewodzie elementarnym).

Skuteczność zastosowanego przeplotu ze względu na ograniczenie strat dodatko-

wych określa współczynnik

zwany współczynnikiem strat od prądów cyrkula-

cyjnych.

CCL

k

3.1. WSPÓŁCZYNNIK STRAT OD PRĄDÓW CYRKULACYJNYCH

Współczynnik strat od prądów cyrkulacyjnych

jest obliczany w zależności od

zastosowanego przeplotu Roebela [6]: oddzielnie dla pręta warstwy dolnej i górnej
turbogeneratora. Jest on zawsze większy od jedności a jego wartość określa skutecz-
ność zastosowanego przeplotu w zmniejszaniu prądów cyrkulacyjnych i opisany jest
równaniem (2)

CCL

k

2

1

1

∑

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

m

i

DC

i

CCL

I

I

m

k

(2)

n

DC

I

m

I

1

=

(3)

w którym:

CCL

k

- współczynnik strat wywołanych prądami cyrkulacyjnymi,

m

- liczba przewodów elementarnych w danym pręcie,

i

I

- prąd i-tego przewodu elementarnego,

n

I

- prąd znamionowy pręta,

DC

I

- prąd przewodu elementarnego przy równomiernym rozkładzie gęstości prą-

du wzdłuż wysokości pręta (brak oddziaływania prądów cyrkulacyjnych).

Straty dodatkowe od prądów cyrkulacyjnych w pręcie danej warstwy uzwojenia tur-
bogeneratora wyznacza się na podstawie współczynnika

CCL

k

(

)

1

−

=

CCL

Cu

CuCCL

k

P

P

(4)

gdzie:

CuCCL

P

- straty dodatkowe od prądów cyrkulacyjnych,

Cu

P

- straty podstawowe,

CCL

k

- współczynnik strat wywołanych prądami cyrkulacyjnymi.

3.2. ROZKŁAD GĘSTOŚCI PRĄDÓW WZDŁUŻ WYSOKOŚCI PRĘTA DLA PRZEPLOTU TYPU

0+180+0

W procesie transpozycji typu (0+180+0) każdy przewód elementarny wykonuje

obieg wokół osi pręta o kąt 180

° [3, 6]. Przy zastosowaniu tej transpozycji rozkład

prądów wzdłuż wysokości pręta jest bardzo nierównomierny dla pręta warstwy dolnej
(BB) i górnej (TB). Spowodowane to jest przepływem prądów cyrkulacyjnych między
przewodami elementarnymi. Prądy te powstają przede wszystkim w strefie części
żłobkowej, gdyż zastosowany przeplot typu (0+180+0) nie zapewnia wystarczającej
kompensacji napięć indukowanych od strumieni rozproszenia w tym obszarze. W
strefie żłobkowej występuje największa gęstość strumienia rozproszenia stąd bardzo
silny wpływ prądów cyrkulacyjnych na rozkład gęstości prądu w pręcie warstwy gór-
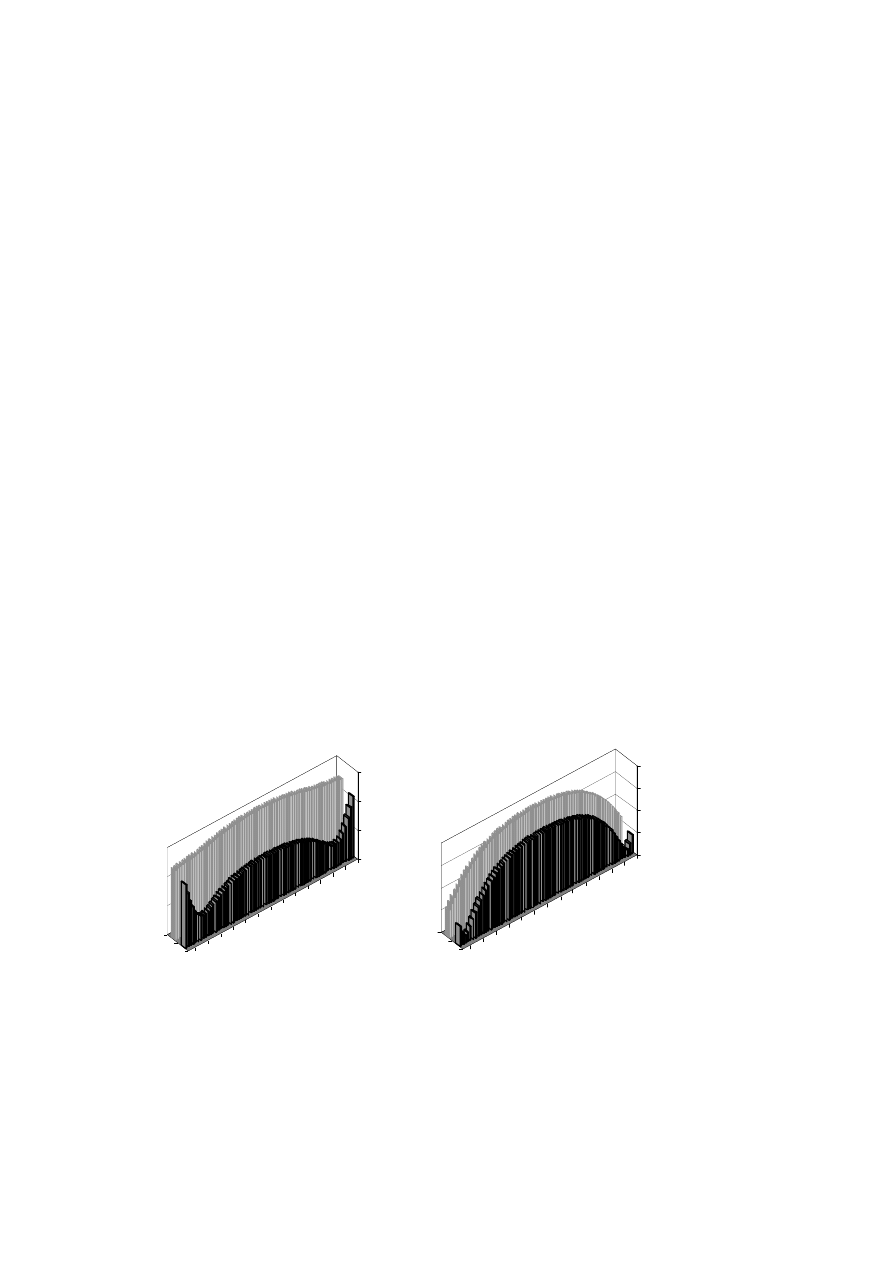
nej (TB) i dolnej (BB) uzwojenia stojana (rys 4).

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

1.0

2.0

3.0

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

a). Żłobek 1, pret dolny (BB), przeplot

0+180+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

2.0

4.0

6.0

8.0

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

b). Żłobek 1, pret gorny (TB), przeplot

0+180+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

1.0

2.0

3.0

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

c). Żłobek 9, pret dolny (BB), przeplot

0+180+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

2.0

4.0

6.0

8.0

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

d). Żłobek 9, pret gorny (TB), przeplot

0+180+0

Rys 4. Rozkład gęstości prądu wzdłuż wysokości pręta uzwojenia stojana (transpozycja 0+180+0)

a) żłobek 1, pręt dolny, b) żłobek 1, pręt górny, c) żłobek 9, pręt dolny, d) żłobek 9, pręt górny,

Fig. 4. Current density distribution as a function of the stator bar height (transposition 0+180+0).

a) slot 1, bottom bar, b) slot 1, top bar, c) slot 9, bottom bar, d) slot 9, top bar,

Zaletą omawianego przelotu jest zmiana pozycji poszczególnych przewodów elemen-
tarnych na wyjściu pręta względem pozycji przewodów na wejściu o kąt transpozycji
180

°. Dzięki temu następuje ograniczenie prądów cyrkulacyjnych wytwarzanych w

strefach czołowych pręta.
Rozkład gęstości prądu wzdłuż wysokości pręta warstwy dolnej i górnej przy zasto-
sowaniu przeplotu typu (0+180+0), przedstawiono na rysunku 4. Rozkład ten jest
bardzo zbliżony dla prętów warstwy dolnej w żłobku nr 1 i 9 oraz dla prętów warstwy
górnej w żłobku 1 i 9. W pręcie warstwy dolnej gęstość prądu

lewej kolumny

przewodów elementarnych jest większa ponad 2,5 krotnie od gęstość prądu

. W

pręcie warstwy górnej rozkład

ac

J

dc

J

dc

ac

J

J

jest jeszcze bardziej niekorzystny. Dla lewej

kolumny przewodów elementarnych

jest większy ponad 6 krotnie od

.

ac

J

dc

J

Tabela 1. Współczynnik strat od prądów cyrkulacyjnych dla przelotu typu 0+180+0

Table 1. The circulating current losses coefficient for transposition 0+180+0

Żłobek 1

Żłobek 9

pręt dolny

pręt górny

pręt dolny

pręt górny

k

CCL

4,57 30,72

4,57

24,15

Duża wartość stosunku

dc

ac

J

J

powoduje wzrost współczynnika strat od prądów

cyrkulacyjnych

(tabela 1) np. dla pręta warstwy dolnej w żłobku nr 9 współ-

czynnik

wynosi 4,57. Straty od prądów cyrkulacyjnych są ponad 3,5 krotnie

CCL

k

CCL

k

większe od strat podstawowych w pręcie. Dla pręta warstwy górnej współczynnik

jest bardzo duży a jego wartość wynosi: ok. 30,72 dla żłobka nr 1 i 24,15 dla

żłobka nr 9.

CCL

k

Ze względu na redukcje prądów cyrkulacyjnych i możliwość uzyskania równomierne-
go rozkładu gęstości prądu wzdłuż wysokości pręta uzwojenia stojana skuteczność
przeplotu 0+180+0 jest bardzo mała. Zastosowanie takiego przeplotu powoduje bar-
dzo duży wzrost strat dodatkowych, przekraczających kilkanaście razy straty podsta-
wowe w pręcie.

3.3. ROZKŁAD GĘSTOŚCI PRĄDU WZDŁUŻ WYSOKOŚCI PRĘTA DLA PRZEPLOTU TYPU

0+360+0

Zastosowanie przeplotu 360

° tylko w strefie żłobkowej powoduje, że każdy z przewo-

dów elementarnych wykonuje pełen obieg wokół osi pręta [2, 3, 6, 9]. Położenie
przewodów elementarnych na wyjściu z pręta jest taka sama jak na wejściu. Przy za-
stosowaniu tej transpozycji nie występują prądy cyrkulacyjne w części żłobkowej w
wyniku całkowitej kompensacji napięć indukowanych od strumienia rozproszenia w
tej strefie.

W strefie czołowej występuje niezrównoważone napięcie indukowane od strumie-

nia rozproszenia wirnika i pozostałych prętów uzwojenia stojana oraz od strumienia
własnego. W pętlach utworzonych przez przewody elementarne płyną prądy cyrkula-
cyjne pod wpływem tych niezrównoważonych napięć w strefie czołowej. Dlatego
rozkład gęstości prądu wzdłuż wysokości pręta warstwy dolnej (BB) i górnej (TB)
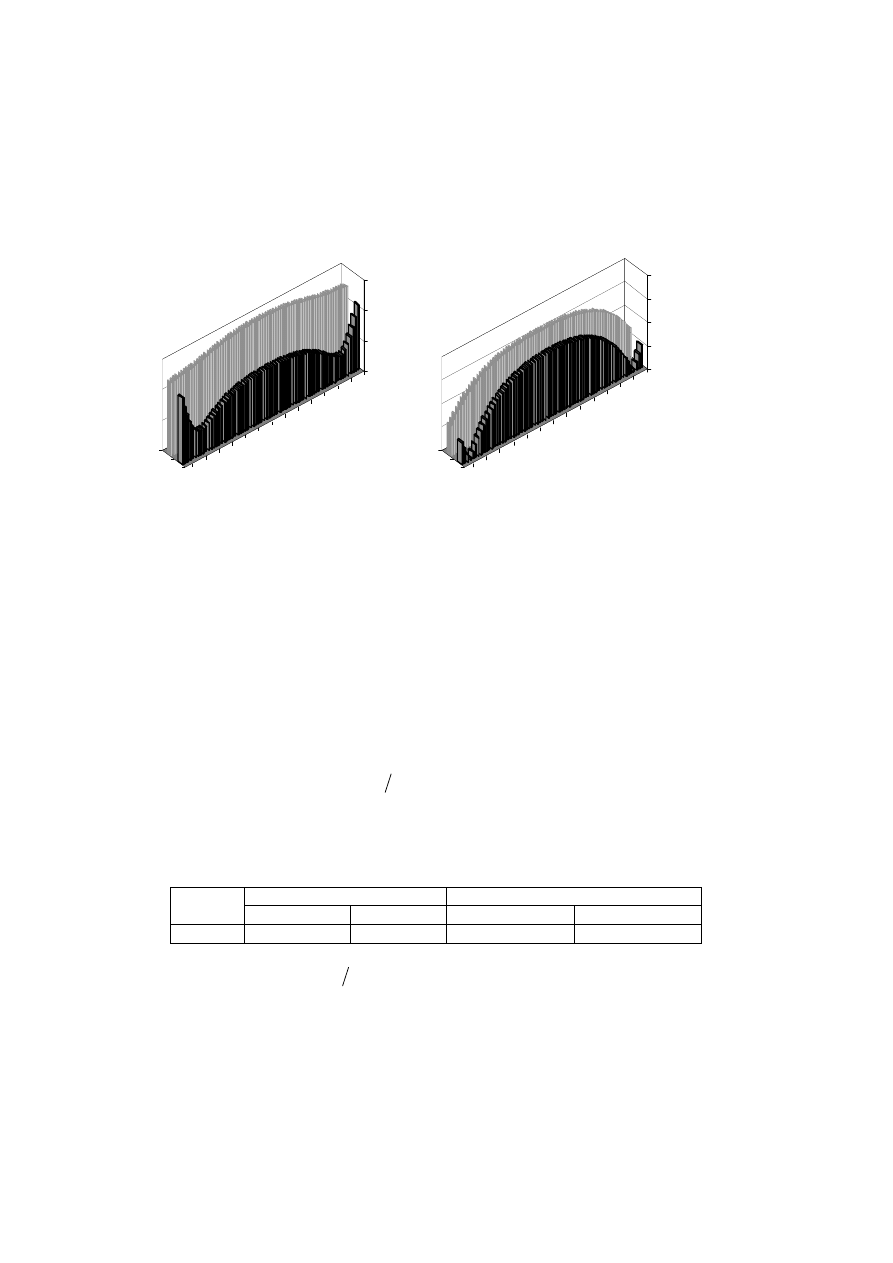
uzwojenia stojana ma nierównomierny przebieg (rys 5).
Wykres rozkładu gęstości prądu przedstawiony na rysunku 5 jest bardzo zbliżony dla
prętów warstwy dolnej w żłobku nr 1 i 9 oraz dla prętów warstwy górnej w żłobku 1 i
9. W pręcie warstwy dolnej gęstość prądu

zwiększa się w miarę oddalania prze-

wodów elementarnych od osi pręta i osiąga największa wartość dla skrajnych przewo-
dów elementarnych. Dla prawej kolumny przewodów elementarnych (rys. 5a i 5c)
stosunek

ac

J

dc

ac

J

J

jest największy i wynosi 3,2 dla najwyżej położonego przewodu

elementarnego w pręcie warstwy dolnej uzwojenia stojana.
Rozkład gęstości prądu pręta warstwy górnej jest bardziej niekorzystny niż pręta war-
stwy dolnej. Stosunek

dc

ac

J

J

jest dużo większy od jedności dla większej liczby

przewodów elementarnych. Wartość maksymalna

dc

ac

J

J

występuje dla skrajnych

przewodów elementarnych kolumny prawej pręta w żłobku 1 (ciemniejsza kolumna na
rysunku 5 b).

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

1.0

2.0

3.0

4.0

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

a). Żłobek 1, pret dolny (BB), przeplot

0+360+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

1.0

2.0

3.0

4.0

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

b). Żłobek 1, pret gorny (TB), przeplot

0+360+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

1.0

2.0

3.0

4.0

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

c). Żłobek 9, pret dolny (BB), przeplot

0+360+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

1.0

2.0

3.0

4.0

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

d). Żłobek 9, pret gorny (TB), przeplot

0+360+0

Rys 5. Rozkład gęstości prądu wzdłuż wysokości pręta uzwojenia stojana (transpozycja 0+360+0)

a) żłobek 1, pręt dolny, b) żłobek 1, pręt górny, c) żłobek 9, pręt dolny, d) żłobek 9, pręt górny,

Fig. 5. Current density distribution as a function of the stator bar height (transposition 0+360+0).

a) slot 1, bottom bar, b) slot 1, top bar, c) slot 9, bottom bar, d) slot 9, top bar,

Wartości współczynników strat od prądów cyrkulacyjnych

dla każdego pręta

żłobka 1 i 9 przedstawiono w tabeli 2.

CCL

k

Tabela 2. Współczynnik strat od prądów cyrkulacyjnych dla przelotu typu 0+360+0

Table 2. The circulating current losses coefficient for transposition 0+360+0

Żłobek 1

Żłobek 9

pręt dolny

pręt górny

pręt dolny

pręt górny

k

CCL

1,41 1,70

1,41

1,73

Z porównania współczynników strat pręta warstwy dolnej i górnej obydwu żłóbków
wynika, iż oddziaływanie prądów cyrkulacyjnych jest większe w pręcie górnym. W

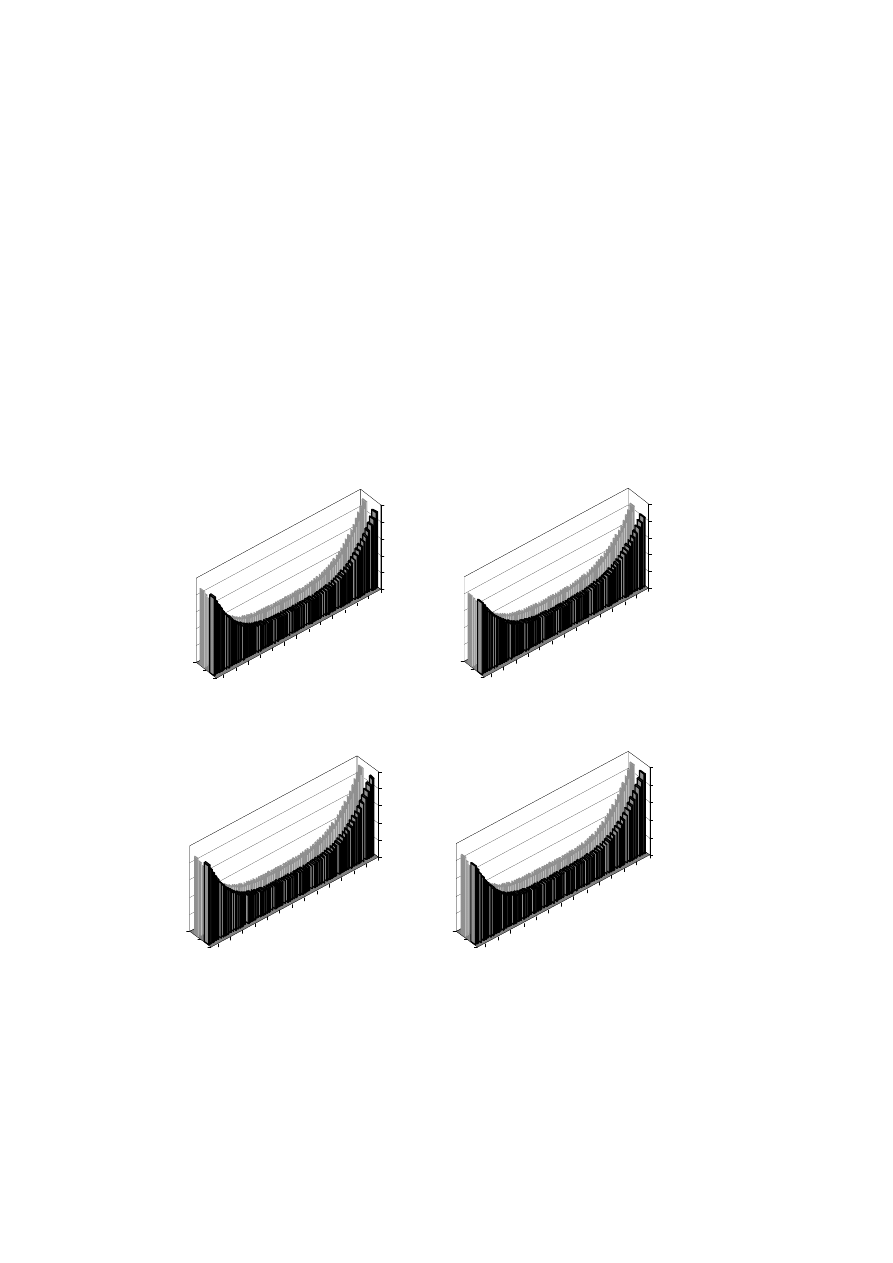
prętach warstwy górnej powstają większe straty dodatkowe wywołane przepływem
prądów cyrkulacyjnych.

3.4. ROZKŁAD GĘSTOŚCI PRĄDU WZDŁUŻ WYSOKOŚCI PRĘTA DLA PRZEPLOTU

TYPU 0+540+0

Przeplot typu 0+540+0 jest nieparzystą wielokrotnością przeplotu 0+180+0, stąd w
procesie transpozycji każdy przewód elementarny wykonuje półtora obiegu wokół osi
pręta [2, 3, 6, 9]. Przy zastosowaniu tej transpozycji następuje eliminacja prądów cyr-
kulacyjnych wytwarzanych w strefie żłobkowej w wyniku całkowitej kompensacji
napięć indukowanych od strumienia rozproszenia w tym obszarze.

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

0.5

1.0

1.5

2.0

2.5

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

a). Żłobek 1, pret dolny (BB), przeplot

0+540+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

0.5

1.0

1.5

2.0

2.5

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

b). Żłobek 1, pret gorny (TB), przeplot

0+540+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

0.5

1.0

1.5

2.0

2.5

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

c). Żłobek 9, pret dolny (BB), przeplot

0+540+0

1

6

11

16

21

26

31

36

41

46

51

56

61

66

0.0

0.5

1.0

1.5

2.0

2.5

Jac/Jdc

[p.u.]

Numer przewodu
elementarnego

d). Żłobek 9, pret gorny (TB), przeplot

0+540+0

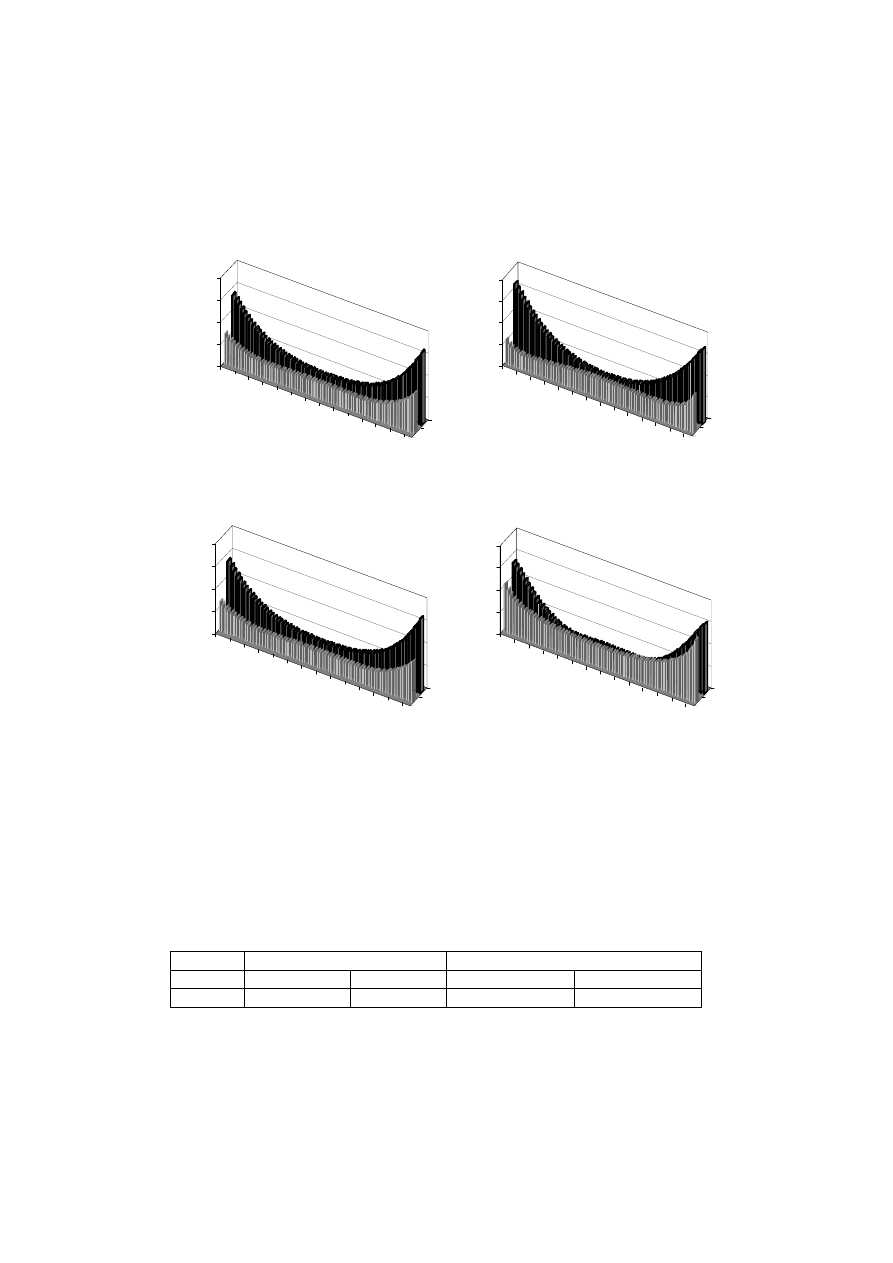
Rys 6. Rozkład gęstości prądu wzdłuż wysokości pręta uzwojenia stojana (transpozycja 0+540+0)

a) żłobek 1, pręt dolny, b) żłobek 1, pręt górny, c) żłobek 9, pręt dolny, d) żłobek 9, pręt górny,

Fig. 6. Current density distribution as a function of the stator bar height (transposition 0+540+0).

a) slot 1, bottom bar, b) slot 1, top bar, c) slot 9, bottom bar, d) slot 9, top bar,

Przeplot ten kompensuje również napięcia w strefie czołowej indukowane od stru-

mieni rozproszenia pozostałych prętów uzwojenia stojana i uzwojenia wirnika. Nato-
miast napięcia indukowane od własnego strumienia rozproszenia w części czołowej
pręta są nieskompensowane. Dlatego od niezrównoważonego napięcia, w pętli utwo-
rzonej przez przewody elementarne, płyną prądy cyrkulacyjne. Prądy te są przyczyną
nierównomiernego rozkładu gęstości prądu wzdłuż wysokości pręta warstwy dolnej
(BB) i górnej (TB) uzwojenia stojana.
Rozkład gęstości prądu wzdłuż wysokości pręta warstwy dolnej i górnej przy zasto-
sowaniu przeplotu typu 0+540+0, przedstawiono na rysunku 6.
Przebieg tego rozkładu jest bardzo zbliżony w prętach warstwy dolnej i górnej w oby-
dwu żłobkach (żłobek 1 i 9). W pręcie warstwy dolnej i górnej gęstość prądu

zwiększa się w miarę oddalania od osi pręta i osiąga największą wartość dla skrajnych
przewodów elementarnych. Dla pręta warstwy dolnej uzwojenia stojana stosunek

ac

J

dc

ac

J

J

osiąga wartość maksymalną równą 2,3 dla najwyżej i najniżej położonych

przewodów elementarnych w pręcie (rys. 6a i 6c).
Z porównania współczynników strat

zestawionych w tabeli 3 wynika, iż prądy

cyrkulacyjne w pręcie dolnym są nieznacznie większe.

CCL

k

Tabela 3. Współczynnik strat od prądów cyrkulacyjnych dla przelotu typu 0+540+0

Table 3. The circulating current losses coefficient for transposition 0+540+0

Żłobek 1

Żłobek 9

pręt dolny

pręt górny

pręt dolny

pręt górny

k

CCL

1,28 1,25

1,29

1,24

4. WNIOSKI

Przedstawiona w pracy metoda i program komputerowy „Bar” umożliwiają obli-

czenie rozpływu i gęstości prądów w przewodach elementarnych oraz strat dodatko-
wych wynikających z prądów cyrkulacyjnych w prętach turbogeneratora dla różnych
typów przeplotu Roebela.

Na podstawie wykonanych obliczeń można wskazać typ przeplotu przewodów

elementarnych, w którym występuje najbardziej równomierny rozkład gęstości prą-
dów w prętach dolnych i górnych oraz najmniejsze straty energii w uzwojeniu maszy-
ny.

LITERATURA

[1]

CARPENTER C.J., The application of the method of images to machine end-winding fields.

Proceedings. IEE,1960 part A, pp. 487-500

[2]

DĄBROWSKI M., Projektowanie maszyn elektrycznych prądu przemiennego. WNT War-

szawa 1994.

[3]

GURAZDOWSKI D, ZAWILAK J., Wpływ przeplotu przewodów elementarnych na stru-

mień skojarzony z prętem turbogeneratora. Prace naukowe Instytutu Maszyn, Napędów i
Pomiarów Elektrycznych PWr. nr 54., 2003, s. 89-100

[4]

GURAZDOWSKI D, ZAWILAK J., Sprzężenia magnetyczne przewodów elementarnych

dwuwarstwowego uzwojenia stojana turbogeneratora. Sympozjum PPEE 2005.

[5]

GURAZDOWSKI D, ZAWILAK J., Indukcja magnetyczna i napięcie indukowane w stre-

fie połączeń czołowych pręta turbogeneratora. Prace naukowe Instytutu Maszyn, Napędów
i Pomiarów Elektrycznych PWr. nr 54, 2004, s. 149-158

[6]

HALDEMAN J., Untersuchung verschiedener Verdrillungsarten in Statorwicklungen gro-

ßer Synchronmaschinen, deren Wirkung auf Strom-und Temperaturverteilung und Zusatz-
verluste in verschiedenen Betriebszuständen. Zürich, 1997, Ausgewählte arbeiten aus dem
Institut für Elektrische Maschinen ETH-ZURICH (ETH Nr. 12291).

[7]

ISELI M. A., Zusatverluste in Statorwicklungen grosser Synchronmaschinen unter Beruck-

sichtigung der Verdrillung und der Stirnraumfelder. Zürich 1991, Ausgewählte arbeiten
aus dem Institut für Elektrische Maschinen ETH-ZURICH (ETH Nr. 9546).

[8] KRAKOWSKI M., Elektrotechnika teoretyczna – pole elektromagnetyczne. PWN War-

szawa 1995 –wydanie piąte poprawione.

[9]

LATEK W., Turbogeneratory. WNT Warszawa 1973.

[10]

REECE. A.B.J., PRAMANIK A., Calculation of the end-region field of a.c. machines.

Proceedings. IEE,1965, pp. 1355-1368

[11] SIKORA R., Teoria pola elektromagnetycznego. WNT Warszawa 1997 –wydanie trzecie

zmienione.

[12]

TRAXLER-SAMEK G., Zusatzverluste im Stirnraum von Hydrogeneratoren mit Roe-

belstabwicklung. Technischen Universitat Wien, Mai 2003, Rozprawa doktorska.

[13]

VOLDEK A.I., Procedure for analyzing the magnetic fields of the end-windings of elec-

trical machines. Leningrad Polytechnical Insitute, 1962.

THE INFLUENCE OF ROEBEL STRANDS TRANSPOSITION ON CURRENT

DENSITY DISTRIBUTION WITHIN TURBOGENERATOR WINDING BAR

The paper presents the influence of Roebel strands transposition on current density distribution as a
function of the top and bottom bar of turbogenerator stator winding. Here is presented the computer
program "Bar" which makes it possible to calculate this current density for different Roebel strands
transposition type within slot and overhang parts. The computations were made for selected tur-
bogenerator, which has power 450MVA, voltage 21kV and frequency 60Hz. The application compu-
tational model takes into consideration the strands magnetic coupling within as well as slot part (fer-
romagnetic environment) and overhang part (non-magnetic environment). The calculation results of
the bar current density distribution are presented for three following transposition types: 0+180+0,
0+360+0, 0+540+0. The calculated bars are located in slot number 1 and 9.