Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych

Nr 58

Politechniki Wrocławskiej

Nr 58

Studia i Materiały Nr

25

2005

__________

Silnik indukcyjny, klatkowy

model polowo-obwodowy, projektowanie

charakterystyki statyczne, dynamiczne

Ludwik ANTAL

*

, Maciej ANTAL

*

, Jan ZAWILAK

F

*

WPŁYW SZEROKOŚCI OTWARCIA ŻŁOBKÓW NA

STATYCZNE I DYNAMICZNE CHARAKTERYSTYKI SILNIKA

INDUKCYJNEGO MAŁEJ MOCY

W pracy przeprowadzono analizę wpływu otwarcia żłobków stojana i wirnika indukcyjnego sil-

nika klatkowego małej mocy na jego charakterystyki statyczne i dynamiczne. Obliczenia charaktery-
styk statycznych momentu i prądu stojana wykonano znajdując rozkład magnetycznego pola harmo-
nicznego w polowo-obwodowym modelu silnika indukcyjnego. Wykonując obliczenia dla różnych
szerokości otwarcia żłobków wirnika i stojana oraz różnych wartości poślizgu zbadano wpływ tych
parametrów na przebiegi momentu i prądu. Z analizy pola nieustalonego w dwuwymiarowym modelu
polowo-obwodowym uzyskano czasowe charakterystyki rozruchowe i charakterystyki ustalonego
stanu obciążenia. Dla tych charakterystyk wykonano obliczenia dla różnych wartości szerokości
otwarcia żłobków stojana.

1. WSTĘP

Obecna sytuacja na rynku silników indukcyjnych wygląda tak, że produkowane są

silniki różnych klas sprawności: zarówno energooszczędne o wysokiej sprawności,
stosowane zwłaszcza wtedy, kiedy silnik musi pracować przez dużą liczbę godzin w
roku, jak i materiałooszczędne o niskiej cenie, których stosowanie jest uzasadnione
ich krótkotrwałą pracą [14, 15]. W tej sytuacji celem wartym wysiłku jest zbliżenie do
siebie tych przeciwstawnych klas silników, poprzez jednoczesne zwiększanie spraw-
ności i zmniejszanie zużycia materiałów. Silnik indukcyjny jest konstrukcją stosun-
kowo prostą i dobrze poznaną. Znane są sposoby podnoszenia ich sprawności i konse-
kwencje tych sposobów [4, 14]. Znane i stosowane są metody optymalizacji ich

*

Politechnika Wrocławska, Instytut Maszyn, Napędów i Pomiarów Elektrycznych, 50-372 Wrocław

ul. Smoluchowskiego 19,

HU

[e-mail]

UH

,

HU

[e-mail]

UH

,

HU

[e-mail]

UH

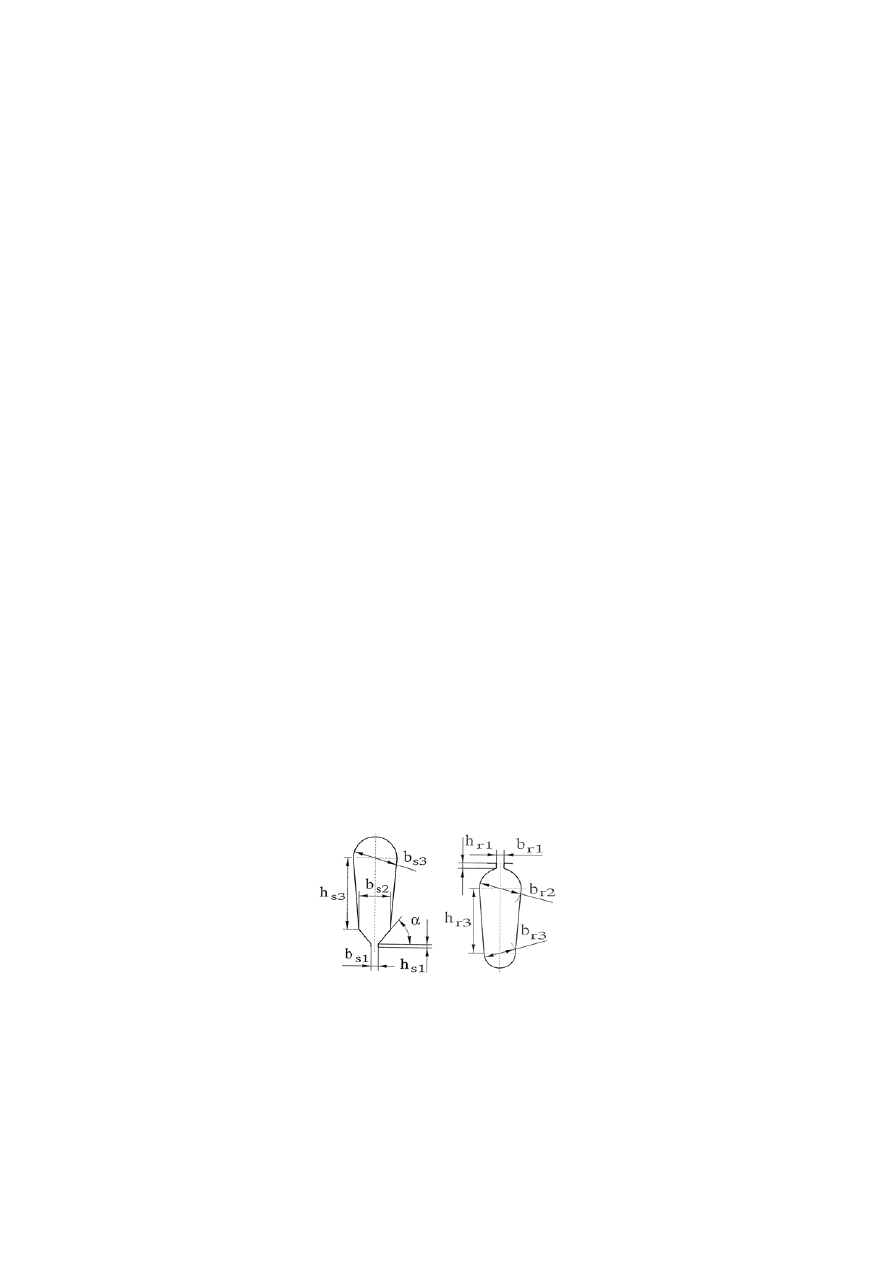
konstrukcji [9, 10, 11, 13]. Jednakże postępy inżynierii materiałowej i technik obli-
czeniowych stwarzają nadzieję na wykorzystanie rezerw tkwiących we własnościach
materiałowych, kształtach i wymiarach. Z tego powodu prowadzone są intensywne
badania nad lepszym odwzorowaniem zjawisk elektromagnetycznych i cieplnych za-
chodzących w silniku indukcyjnym. Pojawiły się zarówno prace dotyczące obliczania
strat mocy (również w laminowanych rdzeniach stalowych) metodą elementów skoń-
czonych [6, 7, 8, 16] jak i prace włączające tę metodę do obliczeń elektromagnetycz-
nych i cieplnych w procesie projektowania maszyny [5, 9, 12]. Ze względu na długi
czas obliczeń modele trójwymiarowe przydatne są do analizy zjawisk, lecz nie mają
jeszcze znaczenia praktycznego w zastosowaniu do projektowania maszyn. W projek-
towaniu mogą jednak być wykorzystywane polowo-obwodowe modele dwuwymiaro-
we. Taki prosty model zbudowany przy użyciu komercyjnego programu Flx2D [3]
posłużył do zbadania wpływu szerokości otwarcia żłobków stojana i wirnika na pod-
stawowe parametry i charakterystyki eksploatacyjne standardowego silnika indukcyj-
nego małej mocy. W pracy [2] przedstawiono wyniki analizy harmonicznej pola w
szczelinie silnika klatkowego i wpływ zmian szerokości otwarcia żłobków na spraw-
ność i współczynnik mocy. Wskazano tam również na możliwość wykorzystania
dwuwymiarowego modelu polowo-obwodowego do optymalizacji konstrukcji zarów-
no silników energooszczędnych jak i silników materiałooszczędnych. W niniejszej
pracy, kontynuującej te badania, przedstawiono wpływ szerokości otwarcia żłobków
na statyczne i dynamiczne charakterystyki momentu i prądu.

2. POLE MAGNETYCZNE W SZCZELINIE SILNIKA KLATKOWEGO

Użyty do obliczeń model polowo–obwodowy został zweryfikowany pomiarowo

[1]. Wobec dobrej zgodności wyników obliczeń i pomiarów wykorzystano opracowa-
ny model do analizy wpływu szerokości otwarcia żłobków stojana i wirnika na kształt
pola magnetycznego w szczelinie. Badany, 4-biegunowy silnik posiada 36 żłobków
stojana i 26 żłobków wirnika. Kształt żłobków i ich podstawowe wymiary pokazano
na rysunku 1.

Rys. 1. Żłobki stojana i wirnika

Fig. 1. Stator and rotor slots

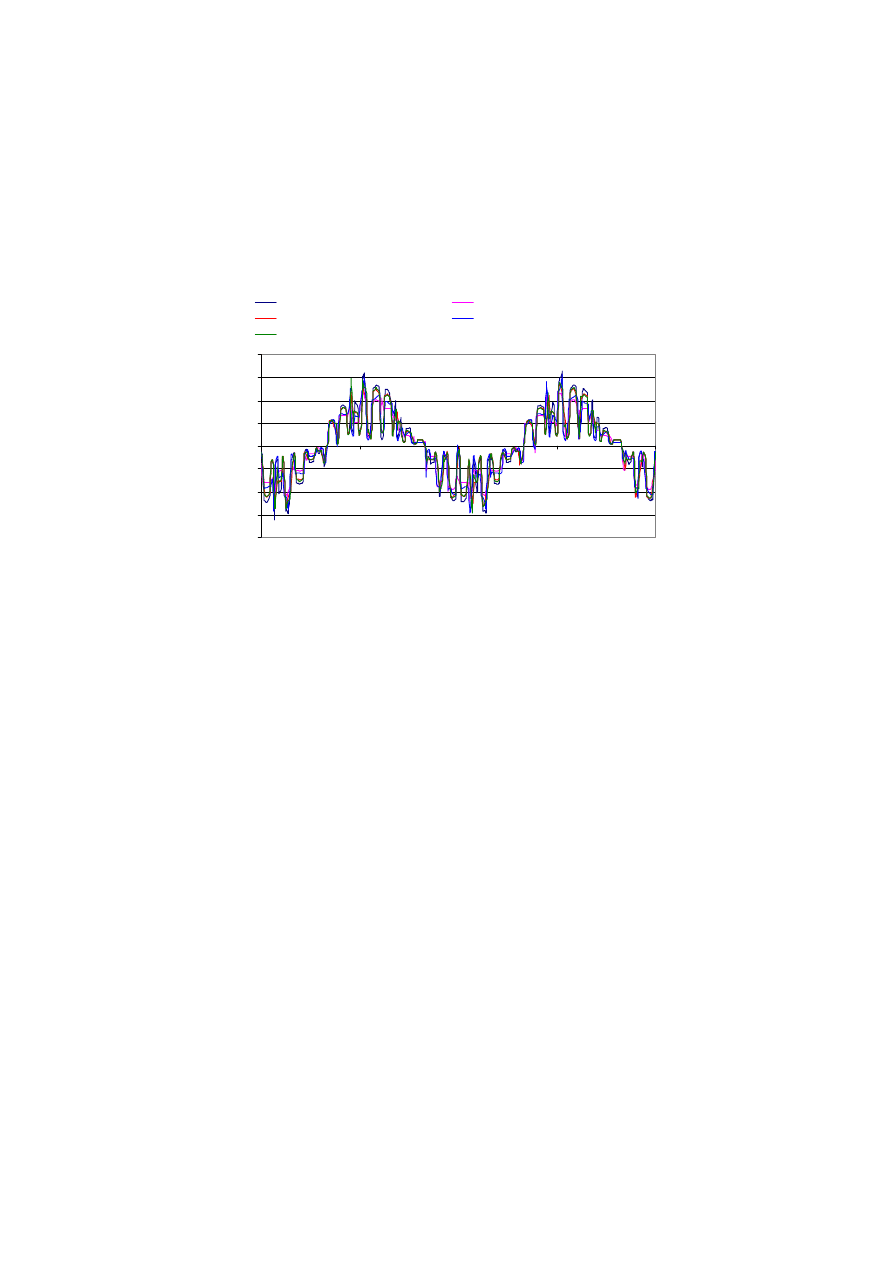
Obwodowy rozkład składowej normalnej indukcji w szczelinie, dla wybranych,

przykładowych wartości szerokości otwarcia żłobków, przedstawiony na rysunku 2,
wskazuje na zależność kształtu pola od rozpatrywanych wymiarów.

-2,0

-1,5

-1,0

-0,5

0,0

0,5

1,0

1,5

2,0

0

90

180

270

360

kąt [deg]

am

pl

itu

da i

nduk

cj

i [

T

]

bs1 = 2,5 mm; br1 = 2,5 mm

bs1 = 0,5 mm; br1 = 0,25 mm

bs1 = 2,5 mm; br1 = 0,25 mm

bs1 = 0,5 mm; br1 = 2,5 mm

bs1 = 2,5 mm; br1 = 1,0 mm

Rys. 2. Rozkład składowej normalnej indukcji w szczelinie silnika

Fig. 2. Distribution of the normal flux density component in the air-gap of the motor

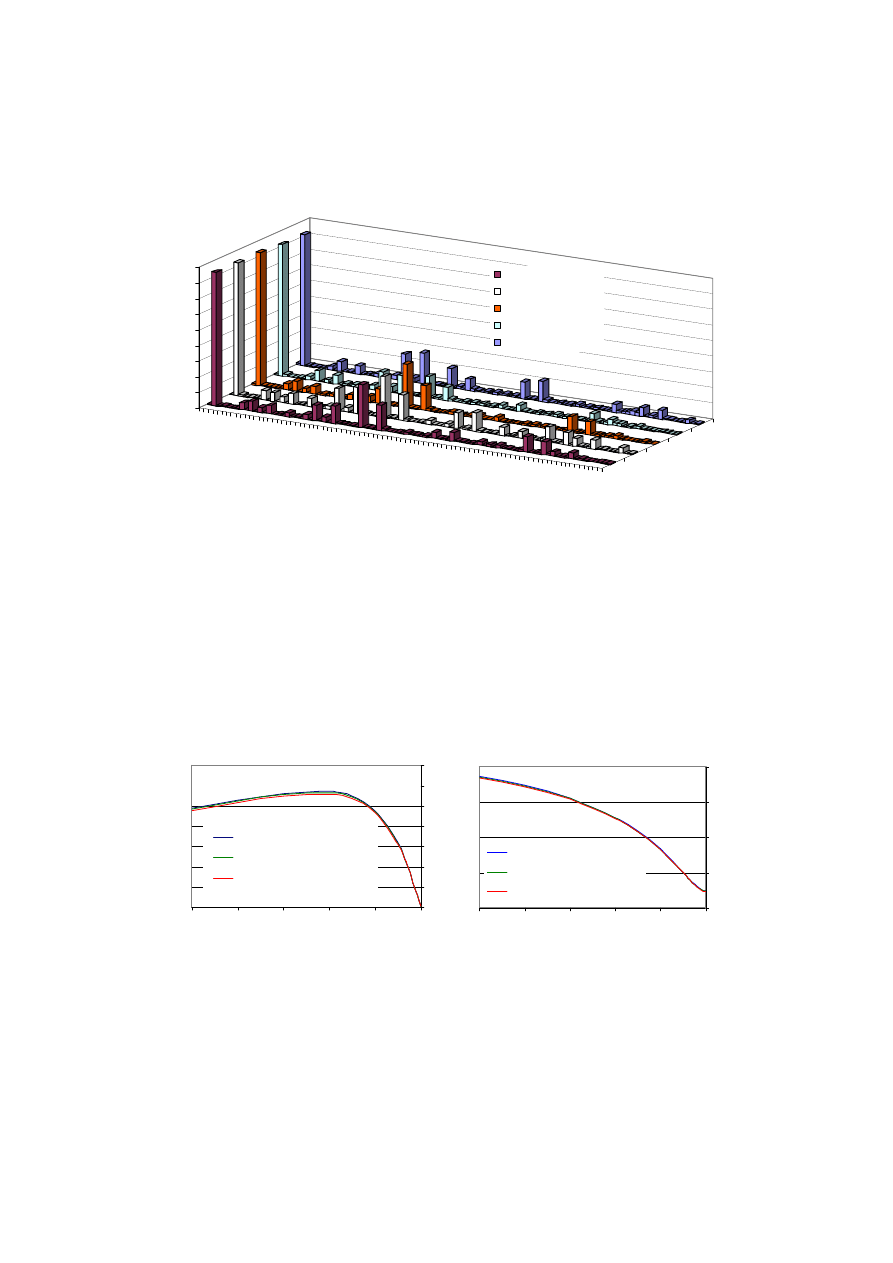
Analiza harmoniczna tych przebiegów (rys. 3) dowodzi, że zależność różnych ro-

dzajów harmonicznych (strefowe n =

νp, żłobkowe stojana n = kŻ

1

± p, żłobkowe

wirnika n = kŻ

2

± p) od wymiarów otwarcia żłobków jest różna. Zależności te szcze-

gółowo omówiono w [2]. Obliczenia magnetycznego pola harmonicznego dla prędko-
ści znamionowej (s =0,06) wykonano zmieniając co 0,25 mm szerokość otwarcia
żłobka stojana b

s1

w zakresie 0,5 – 2,5 mm, i szerokość otwarcia żłobka wirnika b

r1

w

przedziale 0,25 – 2,5 mm, co dało 90 kombinacji otwarcia żłobków. Analiza harmo-
niczna pola w szczelinie dla wszystkich rozpatrzonych przypadków pozwoliła ustalić
zależność poszczególnych rodzajów harmonicznych od wielkości otwarcia żłobków.
Harmoniczna podstawowa n =

ν

p = 2 jak i harmoniczne

ν

= 5 i

ν

= 7 w niewielkim

stopniu zależą od szerokości rozwarć żłobków. Harmoniczne żłobkowe wirnika (n =
24; 28; 50; 54, kŻ

2

± p) rosną ze wzrostem otwarcia żłobków wirnika, natomiast nie-

znacznie zmieniają się na skutek zmian otwarcia żłobków stojana. W identyczny spo-
sób zmieniają się wszystkie harmoniczne żłobkowe wirnika. Harmoniczne żłobkowe
stojana (n = 34; 38; 70; 74, kŻ

1

± p) rosną ze wzrostem otwarcia żłobków stojana,

natomiast w niewielkim stopniu zmieniają się pod wpływem zmian otwarcia żłobków
wirnika. Podobnie zmieniają się wszystkie harmoniczne żłobkowe stojana.

1

5

9 13 17 21

25 29 33 37

41 45 49

53 57 61 65

69 73 77 81

85

14

24 28

50 54

10

2

34

74

70

38

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

am

pl

itu

d

a in

d

u

kc

ji [

T

]

nr harmonicznej (

νp)

bs1 : 2,5 br1 : 2,5
bs1 : 2,5 br1 : 1
bs1 : 2,5 br1 : 0,25
bs1 : 0,5 br1 : 2,5
bs1 : 0,5 br1 : 0,25

Rys. 3. Amplitudy harmonicznych składowej normalnej indukcji w szczelinie silnika

Fig. 3. Amplitudes of harmonics of the normal flux density component in air-gap

3. CHARAKTERYSTYKI STATYCZNE

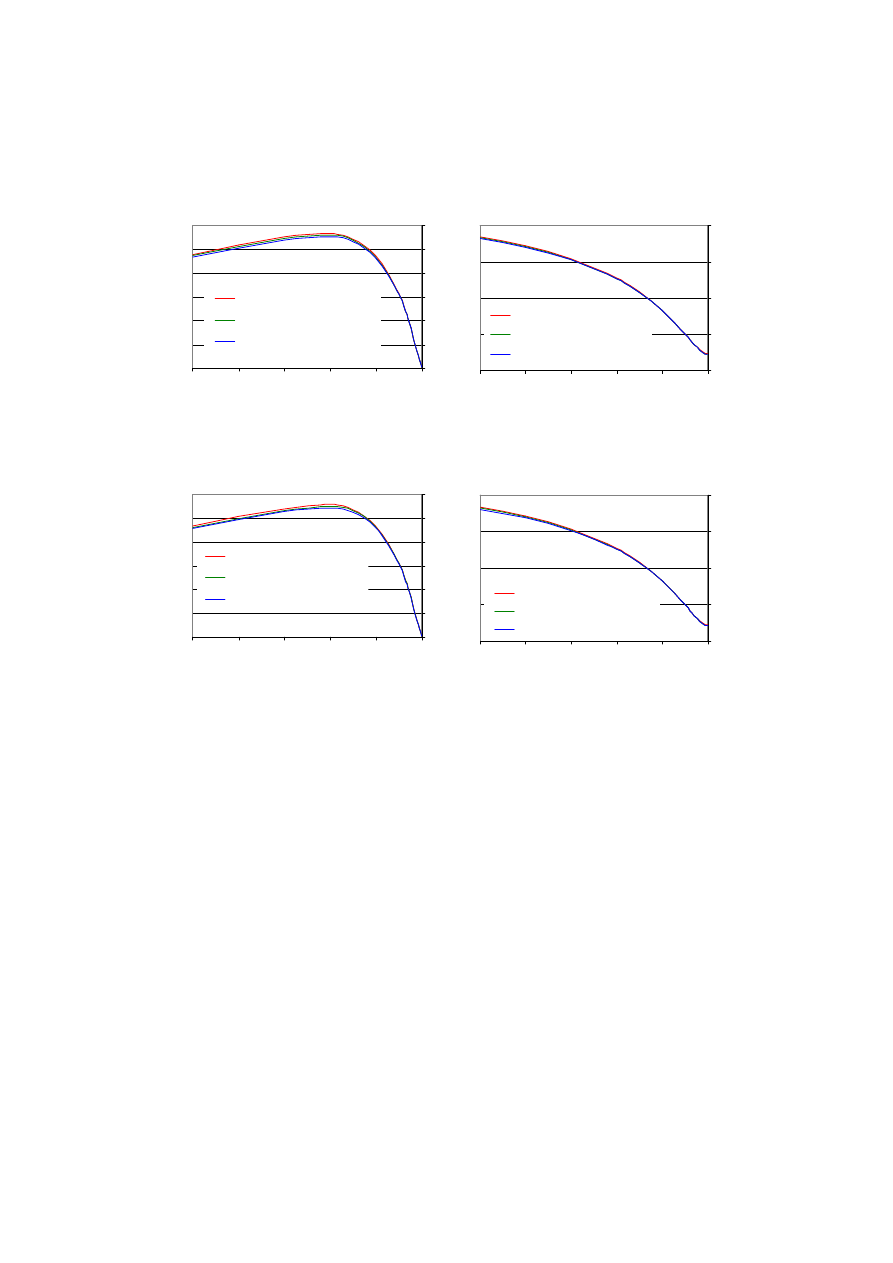
Obliczenia magnetycznego pola harmonicznego dla różnych wartości poślizgu

(s = 0,001–1,0) i różnych wartości szerokości otwarcia żłobków stojana i wirnika po-
zwoliły wyznaczyć charakterystyki momentu i prądu stojana przedstawione na rysun-
kach 4, 5 i 6. Na rysunkach tych kolejność krzywych odpowiada kolejności opisów
legendy.

0

5

10

15

20

25

30

35

0,0

0,2

0,4

0,6

0,8

1,0

poślizg

mo

me

nt

[

N

m]

br1 = 1,5 mm; bs1 = 2,5 mm

br1 = 1,0 mm; bs1 = 2,5 mm

br1 = 0,5 mm; bs1 = 2,5 mm

0

5

10

15

20

0,0

0,2

0,4

0,6

0,8

1,0

poślizg

pr

ąd f

az

ow

y s

toj

ana [

A

]

br1 = 1,5 mm; bs1 = 2,5 mm

br1 = 1,0 mm; bs1 = 2,5 mm

br1 = 0,5 mm; bs1 = 2,5 mm

Rys. 4. Charakterystyki momentu i prądu stojana (b

s1

= 2,5 mm)

Fig. 4. Torque and stator current characteristics (b

s1

= 2,5 mm)

0

5

10

15

20

25

30

0,0

0,2

0,4

0,6

0,8

1,0

poślizg

mo

m

en

t [

N

m]

br1 = 1,5 mm; bs1 = 2,0 mm

br1 = 1,0 mm; bs1 = 2,0 mm

br1 = 0,5 mm; bs1 = 2,0 mm

0

5

10

15

20

0,0

0,2

0,4

0,6

0,8

1,0

poślizg

pr

ąd f

az

ow

y s

toj

ana [

A

]

br1 = 1,5 mm; bs1 = 2,0 mm

br1 = 1,0 mm; bs1 = 2,0 mm

br1 = 0,5 mm; bs1 = 2,0 mm

Rys. 5. Charakterystyki momentu i prądu stojana (b

s1

= 2,0 mm)

Fig. 5. Torque and stator current characteristics (b

s1

= 2,0 mm)

0

5

10

15

20

25

30

0,0

0,2

0,4

0,6

0,8

1,0

poślizg

mo

m

en

t [

N

m]

br1 = 1,5 mm; bs1 = 1,5 mm

br1 = 1,0 mm; bs1 = 1,5 mm

br1 = 0,5 mm; bs1 = 1,5 mm

0

5

10

15

20

0,0

0,2

0,4

0,6

0,8

1,0

poślizg

pr

ąd f

az

ow

y s

toj

ana [

A

]

br1 = 1,5 mm; bs1 = 1,5 mm

br1 = 1,0 mm; bs1 = 1,5 mm

br1 = 0,5 mm; bs1 = 1,5 mm

Rys. 6. Charakterystyki momentu i prądu stojana (b

s1

= 1,5 mm)

Fig. 6. Torque and stator current characteristics (b

s1

= 1,5 mm)

Moment i prąd fazowy stojana słabo zależą od szerokości otwarcia żłobków wirni-

ka. Ze wzrostem tej szerokości rośnie zarówno moment jak i prąd, jednakże zmiany te
są widoczne dopiero dla dużych wartości poślizgu. Wzrost szerokości otwarcia żłobka
wirnika prowadzi więc do zwiększenia momentu maksymalnego oraz momentu i prą-
du rozruchowego. Większy wpływ na analizowane wielkości ma zmiana szerokości
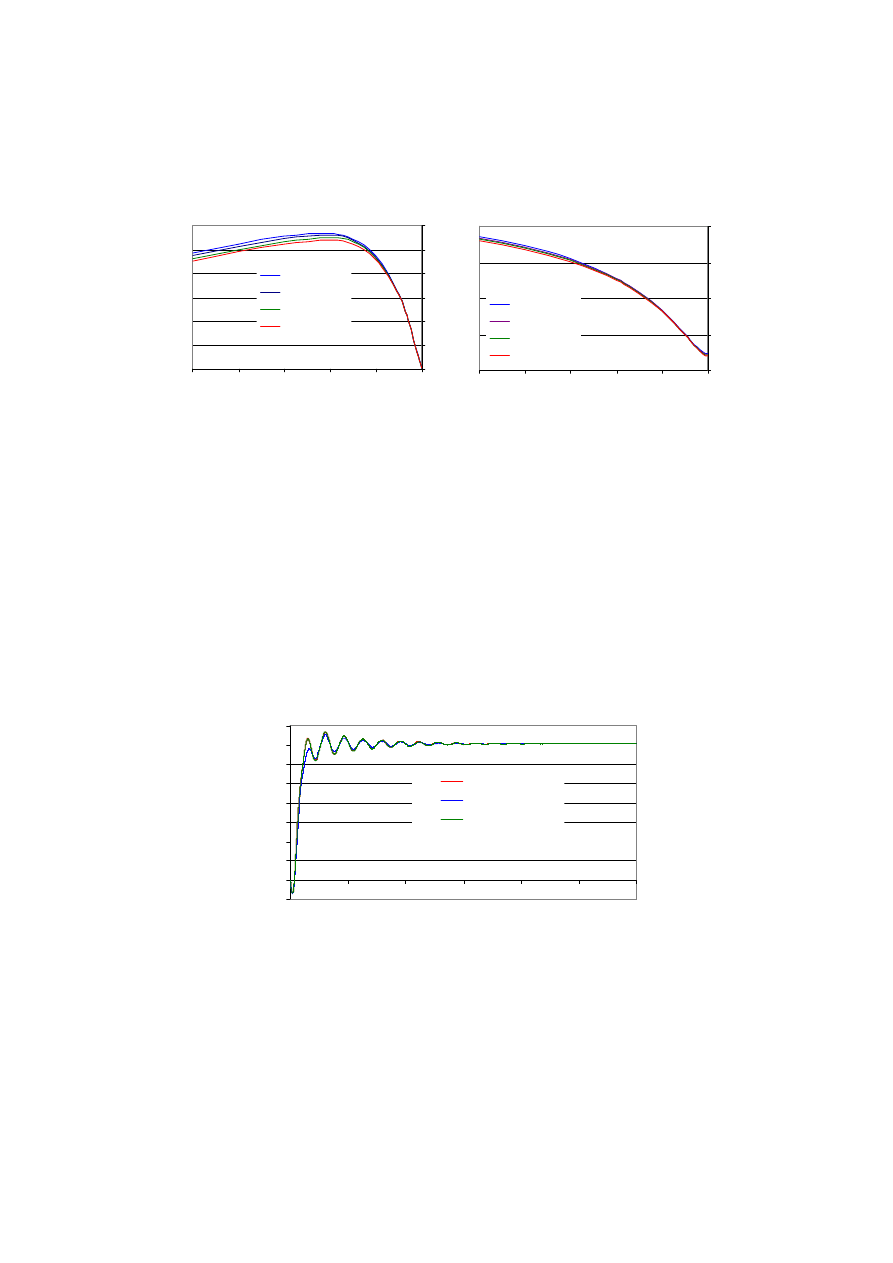
otwarcia żłobków stojana. Na rysunku 7 przedstawiono zmiany charakterystyk mo-
mentu i prądu towarzyszące zmianom szerokości otwarcia żłobka stojana b

s1

. Pokaza-

ne na wykresach charakterystyki zostały wyznaczone dla szerokości otwarcia żłobka
wirnika b

r1

= 1,0 mm. Zmiana szerokości otwarcia żłobka stojana z 2,5 mm na 1,0 mm

zmniejsza moment rozruchowy o 7% i prąd rozruchowy o 3%. Charakter zmian jest
taki sam jak dla żłobka wirnika tzn. moment i prąd rosną ze zwiększaniem szerokości
otwarcia.

0

5

10

15

20

25

30

0,0

0,2

0,4

0,6

0,8

1,0

poślizg

mo

m

en

t [

N

m]

bs1 = 2,5 mm
bs1 = 2,0 mm
bs1 = 1,5 mm
bs1 = 1,0 mm

0

5

10

15

20

0,0

0,2

0,4

0,6

0,8

1,0

poślizg

pr

ąd f

az

ow

y s

toj

an

a [

A

]

bs1 = 2,5 mm
bs1 = 2,0 mm
bs1 = 1,5 mm
bs1 = 1,0 mm

Rys. 7. Charakterystyki momentu i prądu stojana (b

r1

= 1,0 mm)

Fig. 7. Torque and stator current characteristics (b

r1

= 1,0 mm)

3. CHARAKTERYSTYKI DYNAMICZNE

Z analizy pola nieustalonego w dwuwymiarowym modelu polowo-obwodowym

uzyskano czasowe charakterystyki rozruchowe i charakterystyki ustalonego stanu
obciążenia. Pierwsze z nich wyznaczono dla kroku czasowego 0,1 ms, a drugie dla
kroku 0,02 ms. Zwiększenie dokładności było konieczne dla zbadania pulsacji prędko-
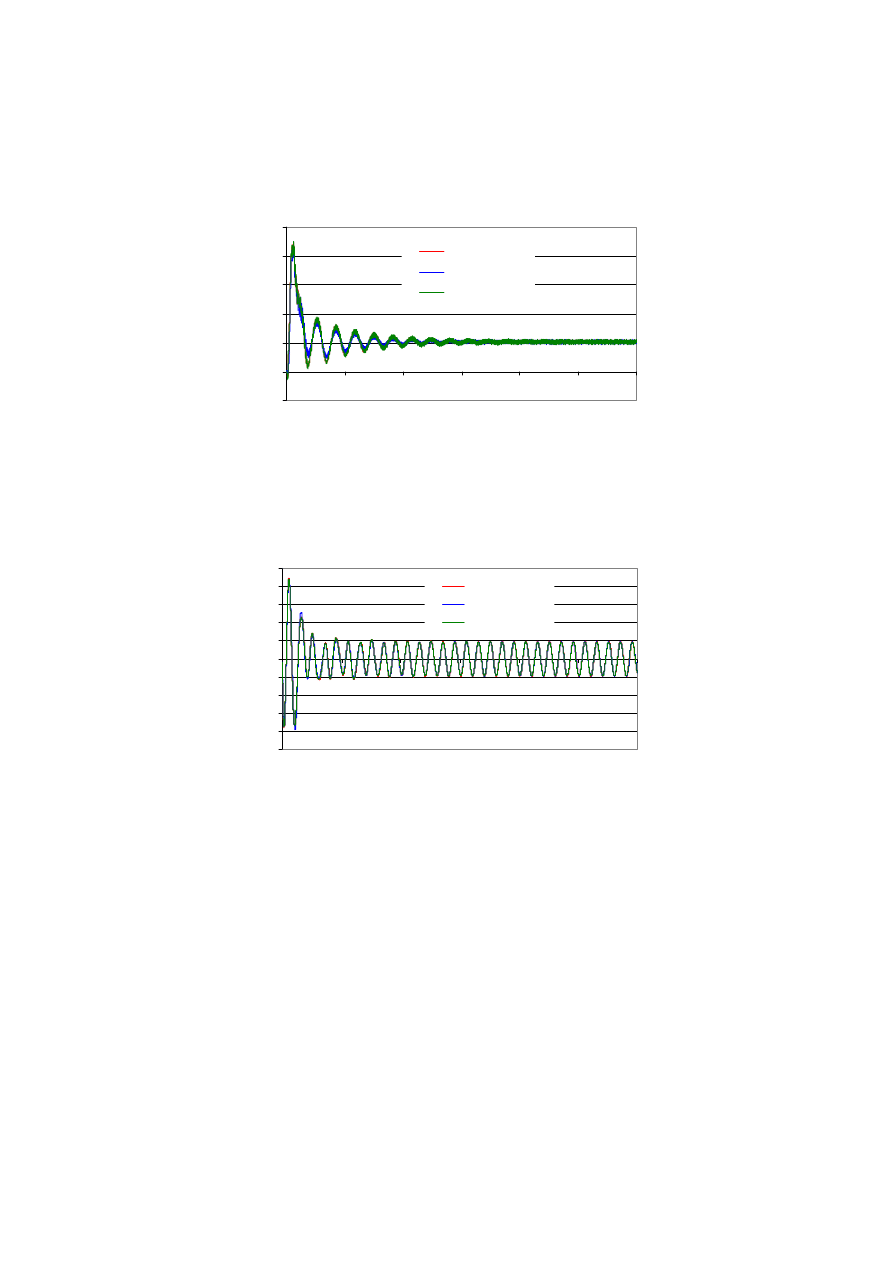
ści obrotowej i momentu. Na rysunkach 8, 9 i 10 przedstawiono rozruch silnika obcią-
żonego stałym, znamionowym momentem, z różnymi szerokościami otwarcia żłobka
stojana i stałą szerokością otwarcia żłobka wirnika (b

r1

= 1,0 mm).

-200

0

200

400

600

800

1000

1200

1400

1600

0,0

0,1

0,2

0,3

0,4

0,5

0,6

czas [s]

pr

ędk

ość

obr

ot

ow

a [

obr

/m

in]

bs1 = 2,5 mm
bs1 = 1,5 mm
bs1 = 1,0 mm

Rys. 8. Prędkość obrotowa podczas rozruchu silnika (b

r1

= 1,0 mm)

Fig. 8. Start-up rotational speed (b

r1

= 1,0 mm)

-10

0

10

20

30

40

50

0,0

0,1

0,2

0,3

0,4

0,5

0,6

czas [s]

mo

me

nt

[

N

m]

bs1 = 2,5 mm

bs1 = 1,5 mm

bs1 = 1,0 mm

Rys. 9. Moment podczas rozruchu silnika (b

r1

= 1,0 mm)

Fig. 9. Start-up torque (b

r1

= 1,0 mm)

-25

-20

-15

-10

-5

0

5

10

15

20

25

0,0

0,1

0,2

0,3

0,4

0,5

0,6

czas [s]

pr

ąd [

A

]

bs1 = 2,5 mm
bs1 = 1,5 mm
bs1 = 1,0 mm

Rys. 10. Prąd stojana podczas rozruchu silnika (b

r1

= 1,0 mm)

Fig. 10. Start-up stator current (b

r1

= 1,0 mm)

Dla największej i najmniejszej z rozpatrywanych szerokości otwarcia żłobka stoja-

na (b

s1

= 1,0 mm i 2,5 mm) przebiegi rozruchowe niemal się pokrywają. Dla b

s1

= 1,5

mm rozruch jest łagodniejszy i trwa krócej. Chociaż moment obciążający ma iden-
tyczną wartość, w końcowej fazie rozruchu prędkości ustalone różnią się wartością
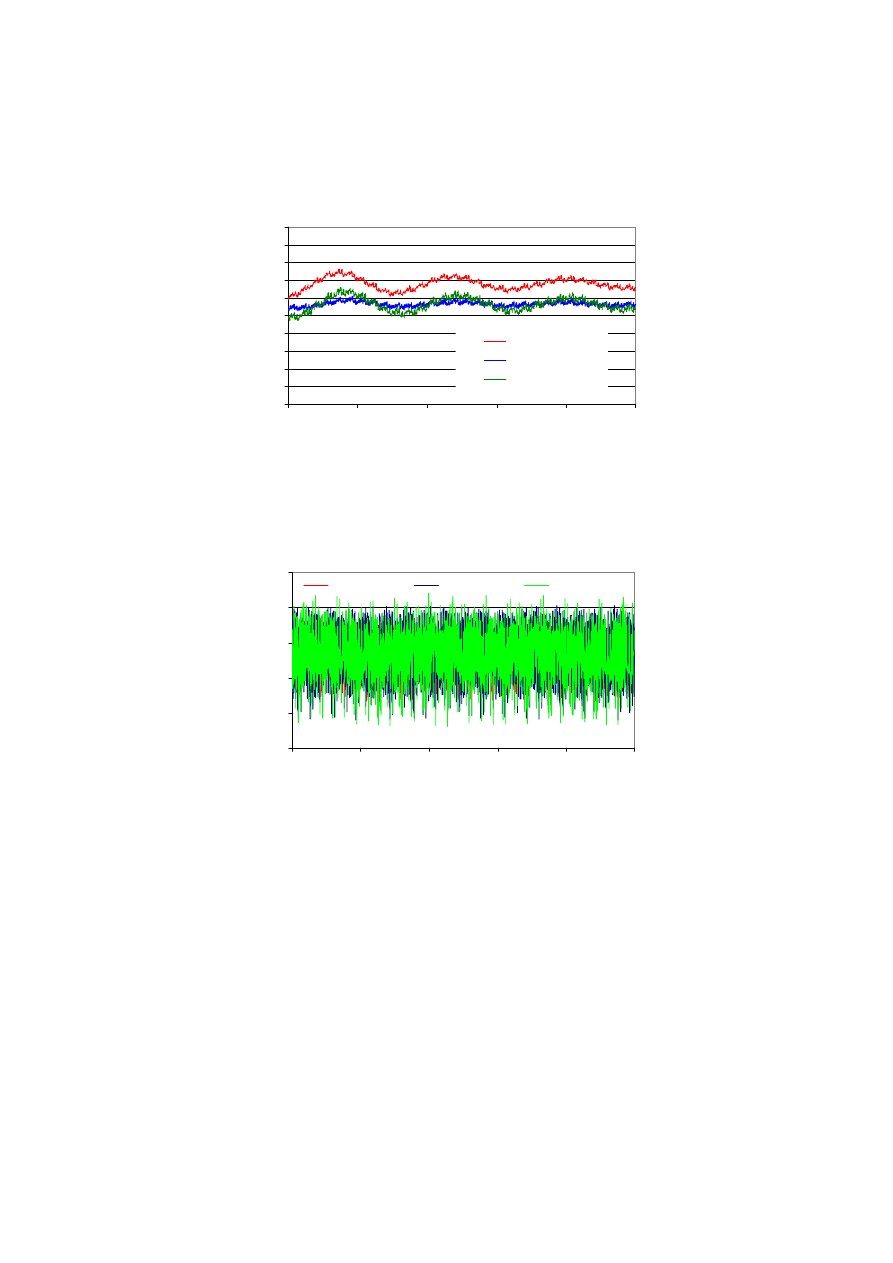
(rys. 11). Moment elektromagnetyczny ma tą samą wartość średnią ale jego pulsacje
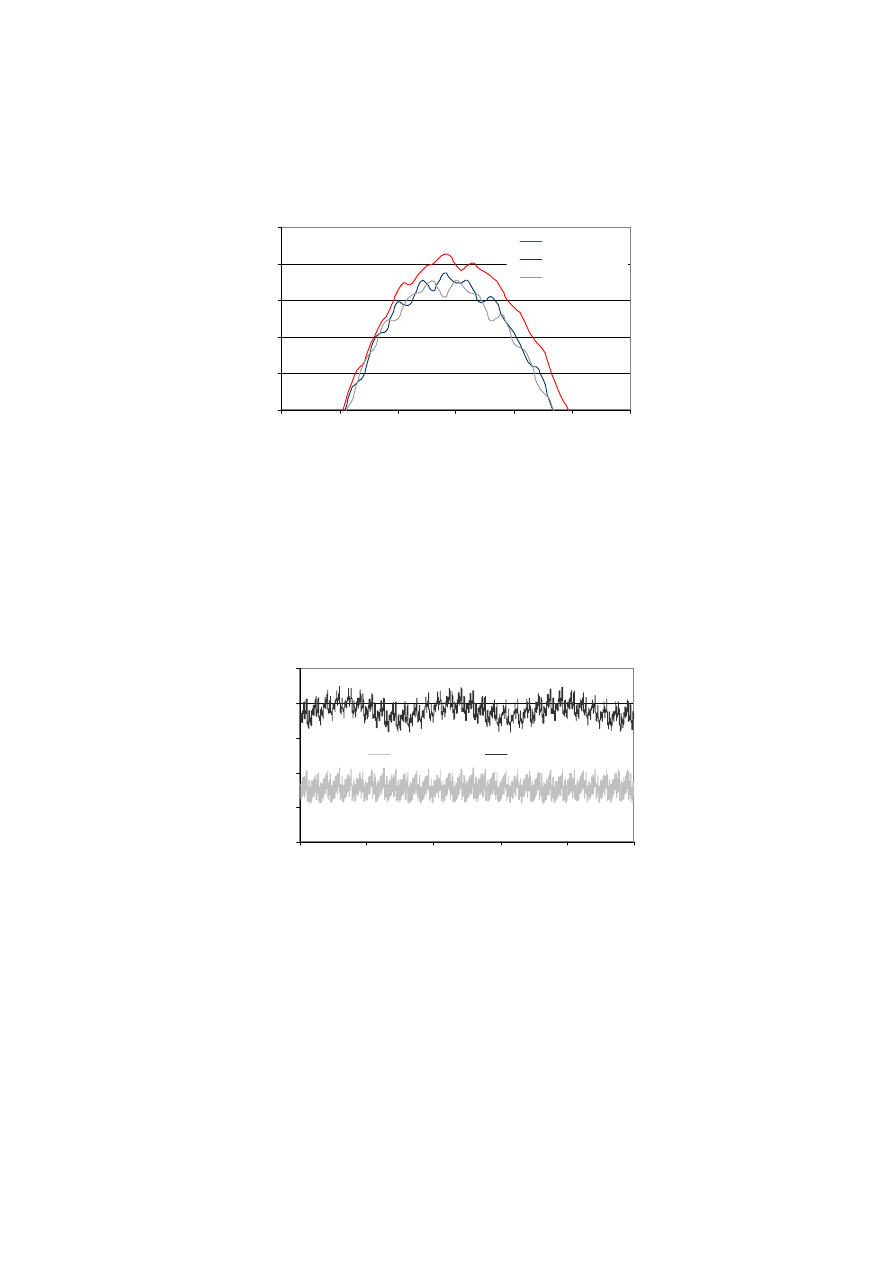
są różne (rys. 12). Prądy stojana minimalnie różnią się wartością, fazą i kształtem (rys.
13).

1405

1406

1407

1408

1409

1410

1411

1412

1413

1414

1415

0,50

0,52

0,54

0,56

0,58

0,60

czas [s]

pr

ędk

ość

obr

ot

ow

a [

obr

/m

in]

bs1 = 2,5 mm
bs1 = 1,5 mm
bs1 = 1,0 mm

Rys. 11. Prędkość obrotowa w końcowej fazie rozruchu silnika (b

r1

= 1,0 mm)

Fig. 11. Rotational speed during a last part of motor start-up (b

r1

= 1,0 mm)

9,0

9,5

10,0

10,5

11,0

11,5

0,50

0,52

0,54

0,56

0,58

0,60

czas [s]

mo

m

en

t [

N

m]

bs1 = 2,5 mm

bs1 = 1,5 mm

bs1 = 1,0 mm

Rys. 12. Moment w końcowej fazie rozruchu silnika (b

r1

= 1,0 mm)

Fig. 12. Torque during a last part of motor start-up (b

r1

= 1,0 mm)

4,0

4,2

4,4

4,6

4,8

5,0

0,589

0,590

0,591

0,592

0,593

0,594

0,595

czas [s]

pr

ąd [

A

]

bs1 = 2,5 mm
bs1 = 1,5 mm
bs1 = 1,0 mm

Rys. 13. Prąd stojana w końcowej fazie rozruchu silnika (b

r1

= 1,0 mm)

Fig. 13. Stator current during a last part of motor start-up (b

r1

= 1,0 mm)

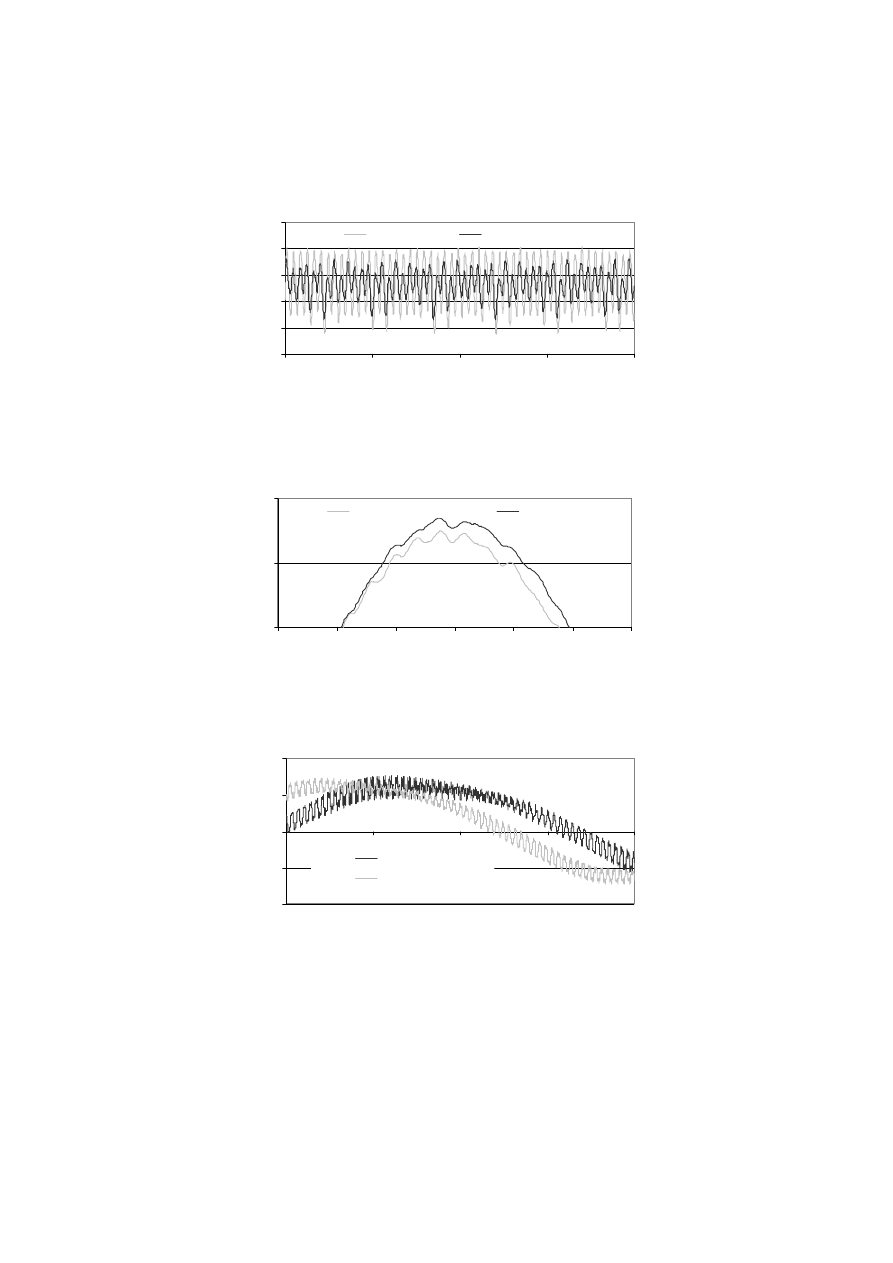
Po ustaleniu się przebiegów rozruchowych (t > 1 s) różnica prędkości ustalonych

dla b

s1

= 1,5 i 2,5 mm jest nieco większa od 1 obr/min. Pulsacje prędkości są większe

(rys. 14), a pulsacje momentu mniejsze (rys. 15) dla większej szerokości otwarcia
żłobka. Dla szerszego otwarcia żłobka wartości amplitudy i fazy prądu stojana są
większe (rys. 16), a prąd wirnika ustala się później (rys. 17).

1410,0

1410,5

1411,0

1411,5

1412,0

1412,5

1,10

1,12

1,14

1,16

1,18

1,20

czas [s]

pr

ędk

ość

obr

ot

ow

a [

obr

/m

in]

bs1 = 1,5 mm

bs1 = 2,5 mm

Rys. 14. Prędkość obrotowa po zakończeniu rozruchu silnika (b

r1

= 1,0 mm)

Fig. 14. Rotational speed after the motor start-up (b

r1

= 1,0 mm)

9,0

9,5

10,0

10,5

11,0

11,5

1,18

1,19

1,19

1,20

1,20

czas [s]

mo

me

nt

[

N

m]

bs1 = 1,5 mm

bs1 = 2,5 mm

Rys. 15. Moment po zakończeniu rozruchu silnika (b

r1

= 1,0 mm)

Fig. 15. Torque after the motor start-up (b

r1

= 1,0 mm)

4,0

4,5

5,0

1,189

1,190

1,191

1,192

1,193

1,194

1,195

czas [s]

pr

ąd f

az

ow

y s

toj

ana [

A

]

bs1 = 1,5 mm

bs1 = 2,5 mm

Rys. 16. Prąd stojana po zakończeniu rozruchu silnika (b

r1

= 1,0 mm)

Fig. 16. Stator current after the motor start-up (b

r1

= 1,0 mm)

-400

-200

0

200

400

1,00

1,05

1,10

1,15

1,20

czas [s]

pr

ąd p

rę

ta

w

irn

ik

a [A

]

bs1 = 2,5 mm

bs1 = 1,5 mm

Rys. 17. Prąd wirnika po zakończeniu rozruchu silnika (b

r1

= 1,0 mm)

Fig. 17. Rotor current after the motor start-up (b

r1

= 1,0 mm)

5. PODSUMOWANIE

Dobór szerokości otwarcia żłobków stojana i wirnika w celu zoptymalizowania

konstrukcji silnika energooszczędnego lub materiałooszczędnego, może nieco popra-
wić lub pogorszyć parametry rozruchowe silnika klatkowego. Pewne kombinacje wy-
miarowe otwarcia żłobków stojana i wirnika mogą złagodzić rozruch, skrócić jego
czas i zmniejszyć pulsacje prędkości lub momentu.

LITERATURA

[1] Antal L., Antal M., Weryfikacja eksperymentalna obwodowo–polowego modelu silnika indukcyjnego,

Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Politechniki Wrocławskiej,
Nr 54, Studia i Materiały Nr 23, Wrocław, 2003, s. 39-48

[2] Antal L., Antal M., Zawilak J., Wpływ szerokości otwarcia żłobków na charakterystyki eksploatacyj-

ne silnika indukcyjnego małej mocy, Maszyny Elektryczne, Zeszyty Problemowe BOBRME Komel,
nr 73, Katowice, 2005, s. 125-130

[3] CEDRAT, FLUX® 9.10 2D application. User’s guide, volume 4, Solving and results post-

processing, March 2005

[4] Chmelik K., Możliwości zwiększenia sprawności silników indukcyjnych, Maszyny Elektryczne, Ze-

szyty Problemowe BOBRME Komel, nr 55, Katowice, 1998, s.60-62

[5] Cistelecan M., Demeter E., Ciumbulea G., High efficiency general purpose small power in-duction

motors: design and development, 15th International Conference on Electrical Machines (ICEM),
Brugge, Belgium, August 25-28, 2002

[6] Dupre L.R., Van Keerb R., Melkebeek J.A.A., A computational model for the iron losses in rotating

electrical machines, International Journal of Engineering Science 36, 1998, pp.699-709

[7] Enokizono M., Morikawa M., Fujiyama S., Distribution of Local Magnetic Properties in Three-

Phase Inducion Motor Model Core, IEEE Transactions on Magnetics, vol.35, Nr 5, September 1999,
pp.3937-3939

[8] Gyselinck L.L.C., Duprè L.R., Vandevelde L., Melkebeek A.A., Calculation of No-load Induction

Motor Core Losses Using the Rate-dependent Preisach Model, IEEE Transactions on Magnetics, vol.
34, Nr 6, November 1998, pp. 3876-3881

[9] Jornet A., Orille A., Pérez A., Pérez D., Optimal design of high frequency induction motors with aid

of finite elements, 15th International Conference on Electrical Machines (ICEM), Brugge, Belgium,
August 25-28, 2002

[10] Jażdżyński W., Wpływ założeń projektowych na optymalne rozwiązania projektowe energooszczęd-

nych silników indukcyjnych, Maszyny Elektryczne, Zeszyty Problemowe BOBRME Komel, nr 55,
Katowice, 1998, s. 63-68

[11] Jażdżyński W., Some economic aspects of designing optimal energy-efficient and high-efficiency

induction motors, 15th International conference on electrical machines (ICEM), Brugge, Belgium,
August 25-28, 2002

[12] Podoleanu I., Schneider J., Müller G., Hameyer K., Simulation system for asynchronous machines,

EPNC 2002, Leuven, Belgium, 1-3 July, 2002; pp. 123-125

[13] Hameyer K., Belmans R., Dular P., Efficient simulation of electromagnetic fields using magnetic

equivalent circuits for numerical optimization, 3rd International Workshop on Electric & Magnetic
Fields, Liege, Belgium, May 6-9, 1996; pp. 207-212

[14] Śliwiński T., Wpływ parametrów rozruchowych silników indukcyjnych na ich koszt produkcji i eks-

ploatacji, Zeszyty Naukowe Politechniki Śląskiej, Seria: Elektryka z. 176, 2001, s.81-86

[15] Śliwiński T., Straty mocy w silnikach indukcyjnych. Nowe aspekty i dylematy, 39th International

Symposium on Electrical Machines SME’2003, 9 – 11 June 2003, Gdańsk – Jurata, Poland

[16] Yamazaki K., Stray load loss analysis of induction motors due to harmonic electromagnetic fields of

stator and rotor, 15th International Conference on Electrical Machines (ICEM), Brugge, Belgium,
August 25-28, 2002

INFLUENCE OF SLOTS WIDTH OPENING ON THE STATIC AND DYNAMIC

CHARACTERISTICS OF A SMALL POWER INDUCTION MOTOR

The work presents calculation results of a small (1.5 kW) squirrel cage induction motor. The influ-

ence of slots width opening on static and dynamic characteristics of the motor was examined. A torque
and a stator current calculations were realized by finding distribution of time-harmonic magnetic field in
a field-circuit motor model. Calculations, for different combination of the stator and the rotor slots width
openings and for different values of a slip, showed influence of these parameters on the torque and the
stator current values. Solution of transient magnetic field in the two-dimensional field-circuit motor
model gives transient characteristics of start-up and steady state for the motor with normal load. These
characteristics were computed for different values of the stator slots width openings.